संभाव्यता सिद्धांत : ही शुद्धद्ध गणिताची एक शाखा असून तिच्यात संभाव्यता या संकल्पनेचा गणिती पद्धतीने अभ्यास केला जातो [→ संभाव्यता २]. ‘संभाव्यतेचे कलनशास्त्र’ या नावानेही ही शाखा ओळखली जाते. आधुनिक सांख्यिकीचा पाया संभाव्यता सिद्धांतावर आधार-लेला आहे. संभाव्यता स्वयंसिद्ध मानून गृहीतकांच्या आधारे संभाव्यता सिद्धांतांची उभारणी करण्याचे श्रेय ए. एन्. कॉल्मॉगॉरॉव्ह (१९३३) ह्या रशियन गणितज्ञाकडे जाते. त्यांनी मांडलेली गृहीतके आता सर्वमान्य झालेली आहेत.
संभाव्यतेच्या गणितीय सिद्धांताचा प्रत्यक्ष व्यवहारात होणारा उपयोग व त्याला प्राप्त होणारा अर्थ प्रत्यक्ष वा काल्पनिक प्रयोगांच्या अथवा निरीक्षणांच्या पुढील काही उदाहरणांनी स्पष्ट होतो : नाणे एकदाच फेकणे किंवा ५०० वेळा फेकणे, किरणोत्सर्गी अणूच्या वा मनुष्याच्या आयुर्मानाचे निरीक्षण, अपघातांची वारंवारता इत्यादी. प्रयोगांची अशी उदाहरणे साहजिकच काहीशी संदिग्ध असतात. संभाव्यता सिद्धांत अर्थपूर्ण होण्यासाठी प्रयोगातून व निरीक्षणातून उद्भवू शकत असलेल्या पर्यायी निष्पन्नांसंबंधी एकमत असणे जरूर असते. उदा., नाणे उडविल्यास ते छाप किंवा काटयाच्या बाजूवरच पडेल असे नाही, तर ते घरंगळून त्याच्या कडेवरसुद्धा उभे राहणे शक्य आहे. तथापि नाणे उडविण्याच्या संकल्पित प्रयोगात छाप किंवा काटयाची बाजू वर येईल हे दोनच निष्पन्न मानण्याचा संकेत असतो. या प्रकारचे आदर्शीकरण विज्ञानात सर्वत्र प्रमाण झालेले असून त्यामुळे सिद्धांताच्या उपयुक्ततेला बाधा न येता त्याला सुलभता येते. अशा प्रकारे पायोगिक व तात्त्विक अडचणी बाजूस ठेवून विमाविज्ञानात माणसाचे वय पूर्णांकाने दर्शविले जाते व प्रत्येक धन पूर्णांक वय होऊ शकतो.
घटना व नमुना-अवकाश : सोयीसाठी प्रयोगांच्या अथवा निरी-क्षणांच्या निष्पन्नांना ‘घटना’ असे संबोधण्याची प्रथा आहे. (‘घटना’ या संकल्पनेची संभाव्यता सिद्धांतातील सम्यक् व्याख्या पुढे दिली आहे). उदा., सहा नाणी उडविली असता त्यांपैकी चार नाण्यांची छापाची बाजू वर येणे, एखादया मोजमापाचे निष्पन्न (५५° से. तापमान, १२० व्होल्ट विद्युत् दाब), एखादया रस्त्यावर ठराविक ठिकाणी ५ मिनिटांत ७ वाहने जाणे इत्यादी. अशी सर्व उदाहरणे घटना म्हणूनच मानण्यात येत असतात. घटनांचे साध्या व संयुक्त असे प्रकार पडतात. ज्या घटनेचे अधिक विघटन करता येत नाही तिला साधी किंवा प्राथमिक घटना म्हणतात. उदा., एक फासा उडविला असता ५ हे दान पडण्याची घटना एकाच प्रकारे घडणे शक्य आहे, तिचे अधिक विघटन होऊ शकत नाही. म्हणून ही घटना साधी आहे. संयुक्त घटना विघटनशील असून तिची साध्या (अविघटनशील) घटनांमध्ये फोड करता येते. उदा., दोन फासे उडविले असता त्यांच्या दानांची ‘बेरीज ६’ होण्याची घटना संयुक्त असून ती (१, ५), (२, ४), (३, ३), (४, २) किंवा (५, १) यांपैकी कोणत्याही एका साध्या घटनेमुळे घडण्याची शक्यता आहे. अशा प्रकारे ‘बेरीज ६’ होण्याच्या संयुक्त घटनेची पाच साध्या घटनांमध्ये फोड होऊ शकते.
प्रयोगाचे निष्पन्न अनिश्चित असून ते काय असेल हे तो प्रयोग पूर्ण होण्यापूर्वी नक्की सांगता येत नाही. अशा परिस्थितीच्या विश्लेषणासाठी संभाव्यता सिद्धांताचा वापर करतात. कोणत्याही प्रयोगात घडणे शक्य असलेल्या सर्व साध्या घटनांच्या समूहाला ‘नमुना- अवकाश’ म्हणतात. तो S या संकेतनाने दर्शविला जातो. या नमुना-अवकाशात प्रत्येक साधी घटना ही एक विवक्षित बिंदू समजली जाते. तिला नमुना-बिंदू म्हणतात.
कोणत्याही (आदर्शीकृत) प्रयोगाशी संबंधित असणाऱ्या सर्व घटनांचे वर्णन नमुना-बिंदूंचा वापर करून आणि पर्यायाने संपूर्ण संकल्पित प्रयोग नमुना-अवकाशाच्या स्वरूपात मांडता येतो. हे सुरूवातीलाच करणे इष्ट असते.
नमुना-अवकाशाची काही उदाहरणे खाली दिली आहेत :
(अ) एखादे नाणे तीन वेळा उडविले तर नमुना -अवकाशात पुढील आठ बिंदू मिळतात (छ – छाप, क – काटा) : छ छ छ, छ छ क, छ क छ, क छ छ, छ क क, क छ क, क क छ, क क क. ‘दोन किंवा अधिक छाप पडणे’ ही घटना पहिल्या चार बिंदूंच्या समूहाने निर्देशित होईल. फक्त एकच काटा ही घटना नमुना-अवकाशातील छ छ क, छ क छ, क छ छ या तीन नमुना-बिंदूंच्या संचाने दाखविली जाईल.
(आ) तीन चेंडूंचे (अ, ब, क) तीन भांडयांमध्ये वितरण करण्याच्या प्रयोगातील निष्पन्ने खाली दाखविली आहेत:
|
(१) (अ ब क /-/-) (२) (-/अ ब क /-) (३) (-/- / अ ब क) (४) (अ ब / क /-) (५) (अ क / ब /-) (६) (ब क / अ /-) (७) (अब /-/ क) (८) (अक /-/ब) (९) (बक /-/ अ) |
(१०) (अ/बक /-) (११) (ब/ अक /-) (१२) (क / अब /-) (१३) (अ/-/ बक) (१४) (ब/-/ अक) (१५) (क /-/ अब) (१६) (-/अब/क) (१७) (-/अक / ब) (१८) (-/बक / अ) |
(१९) (-/अ/ बक) (२०) (-/ब/ अक) (२१) (-/क / अब) (२२) (अ /ब/ क) (२३) (अ/ क /ब) (२४) (ब/ अ/ क) (२५) (ब/ क / अ) (२६) (क / अ / ब) (२७) (क / ब/ अ) |
वरील प्रत्येक रचना ही एक साधी घटना असून ती एक नमुना-बिंदू निर्देशित करते आणि सर्व २७ रचना मिळून नमुना-अवकाश तयार होतो. याच प्रयोगाचे व्यापक स्वरूपम्हणजे r चेंडूंचे n भांडयांत वितरण करण्याचा प्रयोग होय. या व्यापक प्रयोगात r चेंडूंनी एका आठवडयातील निरनिराळ्या दिवशी घडणारे अपघात निर्देशित केले तरआठवडयाचे सात वार ही भांडी मानता येतील मग n = ७ येईल. त्याचप्रमाणे विश्वकिरणांविषयक प्रयोगात गायगर गणकावर आदळणारे कण म्हणजे चेंडू आणि निरनिराळेगणक म्हणजे भांडी असेही म्हणता येईल. अशा प्रकारे हे उदाहरण व्यवहारातील निरनिराळ्या घटना निर्देशित करण्यासाठी अवश्य तेवढे व्यापक आहे.
वरील उदाहरणातील तीन चेंडू टेनिसच्या कोऱ्या चेंडूप्रमाणे तंतोतंत सारखे आहेत असे मानल्यास नमुना-अवकाशात फक्त दहाच नमुना-बिंदू असतील, कारण त्यावेळी (अ / ब / क) व (ब / क / अ) अशा प्रकारच्या वरील उदाहरणात वेगळ्या दिसणाऱ्या रचनांचे स्वरूप (अ / अ / अ) असे समान होईल. यावरून प्रारंभी मांडलेल्याविवक्षित परिस्थितीवर नमुना-अवकाश कशा प्रकारे अवलंबून असतो हे स्पष्ट होते. म्हणून सभाव्यतांसंबंधी बोलताना नमुना-अवकाशाच्या संदर्भातच बोलणे जरूरीचे असते.
वरील (अ) व (आ) या दोन्ही उदाहरणांतील नमुना-अवकाश सांत आहेत. अनंत नमुना-अवकाशाची उदाहरणेही असू शकतात. अनंत नमुना-अवकाश गणनीयकिंवा अगणनीय असू शकतो. उदा., (इ) कारखान्यात तयार झालेल्या उपकरणामधील दोषांची संख्या १, २, ३, ४, …. , n, …. अशी असेल. म्हणून या उदाहरणातीलनमुना-अवकाश अनंत पण गणनीय आहे. तसेच एखादे नाणे छाप येईपर्यंत उडवीत राहण्याच्या प्रयोगात निष्पन्नांची संख्या अनंत परंतु गणनीय असते. (ई) एखादयारस्त्यावरील मनुष्य यादृच्छ पद्धतीने निवडून त्याची उंची मोजणे हा प्रयोग विचारात घेत-ल्यास अशी उंची सर्वसाधारणतः १ मी. ते २ मी. या अंतरालात कितीही असू शकेल.या प्रयोगातील नमुना-अवकाश अनंत व अगणनीय आहे.
नमुना-अवकाश गणनीय असेल तर त्याच्या प्रत्येक उपसंचाला ‘घटना’ म्हणतात. नमुना-अवकाश अगणनीय असेल तर त्याचा उपसंच ‘घटना’ या संज्ञेस पात्र होण्यासाठी काही अटी पाळल्या जाव्या लागतात. पण ते विवेचन फारच तांत्रिक होत असल्याने येथे देण्यात आलेले नाही.
जर A ही एक घटना असेल तर ती न घडणे हीसुद्धा एक घटनाच असेल व ती A अशी दर्शविली जाते. A व A या घटनांना एकमेकांच्या पूरक घटना म्हणतात. A या घटनेत अंतर्भूत नसलेले संबंधित S मधील नमुना-बिंदू A शी संबंधित असतात.
जर A व B या दोन घटना दिलेल्या असल्या आणि A व B यांपैकी एक किंवा दोन्ही घडण्याची घटना C ने दर्शविली तर C ही घटना A व B चा संयोग असतो व ती C = A ∪ B अशी दर्शवितात. अशा घटनेचे विशेष उदाहरण म्हणजे A ∪ A ही घटना असून ती सबंध नमुना-अवकाश म्हणजे S निर्देशित करते. A ∪ A या घटनेमधील नमुना-बिंदू सर्व संभाव्य निष्पन्ने दर्शवीत असल्यामुळे A ∪ A ही घटना निश्चितता दर्शविते.
S हीसुद्धा एक घटनाच असून तिच्यात सर्व नमुना- बिंदूंचा समावेश होतो. S ला ‘निश्चित घटना’ असे म्हणतात. असंभाव्य घटना f या चिन्हाने दर्शवितात. तिच्यात एकही नमुना- बिंदू अंतर्भूत नसतो. साहजिकच S व Ø या घटना परस्परांच्या पूरक घटना आहेत.
A व B या दोन्ही घटना घडून येण्याची घटना D ने दर्शविल्यास ती A व B चा छेदन होते व ती D = A ∩ B अशी दर्शवितात. तिच्यात A व B या दोन्ही घटनांना समाईक असलेल्या नमुना-बिंदूंचा समावेश होतो. जर A व B या दोघांत कोणतेच नमुना-बिंदू समाईक नसतील तर A व B यांना परस्पर अपवर्जित घटना म्हणतात. ते साहजिकच A ∩ B = f असे दाखविता येते.
वरील (आ) या उदाहरणात A = (एकाच भांडयात एकापेक्षा जास्त चेंडू असणे) ही घटना क. (१) ते (२१) या नमुना-बिंदूंमध्ये घडते, तर B =(पहिले भांडे रिकामे नसणे) ही घटना क. (१), (४) ते (१५) आणि (२२) ते (२७) या नमुना-बिंदूंनी दर्शविली जाईल. या उदाहरणाच्या मुना-अवकाशातील प्रत्येक नमुना-बिंदू A किंवा B किंवा दोन्ही घटना दर्शवीत असल्यामुळे A ∪ B = S ही ‘निश्चित घटना’ आहे. D = A ∩ B ही घटना क. (१) आणि (४) ते (१५) या बिंदूंनी दर्शविली जाईल.
संभाव्यता : संभाव्यता या संज्ञेची गणिती व्याख्या अशी केली जाते. S हा नमुना-अवकाश आणि M हा सर्व घटनांचा संच असल्यास P हे (M हा प्रांत आणि सत् संख्या संच हा सहप्रांत असलेले) ⇨ फलन पुढील तीन स्वयंसिद्धकांचे समाधान करीत असेल तर या फलनास संभाव्यता म्हणतात.
(१) अऋणतेचे स्वयंसिद्धक : प्रत्येक A या घटनेसाठी P (A) ≥ ०
(२) संपूर्ण संभाव्यतेचे स्वयंसिद्धक : P (S) = १
(३) गणनीय योगशीलतेचे स्वयंसिद्धक : A1, A2 , A3, …. या घटना असून प्रत्येक i = j साठी Ai ∩ Aj = f असेल,
तर P(A1 ∪ A2 ∪ ….) =å P (Ai)
दिलेल्या घटनांच्या संभाव्यता कशा मिळवावयाच्या याचा विचार ‘संभाव्यता सिद्धांता’ मध्ये केला जात नाही, तर निरनिराळ्या घटनांच्या संभाव्यताएकमेकांशी कशा संबंधित असतात व काही घटनांच्या संभाव्यता दिल्यास त्या संभाव्यता वापरून इतर काही संबंधित घटनांच्या संभाव्यता कशा मिळवावयाच्या या प्रश्नांशी संभाव्यता सिद्धांत निगडित आहे. बऱ्याचशा प्रयोगांत व विशेषतः संधीवर आधारित खेळांच्या संबंधात नमुना-अवकाश सांत असेल, तर बहुतांशी त्यातील सर्व प्राथमिक घटना समसंभाव्य असल्याचे मानता येते. जर A ही घटना S या एकूण n नमुना-बिंदू असलेल्या मुना-अवकाशातील असेल, तर तिची संभाव्यता काढण्यासाठी S मधील किती प्राथमिक घटना A या घटनेशी सुसंगत आहेत, हे पहावे लागते. अशा प्राथमिक घटनांची संख्या जर m असेल तर S मधील एकूण n नमुना-बिंदूंनी दर्शविलेल्या प्राथमिक घटना समसंभाव्य मानून P (A) = असे घेता येते. उदा., दोन समतोल फासे फेकले तर शक्य असलेले सर्व ३६ पर्याय समसंभाव्य आहेत असे मानणे रास्त ठरेल. प्रत्यक्षात फासे इतके समतोल असतीलच असे नाही आणि भारित फाशांच्या बाबतीत प्राथमिक घटनांच्या संभाव्यता निरनिराळ्या घ्याव्या लागतील, कारण अशा वेळी निरनिराळे पृष्ठभाग वर येण्याची संभाव्यता सारखी असणार नाही. तथापि त्यामुळे संभाव्यता सिद्धांतातील विवेचनास बाधा येत नाही. वर उल्लेखिल्याप्रमाणे एखादया प्रयोगातील m आणि n या संख्या निश्चित करण्यासाठी समचयात्मक पद्धतींचा वापर करता येतो.
संभाव्यता सिद्धांतातील प्रमेये : संभाव्यतेच्या व्याख्येचा उपयोग करून संभाव्यता सिद्धांतातील विविध प्रमेये सिद्ध करता येतात. काही महत्त्वाची प्रमेये पुढीलप्रमाणे आहेत :
प्रमेय (१) : (बेरजेचे प्रमेय).
P (A ∪ B) = P (A) + P (B) – P (A ∩ B).
जर A व B या घटना परस्पर अपवर्जित असतील तर या प्रमेयाचा विशेष प्रकार असा होतो :
जर A∩ B = f, तर P (A ∪ B) = P (A) + P (B).
हा विशेष प्रकार वर दिलेल्या संभाव्यतेच्या व्याख्येतील स्वयंसिद्धकच आहे. या प्रमेयाचे, दोनपेक्षा अधिक घटनांसाठी, व्यापकीकरण करता येते. उदा., A, B, C या तीन घटनांसाठी हे प्रमेय असे मांडता येते :
P (A ∪ B ∪ C) = P (A) + P (B) + P (C) – P (A∩B) –
P (A ∩ C) – P (B ∩ C) + P (A ∩ B ∩ C)
आणि A, B, C या तीन घटनांमधील कोणत्याही दोन घटना परस्पर अप-वर्जित असतील, तर
P (A ∪ B ∪ C) = P (A) + P (B) + P (C).
प्रमेय (२) : A ही घटना B या घटनेत अंतर्भूत असेल (म्हणजे जर A ⊂B) तर P (A) < P (B).
प्रमेय (३) : कोणत्याही A या घटनेच्या बाबतीत P (A) ≤ १.
प्रमेय (४) : f या भाव्य घटनेसाठी P (f) = ०.
टीप (१) : प्रमेय (४) चा व्यत्यास खरा नाही म्हणजे P (A) = ० A ही ‘असंभाव्य घटना’ आहे.
हे सत्य पुढीलप्रमाणे विशद करता येते : एक गोल तबकडी घ्या (आ. १). तिच्या परिघावर ० ते १०० हे अंक व त्यातील ०.१, ०.२, …., ०.११, ०.१२, ….असे जास्तीत जास्त उपभाग लिहा. ० व १०० हे दोन्ही एकच बिंदू दाखवतील. समान फरक असलेल्या संख्यांमधील परिघावरील अंतर समान असेल. तबकडीच्या केंद्राशी एक टोक बद्घ असलेला अत्यंत लवचिक काटा असून त्यास थोडासा धक्का दिल्यावर तो बराच वेळ गोलाकार फिरून परिघावरील एका संख्येकडे बाण दाखवीत थांबतो. या बाबतीत संभाव्यता पुढीलप्रमाणे मिळतील :
P (काटा १० ते २० च्या दरम्यान थांबेल) = १०/१००= ०.१
P (काटा १० ते १५ च्या दरम्यान थांबेल) = ५/१००= ०.०५
P (काटा १० ते ११ च्या दरम्यान थांबेल) = १/१००= ०.०१
P (काटा १० ते १०.१ च्या दरम्यान थांबेल) = ०.१/१००= ०.००१
P (T = काटा थांबल्यावर त्याचे टोक १० कडे निर्देश करते) = ०
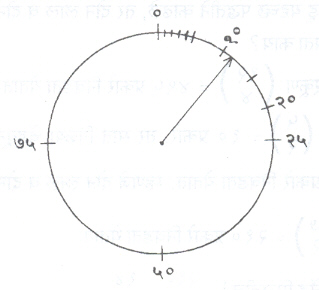T या घटनेची संभाव्यता शून्य आहे. म्हणजे काटा १० वर कधी थांबणारच नाही का ? तसे म्हणता येणार नाही. कारण शून्य ते १०० मधील प्रत्येक संख्येच्या बाबतीत असेच घडेल. मग तो काटा कोणत्याही एका संख्येपाशी थांबणार नाही का ? खूप खूप वेळा असे प्रयोग केल्यास काटा १० वर (किंवा कोणत्याही एका दिलेल्या संख्येपाशी) थांबणे खूप कमी वेळा होईल. पण तसे घडणे अजिबात नाकारता येत नाही. म्हणजे एखादया घटनेची संभाव्यता शून्य असल्यास ती घटना घडणे अतिशय विरळ असते. पण ती घटना ‘असंभाव्य घटना’ असेलच असे नाही.
टीप (२) : संभाव्यतेच्या व्याख्येच्या दुसऱ्या स्वयंसिद्धकाप्रमाणे ‘निश्चित घटने’ ची संभाव्यता १ असते. या विधानाचा व्यत्यासही खरा नाही म्हणजे P (A) = १ A ही ‘निश्चित घटना’ आहे.
सशर्त संभाव्यता : जर A व B या दोन घटना असतील, तर घटना A घडली आहे असे मानून B ही घटना घडण्याच्या संभाव्यतेला ‘ A घडली असता B ची सशर्त संभाव्यता ’ म्हणतात व ती P (B A) अशी दर्शवितात. तिची व्याख्या अशी :
टीप (३) : ‘A घडली असता B च्या सशर्त संभाव्यते’ व्याख्या करण्यासाठी P (A)=० असणे आवश्यक आहे.
टीप (४) : ‘P (B A)’ ला B ची सशर्त संभाव्यता म्हणतात. त्यामुळे P (B) ला B ची बिनशर्त संभाव्यता असे संबोधण्याचा प्रघात आहे.
निरवलंबी घटना : जर P (B | A) = P (B) असेल, तर A व B यांना निरवलंबी घटना म्हणतात. [या ठिकाणी P (A)= ० हे अध्याहृत आहे] … … … (२)
याचाच अर्थ असा की, ‘A या घटनेच्या घडण्यामुळे B या घटनेची संभाव्यता बदलत नसल्यास A व B यांना निरवलंबी घटना म्हणतात ’.
टीप (५) : जर P (B A) = P (B) असेल (म्हणजे A व B या निरवलंबी घटना असतील), तर P (A B) = P (A) हेही खरे असते.
जर A व B या निरवलंबी घटना असतील, तर P (B A) = P (B) असल्याने ‘सशर्त संभाव्यते’ ची समानता (१) मधील व्याख्या वापरून
P (A ∩ B)=P(A).P (A) … … … (३)
असे मिळते. त्यामुळे निरवलंबी घटनेची व्याख्या अशी लिहिता येते :
‘जर P (A ∩ B) = P (A) P (B) असेल, तर A व B यांना निरवलंबी घटना म्हणतात’.
टीप (६) : निरवलंबी घटनांची समानता (३) मधील व्याख्या ही समानता (२) मधील व्याख्येपेक्षा अधिक व्यापक आहे. कारण, दिलेल्या A व B या घटना निरवलंबी आहेत का हे ठरविण्यासाठी समानता (२) मधील व्याख्या वापरल्यास P (B A) मिळवावी लागते व समानता (१) नुसार P (A) = 0 असल्यास P (B A) मिळविता येत नाही. पण समानता (३) मधील व्याख्या वापरल्यास A व B या घटना निरवलंबी आहेत का हे ठरविण्यासाठी P (A) = 0 असल्यास अडचण येत नाही.
प्रमेय (५) : (गुणाकाराचे प्रमेय). P (A ∩ B) = P (A) P (B | A) या प्रमेयाचा विशेष प्रकार असा होतो : A व B निरवलंबी घटना असल्यास P (A ð B) = P (A) P (B). हे वर समानता (३) मध्ये पाहिले आहेच.
दोनपेक्षा अधिक घटनांसाठी या प्रमेयाचे व्यापकीकरण करता येते. उदा., A, B, C या तीन घटनांसाठी हे प्रमेय असे मांडता येते :
P (A ∩ B ∩ C) = P (A) . P (B | A). P (C | A ∩ B).
दोनपेक्षा अधिक घटनांसाठी ‘निरवलंबी घटना’ या संकल्पनेच्या व्याख्येचे व्यापकीकरण करता येते. उदा.,
“जर (१) P (A ∩ B ∩ C) = P (A) . P (B) . P (C).
(२) P (A ∩ B) = P (A) . P (B). (म्हणजे A व B या घटना निरवलंबी आहेत)
(३) P (B ∩ C) = P (B) . P (C). (म्हणजे B व C या घटना निरवलंबी आहेत)
(४) P (A ∩ C) = P (A) . P (C). (म्हणजे C व A या घटना निरवलंबी आहेत)
या चारी अटी पूर्ण झाल्या तरच A, B, C या तीन घटना ‘निरवलंबी घटना’ आहेत असे म्हणतात. चार व अधिक घटनांचे निरवलंबी असणे याची व्याख्या याच प्रकारे मांडता येते.
H1, H2, H3, …, Hn या घटना (१) प्रत्येक i व j या जोडीसाठी Hi ∩ Hj = φ व (२) H1∪ H2∪ …, ∪ Hn = S या अटींचे समाधान करणाऱ्या असतील तर { H1, H2,…, Hn } ला S चे विभाजन म्हणतात.
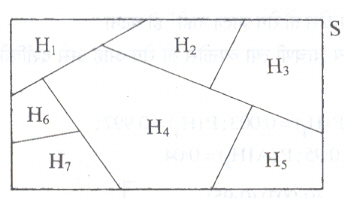
सर्वसाधारण नमुना- अवकाश S हा आयताने दाखविला जातो. आकृती क. २ मध्ये S चे { H1, H2, … , H7} हे विभाजन दाखविले आहे. अशा वेळी H1, H2, … , Hn (आकृतीत n = ७) या घटना प्रत्येक जोडीच्याबाबतीत परस्पर अपवर्जित व निःशेष असतात.
प्रमेय (६) : (संपूर्ण संभाव्य-तेचे प्रमेय). {H1, H2, … , Hn } हे S चे विभाजन असेल व A ही
प्रमेय (७) : (बेझयांचेप्रमेय). {H1, H2, … , Hn } हे नमुना-अवकाश S चे विभाजन असेल आणि A ही S मधील कोणतीही एक घटना असेल तर
येथे P (Hi) ला Hi या घटनेची ‘पूर्ववर्ती संभाव्यता’ आणि P (Hi A) ला Hi ची ‘(A घडल्यानंतरची) पश्चात संभाव्यता’ असे म्हणतात.
उदाहरण (१) : बावन पत्त्यांचा जोड नीट पिसून एक पान यदृच्छ पद्धतीने निवडण्याचा प्रयोग विचारात घ्या. या प्रयोगात ५२ प्राथमिक घटना असून त्या प्रत्येक प्राथमिकघटनेची संभाव्यता १/५२ घेऊ शकतो. जर
A = ‘निवडलेले पान बदाम असणे’ ही घटना आणि B = ‘निवडलेले पान एक्का असणे’ ही घटना तर P (A) = 13/52 P (B) =4/52
∴ (१) A ∩ B =‘निवडलेले पान बदामचा एक्का असणे’ ही घटना व
P (A ∩ B) =1/52
(२) A U B =‘निवडलेले पान बदाम किंवा एक्का किंवा बदामचा एक्का असणे’ ही घटना. म्हणून ‘बेरजेच्या नियमा’नुसार
P (A U B) = P (A) + P (B) – P (A ∩ B)
13/52+4/52–1/52=16/52=4/13
(३) B | A = ‘निवडलेले पान बदामचे आहे हे माहीत असल्यास ते पान एक्का असणे’ ही घटना
येथे P (B A) = P (B) आहे. म्हणजे A व B या घटना निरवलंबी आहेत.
उदाहरण (२) : एखादया गंभीर रोगाने गासलेल्या लोकांचे प्रमाण एकूण लोकसंख्येच्या ०.३ टक्के एवढे आहे असे समजा. हा रोग एखादया व्यक्तीला झाला आहे किंवा नाही हेठरविण्यासाठी वैदयकीय चाचणी उपलब्ध आहे. अशा चाचण्या नेहमीच अचूक उत्तरे देतात असे नाही. असे समजा की रोग खरोखरच झाला असल्यास वैदयकीय चाचणीततो उघडकीस येण्याची संभाव्यता ०.९५ आहे व याउलट रोग झालेला नसल्यास वैदयकीय चाचणीत मात्र तो झाला आहे असा निष्कर्ष येण्याची संभाव्यता ०.०४ आहे. जरएखादी व्यक्ती निवडून तिला वैदयकीय चाचणीत हा रोग झाला आहे असे आढळून आले, तर प्रत्यक्षात त्या व्यक्तीला हा रोग असण्याची संभाव्यता काय ? बेझ यांचे प्रमेयवापरून या प्रश्नाचे उत्तर मिळविता येते. जर
H1 = ‘एखादया व्यक्तीला तो गंभीर रोग झाला आहे’ ही घटना
H2 = ‘ त्या व्यक्तीस तो रोग झाला Zmhr’ ही घटना
A = ‘ वैदयकीय चाचणी त्या व्यक्तीस तो रोग आहे असे दर्शविते ’ ही घटना
उदाहरण (३) : अ, ब, क, ड या चार व्यक्ती एका तिकिटाच्या खिडकीसमोर रांगेत उभ्या आहेत. अ ही व्यक्ती पहिल्या कमांकावर उभी असण्याची संभाव्यता काय ?
चार व्यक्ती एकूण ४ × ३ × २ × १= २४ वेगवेगळ्या प्रकारे रांगेत उभ्या राहू शकतात. जर अ या व्यक्तीसाठी प्रथम कमांक निश्चित केला तर ब, क, ड या उरलेल्या तीन व्यक्तीएकूण ३ × २ × १ = ६ प्रकारे ‘अ’ च्या मागे उभ्या राहू शकतात. म्हणजे या उदाहरणात नमुना- अवकाशात २४ प्राथमिक घटना आहेत. त्यातील सहा प्राथमिक घटना ‘अ प्रथम कमांकावर असणे’ या घटनेशी सुसंगत आहेत.
∴ P (अ ही व्यक्ती प्रथम कमांकावर आहे) =६/२४ =१/४
उदाहरण (४) : एका खोक्यात पाच लाल व सात निळे चेंडू आहेत. जर त्या खोक्यातून चार चेंडू यदृच्छ पद्धतीने काढले, तर दोन लाल व दोन निळे चेंडू मिळण्याची शक्यता काय ?
बारा चेंडूतून चार चेंडू एकूण = ४९५ प्रकारे निवडता येतात. पाच लाल चेंडूतून दोन चेंडू = १० प्रकारे, तर सात निळ्या चेंडूतून = २१ प्रकारे निवडता येतात. म्हणजे दोनलाल व दोन निळे चेंडू एकूण = २१० प्रकारे निवडता येतात.
P[दोन लाल व दोन निळे चेंडू मिळतील]=२१०/४९५ = १४/३३
उउदाहरण (५) : भौतिकीच्या ‘सांख्यिकीय स्थितिगतिशास्त्र’ या उप-शाखेत फोटॉन, इलेक्ट्रॉन यांसारख्या मूलकणांचे प्रावस्था अवकाशामधील वंटन कशा प्रकारचेअसू शकते याचा अभ्यास महत्त्वाचा असतो. फोटॉन कणांच्या बाबतीत कोणतेही दोन कण एकमेकांपासून वेगळे ओळखता येत नाहीत. या तत्त्वानुसार मिळणाऱ्या संख्यांकांना⇨ सत्येंद्रनाथ बोस आणि ⇨ ॲल्बर्ट आइन्स्टाइन यांच्या सन्मानार्थ बोस-आइन्स्टाइन संख्यांक असे म्हटले जाते. फोटॉनाच्या r कणांचे n कोषांमध्ये 
प्रकारे वंटनहोऊ शकते आणि प्रत्येक वंटनाची संभाव्यता सारखीच म्हणजे
इतकी असते.
बोस-आइन्स्टाइन संख्यांक सर्व मूलकणांना लागू होत नाहीत. उदा., इलेक्ट्रॉन, प्रोटॉन व न्यूट्नॉन या कणांच्या अभ्यासात आणखी एक तत्त्व वापरावे लागते. तेम्हणजे ⇨ व्होल्फगांग पाउली यांचे विवर्जन तत्त्व होय. या तत्त्वानुसार कोणत्याही कोषात एकापेक्षा जास्त कण असू शकत नाहीत. सर्व कण अभिन्न आहेत हे गृहीतक आणित्याबरोबरच पाउली यांचे विवर्जन तत्त्व वापरून मिळालेल्या संख्यांकांना फेर्मी-डिरॅक संख्यांक असे म्हणतात. त्यानुसार r कणांचे n कोषांमध्ये
प्रकारे वंटन होऊ शकतेआणि प्रत्येक वंटनाची संभाव्यता सारखीच म्हणजे 
एवढी असते.
बेर्नुली खेळी: अनेक व्यावहारिक प्रश्नांमध्ये फक्त दोनच उत्तरे संभवतात. उदा., एखादी व्यक्ती स्त्री आहे की पुरूष, कारखान्यात तयार होणारी वस्तू सदोष आहे कीनिर्दोष, इत्यादी. जर (१) एखादया प्रयोगाचे दोनच निष्पन्न शक्य असतील व (२) या प्रयोगाची पुनरावृत्ती केल्यास अशा प्रत्येक पुनरावृत्तीत या दोन निष्पन्नाच्या संभाव्यतात्याच कायम राहत असतील, तर अशा प्रत्येक पुनरावर्तित प्रयोगाला बेर्नुली खेळी असे म्हणतात. प्रत्येक खेळीत दोन्हींपैकी प्रत्येक निष्पन्नाची संभाव्यता तीच राहत असल्यानेया सर्व पुनरावर्तित बेर्नुली खेळी निरवलंबी असतात. पहिले याकोप बेर्नुली यांनी अशा प्रकारच्या खेळींची गणितीय मीमांसा विस्तारपूर्वक मांडली, म्हणून त्यांच्या स्मरणार्थ याखेळींना त्यांचे नाव प्राप्त झाले.
बेर्नुली खेळीचे दोन निष्पन्न सर्वसाधारणतः यश (S) व अपयश (F) या नावांनी दाखविण्याची प्रथा आहे. P (S) = p आणि P (F) = १–p = q आहे असे समजू. nबेर्नुली खेळींच्या नमुना-अवकाशात २n नमुना-बिंदू असतात. त्यातील प्रत्येक बिंदू S व F या चिन्हांच्या n सदस्य असलेल्या अनुकमाने मांडता येतो. सर्व खेळी निरवलंबीअसल्याने कोणत्याही अनुकमाची संभाव्यता गुणाकाराचे प्रमेय वापरून मिळविता येते. उदा., दोन बेर्नुली खेळींच्या प्रयोगात चार नमुना-बिंदू असतात व त्यांच्या संभा-व्यताअशा असतात : P (SS) = p२ P (SF) = pq P (FS) = qp =pq
P (FF) = q2. तसेच n बेर्नुली खेळींमध्ये k वेळा यश मिळण्याची संभाव्यता pkqn–k एवढी होते.
‘बेर्नुली खेळी’ या प्रयोगाचे व्यापकीकरण खाली ‘ संयुक्त प्रयोग ’ या नावाने केले आहे.
संयुक्त प्रयोग : ζ हा प्रयोग व त्यामागून F हा प्रयोग केला असल्याचे समजा. अशा वेळी G = (ζ, F) हा संयुक्त प्रयोग आहे असे म्हणता येते. G या प्रयोगातील ζ हीपहिली खेळी व F ही दुसरी खेळी असल्याचे म्हणतात. A ही घटना ζ च्या नमुना-अवकाशातील असून B ही घटना F च्या नमुना -अवकाशातील आहे असे समजा. अशा वेळी‘पहिल्या खेळीत A व दुसऱ्या खेळीत B’ याला ‘संयुक्त घटना’ असे म्हणतात व ती (A, B) अशी दाखवितात. जर सर्व A व B साठी P [(A, B)] = P (A).P (B) असेल, तर ζ व F या खेळी निरवलंबी आहेत असे म्हणतात. तीन अथवा अधिक निरवलंबी खेळींची व्याख्या याच प्रकारे करतात.
या संयुक्त प्रयोगाचा सर्वांत सोपा प्रकार म्हणजे ζ हाच प्रयोग एक- सारख्या परिस्थितीत n वेळा पुनःपुन्हा करणे. हा संयुक्त प्रयोग (ζ, ζ, …, ζ) याऐवजी ζn असादर्शविला जातो. ζ चा नमुना-अवकाश S असेल, तर ζn चा नमुना-अवकाश Sn = {(s1 , s2 , … sn), si ε Si} असा मांडता येतो. संयुक्त प्रयोगाचा एक महत्त्वाचा व खूपप्रसिद्ध असलेला प्रकार म्हणजे ‘बेर्नुली खेळी’ हा होय हे स्पष्ट आहे.
प्रमेय (८) : (बेर्नुली प्रमेय). हे प्रमेय ‘बृहत् संख्यांचे नियम’ या नावाने ओळखल्या जाणाऱ्या नियमांमधील पहिले प्रमेय म्हणून मानण्यात येते. बेर्नुली प्रमेयाचे विधानअसे आहे :
ζ हा प्रयोग एकसारख्या परिस्थितीत n वेळा पुनःपुन्हा केला आहे असे समजा. जर (१) ζ या प्रयोगाच्या सर्व n खेळी निरवलंबी आहेत, (२) S हा ζ चा नमुना-अवकाश आहे, (३) A ही S मधील एक घटना आहे व (४) k (n, A) = ζ च्या एकूण n खेळींपैकी A ही घटना घडणाऱ्या खेळींची संख्या, तर k(n, A)/n हे गुणोत्तर संभाव्यतेच्या अर्थानुसारP (A) च्या
(ξ च्या एकूण n खेळी असल्याने k (n, A) चे मूल्य ०, १, २, … , n यांपैकी एक संख्या असते). व्यावहारिक दृष्ट्या या प्रयोगाचा अर्थ असा होतो : माहीत नसलेल्या P (A) यासंभाव्यतेचे ‘अनुमान’ ζ हा प्रयोग अनेक वेळा करून माहीत असलेल्या या गुणोत्तराने करता येते.
बेर्नुली खेळींच्या संबंधात हेच प्रमेय पुढीलप्रमाणे मांडता येते : ‘बेर्नुली खेळींमध्ये यशाची संभाव्यता p असेल आणि जर n बेर्नुली खेळींमध्ये Sn वेळा यश मिळाले, तर
या विधानाचा अर्थ असा होतो की, जर n बेर्नुली खेळींची संख्या वाढवीत नेली तर यशाचे गुणोत्तर Sn/n आणि p यामधील अंतर ε या आधी ठर-विलेल्या लहान अऋणसंख्येपेक्षाही कमी होण्याची संभाव्यता जवळपास एक असते. उदा., समतोल नाणे काही वेळा उडविले असता छापाचे प्रमाण १/२ येईल असे म्हणता येत नाही परंतु छापांचेप्रमाण १/२ च्या अधिकाधिक जवळ असण्याची संभाव्यता नाणे जास्त वेळा उडवून वाढविली जाऊ शकते व ती संभाव्यता जवळपास एक एवढी होऊ शकते.
उदाहरण (६) : (जन्मदिवस समस्या). १ जानेवारी ते ३१ डिसेंबर या वर्षाच्या ३६५ दिवसांना 1 ते 365 हे कमांक दया. यदृच्छ पद्धतीने n ≥ 2 व्यक्ती निवडून त्यांचेजन्मदिवस नोंदले आहेत असे समजा. या प्रयोगाचे निष्पन्न S = (s1, s2 …. , sn) या अनुकमाने दाखविता येईल. यांत प्रत्येकsi (i = 1, … , n) चे मूल्य 1 ते 365 यापूर्णांकांपैकी एक पूर्णांक असेल. या प्रयोगाच्या नमुना- अवकाशात एकूण (365 )n नमुना-बिंदू असून त्या प्रत्येकाची संभाव्यता (1/(365)n अशी घेता येते. A = ‘निवडलेल्याप्रत्येक व्यक्तीचा जन्मदिवस भिन्नभिन्न आहे’ ही घटना. या घटनेमध्ये (365 ) × (365 ) × (365 ) × … × (366–n) नमुना-बिंदू असतील
जर n = 23 असेल, तर P (A)< 0.5 याचा अर्थ असा की, यदृच्छ पद्धतीने निवडलेल्या तेवीस व्यक्तींच्या समूहात एकापेक्षा जास्त व्यक्तींचा जन्मदिवस एकचअसण्याची संभाव्यता निम्म्याहून अधिक असते. हे तसे सोपे उदाहरण ‘अंतर्ज्ञानावर भरवसा ठेवता येत नाही’ हे सांगते.
मार्कोव्ह साखळी : व्यवहारात अनेक वेळा एकामागून एक घडणाऱ्या घटना निरवलंबी नसतात. आधी घडलेल्या घटनेवर पुढच्या घटनेची निष्पत्ती अवलंबून असते.अशा प्रकारच्या घटनांचा अभ्यास करण्यासाठी ⇨ अंद्येई अंद्येयेव्ह्यिच मार्कोव्ह या रशियन गणितज्ञांनी १९०७ साली मार्कोव्ह साखळीची संकल्पना मांडली.
जर E1, E2 … ह्या निरवलंबी घटना असतील व त्यांच्या संभाव्यता अनुकमे p1, p2 … असतील तर कोणत्याही अनुकमाची संभाव्यता गुणन सिद्धांताने काढता येते.जसे की,
Pr { (E i , Ej , Ek) } = pi pj pk
मार्कोव्ह साखळीव्दारे ह्या सूत्राचे व्यापकीकरण करण्यात आलेले आहे. या सिद्धांतात E१, E२ … ह्या घटना निरवलंबी न मानता प्रत्येक घटना तिच्या लगतच्याआधीच्या (आणि फक्त त्या आधीच्याच) घटनेवर अवलंबून आहे असे मानण्यात येते. त्यामुळे Ek ह्या घटनेची संभाव्यता pk च्याऐवजी, आधीच्या Ej ह्या घटनेवर अवलंबूनअसते व तीpjk ह्या सशर्त संभाव्यतेव्दारे मांडता येते. येथे pjk हिला संकमण संभाव्यता असे संबोधतात व सर्व संकमण संभाव्यता खालीलप्रमाणे मांडता येतात.
वरील आव्यूहामध्ये pj1 + pj2 + = १ आणि pjk > 0 असते. कोणत्याही अनुकमाची मार्कोव्ह साखळीव्दारे मांडणी करण्यासाठी P ह्या संक्रमण संभाव्यता आव्यूहाव्यतिरिक्त { ak } ह्या संभाव्यता वंटनाचीही जरूरी असते. येथे Ek ह्या घटनेने साखळीची सुरूवात होण्याची संभाव्यताak असते. ak ≥ 0 आणि ∑ ak = 1 . वरील विवेचनावरून असेलक्षात येते की,
Pr { (Ej , Ek) } = aj pjk Pr { (Ej , Ek , Er) } = aj pjk pkr
मार्कोव्ह साखळीची संकल्पना एका साध्या उदाहरणाव्दारे स्पष्ट करता येते. समजा, बाजारात A आणि B असे दोन प्रकारचे साबण उपलब्ध आहेत आणिसुरूवातीला हे साबण वापरण्याचे लोकांमधील प्रमाण समान म्हणजे प्रत्येकी ५० टक्के आहे. नंतर A आणि B ह्या कंपनींच्या जाहिरातीमुळे किंवा गुणवत्तेमुळे लोकांच्यासाबणनिवडीच्या प्रक्रियेमध्ये बदल घडून येतो, जो खालीलप्रमाणे मांडता येतो.
येथे कंपनी A चे ९० टक्के ग्राहक तोच साबण वापरणे पसंत करतात, तर कंपनी B चे ५० टक्के गाहक कंपनी A चा साबण वापरू लागतात. अशा प्रकारे कंपनी A चा साबण वापरणाऱ्यांचे प्रमाण,
(0.5) (0.9)+(0.5)(0.5)=0.7
म्हणजे ७० टक्के होते, तर कंपनी B चा साबण वापरणाऱ्यांचे प्रमाण ३० टक्के होते. हीच स्थिती जर कायम राहिली, तर A प्रकारचा साबण वापरणाऱ्यांचे प्रमाण वाढत जाते व Bप्रकारचा साबण वापरणाऱ्यांचे प्रमाण कमी होऊ लागते, जे आपण मार्कोव्ह साखळीच्या सिद्धांताव्दारे निश्चित करू शकतो.
मार्कोव्ह साखळीव्दारे अधिक व्यापक प्रक्रियांचा अभ्यास करता येतो.
चेबिशॉव्ह असमा : यदृच्छ चलांच्या फलनांच्या अपेक्षित मूल्यांसंबंधी चेबिशॉव्ह यांनी एक महत्त्वाची असमा मांडली आहे. X हे यदृच्छ चल असून g (x) हे त्याचेअऋण फलन असल्यास प्रत्येक k (> 0) साठी g(x) हे k पेक्षा मोठे असण्याच्या संभाव्यतेची कमाल मर्यादा या असमेने
P [ g (x) ≥ k ] ≤ E [ g(x) ] / k
g (x) = X – E (x) असेल तर ही असमा बिनमे-चेबिशॉव्ह असमा म्हणून ओळखली जाते.
यदृच्छ चलांचा अभ्यास करताना असे लक्षात येते की, एखादया X या यदृच्छ चलाच्या विचरणाचे मूल्य लहान असल्यास त्या चलाची मूल्ये त्याच्या माध्यापासूनजास्त दूर असणे असंभवनीय असते. E (x) = μ व विचरण (x) = σ2 असल्यास कोणत्याही t (>0) साठी बिनमे – चेबिशॉव्ह असमा पुढीलप्रमाणे आहे :
g (x) = X – E (x) असेल तर ही असमा बिनमे-चेबिशॉव्ह असमा म्हणून ओळखली जाते.
यदृच्छ चलांचा अभ्यास करताना असे लक्षात येते की, एखादया X या यदृच्छ चलाच्या विचरणाचे मूल्य लहान असल्यास त्या चलाची मूल्ये त्याच्या माध्यापासून जास्त दूर असणे असंभवनीय असते. E (x) = μ व विचरण (x) = σ2 असल्यास कोणत्याही t (>0) साठी बिनमे – चेबिशॉव्ह असमा पुढीलप्रमाणे आहे :
येथे (1/ k2) हा P [ | X – μ| ≥ k σ ] यासाठी ऊर्ध्वबंध असून (1–1/k2) हा P [ X –μ < k σ] यासाठी निम्नबंध आहे. उदा., X च्या यदृच्छ पृथक् चलाचे मूल्य –1, 0, 1असण्याच्या संभाव्यता अनुकमे 1/8, 3/4 व 1/8 असतील तर X चे अपेक्षित मूल्य μ = 0 असते व विचरण =σ2=1/4 असते. जर k = २ असेल, तर/
P [ | X –μ | ≥ kσ ] = P [ | X | ≥ 1] ≤ 1/4.
बऱ्याच वेळा चेबिशॉव्हच्या असमेद्वारा मिळणारे बंध हे सम्यक् संभाव्यतेपासून फार जवळ नसल्यामुळे त्यांची उपयोजिता सीमित असते. तरीसुद्धा या असमेस सैद्धांतिक महत्त्व आहे.
बृहत् संख्यांचे नियम : बेर्नुलीचे प्रमेय हे ‘बृहत् संख्यांचे नियम’ नावाने ओळखल्या जाणाऱ्या प्रमेयांतील पहिले प्रमेय म्हणून मानले जात असल्याचे वर पाहिले आहेच.यातील आणखी तीन प्रमेये खालीलप्रमाणे :
तेच सामायिक वंटन असलेले X1, X2, …. , Xn हे n निरवलंबी यदृच्छ चल आहेत असे समजा. याचा अर्थ कोणत्याही x साठी P [ Xn ≤ x ] चे मूल्य प्रत्येक n साठी तेच आहेअसा होतो. X1, X2, …. , Xn यांचे माध्य Xn दर्शवू या. म्हणजे Xn = (X1 + X2 + …. + Xn) / n.
प्रमेय (९) : खिन्चिन यांचा बृहत् संख्यांचा सौम्य नियम.
जर X1 ला सांत अपेक्षित मूल्य असून ते μ असेल, तर
सर्व ε > 0 साठी सीमा P [ | Xn – μ| > ε] → 0
प्रमेय (१०) : कॉल्मॉगॉरॉव्ह यांचा बृहत् संख्यांचा तीव्र नियम.
P [ | Xn → μ | ] = 1 असेल तर आणि तरच X1 चे सांत अपेक्षित मूल्य μ हे असते.
प्रमेय (११) : केंद्रीय सीमा प्रमेय. X1 चे सांत माध्य μ व सांत धन विच-
टीप (७) : बृहत् संख्यांचे सौम्य व तीव्र नियम हे बेर्नुलीच्या प्रमेयाचे व्यापकीकरण देतात. “ प्रतिदर्शाचे माध्य हे समष्टीच्या माध्याचे ‘ चांगले ’ आकल असते “ या अंत:प्रज्ञेनेसांगितलेल्या वाटण्याला केंद्रीय सीमा प्रमेया-कडून समर्थन मिळते. आकलक Xn हा पासून, दिलेल्या x या मूल्याहून किती अधिक प्रमाणात दूर असू शकतो याबद्दलचीकाटेकोर कल्पना केंद्रीय सीमा प्रमेय देते. व्यवहारात किती तरी मापने प्रसामान्य वंटनाप्रमाणे का वागतात यावरही केंद्रीय सीमा प्रमेय प्रकाश टाकते. मुख्यतः निरवलंबीपणेवागणाऱ्या अनेक घटकांचा एखादया मापनावर संपूर्ण परिणामाच्या तुलनेत ‘ थोडा थोडा ’ परिणाम होत असेल, तर त्या मापनाचा प्रसामान्य वंटनानुसार वागण्याकडे कलअसतो. येथे हे लक्षात येते की, व्यवहारात बऱ्याच वेळा प्रसामान्य वंटनाव्यतिरिक्त इतर वंटनेदेखील अगदी सहजगत्या मिळतात.
पहा : वंटन सिद्धांत संभाव्यता -२.
संदर्भ : 1. Chung, K. L. A Course in Probability Theory, 1965.
2. Feller, W. An Introduction to Probability Theory and Its Applications, Vol. I, New York, 1968.
3. Gangolli, R. A. Ylvisakar, N. D. Discrete Probability, 1967.
4. Goldberg, S. Probability : An Introduction, 1987.
5 Hogg, R. V. Craig, A. T. Introduction to MathematicalStatistics,NewYork,1970.
6.Larson,H.J.Introduction to Probability, 1995.
7. Loe’ve, M. Probablity Theory, 2 Vols. 1977-78.
8. Parzen, E. Modern Probability Theory and Its Applications.
देशमुख, शैलजा, चिं. टिकेकर, व. ग.