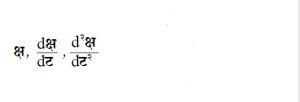सरल हरात्मक गति

सरल हरात्मक गति : ठराविक सरळ रेषेवर मागे-पुढे होणाऱ्या पदार्थाच्या गतीस सरल हरात्मक गती म्हणतात. ही गती कालाच्या ‘ज्या’ वक फलनाने दिली जाते. हा आंदोलन गतीचा सर्वांत साधा प्रकार होय.

अनेक भौतिक प्रणालींमध्ये सरल हरात्मक गती प्रदर्शित होते (येथे ऊर्जेत हानी होत नाही असे गृहीत धरले आहे). लहान परमप्रसर असताना लंबकाची गती जवळजवळ सरल हरात्मक असते [→ लंबक]. उलट-सुलट दिशेत वाहणारा प्रत्यावर्ती प्रवाह वाहून नेणाऱ्या तारेतील इलेक्ट्रॉन, ध्वनितरंगातील माध्यमाचे आंदोलित होणारे कण वगैरे सरल हरात्मक गती दर्शवितात.

सरल हरात्मक गतीत एक प्रेरणाकेंद्र असते व प्रेरणाकेंद्राच्या दोन्ही बाजूंस सारख्या अंतरावर पदार्थाची गती सारखी असते, म्हणून ही गती केंद्राच्या दोन्ही बाजूंस सममित असते. या गतीत प्रेरणाकेंद्राच्या ठिकाणी पदार्थाचा वेग सर्वांत जास्त व प्रवेग शून्य असतो, तर प्रेरणाकेंद्रापासून दूरतम असताना प्रवेग सर्वांत जास्त व वेग शून्य असतो.

सरल हरात्मक गती थोडक्यात समजावून घ्यावयाची झाल्यास एखादया वर्तुळावर फिरणारा बिंदू घेतात. ह्या बिंदूचा वर्तुळव्यासावरील प्रक्षेप व्यासावर मागे-पुढे फिरतो. त्या प्रक्षेपबिंदूची गती म्हणजेच सरल हरात्मक गती होय.

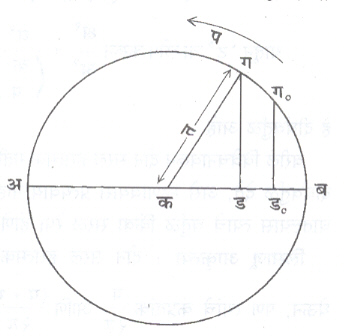
समजा, आ. १ मध्ये ग हा बिंदू वर्तुळावर अपसव्य (घदयाळाच्या काटयांच्या विरूद्ध) दिशेने ‘प ’ या कोणीय वेगाने फिरत आहे. ग चा अब व्यासावरील प्रक्षेप ड हा अब व्यासावर मागे-पुढे फिरत राहणार. ड ची गती म्हणजेच सरल हरात्मक गती होय.

वर्तुळाची त्रीज्या त आहे व मध्य क आहे आणि वर्तुळावर फिरणारा बिंदू हा प्रथम ग_o च्या ठिकाणी आहे. ‘ट’ सेकंदानंतर तो ‘ग’ च्या ठिकाणी आहे, असे मानल्यास आणि Ð बकग = भ घेतल्यास,

क ड = क्ष = त कोज्या ( प ट + भ ) … … … … … (१)

कलनशास्त्राचा [→ कलन] उपयोग करून ड बिंदूचा वेग ‘व’ आणि प्रवेग ‘प्र’ खालील समीकरणे देतील.

 

 

 

 

 

 

समी. (४) वरून क्ष = ० असताना व चे कमाल मूल्य मिळते आणि

क्ष = त असताना व = ० येते.

तसेच समी. (५) वरून प्र चे मूल्य ऋण आहे म्हणून प्र ची दिशा वर्तुळमध्याकडे आहे, हे उघड आहे. तसेच क च्या ठिकाणी प्र = ० आणि अ किंवा ब च्या ठिकाणी प्र चे निर्लेप मूल्य प²त आहे.

आवर्तिता : समीकरणे (१), (२) आणि (३) यांवरून २π/प किंवा याच्या पूर्णांकी गुणकाने ट वाढविल्यास

 

यांची मूल्ये तीच राहतात. म्हणजे सेकंदानंतर ड ची स्थिती वेग व प्रवेग तीच तीच मूल्ये धारण करतात. यास्तव या अवधीला सरल हरात्मक गतीचा आवर्तकाल म्हणतात. या आवर्तकालानंतर बिंदू त्याच ठिकाणी येत असल्याकारणाने हा आवर्तकाल म्हणजे एका आंदोलनास लागणारा अवधी होय.

कंप्रता : एका सेकंदात होणाऱ्या आंदोलन संख्येस कंप्रता म्हणतात. याचा अर्थ सरल हरात्मक गतीची कंप्रता प/२π आहे.

परमप्रसर : केंद्रापासून कोणत्याही बाजूस झालेल्या ‘ड’ च्या कमाल स्थित्यंतरास परमप्रसर म्हणून संबोधतात. हा परमप्रसर म्हणजे दोन दूरतम टोकांतील अंतराचा अर्ध होय.

कला कोन : ∠ बकग = भ या कोनास कला कोन म्हणतात. या कोनाच्या मूल्यावरून कोणत्या क्षणी गतीची सुरूवात झाली हे समजते. सर आयझॅक न्यूटन यांच्या गतिनियमाप्रमाणे,

प्रेरणा = वस्तुमान X प्रवेग

प्रेरणा ‘फ’ ने आणि पदार्थाचे वस्तुमान ‘म’ ने दर्शवून आणि समी. (५) मधील प्र चे मूल्य घेऊन, वरील गतिनियम खालीलप्रमाणे मिळतो.

फ = म प्र = – म प^२ क्ष … … … … … … … (६)

म्हणजे, फ µ क्ष … … … … … … … … … … ..(७)

वरील उदाहरणात ‘ग’ चा प्रक्षेप अब व्यासास लंब असणाऱ्या व्यासावर घेऊन त्याची ‘क’ पासूनची स्थित्यंतरे ‘य’ ने दर्शविल्यास,

य = त ज्या ( प ट + भ ) … … … … … … .(८)

येईल. ‘कोज्या’ किंवा ‘ज्या’ फलनास सर्वसाधारण संज्ञा ‘ज्या’ वक्र फलन आहे, कारण कोनातील फरक π /२ केल्यास ज्या-फलनाचे कोज्या-फलन होते आणि कोज्या-फलनाचे ज्या – फलन होते. म्हणूनच सरल हरात्मक गती म्हणजे कालाचे ‘ज्या’ वक फलन, असे सुरूवातीस केलेले विधान सार्थ आहे.

पदार्थावरील प्रेरणा प्रेरणाकेंद्रापासूनच्या अंतराच्या प्रमाणात असल्यास व प्रेरणेची दिशा केंद्राकडे असल्यास (म्हणजे प्रेरणा आकर्षण असते तेव्हा) पदार्थ सरल हरात्मक गतीत फिरतो.

विलोमत :

क्ष = त कोज्या (प ट + भ)

आणि य = त ज्या (प ट + भ)

या दोन समीकरणांतून (प ट + भ) चा निरास केल्यास

क्ष^२ + य^२ = त^२ असे समीकरण मिळते.

याचा अर्थ एकच परमप्रसर असलेल्या परंतु कला कोनांमध्ये ९०^° चा फरक असलेल्या दोन सरल हरात्मक गतींच्या संयुतीने (संकलनाने) वर्तुळ-बिंदुपथ मिळतो.

ऊर्जा : कोणत्याही गतीत पदार्थाची स्थित्यंतरे होत असल्याकारणाने त्याची स्थितिज ऊर्जा सारखी बदलेल, तसेच वेग बदलल्यास गतिज ऊर्जा बदलेल. स्थितिज ऊर्जा पदार्थावरील प्रेरणेने केलेल्या कार्याने मोजली जाते व ती खालील समीकरणाने दिली जाते.

स्थितिज ऊर्जा = _०∫^क्ष –फ dक्ष (फ ही प्रेरणा होय).

वरील सरल हरात्मक गतीमध्ये फ = – म प^२ क्ष घालून

स्थितिज ऊर्जा = १/२ . म प^२ क्ष^२ तसेच,

गतिज ऊर्जा = १/२ म व^२= १/२ म प^२(त^२–क्ष^२ ) ….[समी.(४) वरून]

∴ स्थितिज ऊर्जा + गतिज ऊर्जा = १/२ म प^२त^२= स्थिरांक.

कारण म, प, त ह्या दिलेल्या गतीतील अचल राशी होत.

दोन सरल हरात्मक गतींची संयुती : एकविध वर्तुळगती दोन सरल हरात्मक गतींच्या संयुतीने होते, हे वर पाहिलेच आहे फक्त दोन्ही गतींच्या कला कोनांतील फरक ९०^° असावयास पाहिजे पण कला कोनांतील फरक ९०^° पेक्षा निराळा असणाऱ्या दोन हरात्मक गतींची संयुती करावयाची झाल्यास परिणामी गती सर्वसाधारणपणे दीर्घवर्तुळाकार येते आणि त्याचे आवर्तकाल असमान असल्यास येणारा बिंदुमार्ग बराच गुंतागुंतीचा असतो. याच वेळी येणारे वक्र म्हणजे लिसाजू आकृत्या होत.

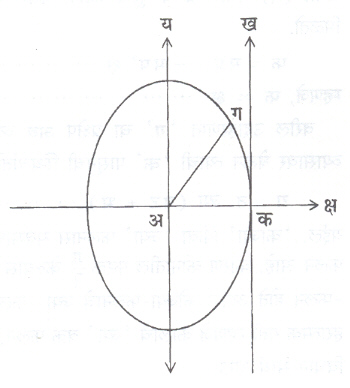
दीर्घवर्तुळ : समजा, आ. २ मध्ये ‘अ’ हा आदिबिंदू प्रेरणाकेंद्र आहे आणि ‘म’ वस्तुमानाचा कण क पासून कख दिशेने व_० गतीने फेकला. अशा वेळी तो कण सरळ रेषेवर फिरणार नाही. समजा, ‘ट’ सेकंदानंतर त्याची स्थिती ‘ग’ च्या ठिकाणी आहे. अक हा क्ष – अक्ष आणि कख याला समांतर अ मधून काढलेली रेषा य– अक्ष घेतली. प्रवेगाचा वरील नियम वापरून येणारे गतिसमीकरण असे येते :

 

यांत अग^→ = र हा सदिश असून क ही संख्या प्रेरणा स्थिरांक आहे.

‘ग’ चे सहनिर्देशक (क्ष, य) ने दर्शविल्यास – क र ह्या प्रेरणेचे संघटक (- क क्ष, – क य ) हे होत. म्हणून वरील समीकरण खालील दोन समीकरणे देईल. ती अशी :

 

यांत क/ म = प^२ लिहिल्यास समीकरणांचे निर्वाह

क्ष = अ ज्या (प ट + भ ) आणि

य = अ′ ज्या (प ट + भ′) असे मिळतात.

कला कोन आणि परमप्रसर निरनिराळे घेतले आहेत, हे ध्यानात घेणे आवश्यक आहे.

प्रारंभीच्या अटी विचारात घेत ट = ० असताना

 

 

 

 

 

 

 

 

 

 

हे दीर्घवर्तुळ आहे.

वरील विवेचनावरून दोन सरल हरात्मक गतींची संयुती सर्वसाधारणपणे दीर्घवर्तुळ देते, असे म्हणावयास प्रत्यवाय नाही. प्रारंभीच विशिष्ट अटी घातल्यास त्याचे वर्तुळ किंवा सरळ रेषा होणे शक्य आहे.

लिसाजू आकृत्या : दोन सरल हरात्मक गतींचे परमप्रसर समान

घेऊन, पण त्यांचे कंप्रतांक प /2π आणि (प + भ) /2π आहेत, असे मानल्यास आणि प्रारंभिक अटी सोयीच्या पडतील अशा घेतल्यास

क्ष = अ कोज्या (प ट)

य = अ कोज्या (प + भ) ट

अशी समीकरणे येतील. ‘य’ चे मूल्य विस्ताराने लिहून व ‘क्ष’ च्या मूल्याचा उपयोग करून

य = अ [कोज्या (प ट).कोज्या (भ ट) -ज्या (प ट).ज्या (भ ट)]

= क्ष.कोज्या (भ ट)- √(अ^२– क्ष२).ज्या (भ ट)

∴ क्ष२ + य^२ – २ क्ष य. कोज्या (भ ट) = अ^२.ज्या२ (भ ट)

हे समीकरण लंबवर्तुळ दर्शविते. फक्त या दीर्घवर्तुळाचे अक्ष ‘ट’ जसजसा बदलेल तसतसे विशिष्ट दिशेने गरगर फिरतील आणि प/भ जर पूर्णांक असेल, तर काही कालानंतर तीच तीच दीर्घवर्तुळे रेखाटली जातील. समजण्यास सोपे जावे म्हणून (प + भ)/प = ७/६ म्हणजे भ = प/६ घेतल्यास क्ष – अक्षावरील एक पूर्ण आंदोलन होत असताना य -अक्षावर ७/६ आंदोलने होणार हे निश्चित आहे. म्हणजे क्ष – अक्षावरील प्रत्येक आंदोलनास य – अक्षावरील आंदोलनाचा कला कोन १/६ (३६०^°) म्हणजे ६०^° ज्यास्त असणार. क्ष – अक्षावरील सहा आंदोलने पूर्ण होतील त्याच क्षणी य – अक्षावर सात आंदोलने पूर्ण होऊन दोन्ही गती पुन्हा सुरूवातीच्या जागी येतील पण असे घडावयाचे झाल्यास प/भ हे गुणोत्तर पूर्णांक असावयास हवे. (आ. ३).

या संयुतीचा मार्ग रेखाटावयाचा झाल्यास सुरूवातीच्या समीकरणामधून ‘ट’ चा निरास करणे अवघड नाही. पण ‘ट’ ला निरनिराळी सोयीस्कर मूल्ये देऊन (क्ष, य) च्या मूल्याचे कोष्टक तयार करणे अधिक सोपे असते व या कोष्टकावरून आलेख काढणे अवघड नाही.

 

 

 

 

 

 

 

 

 

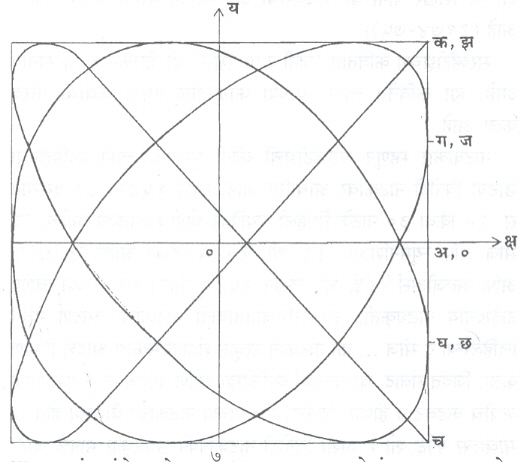
वर दाखविलेली आकृती क. ३ लिसाजू आकृती होय. गुणोत्तर प/भ = २ आणि प/भ = ३ असल्यास येणाऱ्या आकृत्या आ. ४ मध्ये दिल्या आहेत.

लिसाजू आकृत्या दोलनदर्शकाच्या साहाय्याने पडद्यावर पाहता येतात.

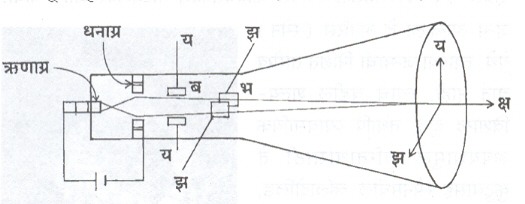
⇨ ऋण किरण नलिके त फिरणारे कण म्हणजे इलेक्ट्रॉन होत. यांचे वस्तुमान सु. ९ X १०२८ गॅम असते. ब आणि भ पट्ट्यांच्या समांतर जोडया एकमेकींस काटकोनांत छेदणाऱ्या प्रतलात घेतल्या आहेत. या पट्ट्यांना निरनिराळ्या कंप्रतांचे विद्युत दाब देऊन पडदयावर फारच गमतीदार आकृत्यांचे नमुने प्रकाशबिंदूंच्या साहाय्याने दाखविणे शक्य आहे. या पडदयावर लिसाजू आकृत्या पाहणे सुलभ आहे, कारण यात दोन सरल हरात्मक गतींची संयुती करणे सोपे असते.

संदमित दोलन : सरल हरात्मक गतीच्या समीकरणात विशिष्ट पदे घालून निरनिराळ्या प्रकारच्या दोलनगती आणता येतात. जसे,