समस्थायित्व

समस्थायित्व : (समस्थिती). पृथ्वीच्या कवचाच्या प्रमुख स्वरूपांची जलस्थैतिक साम्यावस्था असण्याच्या आदर्श स्थितीला सम-स्थायित्व म्हणतात. पृथ्वीचे कवच हे जणू निरनिराळ्या जाडीच्या प्रचंड ठोकळ्यांचे बनलेले आहे व द्रव पदार्थावर समतोल तरंगणाऱ्या घन ठोकळ्याप्रमाणे कवचाचे ठोकळे त्यांच्या खालील पदार्थांवर तरंगत असल्यामुळे त्यांना निरनिराळी उंची प्राप्त होऊन महासागरांचे तळ, खंडे, विस्तीर्ण मैदाने व पठारे, पर्वतरांगा इ. प्रमुख भूमिस्वरूपे उत्पन्न झालेली आहेत, असा समस्थायित्वाच्या तत्त्वाचा आशय आहे. निवांत पाण्यावर लाकडी ठोकळा कसा तरंगतो ते पाहून समस्थायित्वाचे तत्त्व कळण्यास मदत होते. अशा ठोकळ्यांचा काही भाग पाण्यात बुडालेला व काही पाण्याच्या बाहेर असतो व तो जलस्थैतिक  समतोल असतो. पाण्याने मूळ व्यापलेल्या जागेपैकी काही जागा पाण्यापेक्षा हलक्या अशा लाकडाने घेतलेली असते व पाण्याच्या पृष्ठाखालील तेवढय भागात बुडालेल्या लाकडाचा भार व विस्थापित पाण्याचा भार यांच्यामधील फरकाइतक्या द्रव्यमानाची न्यूनता असते. पाण्याच्या पातळीच्या वरील भागात ठोकळ्यांच्या द्रव्यमानाचे जे आधिक्य असते त्याची निष्कृती ( क्षतिपूर्ती वा भरपाई ) पाण्याच्या पातळीखालील भागातल्या तेवढयच द्रव्यमान- न्यूनतेमुळे घडून येऊन समतोलन ( संतुलन ) होत असते.

कवचाच्या ठोकळ्याचे समतोलन कशा प्रकारचे असेल याविषयी ज्या मुख्य कल्पना सुचविल्या गेल्या आहेत त्यांचा सारांश पुढील उदाहरणांवरून कळून  येईल.

समस्थायित्वाची प्रॅट कल्पना : निरनिराळी घनता ( वि. गु.) असणाऱ्या शेवगा, देवदार, सागवान, चारोळी यांसारख्या लाकडांचे सारख्याच जाडीचे, रूंदीचे व वजनाचे ठोकळे घेतले, तर त्यांची उंची निरनिराळी व हलकेपणाच्या प्रमाणात अधिक असेल व सर्वांत कमी घनतेचा ठोकळा सर्वांत उंच असेल. असे ठोकळे पाण्यावर तरंगत ठेवले, तर त्या सर्वांचे तळ एकाच पातळीपर्यंत खोल गेलेले पण पाण्याच्या बाहेर राहणारे भाग निरनिराळ्या उंचीचे व अधिकाधिक हलक्या घनतेचे ठोकळे अधिकाधिक उंच असलेले आढळतात. सर्वांत कमी घनता असणाऱ्या ठोकळ्यांची उंची सर्वांत अधिक असते ( आ. १).

समस्थायित्वाची एअरी कल्पना : एकाच घनतेच्या लाकडाचे निरनिराळ्या उंचीचे ठोकळे पाण्यावर तरंगत असले, तर त्यांचे पाण्याबाहेर राहणारे भाग त्यांच्या उंचीच्या समप्रमाणात असतात. पाण्यात बुडलेले भाग निरनिराळ्या खोलीपर्यंत गेलेले असतात व सर्वांत उंच ठोकळा सर्वांत खोल गेलेला असतो. ( आ. २).

 समस्थायित्वामागील कार्यकारणभाव : एखादया जागी उंच मनोरा बांधला म्हणजे मनोरा हे त्या जागेच्या खडकावरील अधिकभूत ( जादा ) द्रव्यमान असते व त्याला आधार देण्याचे सामर्थ्य पायाच्या खडकांत असते. पर्वतही तसेच म्हणजे खंडावरील अधिकभूत द्रव्यमानाच्या राशी आहेत व ते सर्वस्वी खंडांच्या आधारावर उभे आहेत, अशी कल्पना पूर्वी होती. पर्वत तसे असते तर इमारती बांधताना किंवा सर्वेक्षण करताना जो ओळंबा वापर-तात त्याच्यावर पर्वताच्या आकर्षणाचा परिणाम होऊन तो खृया ऊर्ध्वाधर ( उभ्या ) दिशेपासून विक्षेपित ( विचलित ) झाला असता व विक्षेपाचे परिमाण पर्वताच्या गुरूत्वीय आकर्षणास समानुपाती ( संपाती ) असते परंतु १७३५ साली अँडीज पर्वत प्रदेशाची पाहणी करीत असताना त्या पर्वताच्या द्रव्यमानाच्या मानाने त्याचे आकर्षण जेवढे असावयास पाहिजे त्यापेक्षा ते बरेच कमी आहे, अशी शंका प्येअर बूगेअर यांना आली. त्यानंतर सु. शंभर वर्षांनंतर, भारताच्या सिंधु- गंगा नदयांच्या मैदानी प्रदेशात हिमालयाच्या दक्षिणेजवळच्या भागांचे सर्वेक्षण चालू असताना कल्याणपूर व त्याच्या सरळ उत्तरेस ६०० किमी. अंतरावर असणाऱ्या कल्याणा या गावाचे जमिनीवर सरळ त्रिभुजन करून आणि ज्योतिषशास्रीय उपकरणांच्या साहाय्याने अशा दोन निरनिराळ्या पद्धतींनी जे अक्षांश काढण्यात आले त्यांच्यात चापाच्या सु.५·२३ सेकंद ( विकला ) इतके अंतर दिसून आले.

ज्योतिषशास्रीय उपकरणांचे तलमापन करण्यासाठी ओळंबा वापरला जातो व ओळंब्यावर   उत्तरेस जवळच असलेल्या हिमालयाच्या आकर्षणाचा परिणाम होत असल्या-मुळे अशी चूक येत असावी असे अनुमान करण्यात आले. कारण त्रिभुजन पद्धतीत तशी चूक होणे शक्य नसते. त्यानंतर थोडय वर्षांनी (१८५५) कोलकात्यात राहणारे बिटिश धर्मोपदेशक व भूभौतिकीविद जॉन हेन्री प्रॅट यांनी वरील दोन गावी असणाऱ्या ओळंब्यांवर हिमालयाच्या आकर्षणाचा कमीतकमी किती परिणाम व्हावयास पाहिजे याचे आकलन ( अंदाज ) केले. तेव्हा त्यांना असे दिसून आले की, आकलित परिणामांच्या मानाने प्रत्यक्ष होणारे परिणाम पुष्कळच कमी आहेत. वरील दोन गावांतील ओळं-ब्यांच्या विक्षेपातील आकलित अंतर चापाच्या १५.८८५ सेकंद म्हणजे प्रत्यक्ष आढळणाऱ्या अंतराच्या तिपटीहून किंचित अधिक असावयास पाहिजे होते. सारांश हिमालयाचे आकर्षण अपेक्षित मूल्यापेक्षा बरेच कमी आहे, हे सिद्ध झाले. त्यानंतरच्या काळात हिमालय प्रदेशात व पृथ्वीवरील इतर प्रदेशांत केलेल्या शेकडो मापनांवरून पर्वतरांगांचे आकर्षण अपेक्षित मूल्यापेक्षा सामान्यत: बरेच कमी असते असे कळून आलेले आहे व बूगेअर यांना आलेली शंका खरी ठरली आहे. फान्समधील सर्वेक्षकांना आलेला अनु-भव यापेक्षाही आश्चर्यकारक आहे व तो म्हणजे नैऋर्त्य फान्सच्या बिस्के उपसागराच्या किनाऱ्याजवळच्या प्रदेशात ओळंबा शेजारच्या पर्वताकडे ओढला जाण्याऐवजी त्याच्या विरूद्घ बाजूस म्हणजे समुद्राकडे विक्षेपित होतो हा होय. तसाच विक्षेप इतर पुष्कळ ( उदा., दक्षिण भारताच्या ) किनाऱ्यावर येतो असे त्यानंतरच्या सर्वेक्षणात दिसून आलेले आहे.

पर्वतांचे आकर्षण अपेक्षेपेक्षा कमी असण्याचे एकच भौतिक कारण शक्य आहे व ते म्हणजे पर्वतांच्या दृश्य अशा राशींच्या खाली जे भाग आहेत त्यांच्यात द्रव्यमानाची न्यूनता असली पाहिजे व पर्वतांच्या दृश्य राशींच्या द्रव्यमानाच्या आधिक्याची निष्कृती खोल भागातल्या द्रव्यमान न्यूनतेमुळे होत असली पाहिजे. हिमालयाचे आकर्षण अपेक्षित मूल्यापेक्षा कमी का असावे याचे स्पष्टीकरण करण्यासाठी प्रॅट यांनी वर दिलेल्या  पहिल्या उदाहरणातील द्रव पदार्थावर तरंगणाऱ्या निरनिराळ्या घनतेच्या ठोकळ्यांची कल्पना सुचविली होती (१८५५). त्यांच्या मते हिमालय पर्वताच्या ठोकळ्याचे संघटन सभोवतालच्या ठोकळ्यांपेक्षा किंचित निराळे असून त्याची घनताही किंचित कमी आहे. द्रव पदार्थांवर तरंगणाऱ्या अधिक हलक्या घनतेच्या ठोकळ्यांची उंची अधिक असते व त्यांचे आकर्षण भोवतालच्या अधिक घनतेच्या ठोकळ्यांपेक्षा अर्थात कमी असणार. वरील दुसऱ्या उदाहरणातील कल्पना गेट बिटनमधील ज्योतिषशास्त्रज्ञ ⇨जॉर्ज  बिडेल एअरी यांनी सुचविली होती (१८५९). हिमालयाच्या ठोकळ्याचे संघटन व घनता भोवतालच्या ठोकळ्यांसारखीच आहेत, पण त्याची जाडी अधिक आहे. त्यामुळे तो अधिक उंच असून अधिक खोलही गेलेला आहे. पर्वत हे पाण्यावर समतोल स्थितीत तरंगणाऱ्या बर्फाच्या टेकडयंसारखे   असतात व त्यांचे हलके खडक त्यांच्या खालील अधिक घनतेच्या पदार्थांत एखादया मुळाप्रमाणे खोल गेलेले असल्यामुळे त्यांच्या भाराचे समतोलन झालेले असते, असे एअरी यांचे मत होते.

पृथ्वीच्या कवचाचे ठोकळे ज्या तरंगत आहेत तो अध:स्तर द्रव नसून घनच असतो परंतु प्रदीर्घ काल टिकून राहणाऱ्या दाबांमुळे तो दबला जाऊन अतिमंद गतीने वाहू शकतो व तेवढयपुरते त्याचे वर्तन द्रव  पदार्थासारखे  असते.

समस्थायित्वाच्या तत्त्वात अभिप्रेत असलेली गोष्ट अशी की, समुद्र-सपाटीखाली कमीतकमी खोलीवर अशी एक पातळी असते की, जिच्यावर वरील पदार्थांच्या भाराचा जो दाब पडतो तो सर्वत्र सारखाच असतो. पहिल्या उदाहरणातील ठोकळ्यांच्या तळाची व दुसऱ्या उदाहरणातील सर्वांत उंच ठोकळ्याच्या तळाची पातळी या समान दाबाच्या पातळ्या आहेत. समान दाबाच्या पातळीवर बसणाऱ्या पदार्थांचे, ज्यांच्या अनुप्रस्थ छेदांचे क्षेत्रफळ सारखेच आहे असे विस्तीर्ण स्तंभ घेतले, तर त्या सर्वांचे भार सारखेच असतात. मग त्यांचे माथे ( महासागरांचा तळ, सखल मैदान, पर्वत इ.) कोणत्याही उंचीचे असोत. म्हणून पृथ्वीच्या प्रमुख उठावांची निष्कृती त्यांच्या खालील भागातल्या घनता – भेदांमुळे झालेली असते असे म्हणतात. ज्या आकलित पातळीत निष्कृती पुरी झालेली असते त्या म्हणजे समान दाबाच्या पातळीला निष्कृती समतल ( भूदाबपूर्ती स्तर ) असे म्हणतात. त्या पातळीच्या खालील खडक सुघटय् ( आकार्य ) असल्यामुळे समस्थायित्व घडून येते व टिकवून ठेवले जाणे शक्य असते. समान दाब पातळीच्या खालील खडकांच्या पट्टयला  दुर्बलावरण  म्हणतात.

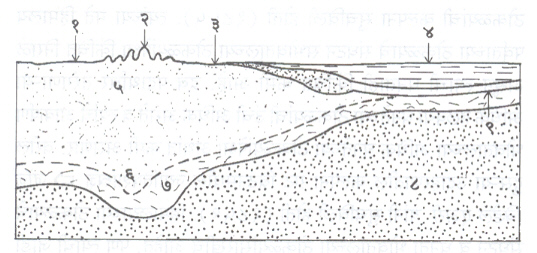
समस्थायी – समतोलनाचे तत्त्व मान्य झालेले असले, तरी खोल भागात निरनिराळ्या घनतेच्या खडकांची वाटणी कशी असेल याविषयी मतभेद आहेत. प्रॅट व एअरी यांच्या कल्पनांशिवाय इतर कित्येक कल्पना सुचविल्या गेल्या आहेत. पृथ्वीवरील बहुतेक सर्व प्रदेशांतल्या खडकांची व त्यांच्या घनतेची माहिती आपणास झालेली आहे. भूकंप – तरंगांच्या साहाय्याने केलेल्या  अन्वेषणाने कवचाच्या खोल भागांविषयी पुढील गोष्टी कळून आल्या आहेत : कवचाचा महासागरांच्या खाली जो भाग आहे त्याच्या (सीमा) खडकांची घनता खंडाच्या (मुख्यत: सियाली) खडकांपेक्षा निश्चित अधिक आहे. सखल मैदानी प्रदेशांखालील कवचाची जाडी सु. ३० किमी. किंवा त्यापेक्षा कमी असते. पर्वतरांगा असलेल्या भागातील कवच अधिक जाड असते व पर्वतांचे (सियाली) खडक मुळांप्रमाणे ५०-६० किमी. पर्यंत खोल गेलेले असतात. वरील सर्व गोष्टी लक्षात घेऊन कवचाची रचना व पृष्ठीय स्वरूप यांचे संबंध कसे असावेत हे स्थूलपणे दाखविणारी एक कल्पना आ. ३ मध्ये दाखविली आहे.

पृथ्वीच्या कवचाची प्रमुख स्वरूपे जलस्थैतिक साम्यावस्थेत ( सम-तोलावस्थेत ) असतात किंवा तशी अवस्था प्राप्त होण्याच्या मार्गावर असतात अशी भूगणित्यांची व भूवैज्ञानिकांची कल्पना आहे. पृथ्वीच्या विस्तीर्ण क्षेत्रांच्या स्वरूपांची निष्कृती खालील पदार्थांच्या वि. गु. मधील किंवा घनतेतील भेदांमुळे जवळजवळ पूर्ण झालेली आढळते. अधि कजाड व कमी घनतेचे खडक असणाऱ्या भागांची खंडे झालेली आहेत व कमी जाडीचे व अधिक घनतेचे खडक असणारे भाग खोल खचून महासागरांचे तळ झालेले आहेत. या गोष्टी समस्थायीत्वाच्या तत्त्वास अनुसरूनच आहेत.नैसर्गिक कियांमुळे पृथ्वीच्या कवचात सतत फेरफार घडून येत असतात. त्यामुळे समतोलनात बिघाड होतात. म्हणून पृथ्वीच्या सर्व भागास आदर्श समतोल अवस्था प्राप्त होणे किंवा झाल्यावर ती दीर्घकाल टिकणे अशक्य असते. नैसर्गिक प्रकियांच्या तीव परिणामांपासून जे प्रदेश दीर्घकाल मुक्त राहिलेले आहेत ते जवळजवळ साम्यावस्थेत असतात व खालील भागातील घनतेच्या भेदांनी त्यांची निष्कृती झालेली असते, असे पृथ्वीच्या निरनिराळ्या भागांत केलेल्या गुरूत्व-मापनांवरून कळून येते परंतु सापेक्षत: अलीकडील काळात विक्षोभित झालेल्या प्रदेशांत मात्र ( उदा., महासागरांच्या खोल खंदक, कोलोरॅडोचे पठार ) गुरूत्वाची मूल्ये अत्यंत विसंगत असतात व त्यांना साम्यावस्था प्राप्त झालेली नाही असे दिसून येते. समस्थायित्वाचे तत्त्व विस्तीर्ण क्षेत्रांतच लावावयाचे असते. एकेकटी शिखरे किंवा दृया यांसारखी लहानसहान स्वरूपे टिकवून धरण्याचे सामर्थ्य कवचाच्या खडकांत असते व त्यांची स्वतंत्र निष्कृती व्हावी अशी अपेक्षा नसते.

 समस्थायी पुन:समायोजन : पर्वतांच्या खडकांचा चुरा नदयांच्या पाण्याबरोबर वाहत जाऊन त्यांच्या मुखाजवळ साचविला जातो. या किया दीर्घकाल घडून आल्या म्हणजे समतोल बिघडविला जातो. पर्वतांचे क्षेत्र हलके होते. त्यांच्या स्तंभांचा अध:स्तरावर पडणारा दाब कमी होतो. गाळ साचलेल्या क्षेत्राचा भार वाढतो व त्याच्या स्तंभांचा अध:स्तरावर पडणारा दाब वाढतो. खोल भागातील पदार्थाचे योग्य तेवढे स्थानांतरण घडून आल्याशिवाय साम्यावस्था साधली जाणे शक्य नसते. भार वाढलेल्या स्तंभांखालील पदार्थ हलक्या झालेल्या स्तंभांखालील भागांकडे अति-मंद गतीने वाहू लागतात. पर्वतांचे स्तंभ वर सरकू लागतात. गाळ साचलेल्या प्रदेशांचे स्तंभ खचू लागतात. दीर्घ कालाने स्थानांतरण पूर्ण होऊन समतोल साधला जातो. या प्रकियांस समस्थायी पुन:समायोजन ( फेरजुळणी ) म्हणतात. ( आ. ४). समस्थायी पुन:समायोजनाचा महत्त्वाचा परिणाम म्हणजे पर्वतांचे किंवा इतर उंचवटयंचे आयुष्य वाढते हा होय. पर्वत झिजून त्यांची उंची कमी होते पण समस्थायी पुन:समायोजनाने ती पुन्हा वाढते. म्हणून कित्येक पर्वत कोटयवधी वर्षे टिकून राहिलेले आहेत.

गेल्या हिमकालात (सु. ६ लाख ते ११ हजार वर्षांपूर्वीच्या काळात) वायव्य यूरोपातील व उत्तर अमेरिकेतील विस्तीर्ण क्षेत्रे बर्फाच्या प्रचंड थरांनी झाकली गेली होती व बर्फाच्या भाराने खचल्यामुळे त्यांची उंची आजच्यापेक्षा कमी होती असे पुरावे आहेत. कालांतराने बर्फाचे थर वितळून गेले. शेवटचे थर सु. आठ ते अकरा हजार वर्षांपूर्वी नाहीसे झाले. भार नाहीसा झाल्यावर ते प्रदेश हळूहळू वर सरकू लाग. त्यांचेले वर सरकणे अदयापि थांबलेले नाही. फिनलंड व स्कँडिनेव्हिया यांचे किनारे २७५ मी.वर सरकलेले आहेत व अजून सु. २१० मी. वर सरकल्यावर त्यांना साम्या-वस्था प्राप्त होईल असे आकलन आहे. बर्फाचा भार नाहीसा होण्याच्या कियेच्या मानाने कवचाचे स्तंभ वर सरकण्याच्या कियेचा वेग फारच मंद असला पाहिजे. पुन:समायोजन पुरे होण्याला किती दीर्घ काल लागतो हे या उदाहरणावरून कळून येईल. पुन:समायोजनाने कवचाच्या हालचाली घडून येतात हे मान्य झालेले आहे पण पृथ्वीच्या कवचात महत्त्वाचे फेरफार घडवून आणणाऱ्या व पर्वतांसाखीर स्वरूपे निर्माण करणाऱ्या वेगळ्याच प्रकारच्या हालचालीही घडून येत असतात.[⟶ पृथ्वीचे अंतरंग]. समस्थायित्वाचे तत्त्व प्रॅट यांनी सुचविलेच होते, पण ‘आयसॉस्टसी’ (सम-स्थायित्व) ही संज्ञा मात्र क्लॅरेन्स एडवर्ड डटन या अमेरिकन भूवैज्ञानिकांनी १८८९ साली सुचविली आणि या तत्त्वाचा उगम हिमालय- प्रदेशाचे सर्वेक्षण चालू  असताना  भारतातच  झाला.

पहा : पृथ्वीचे अंतरंग भूगणित भूविज्ञान.

संदर्भ : 1. Cathles, L. M. The तiscosity of the Earth’s Mantle, 1975.

            2. Holmes, A. Principles of Physical Geology, 1978.

            3. Sabadini, R. Lambeck, K. Boschi, E. Eds., Glacial Isostasy, Sea Leतel and Mantle Rheology, 1991.

केळकर, क. वा.