समतुष्टी वक्र

समतुष्टीवक्र : (इन्डिफरन्स कर्व्ह). सनातनवादयांच्या  मागणी सिद्धांताची जॉन रिचर्ड हिक्स या अर्थशास्त्रज्ञाने केलेली नवी मांडणी. कोणत्याही वस्तूची मागणी रेषा य-भुजेकडून वरून खाली क्ष-भुजेकडे गेलेली  असते. यावरून मार्शलच्या मागणी सिद्धांतानुसार इतर परिस्थिती तशीच असताना वस्तूची  किंमत वाढल्यास, तिच्या मागणीचे परिमाण कमी होते व किंमत कमी झाल्यास तिच्या  मागणीचे परिमाण वाढते. या मागणी सिद्धांताचे स्पष्टीकरण सीमांत उपयोगिता  विवेचन व समतुष्टी वक्ररेषा विवेचन, या दोन पर्यायी मार्गांनी करता येते.  समतुष्टी वक्र विवेचन आधुनिक स्पष्टीकरण असून ते सीमांत उपयोगिता विवेचनाच्या निरनिराळ्या उणिवांमुळे पुढे मांडले गेले आहे.

सीमांत उपयोगिता विवेचनाच्या उणिवा त्याच्या गृहीतकृत्यामुळे निर्माण झाल्या  आहेत. सीमांत उपयोगिता सिद्धांत आणि त्यावर आधारलेल्या मागणीचा सिद्धांत  मांडताना मार्शलने उपयोगिता व समाधान आकडयात मोजता येते, असे गृहीत धरले  होते. हिक्सने आधुनिक समतुष्टी वक्र विवेचनात सीमांत उपयोगिता विवेचनाची  गृहीतकृत्ये बाजूला सारून विवेचन अधिक वस्तुनिष्ठ केले आहे. या विवेचनात  समाधान परिमाणाऐवजी समाधानाच्या पातळीचा निर्देश आहे. म्हणजेच वस्तूंच्या  सेवनांपासून मिळणारे समाधान मूळसंख्यावाचक पद्धतीने न दर्शविता क्रमवाचक संख्या  पद्धतीने दर्शविले आहे. तसेच उपभोक्ता एकत्र वस्तू सेवन करीत आहे असे न मानता, त्याच्यापुढे निरनिरळ्या वस्तूंची परिमाणे संयोगरूपाने समाधानाच्या वेगवेगळ्या  पातळ्या दर्शविणारी आहेत. समतुष्टी वक्र विवेचनाची गृहीतकृत्ये म्हणजे प्रत्येक  उपभोक्त्याचा पसंतीक्रम दिलेला आहे.उपभोक्ताअधिकतम समाधानप्राप्तकरण्याचाम्हणजेसमाधानाचीअत्युच्च पातळी गाठण्याचा  प्रयत्नकरीतअसतो,एवढीचआहेत.

उपभोक्त्याची प्रेयश्श्रेणी किंवा पसंतीक्रम दिलेला असल्यावर उपभोक्त्याचे  कोणत्याही दोन उपभोग्य वस्तूंच्या बाबतींतील समतुष्टी कोष्टक किंवा तटस्थ  कोष्टक मांडता येईल. या कोष्टकात उपभोक्त्याला समाधानाच्या एकाच पातळीत  ठेवणाऱ्या कोणत्याही दोन किंवा अधिक वस्तूंच्या परिमाणांचे संयोग दिलेले  असतात.’ब ‘ आणि’क ‘ या दोन वस्तूंबाबतचे उपभोक्त्याचे तटस्थ कोष्टक  खाली दिल्याप्रमाणे असेल.

समतुष्टी कोष्टक

वरील कोष्टकातील’ब ‘ आणि’क ‘ या दोन वस्तूंचे सर्व संयोग  उपभोक्त्याला एकाच समाधान पातळीत नेऊन पोचविणारे आहेत. अशाच कोष्टकाच्या  साहाय्याने क्ष-भुजेवर’ब ‘ वस्तू व य-भुजेवर’क ‘ वस्तू दर्शवून खालीलप्रमाणे’ इइ ‘ ही समतुष्टी वक्ररेषा काढता येईल. अनेक कोष्टकांच्या साहाय्याने इ_१ इ_१ इ_२ इ_२. … अशा अनेक समतुष्टी वक्ररेषा काढता येतील. प्रत्येक समतुष्टी वक्ररेषा  समाधानाची एक विशिष्ट पातळी दर्शविते.’अ ‘ या मूळ बिंदूपासून दूर असलेल्या इ इ_१ इ_२ समतुष्टी वक्ररेषा समाधानाची अधिकाधिक उंच पातळी दर्शवितात, तर’अ’ बिंदूपासून जवळ असलेल्या समतुष्टी वक्ररेषा समा-धानाची खालची पातळी  दर्शवितात. उपभोक्ता आपल्याजवळ असलेल्या साधनांनी आपले समाधान अधिकतम करण्याच्या हेतूने शक्य त्या दूरच्या समतुष्टी वक्ररेषेला पोहोचण्याचा प्रयत्न करतो. समतुष्टी कोष्टक व समतुष्टी वक्ररेषा यांवरून असे दिसून येते की, जसजसे’ब’ चे परिमाण कमी होते, तसतसे’क’ चे परिमाण वाढत जाते. म्हणजे ‘ब’ चे परिमाण एकएक नगाने कमी केल्याने होणाऱ्या तोट्याची भरपाई’क’ चे परिमाण वाढवून केली जाते, जेणेकरून समाधानाची पातळी कायम राहाते.  समतुष्टी वक्रकोष्टकाला तटस्थ कोष्टक व समतुष्टी वक्राला तटस्थवक्र म्हणतात कारण त्यात दर्शविलेल्या वस्तूच्या परिमाणांच्या संयोगाच्या बाबतीत उपभोक्ता तटस्थ  असतो. समतुष्टी वक्राची प्रमुख वैशिष्टय म्हणजे : (१) प्रत्येक समतुष्टी वक्र’य’ भुजेकडून खाली’क्ष ‘ भुजेकडे उतरतो व दोन्ही भुजांकडे निमुळता होत  जातो. (२) प्रत्येक समतुष्टी वक्र’अ’ ह्या मूळबिंदूशी बहिर्वक असतो. (३) कोणतेही दोन समतुष्टी वक्र एकमेकांना छेदत नाहीत.

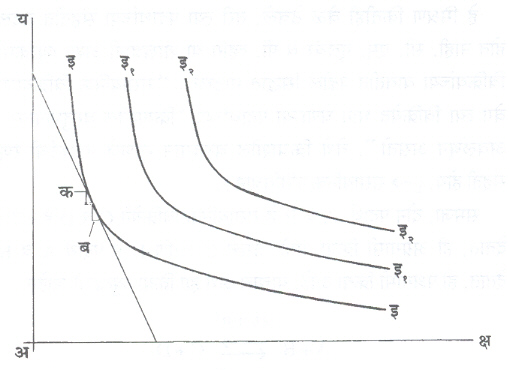
प्रत्येक समतुष्टी वक्र’य ‘ भुजेकडून’क्ष’ भुजेकडे उतरत जातो कारण  जसजसे एका वस्तूचे परिमाण वाढत जाते, तसतसे दुसऱ्या वस्तूचे परिमाण कमीकमी  झाले पाहिजे, तरच समाधानाची पातळी कायम राहील. समतुष्टी वक्राच्या उताराचा कल दोन वस्तूंमधील सीमांत प्रतिस्थापन दराने दर्शविला जातो. समतुष्टी कोष्टकातील कोणत्याही दोन संयोगांची तुलना केल्यास सीमांत प्रतिस्थापन दर काढता येईल. वरील कोष्टकांतील (६) आणि (५) हे संयोग घेतले तर,’ब’ चे परिमाण १६ वरून १५ झाले म्हणजे एकाने कमी झाले, तेव्हा’क ‘ चे परिमाण ४ चे ६ झाले  म्हणजे दोनने वाढले.

 प्रत्येक समतुष्टी वक्र आकृतीत दर्शविल्याप्रमाणे’अ ‘ ह्या मूळबिंदूशी बहिर्वक  असतो. याला कारण दोन वस्तूंमधील आहासी सीमांत प्रतिस्थापन दराचा नियम होय.  या नियमानुसार उपभोक्त्याजवळ एका वस्तूचे परिमाण जसजसे एकएक नगाने वाढत  जाते, तसतसे दुसऱ्या वस्तूचे परिमाण वाढत्या प्रमाणात कमी होत जाते. समजा’ब’ चे परिमाण वाढत आहे, तसतसे’क’ चे परिमाण कमी होत जाते आणि प्रत्येक ’ब’ च्या बदलीत उपभोक्ता’क ‘ चे कमीकमी नग घेत असतो. याउलट जर उपभोक्ता ‘ब’ देत असेल आणि’क’ घेत असेल, तर’ब’ चे परिमाण कमी होत असताना’क’ चे परिमाण वाढत आहे. म्हणून प्रत्येक ’ब’ चा नग सोडून देताना उपभोक्ता’क’ चे अधिकाधिक नग मागू लागेल व’क ‘ आणि’ब’ यांमधील परस्पर पर्याय दर वाढत राहील.

कोणतेही दोन समतुष्टी वक्र एकमेकांना छेदत नाहीत. समजा, जर दोन समतुष्टी  वक्र इ इ आणि इ_१ इ_१ एकमेकांना’फ ‘ बिंदूमध्ये छेदत असतील, तर’फ ‘ हा  छेदनबिंदू दोन्ही समतुष्टी वकांवर असल्यामुळे त्या बिंदूच्या ठिकाणी असलेला  दोन वस्तूंचा संयोग दोन्ही समतुष्टी कोष्टकांत असला पाहिजे. असे असेल,तर ती  दोन्ही समतुष्टी कोष्टके दोन वेगवेगळ्या समाधानांच्या पातळ्या दर्शविणार नाहीत.  म्हणजे दोन्ही समतुष्टी कोष्टके वस्तुत:एक आहेत आणि एक समतुष्टी वक्र  दर्शवीत आहेत, असा  त्याचा अर्थ होईल, म्हणून कोणतेही दोन समतुष्टी वक्र एकमेकांना कदापिही  छेदणार नाहीत.

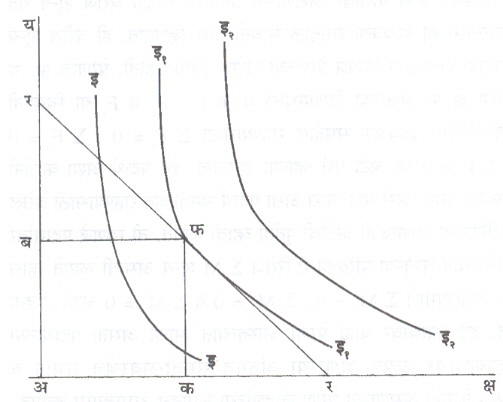
वस्तूच्या किंमती दिलेल्या असल्यास समतुष्टी वकांच्या साहाय्याने उपभोक्ता  आपल्याजवळ असलेल्या रकमेने समाधानाच्या अत्युच्च पातळीवर कसा पोहोचेल हे जाणता  येईल. समजा, उपभोक्त्याजवळ ३६ रू. आहेत आणि ’ब’ ची किंमत नगास रू. २  व ’क’ ची किंमत नगास रू. १ आहे. यावरून उपभोक्त्यास दिलेल्या रक्कमेने मिळू शकणाऱ्या ‘ब ‘ आणि ‘क ‘ च्या परिमाणांच्या संयोगाचे कोष्टक मांडता येईल. या कोष्टकाच्या  साहाय्याने किंमत-रेषा (प्राइस-लाइन) काढता येईल.

ही किंमत-रेषा कोणत्यातरी एका समतुष्टी वक्राला स्पर्शरेषा असेल. ज्या बिंदूत उपभोक्ता संतुलनावस्थेत असतो, म्हणजे त्याला कमाल समाधान मिळत असते, म्हणूनच त्या ठिकाणी असलेला संयोग उपभोक्ता पसंत करतो. म्हणजे दिलेल्या किंमतीत उपभोक्ता ‘ब’ चे किती नग घेईल व ‘क’ चे किती नग घेईल, हे त्या बिंदूपाशी स्पष्ट होते. याच पद्धतीचा अवलंब करून कोणत्याही एका वस्तूची समजा ‘ब’ ची किंमत धरली आणि दुसरीची किंमत म्हणजे ‘क’ ची किंमत कायम राहिली, तर वेगळी किंमत-रेषा काढून वेगळी संतुलावस्था प्राप्त होईल आणि बदललेल्या किंमतीत उपभोक्ता ’ब’ चे किती नग घेतो हे स्पष्ट होईल. अशा रीतीने ‘ब’ च्या बदलत्या किंमतीचे आणि मागणी केलेल्या परिमाणांचे कोष्टक तयार होईल. हेच ‘ब’ च्या मागणीचे कोष्टक होय. यावरून मागणीचा सिद्धांत समतुष्टी वक्राच्या साहाय्याने सिद्ध करता येतो.

 सुर्वे, गो. चिं. भेण्डे, सुभाष