सदिश

सदिश : (व्हेक्टर). सदिश ही गणितातील संकल्पना भौतिकीच्या गरजेपोटी निर्माण झाली. भौतिकीतील वेग, प्रवेग, प्रेरणा व स्थानांतर या संकल्पना अशा आहेत की, त्यांना केवळ संख्यात्मक मूल्य (परिमाण) आहे इतकेच नसून त्यांचे ज्ञान दिशा कळल्याखेरीज पुरे होत नाही. उदा., दुचाकी ताशी चार किमी. वेगाने गेली हे सांगताना ती कोणत्या दिशेने गेली हे सांगणेही आवश्यक असते. संख्यात्मक मूल्य व दिशा या दोन्ही गोष्टी कळल्याखेरीजज्या संकल्पनेचे ज्ञान पुरे होत नाही त्या संकल्पनेला सदिश असे म्हणतात.

सदिश हा दिशादर्शक सरळ रेषाखंडाने दर्शविला जातो. उदा.,

⟶
A         B      येथे

 ⟶
A B

हा दिशाबद्ध सरळ रेषाखंड आहे. त्याची AB ही लांबी सदिशाचे संख्यात्मक मूल्य दाखविते व बाण सदिशाची दिशा दाखवितो. दोन समान व समांतर रेषाखंड एकाच सदिशाचे निर्देशन करतात असे मानले जाते. या सदिशांना स्वैर सदिश म्हणतात. सदिश एका निश्चित रेषेवरील रेषाखंडाने निर्देशित होत असेल तर त्याला रेषा सदिश असे म्हणतात. तो रेषेवरील एका विशिष्ट बिंदूपासूनच रेषाखंड घेऊन निर्देशित केला असेल तर त्याला बंधित सदिश असे म्हणतात.

भौतिकीत अशाही संकल्पना आहेत की,ज्यांना केवळ संख्यात्मक मूल्य असते. घनफळ, ऊर्जा, विद्युत् भार, वस्तुमान, तापमान, घनता अशा दिशाविरहित संकल्पनांना अदिश (स्केलर) असे म्हणतात.

सदिश ही संकल्पना ⇨सर आयझॅक न्यूटन (१६४२-१७२७) यांच्या काळापासून प्रचलित आहे; परंतु सदिशांच्या गणिताची व्यवस्थित रचना ⇨सर विल्यम रोअन हॅमिल्टन आणि हेरमान ग्यूंटर गासमान यांनी एकोणिसाव्या शतकाच्या सुरूवातीस केली.

⇨ऑलिव्हर हेव्हिसाइड व ⇨जोसिआ विलर्ड गिब्ज यांनी एकोणिसाव्या शतकाच्या अखेरीला जी सदिश-गणिताची व्यवस्था लावली तिला अनुसरून येथे मांडणी केली आहे.

सदिश-गणित हे शास्त्र भौतिकी व अभियांत्रिकी या विषयांत महत्त्वाचे साधन ठरले आहेच पण मनोविश्लेषण, मनोविज्ञान व अर्थशास्त्र यांतील कल्पनांची मांडणी करण्यासाठीदेखील या शास्त्रातील संकल्पना उपयोगी पडतात. निरनिराळ्या शास्त्रांतील जटिल कल्पना सदिश-गणिताच्या साहाय्याने सुटसुटीत पद्धतीने व्यक्त करता येतात असा अनुभव आहे.

सदिश-गणितात भूमितीपेक्षाही अधिक स्वातंत्र्य असल्याने भौतिकी हे शास्त्र जसे वाढत गेले तसे त्याच्याबरोबर सदिश-गणितही विकास पावले. भौतिकीच्या आधुनिक शाखा म्हणजे सापेक्षता सिद्धांत, आण्विक भौतिकी यांतही सदिश-गणिताचा उपयोग होतो.

सदिशांची बेरीज : सदिश हा जाड टाइपातील रोमन अक्षरांनी किंवा अक्षराच्या वर बाण असा दाखविला जातो. उदा., a, b, c किंवा

⟶     ⟶      ⟶
a        b        c

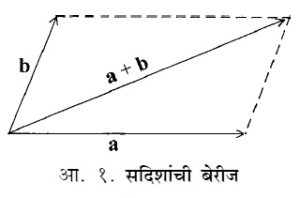
वगैरे. समजा, a व b असे दोन सदिश दिलेले आहेत. तर त्यांची बेरीज दाखविणारे (a + b) हा सदिश समांतरभुज चौकोनीय बेरजेच्या नियमाने शेजारी दिलेल्या आकृतीत दाखविल्याप्रमाणे मिळतो.

 

जर a, b, c अशा तीन संदिशांची बेरीज करावयाची असेल तर प्रथम (a + b) हा सदिश मिळवावा व नंतर (a + b) +  c हा सदिश मिळवावा.

समजा a हा दिलेला सदिश आहे. a हा सदिश विवक्षित लांबीच्या बाणाने दाखविता येतो. या बाणाला समांतर असणारे बाण a चीच दिशा असणारे परंतु लांबीनुसार कमी-अधिक संख्यामूल्य असणारे सदिश आहेत.

 

 

 

उदा., शेजारील आकृतीतील u व v या सदिशांची व a ची दिशा एकच आहे. पण  u चे संख्यामूल्य a च्या संख्यामूल्याहून कमी, तर v चे संख्यामूल्य a च्या संख्यामूल्याहून अधिक आहे. म्हणून असे लिहिता येते की, u = x.a  आणि v = y.a येथे xवy ह्या धन संख्या असूनx &lt 1 &lt y असे आहे. u चे संख्यात्मक मूल्य x व a चे संख्यात्मक मूल्य यांच्या गुणाकाराइतके आहे. हेच । u । = x· । a । असे दाखवितात.

वर x ही धन संख्या घेतली आहे. समजा, x ही ऋण संख्या असेल तर x.a हा सदिश कसा होईल ? x.a या सदिशाचे संख्यात्मक मूल्य x . a इतके असेल. पण x ऋण असल्याने x.a या सदिशाची दिशा a च्या दिशेच्या विरूद्ध असेल. याचाच विवक्षित प्रकार म्हणजे – a = – 1. a हा सदिश होय.

 

 

 

– a या सदिशाचे संख्यात्मक मूल्य a च्या संख्यात्मक मूल्याइतकेच असते. पण त्याची दिशा a च्या विरूद्ध असते. – a व a या सदिशांची बेरीज ० या सदिशाने दाखविली जाते. ० या सदिशाचे संख्यात्मक मूल्य ० इतके असते तर त्याची दिशा संदर्भानुसार कोणतीही घेता येते.

दोन सदिशांची बेरीज (व वजाबाकी) या क्रियेविषयी खालील नियम तयार करता येतात :

(१) a – b = a + (–b) (२) a + b = b + a

(३) (a + b) + c = a + (b + c) (४) x . (a + b) = x . a +x . b

(५) x . (y . a) = (x . y) . a (६) (x + y) . a = x . a + y . a

(७) o.a = o (८) a + o = a (९) a + b = a + c

     ∴b = c वगैरे.

सदिश व सहनिर्देशक : त्रिमितीय अवकाशात सदिशाची कल्पना अधिक सुलभरीतीने मांडता येते.

 

 

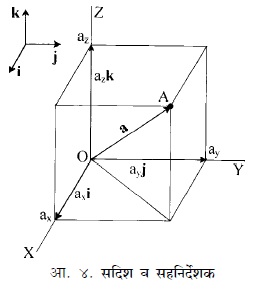
आकृतीमध्ये त्रिमितीय अवकाशात अक्ष-रचना दिलेली असून त्या रचनेचा उगम-बिंदू O आहे. O पासून OX, OY, OZ हे तीन अक्ष परस्परांना लंब आहेत. सदिश आता a हा जर दिलेला असेल, तर तो स्वतःला समांतर अशा रीतीने हलवून a चा उगमबिंदू O याठिकाणी आणता येतो.

⟶
 OA 

हा a हा सदिशद र्शवीत आहे असे मानू या.

A हा ज्यात अक्ष-रचना बसविलेली आहे अशा त्रिमितीय अवकाशातील बिंदू आहे. म्हणून A ला सहनिर्देशक असले पाहिजेत. हे सहनिर्देशक (ax,  ay,  az) आहेत असे मानू.

i, j, k हे एकक संख्यात्मक मूल्य असलेले सदिश O पासून सुरू होऊन OX, OY, OZ या अक्षांवर आहेत. अशा स्थितीत a हा सदिश axi,  ayj व azk या सदिशांच्या बेरजेइतका होतो. हे शेजारच्या आकृती क्र. ४ वरून दिसून येईल.

∴a = axi + ayj + azk

ax, ay, az या संख्यांना a या सदिशाचे सहविभाग असे म्हणतात. जर a = axi + ayj + azk व b = bxi + byj + bzk असे दोन सदिश असतील आणि a, b या संख्या असतील तर aa + bb = (aax + bbx)i + (aay + bby)j + (aaz + bbz) k म्हणजे aa व bb या सदिशांच्या बेरजेचे सहविभाग aa व bb यांच्या तत्सम सहविभागांच्या बेरजेने मिळतात.

वर पाहिले आहे की, प्रत्येक सदिश हा तीन अक्षांच्या समवेत असणाऱ्या सहविभागांच्या बेरजेत मांडता येतो. हा प्रत्येक सहविभाग जर x, y, z व कालदर्शक चल t यांचे फलन असेल तर मूळ सदिश हादेखील x, y, z व t या चलांचे फलन होईल. म्हणजे v(x, y, z, t) हे सदिश फलन मिळेल.

v(x, y, z, t) = vx (x, y, z, t) i + vy (x, y, z, t) j

                                                             + vz (x, y, z, t) k

v या सदिश फलनाला सदिश-क्षेत्र असेही म्हणतात. जर सदिश क्षेत्राच्या चलात कालदर्शक चल t अनुपस्थित असेल; तर त्यास दिशक्षेत्राला कालस्थिर क्षेत्र असे म्हणतात.

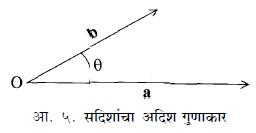
सदिशांचे गुणाकार : a व b हे दिलेले सदिश आहेत.कोणताही सदिश त्याच्या मूळच्या दिशेला समांतर हलविता येत असल्याने असे मानायला हरकत नाही की, a व b यांचे उगम – बिंदू एकाच ठिकाणी आहेत व त्यास दिशांमध्ये q हा कोनआहे.अशा वेळी a व b या सदिशांचा बिंदु-गुणाकार a . b cosq या संख्येने दिला जातो. 

 

 

 

a.b = । a ।.। b। cosq….   ….   …. (१)

येथे हे लक्षात घेणे जरूर आहे की, दोन सदिशांचा बिंदु-गुणाकार करून सदिश न मिळता संख्या मिळते म्हणून या गुणाकाराला सदिशांचा अदिश (संख्यात्मक) गुणाकार असेही म्हणतात. समी. (१) वरून खालील समीकरणे मांडता येतात.

a.b = b . a . . . (२) a.a = |a| २

(a + b) . (c + d) = a . c + a . d+ b . c + b . d . . .  … … (४)

जरi, j, kहेअक्षाशीसंलग्नअसेसदिशअसतीलतर 

जरa = axi + ayj + azkवb = bxi + byj + bzk,

तरa.b = axbx + ayby+ az bz.

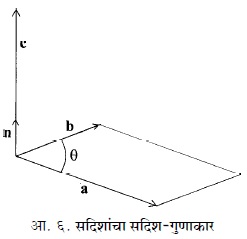
त्रिमितीय अवकाशात a व b हे दोन सदिश आहेत. त्या दोन सदिशांनी एक प्रतलनिश्चित होते. a पासून b कडे जाताना म्हणजे अप-सव्य (घड्याळकाटे विरूद्घ) दिशेने गेल्यास a व b यांच्या प्रतलाला डोक्याच्या दिशेने लंब असणारा सदिश धन-दिशा दर्शवितो. समजा, हासदिश c आहे. अशा स्थितीत a व b यांचा फुली-गुणाकार किंवा सदिश – गुणाकार a x b असा दर्शवितात.

 

 

या गुणाकाराची व्याख्या अशी करतात: (१) a x b हा सदिश असून त्याची दिशा c ची दिशा आहे. c च्या दिशेतील एकक सदिश n आहे, असे समजू.

(२) a x b या सदिशाचे संख्यात्मक-मूल्य a . b sin q असे आहे.

म्हणून axb = |a| .| b| sinq.n दोन सदिशांच्या फुली-गुणाकाराविषयी खालील समीकरणे मांडता येतात.

 

 

 

 

 

 

 

जर a, b, c असे तीन सदिश दिलेले असतील, तर त्यापासून a व (b x c) असे दोन सदिश मिळतील. त्या सदिशांचे a . (b x c) व a x (b x c) असे अनुकमे बिंदु-गुणाकार व फुली-गुणाकार शक्य आहेत. पहिल्याला बिंदु-त्रिगुणाकार व दुसऱ्याला सदिश-त्रिगुणाकार अशी नावे आहेत. येथे हे लक्षात घेणे जरूरी आहे की, a . (b x c) व a x (b x c) यातील पहिली संख्या असून दुसरा सदिश आहे.

 

 

 

 

 

ही संख्या आहे. a, b, c हे सदिश जिच्या बाजू आहेत अशा चितीचे घनफळ ती संख्या दर्शविते.

सदिश-त्रिगुणाकाराबाबत खालील समीकरणे मांडता येतात.

a x (b x c) = (a . c) b — (a . b) c

(a x b) x c = (a . c) b — (b . c) a

कलन : (अ) Φ (x, y, z) हे संख्या-मूल्ये देणारे तीन चलांचे फलन आहे. याचे सदिश-अवकलन

 

 

 

 

 

 

 

 

 

हे सदिश-मूल्य असणारे अवकलन असून त्याला भ्रमिल-अवकलन असे नाव आहे.

त्रिमितीय अवकाशात S हा पृष्ठ आहे. या पृष्ठाचे छोटे तुकडे केले. या तुकडयंचे क्षेत्रफळ किंवा पृष्ठफळ dS आहे. n हा या तुकडयंना लंब असणारा एकक सदिश आहे असे मानू. दर तुकड्यागणिक n दिशा बदलत राहील. n. dS = ds याला dS शी संबंधित लंबपद असे म्हणतात.

f (x, y, z) = f₁(x, y, z) i + f ₂(x, y, z) j + f₃ (x, y, z) k हे सदिश फलन S वरील P (x, y, z) या बिंदूशी सदिश-मूल्य देते. f या फलनाचा S या पृष्ठावरील समाकल ∫_s ∫ f . ds असा दर्शविला जातो. या समाकलाचे मूल्य संख्यात्मक आहे.

पृष्ठाशी संबंधित अशाज्या पृष्ठ-समाकलाची वर व्याख्या दिली, त्याच्याशी संबंधित दोन महत्त्वाची प्रमेय आहेत : (१) समजा की, S हा बंद पृष्ठ असून तो R या घनाकाराचे आवरण आहे. f हे सदिश फलन R च्या (व S च्या) प्रत्येक बिंदूशी एक सदिश मूल्य देते. f चा S या पृष्ठावरील समाकल आणि Ñ. f या संख्यात्मक फलनाचा R या घनाकारावरील समाकल, हे सारखेच असतात म्हणजे

∫_s ∫ f . ds = ∫∫_R∫ (Ñ. f) d T. येथे T हे घनपद आहे.

(२) S हे एक बंद नसलेला पृष्ठ आहे. या पृष्ठाची कड G हा एक बंद वक आहे. f हे सदिश मूल्य देणारे फलन S या पृष्ठावरील (व G या वकावरील) प्रत्येक बिंदूशी व्याख्यात आहे.

f या फलनाचा G या वकावरील समाकल व с X f या फलनाचा S या पृष्ठावरील समाकल यांचे संख्यात्मक मूल्य एकच असते.

∫_r f . dr = ∫_s ∫(сf). ds

येथे r हा G वरील बिंदू दर्शविणारा सदिश आहे. या प्रमेयाला सर जॉर्ज गेबिएल स्टोक्स यांचे प्रमेय असे म्हणतात.

पहा : प्रदिश; सदिश अवकाश.

भावे, श्री. मा.