शून्य : गणितामध्ये शून्य ही संकल्पना एक संख्या म्हणून आणि एखाद्या चलाचे मूल्य म्हणून अशा दोन प्रकारे वापरण्यात येते. संख्या दर्शविण्याकरिता प्रथमपासून प्रतीकात्मक चिन्हे वापरात आलेली असावीत परंतु संख्या एकसारख्या वाढत असल्याकारणाने त्या दर्शविण्याकरिता चिन्हांची संख्या वाढत जाऊ लागली व त्यामुळे मोठमोठ्या संख्या दर्शविणे कठीण जाऊ लागले. मध्ययुगात रोमन लोक २,११२ ही संख्या MMCXII अशी लिहीत असत किंवा ६३९ ही संख्या VIXXXIX अशी लिहीत असत. लिहिण्याची ही अडचण अंकाला दिलेल्या स्थानमूल्यामुळे व शून्याच्या शोधामुळे दूर झाली. द्विमान, त्रिमान, पंचमान, दशमान किंवा विंशतिमान इत्यादी कोणत्याही मानात संख्या दर्शविणे शून्याच्या शोधामुळे सुलभ झाले आहे. [→ अंक संख्या].
हिंदू दशमान पद्धतीत पहिले नऊ अंक झाल्यावर दहा दर्शविण्यास एकावर शून्य ठेवतात आणि पुढील संख्या एकावर एक, एकावर दोन,···· इत्यादी पद्धतीने दर्शवितात. संख्या मांडताना तिच्यातील अंकाच्या स्थानावरून तिची किंमत ठरविली जाऊ लागल्यामुळे संख्या कितीही मोठी असली, तरी ती लिहिण्यास अडचण पडेनाशी झाली. ही दशमान पद्धती प्रथम अरब लोक हिंदूंकडून शिकले. नंतर या पद्धतीचा अरबांमार्फत यूरोपात प्रसार झाला. ⇨ लेओनार्दो फीबोनात्वी यांनी Liber Abaci (१२२८) या ग्रंथात हिंदू पद्धतीने संख्या कशा वाचाव्यात याचे वर्णन केलेले आहे.
शून्य ही भारतीयांनी जगाला दिलेली गणितशास्त्रातील सर्वांत महत्त्वाची देणगी आहे. शून्याविषयीचा सर्वांत जुना उल्लेख पिंगल यांच्या छंदःसूत्रात आढळतो. हा ग्रंथ वि. का. राजवाडे यांच्या मते इ.स. पू. ९०० च्या आसपासचा, तर आर्थर बेरिडेल कीथ या पाश्चात्त्य पंडितांच्या मते इ.स. पू. २०० च्या आसपासचा असावा. या छंदःशास्त्राच्या आठव्या अध्यायातील २८ ते ३१ ही सूत्रे या शोधाच्या दृष्टीने महत्त्वाची आहेत [द्विरर्द्धे ॥ रूपे शून्यम ॥ द्विःशून्ये ॥ तावदर्ध्दे तदगुणितम ॥].
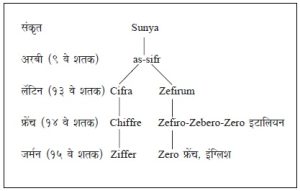शून्याच्या प्रतीकात्मक चिन्हाचा सर्वांत जुना संदर्भ ग्वाल्हेरजवळील एका मंदिरामधील भिंतीवर आढळतो. हा लेख इ. स. ८७० मधील असावा. तो ब्राह्मी लिपीमध्ये आहे. त्यामध्ये मंदिराकरिता दिलेल्या दानाची यादी आहे. त्यात फुलबागेकरिता २७० हात लांब व १८७ हात रुंद अशी जागा नोंदलेली आहे. २७० या संख्येपैकी ० हे छोट्या टिंबाने (.) दर्शविले आहे. त्यातच पुढे माळी देवाला ५० फुलांचे गुच्छ नियमितपणे अर्पण करणार असल्याचे वचन आहे. संस्कृतमध्ये शून्याचा अर्थ रिक्त असा आहे. नवव्या शतकात अरबांचा शून्याशी परिचय झाल्यावर त्यांनी शून्याचे अरबी भाषेतील भाषांतर असिफर या शब्दाने केले. तोच शब्द पुढे कसा बदलत गेला हे पुढील आकृतीवरून दिसून येईल.
चीनमध्ये तेराव्या शतकात प्रथमच शून्याचा वापर लेखनामध्ये केलेला आढळतो. ‘गुबार’ या पश्चिम अरबी अंकलेखन पद्धतीत अंक लिखाणात शून्याची गरज भासत नव्हती. अंकाच्या डोक्यावर टिंबे देऊन त्याचे स्थान दर्शविण्यात येत होते. जसे 
दशम स्थानामरिता एक टिंब, शतकाकरिता दोन टिंबे वगैरे.
शून्याकरिता वापरलेले ० हे चिन्ह ⇨ टॉलेमी या ज्योतिर्विदांना माहीत होते, असा काही शास्त्रज्ञांचा तर्क आहे. ० हे ouden (काही नाही) या ग्रीक शब्दातील पहिले अक्षर असल्यामुळे त्यांनी वरील तर्क मांडला आहे. काही शास्त्रज्ञांच्या मते ० या वर्तुळाच्या आतील भाग रिकामा असल्यामुळे त्याचा वापर शून्याकरिता झाला असावा.
शून्याचा प्रवेश पाश्चिमात्य देशांमध्ये झाला, तेव्हा त्याने त्या लोकांना गोंधळात टाकले. तत्पूर्वी ते लोक ⇨ गोटीचौकटीचा वापर करीत होते. शून्य म्हणजे काहीच नाही असे असेल, तर ते काहीच असू नये परंतु ते काही वेळा काहीच नसते, तर काही वेळा ते काही तरी असते. जसे ३ + ० = ३, ३ – ० = ३ येथे शून्य म्हणजे काहीच नाही परंतु ३० = ३ x १० येथे शून्य म्हणजे काही तरी आहे. यामुळे पाश्चिमात्य लोक गोंधळात पडले. त्या वेळच्या एका फ्रेंच लेखकाने ‘शून्य म्हणजे काही नाही, एक गोंधळ करणारे व अडचणी उत्पन्न करणारे चिन्ह आहे’, असे म्हटले आहे. त्या वेळची पाश्चिमात्यांमधील शून्याबद्दलची प्रतिक्रिया दोन प्रकारची होती. एक म्हणजे शून्य ही सैतानाने उत्पन्न केलेली गोष्ट. दुसरी शून्य ही एक टिंगल करण्याची गोष्ट. पंधराव्या शतकातील एका सुशिक्षित फ्रेंच माणसाने पुढीलप्रमाणे लिहिले आहे : ‘ज्याप्रमाणे गाढवाला सिंह बनावयाचे होते किंवा माकडाला राणी व्हावयाचे होते, तद्वत शून्याने अंकाचा आव आणला’ .
शून्याकरिता इसवी सनानंतर वापरण्यात आलेले शब्द म्हणजे ख, अवकाश इत्यादी. सहाव्या शतकात ब्रह्मगुप्त यांनी शून्याविषयीची कल्पना संपूर्णपणे व्याख्यित केलेली आहे : क + ० = क; क X ० = ० येथे क ही कोणतीही संख्या (पूर्णांक) आहे. क/० + ख = क/० येथे क/० ही नवीन प्रकारची अशी संख्या आहे की, तीमध्ये योग (बेरीज) किंवा वियोग (वजाबाकी) क्रियेने काही फरक पडत नाही. आधुनिक गणितात 
हे अर्थहीन चिन्ह मानतात, म्हणजेच शून्याने भागता येत नाही असे मानतात. क ही शून्याव्यतिरिक्त कोणतीही संख्या असेल, तर क० = १ व ०/क = ० असते. मुळात चिन्ह म्हणून आलेले ० नंतर एक नैसर्गिक संख्या व सम संख्या म्हणून गणले जाऊ लागले, परंतु रुलेट सारख्या जुगारी खेळात ‘०’ ही विषम व ‘००’ ही सम संख्या धरतात.
शून्याविषयी आधुनिक गणितात दुसरा संदर्भ फलनाच्या विचारामध्ये येतो. फलन शून्य असते त्यावेळचे चल पदाचे मूल्य म्हणजे फलनाचे मूल्य शून्य. उदा., न घातीय बहुपदीला न मुळे असतात, म्हणजेच न शून्ये असतात असे म्हटले जाते. बेसेल फलनाची शून्ये म्हणजे जेथे त्याचा आलेख क्ष अक्षाला छेदितो, त्या ठिकाणचे क्ष चे मूल्य.
मापक्रमामध्ये (मोजपट्टीमध्ये) शून्य हा अंक आरंभबिंदू किंवा तटस्थ स्थान दर्शवितो. धन संख्या शून्याच्या उजव्या किंवा वरील बाजूला आणि ऋण संख्या शून्याच्या डाव्या किंवा खालील बाजूला दाखवितात परंतु काही मापक्रमांमध्ये शून्य स्वेच्छपणे मांडलेला असतो. उदा., सेल्सिअस तापमापकामध्ये पाण्याचा गोठणबिंदू दाखविणारे तापमान ०० से. असते.
गुर्जर, ल. वा.; ओक, स.ज.