विश्वस्थितिशास्त्र : (विश्वरचनाशास्त्र). संपूर्ण जड विश्वाचे संबद्ध शास्त्रीय वर्णन करणे हे विश्वस्थितिशास्त्राचे उद्दिष्ट होय. अब्जावधी तारे समाविष्ट करणारी ⇨ आकाशगंगा, ⇨ मॅगेलनी मेघ, ⇨ देवयानी अभ्रिका यांसारख्या लाखो ⇨ दीर्घिका (तारामंडळे)विश्वाचे मूल घटक आहेत, असे विसाव्या शतकारंभी माहीत झाले. या दीर्घिका विश्वाच्या सर्व भागांत सारख्याच दाटीने पसरलेल्या असून सर्व दिशांत त्यांचे वितरण एकसारखेच आढळते. विश्वातील आपली स्थिती कोणत्याही प्रकारे विशिष्ट आहे असे मानण्याचे कारण नसल्याने विश्वाचे वरील चित्र त्यातील कोणत्याही बिंदूवरून हुबेहुब तसेच दिसेल, असे मानले पाहिजे. म्हणजेच विश्व स्थलभेदातीत (समांग) व दिग्भेदातीत (समदिक्) आहे, या विधानास ‘वैश्विक तत्व’ असे म्हणतात. त्याप्रमाणे विश्वातील सरासरी द्रव्यघनता व कोनीय संवेग (वलन करणाऱ्या वस्तूचे निरूढी परिबल-म्हणजे कोनीय वेगाला होणाऱ्या विरोधाचे माप-गुणिले तिचा कोनीय वेग ही राशी) सर्वदूर एकसारखेच असले पाहिजेत. हे साधण्यासाठी संपूर्ण विश्व एक तर निर्गतिक म्हणजे स्थिर तरी असावे, किंवा गती असल्यास ती सर्व दिशांत एकसारखीच असावी. त्या अर्थी विश्वाचे अक्षीय भ्रमण होत नसून ते प्रसरण किंवा आकुंचन पावत असले पाहिजे. सर्वच दीर्विका आपल्यापासून दूर जात असून त्यांचा हा अपसरणाचा (दूरगमनाचा) वेग अंतराच्या समप्रमाणात वाढत जातो, असा शोध १९२९ च्या सुमारास ⇨ एडविन पॉवेल हबल यांनी लावला त्यावरून विश्वप्रसरण पावत आहे, हे सिद्ध होते. v ही दीर्घिकांची अपसरणाची गती व d हे त्याचे अंतर मानल्यास v = Hd हा हृबल नियम मिळतो. यात H ला हबल स्थिरांक म्हणतात. या विश्वप्रसरणाच्या शोधापासून आधुनिक विश्वस्थितिशास्त्राची सुरूवात झाली आणि भौतिकीच्या नियमांनुसार विश्वाच्या सद्य:स्थितीचे वर्णन, पूर्वस्थितीचा अंदाज व भविष्यकाळातील उत्क्रांतीची दिशा जाणून घेण्याचे वैज्ञानिक प्रयत्न सुरू झाले.
ओल्बर्स विरोधाभास :⇨ हाइन्रिक व्हिल्हेल्म (माथेउस) ओल्बर्स यांच्या नावावरून हे नाव पडले आहे. विश्वाची सरासरी द्रव्यघनता सर्वदूर सारखी असली, तरी विश्वातील द्रव्य ताऱ्यांत व दीर्घिकांमध्ये जास्त दाटीने सामावलेले असून आंतरदीर्घिकीय अवकाशात अत्यंत विरलतेने पसरले आहे, ही असमांगता लक्षात घेतली पाहिजे. दीर्घिका स्वत:प्रसरण पावत नसून केवळ त्यांच्या मधील अंतर वाढत आहे, या शोधामुळे ओल्बर्स विरोधाभास (यक्ष प्रश्न) या नावाने ओळखल्या जाणाऱ्या एक जुन्या समस्येचे समाधानकारक उत्तर मिळालेआहे.
अवकाशातील दीर्घिकांची संख्याघनता N मानल्यास r ते r + dr या अंतरावर असणाऱ्या दीर्घिकांची संख्या 4π r2 N dr एवढी होईल. सर्व दीर्घिका L या एकाच दीप्तीच्या आहेत, असे मानल्यास त्यांची r अंतरावरील भासमान (दृश्य) तेजस्विता L/r2 होते. तेव्हा वरील सर्व दीर्घिकांची भासमान तेजस्विता 4π N L dr एवढी होईल. दीर्घिका शून्य ते अनंत अंतरापर्यंत पसरल्या आहेत, असे मानल्यास
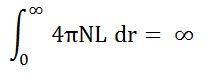 |
या समीकरणाप्रमाणे [⟶ अवकलन व समाकलन ] संपूर्ण आकाश अनंत तेजाने उजळून निघाले पाहिजे. वस्तुस्थिती अशी नाही हे अंधाऱ्या रात्री स्पष्टच दिसते. परंतु एक गोष्ट लक्षात घेण्यास आपण विसरतो. दीर्घिका एकमेकींना झाकत असल्याने कोणत्याही दिशेत सर्वांत जवळचीच दीर्घिका काय ती आपल्याला दिसेल. तरीही विश्व अनंत असल्यास प्रत्येक दृष्टिरेषा कोणत्या ना कोणत्या दीर्घिकेपर्यंत पोहोचेलच. तेव्हा सर्व आकाश अनंत नाही, तरी पण एकाच विशिष्ट सात दीप्तीचे दिसले पाहिजे, परंतु वस्तुत: आकाश काळे किंवा तेजोहीन असून काही दिशांतच दीर्घिका दिसतात. असे का ? हाच ओल्बर्स विरोधाभास होय. त्याचे उत्तर हे की, विश्वप्रसरण पावत असल्याने दूरस्थित दीर्घिकांचा प्रकाश ⇨ डॉप्लर परिणामाने अधिक तरंगलावीचा म्हणजेच कमी ऊर्जेचा दिसतो. त्यामुळे अतिदूरच्या दीर्घिकांची तेजस्विता आपल्याला व्यस्त वर्ग नियमापेक्षा अधिक मंद दिसेल आणि एका विशिष्ट अंतरापलीकडच्या दीर्घिका त्यांचा वेग प्रकाशवेगापेक्षा अधिक झाल्याने आपल्याला दिसणार नाहीत. अशा रीतीने विश्वाला सांत परिसीमा पडल्याने आकाशाचा काळोख समजून येतो व ओल्बर्स विरोधाभासाचे निराकरण होते.
न्यूटनप्रणित विश्वस्थितिशास्त्र : द्रव्यघन दीर्घिका व अतिविरल आंतरदीर्घिकीय अवकाश अशी विश्वाची रचना असली, तरी विश्वस्थितिशास्त्र विश्वाची सरासरी द्रव्यघनता (ρ) सर्वदूर सारखीच मानतात. विश्वप्रसरणामुळे ती सतत कमी होत जाते. तिचे वर्तमान मूल्य ρ0 मानू. तसेच कोणत्याही दीर्घिकेचे स्थान rR(t) मानू. येथे r हा दीर्घिकेचा एक स्थिर अंतरदर्शक प्रचल (अंतर-निर्देशांक) असून R(t) ही कालाबरोबर वाढणारी त्याची गुणक राशी होय, तिचे वर्तमान मूल्य R0 समजू. मग न्यूटनप्रणित गुरूत्वाकर्षण सिद्धांताप्रमाणे पुढील समीकरण मिळते :
यात G हा न्यूटनप्रणित गुरूत्वाकर्षण स्थिरांक आहे. समीकरण (१) वर समाकलन क्रिया [⟶ अवकलन व समाकलन ] केल्यास पुढील समीकरण मिळते.
त्यातील समाकलन स्थिरांक ‘-k’ म्हणजे विश्वातील द्रव्याची ऊर्जाघनमा होय आणि तिच्या मूल्यावरच विश्वस्थितीचे वर्णन अवलंबून असते. k च्या मूल्याप्रमाणे आ. १मध्ये दाखविलेल्या विश्वाच्या तीन प्रमुख प्रतिकृती मिळतात :
(१) k > 0, म्हणजे ऊर्जाघनता ॠण असल्यास सांत विवृत्तीय (दीर्घवर्तुळाकार) व स्पंदमान विश्वप्रतिकृती मिळते आणि
(२) k = 0 असल्यास अनंत अन्वस्तीय [⟶ अन्वस्त ] व
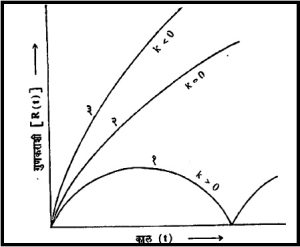
(३) k < 0. म्हणजे ऊर्जाघनता धन असल्यास अनंत अपास्ताकार [⟶ अपास्त ] या दोन प्रसरण पावणाऱ्या विश्वप्रतिकृती मिळतात परंतु अनंत विश्वाचे तर्कशुद्ध विवेचन करण्याच्या कामी न्यूटनप्रणित विश्वस्थितिशास्त्र अपुरे पडते, कारण तत्काल प्रभाव पाडणारे न्यूटनीय गुरूत्वाकर्षण अतिदूरच्या द्रव्याच्या बाबतीत त्याच्या अधिक द्रव्यमानामुळे जवळच्या द्रव्याइतकेच प्रभावी ठरते आणि ओल्बर्स विरोधाभास दीप्तीचे होते. तसेच अनंत विश्वाचे गुरूत्वाकर्षणही आइन्स्टाइनप्रणित व्यापक सापेक्षता सिद्धांताचा उपयोग करावा लागतो. [⟶ सापेक्षता सिद्धांत ]
सापेक्षतावादी विश्वस्थितिशास्त्र : आइन्स्टाइनप्रणित व्यापक सापेक्षता सिद्धांतात नेहमीचा त्रिमितीय अवकाश व काल मिळून झालेला चतुर्मितीय बृहदावकाश (दिक्काल-संबंधता) रीमानीयभूमितीस [⟶ भूमिति ] धरून असतो. त्यात ds अंतर हे पुढील रॉबर्टसन-वॉकर मेट्रिकच्या (मानीयाच्या) साहाय्याने मिळते.
येथे c हा प्रकाशवेग, r, θ, Ø हे त्रिमिति-स्थलनिर्देशांक व k ही त्रिमितीय अवकाशाची वक्रता दाखिविणारी त्रिज्या होय. k चे मूल्य केवळ 0, + 1 किंवा -1 असू शकते. येथील k व न्यूटनप्रणित विश्वस्थितिशास्त्रातील k मधील फरक लक्षात घ्यावा लागतो. येथे k = + 1 असल्यास अवकाश सात विवृत्तीय, k = 0 असल्यास अनंत यूक्लिडीयन [ किंवा सपाट ], k = -1 असल्यास अनंत अपास्ताकार आहे, असे समजावे. खरे विश्व कोणत्या प्रकारचे आहे हे जाणून घेण्यासाठी विश्वप्रसरणाचा प्रतिप्रवेग मोजणे आवश्यक असते. त्याचा स्थिरांक q काढण्यासाठी प्रथम
हा डबल स्थिरांक मोजून नंतर
हे समीकरण वापरतात.
आता गुणक राशी R(t) ठरविणारी पुढील दोन सापेक्षतावादी समीकरणे आहेत.
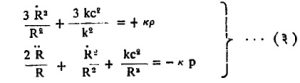 |
येथे k = १·८६ x १०-२७ सीजीएस (सेंटिमीटर, ग्रॅम, सेकंद) एकक हा आइन्स्टाइनप्रणित गुरूत्वाकर्षण स्थिरांक आणि p हा द्रव्य व प्रारण (तरंगरूपी ऊर्जा) यांचा संयुक्त सरासरी विश्वदाब आहे. यांतील पहिले समीकरण न्यूटनप्रणित विश्वस्थितिशास्त्रासारखेच असून k च्या मूल्याप्रमाणे त्यापासून पूर्वीच्याच तीन विश्वप्रतिकृती मिळतात. त्या म्हणजे : (१) k = + 1, सांत विवृत्तीय स्पंदमान विश्व (२) k = 0, अनंत यूक्लिडीयन प्रसरणशील विश्व व (३) k = -1, अनंत अपास्ताकार प्रसरणशील विश्व.
वर्तमान काळी विश्वदाब p जवळजवळ शून्य असल्याने दुसरे समीकरण
असे होते. त्याला Ṙ ने गुणून समाकलन केल्यास Ṙ2 = (A/R)-kc2हे समीकरण मिळते. त्यात A = κρR3/3 घातल्यास आपल्याला पुन्हा पहिले समीकरण मिळते व त्याचे उत्तर म्हणून वरील तीन विश्व प्रतिकृती मिळतात. शिवाय q=(1/2)*[1+(kc2/H2R02)निघत असल्याने
| ( १ ) स्पंदमान विश्वात q >(1/2), | ρ0>3H02/κ ; | |
| ( २ ) यूक्लिडीयन विश्वात q = (1/2), | ρ0=3H02/κ ; आणि | |
| ( ३ ) अपास्ताकार विश्वात 0<q < (1/2), | ρ0 < 3H02/κ |
याप्रमाणे वर्तमान द्रव्यघनता ρ0 व q यांची मूल्ये येतात.
वरील सर्व विश्वप्रतिकृतींत वर्तमान काळी विश्व प्रसरण पावत आहे. हे प्रसरण परतविल्यास पूर्वी एका कालक्षणी विश्वातील सर्व द्रव्य एका बिंदुरूप जागेत अत्यंत दाटीने केंद्रित झाले होते, असा निष्कर्ष निघतो.त्या वेळच्या एकमेवाद्वितीय स्थितीत एक महास्फोट (बिग बँग) हाऊन विश्वप्रसारणास सुरूवात झाली असे दिसते. म्हणून या विश्वप्रतिकृतींना उत्स्फोटित प्रतिकृती म्हणता येईल. (विश्वाची उत्पत्ती आणि उत्क्रांती यांविषयीच्या महास्फोट उपपत्तीनुसार सु.२ x १०१०वर्षापूर्वी विश्वतील सर्व द्रव्य हे बिंदुरूप जागेत केंद्रित होऊन अतिउच्च घनतेचा व तापमानाचा पिंड होता आणि त्याचा स्फोट होऊन सर्व दिशांत द्रव्य पाठविले गेले व यातून प्रसरणशील विश्वाचा जन्म झाला).
काही विशिष्ट विश्वप्रतिकृती : आइन्स्टाइनप्रणित स्थिर विश्व : (ॲल्बर्ट आइन्स्टाइन यांच्यावरून पडलेले नाव). विश्वप्रसरणाचा शोध लागण्यापूर्वी विश्वस्थिर व सांत मानीत. अशी विश्वप्रतिकृती मिळविण्यासाठी (१ते ३) ही समीकरणेअपुरी पडतात. म्हणून आइन्स्टाइन यांनी गुरूत्वाकर्षणाला विरोध करणारी म्हणजेच द्रव्यरूप पदार्थांना एकमेकांपासून दूर सारणारी एक राशी (A) घालून
R2= (A/R)-kc2+(1/3)λR3………… (४)
हे समीकरण मिळविले. त्यातील λ ला वैश्विक स्थिरांक असे नाव आहे.
λ = λc =(4k3c6)/(ρA2) घेतल्यास R = Rc=3A/2kc2 अशी विश्वाची स्थिर त्रिज्या मिळते. या विश्वप्रतिकृतीस आइन्स्टाइनप्रणित स्थिर विश्व म्हणतात.
लमेअत्रप्रणित विश्वप्रतिकृती : (झॉर्झ-आंरी लमेअत्र यांच्या नावावरून पडलेले नाव). λ > λc विश्व प्रथम R ∝ t ⅔ याप्रमाणे हळू प्रसरण पावते व नंतर प्रसरणवेग कमी होऊन R = Rm = (3A/2λ)1/3 झाल्यावर पुन्हा R ∝ exp[ t√( λ/3)] याप्रमाणे जोरात प्रसरण पावते. याला लमेअत्रप्रणित विश्वप्रतिकृति म्हणतात. विश्वप्रसरणाचा शोध लागल्यावर साहजिकच त्याला महत्त्व प्राप्त झाले.
एडिंग्टन-लमेअत्र विश्वप्रतिकृती : λ = λc असल्यावर सुद्धा आणखी दोन पर्यायी विश्वप्रतिकृती मिळतात, असे ⇨सर आर्थर स्टॅन्ली एडिंग्टन यांना दिसून आले. एकात विश्व प्रथम R ∝ t⅔ याप्रमाणे प्रसरण पावून महत्कालानंतर R = Rc या त्रिज्येवर स्थिर होते. दुसऱ्यात R = Rc या स्थिर स्थितीतून विश्व R ∝ exp[ t√( λ/3)] याप्रमाणे जोरात प्रसरण पावू शकते. आइन्स्टाइनप्रणित स्थिर विश्वात दीर्घिका उत्पन्न झाल्यावर अशा प्रकारे विश्व प्रसरण पावू लागले, असे एडिंग्टन व लमेअत्र यांनी सुचविले. म्हणून त्याला एडिंग्टन-लमेअत्र विश्वप्रतिकृती म्हणतात.
डी-सिटरप्रणित पोकळ विश्व : λ >0, k = 0, (Ṙ/R) हा एक स्थिरांक घेऊन व्हिलेम डी-सिटर यांनी ρ = p = 0, R (t) ∝ exp[ t√( λ/3)] या गुणांची एक प्रसरणशील विश्वप्रतिकृती मिळविली, परंतु हिच्यात द्रव्यघनता शून्य असल्याने वास्तविक विश्वाची तिचा संबंध नाही, हे स्पष्ट दिसते.
स्पंदमान विश्व : λ < 0 किंवा λ = 0 व k = + 1 असल्यास विश्वाची त्रिज्या एका विशिष्ट मर्यादेपेक्षा अधिक होत नाही. म्हणून विश्वाचे प्रसरण हळूहळू कमी होऊन त्रिज्येची ऊर्ग्व (वरची) सीमा गाठल्यावर विश्व आकुंचन पावू लागते. अशा रीतीने एकापाठोपाठ प्रसरण व आकुंचन पावणारी स्पंदमान विश्वप्रतिकृती मिळते. हिच्याम विश्वाची सरासरी घनता इतकी असते की, गुरूत्वाकर्षण प्रसरणावर मात करून विश्वाचे प्रसरण थांबवते व त्याच्या आकुंचनास सुरूवात होते आणि अतिघन एकमेवाद्वितीय अवस्था प्राप्त झाल्यावर पुन्हा प्रसरणास सुरुवात होते.
निरंतर स्थितीचा सिद्धांत व तद्नुरूप् विश्वप्रतिकृती : पाख तत्वाप्रमाणे पदार्थांची निरूढी (जडत्व) इ. गुणधर्म संपूर्ण विश्वाच्या घडणी वर अवलंबून असले पाहिजेत. त्याअर्थी G, c यांसारखे स्थिरांक विश्वस्थितीच्या अनुसार बदलू शकतात. तसे असल्यास अतिप्राचीन काळच्या स्थितीची माहिती मिळविण्यासाठी त्यांची वर्तमान मूल्य स्थिर धरून चालणार नाही आणि ती कशी बदलतात ते माहिती नसल्याने विश्वस्थितीची पूर्वकल्पना करणेच कठीण होईल. म्हणून विश्वाचे मानचित्र (नकाशा) सर्व बिंदूवरूनच नव्हे तर सर्व कालक्षणीही एकसारखे असले पाहिजे असे वाटते. या विधानास परिपूर्ण वैश्विक तत्व म्हणतात. ते मानल्यास (Ṙ/R) = H = एक स्थिरांक R = eHt व k = 0 या गोष्टी क्रमप्राप्त होतात. ही प्रतिकृती डी-सिटरप्रणित अन्वस्तीय विश्वप्रतिकृतीसारखी दिसते, परंतु तिच्यातील द्रव्यघनता अशून्य पण स्थिर व संपूर्ण विश्व अनाद्यनंत असते. आता विश्व प्रसरण पावून विरल होत जाईल तेव्हा द्रव्यघनता स्थिर ठेवण्यासाठी नवे द्रव्य सातत्याने उत्पन्न होऊन ती पोकळी भरून निघाली पाहिजे. त्यासाठी विश्वात दर घ. सेंमी. मध्ये दर सेकंदास ३ x १०-४३ग्रॅ. नवे द्रव्य म्हणजे दर लिटरमध्ये दर एक लाख वर्षात एक हायड्रोजन अणू नव्याने उत्पन्न झाला पाहिजे. ही अत्यल्प उत्पती प्रयोगशाळेत तपासून पाहणे शक्य नसल्याने द्रव्याची अखंड उत्पत्ती अशक्य आहे, असे म्हणता येत नाही. परंतु एच्. बॉंडी व टी. गोल्ड यांनी मांडलेल्या या निरंतर स्थितीच्या सिद्धांताप्रमाणे q चे मूल्य – 1 असावे, ते तसे आहे का हे मात्र दूरस्थित स्वस्थ ज्योतींच्या अवलोकनांवरून (निरीक्षणांवरून) ठरविता येईल.

बॉंडी व गोल्ड यांच्या निरंतर स्थितीच्या सिद्धांतास गणिती बैठक देण्यासाठी व द्रव्यनिर्मितीच्या क्रियेसंबंधीचे ज्ञान मिळविण्यासा ⇨फ्रेड हॉईल यांनी आइन्स्टाइनप्रणित सापेक्षता समीकरणात एक उत्पत्तिक्षेत्रराशी C घातली व ⇨जयंत विष्णू नारळीकर यांच्या साहाय्याने त्या नव्या समीकरणाचा सखोल अभ्यास केला. त्यावरून अगोदर द्रव्याने भरलेल्या स्थानीच नवे द्रव्य उत्पन्न होते व C क्षेत्रामुळे ते आपोआप प्रसरण पावू लागले, असा निष्कर्ष निघतो. अतिदीप्तिमान रेडिओ-दीर्घिका व कासार ज्योती हे द्रव्यनिर्मितीचे स्त्रोत असावेत. असे त्यांचे म्हणणे आहे.
या सर्व विश्वप्रतिकृती आ. २मध्ये दाखविल्या आहेत.
विश्वस्थितीसंबंधीचे निरीक्षणात्मक पुरावे : प्रत्यक्ष अवलोकनानक विश्वस्थितीचा अंदाज कसा लावता येईल ते पुढे दिले आहे.
अपसरणाचा वेग व भासमान प्रत यांचा संबंध : प्रारणाच्या λ या तरंगलांबीत अपसरणामुळे जी Δλ वृद्धी होते, ती Z = (Δλ/λ) या राशीने दाखविल्यास हबल नियमानुसार d = (cZ/H) हे अंतर मिळते. यूक्लिडीयन विश्वात भासमान दृश्य दीप्ती lv व्यस्त वर्ग नियमाप्रमाणे बदलते. म्हणून lv ∝ µ (I/Z2) असणार. आता lvच्या लॉगरिथमला – २·५ ने गुणून भासमान दृश्य प्रत mv मिळते म्हणून mv = स्थिरांक + y log Z असे समीकरण येते, परंतु प्रसरणामुळे प्रकाशकणांची (फोटॉनांची) ऊर्जा कमी होते व mv वाढते. ह्या अंतराबरोबर वाढणाऱ्या राशीचे मूल्य Kv (Z) घेतल्यास अंगभूत वा निरपेक्ष प्रत Mv च्या व्याख्येप्रमाणे mv = Mv – y + Kv + y log (cZ/H) असे समीकरण मिळते. इतर विश्वप्रतिकृतींत विश्वप्रसरणचा प्रतिप्रवेग लक्षात घ्यावा लागत असल्याने
mc = mv – Kv = Mv -y + y log (cZ/H) + 1.086 (1-q) Z हे समीकरण वापरले पाहिजे. त्याच्या साहाय्याने mc व log (cZ) यांच्यामधील आलेखावरून q चे मूल्य निश्चित करता येते. अर्थात त्यापूर्वी जवळच्या दीर्घिकांच्या अवलोकनाने H चे मूल्य निश्चित केले पाहिजे. आधुनिक वेधांवरून H = ७५किमी. प्रति-सेंकद प्रति-दक्षलक्ष पार्सेक हा आकडा मिळाला आहे (१ पार्सेक = ३·२५८प्रकाशवर्षे = ३·०८५७२ x १०१३किमी.). त्याचा उपयोग केल्यास छायाचित्रण पट्टीवर दिसणाऱ्या दूरतम दीर्घिकांच्या भासमान प्रतीवरून q = + 1 च्या आसपास असल्याचे दिसते. तेव्हा विश्व स्पंदमान असावे असा निष्कर्ष निघतो आणि विश्वाचे वय ६अब्ज वर्षे व सरासरी द्रव्यघनता २ x १०–२९ग्रॅ./घ. सेमी. येते परंतु तारकीय उत्क्रांतीवरून विश्वाचे वय १०अब्ज वर्षे आणि दीर्घिकांच्या गणनेवरून सरासरी द्रव्यघनता ३ x १०–३१ते १ x १०–३०ग्रॅ./घ. सेमी. निघते. सिद्धांत व अवलोकन (प्रत्यक्ष वेध) यांत मेळ घालावयाचा असल्यास दीर्घिकांची अंगभूत दीप्ती व प्रत Mv कालाबरोबर बदलते, असे मानावे लागते. दीर्घिकांपेक्षा जवळजवळ १००पटींनी अधिक तेजस्वी असलेल्या व म्हणून अतिदूर अंतरापर्यंत दिसणाऱ्या कासार ज्योतींच्या अपसरण वेगांचे अवलोकन करून या प्रश्नाचे उत्तर मिळविण्याचा प्रयत्न झाला आहे, परंतु त्यावरून एवढीच निष्पती झाली की, या ज्योतींची अंगभूत दीप्ती एकसारखी नाही व त्यांची Z – मूल्ये ३पेक्षा कमी आढळतात. कासार ज्योतींच्या भौतिक गुणधर्मांबद्दल अधिक माहिती मिळाल्याशिवाय याची कारणे काय ते समजणार नाही.
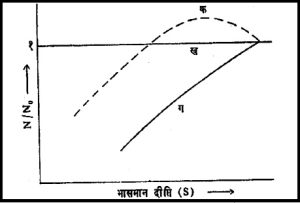
ज्योतींची गणना : यूक्लिडीयन स्थिर विश्वात कोणत्याही प्रकारच्या ज्योतींची (उद्गमांची) संख्याघनता व त्याची दीप्ती या गोष्टी सर्वदुर सारख्या आहेत, असे मानल्यास त्यांची एकंदर संख्या N0 ∝ d3 प्रमाणे वाढेल. त्यांची भासमान दीप्ती S ∝ d-2 याप्रमाणे कमी होईल. म्हणजेच S पेक्षा अधिक तेजस्वी दिसणाऱ्या ज्योतींची संख्या No (S) ∝ S–3/2 याप्रमाणे बदलली पाहिजे. उदा., S ची निम्न सीमा चौपट कमी केल्यास No(S) आठ पटींनी वाढेल. प्रसरणशील पण उत्क्रांतिविरहित विश्वात S व्यस्त वर्ग नियमापेक्षा अधिक त्वरेने कमी होत असल्याने ज्योतींची संख्या N(S) वर निर्देशिलेल्या S–3/2 या नियामापेक्षा कमी राहील. दुसऱ्या शब्दांत N (S) / No (S) ही राशी स्थिर विश्वात एकाबरोबर असेल, तर प्रसरणशील विश्वात ती S बरोबर कमी होत जाईल. (आ. ३).
दीर्घिकांचा प्रकाश आकांशगंगेतील धूलिमेघांत शोषला जातो म्हणून त्यांच्या बाबतीत वरील पडताळा पाहता येत नाही. रेडिओ उद्गमांची रेडिओ ऊर्जा मात्र धूलिमेघांतून आरपार जाते. त्यामुळे आकाशातील सर्व भागांत रेडिओ उद्गमांचे वितरण एकसारखे म्हणजे दिग्भेदातीत किंवा समदिक् आढळते. त्यांच्या गणनेवरून मिळालेली (N/No) हीराशी आ. ३मध्ये तुटक रेषेने दाखविली आहे. मोठ्या तेजस्वितेच्या ज्योतींची संख्या त्यात अपेक्षित संख्येपेक्षा जास्त आढळते. त्यावरून असा निष्कर्ष निघतो की, रेडिओ उद्गमांची संख्या किंवा त्यांची तेजस्विता किंवा दोन्ही गोष्टी पूर्वीच्या काळी अधिक असाव्यात, म्हणजे
भासमान दीप्ति (S) – विश्वाची उत्क्रांती होत आहे असे म्हटले पाहिजे. ही उत्क्रांती Z = ३ या अंतरावर म्हणजे विश्वोत्पत्तीनंतर १अब्ज वर्षांनी सुरू झाली असावी, असे क्कासार ज्योतींच्या अपसरण वेगांवरून दिसते. कदाचित त्याच वेळी दीर्घिका उत्पन्न झाल्या असाव्यात, असा तर्क आहे.
तेजस्विता-आकारमान परीक्षा : यात एखाद्या निवडक प्रतिकृतीतील रेडिओ किंवा प्रकाश उद्गम ज्या अधिकतम अंतरापर्यंत दिसू शकतात, त्या मानाने वस्तुत: ते किती जवळ आहेत, याचा अंदाज घेतात. उद्गमांची संख्याघनता सर्वदूर सारखी असेल, तर त्यांपैकी कोणत्याही उद्गमाचे सरासरी अंतर त्याच्या दूरतम अवलोकनक्षम (निरीक्षण) अंतराच्या ०·८असले पाहिजे. परीक्षणाने ते ०·९इतके आहे असे दिसते. यावरून उद्गमांची संख्याघनता दूर अंतरावर म्हणजे भूतकाळात वर्तमानकाळापेक्षा जास्त होती, असा निष्कर्ष निघतो. ही संख्याघनता (1 + Z)6 याप्रमाणे वाढताना दिसते आणि q = + 1 घेतल्यास त्यांची उत्क्रांती विश्वोत्पत्तीनंतर १अब्ज वर्षांनी सुरू झाली, असाच निष्कर्ष निघतो.
कोनीय व्यास-अपसरण वेग संबंध : यूक्लिडीयन विश्वात दीर्घिकांच्या रेडिओ उद्गमांचा किंवा दीर्घिका समूहांचा कोनीय व्यास अंतराच्या व्यस्त प्रमाणात कमी होत गेला पाहिजे. इतर विश्वप्रतिकृतींत तो सुरूवातीस Z वाढते तसा कमी होतो, पण विशिष्ट अंतरानंतर, म्हणजे विशिष्ट Z मूल्याच्या पुढे परत वाढू लागतो. तव्हा दूरच्या व जवळच्या उद्गमांचा कोनीय व्यास माजून विश्वस्थिती आजमावता येईल. दीर्घिकांच्या कोनीय व्यासांवरून q = +0·3 व रेडिओ उद्गमांच्या कोनीय व्यासांवरून त्यांची संख्याघनता (1 + Z)3 याप्रमाणे वाढते असे आढळते. कोनीय व्यास मोजण्यात बरेच अडथळे येतात म्हणून या आकड्यांत निश्चितता कमी आहे, परंतु विश्व उत्क्रांतिशील आहे. एवढे मात्र त्यावरून दिसून येते.
वैश्विक पार्श्वप्रारण : अतिदूरच्या मंद व अस्पष्ट ज्योतींच्या वा उद्गमांच्या एकत्रित प्रारणास पार्श्वप्रारण म्हणतात. १मेगॅहरर्टसम्हणजे ३००मी. तरंगलांबीच्या रेडिओ तरंगापासून १०० MeV म्हणजे १०-६सेंमी. तरंगलांबीच्या गॅमा-किरणापर्यंत संपूर्ण विद्युत्चुंबकीय वर्णपटात पार्श्वप्रारणाचे अवलोकन झाले आहे. त्यातून आपल्या आकाशगंगचे प्रारण वजा केले म्हणजे इतर बाह्य दीर्घिकांचे व संपूर्ण विश्वाचे दिग्भेदातील किंवा समदिक् वैश्विक पार्श्वप्रारण मिळते. त्याच्या अभ्यासाने विश्वस्थितीचा अंदाज लावता येतो.
मीटर व सेंटिमीटर तरंगलांबीचे रेडिओ प्रारण तसेच प्रकाशीय पार्श्वप्रारण व दूरस्थित सर्वसाधारण दिर्घिकांचेच आहे, असे आढळते. पण १ ते १० मिमी. तरंगलांबीचे रेडिओ प्रारण मात्र अपेक्षेपेक्षा पुष्कळ अधिक आहे, असे आढळते. त्यात अत्यंत सूक्ष्मतम दिग्भेदाचा (असमदिकतेचा) अभाव असून त्याचे तापमान २.७ के. आहे. प्रारंभिक महास्फोट झाला त्या वेळचे अत्युष्ण तापमानाचे प्रारण विश्वाबरोबर प्रसरण पावून त्याचे गेल्या २० अब्ज वर्षांत या सु. ३ के. प्रारणात रूपांतर झाले, असे मानतात. या उर्वरित प्रारणाच्या शोधामुळे महास्फोट सिद्धांतास पुष्टी मिळाली आहे, कारण निरंतर स्थितीच्या सिद्धांतात अशा प्रारणास वाव नाही. यावरूनही विश्व उत्क्रांतीशील आहे, हेच सिद्ध होते.
क्ष-किरण व गॅमा-किरण यांच्या पार्श्वप्रारणाचे अवलोकन १९६० नंतर रॉकेटे, फुगे (बलून) व कृत्रिम उपग्रह यांच्या साहाय्याने झाले आहे. हे प्रारण आंतरदीर्घिकीय अवकाशातील द्रव्यात उत्पन्न झाले असल्यास त्यावरून आंतरदीर्घिकीय द्रव्याचे तापमान, घनता व पूर्वेतिहास यांची माहिती मिळते आणि ते जर प्रकाशवेगाइतक्या वेगवान इलेक्ट्रॉन व ३ के. प्रारण यांच्यातील प्रकीर्णनाने (विखुरले जाण्याच्या क्रियेमुळे याला इन्व्हर्स कॉम्पटन प्रकीर्णन म्हणतात) उत्पन्न झाले असेल, तर त्यावरून वेगवान इलेक्ट्रॉन बाहेर फेकणाऱ्या अतिदीप्त नवतारा, क्वासार इ. अतिदीप्तिमान ज्योतींबद्दल माहिती मिळेल. या दोन्ही गोष्टींचे ज्ञान विश्वस्थितिशास्त्राच्या दृष्टीने फार महत्त्वाचे ठरणार आहे.
इतर विश्वस्थिति-सिद्धांत : आइन्स्टाइनप्रणित व्यापक सापेक्षतेच्या समीकरणांवर न आधारलेले विश्वस्थिति-सिद्धांत खालीलप्रमाणे आहेत.
मिल्न यांचा शुद्धगतिकीय सापेक्षतेचा सिद्धांत : ⇨एडवर्ड आर्थर मिल्न यांनी प्रथम कालमापन व अंतरमापन यांबद्दल खोल विचार करून त्यांच्या मूलभूत मापनपद्धती निश्चित केल्या. उदा., आणवीय, गतिकीय व जीवशास्त्रीय घड्याळे भिन्न असू शकतात, असे त्यांना दिसून आले. विश्वस्थितिशास्त्रासाठी विश्वघटकांच्या अपसरण वेगावर आधारलेली व गतिकीय अशा दोन कालमापन पद्धती सोईस्कर वाटतात. त्यांच्या आधाराने आणि वैश्विक तत्त्वाचा उपयोग करून मिल्न यांना जी विश्वप्रतिकृती मिळाली तिच्यात अपसरण वेग हबल नियमाप्रमाणे अंतराच्या समप्रमाणात वाढतो, द्रव्यघनता काळ पुढे जातो तशी कमी होते, पण ती आदिबिंदूपासून विश्वाच्या सीमेकडे वाढत जाते व विश्वाची सीमा प्रकाशवेगाने पुढे पुढे सरकत जाते. मूळ गृहित विधानांपासून विश्वस्थितीबद्दल वरील निष्कर्ष काढले, एवढेच नव्हे तर त्याहीपुढे जाऊन, मिल्न यांनी न्यूटनप्रणित गुरूत्वाकर्षण सिद्धांत तर्कसंगतीने काढून दाखविला. तसेच प्रकाशकण, विद्युत् चुंबकीय क्षेत्र, आणवीय व अणुकेंद्रीय सिद्धांत इ. भौतिकी नियमही सिद्ध करण्याचा प्रयत्न केला. प्रयोगसिद्ध भौतिकी नियमांपासून विश्वस्थितिशास्त्राकडे जाण्याऐवजी विश्वस्थितिशास्त्रापासून भौतिकी नियम काढून दाखविण्याचा हा एकमेव प्रयत्न होय. त्यात पूर्ण यश मिळालेले नाही, तर पुढील कार्यासाठी बरेच मार्गदर्शन झाले आहे.
एडिंग्टनप्रणित विश्वस्थितिशास्त्र : इलेक्ट्रॉन व प्रोटॉन यांचे विद्युत्आकर्षण त्यांच्यामधील गुरूत्वाकर्षणापेक्षा ०.२ X १०४० पटींनी अधिक आहे, विश्वाची त्रिज्या इलेक्ट्रॉन त्रिज्येपेक्षा ४ X १०४० पटींनी मोठी आहे आणि संपूर्ण विश्वातील प्रोटॉन व न्यूट्रॉन यांची संख्या १०८०= (१०४०)२ इतकी आहे. येथे १०४० ही संख्या पुन्हा पुन्हा आढळते. तेव्हा संपूर्ण विश्वाचे गुणधर्म वआणवीय कणांचे गुणधर्म यांत काही तरी घनिष्ट संबंध असावा, असे वाटते. हे संबंध अंकगणितीय पद्धतीने प्रस्थापित करण्याचा एडिंग्टन यांनी प्रयत्न केला. त्यासाठी त्यांनी तरंग-प्रदिश कलनशास्त्र नावाचे नवे गणिती तंत्र विकसित केले. या पद्धतीने त्यांनी सूक्ष्म संरचना स्थिरांक (hc/2pe2), वैश्विक स्थिरांक l व हबल स्थिरांक H यांची मूल्ये केवळ गणिती तर्काने काढून दाखविली, परंतु एडिंग्टन यांची पद्धत क्लिष्ट व काहीशी कृत्रिम असल्याने शास्त्रज्ञांचा तिच्यावर विश्वास बसला नाही. शिवाय प्रयोगसिद्ध मूल्यांत सुधारणा होत गेली तसा तर्कसिद्ध व प्रयोगसिद्ध मूल्यांतही फरकही वाढला, त्यामुळे एडिंग्टन पद्धती म्हणजे एक केवळ गणिती कसरत वाटते.
डिरॅक सिद्धांत : विश्वाचे वय (1/H) व आणवीय वय (e2/mc3) यांची तुलना केली, तर पुन्हा ०.२ X १०४० ही संख्या येते. यावरून आणवीय व इतर भौतिकी स्थिरांकांचा विश्वाच्या वयाशी संबंध असावा, असे दिसते. यावरून आणवीय स्थिरांक e, m, व गुरूत्वाकर्षण स्थिरांक G हे कालाबरोबर बदलत असावेत, असा तर्क ⇨ पॉल एड्रिएन मॉरिस डिरॅक यांनी केला व त्यावर विश्वस्थितीशास्त्र आधारण्याचा प्रयत्न केला, परंतु तो व्यापक सापेक्षता सिद्धांताशी जुळत नाही. म्हणून अलीकडे सी. ब्रान्स व आर्. एच्. डिक यांनी परिवर्तनशील गुरुत्वाकर्षण स्थिरांकावर आधारलेला स्केलर- टेन्सर सिद्धांत पुढे मांडला आहे.
आल्फव्हेन सिद्धांत : भौतिकीचे नियम द्रव्य व प्रतिद्रव्य यांना सारखेच लागू पडतात. तेव्हा संपूर्ण विश्वात द्रव्याचे हे दोन्ही प्रकार सारख्याच प्रमाणात असावेत, असे ⇨ हान्नेस आल्फव्हेन यांनी सुचविले व त्याप्रमाणे एक विश्वस्थितिशास्त्र रचले. यात सुरूवातीच्या प्रारणविश्वात अतिऊर्जित प्रकाशकणांपासून द्रव्य व प्रतिद्रव्य सारख्या प्रमाणात उत्पन्न झाले. नंतर त्यांच्यातील विनाश प्रक्रियेने जी ऊर्जा उत्पन्न झाली तिच्यामुळे विश्व प्रसरण पावू लागले. परंतु सर्वच जड द्रव्याचा विनाश होण्यापूर्वी द्रव्य व प्रतिद्रव्य ठिकठिकाणी एकमेकांपासून विलग झाले व त्यांच्या संगठनाने दीर्घिका उत्पन्न झाल्या. म्हणजे आपल्याला दिसतात. त्यांपैकी निम्म्या दीर्घिका द्रव्याच्या व निम्म्या प्रतिद्रव्याच्या असाव्यात, असा निष्कर्ष निघतो परंतु द्रव्य व प्रतिद्रव्य एकमेकांपासून खरोखर वेगळे होतील का याबद्दल अजून वाद आहे.
विश्वस्थितिशास्त्रातील काही ज्वलंत प्रश्न : आंतरदीर्घिकीय द्रव्य : विश्व सांत व स्पंदनशील असून त्याचा स्पंदनकाल ७० ते ८० अब्ज वर्षाचा असावा असा बऱ्याच निरीक्षणात्मक पुराव्यांवरून निष्कर्ष निघतो परंतु यासाठी लागणारी सरासरी द्रव्यघनता दीर्घिकांत सामावलेल्या द्रव्यापेक्षा ४०-५० पटींनी अधिक पाहिजे. तेव्हा बाकीचे द्रव्य आंतरदीर्घिकीय अवकाशात विरलतेने पसरले असावे असे वाटते. ते आवेदलित (विद्युत् भाररहित) हायड्रोजनाच्या रूपात असल्यास २१ सेंमी. तरंगलांबीच्या उत्सर्जन व शोषण रेषेच्या अस्तित्वाने जाणवले असते, पण तसे आढळत नाही. त्याचप्रमाणे हायड्रोजनाची लायमन आल्फा शोषणरेषाही [ १२१५ Å तरंगलांबी असलेली शोषणरेषा (१ Å = १ अँगस्ट्रॉम = १ X १०-१० मी.); → वर्णपटविज्ञान] क्वासार ज्योतींच्या वर्णपटात दिसत नाही. तेव्हा आंतरदीर्घिकीय हायड्रोजन व हीलियम संपूर्ण आयनीभूत ( विद्युत् भारित अणूंच्या) अवस्थेत असले पाहिजेत. क्ष-किरण व गॅमा किरण यांच्या पार्श्वप्रारणी तीव्रतेवरून आंतरदीर्घिकीय द्रव्याचे वर्तमान तापमान १० लक्ष केल्व्हिन असावे, असे दिसते. आता असा प्रश्न उत्पन्न होतो की, उष्ण विश्व प्रसरण पावून थंड झाले तसे हे द्रव्यही ३ के. तापमानापेक्षाही थंड होणे क्रमप्राप्त होते, मग ते पुन्हा उष्ण होण्याचे कारण काय? एक तर्क असा आहे की, पुढे दीर्घिका उत्पन्न झाल्या त्या वेळी पुष्कळ ऊर्जा मुक्त झाल्याने आंतरदीर्घिकीय द्रव्याचे तापमान पुन्हा वाढले असावे.
दीर्घिकांचे संगठन : विश्वप्रसरणास सुरुवात झाल्यानंतर दीर्घिकांचे संगठन केव्हा व कसे झाले, याचे निश्चित उत्तर मिळालेले नाही. दाब आणि विरलत्व यांचे तरंग, द्रव्यघनतेत होणारा सूक्ष्म चढ-उतार किंवा संक्षोभ आवर्त (खळबळीचे भोवरे) यांची वाढ होऊन दीर्घिकांचे संगठन होऊ शकते. परंतु वरील तीनही कारणांनी दीर्घिकांचे संगठन होण्यास बराच काल लागतो, असे दिसून येते. म्हणून दिर्घिका सुरूवातीपासून बीजरूपाने अस्तित्वात असाव्यात असे मानण्यात जागा आहे. दीर्घिका उत्पन्न होते वेळी मिलिमीटर तरंगलांबीच्या अतिलघुतरंगांच्या प्रारणात जो फरक पडला असेल, त्याचे वेध घेऊन हा प्रश्न सोडवता येईल.
हीलियमाचा प्रश्न : बहुतेक ताऱ्यांच्या वातावरणात व अंतर्भागात तसेच आंतरतारकीय अवकाशात हीलियमाचे प्रमाण द्रव्यमानाच्या २५ ते ३० टक्के आढळते. ताऱ्यांच्या केंद्रभागी होणाऱ्या अणुकेंद्रीय विक्रियांच्या द्वारे केवळ २ ते ४ टक्के हायड्रोजनाचे हीलियमामध्ये रूपांतर शक्य होते. तेव्हा विश्वातील बहुतेक सर्व हीलियम सुरूवातीच्या महास्फोटात उत्पन्न झाला असला पाहिजे. जॉर्ज गॅमो, राल्फ अल्फर, फ्रेड हॉईल, एडवर्ड टेलर इत्यादींच्या संशोधनाप्रमाणे त्या वेळच्या परिस्थितीत २५ टक्केच हीलियम उत्पन्न होतो. अशा रीतीने महास्फोट सिद्धांतास पुष्टी मिळते. परंतु गोलाकार तारकागुच्छातील जुन्या ताऱ्यांत हीलियमाचे प्रमाण याहून कमी असण्याची शक्यता आहे. तितके कमी प्रमाण मिळविण्यासाठी विश्वाचे सुरूवातीचे प्रसरण फार वेगात झाले असले पाहिजे. तसे होण्यास पूर्वी अधिक असलेला परिवर्तनशील गुरूत्वाकर्षण स्थिरांक (ब्रान्स-डिक सिद्धांत) किंवा सुरूवातीचे असमदिक्(विषमदिक्) प्रसरण कारणीभूत होऊ शकते असे सौद्धांतिक दृष्ट्या आढळून येते.
कालप्रवाहाची दिशा : भौतिकीचे नियम भविष्य व भूत दोन्ही कालांस सारखेच लागू होतात. मग आपणास काल पुढेच जात आहे असे का वाटते? कालप्रवाहाची दिशा (कालाची बाणरेषा) ठरविण्यास ऊष्मागतिकीच्या दुसऱ्या नियमाप्रमाणे ⇨ एंट्रॉपीची वाढ, ⇨ विद्युत् गतिकीतील नियंमाप्रमाणे विद्युत् भारांपासून प्रारणाचे ऊत्सर्जन व विश्वस्थितिशास्त्रातील विश्वाचे प्रसरण ह्यांचा उपयोग होतो. तेव्हा या तिन्ही गोष्टी एकमेकींवर अवलंबून असल्या पाहिजेत आणि हे कोणत्या विश्वस्थिति-सिद्धांतात शक्य असेल ते ठरविता येईल. उदा., विद्युत् चुंबकीय क्षेत्रासंबंधीच्या मॅक्सवेल समीकरणांवरून विद्युत् भारांचे प्रगतिरोधी व प्रगत असे दोन परिणाम घडू शकतात [⟶ मॅक्सवेल विद्युत् चुंबकीय समीकरणे]. त्यांपैकी प्रगतिरोधी परिणामाचाच अनुभव येतो. याचे कारण शोधण्याचा व्हीलर व ⇨ रिचर्ड फिलिप्स फाइनमन यांनी प्रयत्न केला आहे. त्यांच्या कल्पनेप्रमाणे एखाद्या विद्युत् भारावर होणाऱ्या संपूर्ण विश्वाच्या प्रतिक्रियेमुळे प्रगत परिणाम नष्ट होऊन केवळ प्रगतिरोधी परिणाम शिल्लक राहतो. परंतु निरंतर स्थितीच्या सिद्धांतातच असे होऊ शकते. याच्या उलट उत्क्रांतिशील विश्वात प्रगत परिणामच शिल्लक राहील, असे सिद्ध करता येते. अशा रीतीने विद्युत् गतिकी, ⇨ ऊष्मागतिकी आणि विश्वस्थितिशास्त्र यांचा मेळ घालता येऊन कालाच्या प्रवाहाची दिशा समजू शकते, परंतु विश्वासार्ह निष्कर्ष काढण्यासाठी अधिक सैद्धांतिक संशोधनाची आवश्यकता आहे.
विश्वारंभीची एकमेवाद्वितीय स्थिती : वेधसिद्ध विश्वप्रसरण सुरू झाले त्या वेळी विश्वाची द्रव्यघनता अनंताच्या जवळपास असल्याने त्या एकमेवाद्वितीय स्थितीत नेहमीचे भौतिकीय नियम लागू होतात की नाही ते निश्चितपणे सांगता येणार नाही. म्हणून अशी एकमेवाद्वितीयता टाळण्याचे गणिती प्रयत्न चालू आहेत, परंतु गुरुत्वाकर्षण दाखविणाऱ्या व सांत विश्वात ही स्थिती अपरिहार्य वाटते. मग त्या अतिधन अवस्थेत गुरुत्वाकर्षणाचे पुंजीकरण होत असेल का ? सर्व प्रकारचे चढ-उतार तीव्र होऊन दीर्घिकांची बीजरूप सुरूवात होत असेल का ? कणयुग्मांची उत्पत्ती होण्यास लागणारे अंतर दृश्य क्षितिजापेक्षा मोठे असल्याने विश्वास समदिक्ता आली असेल का? इ. प्रश्न उत्पन्न होतात. अतिधन अवस्थेतील नवे भौतिकी नियम समजल्याशिवाय या प्रश्नाचे उत्तर मिळणार नाही.
पहा : अभ्रिका अवकाश-काल आकाशगंगा एंट्रॉपी क्वासार खगोल भौतिकी ज्योतिषशास्त्र दीर्घिका भौतिकी रेडिओ ज्योतिषशास्त्र विश्वोत्पत्तिशास्त्र.
संदर्भ : 1. Berry, M. I. An Introduction to Relativity and Cosmology, New York, 1889.
2. Bondi, H. Cosmology, Cambridge, 1960.
3. Partridge, R. B. Three K : The Cosmic Microwave, Background Radiation, New York, 1993.
4. Peebles, P. J. E. Principles of Physical Cosmology, New York, 1993.
5. Rowan-Robinson, M. The Cosmological Distance, Ladder Distance and Time in the Universe, New York, 1985.
6. Tucker, W. H. Tucker, K. The Dark Matter: Contemporary Science’s Quest for the Mass Hidden in our Universe, New York, 1988.
अभ्यंकर, कृ. दा.
“