विद्युत् चुंबकीय प्रारण

विद्युत् चुंबकीय प्रारण :अवकाशातून (निर्वातातून) अथवा द्रव्यरूपातील माध्यमातून ⇨विद्युत् चुंबकीय तरंगांच्या रूपात प्रेषित होणारी (एका ठिकाणाहून दुसऱ्या ठिकाणी जाणारी) ऊर्जा म्हणजे विद्युत् चुंबकीय प्रारण होय. अशा प्रकारच्या ऊर्जेच्या उत्सर्जनाला आणि प्रसारणालाही हीच संज्ञा वापरतात.जेव्हा विद्युत् भार आंदोलित होतो किंवा प्रवेगित होतो (वेगाची त्वरा वाढते).तेव्हा त्याच्यापासून एका क्षोमाचे (खळबळीचे) प्रसारण होते. विद्युत् व चुंबकीय क्षेत्रांमध्ये क्षोम निर्माण होऊन विद्युत् भारापासून दूरवर प्रसार होत असल्याने विद्युत् व चुंबकीय क्षेत्रांचे अस्तित्व हे या क्षोमाचे वैशिष्ट्य असून या क्षोमाला विद्युत् चुंबकीय तरंग असे म्हणतात. अशा तरंगाच्या कंप्रतांचा (दर सेकंदास होणाऱ्या आवर्तनांच्या संख्येचा) पल्ला फार मोठा हे. प्रकाश तरंग, उष्णता प्रारण, रेडिओ तरंग ही विद्युत् चुंबकीय प्रारणांची सर्वाधिक परिचित उदाहरणे होत. यांशिवाय जंबुपार व अवरक्त प्रारण (दृश्य वर्णपटातील जांभळ्या व तांबड्या रंगांच्या पलीकडील अदृश्य किरण), क्ष-किरण, गॅमा किरण ही त्याची अन्य उदाहरणे आहेत. विद्युत् चुंबकीय प्रारणाच्या या सर्व रुपांच्या पोकळीतील प्रसारणाचा वेग एकच असतो. मराठी विश्वकोशात अवरक्त प्रारण, उष्णता प्रारण, जंबुपार प्रारण, प्रकाश प्रारण, विद्युत् चुंबकीय तरंग, सूक्ष्मतरंग, क्ष-किरण अशा स्वतंत्र नोंदी असून किरणोत्सर्ग या लेखात गॅमा किरणांविषयीची माहिती आलेली आहे.

ऊर्जेचे प्रेषण वा प्रसारण तीन प्रकारांनी होते. त्यांपैकी सर्वसाधारण प्रकारचे प्रारण हा एक प्रकार होय. (भौतिक कणांच्या हालचालीतून होणारे प्रसारण म्हणजे अभिसरण आणि एका कणाकडून लगतच्या दुसऱ्या कणाकडे ऊर्जेचे हस्तांतरण होऊन होणारे प्रसरण म्हणजे संवहन हे ऊर्जा-प्रसारणाचे इतर दोन प्रकार आहेत). मात्र विद्युत् चुंबकीय प्रारणाच्या प्रसारणासाठी द्रव्यरूप माध्यम असलेच पाहिजे असे बंधन नसते. अवकाशातील तंरगगतीच्या रूपात विद्युत् चुंबकीय प्रारणाचे प्रसारण होते. मात्र काही परिस्थितींत प्रारण हे तरंगाऐवजी पुंजाचे किंवा कणांचे बनलेले आहे, असे सैद्धांतिक दृष्ट्या मानावे लागते.

इतिहास:जे. सी. मॅक्सवेल यांनी विद्युत् चुंबकीय सिद्धांत १८६५ साली मांडला. यानुसार निर्वातातून प्रत्यावर्ती (ठराविक काळाने ज्यांची दिशा आणि परिणाम बदलते अशा) विद्युत् क्षेत्राचे आणि त्याच्याशी निगडित, लंबरूप प्रतलातील चुंबकीय क्षेत्राचे प्रसारण होऊ शकते. अशा तऱ्हेने विद्युत् चुंबकीय तरंगाचे भाकीत या सिद्धांताने केले गेले आणि प्रसारित होणाऱ्या परस्परसंलग्न क्षेत्रांना विद्युत् चुंबकीय तरंग हे नाव देण्यात आले. या तरंगाचा वेग प्रकाशाच्या वेगाएवढाच असल्याचे आढळले. यावरून प्रकाश विद्युत् चुंबकीय तरंगाचे रूप असावे ही कल्पना पुढे आली. १८८७ च्या सुमारास एच. आर. हर्ट्झ यांनी विद्युत् चुंबकीय तरंग प्रयोगाद्वारे निर्माण करून त्यांचे अभिज्ञान केले. म्हणून या तरंगाना ‘हर्टझियन’ तरंग असेही म्हणतात. विद्युत् चुंबकीय प्रारणासंबंधीच्या अभ्यासाची जी वाटचाल झाली तिच्यात न्यूटन यांचा कण सिद्धांत, तरंग सिद्धांत, विद्युत् चुंबकीय क्षेत्राची संकल्पना, पुंज सिद्धांत हे महत्त्वाचे टप्पे असून त्यांच्याविषयीची माहिती प्रकाश या नोंदीत दिलेली आहे.

विद्युत् चुंबकीय प्रारण निर्वात पोकळीतून प्रकाशाच्या वेगाने (c) आणि द्रव्य माध्यमातून

या वेगाने प्रसार पावते. येथे ही माध्यमाची विद्युत् पार्यता असून µ ही त्याची चुंबकीय पार्यता आहे [⟶ चुंबकत्व]. हे प्रारण म्हणजे तरंग आणि पुंज अशी द्वित्त प्रकृती दाखविते. तरंग प्रकृती अभिजात आविष्कारात प्रत्ययाला येते. पण द्वित्त प्रकृती समजून घेण्यासाठी आधुनिक पुंज विद्युत् गतिकीचा आधार घ्यावा लागतो. विद्युत् चुंबकीय प्रारणाच्या पुंज सिद्धांताप्रमाणे प्रारण हे प्रारण पुंजाचे बनलेले असून अशा एका पुंजास ⇨फोटॉन किंवा प्रकाशकण असे म्हणतात. फोटॉन हा विद्युत् चुंबकीय क्षेत्र वाहक असून त्याची ऊर्जा ħω असते आणि परिवलन ħ या एककात एक असते

ω= कोनीय कंप्रता, h = प्लांक स्थिरांक. ऊर्जा पुंज (फोटॉन) विद्युत् भाररहित असून त्याचे वस्तुमान नगण्य आहे [⟶ पुंज क्षेत्र सिद्धांत].

या प्रारणाचे साधारणपणे दोन प्रकार केले जातात. पहिला, विद्युत् चुंबकीय तरंग आणि दुसरा, कण प्रारण, मॅक्सवेल सिद्धांताप्रमाणे प्रकाश म्हणजे विद्युत् चुंबकीय तरंग आहे. विद्युत् गतिकी ही शाखा यांवरच आधारलेली आहे.

विद्युत् चुंबकीय तरंग :प्रवेगित अगर आंदोलित असणाऱ्या विद्युत् भारामुळे विद्युत् चुंबकीय क्षेत्रात क्षोभ निर्माण होतो व तो तरंगरूपाने माध्यमातून प्रसारित होतो. त्याचप्रमाणे विद्युत् भारित कणांच्या समूहातील विद्युत् आणि चुंबकीय परिबलांत बदल होतात, त्यावेळी विद्युत् चुंबकीय प्रारण तरंगाद्वारे बाहेर उत्सर्जित केले जाते. या तरंगाना विद्युत् चुंबकीय तरंग असे संबोधिले जाते. या तरंगनिर्मितीमुळे विद्युत् भारित कणांच्या ऊर्जेचा ऱ्हास होतो. तरंगरूपाने विद्युत् आणि चुंबकीय क्षेत्रांची प्रणाली बाह्य दिशेला प्रसारण पावते. त्यामुळे प्रसारित होणाऱ्या क्षोभामध्ये विद्युत् आणि चुंबकीय क्षेत्रांचे अस्तित्व असते.

विद्युत् चुंबकीय तरंग अवतरंग आहेत म्हणजे तरंग प्रसारण दिशेला लंबरूप

आणि

सदिश क्षेत्र असते. [⟶ सदिश].

विद्युत् चुंबकीय प्रारणाच्या वर्णपटाकडे पाहिल्यावर या तरंगांची व्याप्ती किती विस्तृत आहे याची कल्पना येते. भिन्न तरंगलांबी विभागात या तरंगाचे स्वरूप भिन्न असते [⟶ विद्युत् चुंबकीय तरंग].

एकजिनसी, समदिक्, विद्युत् निरोधक माध्यमासाठी खालील विद्युत् आणि चुंबकीय क्षेत्र समीकरणे लिहिता येतात [⟶ मॅक्सवेल विद्युत् चुंबकीय समीकरणे].

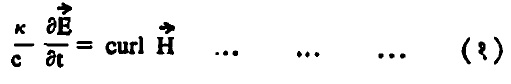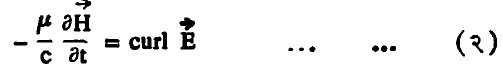c ही निर्वात पोकळीतील तरंग प्रसारण गती आहे. निर्वात पोकळीमध्ये κ= µ= 1. वरील समीकरणांच्या संयोगातून जे. सी .मॅक्सवेल यांनी तरंग समीकरण (५) मिळविले व विद्युत् चुंबकीय तरंगांच्या अस्तित्वाबद्दल प्राक्‌कथन केले.

या समीकरणात  ∇² हा अदिश कारक [⟶ कारक सिद्धांत] असून त्याला लाप्लाशियन असे नाव आहे. या तरंगांचा वेग प्रकाशाच्या वेगाएवढाच असल्याचे लक्षात आल्यावर प्रकाश विद्युत् चुंबकीय तरंगाचे रूप असावे ही कल्पना पुढे आली. निर्वात पोकळीत या तरंगांना समीकरणे (६) आणि (७) ही लागू पडतात. ही दोन्ही समीकरणे (५) वरून मिळविता येतात.

तरंगाचे प्रकार :मॅक्सवेल यांनी दाखवून दिले कि, प्रकाश हा विद्युत् चुंबकीय तरंगाचा एक प्रकार असून ह्या तरंगाची गती प्रकाशाच्या गतीएवढी आहे. या तरंगांची कंप्रता सेकंदाला १० आवर्तने किंवा त्याहूनही कमी ते १०^२५ आवर्तने किंवा त्याहूनही जास्त एवढी असते. तरंगलांबी आणि तरंग कंप्रता यांचा गुणाकार प्रकाशाच्या गती (३ ×१०^८ मी./ सेकंद) एवढा असतो. विद्युत् चुंबकीय तरंगाचे अनेक प्रकार आहेत. या तरंगांचे काही मूलभूत गुणधर्म आहेत. पण काही गुणधर्म तरंगांच्या कंप्रतेवर अवलंबून असतात. दृश्य प्रकाश तरंगांची लांबी ०.४ × १०^-६ मी. (निळा प्रकाश) ते ०.७५ × १०^-६ मी. (तांबडा प्रकाश) या सीमांमध्ये असते. विद्युत् चुंबकीय तरंगांच्या ह्या विभागास दृश्य प्रारण असे म्हणतात.  फक्त ह्या विभागातील विद्युत् चुंबकीय तरंगानाच मानवी डोळ्यांकडून प्रतिसाद मिळतो आणि या तरंगामुळेच आपण द्दश्य जग पाहू शकतो. ह्या विभागाच्या बाहेरील विद्युत् चुंबकीय तरंगाचे अभिज्ञान फक्त विशिष्ट उपकरणांद्वारेच होऊ शकते. विद्युत् चुंबकीय तरंगांचा संपूर्ण वर्णपट आ.१ मध्ये दाखविला आहे [⟶ प्रकाश रेडिओ प्रेषण]. आ.१. मध्ये दर्शविलेल्या निरनिराळ्या विभागांतील तरंगांची निर्मिती कशी होते हे खाली दिले आहे.

गॅमा किरण: काही किरणोत्सर्गी (भेदक कण अथवा किरण बाहेर टाकणाऱ्या) पदार्थाच्या अणुकेंद्रातून आणि क्षोभावस्थेतील अणुकेंद्रातून १ किलो इलेक्ट्रॉन-व्होल्टपासून १०० दशलक्ष इलेक्ट्रॉन व्होल्टपर्यंत ऊर्जेचे गॅमा किरण उत्सर्जित होतात. हे उत्सर्जन म्हणजे निम्न स्थितीला येण्यासाठी स्वत:च्या आंतररचनेत बदल करण्याच्या क्षोभावस्थेतील अणुकेंद्राच्या प्रक्रियेचाच एक भाग होय.

गॅमा किरणांचे उत्सर्जन करणारी अणुकेंद्रे निर्माण करण्यासाठी उच्च ऊर्जेच्या प्रोट्रॉनांचा, त्याचप्रमाणे मंदगती न्यूट्रॉनांचा विशिष्ट अणूंवर भडिमार करतात. त्याशिवाय विशिष्ट अणुकेंद्रांच्या संघटन प्रक्रियेतून आणि काही अणुकेंद्रांमध्ये भंजन प्रक्रिया प्रवर्तित करून गॅमा किरणोत्सर्गी अणुकेंद्रे तयार करतात.

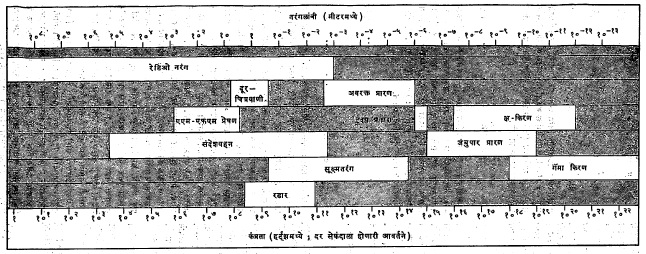
विद्युत् चुंबकीय प्रारणाच्या वर्णपटात अतिउच्च कंप्रता टोकाकडील भागात गॅमा प्रारण येते. त्याची तंरगलांबी ०.०१ नॅनोमीटरपेक्षा (नॅनो म्हणजे एक अब्जांश) कमी असते. बहुतेक गॅमा किरणांच्या ऊर्जेचा पल्ला ५० ते ६,००० दशलक्ष इलेक्ट्रॉनव्होल्ट इतका असतो. तरंग आणि कण या प्रवृत्तींच्या अनुषंगाने गॅमा किरणांच्या द्वित्त प्रकृतीचे आकलन झाले आहे.

क्ष-किरण:क्ष-किरणांची निर्मिती खालील तीन प्रकारांनी होऊ शकते. अणुकेंद्र क्षोभावस्थेत असलेल्या काही अणूंमध्ये आंतरिक रूपांतर प्रक्रिया होते. ज्यामुळे अणुकेंद्रातील जादा ऊर्जेचे स्थानांतरण अणूच्या आंतर-कवचातील इलेक्ट्रॉनांकडे होऊन अणूकेंद्र निग्म स्थितीला येते. याच प्रक्रियेचा एक भाग म्हणून अणूच्या आंतर-कवचातून विशिष्ट क्ष-किरणांचे उत्सर्जन होते. उत्सर्जित क्ष-किरणांची तरंगलांबी अणूच्या रचनेवर अवलंबून असून क्ष-किरणांचा रेषा वर्णपट असतो.

उच्च अणुभाराच्या द्रव्यावर वेगवान इलेक्ट्रॉनांचा मारा केल्यावर द्रव्याच्या अणूतील इलेक्ट्रॉनांच्या ऊर्जास्थितीतील संक्रमणातून क्ष-किरण निर्माण होतात. या किरणांची तरंगलांबी मारा करणाऱ्या इलेक्ट्रॉनांच्या वेगावन अवलंबून न राहता  लक्ष्यातील अणुंच्या रचनेवर अवलंबून असते आणि त्यांचा रेषा वर्णपट असतो. तिसऱ्या प्रकारात, क्ष-किरण नलिकेत विद्युत् वर्चसांतर निर्माण करून वेगवान इलेक्ट्रॉनांचा प्रवाह तयार करून धातुच्या धनाग्रांच्या लक्ष्यावर त्यांचा मारा करतात. यामुळे लक्ष्यातील उच्च अणुभारांच्या विद्युत् क्षेत्रात प्रवाहातील इलेक्ट्रॉन ऋण प्रवेगित होऊन क्ष-किरणांचे उत्सर्जन होते. या किरणांच्या वर्णपट अखंड असून त्यांची किमान तरंगलांबी नलिकेच्या दोन टोकांमधील विद्युत् वर्चसांतरांच्या समप्रमाणात असते. याशिवाय स्फुल्लिंगी विसर्जनामध्ये अणूपासून क्ष-किरण रेषीय प्रारण उत्सर्जित होऊ शकते. अवकाशात सुर्य, तारे, तारकागुच्छ, क्ष-किरणोत्सर्गी तारकायुगुल आणि गोलाकार तारकागुच्छातील अभ्रिकांतून क्ष-किरण उत्सर्जित होतात. पृथ्वीचे वातावरण क्ष किरणांना अपारदर्शक असून वातावरणात क्ष-किरणांचे शोषण होते व ते जमिनीवर पोहोचू शकत नाहीत. त्यामुळे खगोलीय क्ष-किरणांचे अवलोकन वातांवरणाच्या पलीकडे अवकाशातील उपग्रहामार्फत करावे लागते. [⟶ क्ष-किरण].

जंबुपार प्रारण:वायुरूप पदार्थांतील अणू वा रेणू क्षोभावस्थेत असताना इलेक्ट्रॉनांचे उच्च ऊर्जा स्थितीतून निम्न स्थितीमध्ये संक्रमण झाल्यावरदोन्ही स्थितीतील ऊर्जाभिन्नता प्रकाशाच्या स्वरूपात उत्सर्जित होते. अशा रीतीने योग्य ऊर्जांतराच्या स्थितीमधील संक्रमणातून जंबुपार प्रारण उत्सर्जित होते. स्फुल्लिंगी विसर्जनातून, पाऱ्याचा बाष्पदीप  हायड्रोजन वायुदीप आणि कार्बन, हायड्रोजन पारा यांच्या प्रज्योत विसर्जनातून जंबुपार प्रारण उत्सर्जित होते.अत्यंत तप्त तारे, सूर्य, सौर शिखा यांमधूनही जंबुपार प्रारण उत्सर्जित होते, परंतु पृथ्वीच्या वातावरणातील वरच्या थरात त्याचे बऱ्याच प्रमाणात शोषण होते. [⟶ जंबुपार प्रारण].

दृश्य प्रकाश : तप्त पदार्थापासून दृष्य प्रारण मिळते. खगोलातील तारे व सूर्य आणि जमिनीवरील विद्युत् दिवे या उद्‌गमांपासून या तऱ्हेने मिळणारे प्रारण अखंड वर्णपटाच्या स्वरूपात असते. वायुरूप पदार्थांतील उद्दीपित अणू वा रेणूतील इलेक्ट्रॉनांच्या भिन्न ऊर्जास्थितींतील संक्रमणातून दृश्य प्रारण पुंजाच्या स्वरूपात उत्सर्जित होते. पुंजाला प्रकाशकण असे नाव आहे. हे प्रारण रेषा वर्णपट (अणूपासून) किंवा पट्ट वर्णपट (रेणूपासून) या स्वरूपात असते.

सोडियमाची वाफ, पाऱ्याचे बाष्प, हायड्रोजन, निऑन, आर्‌गॉन इ. वायू भरलेल्या विसर्जन नलिका, अनुस्फुरक नळ्या, कार्बन, पारा इत्यादींच्या प्रज्योत विसर्जनातून या प्रकारचा प्रकाश मिळतो. निरनिराळ्या तरंगलांबींचा प्रकाश डोळ्यांना निरनिराळ्या रंगाचा दिसतो. [⟶ प्रकाश].

अवरक्त प्रारण : यालाच उष्णता प्रारण असेही नाव आहे. सूर्यापासून व इतर तप्त पदार्थांपासून अखंड वर्णपट स्वरूपात अवरक्त प्रारण उत्सर्जित होते. विद्युत् रोधक तारेतून विद्युत् प्रवाह पाठवून ती तापून लाल झाल्यावर अवरक्त प्रारण उत्सर्जित करते. विद्युत् तापकापासून देखील हे प्रारण मिळते. थंडीमध्ये उबदारपणासाठी या साधनांचा वापर करतात.

वायुरूप पदार्थांतील रेणूंना कंपन आणि परिवलन या गती असतात. आणि त्यांच्याशी संबंद्ध ऊर्जास्थिती असतात. रेणूतील इलेक्ट्रॉनांच्या भिन्न ऊर्जास्थितींतील संक्रमणामुळे अवरक्त प्रारण उत्सर्जित होते. ते पट्ट वर्णपटाच्या स्वरूपात असते. पृथ्वीच्या वातावरणातील काही वायू अशा प्रकारे अवरक्त प्रारण उत्सर्जित करतात. [⟶ अवरक्त प्रारण].

सूक्ष्मतरंग प्रारण: १ मिमी.पेक्षा जास्त व १ मी पेक्षा कमी तरंगलांबीच्या रेडिओ तरंगांना सूक्ष्मतरंग प्रारण असे नाव आहे. अवरक्त प्रारणाचे काही गुणधर्म सूक्ष्मतरंगांनाही लागू पडतात. अवरक्त प्रारणाचे काही गुणधर्म सूक्ष्मतरंग प्रारण असे नाव आहे. अवरक्त प्रारणाचे काही गुणधर्म सूक्ष्मतरंगांनाही लागू पडतात. अवरक्त व सूक्ष्मतरंग यांच्यातील तरंगलांबीची सीमारेषा १ मिमी. च्या जवळपास असते. सूक्ष्मतरंग इलेक्ट्रॉनाने निर्माण करतात. याउलट अवरक्त प्रारण ऊष्मीयतेने निर्माण करतात. सूर्यापासून अखंड वर्णपटाच्या स्वरुपात हे प्रारण उत्सर्जित होते. [⟶ सूक्ष्मतरंग].

रेडिओ तरंग प्रारण: तरंगलांबी १ मी. हून अधिक असणारे प्रारण रेडिओ तरंग प्रारण म्हणून ओळखले जाते. कंप्रतेनुसार याची उच्चतम, उच्च आणि नीच कंप्रता विभाग अशी विभागणी केली जाते.

रेडिओ प्रेषकात हे तरंग निर्माण केले जातात. विद्युत् प्रवाह शीघ्र गतीने चालू- बंद होत राहील यावर रेडिओ प्रेषकाचे कार्य चालते. ज्या कंप्रतेला प्रेषकातील प्रवाह चालू-बंद होत राहील त्या कंप्रतेचे विद्युत् चुंबकीय (रेडिओ) तरंग निर्माण होतात. उच्च कार्यक्षमतेसाठी प्रारणाची तरंगलांबी आणि आकाशकाची (अँटेनाची) लांबी एकच असणे इष्ट असते.

सूर्याने उत्सर्जित केलेल्या प्रारणामध्ये रेडिओ प्रारण असते. त्याच प्रमाणे इलेक्ट्रॉनिकीतून नीच कंप्रतेच्या रेडिओ तरंगांपासून जास्तीत जास्त ३ ×१०^१५ हर्टझ कंप्रतेपर्यंतचे तरंग (सूक्ष्मतरंग) निर्माण करता येतात. यांची तरंगलांबी १ मिमी. असते.

कृष्ण पदार्थ प्रारण:सृष्टीतील प्रत्येक पदार्थ त्याच्या तापमानानुसार विद्युत् चुंबकीय प्रारणाच्या स्वरूपात ऊर्जा उत्सर्जित करीत असतो. सूर्यापासून मिळणारे प्रारण याच प्रकारे मिळते. पदार्थांचे नैसर्गिक गुणधर्म आणि त्याचे तापमान यांवर उत्सर्जित प्रारणाची तीव्रता व तिचे वर्णपटातील वितरण अवलंबून असते. यामुळे प्रारणाला (उत्सर्जित) तापमानाचा संदर्भ देण्याची पद्धत आहे.

ज्याप्रमाणे प्रत्येक पदार्थातून प्रारण उत्सर्जित होत असते, त्याचप्रमाणे त्याच्यावर बाहेरून प्रारणाचे आपतन होत असते. हे आपाती प्रारण पदार्थांत शोषले जाऊन त्यांचे उष्णतेत रूपांतर होत असते. या क्रियेमध्ये आपाती प्रारणाचे तापमान आणि त्याचे शोषण करणाऱ्या पदार्थांचे तापमान यांचा विचार केला जातो.

विद्युत् चुंबकीय प्रारणाच्या उत्सर्जन-शोषण क्रियांच्या शोषण क्रियांच्या संबंधात एक संदर्भ पदार्थ म्हणून कृष्ण पदार्थाला विशेष सैद्धांतिक स्थान आहे आणि कृष्ण पदार्थांच्या व्याख्येवरून त्याचे महत्त्वाचे गुणधर्म स्पष्ट होतात. व्याख्येनुसार कृष्ण पदार्थांवरील आपाती प्रारण पूर्णपणे शोषले जाते. त्याचप्रमाणे कृष्ण पदार्थांने कोणत्याही तापमानाला उत्सर्जित केलेल्या प्रारणाची तीव्रता त्याच तापमानाच्या इतर कोणत्याही पदार्थाच्या उत्सर्जित प्रारणाच्या तीव्रतेहून जास्त असते. या गुणधर्मामुळे कृष्ण पदार्थ प्रारण वैशिष्ट्यपूर्ण ठरून त्याचे वर्णपट वितरण इतर पदार्थांच्या उत्सर्जित प्रारणाच्या वर्णपट वितरणाहून भिन्न असते आणि म्हणून ते ओळखता येते. कृष्ण पदार्थ प्रारणासंबंधी वेगवेगळे नियम सिद्ध केले आहेत. [⟶ उष्णता प्रारण].

कोणत्याही पदार्थाच्या दर एकक क्षेत्रफळाने उत्सर्जन केलेली ऊर्जा व आपाती प्रारणाचा पदार्थाने शोषलेला भाग यांच्यातील गुणोत्तराचा पदार्थाचे तापमान व उत्सर्जित प्रारणाची तरंगलांबी यांच्याशी फलनरुपी [⟶ फलन] संबंध असतो. याला किरखोफ नियम म्हणतात. व तो असा दर्शवितात.

कृष्ण पदार्थाचा आपाती प्रारणांचा शोषित भाग =१ = E_ab म्हणून कृष्ण पदार्थाच्या दर एकक क्षेत्रफळाने उत्सर्जित केलेली कोणत्याही तरंगलांबीची ऊर्जा तर कोणत्याही पदार्थापेक्षा जास्त असते.

कृष्ण पदार्थ प्रारणाच्या वर्णपटातील ऊर्जा वितरणाबाबत प्लांक नियम आहे. परिसराशी ऊष्मीय समतोलात असणाऱ्या कृष्ण पदार्थाने ऊत्सर्जित केलेली रैखिक दिशादिष्ट ऊर्जा माक्स प्लांक सूत्रानुसार खालीलप्रमाणे मांडली आहेत.

येथे E_λdλ म्हणजे कृष्ण पदार्थाच्या दर एकक क्षेत्रफळाने प्रलंबाशी θ कोनात, दर एकक घनकोनात λ ते λ+dλ या तरंगलांबी विस्तारात दर सेकंदास ऊत्सर्जित केलेली रैखिक दिशादिष्ट ऊर्जा होय. h हा प्लांक स्थिरांक (६.६२६ ×१०^-३४ जूल-सेकंद) k हा बोल्टसमान स्थिरांक ( १.३८०७ ×१०^-२४जूल/अंश के) आणि c हा प्रकाशाचा वेग आहे.

प्लांक नियम वापरून वीन नियम साध्य करता येतो. सूत्ररूपाने तो असा लिहितात.

λmT	= ०.२८८ सेंमी. अंश के
	=  ०.२८८ × १०-२ मी. अंश के

(येथे λ_m म्हणजे T निरपेक्ष तापमानाच्या कृष्ण पदार्थाने उत्सर्जित केलेल्या ऊर्जा वितरणपटातील कमाल बिंदूची तरंगलांबी होय).

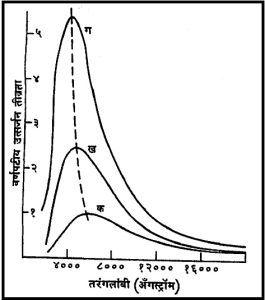
या नियमावरून असे समजते की, λ_m आणि T यांच्या गुणाकाराचे मूल्य स्थिर असल्याने T चे मूल्य वाढले, तर त्याच्याशी संबद्ध λ_m मूल्य घटून गुणाकार पूर्वीइतकाच राहणार. याचा अर्थ प्रारणाचे उत्सर्जन वाढत्या तापमानाला होऊ लागल्यास कमाल तीव्रता बिंदू वर्णपटातील कमी तरंगलांबीकडे सरकतो असा आहे. (आ. २). श्टेफान- बोल्ट्समान नियमान्वये T निरपेक्ष तापमानाच्या कृष्ण पदार्थांच्या दर एकक क्षेत्रफळाने दर सेकंदाला उत्सर्जित केलेली एकूण ऊर्जा (E_em) काढण्यासाठी खालील सूत्र आहे.

E_em = σT⁴

येथे  σ हा श्टेफान -बोल्टसमान स्थिरांक आहे.)

वरीलपैकी कोणत्याही नियमाचा उपयोग करून कृष्ण पदार्थांचे निरपेक्ष तापमान गणिताने काढता येते. [⟶ कृष्ण पदार्थ].

सौर प्रारण व पार्थिव प्रारण ही दोन्ही विद्युत् चुंबकीय प्रारणे आहेत. सूर्याचे तापमान सु. ६,०००° अंश के व पृथ्वीचे तापमान सु. २८८° अंश के हे त्यामुळे सौर प्रारणाचा वर्णपट ४ मायक्रॉनांच्या (मीटरच्या एक दशलक्षांश अंतर म्हणजे मायक्रॉन) आत असून प्रारणाची कमाल तरंगलांबी ०.४७ मायक्रॉन आहे, तर पार्थिव प्रारणाचा वर्णपट ४ मायक्रॉन ते ८० मायक्रॉन या सीमांमध्ये असून उत्सर्जित प्रारणाची कमाल तरंगलांबी १० मायक्रॉन आहे.

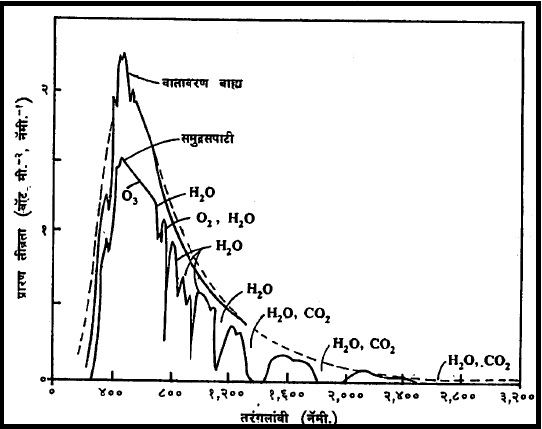
विद्युत् चुंबकीय प्रारणाचे पृथ्वीच्या वातावरणात होणारे शोषण : प्रकाशीय माध्यम या दृष्टीने पृथ्वीचे वातावरण बरेचसे जटील असून वातावरणाचे संघटन त्याच्यातून संक्रमित होणाऱ्या प्रकाशाची तरंगलांबी व प्रकाशीय मार्ग या गोष्टींना संवेदनशील असणारे त्याचे गुणधर्म आहेत. त्यामुळे पृथ्वीच्या वातावरणातून सूर्यप्रकाशाचे संक्रमण होताना हवेतील अणू व रेणू, वायुकालिल, ढग इत्यादी प्रकाशाचे शोषण, प्रकीर्णन (विखुरले जाण्याची क्रिया) आणि विसरित परावर्तन होऊन त्याचे शोषण होते.

सूर्याच्या वर्णपटातील प्रारण तीव्रता (ऊर्जा) वितरणाचे समुद्रसपाटीवर आणि पृथ्वीच्या वातावरणापलीकडे (अवकाशात) मापन करून त्याचे तुलनात्मक निरीक्षण केल्यास दोहोंमध्ये खूप फरक असल्याचे स्पष्ट होते (आ ३). हा फरक पडण्याचे प्रमुख कारण म्हणजे वातावरणातील अणू व रेणूंमध्ये विशिष्ट कंप्रतेचे प्रारण शोषून घेण्याची असलेली क्षमता होय. वातावरणाच्या वेगवेगळ्या थरांतून विद्युत् चुंबकीय प्रारणाचे संक्रमण होत असताना त्या त्या थरातील अणू व रेणू त्यांच्या गुणधर्मानुरूप कंप्रतेच्या प्रारणाचे आपापल्या क्षमतेप्रमाणे कमीअधिक शोषण करतात व अशा प्रकारे भूमिगामी ऊर्जेमध्ये वर्णपटाच्या निरनिराळ्या तरंगलांबी विभागात कमीअधिक बदल घडवून आणतात. शोषण झालेली ऊर्जा वातावरणाच्या त्या त्या थरातील हवेचे तापमान वाढविण्यामध्ये त्याचप्रमाणे प्रकाशविद्युत् आणि प्रकाशरासायनिक विक्रिया घडविण्यामध्ये खर्च होते. [⟶ वातावरण]. निरनिराळ्या कंप्रता विभागांतील प्रमुख वातावरणीय शोषक कोष्टक क्र. १ मध्ये दिले आहेत.

जेव्हा λ तरंगलांबीचे आणि E_λ तीव्रतेचे एकवर्णी प्रारण वातावरणाच्या किंवा वायूच्या ds जाडीच्या थरातून जाते तेव्हा थोडेसे प्रारण (ds_λ) त्या थरामुळे शोषिले जाते. थरातून बाहेर पडणाऱ्या प्रारणाची तीव्रता कमी होते. मूळ प्रारणाच्या काही भागाचे शोषण होते. शोषिलेला भाग aλ आहे असे समजता येईल. त्यामुळे

d E_λ= – a_λ E_λ… … (८)

वायूची घनता (r) आणि जाडी (ds) यांच्याशी a_λ प्रमाणात्मक आहे, असे काही मापनांवरून दिसून येते. त्यामुळे a_λ = k_λrds. येथे k_λ हा शोषण स्थिरांक आहे. समी. (८) मध्ये a_λचे मूल्य घातले म्हणजे

dE_λ= – K_λp E_λ ds … … (९)

कोष्टक क्र. १. विद्युत्‌ चुंबकीय प्रारणाचे शोषण
कंप्रता/ तरंग लांबी विभाग	वर्णपट विभागाचे नाव	प्रमुख वातावरणीय शोषक
१० मेगॅहॅटझ-२० गिगॅहॅटझ	सूक्ष्मतरंग व रेडिओ तरंग	सर्वसाधारणपणे वातावरण पारदर्शक असते.
२० गिगॅहर्टझ-१, ००० गिगॅहर्टझ	रेणवीय परिवलन शोषण वर्णपट	प्रमुख शोषक H2O व O2 रेणूचे परिवलन शोषण
२५ मायक्रोमीटर १५ मायक्रोमीटर	अवरक्त विभाग रेणवीय कंपन शोषण वर्णपट	अर्धपारदर्शक, H2O, Co2 O3 या रेणूंचे कंपन शोषण.
०.८मायक्रोमीटर- ०.४ मायक्रोमीटर	दृष्य प्रारण विभाग	प्रमुख शोषक H2O  त्याखालोखाल O2 ओझोनाचा शोषण पट्ट ४४० – ७४० नॅनोमीटर
०.४ मायक्रोमीटर – ०.२ मायक्रोमीटर	लगतचा व मध्य जंबुपार विभाग	प्रमुख शोषक : ओझोन (o3). शोषित ऊर्जेमुळे ओझोनाचे विदलन (O3 ® O2)
२०० नॅनोमीटर – १३५ नॅनोमीटर	मध्य आणि दीर्घ जंबुपार विभाग	प्रमुख शोषक: ऑक्सिजन रेणू (o2)
१०० नॅनोमीटरहून कमी याहूनही कमी तरंगलांबीचा भाग		प्रमुख : नायट्रोजन रेणू (N2) प्रमुख शोषक : ऑक्सिजन (O) आणि                 नायट्रोजन (N) अणू

हे समीकरण प्राप्त होते. याचे 0 आणि S या सीमांमध्ये समाकलन करून समी (१०) मिळते.

प्रारणाने वायूतून s अंतर प्रवास केल्यावर प्रारणाची तीव्रता किती प्रमाणात कमी होते. हे या समीकरणावरून कळते. या समीकरणास बीअर शोषण असे संबोधिले जाते.

सौर प्रारणातील λ तरंगलांबीच्या प्रारणाचा शिरोबिंदू कोन जर θ असेल तर ds = -dz sec θ वरच्या दिशेत आपण z धन आहे, असे समजतो. म्हणून ds ला ऋण चिन्ह आहे. बीअर शोषण नियमाप्रमाणे सौर प्रारणातील λ तरंगलांबीचे प्रारण सूर्यापासून वातावरणात z उंची वर येईल तेव्हा त्याची कमी झालेली तीव्रता  (E_λz) समी. (११) वरून प्राप्त होईल.

या सूत्राचा विकास करण्यात आपण गृहीत धरले आहे की, आपाती प्रारणाच्या मानाने वातावरणातील वायूपासून उत्सर्जित झालेल्या प्रारणाचे प्रमाण नगन्य आहे. हे गृहीत दृश्य प्रारणाच्या बाबतीत बरोबर आहे.

विद्युत् चुंबकीय प्रारणाचे प्रकीर्णन: विद्युत् चुंबकीय प्रारण कोणत्याही माध्यमातून संक्रमित होताना माध्यमातील कणांवर पडते. काही प्रमाणात कण प्रारण शोषतात आणि उरलेल्या प्रारणाचे प्रकीर्णन होते. प्रारणाच्या किरणांमधील ऊर्जेचा काही भाग अलग होऊन तो वेगवेगळ्या दिशांनी केला, तरंगलांबी यांतील बदलासह ऊत्सर्जित होणे या प्रक्रियेला प्रकिर्ण असे नाव आहे. प्रारणाच्या लघुतरंगांच्या (म्हणजे उच्च ऊर्जा) भागात प्रारण फोटॉन स्वरूपात उल्लेखिले जाते. त्या भागात या प्रक्रियांना फोटॉन प्रकीर्णन आणि कॉम्पटन प्रकीर्णन अशी नावे आहेत. त्यापेक्षा दीर्घ तरंगलांबीच्या क्ष-किरण विभागात घनावस्थेतील स्फटिकांच्या रचनेच्या अभ्यासाचे परिणामकारक साधन क्ष किरण प्रकीर्णनाद्वारे उपलब्ध होते. दृश्य प्रारण विभागात प्रकाशाच्या प्रकिर्णन गुणधर्मावरून सूर्यास्ताच्या वेळचे तांबडे आकाश पांढरे शुभ्र ढग आणि निळे आकाश यांच्या रंगांचा उलगडा होतो. त्यापलीकडे रेडिओ तरंग विभागात पृथ्वीच्या वातावरणातील त्यांच्या प्रकीर्णनावरुन रेडीओ तरंगाचे गुणधर्म समजतात.

प्रकिर्णन प्रक्रियांचे विविध प्रकार आहेत. आपाती किरणातील ऊर्जेचे शोषण आणि नंतर तिचे विकिरण यांमधील कालावधीवरून प्रकीर्णनाचे वर्गीकरण करतात. ज्या क्रिया प्रत्यक्षात तत्कालिक होतात. त्यांना प्रकीर्णन असे नाव आहे. ऊर्जा शोषण आणि पुनरुत्सर्जन यांमध्ये मोजण्यायोग्य विलंब कालावधी असल्यास ती प्रक्रिया दीप्ती म्हणून ओळखली जाते. विलंबकाल एक मायक्रोसेकंदाहून जास्त असल्यास प्रक्रियेला अनुस्फुरण असे नाव आहे. एक सेकंदापेक्षा जास्त विलंबाने होणाऱ्या प्रक्रियेला प्रस्फुरण प्रक्रिया म्हणतात.

तत्काळ घडणाऱ्या प्रकीर्णनाचे देखील दोन प्रकार आहेत. यांमध्ये तरंगलांबीतील अगर ऊर्जेतील स्थानच्युतीचा विचार केला जातो. पहिल्या प्रकारातील प्रकीर्णन स्थितिस्थापक म्हणजे ऊर्जाक्षय नसणारे असते. यामध्ये आपाती प्रकाशाच्या ऊर्जेमध्ये अथवा तरंगलांबीमध्ये प्रकीर्णनानंतर बदल न होता फक्त कलेमध्ये आणि विकिरण दिशेमध्ये बदल होतो.

दुसऱ्या प्रकाराला अस्थितिस्थापक प्रकीर्णन असे नाव आहे. यात आपाती प्रकाशाच्या ऊर्जेमध्ये अगर तरंगलांबीमध्ये स्थानच्युती होते. या प्रकारच्या प्रकीर्णनाचा सर सी. व्ही. रामन आणि के. एस्. कृष्णन यांनी १९२८ मध्ये शोध लावला. यामध्ये द्रवातील अगर घनस्फटिकातील रेणूंनी अस्थितिस्थापक प्रकीर्णन केलेल्या ऊर्जेमध्ये रेणूंच्याकंपन ऊर्जेइतकी वाढ अगर घट होते. यांपैकी ऊर्जेमध्ये घट होणाऱ्या प्रकीर्णनाच्या रेषीय वर्णपटाबद्दल अगोदर माहिती होती. या रेषांना स्टोक्स रेषा असे नाव आहे. ऊर्जेमध्ये वाढ होणाऱ्या प्रकीर्णनाच्या रेषीय वर्णपटाचा रामन यांनी शोध लावला. या रेषांना रामन रेषा, प्रकीर्णनाला रामन प्रकीर्णन आणि आविष्काराला रामन परिणाम अशी नावे आहेत. [⟶ रामन परिणाम].

रामन परिणामाचा वापर करून द्रायूंमधील (द्रव अथवा वायूंमधील) रेणूंची परिभ्रमण आणि कंपन ऊर्जास्थितींबद्दल प्रयोगाद्वारे माहिती मिळविता येते. दोन्ही अणुकेंद्रे समान असणारे रेणू कंपन परिभ्रमण वर्णपट उत्सर्जित करीत नसल्याने अशा रेणूंबाबत ऊर्जास्थितींची माहिती मिळविण्यासाठी रामन परिणाम फारच उपयोगी पडतो. यासाठी द्रायूंच्या पारदर्शक माध्यमावर योग्य त्या कंप्रतेचा एकवर्णी प्रखर प्रकाशझोत सोडतात. आपाती प्रकाशझोताला लंबरूप दिशेत प्रकीर्णन प्रकाशामध्ये साधारणपणे आपाती कंप्रतेचा ( उद्दीपन कंप्रतेचा) प्रकाश दिसेल परंतु याशिवाय त्यापेक्षा जास्त आणि कमीकंप्रतेच्या वर्णरेषा देखील दिसतात. (आ. ४). यांपैकी मोठी स्थानच्युती असणाऱ्या रेषा कंपन ऊर्जास्थितीशी संबंधित असतात, तर कमी स्थानच्युतीच्या रेषा परिभ्रमण ऊर्जास्थितीशी निगडित असतात. उद्दीपन कंप्रतेच्या वरील बाजूस असणाऱ्या जास्ती आणि कमी स्थानच्युतीच्या वर्णरेषांना रामन वर्णरेषा असे नाव आहे. रामन वर्णपटावरून मिळणाऱ्या माहितीचा उपयोग करून रेणूच्या रचनेतील महत्त्वाचे स्थिरांक मिळविता येतात. त्याशिवाय रेणूंमधील अणूकेंद्रांचे परिवलन माहित होते. हा रामन परिणामाचा महत्त्वाचा उपयोग आहे.

अलीकडील काळात रामन परिणाम ही संज्ञा जास्त व्यापक अर्थाने वापरली जाते. मग ते चुंबकीय स्फटिकातील परिवलन तरंगांद्वारे होणारे प्रारणाचे प्रकीर्णन असो, अथवा अर्धसंवाहकात (ज्याची संवाहकता धातू व निरोधक यांच्या दरम्यानची असते अशा पदार्थात) [→ आयनद्रायू भौतिकी] तरंगांद्वारे होणारे प्रारणाचे प्रकीर्णन किंवा आधिद्रायू हीलियमामधील रोटॉनांसारख्या मूलभूत पुंजांद्वारे होणारे प्रारणाचे प्रकीर्णन असो. या सर्वांमध्ये होणाऱ्या प्रारणाच्या अस्थितिस्थापक प्रकीर्णनाला रामन परिणाम असे म्हटले जाते.

द्रव अगर वायूंमध्ये दोन भिन्न क्रिया अस्थितिस्थापक प्रकीर्णन घडवितात. त्यांपैकी एक म्हणजे दाबतरंगांमुळे होणारे ब्रीयवँ प्रकीर्णन होय. माध्यमातून ध्वनितरंग प्रसारित होत असल्यास संपीडन (दाबले जाण्याची क्रिया) व विरलीकरण विभाग अर्ध्या तरंगलांबी अंतराने निर्माण होऊन दाबतरंग प्रसारित होतात. माध्यमावर पडणाऱ्या प्रकाशाचे हे दाबतरंग प्रकीर्णन होतात. दाबतरंगांची गती एकतर प्रकाश उद्‌गमाकडे अथवा त्यापासून दूर असल्याने प्रकाशीय डॉप्लर परिणामामुळे प्रकीर्णन प्रकाशाच्या कंप्रतेत वाढ अगर घट होऊन लहान प्रमाणात स्थानच्युती आढळून येते. [→ डॉप्लर परिणाम].

अस्थितिस्थापक प्रकीर्णन घडविणारी द्रायू अगर वायूंमधील दूसरी प्रक्रिया म्हणजे ⇨एंट्रॉपीतील किवा तापमानातील चढउतार होत. या घटनेमध्ये प्रकीर्णनामुळे होणारी स्थानच्युती उद्दीपन तरंगलांबीच्या दोन्ही बाजूंस पसरून उद्दीपन तरंगलांबी रुंदावते. साधारण द्रवांमध्ये एंट्रॉपी चढउतार ध्वनितरंगांप्रमाणे प्रसारित न होता सगळीकडे पसरत असल्याने तसेच त्यांची वैशिष्ट्यपूर्ण कंप्रता नसल्याने असे घडते. काही विशेष परिस्थितीत मात्र हे चढउतार प्रसारित होऊ शकतात. ही घटन अधिद्रायू हीलियमामध्ये आणि शीत तापमानाला सोडियम फ्ल्युओराइड स्फटिकात आढळलेली असून हा आविष्कार ‘दुसरा ध्वनी’, या नावान ओळखला जातो.

एंट्रॉपीतील किंवा तापमानातील चढउतारामुळे होणाऱ्या प्रकीर्णनाला रॅली प्रकीर्णन असे नाव आहे. घन पदार्थातील विकृती आणि अशुद्धीमुळे देखील प्रकीर्णन होते. व त्यापुढे चढउतारामुळे होणारे रॅली प्रकीर्णन अस्पष्ट होते.

वायू व द्रवांमधील प्रकीर्णन उद्दीपन तरंगलांबीपेक्षा लहान आकारमानाच्या कणांमुळे होते. या गृहीतावर आधारून लॉर्ड रॅली यांनी १८७१ साली या प्रकीर्णनासाठी पुढील समीकरण सुचविले.

यामध्ये कणापासून r अंतरांवर प्रकीर्णित प्रकाशाची तीव्रता I(θ) असून उद्दीपन तरंगलांबी λ आणि आपाती प्रकाशाची तीव्रता I₀ आहे प्रकीर्णन करणाऱ्या कणांची संख्या d असून विक्षोभक कणांचे घनफळ V  आहे. n हा द्रायूचा प्रणमनांक (वक्रीभवनांक) आहे. Cos  θ ही राशी अध्रुवित प्रकाशासाठी असून q हा प्रकीर्णनाचा कोन आहे.

ॲव्होगाड्रो संख्या (N) किंवा माध्यमाचा रेणुभार (M) यांपैकी एक माहीत असेल तर रॅली यांच्या समीकरणातील

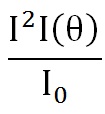या गुणोत्तराच्या मापनावरून दुसरी राशी काढता येते. समी. (१२) मध्ये प्रकीर्णन प्रकाशाची तीव्रता तरंगलांबीच्या चतुर्थ घाताच्या व्यस्त प्रमाणात (λ-⁴) असल्याने सूर्यप्रकाशातील निळ्या रंगाचे तांबड्या रंगाच्या प्रकाशापेक्षा सोळा पट जास्त प्रकीर्णन होते. त्यामुळे दिवसा आकाशाचा रंग निळा दिसतो. त्याचप्रमाणे सूर्योदय अगर सूर्यास्ताच्या वेळचे आकाश लाल दिसते. कारण हवेतील रेणूंमुळे सूर्यप्रकाशातील निळा रंग प्रकीर्णनामुळे सगळीकडे विखुरला जाऊन थेट डोळ्यापर्यंत पोचणाऱ्या सूर्यप्रकाशात लाल रंगाचे प्राबल्य राहते.

रॅली प्रकीर्णन करणारे कण उद्दीपन तरंगलांबीपेक्षा लहान आकारमानाचे असून ते स्वतंत्रपणे कार्य करतात, असे गृहीत धरले आहे. काही महत्त्वाच्या परिस्थितींत ही दोन्ही गृहीते निष्फळ होतात. प्रकीर्णन करणाऱ्या कणांची त्रिज्या जेव्हा उद्दीपन तरंगलंबीच्या समतुल्य होते. तेव्हा रॅली प्रकीर्णनाचे निष्कर्ष लागू होत नाहीत. कलिली निलंबनाभ प्रणालीमध्ये प्रकीर्णन करणारे कण दृश्य प्रकाशाच्या तरंगलांबीच्या आकारमानाचे अगर त्याहून मोठे असतात. या कणांमुळे होणारे प्रकीर्णन उद्दीपन तरंगलांबीशी निरवलंबी असते म्हणजे कोणत्याही तरंगलांबीचा प्रकाश सारख्याच प्रमाणात प्रकीणत होतो. या गुणधर्माला ‘शुभ्र प्रकीर्णन वर्णपट’ असे म्हणतात. हा आविष्कार टिंड्‌ल परिणाम या नावाने ओळखला जातो. आकाशातील ढग पांढरे शुभ्र दिसण्याचे कारण टिंड्‌ल परिणाम आहे. ढगातील पाण्याचे थेंब आकारमानाने दृश्य प्रकाशाच्या तरंगलांबीपेक्षा मोठे असल्याने शुभ्र प्रकीर्णन होते.

प्रकीर्णन करणाऱ्या कणांचे स्वतंत्रपणे कार्य करण्याबाबतचे रॅली प्रकीर्णनातील गृहीत द्रवांमधील प्रकीर्णनाला लागू पडत नाही. द्रवांत शेजारील रेणूंच्या हालचालींमध्ये प्रबल परस्परसमन्वय असतो. यामुळे प्रकीर्णन झालेल्या प्रकाशकिरणात स्थायी कलासंबंधी आणि भंजक व्यतिकरण होते. व बराचसा प्रकाश लुप्त होतो. द्रवाच्या घनतेतील उतारामुळे होणारे टिंड्‌ल प्रकीर्णन तेवढे शिल्लक राहते. या आविष्काराचा सैद्धांतिक स्मॉलुकॉव्हस्की यांनी १९०८ मध्ये आणि अलबर्ट आइन्स्टाईन यांनी १९१० मध्ये केला.

रॅली यांच्या पायाभूत सिद्धांताचा त्यांच्या नंतर अनेक संशोधकांनी विस्तार केला. स्वतः रॅली यांनी १९११ मध्ये आणि आर, गान्स यांनी १९२५ मध्ये परिमित गोलकांच्या प्रकीर्णनाची ही सूत्रे तयार केली. यदृच्छ कुंडल बहुवारिकांच्या प्रकीर्णनाला ही सूत्रे लागू पडण्याच्या दृष्टीने पी. डेबाय यांनी १९४७ मध्ये रॅली−गान्स सुद्धांताचा विस्तार केला. या तिन्ही संशोधकांच्या निष्कर्षांचा समन्वय असलेला रॅली−गान्स−डेबाय या नावाने ओळखला जाणारा सिद्धांत कोणत्याही आकारमानाच्या कणाच्या प्रकीर्णनाला लावता येतो, मात्र त्यासाठी कणाचा  तरंगलांबीहून लहान आकारमानाच्या कणांच्या प्रकीर्णनाला लावता येतो.

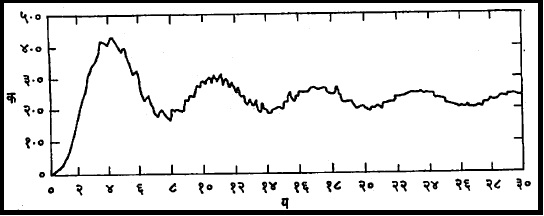
वास्तविक पाहता रॅली-गान्स-डेबाय सिद्धांताअगोदर, १९०८ मध्ये, याहूनही पूर्णत्वाकडे जाणारा जास्त विकसित सिद्धांत जी. मी यांनी गणिती-भौतिकी पद्धतीने मांडला होता, परंतु मी यांचा सिद्धांत लावताना संख्यात्मक उत्तर काढणे आवश्यक असल्याने व त्यासाठी खूप आकडेमोड करावी लागत असल्याने त्याचा वापर मागे पडला. प्रकाशाच्या तरंगलांबीपेक्षा मोठ्या आकारमानाच्या कणांच्या प्रकीर्णनासाठी देखील मी यांचा सिद्धांत लावता येतो. अशा कणांच्या बाबतीत प्रकीर्णन झालेल्या प्रकाशामध्ये मोठे कलांतर होतात. या सिद्धांतान्वये प्रकीर्णन करणाऱ्या कणांचे आकारमान जसे बदलेल तशी प्रकीर्णन प्रकाशाची तीव्रता पुष्कळ वेळा वर-खाली होत राहते. (आ. ५)

गोल कणांचा व्यास आणि तरंगलांबी यांचे गुणोत्तर कितीही असले तरी मी प्रकीर्णन सिद्धांत लावता येतो. वातावरणातील प्रकीर्णनाच्या अभ्यासात याचा उपयोग होतो. ढगातील पावसाचे मोठे थेंब रडार प्रारणाच्या तरंगलांबीपेक्षा मोठे असून देखील मी सिद्धांत लावता येत असल्यामुळे रडार यंत्रणेचा वादळ आणि पाऊस यांच्या अभ्यासासाठी उपयोग करता येतो. प्रकीर्णन फलनांची विस्तारित कोष्टके वापरून आणि संगणकाच्या मदतीने प्रकीर्णन फलनाचे संख्यात्मक मूल्य काढण्यातील अडचण दूर झाली आहे.

पहा : अवरक्त प्रारण उष्णता प्रारण जंबुपार प्रारण प्रकाश प्रारण विद्युत् चुंबकीय तरंग सूक्ष्मतरंग क्ष-किरण.

संदर्भ : 1. Barut, A. O. Foundation of Radiation Theory and Quantum Electrodynamics, New York, 1989.

2. Doren, R. Basic Engineering Electromagnetics, New York 1989

3. Heitler, W. The Quantum Theory of Radlation, Ozford 1984.

4. Jackson, J. D. Classical Electrodynamics, New York, 1962.

5. Marion, J. B. Classical Electromagnetic Radiation, New York, 1968.

6. Neff, H. P. Basic Electromagnetic Fields, New York, 1981.

7. Paul, C. R. Nasar, S. A. Introduction to Electronmagnetic Fields, 1982.

8. Read, F. H. Electromagnetic Radiation, New York, 1980.

9. Sadiku M. Elements of Electromagnetics, New York, 1980.

10. Wangsness, R. K. The Electromagnetic Fields, 1979.

ताकवले, रा. गो.; साठे, ल. ना.; आगाशे, वसंत वा.