बांधकाम संरचना सिद्धांत व अभिकल्प – ६

मुख्य भागावर जाण्यासाठी येथे क्लिक करा

मॅक्सवेल पारस्परिक विचलनाचे प्रमेय : संरचनेच्या एका बिंदूचे [आ. २० (अ) मध्ये C बिंदूचे] दुसऱ्या (D) बिंदूवरील भारामुळे होणारे विचलन (CC₁) हे तोच भार पहिल्या (म्हणजे C) बिंदूवर घेतला असता दुसऱ्या (म्हणजे D) बिंदूच्या होणाऱ्या विचलनाबरोबर (म्हणजे DD₁ बरोबर) असते [आ. २० (आ)]. संरचनांच्या विचलानांच्या विश्लेषणात या प्रमेयाचा अनेक वेळेला आधार घेऊन गणन सोपे केले जाते.

ऑयलर-बेर्नुली समाकलन सूत्रे : घटकाची वक्रता नमन परिबलाशी जोडणाऱ्या I/R = M/EI या पदार्थबलविज्ञाननातील [⟶पदार्थांचे बल] सूत्रामध्ये कलनशास्त्रातील 1/R≈ d²y/dx² ह्या सूत्राचा उपयोग करून ऑयलर-बेर्नुली यांनी खालील समाकलन सूत्रे मांडली :

d2y

=

M

∴ θ =

dy

=

∫

M

.dx आणि

y =

∫

dx

∫

M

dx

या सूत्रावरून नमनामुळे होणारे विचलन काढता येते.

dx2

EI

dx

EI

EI

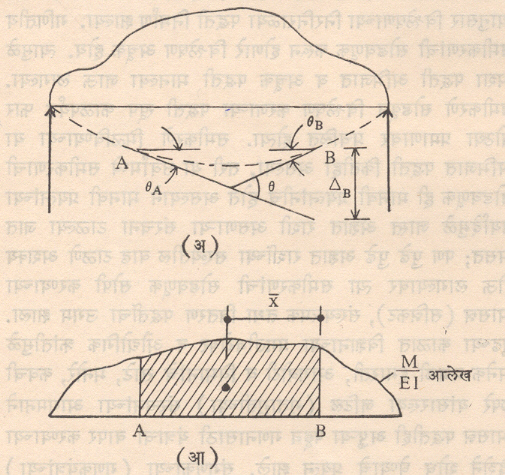
मोर परिबल क्षेत्र प्रमेये : यांतील पहिल्या प्रमेयानुसार कोणत्याही दोन बिंदूंमधील उतार कोनांतील फरक हा त्या बिंदूंमधील (नमन परिबल/दृढता) या राशीच्या आलेखाच्या क्षेत्रफळाइतका असतो. आ. २१ (अ) मध्ये A आणि B या बिंदूंमधील उतार-कोनांतील फरक = θ= θ_B‒(‒θ_A) हा या प्रमेयानुसार B व A बिंदूमधील M/EI आलेखाचे छायांकित क्षेत्रफळ होय. [आ. २१ (आ)].

दुसऱ्या प्रमेयानुसार B या एका बिंदूचे A या दुसऱ्या बिंदूच्या स्पर्शरेषेपासूनचे रेषीय विचलन (∆_B) हे त्या दोन बिंदूमधील M/EI या राशीच्या आलेखाच्या क्षेत्रफळाचे [आ. २१ (आ) मध्ये छायांकित क्षेत्राचे] त्याच (B) बिंदूभोवती घेतलेल्या परिबलाइतके असते. म्हणजे ∆_B = ∫ B_A Mx.dx/EI किंवा छायांकित क्षेत्रफळ गुणिले x.` येथे x` म्हणजे छायांकित भागाच्या गुरूत्वबिंदूचे B पासूनचे अंतर आहे. हे प्रमेय व ऑयलर-बेर्नुली यांचे वरील सूत्र यांमधील साम्य सहज लक्षात येईल.

---

कास्तिल्येनो स्थितीस्थापक ऊर्जा प्रमेय : हे प्रमेय संरचनेच्या विचलानाचा संरचनेच्या स्थितिस्थापक ऊर्जेशी संबंध दाखविते. स्थितिस्थापक ऊर्जा हीच मुळात संरचनांच्या घटकांतील अंतर्गत प्रेरणा व प्रतिविकृती यांच्याशी संबंधित असल्याने अप्रत्यक्षपणे हे प्रमेय विचलनाचा प्रेरणेशी संबंध जोडतो. या प्रमेयानुसार ∂ U/∂ P = ∆ येथे U ही संरचना स्थितिस्थापक ऊर्जा, P हा ज्या ठिकाणचे विचलन काढावयाचे असते त्या ठिकाणचा भार व ∆ हे त्या बिंदूचे विचलन होय.

संरचनेतील स्थितिस्थापक ऊर्जा प्रतिबलाच्या प्रकारानुसार खालील सूत्रांनी मिळते. 

स्थितिस्थापक ऊर्जा = (प्रतिबल प्रतिविकृती) / २
अंतर्गत प्रेरणेचा / प्रतिविकृतीचा प्रकार	स्थितिस्थापक ऊर्जा (U)
अक्षीय प्रेरणा (P)	∫ P2ds 2AE
कर्तन प्रेरणा (V)	∫  V2ds  2AG
नमन परिबल(M)	∫  M2ds  2EI
धूर्णीय परिबल (T)	∫  T2ds  2GI

येथे s = घटकाची लांबी, A = काटच्छेदाचे क्षेत्रफळ, I = निरूढी परिबल, J = ध्रुवीय निरूढी परिबल, E = स्थितिस्थापकता गुणांक व G= दृढता मापांक. ह्या प्रमेयावरून संरचनेचे विचलन सरळ सरळ मिळत असल्याने हे प्रमेय विचलनांच्या गणनासाठी व मुख्यतः स्थितिकीदृष्ट्या अनिर्धार्य संरचनांच्या विश्लेषणास अतिशय उपयुक्त ठरते.

---

आभासी कार्य प्रमेय : हे प्रमेय संरचनेस काही विशिष्ट हेतूने देण्यात येणारा आभासी (काल्पनिक) भार व त्यामुळे निर्माण होऊ शकणारी स्थितिस्थापक ऊर्जा यांचा संबंध दर्शविते. या प्रमेयानुसार कोणत्याही संरचनेस अतिसूक्ष्म आभासी भार दिल्यास संरचनेच्या बहिर्गत विचलनामुळे होणारे कार्य हे संरचनेत निर्माण झालेल्या अंतर्गत प्रेरणांनी केलेल्या कार्याइतके असते. अंतर्गत कार्य हे स्थितिस्थापक ऊर्जेइतके असल्याने,

बहिर्गत आभासी कार्य = अंतर्गत आभासी स्थितिस्थापक ऊर्जा. विचलनांचे गणन करताना आभासी भार एकक मूल्याचा घेतला जातो. त्यानुसार विचलन खालील सूत्रांनी मिळते :  

प्रेरणा / प्रतिविकृतीचा प्रकार	विचलन
अक्षीय प्रेरणा	∑ PpL AE
कर्तन प्रेरणा	∑  Vvds AG
नमन परिबल	∑  Mmds EI
धूर्णीय परिबल	∑  Tt.ds GI

येथे p, v, m, t ह्या त्या त्या प्रकारच्या एकक आभासी भारामुळे आलेल्या त्या त्या प्रकारची अंतर्गत प्रेरणा असून P, V, M व T या बाहेरील प्रत्यक्ष भारांमुळे आलेल्या अंतर्गत प्रेरणा आहेत.

विचलन गणनाच्या पद्धती : वरील विविध तत्त्वांचा, प्रमेयांचा किंवा सिद्धांताचा आधार घेऊन विचलनांचे गणन करण्याच्या पुढील विविध पद्धती आहेत : (१) आनुक्रमिक समाकलन पद्धती, (२) परिबल क्षेत्र पद्धती (३) अनुबद्ध संरचना अर्थात स्थितिस्थापक भार पद्धती, (४) सांत अंतर पद्धती, (५) प्रसरण पद्धती, (६) त्रिकोणमितीय श्रेढी पद्धती, (७) स्थितिस्थापक ऊर्जा पद्धती, (८) आभासी कार्य पद्धती अर्थात एकक भार पद्धती, (९) एम्. विलियट व ओटो मोर यांची भूमितीय रचना पद्धती.

---

आनुक्रमिक समाकलन पद्धती ऑयलर-बेर्नुली सूत्रांवर आधारित असून तुळईचे विचलन काढण्यासाठी त्यांचा उपयोग होतो. कैची किंवा चौकटीचे विचलन या पद्धतीने काढता येत नाही. परिबल क्षेत्र पद्धती मोर यांच्या प्रमेयांवर आधारित असून या पद्धतीने सुद्धा फक्त तुळईची विचलने काढता येतात. ह्याच पद्धतीचे सुधारित स्वरूप म्हणून अनुबद्ध संरचना पद्धती अर्थात स्थितिस्थापक भार पद्धीतचा उगम झाला. या पद्धतीत तुळईवरील नमन परिबलाचे वितरण हेच अनुबद्ध तुळईवरील स्थितिस्थापक भार धरून त्यावरून या अनुबद्ध तुळईची कर्तन प्रेरणा ही मूळ तुळईचे उतार फलन व अनुबद्ध तुळईचे नमन परिबल हे मूळ तुळईचे विचलन होते. ही पद्धती विशेष प्रचलित नाही.

 

तुळईच्या विचलनासाठी थीओडोर फोन कार्मन यांनी सांत अंतर पद्धती [⟶सांत अंतर कलन] सुचविली असून तिच्यात तुळईच्या वक्राच्या कोणत्याही बिंदूवरील उतार व वक्रता dy/dx व d²y/dx² या अवकलज स्वरूपात न घेता सांत अंतर राशींच्या स्वरूपात घेऊन समीकरणे मिळवून ती सोडवून विश्लेषण केले जाते. या अंतर समीकरणांच्या सोडवणुकीसाठी डी. एन्. ॲलन यांनी गणितातील समीकरण प्रणाली सोडविण्याच्या आनुक्रमिक आसन्नीकरणाच्या प्रसरण पद्धतीचा वापर सुचविला. एस्. पी. ट्यिमशेन्कॉ यांनी EId²y/dx² = M या मूलभूत अवकल समीकरणाच्या सोडवणुकीसाठी त्रिकोणमितीय श्रेढींचा उपयोग सुचवून त्यांच्या साहाय्याने विचलन गणन करण्याची पद्धती मांडली. या तिन्ही पद्धतींचा उपयोग ज्यांचे विचलन मूळ स्थितिस्थापक वक्राचे अवकल समीकरण सोडविण्याने मिळते, अशा तुळ्या व पाट यांसारख्या संरचनांसाठीच प्रामुख्याने होतो.

स्थितिस्थापक ऊर्जा पद्धती ही कास्तिल्येनो यांच्या प्रमेयावर आधारित असून या प्रमेयाच्या उपयोगाने कोणत्याही प्रकारच्या संरचनेचे कोणत्याही प्रकारचे विचलन काढता येते. त्यामुळे ही पद्धती सांरचनिक विश्लेषणात आपले स्थान अजूनही टिकवून आहे. तुळईसारख्या घटकांसाठी वर आलेल्या सोप्या पद्धती उपलब्ध असल्याने ही पद्धती विशेषेकरून कैच्या व चौकटी यांसाठी वापरली जाते. स्थितिसकीदृष्ट्या अनिर्धार्य संरचनेच्या विश्लेषणात तर याच पद्धतीचा आधार घेतला जातो.

 

आभासी कार्य पद्धती आभासी कार्य प्रमेयावर आधारित असून हिचा वापरही कैच्या व चौकटी यांसाठी करतात. ह्या पद्धतीमध्ये व स्थितिस्थापक ऊर्जा पदधतीमध्ये खूप साम्य आहे. या पद्धतीमध्ये आभासी भार एकक मूल्याचा वापरला जात असल्याने हिला एकक भार पद्धती सुद्धा म्हणतात (याच आभासी कार्य प्रमेयाचा दृढता पद्धतीमध्ये एकक विचलन देऊन निर्माण होणाऱ्या प्रेरणा काढण्यासाठी उपयोग करतात. या पद्धतीस एकक विचलन पद्धती म्हणतात).

 

कैच्यांच्या विश्लेषणासाठी विलियट व मोर या शास्त्रज्ञांनी भूमितीय कृतींच्या आधारे एक पद्धतीं सुचविली असून या कृतीच्या आधारे येणाऱ्या विचलन आलेखास ‘विलियट-मोर’ आलेख म्हणून ओळखतात. पुलाच्या कैच्यांच्या विचलनासाठी या पद्धतीचा उपयोग होतो.

 

स्थितिकीदृष्ट्या अनिर्धार्य संरचनांचे स्थितिस्थापक विश्लेषण : स्थितिकीदृष्ट्या अनिर्धार्य संरचनांतील अज्ञात राशी काढण्यासाठी केवळ संतुलन समीकरणे अपुरी ठरतात व सुसंगत विचलनाच्या तत्त्वाचा अर्थात संरचनेच्या अखंडतेचा आधार घेऊन जास्तीची समीकरणे मिळवावी लागतात, याचे वर विवरण आलेले आहे.संरचनेचे विश्लेषण करताना अज्ञात राशी कोणत्या घ्याव्यात यावर अनिर्धार्य संरचना विश्लेषणाच्या पद्धतींचे दोन प्रमुश वर्ग पडतात. संरचना विश्लेषणाच्या प्रेरणा आणि विचलन या प्रमुख राशी होत. कोणती राशी अज्ञात धरावी यावरून हे दोन वर्ग पडतात. अनिर्धार्य संरचनामध्ये संतुलनास पाहिजे त्यापेक्षा जास्त आधार-प्रतिक्रियाची संख्या त्या संरचनेची अनिर्धार्यता दाखवते. उदा., आ. २२ मधील दोन्ही टोकांकडे बद्ध आधार असलेल्या तुळईत दोन्ही टोकांना उभ्या आधार-प्रतिक्रिया व नमन-परिबले येतात. संतुलनाच्या दृष्टीने तुळई दोन्ही टोकांना मुक्ताधारित असली तरी चालेल. याचाच अर्थ दोन्ही टोकांकडे बद्ध आधार असलेल्या तुळईत दोन्ही टोकांना उभ्या आधारप्रतिक्रिया व नमन-परिबले येतात. संतुलनाच्या दृष्टीने तुळई दोन्ही टोकांना मुक्ताधारित असली तरी चालेल. याचाच अर्थ दोन्ही टोकांकडील नमन-परिबले ही अतिरिक्त होत. संरचना विश्लेषणाच्या एका वर्गामध्ये ही अतिरिक्त प्रतिबले अज्ञात राशी म्हणून मानली जाऊन जेवढ्या अतिरिक्त आधार-प्रतिरिक्त असतील तेवढी अतिरिक्त समीकरणे सुसंगत विचलनाच्या तत्त्वाच्या आधारे काढली जाऊन ती संतुलन समीकरणाबरोबर सोडवून विश्लेषण केले जाते. या वर्गात मोडणाऱ्या पद्धती सुसंगत विचलनाच्या पद्धती म्हणून मानल्या जातात. यांत अतिरिक्त-आधार-प्रतिक्रिया या अज्ञात राशी असल्याने ह्यास विश्लेषणाची प्रेरणा पद्धतसुद्धा म्हणतात. विश्लेषणाच्या या अभिमार्गाचे जेम्स क्लार्क मॅक्सवेल, ओटो मोर व एच्. एम्. ब्रेसलाऊ हे उद्गाते मानले जातात.

---

दुसऱ्या वर्गामध्ये संरचनेच्या विचलनीय अनिर्धार्यतेचा उपयोग केला जातो. बद्ध आधाराचे विचलन शून्य होय. संरचनेची एकूण आधार विचलने किती आहेत तेवढी संरचनेची विचलनीय अनिर्धार्यता मानली जाते. उदा., आ. २२ मधील बद्ध तुळईत आधार विचलने शून्य आहेत. त्यामुळे ही तुळई विचलनीय दृष्ट्या निर्धार्य होय. याउलट आ. ४ मधील तुळईत उजव्या टोकाला परिवलनीय विचलन होई शकत असल्याने ह्या तुळईची विचलन अनिर्धार्यता एक होय. दोन्ही टोकांकडे मुक्ताधार असलेल्या तुळईच्या दोन्ही टोकांना परिवलनीय विचलने येऊ शकत असल्याने ह्या तुळईची विचलना अनिर्धार्यता दोन होय. आ. ५ मधील तुळईत उजव्या टोकास परिवलनीय विचलनाशिवाय तारेच्या दिशेने रेषीय विचलनही होऊ शकते म्हणून या तुळईची विचलन अनिर्धार्यता दोन होय. ह्या दुसऱ्या वर्गामध्ये आधार विचलने ही अज्ञात राशी म्हणून धरतात. त्यामुळे या प्रकारच्या पद्धतींना विश्लेषणाच्या विचलन पद्धती म्हणतात. या पद्धतींचा मूळ शोध ओटो मोर व जी. ए. मॅनी या शास्त्रज्ञांनी लावला. या पद्धतीमध्येही विविध सांरचनिक प्रमेये, तत्त्वे व सिद्धांत यांच्या साहाय्याने जेवढी अनिर्धार्य विचलने असतील तेवढी समीकरणे मिळवून ती सोडवून विश्लेषण केले जाते.

 

विविध विश्लेषण पद्धती : स्थितिकीदृष्ट्या अनिर्धार्य संरचनांच्या विश्लेषणाचा विविध शास्त्रज्ञांकडून विविध अंगाने विचार व अभ्यास केला गेल्याने व शोध घेतला गेल्याने अनेक प्रकारच्या विश्लेषण पद्धती उदयास आल्या. विश्लेषणामध्ये अनिर्धार्य अज्ञात राशींची सोडवणूक ही मुख्य गोष्ट होय. सुरूवातीच्या काळात ह्या राशींच्या सोडवणुकीसाठी लागणारी समीकरणे मिळविण्यासाठी वेगवेगळ्या शास्त्रज्ञांकडून वेगवेगळ्या संरचना सिद्धांतांचा किंवा तत्त्वांचा आधार घेतला गेला. ही समीकरणे मिळविण्याच्या पद्धतीनुसार किंवा ती मिळविण्यासाठी ज्या तत्त्वांचा किंवा सिद्धांतांचा वापर केला गेला त्यानुसार विश्लेषणाच्या निरनिराळ्या पद्धती निर्माण झाल्या. गणितीय समीकरणांची सोडवणूक करून होणारे विश्लेषण अचूक होय. त्यामुळे अशा पद्धती अभिजात पद्धती कितीही असल्या, तरी या सर्वांमध्ये समीकरणाची सोडवणूक ही मानवी प्रयत्नांनीच होत असल्याने मानवी प्रयत्नांच्या मर्यादेमुळे जास्त अज्ञात राशी असणाऱअया संरचना टाळल्या जात असत पण पुढे पुढे अज्ञात राशींच्या संख्येतील वाढ टाळणे अशक्य होऊ लागल्यावर त्या समीकरणांची सोडवणूक सोपी करण्याच्या आसन्न (सन्निकट), संख्यात्मक तथा वितरण पद्धतींचा उगम झाला. पुढच्या काळात विज्ञानाच्या प्रगतीबरोबर व औद्योगिक क्रांतीमुळे अनेक मजली इमारती, आगबोटी व विमानांचे साटे, मनोरे, कवची छपरे यांसारख्या जटिल (गुंतागुंतीच्या)संरचनांच्या आगमनाने आसन्न पद्धतीही अपुऱ्या पडून गणनासाठी यंत्राचा वापर करण्याच्या दिशेने शोध घेण्याचे प्रयत्न झाले. संगणकांच्या (गणकयंत्रांच्या) आगमनाबरोबर पूर्वीच्या अभिजात व नंतरच्या आसन्न पद्धती बाजूला पडून समीकरणे गणितातील आव्यूह पद्धतीने [⟶आव्यूह सिद्धांत] संगणकाच्या साहाय्याने सोडविणाऱ्या विश्लेषण पद्धती वापरात येऊ लागल्या. आज या संगणकी आव्यूह पद्धतींनी यामागील सर्व पद्धतींना बाजूस सारून आपले वैशिष्टयपूर्ण स्थान प्राप्त केले आहे. त्यामुळे या आधुनिक संगणकी पद्धतींच्या पूर्वीच्या सर्व विश्लेषण पद्धतींचा त्रोटक आढावा केवळ त्यांच्या संरचनाशास्त्राच्या इतिहासातील स्थानामुळे घेतला आहे. संगणकाच्या अभावी ज्या पद्धती अजूनही वापरल्या जातात त्यांचे थोडक्यात विवरणही केलेले आहे. या विश्लेषणाच्या विविध पद्धती त्यांच्या वर्गांसह व संशोधकांसह पुढीलप्रमाणे आहेत :

अभिजात पद्धती :

(१) सुसंगत विचलन पद्धथी (मॅक्सवेल, मोर)

   (अ) आभासी कार्य पद्धती (मॅक्सवेल, मोर)

   (आ) स्थितिस्थापक केंद्र पद्धती (कूलमान)

   (इ) स्तंभविश्लेषण सादृश्य पद्धती (हार्डी क्रॉस)

   (ई) स्थितिस्थाक भार पद्धती

(२) किमान कार्य अर्थात किमान स्थितिस्थापक ऊर्जा पद्धती (कास्तिल्येनो)

(३) त्रिपरिबल प्रमेय पद्धती (क्लॅपिरॉन)

(४) उतार-विचलन पद्धती (मोर व मॅनी)

(५) विशिष्ट बिंदू पद्धती (क्लॅक्स्टन फिड्लर)

(६) क्रमिक समाकलन पद्धती 

---

वितरण व उपसादन पद्धती :

(१) नमन परिबल वितरण पद्धती (हार्डी क्रॉस) 

(२) आनुक्रमिक सुधार पद्धती अर्थात कर्तन प्रतिबल वितरण पद्धती (एल्. ई. ग्रींटर) 

(३) परिवलन अंशदान अर्थात कानी पद्धती (कानी) 

(४) आधार-प्रतिक्रिया वितरण पद्धती (ए. सी. स्कॉरडेलीस) 

आसन्न पद्धती :

(१) चौकोनी कमान पद्धती 

(२) प्रक्षेप बहाल पद्धती

आधुनिक संगणकी आव्यूह पद्धती :

(१) आव्यूह प्रेरणा पद्धती अर्थात नम्यता पद्धती 

(२) आव्यूह विचलन पद्धती अर्थात दृढता पद्धती 

(३) परिमित घटक पद्धती 

वरीलपैकी काही महत्त्वाच्या पद्धतींचे खाली थोडक्यात वर्णन दिले आहे. 

---

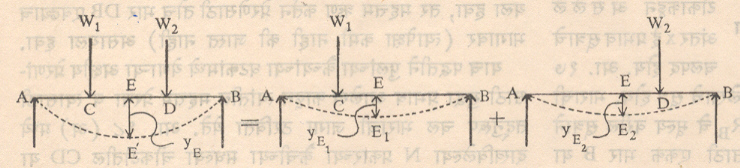
अभिजात पद्धती : (१) सुसंगत विचलन पद्धती : स्थितिकीदृष्ट्या अनिर्धार्य संरचनांच्या विश्लेषणाच्या विविध पद्धतींपैकी सुसंगत विचलन पद्धती ही सर्वांत जुनी अभिजात पद्धती होय. १८६४ मध्ये मॅक्सवेल यांनी तिचा शोध लावला व मोर यांनी १८७४ मध्ये तिला आजचे स्वरूप दिले. या पद्धतीत संरचनेतील अतिरिक्त आधार काढून टाकून संरचना स्थितिकीदृष्ट्या निर्धार्य केली जाते व अशा निर्धार्य संरचनेचे प्रत्येक अतिरिक्त आधाराच्या दिशेने बाहेरील प्रेरणांमुळे होणारे व अज्ञात आधार-प्रतिक्रियांमुळे होणारे विचलन अज्ञात राशीच्या रूपात काढले जाते. प्रत्यक्षात आधाराच्या जागी विचलन होत नसल्याने दोन्ही विचलनांची बेरीज शून्य होते. या सुसंगत विचलनाच्या तत्त्वाचा वापर करून अतिरिक्त आधार-प्रतिक्रियांच्या संख्येइतकी समीकरणे मिळतात. ही समीकरणे सोडवून अतिरिक्त आधार-प्रतिक्रिया काढल्या जातात. बाकीच्या आधार-प्रतिक्रिया व घटकांमधील प्रेरणा यांचे विश्लेषण संतुलन समीकरणांच्या साह्याने करणे शक्य होते. उदा., आ. २३ मध्ये दाखविलेल्या बद्ध तुळईत दोन्ही आधारंकडील बद्ध परिबले अतिरिक्त आधार-प्रतिक्रिया धरून ह्या अगोदर ती काढून टाकली असता, म्हणजेच तुळई मुक्ताधारित धरून सुसंगत विचलन तत्त्वाच्या आधारे खालील समीकरणे मिळतात : θ_A = θ_A1+ θ_A2+ θ_A3 = 0 आणि θ_B = θ_B1+ θ_B2+ θ_B3 = 0 येथे θ_A1 व θ_B1 ही w भारामुळे A व B येथे होणारी परिवलने, θ_A2 व θ_B2 ही M_A या आधार-प्रतिक्रियामुळे A व B येथे होणारी परिवलने आणि θ_A2 व θ_B3 ही M_B या आधार-प्रतिक्रियेमुळे A व B येथे होणारी परिवलने आहेत. या ठिकाणी

θ_A1 = θ_B1= wL³/ 24EI,

θ_A2 = M_AL, θ_B2 = M_AL, θ_A3 = M_BLθ_B3 = M_BL 

3EI                6EI                 6EI               3EI

यावरून wL³ + M_AL + M_BL = 0 आणि   wL³ + M_AL + M_BL = 0

24EI     3EI       6EI                    24EI      6EI      3EI

ही समीकरणे तयार होतात आणि ती सोडविली असता  

M_A = M_B = ‒ wL² हे उत्तर मिळते.

१२

 

आव्यूह प्रेरणा पद्धथी म्हणजे याच पद्धतीचे आव्यूह स्वरूप होय. या पद्धतीत विचलनांचे गणन ही महत्तवाची क्रिया होय. विचलन गणनाच्या या अगोदर दर्शविलेल्या विविध पद्धतींचा यासाठी उपयोग होतो.प्रामुख्याने आभासी कार्य पद्धती म्हणजेच एकक भार पद्धथी, परिबल क्षेत्र पद्धती व आनुक्रमिक समाकलन पद्धती यासाठी वापरली जाते. असमपार्श्वाकार तुळईसाठी स्थितिस्थापक भार पद्धतीचा उपयोग केला जातो. एका गाळ्याच्या चौकोनी चौकटींसाठी किंवा समानीसाठी कार्ल कूलमान यांनी १८६६ मध्ये स्थितिस्थापक केंद्र पद्धती व नंतर हार्डी क्रॉस यांनी १९३० मध्ये स्तंभविश्लेषण सादृश्य पद्धती सुचविल्या पण त्यांच्या मर्यादित उपयोगामुळे या पद्धती आता इतिहासजमा झाल्या आहेत.

(२) स्थितिस्थापक ऊर्जा पद्धती : सर्व प्रकारच्या संरचनांचे कोणत्याही प्रकारचे विचलन कास्तिल्येनो यांच्या प्रमेयाने करता येत असल्याने स्थितिस्थापक ऊर्जा पद्धतीचा वापर विचलनांच्या गणनाबरोबरच स्थितिकीदृष्ट्या अनिर्धार्य अशा संरचनांच्या विश्लेषणासाठी होऊ लागला. या पद्धतीच्या व्यापक व मूलभूत अशा स्वरूपामुळे अनिर्धार्य संरचनांच्या विश्लेषणाच्या अभिजात पद्धतीमध्ये हिचे स्थान अनन्यसाधारण आहे. असे असले, तरी इतर सुलभ पद्धतींच्या मानाने ती क्लिष्ट असल्यामुळे तिचा वापर तितकासा होत नाही. मात्र संरचना विश्लेषणाच्या सर्व आधुनिक पद्धतींमध्ये स्थितिस्थापक ऊर्जा तत्त्वाचा आधार नेहमीच घेतला जातो.

(३) त्रिपरिबल, चतुःपरिबल प्रमेय पद्धती : अखंड, अनेकाधार तुळ्यांच्या विश्लेषणासाठी फार पूर्वी म्हणजे १८५७ मध्ये क्लॅपिरॉन यांनी त्रिपरिबल व चतुःपरिबल प्रमेये मांडली. त्यांचा आजसुद्धा वापर केला जातो. तुळईच्या आधारच्या दोन्ही बाजूंकडील परिवलने तुळईच्या अखंडतेमुळे सारखीच असली पाहिजेत या सुसंगत विचलन तत्त्वाचा आधार घेऊन खालील प्रमेय मांडले गेले. 

M_AL₁ + 2M_B (L₁+L₂) + M_C L₂ =  I₁ I₁ I₂ I₂

‒6 Q_AB + Q_BC ‒ E δ_A‒ E δ_C 

I₁L₁ I₂L₂ L₁ L₂

यात M_A, M_B व M_C ही A, B व C येथील नमन परिबले I₁, I₂ ही AB व BC या गाळ्यांमधील तुळईची घूर्णीय परिबले L₁, L₂ ही AB व BC या गाळ्यांची लांबी Q_AB व Q_BC ही अनुक्रमे AB व BC या गाळ्यांवरील नमन परिबल आलेखांची A व C भोवतीची परिबले δ_A, δ_C ही A व C या आधारांची B च्या आधार पातळीपासूनची उभी अंतरे आणि E हा स्थितिस्थापकता गुणांक होय. या प्रमेयास त्रिपरिबल प्रमेय म्हणतात.

जेव्हा एखाद्या (समजा B या) आधाराशी तुळईच्या दोन बाजूंशिवाय तिसरा घटक जोडला असेल, तर अशा वेळी खालीलप्रमाणे चतुःपरिबल प्रमेय मिळते :

M_A L₁ + M_B1 L₁ + M_B2 L₂ +

I₁ I₁ I₂

M_C L₂ = ‒ 6 (Q_AB + Q_BC ‒ E δ_A‒ E δ_C )

I₂ I₁L₁ I₂L₂ L₁ L₂

व M_B1 – M_B2 = M_O यात M_O हे B येथील तिसऱ्या घटकामधील नमन परिबल आणि M_B1 व M_B2 ही B येथील AB व BC या भागांतील नमन परिबले होत.

---

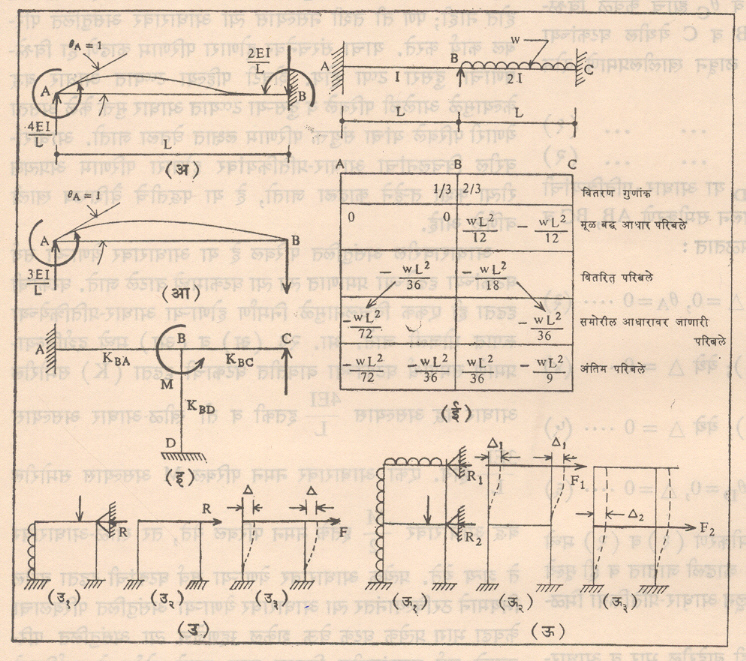
(४) उतार-विचलन पद्धती : अभिजात पद्धतींमध्ये उतार-विचलन पद्धतीचे स्थान सुसंगत विचलन पद्धतीइतकेच महत्त्वाचे आहे. कारण आधुनिक संगणकी विचलन पद्धतीचे हे मूळ रूप होय. ह्या पद्धतीची मूळ कल्पना ओटो मोर यांनी १८९२‒९३ मध्ये प्रथम मांडली व जी. ए. मॅनी यांनी १९१५ मध्ये तिला आजचे विश्लेषण पद्धतीचे स्वरूप दिले. या पद्धतीत आधाराची अज्ञात विचलनांच्या रूपामध्ये आधार-प्रतिक्रिया प्रेरणा-विचलन संबंधाचा उपयोग करून मांडली जातात. आधार-विचलने व आधार-प्रतिक्रिया यांना जोडणारी ही समीकरणे उतार-विचलन समीकरणे म्हणून ओळखली जातात. ह्यातील प्रत्येक समीकरण एका वेली एकाच आधार-विचलनाचा आधार-प्रतिक्रियेवर होणारा परिणाम काढून सर्व विचलनांमुळे होणाऱ्या परिणामांची बेरीज करून मिळविले जाते उदा., आ. २५ मध्ये AB या घटकाची θ_A, θ_B व ∆ ही तीन विचलने होत, तर M_AB व M_BA या आधार-प्रतिक्रिया होत. आ. २५ (आ) मध्ये सुरूवातीस सर्व विचलने शून्य असताना (म्हणजे दोन्ही आधार बद्ध असताना) बाहेरील भारामुळे येणाऱ्या आधार-प्रतिक्रिया दाखविल्या आहेत. आ. २५ (इ, ई व उ) मध्ये अनुक्रमे फक्त θ_A, θ_B आणि ∆ आणि या विचलनांमुळे येणाऱ्या आधार-प्रतिक्रिया दाखविल्या आहेत. एकूण आधार-प्रतिक्रिया ही चारही प्रतिक्रियांची बेरीज होय. म्हणजेच-

---

M_AB =  M_ABF + M’_AB + M”_AB + M”‘_AB

आणि M_BA = M_BAF + M’_BA + M”_BA + M”‘_BA

येथे M’_AB = 4EI θ_A, M’_BA =  2 EI θ_A

L                         L

M”_AB = 2 EI θ_B, M”_BA = 4 EI θ_B

L                          L

M””_AB = ‒6EI∆ , M'”BA = ‒ 6EI∆

L² L²

∴ M_AB = M_ABF +  4EIθ_A + 2EIθ_B‒ 6EI∆ 

L            L           L²

∴M_AB = M_ABF + 2EI (2 θ_A + θ_B‒ 3 ∆ )

L                           L

त्याचप्रमाणे M_BA = M_BAF + 2EI (2θ_A + θ_B‒ 3∆ )

L                        L

 ही समीकरणे संरचनेच्या प्रत्येक घटकास लावून प्रत्येक घटकाच्या आधार-प्रतिक्रिया आधार-विचलनांच्या रूपामध्ये काढली जातात. नंतर प्रत्येक आधारावर सर्व घटकांकडून येणाऱ्या आधार-प्रतिक्रियांना संतुलन समीकरणे लावून ती एकमेकांस जोडली जातात. अशा तऱ्हेने संरचनेत जेवढी आधार-विचलने असतील तेवढी समीकरणे मिळविली जातात. ती समीकरणे सोडवून आधार-विचलने काढली जातात. काढलेल्या आधार-विचलनांवरून प्रत्येक घटकाच्या टोकाकडील आधार-प्रतिक्रिया वरील सुरूवातीस काढलेल्या उतार-विचलन समीकरणांच्या साहाय्याने मिळविल्या जातात आणि अशा तऱ्हेने संरचनेचे विश्लेषण पूर्ण होते. उदा., आ. २५ (ऊ) मधील अनेकाधार अखंड तुळईची B व C येथील परिवलने θ_B व θ_C ह्याच केवळ विश्लेषणाच्या अज्ञात राशी होत. त्यासाठी B व C येथील घटकांच्या आधार-प्रतिक्रियांना संतुलन समीकरणे लावून खालीलप्रमाणे दोन समीकरणे मिळतात :

M_BA + M_BC = 0…  …  …   (१)

M_CB + M_CD = 0…  …  …   (२)

यामधील M_BA, M_BC, M_CB व M_CD या आधार-प्रतिक्रियांची मूल्ये θ_B व θ_C यांच्या रूपात उतार-विचलन समीकरणे AB, BC व CD या घटकांना लावून खालीलप्रमाणे मिळतात :

M_BA = M_BAF + 2EI₁(2 θB) येथे ∆=0, θ_A = 0 ……. (३)

L₁

M_BC = M_BCF + 2EI₂ (2 θ_B + θ_C) येथे ∆=0 ……… (४)

L₂

---

M_CB = M_CBF + 2EI₂ (θ_B + 2 θ_C) येथे ∆=0 ……… (५)

L₂

M_CD = M_CDF + 2EI₃ (2 θ_C) येथे θ_D = 0, ∆=0 ……(६)

L₃

समीकरणे (३) ते (६) मधील राशी समीकरणे (१) व (२) मध्ये घालून ती सोडवून व यांची मूल्ये काढली जातात θ_B व θ_C ही मूल्ये (३) ते (६) या समीकरणांत पुन्हा घालून आधार-प्रतिक्रिया मिळविल्या जातात. चौकटी संरचनांमध्ये आडव्या दिशेनेही बाहेरील भार व आधार-प्रतिक्रिया येत असल्याने अशा संरचनांच्या विश्लेषणात ∑H=0 ह्या समीकरणाचाही वापर करावा लागतो, कारण अशा संरचनांमध्ये सांध्यांच्या परिवलनाबरोबर चौकटीचे आडव्या दिशेने होणारे रेषीय विचलन हे सुद्धा अज्ञात असते. संरचनेचा एखादा आधार कोणत्याही तऱ्हेने खचत असल्यास त्यामुळे संरचनेत निर्माण होणाऱ्या आधार-प्रतिक्रियाही या पद्धतीत काढता येतात. या पद्धतीचा उपयोग अर्थात ज्या संरचनेत कमीतकमी आधार-विचलने असतील अशा संरचनांच्या विश्लेषणात सोपा ठरतो. संरचनेची अनिर्धार्य विचलने जितकी जास्त तितके विश्लेषण करणे कठीण होते.

वितरण व उपसादन पद्धती : (१) नमन परिबल वितरण पद्धती : ही पद्धीत यापूर्वी विशद केलेल्या पद्धतींप्रमाणे अभिजात पद्धती म्हणता येणार नाही. ती एक विश्लेषणाची संख्यात्मक आसन्न वितरण पद्धतीच होय. तरी पण संरचनेच्या विश्लेषणासाठी होणाऱ्या वापराच्या दृषअटीने पाहता हिचा क्रम सर्वांत वर लागेल. याचे मुख्य कारण म्हणजे यात कोणत्याही प्रकारची समीकरणे सोडवावी लागत नाही. अर्थात त्यमुळे उपसादन (क्रमाक्रमाने अधिकाधिक जवळचा अंदाज काढण्याच्या) मार्गाचा अवलंब करणे या पद्धतीत अपरिहार्य ठरते. आधुनिक काळात सुद्धा जेव्हा संगणकाचे साहाय्य उपलब्ध नसेल, तेव्हा हात-गणनासाठई हिचा अतिशय उपयोग होतो. हार्डी क्रॉस यांनी १९३० मध्ये या पद्धतीचा शोध लावला. ही पद्धतही विश्लेषणाच्या विचलन पद्धतींच्या समूहापैकीच एक होय. तरीसुद्धा या पद्धतीत विचलने प्रत्यक्ष शोधून काढली जात नाहीत पण त्यांचा होणारा परिणाम मात्र अप्रत्यक्ष रीत्या काढला जातो हे या पद्धतीचे वैशिष्ट्य, सोपेपणा व गुण होय. या पद्धतीतही प्रथम संरचना विचलनीय दृष्ट्या बद्ध करून प्रत्येक घटकाच्या टोकास येणारी बद्ध-आधार परिबले काढली जातात. हा विश्लेषणाचा पहिला टप्पा होय. यानंतर जो आधार विचलनास मुक्त असेल तो मुक्त केला जातो. म्हणजेच त्या ठिकाणी उलटी बद्ध-आधार परिबले कार्यान्वित केली जातात. आधाराच्या सर्व बाजूंकडील एकूण परिबले संतुलित असल्यास आधार मुक्त करण्याचा संरचनेवर काहीच परिणाम होत नाही पण ती तशी नसल्यास त्या आधारावर काहीच परिणाम असंतुलित परिबल कार्य करते. याचा संरचनेवर होणारा परिणाम काढणे हा विश्लेषणाचा दुसरा टप्पा होय. शेवटी पहिल्या टप्प्यात आधार बद्ध केल्यामुळे आलेली परिबले व दुसऱ्या टप्प्यात आधार मुक्त केले असता येणारी परिबले यांचा संयुक्त परिणाम लक्षात घेतला जातो. आधारंवरील विचलानंचा आधार-प्रतिक्रियांवर होणारा परिणाम अप्रत्यक्ष रीत्या कशा तऱ्हेने काढला जातो. हे या पद्धतीचे वैशिष्टय खाली वर्णिले आहे.

---

आधारावरील असंतुलित परिबल हे या आधारावर येणाऱ्या सर्व घटकांच्या दृढतेच्या प्रमाणात त्या त्या घटकामध्ये वाटले जाते. घटकाची दृढता ही एकक विचलनामुळे निर्माण होणाऱ्या आधार-प्रतिक्रियेच्या रूपात मोजली जाते. आ. २६ (अ) व (आ) मध्ये दर्शविल्याप्रमाणे समपार्श्व घटकाच्या बाबतीत घटकाची दृढता (K) समोरील आधार बद्ध असल्यास 4EI/L इतकी व तो खीळ-आधार असल्यास 3EI/L होय. एका आधारावर नमन परिबल M असल्यास समोरील बद्ध आधारावर M/2 इतके नमन परिबल येते, तर खील-आधारावर ते शून्य येते. प्रत्येक आधारावर येणाऱ्या सर्व घटकांची दृढता वरील नियमाने ठरविल्यानंतर त्या आधारावर येणाऱ्या असंतुलित परिबलाचा केवढा भाग प्रत्येक घटक घेऊ शकेल म्हणजेच त्या असंतुलित परिबलाचे सर्व घटकांमधील वितरण कशा प्रकारे होईल हे दर्शविणारे वितरण गुणांक प्रत्येक आधारासाठी काढणे शक्य होते. हा गुणांक अर्थातच कोणत्याही घटकाच्या दृढतेशी जे प्रमाण असेल त्यावरून ठरतो. उदा., आ. २६ (इ) मध्ये B या आधारावर BA या घटकासाठीच वितरण गुणांक = K_BA / (K_BA + K_BC + K_BD). यावरून BC व BD साठी सुद्धा वितरण गुणांक मिळतात. त्या सर्वांची बेरीज अर्थातच १ होय. अशा तऱ्हेने प्रत्येक आधारावरील प्रत्येक घटकाचा वितरण गुणांक मिळवून त्यानुसार असंतुलित परिबलांचे वितरण केले जाते. या वितरणामुळे मुक्त केलेला आधार संतुलित होतो पण प्रत्येक घटकाच्या समोरील आधार त्यावर वितरण क्रियेमुळे गेलेल्या परिबलांमुळे असंतुलित होतो. त्यामुळे समोरील आधारावर नवीन आलेल्या परिबलांचे पुनः वितरण केले जाते व ही वितरण क्रिया समोरील आधारावर जाणारी परिबले कमीत कमी होईपर्यंत करावी लागते आणि शेवटी विश्लेषणाच्या पहिल्या टप्प्यात आलेली प्रत्येक घटकाची बद्ध-आधार परिबले व दुसऱ्या टप्प्यामध्ये आधार मुक्त करण्याने असंतुलित परिबलांचे वितरण केल्यामुळे आलेली आधार परिबले यांची बेरीज करून अंतिम आधार परिबले मिळतात. ही पद्धती एक प्रकारे उपसादन पद्धतीच होय. या पद्धतीत घटिवत (घड्याळाच्या काट्यांच्या गतीच्या दिशेतील) परिबले धन (+) आणि प्रतिघटवित परिबले ऋण (‒) धरली जातात. यानुसार आ. २६ (ई) मध्ये ABC या अखंड तुळईचे A, B, C हे तिन्ही आधार बद्ध धरून पुढील बद्ध-आधार परिबले मिळतात. M^F_AB = 0 = M^F_BA, M^F_BC = wL²/12 आणि M^F_CB = -wL²/12 ही परिबले आकृतीमधील कोष्टकात पहिल्या ओळीत दाखवली आहेत. B हा आधार परिवलनास मुक्त असल्याने तो मुक्त केला जातो. म्हणजेच दोन्ही बाजूंकडील बद्ध-आधार परिबल विरोधी परिबले कार्यान्वित केली जातात. दोन्ही बाजूंकडील ही परिबले एकमेकांस संतुलित नसल्याने ‒wL²/12 इतके असंतुलित परिबल या आधारावर राहते. त्याचे BA व BC यांच्या दृढतेच्या प्रमाणात वितरण करावे लागते. आता AB व BC यांची दृढता १ : २ या प्रमाणात धरता B येथील BA व BC या घटकांसाठीचे परिबल वितरण गुणांक अनुक्रमे १/३ व २/३ होतील. याचा अर्थ ‒wL²/12 एवढ्या असंतुलित परिबलापैकी ‒wL² /12 X 1/3 = ‒wL² /36 एवढे परिबल BA हा घटक घेतो, तर ‒wL² /18 एवढे परिबल BC हा घटक घेतो. ही परिबले आकृतीमधील कोष्टकात दुसऱ्या ओळीत दाखवली आहेत. B येथील ह्या टोकाकडील वितरित परिबले समोरील A व C या आधारांवर(ते बद्ध असल्याने) निम्म्या प्रमाणात (म्हणजे A आधारवर १/२X wL² /36=  wL² /72 व C या आधारावर १/२X wL² /18 = wL² /36 इतकी) परिबले निर्माण करतात. आता A व C हे दोन्ही आधार बद्ध असल्याने ते नेहमीच संतुलित असतात कारण बद्ध-आधार त्यावर येणाऱ्या परिबलाइतकेच विरोधी परिबल स्वतःहून निर्माण करतो. त्यामुळे या उदाहरणात ही वितरण क्रिया येथेच संपून आकृतीमधील कोष्टकात दाखविल्याप्रमाणे सुरूवातीपासून अखेरपर्यंतच्या सर्व टप्प्यांमधील (असंतुलित व वितरित अशा सर्व) परिबलांची बेरीज करून अंतिम परिबले मिळतात. वरील उदाहरणात तुळई  C या आधाराच्याही पुढे CD एवढ्या आणखी एका गाळ्यावर अखंड असली, तर C हा आधारही परिवलन दृष्ट्या मुक्त होऊन त्यावर गेलेल्या wL²/36 या परिबलामुळे नव्याने असंतुलित होतो व सुरूवातीस विशद केल्याप्रमाणे ही परिबल वितरण क्रिया आणखी पुढे चालू ठेवावी लागते. यावरून हे लक्षात येईल की, या पद्धतीत आधारचे परिबल असंतुलन टप्प्याटप्प्याने वितरण क्रियेने कमी कमी केले जाते. या पद्धतीचा मोठा दोष असा की, वितरणाचे अनेक टप्पे असल्याने चुका होण्याची शक्यता जास्त व सर्वांत मोठा दोष म्हणजे कोणत्याही एखाद्या टप्प्यावर झालेली चूक शेवटपर्यंत तशीच अवशिष्ट राहाते (ओढली जाते) व त्यात स्वयं-सुधारणेस वाव नसतो. पुढे विशद केलेल्या गास्पर कानी यांच्या विश्लेषण पद्धतीत हा दोष नाही. जास्त घटक असलेल्या संरचनांसाठी ही पद्धती अर्थातच कष्टदायकक ठरते.

चौकटीचे विश्लेषण करताना आडव्या प्रतलात येणाऱ्या वायुभारासारख्या भारांचाही विचार करावा लागतो. यासाठी विश्लेषण तीन टप्प्यांत केले जाते. पहिल्या टप्प्यात चौकटीचे आडव्या प्रतलात विचलन होत नाही असे धरून-विश्लेषण केले जाते. त्यासाठी हे विचलन अवरूद्ध करणारी आधार-प्रतिक्रिया द्यावी लागते [पहा : आ. २६ (उ_१)]. अशा तऱ्हेने केलेले संरचनेचे पहिल्या टप्प्यातील विश्लेषण हे अवरूद्ध विचलन विश्लेषण म्हणून मानले जाते. या विश्लेषणावरून संतुलन समीकरणांत्या साहाय्याने आडव्या प्रतलातील विचलन अवरूद्ध करणारी आधार-प्रतिक्रिया (R) काढली जाते. आता प्रत्यक्षात असा विचलन अवरोधी आधार-प्रतिक्रियेच्या उलट प्रेरणा चौकटीवर कल्पित आधारच्या ठिकाणी कार्यान्वित केली जाते [पहा : आ. २६ (उ_२)] आता आडव्या दिशेने येणाऱ्या वरील प्रेरणेमुळे चौकटीत निर्माण होणाऱ्या परिबलांचे विश्लेषण करावे लागते. हा विश्लेषणाचा दुसरा टप्पा होय. या टप्प्यात प्रत्येक सांध्याचे परिवलन अवरूद्ध करून विश्लेषण केले जाते. यास अवरूद्ध परिवलन विश्लेषण म्हणतात. ह्या टप्प्यातील विश्लेषण तसे सरळ पद्धतीने करणे शक्य नसते.

---

त्यासाठी वरील कल्पित आधारचे यादृच्छिक आडवे रेषीय विचलन ∆ गृहीत धरून [पहा : आ. २६ (उ३)] त्यामुळे येणाऱ्या बद्ध-आधार परिबलांचे वर चर्चिलेल्या परिबल वितरण पद्धतीने विश्लेषण करून त्यावरून संतुलन समीकरणांच्या साहाय्याने ∆ विचलनासाठी लागणारा आडवा भार काढला जातो. आता चौकटीच्या घटकांमधील परिबले स्थितिस्थापक तत्त्वानुसार या F भाराच्या सम प्रमाणात होत असल्याने पहिल्या टप्प्याच्या अखेरीस कार्यान्वित होणाऱ्या R या भारामुळे चौकटीच्या घटकात निर्माण होणारी परिबले ही R/F X (F मुळे निर्माण झालेली परिबले) इतकी असतील. येथे विश्लेषणाचा दुसरा टप्पा पूर्ण होतो. विश्लेषणाच्या अंतिम टप्प्यात सर्व घटकांतील अंतिम परिबले दोन टप्प्यांतील परिबलांची बेरीज करून मिळविली जातात. वर फक्त एक मजली चौकट गृहीत धरण्यात आली आहे. अनेक मजली चौकटींच्या बाबतीत हे विश्लेषण आणखी कष्टदायक होते. कारण दुसऱ्या टप्प्यातील विश्लेषणात अनेक मजली चौकटींसाठी प्रत्येक मजल्यावर होणाऱ्या ∆¹, ∆² [पहा आ. २६ (ऊ)] या विचलनांसाठी संरचनेचे स्वतंत्र विश्लेषण संपूर्ण चौकटीसाठी करावे लागते व शेवटी सर्व विश्लेषणांमधून आलेल्या परिबलांची बेरीज करून खालीलप्रमाणे अंतिम परिबले (M) मिळतात. 

M = M_P + R₁/_F1.M_s1 + R₂/_F2.M_s2 + …..

यात MP व MS ही अनुक्रमे अवरूद्ध विचलन विश्लेषण व अवरूद्ध परिवलन यांतून मिळालेली परिबले आहेत. या दुसऱ्या टप्प्यातील अवरूद्ध परिवलन विश्लेषणासाठी एल्. ई. ग्रींटर यांनी आनुक्रमिक सुधार पद्धती किंवा कर्तन प्रेरणा वितरण पद्धती सुचविली होती.

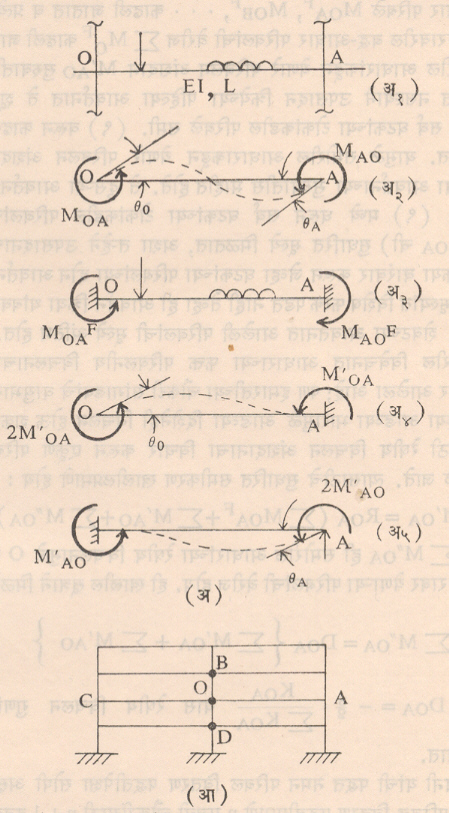
(२) कानी यांची परिवलन अंशदान पद्धती : उपसादन प्रकारातील दुसरी महत्त्वाची विश्लेषण पद्धती म्हणजे १९४७ मध्ये गास्पर कानी यांनी प्रतिपादन केलेली परिवलन अंशदान पद्धती होय. ही पद्धतीसुद्धा नमन परिबल वितरण पद्धतीप्रमाणेच अभिजात पद्धती-ऐवजी आजही (विशेषेकरून अनेक मजली सांगाड्यांच्या विश्लेषणासाठी) वापरली जाते. संगणकी विश्लेषणासाठीही या पद्धतींचा वापर होतो. ही पद्धतीसुद्धा विश्लेषणाच्या विचलन पद्धतीपैकीच होय. हिच्यातही उतार-विचलन समीकरणांचा आधार घेतला जातो. आ. २७ (अ) मध्ये अखंड संरचनेतील एका OA या घटकातील आधार-प्रतिक्रिया व आधार-विचलने दाखविली आहेत. त्यावरून या पद्धतीचे प्रथम खालील मुख्य समीकरण मिळते :

M_OA = M_OA^F + 2M’_OA + M’_AO ……………. (७)

येथे M_OA^F = फक्त बाहेरील भारामुळे येणारे O येथील बद्ध-आधार परिबल (यात θ_O = θ_A शून्य होय), 2M’_OA = फक्त θ_O या परिवलनामुळे येणारे O येथील परिबल (यात θ_A शून्य होय) आणि M’_AO = फक्त θ_A या विचलनामुळे येणारे O येथील परिबल (यात θ_O शून्य होय). M’_OA व M’_AO यांना परिवलन अंशधान म्हणतात. यावरून ही पद्धती परिवलन अंशदान पद्धती म्हणून ओळखली जाते.

---

आता आ. २७ (आ) मध्ये दाखविल्याप्रमाणे संरचनेत कोणत्याही सांध्याशी (समजा ‘O’ या सांध्याशी) अनेक घटक येऊ शकतात. या सांध्यास समीकरणे लावली असता खालील दुसरे महत्त्वाचे समीकरण मिळते.

∑M_O = M_OA + M_OB + ………. = 0 = ∑M_OA

पण  

MOA = MOAF + 2M’OA + M’AO

 ∴ ∑M_OA^F + 2 ∑M’_OA + ∑M’_AO = 0

∴∑M’_OA = – ½ [∑M_OA^F + ∑M’_AO] … (८)

यात ∑ M_OA^F ही O भोवतालच्या सर्व घटकांच्या बद्ध-आधार परिबलांची बेरीज, ∑M’_OA ही O येथील परिवलनामुळे O येथे येणाऱ्या सर्व घटकांच्या परिवलन अंशदानांची बेरीज व ∑M’_AO ही समोरील सर्व आधारांच्या परिवलनामुळे O येथे येणाऱ्या परिवलन अंशदानांची बेरीज होय.

आता O या ठिकाणी येणाऱ्या सर्व घटकांचे परिवलन सारखेच असल्यामुळे O या घटकातील परिबल पुढीलप्रमाणे मिळते.

M’_OA = – १/२ K_OA ∑ M’_OA = ROA ∑M’_OA

                         ∑KOA

∴ M’_OA = R_OA (∑ M_OA F + ∑ M’AO) ….. (९)

येथे R_OA = ‒ १/२K_OA ………………………..(१०)

                                 ∑K_OA

यात K_OA ही OA घटकाची दृढता होय. R_OA यास परिवलन गुणांक म्हणतात. समी. (९) हे या पद्धतीतील प्रधान सूत्र होय.

या पद्धतीने विश्लेषण करताना प्रथम प्रत्येक आधाराचे सर्व घटकांकडील परिवलन गुणांक R_OA, R_OB, .. काढले जातात. त्याचप्रमाणे नमन परिबल वितरण पद्धतीप्रमाणे प्रत्येक घटकाच्या टोकाकडील बद्ध-आधार परिबले M_OA^F, M_OB^F, … काढली जातात व प्रत्येक आधारावरील बद्ध-आधार परिबलांची बेरीज काढली ∑M_O^F काढली जाते. समोरील आधारांकडून येणारे परिवलन अंशदान M’_AO सुरूवातीस माहीत नसल्याने उपसादन क्रियेच्या पहिल्या आवर्तनात ते शून्य धरून सर्व घटकांच्या टोकांकडील परिबले समी. (९) वरून काढली जातात. यामुळे समोरील आधारकडून येणारे परिवलन अंशदान दुसऱ्या आवर्तनाच्या सुरूवातीस माहीत होते. ते दुसऱ्या आवर्तनात समी. (९) मध्ये धरून सर्व घटकांच्या टोकांकडील परिवलांची (M’_OAची) सुधारित मूल्ये मिळतात, अशा तऱ्हेने उपसादनाची ही क्रिया वारंवार करून जेव्हा घटकांच्या परिबलांच्या दोन आवर्तनांतील मूल्यांत विशेष फरक पडत नाही तेव्हा ही आवर्तन क्रिया थांबवली जाते. शेवटच्या आवर्तनात आलेली परिबलांची मूल्ये अंतिम होत.

---

वरील विवेचनात आधाराच्या फक्त परिवनीय विचलनाचाच विचार आलेला आहे पण इमारतीच्या चौकटी सांगाड्यांचे वायुभारासारख्या आडव्या भारामुळे आडव्या दिशेनेही विचलन होऊ शकते. यासाठी रेषीय विचलन अंशदानाचा विचार करून एकूण परिबल काढले जाते. त्यासाठीचे सुधारित समीकरण खालीलप्रमाणे होय :

M’_OA = R_OA (∑M_OA^F + ∑M’_AO + ∑M”_OA)

येथे ∑M”_OA ही समोरील आधारांच्या रेषीय विचलनामुळे O या आधारावर येणाऱ्या परिबलांची बेरीज होय. ही खालील सूत्राने मिळते.

∑M”_OA = DOA { ∑M’_OA + ∑M’_AO}

यात D_OA = ‒3/2 . KOA यास रेषीय विचलन गुणांक म्हणतात.

                                 ∑KOA

कानी यांची पद्धत नमन परिबल वितरण पद्धतीपेक्षा सोपी असून नमन परिबल वितरण पद्धतीप्रमाणे n मजली चौकटींसाठी n + 1 इतकी स्वतंत्र विश्लेषणे या पद्धतीत करावी लागत नाहीत. इतकेच नव्हे, तर पहिल्यापासूनच्या सर्व आवर्तनांतील मूल्यांची बेरीजही या पद्धतीत करावी लागत नाही. शिवाय मधल्या एखाद्या आवर्तनात काही चूक झाल्यास ती पुढील आवर्तनात आपोआप सुधारली जाऊन नाहीशी होते. शिवाय प्रत्येक आवर्तनाअखेर घटकामधील परिबल सरळ मिळते. या पद्धतीचा वापर जर्मनीत व भारतात विशेषेकरून होतो. अमेरिकेची संयुक्त संस्थाने व ब्रिटन या देशांतून नमन परिबल वितरण पद्धती स्थान टिकवून आहे. वरील दोन्ही पद्धती (नमन परिबल वितरण पद्धती व कानी पद्धती) या नमन परिबलाशा संबंधित असल्याने ज्या संरचनांच्या घटकांमध्ये नमन परिबले येतील अशा संरचनांच्या (उदा., अखंड तुळ्या, बद्ध-आधार चौकटी इ.) विश्लेषणासाठीच होई शकतो. खीळ सांध्यांनी युक्त अशा कैच्यांसाठी त्यांचा वापर होऊ शकत नाही. अशा संरचनांसाठी अभिजात पद्धतींचाच वापर करण्यात येतो.

आडव्या प्रतलातील तुळईच्या जालांसाठी अभिजात पद्धतींशिवाय डब्ल्यू. डब्ल्यू. यूएल या शास्त्रज्ञांनी नमन परिबल पद्धतीचा व ए. सी स्कॉरडेलीस या शास्त्रज्ञांनी आधार-प्रतिक्रिया वितरण पद्धतीचा वापर सुचविला. या पद्धतीचा वापर सुचविला. या पद्धतीसुद्धा एक उपसादन पद्धतीच होत.

---

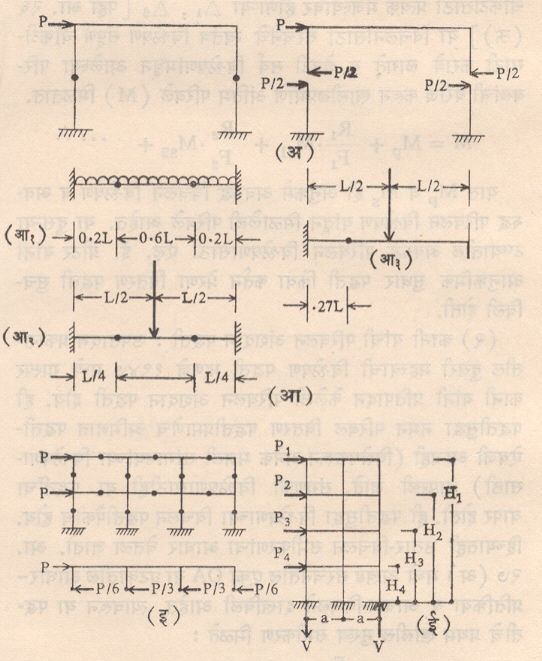
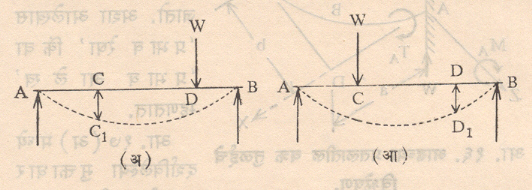
आसन्न पद्धती : वर विशद केलेल्या अभिजात पद्धती व उपसादन पद्धती या संरचनेच्या जास्तीत जास्त अचूक विश्लेषणास योग्य होत पण प्रत्यक्षात कित्येक संरचनासाठी विशेषतः संरचनांच्या प्राथमिक अभिकल्पांसाठी इतक्या परिशुद्ध पद्धतींपेशक्षा सोप्या, जलद विश्लेषण करणाऱ्या आसन्न पद्धतींचा वापर जास्त उपयुक्त ठरतो. या सोप्या पद्धतींचा पाया म्हणजे अनिर्धार्य संरचनांची क्लिष्टता कमी करणाऱ्या काही गृहीतकांचा वापर करणे हा होय. या मागे विश्लेषण सोपे व लवकर व्हावे पण त्याचबरोबर ते अंतिम अचूक उत्तरापासून फार दूर व भरकटलेले असू नये हा हेतू असतो. या पद्धतीत अनिर्धार्य संरचनांमध्ये पूर्वानुभवाच्या आधारे योग्य त्या ठिकाणी परिवलनास मुक्त अशा संधी (खिळी) गृहीत धरून संरचना स्थितिकीदृष्ट्या निर्धार्य केल्या जातात. अशा खिळींच्या ठिकाणी नमन परिबल शून्य असल्याने जेवढ्या खिळी गृहीत धरल्या जातील तितकी आणखी समीकरणे मिळून संरचनेचा प्रत्येक भाग संतुलन समीकरणांनी स्वतंत्र रीत्या सोडविता येतो. उदा., आ. २८ (अ) मध्ये दाखविल्याप्रमाणे दृढपाया असलेल्या चौकटींच्या स्तंभांच्या मध्यभागी खिळी म्हणजे शून्य नमन परिबलाचे बिंदू धरून विश्लेषण केले जाते. दोन्ही स्तंभ सर्वार्थाने सारखे असल्यास चौकटीवर येणारा आडवा भार दोन्ही स्तंभ समान प्रमाणात घेतात व त्यावरून घटकाच्या टोकांकडील नमन परिबलेही (वरील उदाहरणात p/2 . h/2 = ph /4 इतकी) मिळतात. विविध बद्ध तुळ्यांमधील खिळींच्या गृहीत जागा आ. २८ (आ) मध्ये दाखविल्या आहेत. याच तत्त्वावर आधारित अनेक मजली दृढ चौकटींच्या विश्लेषणासाठी चौकोनी कमान पद्धती व प्रक्षेप बहाल पद्धती अशा दोन आसन्न पद्धती उपलब्ध आहेत.  

(१) चौकोनी कमान पद्धती : कमी उंचीच्या व जास्त रूंदीच्या (जास्त गाळ्यांच्या) चौकोनी चौकटीसाठी व आडव्या भारांसाठी ही पद्धत योग्य होय. या पद्धतीत खालील गृहीतके धरली जातात : (१) शून्य नमन परिबल बिंदू प्रत्येक उभ्या व आडव्या घटकाच्या मध्यावर असतो. (२) आडवा भार हा सर्व स्तंभांकडून (उभ्या घटकांकडून) सारख्या प्रमाणात घेतला जातो. अर्धात आतील बाजूकडील स्तंभ बाहेरील बाजूकडील स्तंभांपेक्षा दुप्पट भार घेतात. आ. २८ (इ) मध्ये बाहेरील दोन स्तंभ एक धरून एकूण ३ स्तंभ होत असल्याने आतील प्रत्येक स्तंभ P/3 इतका भार घेईल, तर बाहेरील प्रत्येक स्तंभ P/6 इतका भार घेईल. प्रत्येक शून्य परिबल बिंदूवरील आडवे भार काढल्यानंतर चौकटीच्या दृढ सांध्यावर येणारी नमन परिबले सहज काढता येतात.

(२) प्रक्षेप बहाल पद्धती : ही पद्धत प्रामुख्याने रूंदीपेतक्षा उंची जास्त असलेल्या अनेक मजली उंच इमारतींना जास्त योग्य होय. या पद्धतीत खालील गृहीतके धरली जातात : (१) शून्य नमन परिबल बिंदू प्रत्येक उभ्या व आडव्या घटकाच्या मध्यावर असतो. (२) आडव्या भारामुळे उभ्या स्तंभामध्ये येणारा भार हा त्या स्तंभसमूहाच्या ⇨गुरूत्वमध्यापासून त्या स्तंभाच्या असलेल्या अंतराच्या प्रमाणात असतो. आ. २८ (ई) तिन्ही स्तंभामध्ये अंतर सारखे असताना स्तंभसमूहाचा गुरूत्वमध्य मधल्या स्तंभाशी असेल. त्यामुळे आडव्या भारामुळे उजवीकडील स्तंभामध्ये V एवढा संकोची भार येईल, तर डावीकडील स्तंभामध्ये V एवढा ताणभार येईल, तर मधल्या स्तंभावर काहीच भार येणार नाही.

V चे मूल्य P₁, P₂, P₃ P₄ या आडव्या भारांचे व V या उभ्या भाराचे पायाकडील कोणत्याही बिंदूभोवती परिबल घेऊन मिळू शकते. वरील उदाहरणात

V = ∑Ph / 2a

संगणकी आव्यूह पद्धती : आधुनिक युगातील संगणकाच्या आगमनाने व संरचना तंत्रात होणाऱ्या बदलाच्या प्रचंड वेगामुळे विविध प्रकारची रचना, मांडणी, आकार यांनी युक्त अशा क्लिष्ट संरचना वापरात येऊ लागल्याने अशा संरचनांच्या अनिर्धार्यतेचे प्रमाण इतके वाढले आणि विश्लेषण इतके क्लिष्ट व कष्टदायक होऊ लागले की, अशा विश्लेषणासाठी शास्त्रज्ञांना संगणकी पद्धतीचा अवलंब करणे भागच पडले. अर्थात संगणकी पद्धतींमध्ये सुद्धा अभिजात पद्धतींचा आधार घेतला जाणे अपरिहार्य होते. फक्त पूर्वीच्या थोड्या अज्ञात राशींच्या ऐवजी आता अज्ञात राशींचे समूहाच्या समूह येऊ लागल्याने सर्व राशींचा सामूहिक दृष्ट्या विचार करू शकणाऱ्या आव्यूह विचलन पद्धती व आव्यूही स्वरूप संगणाकाच्या सोयीसाठी आवश्यकच होते. यावरून हे स्पष्ट व्हावे की, या आव्यूह पद्धती मानवी प्रयत्नाने विश्लेषण करण्यासाठी किंवा हात-गणनासाठी नाहीत. त्या केवळ क्लिष्ट अशा संरचनांच्या (ज्यांची अनिर्धार्यता ३ पेक्षा जास्त असेल अशा संरचनांच्या) विश्लेषणासाठीच होय.

आपण या पूर्वीच पाहिले आहे की, प्रेरणा-विचलन संबंधाची सूत्रे घटकाची नम्यता किंवा दृढता दर्शवितात. D = FP या सूत्रातील D हे विचलन व P ही प्रेरणा होय, तर F हा नम्यता मापांक होय. अर्थात F म्हणजे एकक मूल्याच्या प्रेरणेमुळे (P=1) येणारे विचलन होय. तसेच P = SD या सूत्रात S हा दृढता (ताठरता) गुणांक होय. अर्थात S म्हणजे एकक मूल्याइतक्या विचलानमुळे निर्माण होणारी किंवा एकक मूल्याइतक्या विचलनासाठी लागणारी प्रेरणा होय. या मूलभूत सूत्रांच्या आधारावर अनुक्रमे नभ्यता पद्धती व दृढता पद्धती यांची उभारणी झाली आहे.

---

 (१) आव्यूह प्रेरणा पद्धती अर्थात नम्यता पद्धती : ही पद्धती सुसंगत विचलन पद्धती या अभिजात पद्धतीचे आव्यूह स्वरूप होय. ह्या पद्धतीमध्ये संरचनेवरील प्रेरणांना महत्व असून त्यामुळे संरचनेच्या स्थितिकीय अनिर्धार्यतेकडे लक्ष दिले जाते. संरचनेच्या अतिरिक्त आधार-प्रतिक्रिया (R) या पद्धतीत अज्ञात राशी म्हणून मानल्या जातात. विश्लेषणाच्या पहिल्या टप्प्यात अतिरिक्त आधार-प्रतिक्रिया काढून टाकून संरचना निर्धार्य केली जाते. अशा संरचनेस प्राथमिक संरचना म्हणतात. अशा निर्धार्य संरचनेची जरूर ती विचलने काढणे शक्य असते. विश्लेषणात अतिरिक्त आधार-प्रतिक्रिया काढणे हे ध्येय असल्याने व त्या सुसंगत विचलन तत्त्वाच्या उपयोगाने काढणे शक्य असल्याने विश्लेषणाच्या पहिल्या टप्प्यात अतिरिक्त आधार-प्रतिक्रियेच्या ठिकाणी व प्रतिक्रियेच्या दिशेने बाहेरील भारामुळे होणारी विचलने (DP) काढली जातात. आता प्रत्यक्षात संरचनेमध्ये अतिरिक्त आधार असल्याने दुसऱ्या टप्प्यात ते कार्यान्वित केले जातात व फक्त या कार्यान्वित केलेल्या आधार-प्रतिक्रियांमुळे त्या त्या प्रतिक्रियांच्या दिशांनी होणारी विचलने (D_R) अज्ञात आधार-प्रतिक्रियांच्या (R च्या) रूपात काढली जातात. हे संरचनेचे दुसऱ्या टप्प्यातील पूरक विश्लेषण होय. आता अतिरिक्त आधारांना सुसंगत विचलनाचे तत्त्व लागू केले जाते.

त्यानुसार आधाराचे विचलन शून्य असल्याने D_P + D_R = 0. D_R हे R च्या रूपात असल्याने वरील सूत्रामुळे चे मूल्य मिळते. एकदा या अतिरिक्त आधार-प्रतिक्रिया मिळाल्या की, पुढील सर्व विश्लेषण संतुलन समीकरणांच्या साहाय्याने करता येते. वरील विवेचनात D, P, D_P, D_R, R या सर्व राशी आव्यूहाच्या स्वरूपात आहेत. वर विशद केलेल्या कार्यपद्धतीवरून विश्लेषणास खाली दर्शविल्याप्रमाणे स्वरूप मिळते.

---

स्थितिस्थापक विश्लेषणात अध्यारोपणाचे तत्त्व लागू असल्याने संरचनेवर कार्यान्वित असलेल्या P₁, P₂, …., P_N या N प्रेरणांमुळे एखाद्या प्रेरणेच्या दिशेने होणारे विचलन हे प्रत्येक प्रेरणा स्वतंत्र रीत्या कार्यान्वित होत असताना येणाऱ्या D₁, D₂, …, D_N या सर्व विचलनांची बेरीज होय. म्हणजेच

	j=N		j=N
Di = Di1 + Di2 +….. + DiN =	∑	Dij =	∑	FijPj आव्यूहाच्या स्वरूपात D = F P	…	…	(११)
	j=1		j=1

आता संरचनेवर कार्यान्वित होणाऱ्या प्रेरणा ह्या बाहेरील भार L व अतिरिक्त आधार-प्रतिक्रिया R अशा दोन्ही मिळून होत. या आधारे वरील आव्यूही समीकरणातील प्रत्येक आव्यूहाचे खालीलप्रमाणे खंडकरण (विभाजन) करता येते.

[

DL

]

=

[

FLL FLR

]

[

L

]

…

…

(१२)

DR

FRL FRR

R

यात D_L म्हणजे बाहेरील भारांच्या (L च्या) दिशेने होणारी विचलने आणि DR म्हणजे अतिरिक्त आधार-प्रतिक्रियांच्या (R च्या) दिशेने होणारी विचलने होत. संरचना निर्धार्य असल्यास R व D_R शून्य होतात व त्या परिस्थितीत संरचनेतील एखाद्या प्रेरणा बिंदूचे प्रेरणेच्या दिशेने होणारे विचलन D_L = F_LL.L या सूत्राने मिळेल ज्या बिंदूचे एखाद्या दिशेकडील विचलन काढावयाचे असेल त्या बिंदूवर त्या दिशेने कोणतीच प्रेरणा कार्य करीत नसल्यास अशा ठिकाणी विचलन काढावयाच्या दिशेने काल्पनिक शून्य प्रेरणा धरून विश्लेषण केले जाते.

अनिर्धार्य संरचनांचे विश्लेषण करताना प्रथम अतिरिक्त आधार-प्रतिक्रिया R काढणे आवश्यक असते. वरील समीकरणावरून

D_R = F_RL.L + F_RR.R = D_RL + D_RR

R = F_RR^‒1 [D_R – F_RL L] = F_RR^‒1 [D_R – D_RL] …… (१३)

यात D_RL = R च्या दिशेने L मुळे होणारे विचनल आणि D_RR = R च्या दिशेने R मुळे होणारे विचलन होय. बहुतेक वेळा आधाराकडील विचलन शून्य असते, तेव्हा D_R = 0 म्हणून R = -F_RR^‒1 . D_RL. आ. २९ (अ) मधील तुळईचे अनिर्धार्यतामान २ होय. B व C येथील आधार-प्रतिक्रिया R1 व R2 म्हणून अतिरिक्त आधार-प्रतिक्रिया धरता B व C येथील आधार-प्रतिक्रियांच्या दिशेने होणारे DR हे विचलन शून्य होय. अशा वेळी R = -F^-1_RR . D_Rl

[

R1

]

= ‒

[

F11 F12

]

-1

[

DR1L

]

…

…

(१४)

R2

F21 F22

DR2L

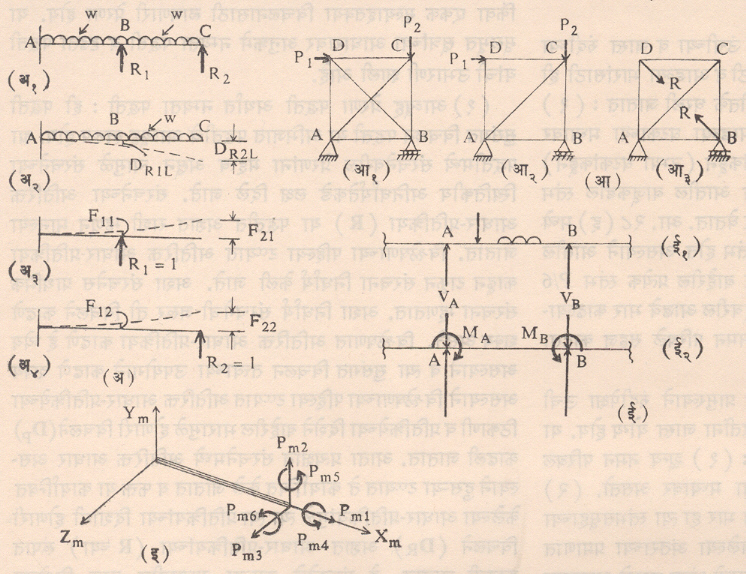
या उदाहरणात D_R1 म्हणजे बाहेरील भार w मुळे B व C ची R₁ व R2 या दिशांनी होणारी विचलने होत. ही विचलने विचलन-गणनाच्या विविध पद्धतींपैकी कोणत्याही पद्धतीने काढता येतात. त्याचप्रमाणे FRR या नम्यता आव्यूहाचे गुणांक R₁ = 1 व R₂ = 1 धरून R₁ व R₂ च्या दिशेने येणारी विचलने काढून मिळविता येतात. अशा तऱ्हेने अतिरिक्त आधार-प्रतिक्रिया मिळतात व पुढील विश्लेषण संतुलन समीकरणांनी करता येते.

---

यात D_RL = R च्या दिशेने L मुळे होणारे विचनल आणि D_RR = R च्या दिशेने R मुळे होणारे विचलन होय. बहुतेक वेळा आधाराकडील विचलन शून्य असते, तेव्हा D_R = 0 म्हणून R = -F_RR^‒1 . D_RL. आ. २९ (अ) मधील तुळईचे अनिर्धार्यतामान २ होय. B व C येथील आधार-प्रतिक्रिया R1 व R2 म्हणून अतिरिक्त आधार-प्रतिक्रिया धरता B व C येथील आधार-प्रतिक्रियांच्या दिशेने होणारे DR हे विचलन शून्य होय. अशा वेळी R = -F^-1_RR . D_Rl

[

R1

]

= ‒

[

F11 F12

]

-1

[

DR1L

]

…

…

(१४)

R2

F21 F22

DR2L

या उदाहरणात D_R1 म्हणजे बाहेरील भार w मुळे B व C ची R₁ व R2 या दिशांनी होणारी विचलने होत. ही विचलने विचलन-गणनाच्या विविध पद्धतींपैकी कोणत्याही पद्धतीने काढता येतात. त्याचप्रमाणे FRR या नम्यता आव्यूहाचे गुणांक R₁ = 1 व R₂ = 1 धरून R₁ व R₂ च्या दिशेने येणारी विचलने काढून मिळविता येतात. अशा तऱ्हेने अतिरिक्त आधार-प्रतिक्रिया मिळतात व पुढील विश्लेषण संतुलन समीकरणांनी करता येते.

आ. २९ (आ) मध्ये अतिरिक्त घटकयुक्त अंतर्गत अनिर्धार्यता असलेली कैची दाखविली आहे. यातील BD हा घटक अतिरिक्त धरून तो काढून टाकून कैची निर्धार्य केली जाते. अशा प्राथमिक कैचीत R च्या दिशेने बाहेरील भारामुळे येणारे विचलन D_RL = F_RL . P होय, तर प्रत्यक्ष R मुळे येणारे विचलन D_RR होय. आता अशा उदाहरणात F_RR व F_RL हे नम्यता आव्यूह संरचनेच्या निर्देशक दिशांमध्ये माहीत असतो. तसा तो काढणे सोपे असते. अशा वेळी प्रथम घटकाचा नम्यता आव्यूह घटकाच्या निर्देशक दिशांमध्ये काढून मग तो संरचनेच्या निर्देशक दिशांमध्ये रूपांतरित केला जातो. हे रूपांतर तुळईसारख्या संरचनेत लागत नाही, कारण तेथे संरचनेच्या निर्देशक दिशांमध्ये रूपांतरित केला जातो. हे रूपांतर तुळईसारख्या संरचनेत लागत नाही, कारण तेथे संरचनेच्या व घटकाच्या निर्देशक दिशा एकच असतात. हे रूपांतर या पूर्वी विशद केलेल्या विविध सांरचनिक तत्त्वांच्या (उदा., स्थितिस्थापक ऊर्जा तत्त्व, आभासी कार्य तत्त्व, कास्तिल्येनो प्रमेय इत्यादींच्या) साहाय्याने खालीलप्रमाणे मिळते.

P_m = AP …………… (१५)

व 

F = A’F_mA ………….(१६)

यात P_m = घटकाच्या निर्देशक दिशांतील घटकातील प्रेरणा, P = संरचनेच्या निर्देशक दिशांतील संरचनेवरील प्रेरणा, A = बाहेरील भारांचे घटकांमधील अंतर्गत प्रेरणांत रूपांतर करणारा आव्यूह, F_m = घटकाच्या निर्देशक दिशांतील घटकाचा नम्यता आव्यूह, F = संरचनेच्या निर्देशक दिशांतील संरचनेचा नम्यता आव्यूह.

अनिर्धार्य संरचनांच्या बाबतीत एकूण प्रेरणा P या बाहेरील भार L व अतिरिक्त आधार-प्रतिक्रिया R यांनी युक्त असल्याने

Pm = [A_L A_R] [L] ……… (१७)

[R]

F_RL = A’_R F_m A_L

व                              ………(१८)

F_RR = A_‘R F_m A_R

F_m1 0

येथे Fm =        F_m2 ………….. (१९)

⫶ 0  F_mn

यात F_mn हा n व्या घटकाचा त्याच्याच निर्देशक दिशेतील नम्यता आव्यूह होय. कैच्यांमधील फक्त अक्षीय भार असलेल्या घटकाचा हा नम्यात आव्यूह फक्त l /aE इतका असतो (येथे ι = घटकाची लांबी, a = घटकाच्या काटच्छेदाचे क्षेत्रफळ व E = स्थितिस्थापकता गुणांक). आता BD या अतिरिक्त घटकाच्या दिशेने अंतिम विचलन D_R हे I /aE इतके असल्याने D_R चे मूल्य आणि F_RL व F_RR यांची समी. (१८) वरून मिळालेली मूल्ये समी. (१३) मध्ये घातली असता अतिरिक्त आधार-प्रतिक्रिया R मिळू शकते. हे मिळाल्यावर समी. (१७) वरून घटकातील अंतर्गत प्रेरणा Pm मिळतात, तर

---

-D_L = F_LL L + F_LR R

यात F_LL = A’_L Fm A_L आणि

F_LR = A’_L Fm . A_R

या सूत्रांवरून कोणत्याही बिंदूचे विचलन मिळू शकते.  

या पद्धतीचा वापर करताना घटकावर कोणत्या तऱ्हेची सांरचनिक विरूपण क्रिया होते (उदा., अक्षीय विचलन, नमन, घूर्णीय वलन इ.) तीनुसार त्या घटकाचा घटक नम्यता आव्यूह काढावा लागतो. तसेच बाहेरील प्रेरणांमुळे घटकांमध्ये येणाऱ्या अंतर्गत प्रेरणा काढणारे प्रेरणा-रूपांतर आव्यूहही काढावे लागतात. सर्वसाधारणपणे कोणत्याही घटकावर कोणत्याही टोकाकडे खालील ६ (३ रेषीय व ३ परिवलनीय) प्रेरणा येऊ शकतात [पहा : आ. २९ (इ)]. अशा घटकाचा नम्यता आव्यूह खालीलप्रमाणे होय :

येथे ι = घटकाची लांबी, a = घटकाच्या काटच्छेदाचे क्षेत्रफळ, I = घटकाचे घूर्णीय परिबल (त्या त्या अक्षाभोवतीचे), E = स्थितिस्थापकता गुणांक, G = कर्तन दृढता मापांक.

जेव्हा एखादी विरूपण क्रिया एखाद्या घटकावर होत नसेल तेव्हा तेवढा नम्यता गुणांक शून्य घेऊन शेष नम्यता आव्यूह विश्लेषणात घेतला जातो. वेगवेगळ्या विरूपण क्रियांसाठी यावरून स्वतंत्र नम्यता आव्यूहही मिळू शकतात. 

कोणत्याही आव्यूह पद्धतीत बाहेरील प्रेरणा फक्त घटकांच्या सांध्यावर कार्यान्वित होणे आवश्यक असते. जेव्हा एखादा भार घटकाच्या मध्यावर कार्यान्वित होतो तेव्हा तो घटक त्याच्या दोन्ही टोकांस बद्ध धरून अशा भारामुळे त्या टोकाकडे येणाऱ्या प्रेरणा सांध्यावर धरून विश्लेषण केले जाते [पहा : आ. २९ (ई)]. जेव्हा असा परिणाम काढणे शक्य नसेल तेव्हा त्या भाराच्या जागी काल्पनिक सांधा धरून विश्लेषण केले जाते. या पद्धतीने औष्णिक फरकामुळे होणारी विचलने, एखाद्या घटकाची लांबी कमी किंवा जास्त असताना तो संरचनेत बसविण्यामुळे येणाऱ्या दुय्यम प्रेरणासुद्धा काढता येतात.

---

(२) आव्यूह विचलन पद्धती अर्थात दृढता पद्धती : या पद्धतीत नम्यता पद्धतीच्या उलट संरचनेची विचलनीय अनिर्धार्यता लक्षात घेऊन संरचनेच्या आधारांची विचलने अज्ञात राशी म्हणून मानली जातात. संरचनेच्या विश्लेषण करताना प्रथम पहिल्या टप्प्यात संरचना विचलनीय दृष्ट्या निर्धार्य करून म्हणजेच सर्व आधार बद्ध करून प्रत्येक घटकाच्या टोकाकडील बद्ध आधार-प्रतिक्रिया काढल्या जातात. ही संरचना प्राथमिक संरचना व बद्ध-आधार-प्रतिक्रिया या प्राथमिक विश्लेथणाच्या राशी मानल्या जातात. प्रत्यक्षात आधार विचलनीय दृष्ट्या बद्ध नसल्याने ते विश्लेषणाच्या दुसऱ्या टप्प्यात मुक्त केले जातात. म्हणजेच बद्ध-आधार-प्रतिक्रियांच्या विरोधी प्रेरणा सांध्यांवर कार्यान्वित केल्या जातात. त्यामुळे होणारी सांध्यांची विचलने मिळविणे व घटकांमधील प्रेरणा काढणे हा विश्लेषणाचा दुसरा टप्पा होय. या टप्प्यास पूरक विश्लेषण महणतात. संरचनेवर कार्य करणाऱ्या प्रेरणांमुळे होणारी संरचनेची विचलने मिळविणे हे कित्येक संरचनांच्या बाबतीत तितकेसे सोपे नसल्याकारणाने पण संरचनेच्या घटकांचे विचलन व त्यामधील प्रेरणा यांचा संबंध प्रस्थापित करणारी घटकांचे प्रेरणा-विचलन सूत्रे मिळविणे सहज शक्य असल्याने या पद्धतीत घटकाकडून संरचनेकडे असा प्रवास करणे सोयीचे ठरते. त्यामुळे या पद्धतीत सर्वांत प्रथम P_m = s_mD_m ह्या प्रेरणा-विचलन संबंधाच्या आधारे घटकाचा दृढता आव्यूह घटकाच्याच निर्देशक दिशांमध्ये काढला जातो. ह्या आव्यूहाचे गुणांक अर्थातच त्या घटकावर होणाऱ्या सांरचनिक विरूपण क्रियेच्या प्रकारावरून ठरविले जातात. या दृढता आव्यूहाच्या प्रत्येक स्तंभातील गुणांक म्हणजे घटकावरील D_m या सर्व विचलनांपैकी एका वेळी एक विचलन एकक मूल्याचे धरून (व त्याच वेळेस अन्य विचलने शून्य धरून) घटकाच्या दोन्ही टोकांना येणाऱ्या अंतर्गत प्रेरणा होत. उदा., केवळ अक्षीय भार घेऊ शकणाऱ्या घटकाच्या दोन टोकांकडे P₁, P₂ इतक्या दोन प्रेरणा (आधार-प्रतिक्रिया) व दोन अक्षीय विचलने D₁, D₂ येऊ शकतात [पहा : आ. ३० (अ)] म्हणजेच या घटकाचा दृढता आव्यूह २×२ या श्रेणीचा (क्रमाचा) असेल.

आ. ३० (आ) मध्ये D₁ = 1 व D₂ = 0 धरता, १ व २ या टोकांकडील आधार-प्रतिक्रिया I /aE व – l /aE या दृढता आव्यूहाच्या पहिल्या स्तंभातील गुणांक होत आणि आ.३० (इ) मध्ये D₁ व D₂ धरता, १ व २ टोकांकडील आधार-प्रतिक्रिया ‒ /aE व – l /aE या दृढता आव्यूहाच्या दुसऱ्या स्तंभातील गुणांक होत. यावरून या घटकाचा दृढता आव्यूह खालीलप्रमाणे मिळतो. 

sm = s₁₁ s₁₂ l 1 ‒1 

s₂₁ s₂₂ = aE ‒1     1  

सर्वसाधारणपणे कोणत्याही घटकाच्या टोकास येणारी ६ विचलने धरल्यास घटकाचा सर्वसाधारण दृढता आव्यूह १२×१२ या श्रेणीचा येईल. तुळईमध्ये घटकाच्या टोकाकडील फक्त परिबलने लक्षात घेतल्यास २×२ श्रेणीचा, परिवलनांबरोबर पार्श्व दिशेने येणारी रेषीय विचलने लक्षात घेतल्यास ४×४ श्रेणीचा, उभ्या प्रतलातील चौकटींच्या सांध्यावरील उभ्या व आडव्या दिशेने येणारी रेषी विचलने व परिवलन लक्षात घेतल्यास ६×६ श्रेणीचा, तर आडव्या प्रतलातील जात्य (एकमेकांना काटकोनात असलेल्या) जालांच्या बाबतीत प्रत्येक सांध्यावरील दोन अक्षांभोवतालची परिवलने व उभ्या भाराच्या दिशेने येणारे रेषीय विचलन लश्रात घेता ६ × ६ श्रेणीचा असे घटक दृढता आव्यूह येतात.

संरचनेच्या विश्लेषणासाठी संरचनेच्या सांध्यांवर कार्यान्वित होणाऱ्या प्रेरणा व संरचनेच्या सांध्यांचे विचलन या सर्वांना जोडणारा संरचनेचा एकूण दृढता आव्यूह मिळवणे हे आवश्यक असते. संरचना अनेक घटकांनी बनलेली असल्याने संरचनेचा एकूण दृढता आव्यूह सर्व घटकांचे स्वतंत्र दृढता आव्यूह एकत्र करून मिळू शकतो पण वेगवेगळ्या घटकांच्या दिशा वेगवेगळ्या असल्याने व घटकांचे दृढता आव्यूह त्या त्या निर्देशक दिशांना असल्याने सर्व घटकांच्या दृढता आव्यूहाचे एकत्रीकरण करण्यापूर्वी ते सर्व संरचनेच्या निर्देशक दिशांमध्ये निर्देशक-दिशा-रूपांतर आव्यूहाच्या साहाय्याने खाली दर्शविल्याप्रमाणे रूपांतरित करून घ्यावे लागतात.

s = T’.s_m.T

येथे T हा निर्देशक-दिशा-रूपांतर आव्यूह असून s व s_m हे घटकाचे अनुक्रमे संरचनेच्या व घटकाच्या निर्देशक दिशांमधील दृढता आव्यूह होत.

---

वरील रूपांतर झाल्यावर सर्व घटकांच्या संरचनेच्या निर्देशक दिशांतील रूपांतरित घटक आव्यूहांचे एकत्रीकरण करून संरचनेचा एकूण दृढता आव्यूह S मिळविला जातो. हा संरचनेवरील भार व तिचे विचलन यांचा खालील संबंध प्रस्थापित करतो.

P = S.D

वरील समीकरणामध्ये संरचनेच्या D या एकूण विचलनांपैकी काही विचलने ज्ञात असतात, तर काही अज्ञात असतात. ज्ञात विचलने अर्थातच संरचनेच्या आधाराकडील होत. बद्ध-आधाराचे रेषीय परिवलनीय विचलन शून्य होय. खचलेल्या आधाराचेही विचलन हे ज्ञातच असते. विश्लेषणामध्ये अज्ञात विचलन ठरविणे एवढाच भाग प्रमुख असल्याने वरील समीकरणाच्या विश्लेषणाच्या सोयीसाठी खालीलप्रमाणे खंडकरण केले जाते.

 P =      P_L =   S_LL S_LR D_L

P_R S_RL S_RR D_R

यात D_L = अज्ञात विचलने, D_R = ज्ञात विचलने, P_L अज्ञात विचलनाचे जागी असणाऱ्या प्रेरणा आणि P_R = ज्ञात विचलनांचे जागी असणाऱ्या प्रेरणा. यावरून

P_L = S_LL D_L + S_LR D_R

∴D_L = S^-1_LL [P_L –S_LR D_R]

 D_R ही ज्ञात विचलने सर्वसाधारणपणे आधारकडील असल्याने शून्य असतात अशा वेळी

D_L = S^-1_LL P_L

हे दृढता पद्धतीतील प्रधान समीकरण होय.  यावरून हे लक्षात येईल की, संरचनेच्या एकूण दृढता आव्यूहापैकी फक्त अज्ञात विचलनांशी संबंधित असलेला दृढता आव्यूहाचा भागच फक्त विश्लेषणात आवश्यक असतो आणि कित्येक वेळा तेवढाच भाग स्वतंत्रपणे मिळवून विश्लेषण केले जाते. एकदा D_L ही विचलने काढल्यावर शून्य विचलन असलेल्या आधाराच्या प्रतिक्रिया P_R या खालील समीकरणावरून मिळतात.

 P_R – S_RL D_L + S_RR D_R

अज्ञात विचलने D_L मिळाल्यानंतर त्यावरून घटकांमध्ये येणाऱ्या प्रेरणा P_m = s_mD_m या समीकरणाने मिळतात. त्यासाठी संरचनेच्या निर्देशख दिशांमधील D_L ही विचलने अक्षांच्या परिवलन रूपांतर आव्यूहाने D_m मध्ये रूपांतरित करून घ्यावी लागतात. तुळईमध्ये D_L व D_M ही एकच असतात कारण घटक व संरचना यांच्या निर्देशक दिशा एकच असतात. विश्लेषणाची ही दुसऱ्या टप्प्यातील क्रिया पूरक विश्लेषण म्हणून मानली जाते व यातील राशी पूरक राशी म्हणून समजल्या जातात. विश्लेषणाचे अंतिम उत्तर प्राथमिक राशी व पूरक राशी यांच्या बेरजेने मिळते.

---

या सर्व विवेचनावरून हे लक्षात येईल की, ही पद्धती व अभिजात पद्धतींमधील उतार-विचलन पद्धती यांत खूप साम्य आहे. यात फरक इतकाच की, उतार-विचलन पद्धती लहान संरचनांनाच फक्त सुयोग्य ठरते व मानवी प्रयत्नाने हात-गणनाने सोडविता येते, तर ही आव्यूह पद्धती अनेक अज्ञात राशी असलेल्या मोठ्या संरचनांच्या विश्लेषणासाठी व तीही संगणाकाचे साहाय्य उपलब्ध असल्यासच उपयोगी पडते. ही पद्धती अनेकाधार तुळ्या, स्थितिस्थापक आधारावरील तुळ्या, तुळ्यांचे जाल, दृढ चौकटी, अनेक मजली सांगाडे, कैच्या, त्रिमितीय कैच्या, मनोरे इ. जालक रचना, कमानी वगैरे रेषीय घटकांनी युक्त अशा कोणत्याही संरचनांच्या विश्लेषणासाठी आपले एकमेवाद्वितीय असे स्थान १९८० सालामध्येही टिकवून आहे. नवीन प्रचारात येत असलेल्या सूक्ष्म प्रक्रियकांसाठी [⟶संगणक] व कित्येक संगणकांसाठी या पद्धतीच्या विश्लेषणाची कार्यक्रमणे (क्रमवार करावयाच्या क्रियांच्या तपशीलवार याद्या) सुद्धा उपलब्ध झालेली आहेत. त्यामुळे ह्या पद्धतीत जवळ जवळ विश्लेषणाच्या अजाराचेच स्वरूप आज आले आहे.

(३) परिमित घटक पद्धती : १९५० ते १९६० या दशकात विमानांच्या सांगाड्यांसारख्या क्लिष्ट संरचनांच्या विश्लेषणासाठी झालेल्या संशोधन प्रयत्नांतून एका व्यापक व क्रांतिकारी अशा परिमित घटक पद्धतीचा जन्म झाला. आज ही पद्धती फक्त संरचनाशास्त्रज्ञांची किंवा गणितज्ञांची मक्तेदारी राहिली नसून या पद्धतीचा वापर शास्त्रीय जगतातील व तंत्रविद्येच्या सर्व शाखांमधून सातत्यक (संततीय) किंवा क्षेत्रीय समस्या वा प्रश्नांची [⟶ क्षेत्र सिद्धांत] उकल करण्यासाठी या पद्धतीया कशा तऱ्हेने उपयोग होतो या दृष्टिकोनातूनच ओळख करून दिलेली आहे. संरचना विश्लेषणाच्या आव्यूह पद्धतींचा उपयोग फक्त रेषीय घटकांनी युक्त अशा संरचनांच्या विश्लेषणासाठीच होत असल्याने प्रतलीय किंवा घन घटकांनी युक्त अशा वेगवेगळ्या सातत्यक संरचनांसाठीही आव्यूह पद्धतींचा वापर कसा करता येईल या प्रयत्नातून सातत्यकाच्या विश्लेषणासाठी परिमित घटकाच्या कल्पनेचा उगम झाला. या परिमित घटक पद्धतीत सातत्यक म्हणजे संततीय क्षेत्र हे पृथक् पृथक् अशा छोट्या छोट्या परिमित घटकांनी बनले आहे असे गृहीत धरले जाते. परिमित घटकांचा आकार, प्रकार व घटकांचे वितरण हे संरचनेचा आकार, प्रकार, समस्येचे स्वरूप यांनुसार पाहिजे तसा घेता येणे या पद्धतीत शक्य असल्याने वाटेल त्या अनियमित आकारांच्या, सीमांच्या, अनियमित गुणधर्म असलेल्या संरचनांचे कोणत्याही प्रकारचे (स्थितिकीय, गतिकीय, औष्णिक, कंपन इ.) विश्लेषण करणे या पद्धतीने शक्य होते, हा या पद्धतीचा सर्वांत मोठा लक्षणीय गुण होय (उदा., वेगवेगळ्या गुणधर्मांनी युक्त अशा मातीचे थर असलेल्या मातीच्या धरणाचे विश्लेषण, पायातील मातीचे विविध थर व प्रकार असलेल्या स्तरांमधून होणारे प्रतिवलांचे, भूमिगत पाण्याच्या प्रवाहाचे, पाण्याच्या दाबाचे विश्लेषण, औष्णिक पात्रातून होणारे उष्णतेचे वहन, यंत्रे व अवजारांतील प्रतिबलांचे केंद्रीभवन इ. असंख्य व विविध प्रकारच्या समस्या). मूलतः ही पद्धती संरचनांच्या बाबतीत आव्यूह पद्धथी प्रतलीय व घन घटकांनी युक्त अशा संरचनांना लावायच्या प्रयत्नातून झाल्याने दोन्हीची कार्य पद्धती तत्त्वतः जवळ जवळ एकसारखीच आहे, हे खालील विवेचनावरून कळेलच.

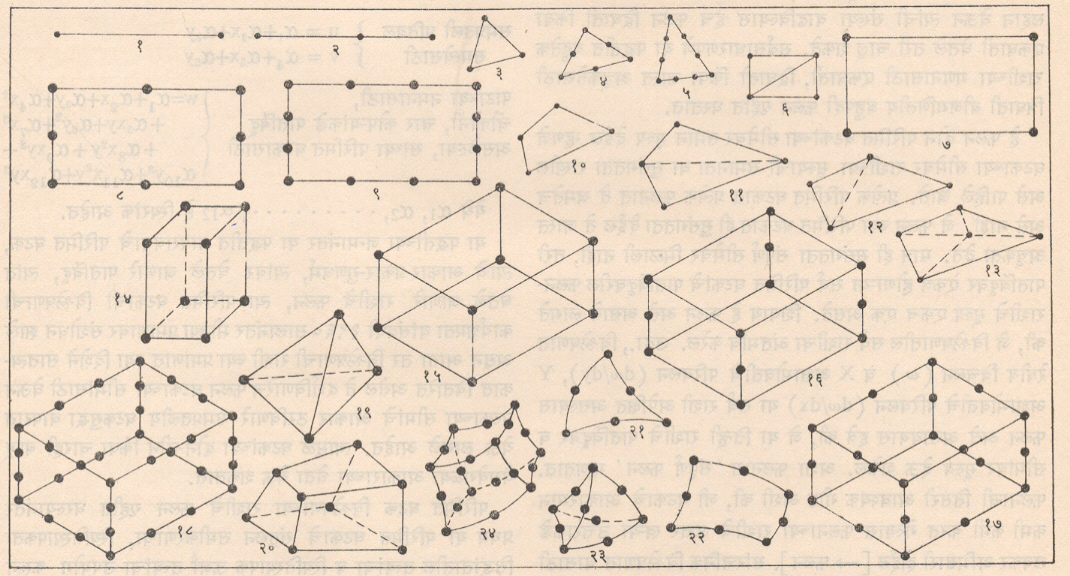
सर्वांत प्रथम संरचनेच्या आकारनुसार, समस्येच्या प्रकारानुसार, पदार्थांच्या गुणधर्मांनुसार, संरचनेतील पदार्थांच्या वितरणानुसार व एकूण विश्लेषणाच्या कोणत्या बाबीत वा भागात आपल्याला स्वारस्य आहे त्यानुसार योग्य अशा छोट्या छोट्या परिमित घटकांमध्ये संरचनेचे काल्पनिक पृथकीकरण केले जाते. हे परिमित घटक एकरेषीय, एकप्रतलीय, त्रिमितीय अर्थात घन असे, वक्र किंवा सरण रेषा वा प्रतल यांनी सीमांकित असलेले असे कोणत्याही आकाराचे व आकारमानाचे भाग किंवा खंड असू शकतात. चौकोनी पाट किंवा लाद्यांसाठी आयताकृती, वर्तुळाकार संरचनांसाठी वृत्तखंडाच्या आकारचे तर अनियमीत सीमांकित संरचनांसाठी त्रिकोणाकृती किंवा चौकोनाकृती परिमित घटक घेतले जातात. विश्लेषणात ज्या श्रेणीची अचूकता हवी असेल त्यानुसार परिमित घटकांची संख्या व आकारमान ठरविले जाते. संरचनेच्या विश्लेषणात वापरले जाणारे परिमित घटकांचे विविध नमुने आ. ३१ मध्ये दाखविले आहेत. 

---

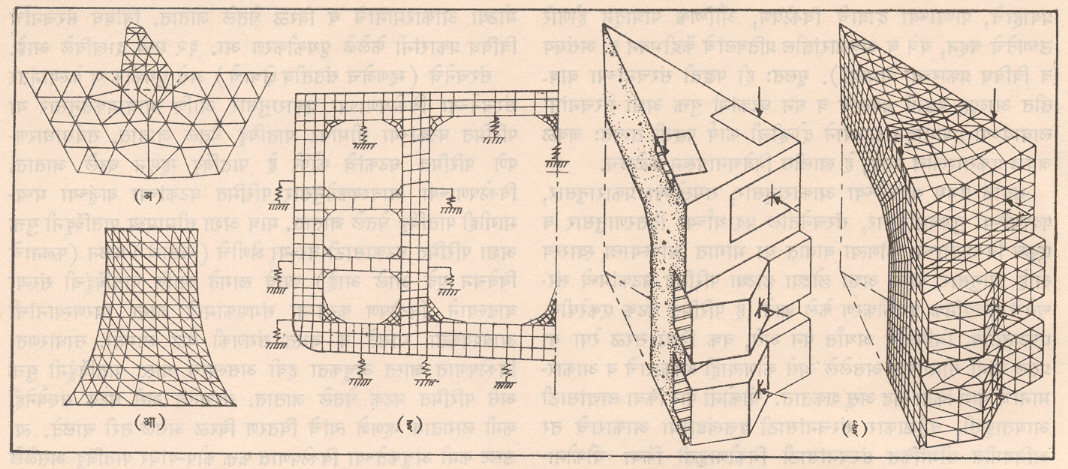
जास्त अचूकता अपेक्षित असल्यास घटकांची संख्या जास्त व आकारमान लहान असावयास हवे. संरचनेतील ज्या एखाद्या विशिष्ट भागामध्ये (उदा., चक्राच्या दात्यांच्या टोकाकडील भागांत) प्रतिबलाचे (फलनाचे) केंद्रीकरण अपेक्षित असल्यास तेवढ्या ठिकाणी घटकांचे केंद्रीकरण केले जाते (म्हणजे ते जवळजवळ व लहान आकारमानाचे घेतले जातात). ठोकळमानाने विश्लेषण करावयाचे असल्यास (उदा., मोठ्या आकारमानाची धरणे, पायामधील दूरचा भाग इ.) घटक मोठ्या आकारमानाचे व विरळ घेतले जातात. विविध संरचनांचे विविध प्रकारांनी केलेले पृथकीकरण आ. ३२ मध्ये दाखविले आहे.

संरचनेचे (म्हणजेच संततीय क्षेत्राचे) असे पृथकीकरण केल्यानंतर संरचनेच्या विश्लेषणाच्या प्रकारानुसार आणि आवश्यकतेनुसार या परिमित घटकांच्या सीमांवर पातबिंदू घेतले जातात. सर्वसाधारणपणे परिमित घटकाचे कोपरे हे पातबिंदू म्हणून धरले जातात. विश्लेषणाच्या आवश्यकतेनुसार परिमित घटकांच्या बाजूंच्या मध्यभागीही पातबिंदू घेतले जातात. मात्र अशा सीमामध्य पातबिंदूंनी युक्त अशा परिमित घटकासाठी वरच्या श्रेणीचे (घाताचे) फलन (फलनाचे विवेचन पुढे आले आहे) घ्यावे लागते आणि पातबिंदूंची संख्या वाढल्याने विश्लेषण करताना संगणकामध्ये जास्त स्मरणस्थानांची आवश्यकता भासते व जास्त संगणकी वेळ लागतो. साधारणतः विश्लेषणात जास्त अचूकता हवी असल्यास जास्त पातबिंदूंनी युक्त असे परिमित घटक घेतले जातात. संरचनेत असे घटक संख्येनेही कमी लागतात म्हणजे त्यांचे वितरण विरळ असले तरी चालते. त्या उलट कमी अचूकतेच्या विश्लेषणात फक्त कोपऱ्यांवर पातबिंदू असलेले परिमित घटक घेणे हे संगणकी वेळ, लागणारी स्मरणस्थाने व सुकरता या दृष्टीने सोयीचे ठरते. सर्व परिमित घटक या पातबिंदूंशी एकमेकांस जोडले आहेत असे धरले जाते म्हणजे या पातबिंदूंच्या सर्व बाजूंनी येणाऱ्या परिमित घटकांचे या पातबिंदूवरील फलन एकच असते. विश्लेषणाची जी राशी असेल (उदा., विचलन, प्रेरणा, प्रतिबल, परिबल, तापमान, कंप्रता-एका सेकंदात होणाऱ्या कंपनाची संख्या इ.) ती सर्व पातबिंदूंवर काढली जाते. म्हणून ज्या ठिकाणी ही राशी काढावयाची असेल त्या जागी पातबिंदू घेणे आवश्यक असते. यानंतर परिमित घटकाच्या अंतर्गत क्षेत्रातील विश्लेषणाच्या राशीचे वितरण दर्शविणारे फलन (उदा., विचलन काढावयाचे असल्यास विचलनाच्या वितरणाचे फलन) गृहीत धरले जाते. उदा., एककेंद्री भारामुळे होणाऱ्या तुळईच्या रेषीय विचलनासाठी तृतीय घाती फलन हे सर्वांत अचूक होय पण परिमित घटकाचे आकारमान लहान घेऊन त्यांची संख्या वाढविल्यास हेच फलन द्विघाती किंवा एकघाती घेतले तरी चालू शकते. सर्वसाधारणपणे या पद्धतीत बहुतेक राशींच्या गणनासाठी एकघाती, द्विघाती किंवा जास्त अचूकतेसाठी त्रिघाती बीजगणितीय बहुपदी फलन गृहीत धरतात.

---

हे फलन दोन परिमित घटकांच्या सीमेवर समान मूल्य देईल म्हणजे घटकाच्या सीमेवर राशीच्या मूल्याची समानता वा सुसंगतता राखील असे पाहिले जाते. प्रत्येक परिमित घटकात प्रत्येक फलनात ते जमतेच असे पाहिले जाते. प्रत्येक परिमित घटकात प्रत्येक फलनात ते जमतेच असे नाही. जे फलन ज्या परिमित घटकात ही सुसंगतता देईल ते जास्त अचूकता देते. मात्र ही सुसंगतता संपूर्ण सीमेवर मिळाली नाही, तरी पातबिंदूवर एकत्र होणाऱ्या सर्व परिमित घटकांचे पातबिंदूवरील फलन-राशीचे मूल्य एकच एक असते. शिवाय हे फलन असे असावे लागते की, जे विश्लेषणातील सर्व राशींचा अंतर्भाव करेल. उदा., विश्लेषणात रेषीय विचलन (ω) व X अक्षाभोवतीचे परिवलन (dω/dy), Y अक्षाभोवतीचे परिवलन (dω/dx) या सर्व राशी अपेक्षित असल्यास फलन असे असावयास हवे की, जे या तिन्ही राशींचे पातबिंदूवर व सीमांवर मूल्य देऊ शकेल. अशा फलनास ‘संपूर्ण फलन’ म्हणतात. फलनाची तिसरी आवश्यक गोष्ट अशी की, जी घटकाचे आकारमान कमी कमी करत गेल्यास फलनाच्या राशीचे उत्तर खऱ्या उत्तराकडे लवकर अभिसारी होईल [⟶फलन]. सांरचनिक विश्लेषणात यासाठी फलनास पुढील तीन गोष्टी साध्य करणे आवश्यक असते : (१) दृढ वस्तूच्या एकविध गतीमुळे कोणतीही प्रतिविकृती घटकात येता कामा नये. (२) पातबिंदूच्या विचलनाशी सुसंगत अशी स्थिर प्रतिविकृती अवस्था ह्या फलनाने दिली पाहिजे. (३) सीमेवरील प्रतिविकृती अपरिमित असता कामा नये. अशा तऱ्हेने गृहीत धरल्या जाणाऱ्या फलनाकडून राशींची दोन घटकांच्या सीमांवरील सुसंगता, संपूर्णता व द्रुत अभिसारिता या तीन अटींची पूर्तता होणे अपेक्षित असते. जे फलन जास्तीत जास्त अटी पूर्ण करू शकेल ते चांगले मानले जाते. अशा चांगल्या फलनांनी युक्त चांगले परिमित घटक जास्त अचूकता देतात पण संगणकी वेळही जास्त घेतात. स्थितिस्थापक विश्लेषणातील समप्रतली प्रतिबल समस्येसाठी व पाटांच्या नमन विश्लेषणासाठी त्रिकोणी व चौकोनी घटकांसाठी वापरली जाणारी काही फलने खाली दिली आहेत :

समप्रतली प्रतिबल समस्येसाठी	}	u = α1+α 2x+ α3y
		v = α4+α 5x+ α6y

पाटाच्या नमनासाठी, चौकोनी,चार कोपऱ्यांकडे पातबिंदू असलेल्या,साध्या परिमित घटकासाठी } w = α₁+α₂x+ α₃y + α₄x² +α₅xy+ α₆y²+α₇x³ +α₈x³y+ α₉xy²+ α₁₀y³+α₁₁x³y+ α₁₂xy³

येथे α₁, α₂, ……., α₁₂ हे स्थिरांक आहेत. 

या पद्धतीच्या जन्मानंतर या पद्धतीत वापरावयाचे परिमित घटक, त्यांचे आकार-प्रकार-गुणधर्म, त्यांवर घेतले जाणारे पातबिंदू, त्यांत घेतले जाणारे राशीचे फलन, त्या परिमित घटकाची विश्लेषणाची कार्यक्षमता यांसंबंधी १९६० सालानंतर मोठ्या प्रमाणावर संशोधन झाले असून आता तर विश्लेषणाची राशी ज्या प्रमाणात ज्या दिशेने सातत्यकात वितरित असेल ते दर्शविणारेच फलन घटकाच्या सीमांसाठी घेऊन घटकाच्या सीमांचे आकार ठरविणारे समप्रतलीय घटकसुद्धा वापरात येऊ लागले आहेत. त्यामुळे घटकांच्या दोन-तीन किंवा चारही बाजू वेगवेगळ्या आकारच्या घेता येऊ शकतात.

परिमित घटक विश्लेषणाच्या राशीचे फलन गृहीत धरल्यानंतर प्रथम या परिमित घटकाचे संतुलन समीकरणाचा, स्थितिस्थापकता सिद्धांततील तत्त्वांचा व स्थितिस्थापक ऊर्जा तत्त्वाचा उपयोग करून अंतर्गत विश्लेषण करून त्या घटकाचे दृढता आव्यूह व अंतर्गत प्रेरणा-विचलन संबंध दर्शविणारा आव्यूह त्या घटकाच्या निर्देशक दिशांनी काढले जातात. यानंतर या परिमित घटकाच्या दृढता आव्यूहाचे संरचनेच्या निर्देशक दिशांना रूपांतर करून अध्यारोपणाच्या संरचनेच्या तत्त्वाच्या आधारे संरचनेचा एकूण दृढता आव्यूह काढला जातो. या आव्यूहाच्या साहाय्याने दृढता पद्धतीतील तत्त्वांच्या साहाय्याने पातबिंदूवर कार्यान्वित असलेल्या प्रेरणांवरून या पातबिंदूचे विचलन काढले जाते. एकदा पातबिंदूचे विचलन काढल्यावर घटकांमधील अंतर्गत प्रेरणा प्रेरणा-विचलन संबंध दर्शविणाऱ्या आव्यूहावरून मिळविल्या जातात आणि असा तऱ्हेने संरचनेचे विश्लेषण पूर्ण होते. थोडक्यात, या विश्लेषण पद्धतीचे पुढील प्रमुख टप्पे होत : (१) संरचनेचे पृथकीकरण, (२) परिमित घटकाची निवड व घटकाच्याच गुणधर्मांचे अंतर्गत विश्लेषम व त्यावरून घटकांचा दृढता आव्यूह मिळविणे, (३) सर्व घटकांच्या दृढता आव्यूहाच्या एकत्रीकरणाने संरचनेचा दृढता आव्यूह मिळविणे, (४) तो सोडवून पातबिंदूंच्या विचलनांचे निर्धारण आणि शेवटी (५) घटकातील अंतर्गत प्रेरणांचे गणन.

वर फक्त दृढता पद्धतीचा परिमित घटक पद्धतीतील वापर विशद केला आहे. याच तऱ्हेने नम्यता पद्धतीचाही परिमित घटक विश्लेषणात उपयोग केला जातो. इतकेच काय पण आता तर नम्यता-दृढता या दोन्ही पद्धतींचा मिश्र (संकरित) वापरसुद्धा केला जातो.  

पुढील भाग पाहण्यासाठी येथे क्लिक करा

“