बांधकाम संरचना सिद्धांत व अभिकल्प

बांधकाम :संरचना सिद्धांत व अभिकल्प : निवारा ही मानवमात्राची एक प्रमुख गरज होय. हा निवारा मानवास निसर्गाच्या ऊन, पाऊस, वारा, अग्नी, भूकंप यांसारख्या घटकांपासून संरक्षण देतो. त्यासाठी निसर्गानेच उपलब्ध करून दिलेल्या सामग्रीचा उपयोग करून मानव अशी काही वास्तुरचना निर्माण करतो की, जीमुळे त्याला हा निवारा मिळतो. वास्तूच्या या रचना स्वरुपास संरचना म्हणतात. निसर्गाच्या विविध घटकांपासून संरक्षण देणे एवढाच हेतू या वास्तूचा नसून कार्यासाठी लागणारी जरुर ती जागा उपलब्ध करून देणे, त्या वास्तूवर येणारे विविध प्रकारचे अचल व चल भार विविध घटकांमधून पायाकडे सुरक्षितपणे वाहून नेणे हेही तितकेच महत्त्वाचे अन्य हेतू आहेत. औद्योगिक क्रांतिपूर्व काळापर्यंत स्थापत्याविषयक वास्तू उदा., इमारती, पूल, धरणे, जलसेतू, धारकभिंती इत्यादींचाच फक्त संरचना म्हणून विचार केला जात असे पण औद्योगिक क्रांतीनंतर झालेल्या प्रगतीमुळे त्या पुढील काळात आगगाड्यांचे डबे, मोटारींचे साटे, जहाजे, विमानांचे सांगाडे, दाबपात्रे, बाष्पपात्रे, पाण्याच्या व तेलाच्या टाक्या, औष्णिक विद्युत् केंद्रांना लागणारे शीतक मनोरे, अन्नधान्य किंवा खते साठविण्याची कोठारे, कोठ्या व कणग्या, कोळसा, खनिज इ. साठविणारे पेटारे, धरणाचे दरवाजे, कालव्यातील जलपाश, खनिज इ. साठविणारे पेटारे, धरणाचे दरवाजे, कालव्यातील जलपाश, विमानगृहे, विमानतळाच्या धावपट्ट्या, बंदरातील धक्के, विजेच्या तारांसाठी उंच मनोरे, रेडिओ दूरदर्शक (दुर्बिणी), रेडिओ व दूरचित्रवाणी प्रेषणाच्या आकाशकांचे (अँटेनांचे) मनोरे आणि अत्याधुनिक काळातील रॉकेट, अवकाशयाने व कृत्रिम उपग्रह यांचे सांगाडे, मोठमोठ्या यंत्रांचे साटे व त्यांचे भाग या सर्वांचा‘संरचना’म्हणून विचार करावा लागतो. यावरून असे दिसून येईल की, अशा विविध प्रकारच्या वस्तू व वास्तू यांसाठी संरचना लागत असल्याने संरचनेचा हेतू केवळ निसर्गाच्या घटकांपासून संरक्षण देणे, कार्योपयुक्त जागा देणे व तिच्यावर येणाऱ्‍या भारांचे सुरक्षितपणे वहन करणे एवढाच राहिलेला नसून पाणी, विविध द्रव अथवा इतर पदार्थ सुरक्षितपणे धारण करून त्यांचा साठा करणे, चलभारामुळे होणाऱ्‍या कंपनांपासून संरक्षण करणे इ. हेतूसुद्धा संरचनेस साध्य करावे लागतात.

संरचनांचे वर्गीकरण व प्रकार : संरचनांचे खाली दर्शविल्याप्रमाणे विविध प्रकारे वर्गीकरण केले जाते.

(१) संरचनेच्या स्वरुपावर आधारित वर्गीकरण : (अ) रैखिक संरचना : या रेखीय घटकांनी युक्त असतात उदा., खांब, तुळ्या, बहाल, कैच्या, कमानी, मनोरे व इतर जालक रचना (आ) पृष्ठीय संरचना : या पृष्ठीय घटकांनी युक्त असतात उदा., लाद्या, पाट, घडीच्या लाद्या, कवचे, घुमट इ. (इ) सघन त्रिमितीय संरचना : उदा., यंत्राचे भाग, लाटारोधक ठोकळे आणि (ई) संयुक्त संरचना : ज्यांत रेखीय व पृष्ठीय अशा दोन्ही प्रकारच्या घटकाचा संयुक्तपणे वापर होतो उदा, आधारतीरयुक्त लाद्या, वक्रतीरयुक्त कवचे, तीरयुक्त घुमट इत्यादी.

(२) संरचनेच्या कार्याच्या प्रकारावर आधारित वर्गीकरण : (अ) निवारा देणे : उदा., इमारती (आ) वाहतूक चलभार वाहून नेणे : उदा., पूल, जलसेतू (इ) द्रव किंवा अन्य वस्तू साठविणे अथवा धारण करणे : उदा., टाक्या, कोठारे, कणग्या, धरणे, धारकभिंती, जलधारक दरवाजे, जलपाश इ. (ई) आधार देणे : उदा., मचाण, पहाड, आडके, रेडिओ व दूरदर्शक मनोरे (उ) साटा होणे : उदा., यंत्रे, मोटारी, आगगाड्यांचे डबे व एंजिने, विमाने, जहाजे इत्यादींचे सांगाडे (ऊ) आच्छादन देणे : उदा., छप्परे.

(३) भारवहन कशा तऱ्‍हेने होते यावर आधारित वर्गीकरण : (अ) भारवाही संरचना : (लादी व भिंतीयुक्त इमारती). ज्यांत भारांचे वहन प्रामुख्याने लादी व भिंती यांमधून होते (आ) सांगडी संरचना : ज्यात भारांचे वहन प्रामुख्याने तुळई, बहाल, कमान व स्तंभ यांसारख्या रेखीव घटकांद्वारे होते. यात भिंतीवर भार येत नाही (इ) पटल-तीरयुक्त संयुक्त संरचना : ज्यांत भारांचे वहन तीर व पटल यांच्या संयुक्त क्रियेने होते. उदा., विमानांचे सांगाडे, तीरयुक्त तल.

(४) संरचनेच्या घटकांच्या जोडणीच्या प्रकारावर आधारित वर्गीकरण : (अ) दृढ चौकटी संरचना: यांत संरचनेचे घटक दृढ (परिबल-निरोधी अर्थात परिवलन होण्यास रोध करणाऱ्‍या) सांध्यांनी जोडलेले असतात (आ) साधी संरचना : यांत घटक साध्या कीलयुक्त संध्यांनी जोडलेले किंवा नुसते एकावर एक टेकलेले असतात. साधे सांधे परिबल-निरोधन करू शकत नाहीत.

(५) भारवहन करताना संरचनेच्या घटकांवर येणाऱ्‍या बलांच्या प्रकारांवर आधारित वर्गीकरण : (अ) ताण संरचना : ज्यांत भारांचे वहन घटकांमधील ताण प्रेरणेने होते उदा., निलंबी पूल, पोलादी दोरखंडयुक्त छपरे, रज्जु-आधारित पूल (आ) संकोची प्रेरणायुक्त संरचना : ज्यांत भारांचे वहन घटकांतील संकोची प्रेरणेने होते उदा., कमानी, घुमट, कवचे (इ) अक्षीय प्रेरणायुक्त संरचना : ज्यांत घटकांमध्ये फक्त अक्षीय प्रेरणा येते (मग ती ताण प्रेरणा किंवा संकोची प्रेरणा अशा कोणत्याही प्रकारची असो) उदा., कैच्या (ई) नमन प्रेरणायुक्त संरचना : ज्यांत घटकांमध्ये भाराचे वहन घटकांतील नमन (वाकविणाऱ्‍या किंवा वळविणाऱ्‍या) प्रेरणेने केले जाते उदा., पाट, तुळई, बहाल, लादी (उ) संयुक्त प्रेरणायुक्त संरचना : ज्यांत अक्षीय प्रेरणा व नमन प्रेरणायुक्त अशा दोन्हीद्वांरे भारांचे वहन होते उदा., दृढ चौकटी.

(६) बांधकामात वापरण्यात आलेल्या पदार्थाच्या प्रकारावर आधारित वर्गीकरण : दगडी संरचना, लाकडी संरनचा, पोलादी संरचना, काँक्रीटची संरचना, पूर्वप्रतिबलित (काँक्रीटमधील सळ्यांना ताण देऊन नंतर त्या काँक्रीटमध्ये गाडून तयार केलेल्या) काँक्रीटची संरचना, पूर्वप्रतिबलित धातूची संरचना, लघुभारी (वजनाने हलक्या) धातूची संरचना इत्यादी.

(७) शास्त्रीय विश्लेषणावर आधारित वर्गीकरण : (अ) स्थितिकीदृष्ट्या (समतोलाच्या समीकरणांनी) निर्धार्य संरचना व (आ) स्थितिकीदृष्ट्या अनिर्धार्य संरचना.

(८) संरचनेच्या पदार्थांच्या सांरचनिक गुणधर्मांवर आधारित वर्गीकरण : (अ) स्थितिस्थापक संरचना : ज्यांत सर्व घटक व संरचना स्थितिस्थापक गुणधर्मानुसार (आकार व आकारमान यांत बदल करणारी प्रेरणा काढून घेतल्यावर मूळ स्थिती परत प्राप्त होण्याच्या गुणधर्मानुसार) वर्तन करतात (आ) अस्थितिस्थापक संरचना (इ) आकार्य संरचना : ज्यांत संरचनेचे घटक आकार्य गुणधर्मानुसार (एका ठराविक मर्यादेपक्षा जास्त प्रेरणा लावल्यास आकारात वा आकारमानात कायम स्वरुपाचा बदल होण्याच्या गुणधर्मानुसार) वर्तन करतात (ई) भंजनशील संरचना : ज्यांत संरचनेचे घटक लवचिकपणाच्या अभावाचा म्हणजे ठिसूळपणाचा गुणधर्म दाखवितात.

वास्तुरचनेचा इतिहास, उत्क्रांती व विकास : वास्तूच्या बांधकामाचा विचार करता वास्तूच्या संरचनेचे स्वरुप व तीवरील भाराच्या वहनाचे संरचनाशास्त्र हे एकमेकांशी अत्यंत निगडित असल्याचे लक्षात येते. तेव्हा संरचनाशास्त्राचा व तंत्राचा विकास पाहत असताना वास्तुरचनेच्या इतिहासाचा मागोवा घेणे प्राप्त ठरते. बांधकामासाठी वापरण्यात येणाऱ्‍या सामग्रीच्या प्रकारांवर आणि गुणधर्मांवर संरचनेचे स्वरुप प्रामुख्याने अवलंबून असल्याने बांधकामास उपलब्ध असणाऱ्‍या पदार्थांमध्ये कालमानाप्रमाणे कसकसे बदल होत गेले याच्याशी वास्तुरचनेचा इतिहास निगडित आहे. अती प्राचीन काळी बांधकामास सुरूवात झाली तेव्हा कायम स्वरुपाच्या बांधकामात प्रामुख्याने निसर्गात भरपूर प्रमाणात उपलब्ध होत असे. उपलब्ध इतिहासानुसार इ.स.पू. ४००० या काळात मेसोपोटेमियन संस्कृतीतदगड एकावर एक ठेवून ते दोन्ही बाजूंनी झुकाव पद्धतीने पुढे आणून होणाऱ्‍या प्रक्षेपी कमान रचनेस सुरूवात झाली [⟶पूल]. ज्या ठिकाणी दगड सहज उपलब्ध होत नाहीत अशा प्रदेशात विटांच्या साहाय्याने केलेली अशीच रचना भारतातील आर्यपूर्व संस्कृतीच्या काळात होत असल्याचे मोहें-जो-दडो व हडप्पा येथील अवशेषांवरून लक्षात येते. याच काळात ईजिप्शियन. मेसोपोटेमियातील सुमेरियन, भारतातील सिंधू संस्कृती व त्यानंतरच्या ग्रीक संस्कृतीत खांब-तुळईची रचनाच बांधकामात मोठ्या प्रमाणात आढळून येते. इ. स. पू. २८००–१७०० या काळात ईजिप्तमध्ये बांधले गेलेले ⇨ पिरॅमिड, इ.स.पू. २५००–१५०० या काळातील सिंधू संस्कृतीतील मोहें-जो-दडो व हडप्पा या नगरांचे अवशेष,इ.स. पू. २२०० ते ५०० या काळात मेसोपोटेमियामध्ये सुमेरियन,अँसिरियन व बॅबिलोनियन संस्कृतींत बांधली गेलेली ⇨ झिगुराते (मंदिर-मनोरे), इ. स. पू. १९०० च्या सुमारास मेसोपोटेमियात युफ्रेटीस नदीच्या किनाऱ्‍यावर बांधले गेलेले बॅबिलन शहर व तेथील बॅबेलचा मनोरा, इ. स. पू. १५०४ मध्ये ईजिप्तमध्ये नाईल नदीच्या किनाऱ्‍यावरील थीब्झ येथे वास्तुरचनेची पहिली राणी म्हणून ओळखल्या जाणाऱ्‍या हॅटशेपशूट नावाच्या राणीने सेनमट या वास्तुशिल्पज्ञांच्या मदतीने बांधलेले डेर-एल-बाहरीचे भव्य मंदिर ही सर्व अती प्राचीन कालीन वास्तुरचनेची साक्ष देतात. इ. स. पू. ९८० मध्ये पूर्ण झालेले कारनॅक येथील अँमन देवतेच्या प्रचंड मंदिराचे बांधकाम जवळजवळ ७०० वर्षे चालू होते. ३६६ मी. लांब, १०७ मी रुंद असे हे मंदिर २० मी. उंच व ३.२२५ मी. व्यासाच्या असंख्य दगडी खांबांवर १०.९ मी. लांब व १.२ मी. जाडीच्या अखंड दगडी लाद्या व तुळ्यांनी बांधले गेले होते. वस्तुमानात जगातील कोणतीही वास्तू (धरणे सोडून) याची बरोबरी करू शकणार नाही. फार तर याची तुलना अनेरिकेतील ओहायओ राज्यातील अँक्रन येथील ३५८ मी. लांब, ९९ मी. रुंद व ६१ मी. उंच अशा विमानगृहाशीच फक्त करता येईल.

यानतंर इ. स. पू. सहाव्या ते चौथ्या शतकांमध्ये वास्तुरचनेचा वा वास्तुशिल्पाचा फार मोठा इतिहास घडून आला. याच काळात तुळई-खांब रचना फार प्रगत अवस्थेत पोहोचली होती. ⇨ अक्रॉपलिस (अथेन्स) येथे कॅलिक्राटीझ, इक्टायनस व फिडीयस या वास्तुशास्त्रज्ञांनी बांधलेल्या ऑलिंपियन झ्यूस, अथीना, प्रॉपिलीया व सुप्रसिद्ध ⇨ पार्थनॉन या भव्य मंदिराचे अवशेष त्या काळाच्या वास्तुरचनेच्या वैभवाची साक्ष देतात.

भारतात भगवान बुद्ध, मौर्य राजे व सम्राट अशोक यांच्या काळामध्ये (इ. स. पू. २७३–२३२) बांधलेली चैत्यगृहे, सारनाथ व सांची येथील स्तूप महिरपी तुळ्या, कमानी, घुमट, खांब व झुकाव टेकू या पद्धतीची रचना आढळते. युरोपमध्ये ग्रीकांनंतंर रोमन लोक महान वास्तुरचनाकार म्हणून इतिहासात प्रसिद्ध झाले. रोमन वास्तुशिल्पज्ञांनी भारवहनासाठी तुळईऐवजी अर्धवर्तुळाकार कमानी रचना व घुमटाची रचना वापरण्यास सुरूवात केली. या अर्धवर्तुळाकार कमानी-रचनेचे वैशिष्ट्य हे की, चुना किंवा सिमेंट यासारख्या संयोजी पदार्थाचा वापर न करता दगडी ठोकळ्यांची वर्तुळाकार कंसाच्या तुकड्यांच्या आकारात घडाई करून तसे घडविलेले ठोकळे नुसते एका शेजारी एक रचून कमान तयार केली जात असे. भुयारांसाठी, कोठारांसाठी दंडगोलाकार छपरे, पुलांसाठी वर्तुळाकार कमानी व देवळांमध्ये घुमटांचा मोठ्या प्रमाणावर वापर करण्यात येऊ लागला. इ. स. पू. २७ मध्ये रोममध्ये बांधलेल्या भव्य अशा पेंथीऑन या वास्तूमध्ये ४३ मी. व्यासाचा २१.६ मी. उंचीचा अर्धगोल आकाराचा घुमट वापरला गेला. अंतर्गत स्तंभाचा वापर न करता एवढ्या मोठ्या प्राकाराला आधार देणारी वास्तू एकोणिसाव्या शतकापर्यंत एकमेवाद्वितीय असे स्थान राखून होती. इ. स. ८० मध्ये रोममध्येच ⇨ कॉलॉसिअम म्हणून ओळखल्या गेलेल्या १८७ मी. लांब व १५६ मी. रुंद अशा दीर्घवर्तुळाकार भव्य प्रेक्षागारासाठी त्रिस्तरीय अर्धवर्तुळाकार कमानीची रचना ४८ मी. उंचीपर्यंत केली गेली. रोमन वास्तुरचनेमध्ये वास्तुमानातून किंवा सघनतेतून मिळत असे. त्यामुळे या रचनेत अवाढव्यपणा व बोजडपणा हे दोष आले. हे दोष पुढे आलेल्या गॉथिक पद्धतीतील दोन कंसाकार बाहूंच्या साहाय्याने होणाऱ्‍या टोकदार कमानी रचनेत दूर झाले. या रचनेत वास्तूचे स्थैर्य सघनतेऐवजी भूमितीय आकाराच्या गुणधर्माच्या उपयोगाने साध्य केले गेले. इतकेच नव्हे, तर या रचनेत वास्तूस खूप उंची मिळून तिच्या भव्यतेत व सौंदर्यात भरच पडली.

रोमन काळानंतरची पुढील जवळजवळ १,५०० वर्षे वास्तुरचना दृष्ट्या युरोप व मध्यपूर्वेत अंधाराची गेली. पण याच काळात भारतामध्ये वास्तुरचनेला मोठा बहर आलेला दिसतो. आंध्र प्रदेशातील राजांनी (इ. स. पू. ७२ ते इ. स. ३२० या काळात) बांधलेली नागार्जुनकोंडा येथील चैत्यगृहे, गुप्तकाळातील (इ.स. ३२०–४९९) अजिंठा य़ेथे खोदल्या गेलेल्या गुंफा, राष्ट्रकुटांनी (७२५–५५ मध्ये) बांधलेले वेरूळचे कैलास मंदिर, मध्य प्रदेशात बुंदेलखंडात चंदेल्लांनी (९५४–१००२) बांधलेले खजुराहो येथील कंदरिया महादेव मंदिर, दक्षिणेत तंजावर इ. ठिकाणी चौल राजांनी (९८५–१०१४) बांधलेली उंच गोपूरांनी युक्त मंदिरे, पांड्य राजांनी मदुराई येथे बांधलेले मीनाक्षीसुंदरम देवालय, अकराव्या शतकात व त्यानंतरच्या काळात संगमरवरी दगडात बांधलेली अबू पर्वतातील दिलवाड्याची जैन मंदिरे, कर्नाटकात होयसळ व बल्लवा यांनी (११११–४२ या काळात) बांधलेली बेलूर व हळेबीड येथील मंदिरे, ओरिसामध्ये राजा नरसिंह देव यांनी (१२३८–६४ मध्ये) बांधलेले कोनारकचे सुप्रसिद्ध सूर्यमंदिर, कर्नाटकात १२६८ मध्ये बांधलेले सोमनाथपूर येथील मंदिर, हरिहर यांनी (१३३६–५४ या काळात) विजयानगर साम्राज्याची हंपी येथे बांधलेली राजधानी, राजस्थानमध्ये चितोडगड येथे (१४५८–८४ मध्ये) राणा कुंभ यांनी बांधलेला विजयस्तंभ, मुहम्मद आदिलशाह (१६२६–५६) यांनी विजापूर येथे बांधलेला गोलघुमट ह्या सर्व वास्तू त्या काळातील वास्तुरचनेची कल्पना देतात. घडीव दगडी खांब, महिरपीयुक्त तुळ्या, घुमट, मेघडंबरी यांनी युक्त अशाच या रचना होत. मुसलमान अमदानीत १२०६–१० मध्ये बांधलेला कुतुबमिनार, सम्राट अकबर (१५४२–१६०५) यांनी बांधलेली फतेपुर-सीक्री येथील राजधानी व आग्ऱ्‍याचा किल्ला, शहाजहान (१६२८–५७) यांच्या काळातील जगप्रसिद्ध ताजमहाल व लाल किल्ला आणि त्याच काळात दक्षिणेत मदुरा येथे तिरुमल नायक (१६२३–५९) या राजांनी बांधलेले प्रासाद ह्या त्यानंतरच्या महत्त्वाच्या वास्तुरचना होत. विविध घराण्यांतील राजांच्या मदतीने बाराव्या शतकापासून अठराव्या शतकापर्यंतच्या प्रदीर्घ कालावधीत बांधलेले व त्याच्या वैशिष्ट्यपूर्ण प्रचंड ओवऱ्‍‍यांच्या बांधणीकरिता प्रसिद्ध असलेले रामेश्वरम् येथील मंदिरही उल्लेखनीय वास्तुरचना आहे.

या मधल्या १,५०० वर्षांच्या काळात प्रामुख्याने दगड व विटा हेच बांधकामाचे साहित्य राहिल्याने तुळई-खांब, कमानी-घुमट हीच रचना राहिली. फक्त अर्धवर्तुळावर कमानीऐवजी लंबवर्तुळाकार वा कंसाकार कमानी असा आकारामधील फरकासारखा किरकोळ फरक जाणवतो. बांधकाम संरचनेच्या नवीन संकल्पना, नवीन साहित्याचा वापर ह्या सर्व गोष्टी यूरोपातील प्रबोधन काळानंतरच्या होत. संरचनेवर येणाऱ्‍या विविध प्रकारच्या भारांचा संरचनेच्या विविध घटकांवर परिणाम कोणत्या प्रकारे होतो (उदा., अक्षीय विरुपण, नमन, व्याकुंचनलपकणे, परिवलन इ.), तसेच बांधकामात वापरल्या जाणाऱ्‍या पदार्थांचे भाराखाली वर्तन कसे होते या सर्व गोष्टींचा शास्त्रशुद्ध अभ्यास व प्रयोगावर आधारित संशोधन यास प्रबोधनकाळात मोठ्या प्रमाणावर चालना मिळून त्या अभ्यास व संशोधनावर आधारित प्रमेये व सूत्रे मांडली जाऊन ती बहुचर्चेने मान्य होऊन ग्रंथबद्ध होऊ लागली. या प्रमेयांवर आधारित शास्त्रीय विश्लेषणाच्या पद्धती निर्माण होऊ लागल्या. या पद्धतींच्या आधारे अमुक एका प्रकारचा सांरचनिक घटक वेगवेगळ्या प्रकारे किती भार घेऊ शकेल याचे गणित करणे शक्य होऊ लागले. याच काळात जास्त संशोधनाने संरचनेच्या नवीन संकल्पना प्रचारात येऊ लागल्या. रोमन काळातील सम्राट ट्रेजन यांच्या सेतुशिल्पज्ञाची कैची, सांगाडी किंवा जालक संरचना पंधराव्या शतकात लिओनार्दो दा व्हींची या महान शास्त्रज्ञांनी अभ्यासून त्याचा वापर पुलाचे बहाल व लांब गाळ्याच्या कमानीच्या उभारणीकरिता लागणाऱ्‍या आडक्यांसाठी करून बांधकामाचे तंत्रही त्याबरोबर विकसित केले. ह्या संरचनेचा वापर अर्थात लाकडी वास्तूंसाठीच होत असे. अठराव्या शतकात ओतीव व घडीव लोखंडाचा वापर कैची रचनेत मोठ्या प्रमाणात होऊन विविध प्रकारच्या आणि विविध आकारांच्या कैच्यांची निर्मिती सुरू झाली. इंग्लंडमध्ये एकोणिसाव्या शतकाच्या पूर्वार्धात ओतीव लोखंडी घटकांचा वापर करून सांगाडी संरचनेच्या साहाय्याने अनेक मजली इमारती बांधल्या गेल्या. १८५१ मध्ये बांधली गेलेली क्रिस्टल पॅलेसची इमारत ही पहिली संपूर्ण लोखंडी सांगाड्याची इमारत हेय. १८५५ साली पॅरिसमधील प्रदर्शनाच्या भव्य दालनासाठी ४२.३ मी. गाळ्याची ओतीव लोखंडी घटकांची कमान वापरली गेली. हे लोखंडी बांधकाम पुढे पोलादाच्य़ा निर्मितीनंतरच्या पोलादी इमारतींच्या बांधणीस पायाभूत ठरले. एकोणिसाव्या शतकाच्या मध्यास हेन्री बेसेमर यांनी आधुनिक पोलादनिर्मितीच्या पद्धतीच्या लावलेल्या शोधाने तर बांधकामशास्त्रात मोठी क्रांती घडवून आणली. लाटीव छेदाच्या निर्मितीमुळे भिंती आणि कमानीच्या जागी पोलादी खांब व तुळ्यांचा वापर सर्रास होऊन सांगाडी संरचनेस सुरूवात झाली. छोटे पोलादी तुकडे रिव्हेट किंवा नटबोल्टने जोडून सहज बांधणी करता येणाऱ्‍या जालक संरचनेचा उपयोग करून लाटीव पोलादी घटकांच्या साहाय्याने लांब गाळ्यांच्या कैच्यांचे पूल, पाटतुळ्यांचे पूल, उंच मनोरे आणि कैचीयुक्त कमानी बांधल्या जाऊ लागल्या. विजेच्या पाळण्याच्या (लिफ्टच्या) शोधामुळे सांगाडी संरचनेच्या गगनचुंबी इमारतींची निर्मिती मोठ्या प्रमाणावर सुरू झाली. या काळात झालेल्या औद्योगिक क्रांतीमुळे संरचनाकारांसमोर नवनवीन स्वरुपाचे प्रश्न उभे राहिले. उदा., परिवहन क्षेत्रात आगगड्यांच्या आगमनाने चक्रीय व अतिशीघ्र भार वाहू शकतील अशा लांब गाळ्यांच्या पुलांची आवश्यकता, कालव्यामधून होणाऱ्‍या वाहतुकीसाठी जलपाशाच्या दरवाजाची निर्मिती मोटारींचे साटे, जहजांचे सांगाडे, यंत्रांचे साटे, अल्प वजनात जास्त सामर्थ्य देणाऱ्‍या पदार्थाचा वापर करून होणारी विमानांची निर्मिती रेडीओ व दूरसंदेशवहन आणि विद्युत् शक्तीचे प्रेषण यांसाठी लागणारे उंच मनोरे अशा विविध संरचनांची बांधणी अशा समस्यांची शीघ्रतम उकल करणेही आवश्यक असे व त्यासाठी चाचपणी (चुकतमाकत सुधार) पद्धतीस वेळ नसे आणि तऱ्‍हेच्या संरचना पूर्वी वापरीत नसल्याने अनुभवजन्य सूत्रांचा वापरही शक्य नसे. त्यामुळे अशा सारंचनिक प्रश्नाची उकल प्रयोगिक चाचण्या घेऊन करण्याची पद्धत अमलात येऊन त्या चाचण्यांमधून काही शास्त्रीय सिद्धांत अथवा सूत्रांची निर्मिती करता आली. जेथे उपलब्ध साहित्य वा पदार्थ चालू शकत नसेल तेथे नवीन साहित्याच्या संशोधनास चालना मिळाली. नैसर्गिक दगडाऐवजी पाहिजे तो आकार घेऊ शकणारा दगडासारखा कृत्रिम पदार्थ निर्माण करण्यास चालना मिळून त्यातून काँक्रीटचा शोध लागला. पोलादाप्रमाणेच काँक्रीटच्या शोधानेही संरचनेच्या इतिहासात नवीन अध्याय सुरू केला. १९३४ साली स्पेनमध्ये एद्वारदोटॉरोहा या वास्तुशिल्पज्ञांनी बाजारपेठेच्या इमारतीसाठी रोमन कालीन पँथीऑनपेक्षा मोठा असा अर्धगोलाकृती व वरच्या बाजूस अवघी ८.३ सेंमी. जाडी असलेला घुमट काँक्रीटच्या साहाय्याने बांधला. काँक्रीट ताण घेऊ शकत नसल्याने तो घेण्यासाठी पोलादी सळ्यांचा वापर करून काँक्रीट प्रबलित करण्याची पद्धती १८९० मध्ये फ्रान्स व अमेरिकेत सुरू झाली आणि हे प्रबलित काँक्रीट म्हणून ओळखले जाऊ लागले. पूल व इमारती यांच्या बांधकामात दगडाची जागा प्रबलित काँक्रीटने घेतली. काँक्रीटच्या घटकात ताण घेण्यासाठी पोलादाचा वापर करण्याऐवजी त्यामध्ये बाहेरील भार येण्यापूर्वीच विरोधी प्रकारची म्हणजे संकोची प्रेरणा निर्माण करण्याच्या कल्पनेने अधिक सामर्थ्यशाली अशा पूर्वप्रतिबलित काँक्रीटला जन्म दिला. लांब गाळ्याच्या संरचनांच्या निर्मितीमध्ये पूर्वप्रतिबलित काँक्रीटने एक विशिष्ट स्थान प्राप्त केले [⟶काँक्रीट]. विमानाच्या निर्मितीमध्ये अल्प वजनता जास्त सामर्थ्य मिळविण्यासाठी अँल्युमिनियम व मॅग्नेशियम यांनी युक्त अशा मिश्रधातुची उत्पत्ती विसाव्या शतकाच्या मध्यास झाली [⟶बांधकाम, हलक्या धातूंचे]. अशा विविध प्रकारच्या बांधकामाच्या साहित्याचे गुणधर्म अगदी वेगळे असल्याकारणाने त्या प्रत्येक पदार्थाच्या संरचनेचे स्वतंत्र असे शास्त्र निर्माण झाले.

प्राचीन कालीन तुळई-खांब संरचनेमध्ये हे दोन्ही घटक एकत्र काम करीत नसत. तुळई खांबावर नुसती ठेवली वा टेकवली जात असे. अशी संरचना बांधणीस सोपी असली, तरी जास्त खर्चाची व दृढतेच्या दृष्टीने कमी दर्जाची असते. या संरचनेमध्ये तुळईचे आकारमान मोठे व खांबाचे लहान असा असम प्रकार आढळतो. पोलादाच्या बांधकामात वितळजोडकाम (वेल्डिंग) तंत्राच्या आगमनामुळे व काँक्रीटच्या घटकाच्या एकसंघ निर्मितीच्या शक्यतेमुळे एकसंघ संरचनेची कल्पना मूळ धरू लागली. संरचनाशास्त्राच्या प्रगतीमुळे एकसंघ संरचनेचे विश्लेषण करणेही शक्य झाले. अशा संरचनेत साहित्य कमी लागून दृढताही जास्त येते. एकसंघ संरचनेच्या कल्पनेमुळे पूर्वी भारवहनासाठी भिंती-तुळ्या व कमानीचा वापर होत असे त्याऐवजी इमारतीचा लादी, तुळई व खांबयुक्त एकसंघ सांगाडा आणि नैसर्गिक घटकांपासून (ऊन, पाऊस, वारा इ.) संरक्षण मिळविण्यासाठी अल्पभारी पडद्यांचा (पार्टिशन्सचा) अथवा काचांचा वापर होण्यास सुरूवात झाली. पुढे लांब गाळ्याच्या तक्तपोशी व छतासाठी तीरांचा वापर करून लादीचे किंवा घुमटाचे सामर्थ्य व दृढता वाढविण्याच्या कल्पना प्रसृत होऊन आधारतीरयुक्त लाद्या, तीरयुक्त घुमट अशा संरचना प्रचलित झाल्या. १९५० मध्ये एका इमारतीच्या सु. १०७ मी. गाळ्यासाठी अँल्युमिनियम तीरयुक्त घुमट बांधला गेला. आगगाड्यांचे डबे, जहाजे, मोटारी व विमाने यांच्या सांगाड्यांसाठी प्रधान चौकट,तीर दृढक आणि बाहेरील पटलयुक्त संयुक्त संरचना उदयास आली. उंच मनोरे, लांब गाळ्याची छपरे, लांब गाळ्याचे पूल यांसाठी रज्जु-आधाराचा उपयोग केल जाऊ लागला. मोठ्या शहरांतील जमिनीच्या वाढत्या किंमतीमुळे गगनचुंबी इमारतींची निर्मिती सुरू झाली. काँक्रीटच्या आगमनाने संरचनेला कसा आकार दिला असता त्यात फक्त संकोची प्रेरणा येईल या दिशेने विचार होऊन काँक्रीटच्या कवची छपरांचे आणि घडीच्या छतांचे दालन खुले झाले. संरचनेच्या या विविध संकल्पनांमध्ये संरचनेच्या घटकांना सुयोग्य आकार व स्वरुप देऊन संरचनेचे सामर्थ्य व सौंदर्य मिळविण्याचा प्रयत्न दिसतो. विसाव्या शतकाच्या मध्यास पदार्थांच्या स्थितिस्थापक गुणधर्माबरोबरच आकार्य गुणधर्माचा विचार होऊन संरचनेच्या अभिकल्पाच्या (आराखड्याच्या) कल्पनेतच क्रांतिकारक बदल करणाऱ्‍या परम भार पद्धतीचा उगम झाला. संगणकाच्या (गणकयंत्राच्या) आगमनाने, तर कोणत्याही आकाराच्या संरचनेचे विश्लेषण व अभिकल्पन करणे सुलभ झाल्याने वास्तुशिल्पज्ञांना आपल्या प्रज्ञेची आणि कल्पनांची भरारी दाखविण्यास एक प्रकारे आव्हानच दिले गेले आहे. त्यातूनच आज जगात वैशिष्ट्यपूर्ण व एकमेवाद्वितीय अशा संरचनांची निर्मिती सुरू झाली आहे. त्यांतील आधुनिक काळातील आश्चर्य म्हणून उल्लेख करता येईल अशा जगातील काही संरचनांची माहिती कोष्टक क्र.१ (अ) मध्ये दिली आहे, तर भारतातील १९६०–८० या काळातील काही उल्लेखनीय संरचनांची माहिती कोष्टक क्र. १ (आ) मध्ये दिली आहे. यांत धरणे व पूल यांचा समावेश केलेला नाही.

कोष्टक क्र.१. काही उल्लेखनीय संरचना
(अ) जगातील (१९७६ अखेरपर्यंतच्या).
(१)	सर्वांत उंच संरचना	:	फ्लॉक (पोलंड) येथील वॉर्सा रेडिओ प्रेषण आकाशक. उंची ६४५ मी. हे सर्वांत उंच पोलादी बांधकामसुद्धा होय.
(२)	सर्वांत लांब संरचना	:	चीनची सुप्रसिद्ध भिंत. लांबी ३,४६० किंमी.
(३)	सर्वांत लांब गाळा	:	नॉर्वेमधील सॉग्ना फ्योर्डवर उच्च दाबाच्या विद्युत् वाहक तारांच्या दोन मनोऱ्‍यांमधील गाळा. लांबी  ४,८८८ मी.
(४)	सर्वांत लांब गाळ्याचा पुल	:	इंग्लंडमध्ये हंबर नदीवरील १,४१० मी. लांब गाळ्याचा निलंबी पूल.
(५)	सर्वांत लांब पूल	:	अमेरिकेतील लुइझिॲना राज्यातील न्यू ऑर्लीअन्सजवळ पाँचरट्रेन सरोवरावरील ३८.४ किमी. लांबीचा पूर्वप्रतिबलित काँक्रीटचा पूल.
(६)	सर्वांत खोल पाया	:	उत्तर समुद्रातील फॉर्टिज येथील तेलविहिरीच्या धक्क्याचा स्तंभिका पाया. समुद्रतळाच्या खाली १०० मी. खोल व समुद्र सपाटीपासून २३० मी. खोल.
(७)	सर्वांत उंच इमारत	:	अमेरिकेतील शिकागो येथील सिअर्स टॉवर. एकूण १०९ मजले, ४४२ मी. उंच. त्यावरील आकाशकासह उंची ५४८ मी. इमारतीची नलिकाकार संरचना.
(८)	सर्वांत उंच काँक्रीटची चिमणी	:	कॅनडात आँटॅरिओ-सडबरी येथील इंटरनॅशनल निकेल कंपनीची ३८१ मी. उंच काँक्रीटची गोल चिमणी. वरच्या बाजूकडील व्यास १७.८ मी., पायाकडील व्यास ३५.४मी.

(९)	सर्वांत उंच काँक्रीटचे बांधकाम	:	कॅनडातील टोराँटो येथील सीएन टॉवर. उंची ४४६ मी.
(१०)	सर्वांत उंच लोखंडी बांधकाम	:	फ्रान्समध्ये पॅरिस येथील आयफेल मनोरा. उंची ३०५ मी. (सर्वांत उंच पोलादी बांधकाम या कोष्टकातील क्र.१ चे होय).
(११)	सर्वांत उंच दगडी बांधकाम	:	अमेरिकेतील वॉशिंग्टन येथील वॉशिंग्टन स्मारकाची इमारत. उंची १६९ मी.
(१२)	सर्वांत लांब गाळ्याचे कवची छप्पर	:	अमेरिकेतील इलिनॉय विद्यापीठाच्या प्रेक्षागारावरील १२१.९ मी. व्यासाचे व कडी तुळईपासून १९ मी. उंची असलेले घडीच्या लादींनी युक्त घुमटाकार कवची छप्पर. कवचाची जाडी अवघी ९ सेंमी., तर घड्यांची सर्वांत जास्त उंची २.३ मी.
(१३)	सर्वांत लांब गाळ्याचे पोलादी जालक छप्पर	:	अमेरिकेतील न्यू ऑर्लिअन्स येथील लुइझिअँना सुपरडोम. २०७.३ मी. व्यास व ८३ मी. उंच पोलादी कैच्यांचे घुमटाकार छप्पर.
(१४)	सर्वांत लांब गाळ्याचे कमानी छप्पर	:	अमेरिकेतील टेक्सस राज्यामधील अर्व्हिंग येथील क्रीडागार. २४०.३ मी. ☓१९०.५ मी. दीर्घ वर्तुळाकार.  सहा पोलादी कमानी.
(१५)	सर्वांत लांब गाळ्याची तन्य संरचना	:	इटलीमधील मिलान येथील पॅलॅसपोर्ट प्रेक्षागार. १२८ मी. गाळ्यावर अघोदृश्यात वर्तुळाकार असलेल्या ६ ☓ २.५ मी. काटच्छेदाच्या पेटी तुळईवर आधारलेले पोलादी रज्जुबंधित छप्पर.

(आ) भारतातील (१९६० –८० या कालखंडात बांधलेल्या).
(१)	मुंबईतील मरीन ड्राइव्ह उड्डाण मार्ग. भारतातील शहरी भागातील सर्वांत लांब पूल. लांबी ७३१.५ मी.
(२)	मुंबई येथील सांताक्रुझ विमानतळावरील इंडियन एअरलाईन्सचे     विमान गृह. १५२ मी. रुंद असा मुक्त गाळा. पूर्व प्रतिबलित काँक्रीटच्या रज्जुआधारित घडीच्या लाद्यांचे छप्पर.
(३)	भीमा नदीवरील जलसेतू. पूर्वप्रतिबलित काँक्रीटच्या ४.८ मी. व्यासाच्या व अवघ्या २० सेंमी. जाडीच्या ४१.५ मी. गाळ्याच्या नलिका. एकूण लांबी ९४७ मी.
(४)	नानगल (पंजाब) येथील खत कारखान्याचे अन्वस्तीय (पॅराबोलिक) कोठार. गाळा ३४ मी., उंची १९.५ मी. पूर्वरचित घडीच्या कमानीचा वापर.
(५)	हिंदुस्थान एरॉनॉटिक्स, बंगलोर येथील १० लक्ष लिटर क्षमतेचा जलस्तंभ. उंची ३० मी. वरच्या बाजूस टाकीचा व्यास २५ मी. खालील नलिकाकार काँक्रीटचा आधारस्तंभ व वरील टाकीची एकसंघ रचना.
(६)	तमिळनाडूमधील कल्पकम येथील अणुऊर्जा केंद्राचे धारक पात्र. जगातील दुपदरी धारक योजना असलेली पहिली संरचना. आतील कवच पूर्वप्रतिबलित काँक्रीटचे, तर बाहेर दगडी बांधकामाची ६०० मिमी. जाड भिंत, बाहेरील व्यास ४५ मी., उंची ४० मी., २३५ मेगॅवॉट ऊर्जाक्षमतेच्या अणुभट्टीसाठी जगातील हे सर्वात स्वस्त धारक पात्र मानले गेले आहे.
(७)	राजस्थानातील कोटा येथील अणुऊर्जा केंद्रासाठी मुख्य अणुभट्टी इमारतीवरील छपराचा ३९.६ मी. व्यासाचा पूर्व प्रतिबलित काँक्रीटचा घुमट हा जगातील अशा तऱ्‍हेचा तिसऱ्‍या क्रमांकाचा घुमट मानला जातो. पहिले दोन फ्रान्समध्ये आहेत.
(८)	मुंबई येथील शेअर बाजाराची अनेक मजली गगनचुंबी इमारत. १३० मी. उंचीच्या मध्यभागाची बांधणी केवळ ३५ दिवसांत पूर्ण झाली.
(९)	मुंबई येथील महाराष्ट्राच्या नवीन विधान भवनाची इमारत. ७९ मी. उंचीच्या २१ मजली मुख्य इमारतीच्या पुढे ३६ मी. व्यासाची गोल पाच मजली इमारत. तळमजला आणि पहिला मजला येथे मुख्य विधान भवन. पहिल्या मजल्यावर ८.४ मी. रुंद सज्जे. छप्पर घडीच्या लाद्याचे, पाकळीच्या आकाराचे, ५० मी. उंच घुमटाकार.
(१०)	मुंबई येथील नॅशनल इन्स्टिट्यूट फॉर परफॉर्मिग आर्ट्सचे टाटा प्रेक्षागृह. इंटिमेट थिएटर पद्धतीचे वैशिष्टयपूर्ण वास्तुरचनेचे एक हजार प्रेक्षक बसण्याची क्षमता. मध्यभागी वर्तुळाकार रंगमंच.
(११)	ऑरोव्हिल (पाँडिचेरी) येथील ३० मी. व्यासाचे गोल अल्पोपहारगृह. त्याच्या वैशिष्टयपूर्ण स्थापत्य शिल्पासाठी प्रसिद्ध. ४१ मी. गाळ्याचे त्रिकोणाकार जालांचे छप्पर. त्याचे छत मूळ इमारतीच्या २१ मी. पुढे प्रक्षेपित होत असलेले.
(१२)	मुंबईतील तुर्भे येथील भाभा अणुसंशोधन केंद्रातील आइसक्रीमच्या पेल्याच्या आकाराच्या पूर्वप्रतिबलित काँक्रीटच्या पाण्याच्या टाक्या. क्षमता २.२५ दशलक्ष लिटर.
(१३)	विजयवाडा औष्णिक विद्युत् केंद्रासाठी इब्राहिमपट्टण येथील काँक्रीटची चिमणी. ही भारतातील सर्वात उंच व अनेक धूममार्ग असलेली चिमणी होय. उंची १८० मी. प्रत्येक धूममार्ग ४ मी. व्यासाचा. बाहेरील व्यास वरच्या बाजूस १३ मी. व खालच्या बाजूस १८.३ मी.
(१४)	ग्वाल्हेरजवळील पाटबंधाऱ्‍याचा कालवा. चंबळ नदीचे खोल पात्र पार करण्यासाठी बांधलेला, जगातील सर्वात लांब कुनू वक्रनाल (सायफन). याचा अंतर्गत व्यास ६ मी., एकूण लांबी १.७५ किमी. असून त्यापैकी २८० मी. लांबीचा भाग नदीवरून पुलासारखा नेलेला. सर्वात खालच्या बाजूस पाण्याचा भार २५.८ मी. उंचीचा.

 

संरचनाशास्त्राचा इतिहास व विकास : वास्तुरचना पुरातन कालापासून होत असली, तरी संरचनेचे अभिकल्पन हे अगदी सोळाव्या शतकापर्यंत संरचनाकाराची कल्पनाशक्ती, अंतःप्रज्ञा, समान वास्तूंच्या निर्मितीचा पूर्वानुभव आणि संरचनांच्या प्रवृत्तीचा अभ्यास यांवरच आधारित असे. वरील गुणांच्या साहाय्याने प्राचीन संरचनाकारांनी ठोक ताळ्याचे तंत्र वापरून हजारो वर्षे वास्तूंची निर्मिती केली. असे असले, तरी पूर्वीच्या अनुभवाच्या व निरीक्षणाच्या आधारे संरचनेच्या सिद्धांताचा शास्त्रीय अभ्यासही कित्येक शास्त्रज्ञ करीत होतेच. संरचनाशास्त्र संरचनेवर येणारे भार व विचलन यांच्याशी संबंधित असल्याने संरचनाशास्त्राचा मूलस्त्रोत भौतिकीतील ⇨ यामिकीशास्त्रात सापडतो. पदार्थांवर, वस्तूंवर व वास्तूंवर होणारा भारांचा परिणाम, पदार्थांचे अथवा वास्तूंचे या भाराखाली होणारे वर्तन याचा अभ्यास यामिकीशास्त्रात होतो. अँरिस्टॉटल (इ. स. पू. ३८४–३२२), आर्किमिडीज (इ. स. पू. सु. २८७–२१२) व टॉलेमी (इ. स. सु. ९०–१६९) हे या शास्त्रचे अध्वर्यू होत. त्यांनी मांडलेल्या यामिकीय सूत्रांचा वापर ग्रीक व रोमन वास्तुरचनेत केलेला आढळतो. रोमन सम्राट ऑगस्टस यांच्या काळात व्हिट्रूव्हिअस (इ. स. पू. पहिले शतक) नावाच्या वास्तुशिल्पकारांनीDe Architecturaहा बांधकामावरील पहिला शास्त्रीय ग्रंथ लिहून त्यात त्या काळापर्यत माहीत असलेली बांधकामशास्त्राची सूत्रे व तत्त्वे ग्रंथबद्ध केली. त्यानंतर सोळाव्या शतकापर्यतचाकाळ वास्तुशास्त्राच्या दृष्टीनेही अंधारयुगच मानला जातो. यानंतरच्या प्रबोधन काळामध्ये सर्वच शास्त्रांच्या प्रगतीबरोबर वास्तुशास्त्र आणि संचरनाशास्त्राचाही विकास होऊ लागला. लिओनार्दो दा व्हींची, गॅलिली गॅलिलीओ, आयझॅक न्यूटन, रॉर्बट हुक, एद्म माऱ्‍यॉत व लेनर्ड ऑयलर हे या संरचनाशास्त्राचे पूर्वसुरी मानले जातात. गॅलिलीओ यांचे Discorsl e Dimostrazionl Matematiche intorno a due nuvoe Scienze(इंग्रजीत टू न्यू सायन्सेस या नावाने ओळखण्यात येणारे) हे संरचनेशी संबंधित पदार्थबलविज्ञानावरील पहिले पुस्तक मानले जाते. यानंतरच्या तीन-चार शतकांमध्ये संरचनाशास्त्राची प्रगती सर्व आढावा घेणे अतिशय कठीण असले, तरी कोष्टक क्र. २ मध्ये दिलेल्या संक्षिप्त माहितीवरून सुद्धा या प्रगतीच्या प्रवाहाची कल्पना येऊ शकेल.

संरचनेच्या अभिकल्पाची मूलतत्त्वे, कल्पना व क्रम : वास्तूच्या प्रत्यक्ष बांधकामाअगोदर किंवा निर्मितीपूर्वी, अवगत शास्त्रीय सिद्धांताच्या आधारे वास्तूच्या संरचनेचा अभिकल्प करणे अत्यावश्यक असते. संरचनेची सुरक्षितता, सेवायोग्यता, कमीत कमी खर्चात निर्मिती, सौंदर्य व टिकाऊपणा ही संरचनेच्या अभिकल्पाची आधारभूत तत्त्वे मानली जातात. वास्तुवर येणारे भार सुरक्षितपणे सुयोग्य साहित्याचा वापर करून कमीत कमी खर्चात वाहू शकणारी, सौंदर्यपूर्ण व टिकाऊ संरचना निर्माण करणे हे अभिकल्पकाचे ध्येय असते. बाहेरील भारामुळे संरचनेचा कोणताही घटक कोसळू नये, मोडू नये वा भंग पावू नये, या गोष्टींचा विचार सुरक्षिततेत अभिप्रेत असतो, तर सेवायोग्यतेच्या किंवा कार्योपयुक्ततेच्या बाबतीत भारामुळे आत्यंतिक विरूपण होऊन किंवा तडे जाऊन अथवा स्थान भ्रष्ट होऊन संरचना निकामी होऊ नये या गोष्टींचा विचार अभिप्रेत आहे. उदा., खांबावर किंवा भिंतीवर येणाऱ्‍या अवजड भाराखाली ती भंगणे, कोसळणे, पाया खचणे, खांब लपकणे तुळई अतिशय वाकणे (न तुटणाऱ्‍या पण अतिशय वाकणाऱ्‍या फळीवरून जाताना माणसाला असुरक्षित वाटते म्हणून अशी फळी सेवायोग्य नसते), तुळई किंवा लादीला तडे जाणे (तडे गेलेल्या काँक्रीटच्या तुळई खाली काम करायलाही माणसास असुरक्षित वाटते), पाण्याच्या टाकीच्या किंवा धरणाच्या भिंतीला तडे जाणे (ज्यामुळे तिची जलाभेद्यता नष्ट होऊन पाणी झिरपून वास्तू निकामी होते), संरचनेच्या अतिविरूपणामुळे दरवाजे-खिडक्यांच्या चौकटी वाकून दरवाजे-खिडक्या न लागणे, पूल किंवा वाहनाचे सांगाडे यांसारख्या संरचनांवर मोठया प्रमाणात येणाऱ्‍या कंपनामुळे संरचना खिळखिळी होणे किंवा तिचे सामर्थ्य/आयुष्य कमी होणे या सर्व गोष्टी टाळणे म्हणजेच संरचना सुरक्षित व सेवायोग्य राखणे होय. विसाव्या शतकाच्या मध्यापर्यत संरचनेच्या फक्त सुरक्षितेचाच विचार अभिकल्पात केला जात असे पण त्यानंतरच्या वीस वर्षात सुरक्षिततेबरोबर संरचनेच्या सेवायोग्यतेकडेही लक्ष दिले जाऊ लागले आहे. हे दोन्ही उद्देश साध्य होण्यासाठी वेगवेगळ्या देशांच्या मानक संस्था किंवा वास्तुरचनेशी संबंधित असलेल्या मोठया संस्था अभिकल्पासंबंधीचीसूत्रे व नियम ग्रंथित केलेल्या संहिता व नियमावली प्रसृत करतात. त्यानुसार अभिकल्पकांना किंवा वास्तुकारांना संरचेना अभिकल्प करमे कायद्याने, नियमाने, बांधकामाच्या अटींनी किंवा संकेतानी अनिवार्य केले जाऊन संरचनेची सुरक्षितता व सेवा योग्यता यांची निश्चिती साध्य केली जाते. मात्र आर्थिक काटकसर, सौंदर्य आणि टिकाऊपणा या गोष्टी मात्र अभिकल्पकास आपला अनुभव, ज्ञान, प्रज्ञा व अनुमान यांच्या आधारेच साधाव्या लागतात.

कोष्टक क्र. २. संरचनाशास्त्राचा संक्षिप्त इतिहास, विकास, संशोधक व त्यांचे कार्य
काल (१)	शास्त्रज्ञ/संशोधक (२)	ओळख, कार्य व संशोधन (३)
इ. स. पू. सु.२८७-२१२	आर्किमिडीज	महान ग्रीक शास्त्रज्ञ. संतुलनाचा सिद्धांत गुरुत्वबिंदूचे स्थान तरफेची तत्त्वे कप्प्यांचा उपयोग व त्यांची सूत्रे.
इ. स. पू. ६३ ते इ. स. १४	व्हिट्रव्हिअ	रोमन वास्तुशास्त्रज्ञ. इमारतीच्या बांधकाम तंत्रावर पहिले पुस्तक लिहिले तुळई खांब व कमानी यांच्या संरचनेसंबंधीची सूत्रे.
इ. स. १४५२	लिओनार्दो दा व्हींची	१,५०० वर्षाच्या अंधारयुगानंतरचे पहिले महान १५१९ इटालियन शास्त्रज्ञ. परिबलाचे तत्त्व प्रेरणांचे संतुलन.आभासी कार्याचे तत्त्व तुळई, खांब, कैच्या व कमानी यांमधील प्रेरणांचा अभ्यास.
१५१८-१५८०	आंद्रेआ पाल्लाद्यो	रोमन लोकांनंतर लाकडी कैच्या पुलांसाठी प्रथम वापरणारे इटालियन अभियंते.
१५४८-१६२०	सायमन स्टेव्हाइन	डच शास्त्रज्ञ, स्थितिकीशास्त्रातील महत्त्वाची सूत्रे.
१५६४-१६४२	गॅलिली गॅलिलीओ	महान इटालियन संशोधक व शास्त्रज्ञ खगोलशास्त्र व गतिकीशास्त्राचा गाढ व्यासंग व अभ्यास. पडणाऱ्‍या वस्तूंच्या गतीसंबंधीची सूत्रे. पदार्थाचे बल व गतिकीशास्त्र यांवर पहिला ग्रंथ लिहिला
१६२०-१६८४	एद्म माऱ्‍यॉत	फ्रेंच अँकॅडेमी ऑफ सायन्सेसमधील नावाजलेले पहिले फ्रेंच शास्त्रज्ञ. स्थितिस्थापक वस्तूंच्या आधाताचे नियम तुळईच्या नमन सामर्थ्याचा अभ्यास.
१६३५-१७०३	रॉबर्ट हुक	‘हुक नियम’ म्हणून प्रसिद्ध असलेल्या स्थितिस्थापकतेविषयीच्या सिद्धांताचे जनक सर्वगामी जोडाची कल्पना.
१६४०-१७१८	फिलिप लाईर	फ्रेंच शास्त्रज्ञ. दगडी कमानींच्या विश्लेषणात भूमितीय आरेखन पद्धतीचा वापर दगडी कमानींच्या विश्लेषणावर पहिला ग्रंथ लिहिला.
१६४२-१७२७	आयझॅक न्यूटन	महान इंग्रज संशोधक. यामिकीशास्त्रातील वस्तुंच्या प्रेरणा-प्रतिक्रिया व प्रेरणा-गती यांसंबंधीच्या सुप्रसिद्ध नियमांचे जनक समाकलन शास्त्रातील सूत्रासंबंधी अभ्यास.
१६५४-१७०५	याकोप बेर्नुली	बेर्नुली या सुप्रसिद्ध स्विस संशोधन कुटुंबातील आद्य शास्त्रज्ञ. नमनाचा व नमन- विचलनाचा सुप्रसिद्ध सिद्धांत.
१६५४-१७२२	प्येअर व्हॅरिग्नॉन	फ्रेंच शास्त्रज्ञ सुप्रसिद्ध परिबल प्रमेयाचे जनक.
१६६६-१७१६	आंत्वान पेरँ	फ्रेंच शास्त्रज्ञ, महत्तम नमन सामर्थ्या्या तुळईचा सिद्धांत.
१६६७-१७४८	योहान बेर्नुली	बेर्नुली कुटूंबातील एक गणितज्ञ, आसामी विचलनाचे तत्त्व.
१७१६	यूबेअर गोत्ये	महान फ्रेंच पूल-रचनाकार व शास्त्रज्ञ पूलबांधणी.तंत्रावर पहिला ग्रंथ [Trait de Ponts] लिहिला व तो पुढे ७० वर्षे वापरात राहिला.
१६९२-१७६१	पीटर व्हान	डच शास्त्रज्ञ. पदार्थाच्या बलाच्या चाचणी पद्धतीचा शोध.
१७००-१७८२	डानिएल बेर्नुली	बेर्नुली कुटुंबातील एक शास्त्रज्ञ, स्थितिस्थापकता आलेखावर संशोधन.

 

सांरचनिक अभिकल्पातील टप्पे : संरचनेचे संकल्पन, योजना व तिचा प्राथमिक अभिकल्प, गणितीय विश्लेषण, घटकांचा अंतिम अभिकल्प व संरचनेचे आरेखन हे संरचनेच्या अभिकल्पाचे प्रमुख टप्पे होत. प्राथमिक अभिकल्पामध्ये-(१) वास्तूच्या उद्देशानुसार, तीवर येणाऱ्‍या भारांच्या प्रकारानुसार, धनाच्या उपलब्धतेनुसार आणि वास्तुच्या प्रकाराप्रमाणे तिच्या सौंदर्य व टिकाऊपणाच्या मागणीनुसार संरचनेच्या स्वरूपाची व आकारमानाची निवड करणे (उदा., लांब गाळ्याच्या पुलासाठी पुलाच्या जागेवरील परिस्थितीनुसार कमान, तुळई किंवा कैची संरचनेची निवड करणे, कैची संरचना ठरविल्यास कैचीचे आकारमान व प्रकार ठरविणे लांब गाळ्यांच्या छपरांसाठी कमान, कवची छप्पर, कैची, घुमट की घडींच्या लाद्यांची संरचना वापरावयाची हे ठरविणे, लांब गाळ्याच्या तक्तापोशीसाठी तुळई-लादी संरचना की जालकाकार दृढकयुक्त लादी हे ठरविणे इ.) (२) संरचनेच्या प्रकाराची निवड (उदा., एकसंघ की साधी) (३) मोकळ्या जागेच्या मागणीनुसार संरचनेच्या घटकांची मांडणी (उदा., तुळ्या किंवा कैच्यांचे गाळे व दोघांमधील अंतर ठरविणे. स्तंभाची उंची व स्तंभांमधील अंतर ठरविणे) (४) संरचनेच्या घटकांचे जरूर तेथे ठोकळमानाने आकारमान ठरविणे (उदा., काँक्रीटच्या इमारतींमध्ये लादीची जाडी, तुळई व खांबाचे तौलनिक आकारमान, धरण व धारक भिंती यांमध्ये उंचीच्या प्रमाणात पायाची रुंदी घेणे इ.) आणि (५) संरचनेच्या बांधकाम सामग्रीची निवड (उदा., प्रबलित काँक्रीट, पूर्वप्रतिबलित काँक्रीट, पोलाद, लाकूड इ.) या सर्व गोष्टींचा समावेश होतो या सर्व गोष्टींवरून लक्षात येईल की, संरचनेचे प्राथमिक अभिकल्पन हे कुठल्या गणिती सूत्रांवर किंवा शास्त्रीय सिद्धांतांवर आधारित नसून ते अभिकल्पकाचे ज्ञान, अनुभव, प्रज्ञा व अनुमान यांवरच प्रायः अवलंबून असते. अभिकल्पक जितका ज्ञानी, अनुभवी व प्रज्ञावंत असेल त्या प्रमाणात संरचनेचा प्राथमिक अभिकल्प योग्य व अचूक असेल

कोष्टक क्र. २ (पुढे चालू)
१	२	३
१७२९	बेर्नार बॅलिदॉर	फ्रेंच शास्त्रज्ञ. धारक भिंतीवर येणाऱ्या भरावाच्या आडव्या रेट्यांसंबंधी संशोधन अभियांत्रिकी विज्ञानावर पहिला ग्रंथ लिहिला आणि तो पुढे १०० वर्षे वापरात राहिला.
१७०७–१७८३	लेनर्ड ऑयलर	सुप्रसिद्ध स्विस गणितज्ञ. स्थितिस्थापकतेच्या स्थैर्याच्या सिद्धांताचे जनक तुळईच्या नमन-विचलन आलेखासंबंधी डानिएल बेर्नुली यांच्याबरोबर संशोधन वत्यावर आधारित नमन-विचलनाची सुप्रसिद्ध समाकलन सूत्रे मांडली.स्तंभांच्याव्याकुंचनाशी संबंधित सुप्रसिद्ध सूत्रे. दंडाच्या कंपनावर संशोधन.
१७१७–१७८३	झां ल राँ द ॲलांबेर	फ्रेंच गणितज्ञ. गतिकीशास्त्रातील सुप्रसिद्ध गतिकी संतुलनाचे तत्त्व मांडले गतिकीवर ग्रंथ लिहिला.
१७२४–१७९२	जॉन स्मीटन	घडीव लोखंडाचा बांधकामात वापर करणारा पहिला इंग्लिश वास्तुरचनाकार. १७७६-७९ मध्ये कोल-ब्रुकडेल येथे बांधल्या गेलेल्या घडीव लोखंडाच्या पहिल्या सुप्रसिद्ध कमानी पुलाचे निर्माते.
१७३२–१८०७	ई. एम्. गॉत्यी	फ्रेंच अभियंते. दगडाच्या भंजन सामर्थ्याचा प्रथम शास्त्रीय अभ्यास तुळईतील कर्तन प्रेरणांचा अभ्यास परिपीडन तराजूची निर्मिती.
१७३६–१८१३	शार्ल ऑग्युस्तीन द कुलंब	फ्रेंच शास्त्रज्ञ. घर्षणाची तत्त्वे. धारक भिंतीवरील भरावाच्या रेट्याची सूत्रे संकोची भाराखाली घना-कार ठोकळ्याचे कर्तन क्रियेने होणारे भंजन औष्णिकक्रियांचा धातूंच्या गुणधर्मांवर होणाऱ्या परिणामांचा अभ्यास तुळईतीलकर्तन प्रतिबले
१७३६–१८०६	झोझेफ ल्वी लाग्रांझ	सुप्रसिद्ध फ्रेंच गणितज्ञ. आभासी कार्याचे तत्त्व व स्तंभाचे व्याकुंचन यांवर संशोधन.
१७४६–१८१८	गास्पार माँझ	फ्रेंच शास्त्रज्ञ. तांत्रिक शिक्षणाचे पितामह पॅरिस येथील सुप्रसिद्ध एकोल पॉलिटेक्निकचे संस्थापक तांत्रिक शिक्षणात प्रायोगिक व आरेखनाच्या शिक्षणास सुरूवात
१७५५–१८३९	रीश बॅरन द प्रॉनी	फ्रेंच अभियंते. धारक भिंतीच्या स्थैर्यासंबंधी संशोधन.
१७५७–१८३४	टॉमस टेलफर्ड	सुप्रसिद्ध इंग्रज स्थापत्य अभियंते. इंग्लंडमधील असंख्य पुलांचे निर्माते
१७५९–१७८९	याकोप बेर्नुली	बेर्नुली कुटुंबातील एक शास्त्रज्ञ. स्थितिकीदृष्या अनिर्धार्य संरचना तत्त्वाचे प्राथमिक प्रस्तुतीकरण.
१७६१–१८२१	जॉन रेनी	इंग्लंडचे सुप्रसिद्ध पूल अभियंते. इंग्लंडमध्ये मोठ्या प्रमाणात पूलनिर्मिती पुलाच्या बांधकाम तंत्राचे शिक्षण देणारी इंग्लंडमधील पहिली संस्था स्थापन केली.
१७६८–१८३०	जे. बी. जे. फूर्ये	फ्रेंच गणितज्ञ. सुप्रसिद्ध फूर्ये श्रेढींच्या संकल्पनेचे जनक.
१७७३–१८२९	टॉमस यंग	स्थितिस्थापकता गुणांकाकरिता प्रसिद्ध असलेलेइंग्रज शास्त्रज्ञ. विकेंद्रभारित स्तंभ व ताण घटक यांवर संशोधन. जहाजाच्या सांगाड्याच्या विश्लेषण पद्धतीचा शोध.

 

अभिकल्पाचा दुसरा टप्पा म्हणजे संरचनेवर येणाऱ्या भारांची माहिती करून घेणे व संरचनेच्या बांधकामात जी सामग्री वापरावयाची असेल तिच्या बलाची (सामर्थांची) व वर्तनाची चाचण्यांच्या आधारे जरूर ती माहिती करून घेणे. संरचनेवर येणाऱ्या भारांची माहिती व नैसर्गिक घटकांच्या (उदा., वारा, भूकंप. तापमान इ.) क्रियांची माहिती ही अशाच समान संरचनेवर पूर्वी आलेल्या भारांसंबंधीच्या सांख्यिकीय माहितीच्या आधारे किंवा मानक संस्थांनी दिलेल्या संहितेच्या आधारे घेतली जाते. जेव्हा एखादी संरचना प्रथमच निर्माण केली जात असेल (उदा., अवकाशयानाची किंवा अंतराळ उपग्रहाची रचना) तेव्हा तिच्यावर येणाऱ्या कित्येक भारांची अथवा नैसर्गिक घटकांच्या परिणामांची कल्पना अनुमान धपक्यानेच करावी लागते. बांधकामाच्या पदार्थांच्या बलाची आणि वर्तनाची माहिती प्रत्यक्ष चाचणी करून वेळोवेळी  घेता येते.

कोष्टक क्र. २ (पुढे चालू)
१	२	३
१७८१–१८४९	एस्. जी. प्वासाँ	फ्रेंच शास्त्रज्ञ. सुप्रसिद्ध प्वासाँ गुणोत्तराचा शोध पाटाचे विचलन व कंपने यांवर संशोधन.
१७८१–१८६८	डेव्हिड ब्रूस्टर	स्कॉटिश शास्त्रज्ञ. प्रकाश-स्थितिस्थापकता (प्रत्यास्थता) पद्धतीमधील सुप्रसिद्ध ब्रूस्टर परिणामाचे जनक.
१७८५–१८३६	सी. एल्. एम्. एच्. नेव्हिअर	सुप्रसिद्ध फ्रेंच शास्त्रज्ञ व संशोधक. पदार्थांचे बल या विषयावर तोपर्यंतच्या संशोधनावर आधारित व पुढच्या काळातील या शास्त्रावरच्या पाठ्यपुस्तकांना आधारभूत ठरलेला पहिला ग्रंथ लिहिला. स्थितिस्थापकता सिद्धांतावर आधारित विश्लेषणअनिर्धार्य संरचनांच्या विश्लेषणाचे सर्वप्रथम प्रस्तुतूकरण तुळ्या, वक्रदंड, पाट, लाद्या, कवचे इत्यादींचे विश्लेषण.
१७८८–१८६७	झां व्हीक्तॉर पाँस्ले	फ्रेंच अभियंते व गणितज्ञ. तुळईतील कर्तनी विरूपण व धातूच्या घटकातील शिणवटा यांसंबंधी संशोधन महत्तम स्थितिस्थापकता ऊर्जा सिद्धांत.
१७८९–१८५७	ऑग्युस्तीन ल्वी कोशी	सुप्रसिद्ध फ्रेंच गणितज्ञ. स्थितिस्थापकता सिद्धांतातील घटकांवर संशोधन.
१७८९–१८६१	ईटन हॉजकिनसन	इंग्रज शास्त्रज्ञय तुळईचे नमन व ओतीव पोलादाच्या तुळ्यांचे बल यांवर संशोधन पदार्थांच्या बलाच्या प्रायोगिक चाचण्या स्तंभाच्या सामर्थ्यावरील निबंधास रॉयल पदकाचा सन्मान.
१७८९–१८७४	विल्यम फेअरबर्न	स्कॉटिश अभियंते. सुप्रसिद्ध ब्रिटानिया पुलाच्या निर्मितीस हातभार व त्यानिमित्ताने पदार्थांच्या बलाच्या प्रायोगिक चाचण्यांच्या पद्धती, सांध्याची चाचणी व दाबपात्राच्या चाचण्या यांसंबंधी प्रयोग बांधकामात लोखंडाचा वापर’ या विषयावर ग्रंथ लिहिला.
१७९०–१८६८	ए. एफ्. मबिउस	जर्मन शास्त्रज्ञ. कैच्यांच्या विश्लेषणावर संशोधन पुढील काळात ओटो मोर यांनी मांडलेल्या प्रमेयांना मूळ आधार ठरलेले संशोधन त्रिमिती कैच्यांचा अभ्यास.
१७९३–१८४१	जॉर्ज ग्रीन	इंग्रज गणितज्ञ. स्थितिस्थापकता सिद्धांतातील प्रमेये.
१७९५–१८७०	गाब्रीएल लामे	फ्रेंच गणितज्ञ. स्थितिस्थापकता सिद्धांतावर प्रथम ग्रंथ लिहिला (१८५२) प्रतिबल विवृत्तजाचा सिद्धांत जाड चितीसंबंधीची सुप्रसिद्ध प्रमेये.
१७९७–१८७२	जे. एम्. सी. द्युआमेल	फ्रेंच शास्त्रज्ञ. औष्णिक क्रियेमुळे येणाऱ्या प्रतिबलांवर संशोधन.
१७९७–१८८६	ए. जी. सी.    सँ-व्हिजन	फ्रेंच संशोधक व शास्त्रज्ञ. क्षेत्रावरील प्रतिबलाचे सुप्रसिद्ध तत्त्व स्थितिस्थापकता सिद्धांत, दंडाचे घूर्णीय सामर्थ्य, कंपने व आघात यांचे परिणाम यांवर संशोधन.
१७९८-१८९५	एफ्. ई. नॉइमान	जर्मन शास्त्रज्ञ. प्रकाश-स्थितिस्थापकतेवर संशोधन.
१७९९-१८६४	बी. पी. ई. क्लॅपिरॉन	फ्रेंच शास्त्रज्ञ. रेल्वे पुलांचे अभिकल्प अखंड तुळईच्या विश्लेषणाच्या सुप्रसिद्ध त्रिपरिबल प्रमेयाचे जनक.

 

अभिकल्पाचा या पुढचा तिसरा टप्पा म्हणजे संरचनेचे गणितीय विश्लेषण करणे हा होय. संरचनेचे विश्लेषण म्हणजे भारांमुळे किंवा बाहेरील नैसर्गिक क्रियांमुळे तिच्या घटकांमध्ये कोणत्या प्रकारच्या व किती प्रेरणा येतात व त्या प्रेरणांमुळे ते घटक कसे वर्तन करतात, त्यांचे विरूपण किती होते या सर्व गोष्टींचे गणित करणे होय. हे गणित करताना सुरक्षिततेच्या दृष्टीने संरचनेवरील भार काही पटींनी वाढविले जातात, तर पदार्थाचे बल काही अंशाने की केले जाते. अभिकल्पासाठी धरावयाचा अंतिम भार व प्रत्यक्ष येणारा भार यांच्या गुणोत्तरास भारांचा सुरक्षा गुणांक [⟶सुरक्षा गुणांक] किंवा भार गुणांक म्हणतात, तर पदार्थाचे प्रत्यक्ष बल आणि अभिक्लापत धरावयाचे बल यांच्या गुणोत्तरास पदार्थ-बलाचा सुरक्षा गुणांक म्हणतात. संपूर्ण संरचनेचा एकूण सुरक्षा गुणांक हा ह्या गुणोत्तरांचा गुणाकार होय. हा गुणांक संरचनेचे एकूण सुरक्षामान ठरवितो. भाराचा व पदार्थ-बलाचा असे दोन्ही सुरक्षा गुणांक हे प्रायः संरचनेच्या मंजनाची संभाव्यता व त्या भंजनामुळे होणारे परिणाम या दोन गोष्टींच्या आधारे ठरविले जातात. संरचनेच्या भंजनाची संभाव्यता ही संरचनेवर येणाऱ्या भारांच्या माहितीतील अचूकता, पदार्थ-बलांच्या माहितीतील अचूकता व संरचनेच्या विश्लेषणाची अचूकता (म्हणजेच गृहीत गोष्टी व प्रत्यक्षातील फरकांचे मान) यांवर अवलंबून असते. ही अचूकता जितकी जास्त तितकी भंजनाची संभाव्यता कमी. संरचनेमध्ये ही अचूकता ज्या प्रमाणात साध्य करणे शक्य असते त्या प्रमाणानुसार सुरक्षा गुणांक ठरवावा लागतो.उदा., काँक्रीटच्या संरचनेत पदार्थ-बलाची अचूकता खूपच कमी. काँक्रीट ठोकळ्यांच्या चाचणीने ठरविलेले बल व प्रत्यक्ष जागेवरील घटकातील काँक्रीटचे बल यांत खूपच तफावत असते, कारण चाचणीच्या ठोकळ्यांची स्थिती व प्रत्यक्ष जागेवरील काँक्रीटची स्थिती यांत खूप फरक असतो. काँक्रीटच्या बांधकामात जरूर ते कसब, कार्यकुशलता उपलब्ध असे कित्येक कारणांनी शक्य नसल्याने किंवा कठीण असल्याने घटकांचे अभिकल्पित आकारमान व निर्मितीनंतरचे प्रत्यक्ष आकारमान यांतही तफावत आढळते. अकुशल कामामुळे कित्येक वेळा खांबावर भार विकेंद्रित होतात, तर अभिकल्पामध्ये मात्र ते अक्षीय धरलेले असतात. त्यामुळे काँक्रीटसारख्या पदार्थांसाठी पदार्थबलाचा सुरक्षा गुणांक पोलादपेक्षा खूप जास्त घ्यावा लागतो. संरचनेचे अगदी अचूक (परिशुद्ध) विश्लेषण करणे, तर कित्येक वेळेला अशक्य तर कित्येक वेळेला अतिशय कठीण व क्लिष्ट होते. ते सुलभ करण्यासाठी कित्येक वेळेला अशा काही गोष्टी गृहीत धराव्या लागतात की, ज्या प्रत्यक्ष संरचनेत साध्य करता येतातच असे नाही (उदा., तापमानातील बदलाचे परिणाम, काँक्रीट संरचनेत होणारे विसर्पण म्हणजे थोड्याशा प्रतिबलाने दीर्घ कालात होणारे आकार्य विरूपण-व शिणवटा यांचा परिणाम). अशा परिस्थितीत हे विश्लेषण स्थूलमानानेच होते. अशा वेळी सुद्धा सुरक्षा गुणांक ठरविताना संरचनेच्या भंजनाच्या संभाव्यतेबरोबर  त्या भंजनामुळे होणाऱ्या परिणामाचाही विचार करावा लागतो. भंजनामुळे होणाऱ्या परिणामामध्ये तशा संरचनेच्या पुनर्निर्मितीची आवश्यकता व निवड आणि आवश्यकता असल्यास पुनर्निर्मितीस लागणारा वेळ व खर्च, भंजनामुळे होणारी प्राणहानी, वित्तहानी व आय-व्यय व्यवहारावर होणारा परिणाम यांचा विचार करावा लागतो. उदा., विजेचा साधा खांब तुफान वाऱ्यामुळे मोडल्यामुळे किंवा वाकल्यामुळे होणाऱ्या परिणामापेक्षा उच्च दाबाचा विद्युत् प्रवाह वाहून नेणाऱ्या कोसळल्यास होणारे परिणाम निश्चितच जास्त गंभीर असतात. तसेच साध्या वखारीच्या संरचनेतील तुळईपेक्षा प्रेक्षागृहातील सज्जाचा (बाल्कनीचा) बहाल कोसळल्याने मोठ्या प्रमाणावर प्राणहानी होते. साध्या नलिका मोरीपेक्षा मोठ्या नदीवरील लांब गाळ्याचा रेल्वे पूल वाहून गेल्यास होणारी हानी किती तरी पट मोठी असते. असा पूल पुन्हा ताबडतोब कमीत कमी वेळात बांधणे, तर आवश्यक असतेच शिवाय मधल्या काळात वाहतुकीवर पडणारा ताण व आय-व्यय व्यवहारावर होणारा प्रचंड परिणाम आणि पूल कोसळत असताना त्यावरून गाडी जात असल्यास होणारी प्राणहानी हे सर्व परिणाम अतिशय गंभीर स्वरूपाचे असतात. त्यामुळे अशा पुलाच्या अभिकल्पात जास्त सुरक्षा गुणांक घेणे अधिक तर्कशुद्ध ठरते. अशा तऱ्हेने विविध गोष्टींचा संरचनेच्या सुरक्षिततेवर व सेवायोग्यतेव होणारा परिणाम आणि संरचनेच्या असुरक्षिततेचा इतर गोष्टींवर होणाऱ्या परिणामांचे गांभीर्य या आधारे एकूण सुरक्षा गुणांक ठरवून त्या आधारे वाढीव भार घेऊन व कमी पदार्थ-बल धरून संरचनेचे विश्लेषण करावे लागते.

---

कोष्टक क्र. २ (पुढे चालू)
१	२	३
१८०१–१८६१	एम्. व्ही ऑस्ट्रोग्राडस्की	रशियन शास्त्रज्ञ. चलनकलनशास्त्र व स्थितिस्थापक वस्तूमधील तरंग यांवर कार्य.
१८०१–१८९२	जॉर्ज बिडेल	इंग्रज शास्त्रज्ञ. स्थितिस्थापकता सिद्धांतातील सुप्रसिद्ध प्रतिबल फलनाचे जनक
१७४४–१८४८	आय्. टाउन	}     सर्व अमेरिकन अभियंते. प्रत्येकाची स्वतंत्र अशी कैची रचना प्रसिद्ध आहे.
१७८३–१८६०	रसेल वॉरेन
१८०४–१८८८	एस्. व्हिपल
१८१२–१८७५	टी. डब्ल्यू. प्रॅट
१८४०	विल्यम्स हौ
१८०३–१८५९	रॉबर्ट स्टीव्हेन्सन	इंग्रज रेल्वे अभियंते. इंग्लंडमधील सुप्रसिद्ध ब्रिटानिया पुलासह इतर अनेक रेल्वे पुलांच्या निर्मितीस हातभार.
१८०६–१८५९	आय्. के. ब्रूनेल	प्रसिद्ध इंग्रज पूल अभियंते, पोलादी पाट-बहालाच्या वापरास सुरुवात इंग्लंडमध्ये अनेक पोलादी पूल बांधले.
१८०६–१८७१	जे. एल् वाईस्बाख	जर्मन शास्त्रज्ञ. पदार्थबलविज्ञानाचा यंत्रांच्या व त्यांच्या भागांच्या निर्मितीमध्ये वापर.
१८०९–१८६३	फेर्डिनांट याकोप रेडटेनबॅखर	जर्मन शास्त्रज्ञ. पदार्थबलविज्ञानाचा यंत्रांच्या व त्यांच्या भागांच्या निर्मितीमध्ये वापर.
१८१९–१९०३	जी. जी स्टोक्स	ब्रिटिश शास्त्रज्ञ. पदार्थांची आकार्यता व प्रेरित कंपने यांवर संशोधन
१८१९–१९१४	आउगुस्ट व्हलर	जर्मन शास्त्रज्ञ. पदार्थातील शिणवटा अंतर्वक्री टोकदार कोपऱ्यांमुळे होणारे परिबलांचे केंद्रीभवन व आकार्य नमनामुळे शेष बलांची निर्मिती यांवर संशोधन
१८२०–१८७२	डब्ल्यू. जे. एम्. रँकिन	स्कॉटिश संशोधन-शास्त्रज्ञ. इंग्लंडमधील अनुप्रयुक्त यामिकीवर पहिले पुस्तक लिहिले प्रतिबल, प्रतिविकृती व स्थितिस्थापकता यांचा पुस्तकात प्रथम समावेश या पुस्तकाच्या त्या काळी १५ आवृत्त्या निघाल्या निलंबी पुलाच्या दृढक तुळ्या, धारक भिंतीवरील मातीचा भार यांवरील सुप्रसिद्ध सिद्धांताचे जनक. रेल्वेच्या डब्यांच्या अक्षदंडांमध्ये आवर्ती भारामुळे येणाऱ्या शिणवट्यावर संशोधन.
१८२१–१८८१	कार्ल कूलमान	जर्मन शास्त्र व पूल अभियंते. निलंबी पुलाच्या दृढक तुळ्यांवर संशोधन कैच्यांच्या विश्लेषणाच्या भूमितीय आरेखन पद्धतीवर पहिला ग्रंथ लिहिला. (१८६६) गुरुत्वमध्य ठरविण्यासाठी, निरूढी परिबल ठरविण्यासाठी व प्रधान परिबलांच्या निश्चितीकरणासाठी आलेख पद्धती शोधून काढली.
१८२१–१८८१	ई. फिलिप्स	फ्रेंच शास्त्रज्ञ. रेल्वे डब्यांच्या आधारासाठी पट्ट्यांच्या स्प्रिंगांचा वापर.
१८२१–१८९१	डी. जे. झुराव्हस्की	रशियातील रेल्वे पुलांच्या निर्मितीस हातभार संयुक्त तुळईतील कर्तन प्रेरणांवर संशोधन व या संशोधनाच्या आधारे ब्रिटानिया पुलाच्या अभिकल्पातील दोषांचे विश्लेषण.

सांरचनिक अभिकल्पाचा या पुढील चौथा टप्पा म्हणजे विश्लेषणामुळे ज्ञात झालेल्या घटकातील प्रेरणा व संरचनेत  वापरावयाच्या पदार्थांचे अवगत बल यांच्या आधारे संरचनेच्या घटकांचे अंतिम आकारमान ठरविणे किंवा गृहीत आकारमानाच्या सुरक्षिततेची खात्री करून घेणे हा होय. घटकांचे अंतिम आकारमान ठरविताना संरचनेच्या घटकांचे विविध सांरचनिक विरूपण क्रियांनुसार असलेले प्रतिबल अथवा सामर्थ्य  (उदा., ताणबल, संकोची बल, नमन परिबल, वूर्णीय परिबल, व्याकुंचनरोधी बल इ.). हे त्यावर येणाऱ्या प्रेरणांपेक्षा जास्त आहे की नाही आणि घटकांचे  होणारे सांरचनिक विरूपण अथवा विचलन एका ठराविक मर्यादेत आहे की नाही, हे पहाणे संरचनेच्या सुरक्षिततेच्या व सेवायोग्यतेच्या दृष्टीने अत्यावश्यक ठरते. यामुळे घटकाच्या गृहीत आकारमानामध्ये वाढ करावी लागत असल्यास घटकाच्या स्वतःच्या भारामध्ये वाढ होत असल्याने संरचनेचे पुनर्विस्लेषण करणे भाग पडते. अभिकल्पाचा अंतिम व पाचवा टप्पा म्हणजे संरचनेची उभारणी व बांधणी यांस उपयुक्त असे कार्यकारी आरेश तयार करणे होय. या आरेखांमध्ये संरचनेचा आराखडा, मांडणी, घटकांचे आकारमान, पदार्थांचा प्रकार, अपेक्षित बल इ. गोष्टी मापांसह व परिमाणांसह दिल्या जातात.

---

कोष्टक क्र. २ (पुढे चालू)
१	२	३
१८२२–१८८३	झाक ए. सी. ब्रीझ	फ्रेंच शास्त्रज्ञ. पदार्थबलविज्ञानावर दोन ग्रंथ लिहिले वक्रदंडातील प्रेरणांवर संशोधन.
१८२४–१८८७	जी. आर्. किरखोफ	जर्मन शास्त्रज्ञ. पाट व लाद्या यांच्या विश्लेषणांचे सिद्धांत पाटांचे कंपन.
१८२४–१९०७	विल्यम टॉमसन केल्व्हिन	ब्रिटिश शास्त्रज्ञ. स्थितिस्थापकता सिद्धांतात संशोधन
१८२६–१८९३	फ्रांट्स ग्राशॉफ	जर्मन शास्त्रज्ञ. स्थितिस्थापकता व आकार्यता सिद्धांतावर ग्रंथ लाद्यांच्या विश्लेषणावरील सिद्धांत.
१८३१–१८७९	जेम्स क्लार्क मॅक्सवेल	स्कॉटिश शास्त्रज्ञ. संरचना विश्लेषण सिद्धांतांचे अध्वर्यू सुप्रसिद्ध पारस्परिक विचलनाच्या प्रमेयाचे व विश्लेषणाच्या प्रभाव गुणांक पद्धतीचे जनक संरचना विश्लेषणाच्या आलेखन पद्धतीचा शोध कैच्यांचे विश्लेषण व विचलनांचे गणन.
१८३३–१८९३	योहान बॉशिंगर	जर्मन शास्त्रज्ञ. पदार्थांच्या भंजनाचा सिद्धांत पदार्थातील शेष प्रतिबलांवर संशोधन.
१८३५–१८८८	ई. विंक्लर	वक्रदंड, साखळ्या व आकडे (हूक) यांचे नमन स्थितिस्थापक आधारवरील तुळ्यांचे विश्लेषण.
१८३५–१९१६	ओटो मोर	जर्मन शास्त्रज्ञ व रेल्वे अभियंते. संरचनेच्या विश्लेषण शास्त्रात मॅक्सवेल यांच्या इतकेच महत्त्वाचे कार्य विश्लेषणाच्या विविध पद्धती व प्रमेये मांडली विश्लेषणाच्या नमन-परिबल पद्धतीचे जनक प्रधान प्रतिबलांसाठी भूमितीय आरेखन पद्धती शोधून काढली. आभासी कार्याच्या सिद्धांतावर आधारित विश्लेषण पद्धथी मांडली विचलनांच्या गणनासाठी प्रभाव आलेखांचा सर्वप्रथम उपयोग.
१८३८–१९१०	मॉरिस लेव्ही	फ्रेंच गणितज्ञ व अभियंते. पट्ट विश्लेषणाचा सिद्धांत.
१८४२–१९१९	जे. डब्ल्यू. एस्. रॅली	इंग्रज शास्त्रज्ञ. संरचनेच्या स्थितिसाथापक स्थैर्याचा सिद्धांत कंपनांचा अभ्यास विचलनाच्या अवकल समीकरणाच्या समाकलनाच्या आधारे संरचनेचे विश्लेषण करणाऱ्या पद्धतीचे जनक.
१८४२–१९२९	झोझेफ व्हालांतँ बूसँक्यू	फ्रेंच शास्त्रज्ञ. केंद्रीय भारामुळे पायाखाली येणाऱ्या प्रतिबलांवर संशोधन.
१८४७-१८८४	आल्बेर्तो कास्तिल्येनो	इटालियन शास्त्रज्ञ. सुप्रसिद्ध स्थितिस्थापक ऊर्जा सिद्धांताचे जनक यांच्या संशोधनाने संरचना विश्लेषणास पायाभूत तत्त्वज्ञान प्राप्त झाले.
१८४७–१९२१	एन्. झुकॉव्हस्कई	रशियन शास्त्रज्ञ. वायुगतिकी शास्त्रात महत्वाचे संशोधन.
१८४८–१९३१	फ्रीड्रीख एंगेझर	जर्मन शास्त्रज्ञ. कास्तिल्योनो यांच्या स्थितिस्थापक ऊर्जा सिद्धातास समांतर असा पूरक स्थितिस्थापक ऊर्जा सिद्धांत यांनी मांडला.
१८७३	रॉबर्ट बो	कैच्यांच्या विश्लेषणाची भूमितीय आरेख पद्धती शोधून काढली.
१८७३	सी. ई. ग्रीन	अमेरिकन शास्त्रज्ञ. संरचना विश्लेषणाच्या अनुबद्ध संरचना पद्धतीचा शोध लावला.
१८८६	हाइन्रिख म्यूलर ब्रेसलाऊ	जर्मन शास्त्रज्ञ. मॅक्सवेल व मोर यांच्याप्रमाणेच संरचना विश्लेषणात महान कार्य अनिर्धार्य संरचनांच्या विचलनाच्या सुप्रसिद्ध पमेयाचे जनक.

 

सांरचनिक विश्लेषण व अभिकल्पाचे विविध प्रकार : संरचनेत वापरल्या जाणाऱ्या पदार्थांच्या वर्तन-प्रवृत्तीनुसार संरचना विश्लेषणाच्या (१) स्थितिस्थापक पद्धती, (२) अस्थितिस्थापक पद्धती, (३) आकार्य पद्धती, (४) परम भार पद्धती व (५) स्थिती-सीमा पद्धती अशा पाच पद्धती आहेत. स्थितीस्थापक पद्धतीमध्ये संरचना व संरचनेत वापरला जाणारा पदार्थ हा स्थितिस्थापक गुणधर्मांचा आहे असे धरून विश्लेषण केले जाते. म्हणजेच या पदार्थांचे व संरचनेचे विचलन हे त्यावर येणाऱ्या भाराच्या सम प्रमाणात होते असे मानले जाते पण प्रत्यक्षात मात्र कोणताच पदार्थ (अगदी पोलादसुद्धा) भंजनाच्या अवस्थेतपर्यंत स्थितिस्थापक प्रवृत्ती दाखवीत नाही. पोलादसुद्धा एका मर्यादेपर्यंतच स्थितिस्थापक प्रवृत्ती दर्शविते, मात्र त्यानंतर ते आकार्य प्रवृत्ती दाखविते. स्थितिस्थापक पद्धतीमध्ये संरचनेच्या घटकांमध्ये बाहेरील भारामुळे येणारी महत्तम प्रत्यक्ष प्रतिबले अनुज्ञात प्रतिबलांपेक्षा कमी राहातील हे पाहिले जाते. अनुज्ञात प्रतिबले ही पदार्थाच्या परम प्रतिबलावरून किंवा शरण प्रतिबलावरून (भार न वाढविता ज्या किमान प्रतिबलाला घटकाचे प्रसरण वाढत राहते अशा प्रतिबलावरून) सुरक्षा गुणांकांच्या आधारे ठरविली जातात. परम प्रतिबल व अनुज्ञात प्रतिबल यांचे गुणोत्तर हा या पद्धतीत सुरक्षा गुणांक धरला जातो म्हणजे या पद्धतीत असे गृहीत धरले जाते की, संरचनेच्या कोणत्याही भागामध्ये कोणत्याही ठिकाणी कोणत्याही परिस्थितीत परम प्रतिबल येणे असुरक्षित होय. प्रत्यक्षात मात्र संपूर्ण संरचना किंवा तिचा भाग किंवा तिचा घटक हा कोणत्या एखाद्याच ठिकाणी परम प्रतिबल आल्याने भंग पावत नाही. त्यामुळे ही पद्धती खरोखरीच केवढ्या भारामुळे संरचना भंग पावेल–म्हणजेच भंग पावण्यापूर्वी तिची खरीखुरी माया किती आहे, हे दर्शवीत नाही. ज्या भारामुळे संरचना भंग पावेल, मोडेल वा कोसळेल असा भंग-भार शोधून काढावयाचा गेल्या दोन-तीन शतकांत प्रयत्न होऊन संरचना भंग पावेपर्यंत संरचनेचे वर्तन कसे होते व त्यावरून सुरक्षिततेत्या दृष्टीने माया ठरवून संरचना किती भार घेऊ शकेल या सर्व गोष्टींचे संशोधन व त्याचा अभ्यास होऊन त्यावर आधारित आकर्य पद्धती व परम भार पद्धती यांचा उगम झाला. आकार्या पद्धती ही पोलादासारख्या आकार्य गुणधर्म असलेल्या पदार्थांच्या संरचनेसाठी वापरली जाते. पोलाद हे ठराविक मर्यादेपर्यंत स्थितिस्थापक व त्यानंतर प्रायः आकार्य गुणधर्म दाखवते. पोलादच्या या आकार्य वर्तनामुळे संरचनच्या एखाद्या घटकामध्ये एखाद्या ठिकाणी स्थायी विकृती मर्यादित प्रमाणात येऊ दिल्याने प्रेरणांचे संरचनेच्या सर्व भागांवर पुनर्वितरण होऊन संरचनेचा परम भार वाढतो. या गोष्टींचा आकार्य पद्धतीत उपयोग करून घेतला जातो. म्हणजेच आकार्य पद्धती ही पदार्थाचा भंजनापर्यंतच्या वर्तनाच्या सर्व टप्प्यांचा विचार करून संरचनेचा भंग-भार शोधून काढते व त्याच्याशी संरचनेचे विश्लेषण निगडित करते.

---

कोष्टक क्र. २ (पुढे चालू)
१	२	३
१८५७–१९३६	कार्ल पीअर्सन	इंग्रज शास्त्रज्ञ. आयझॅक टॉडहंटर या शास्त्रज्ञांबरोबर त्यांनी स्थितिस्थापकता सिद्धांत व पदार्थबलविज्ञानाचा इतिहास प्रथमच ग्रंथबद्ध केला (१८८६–९३).
१८६३–१९४०	ए. ई. एच्. लव्ह	इंग्रज शास्त्रज्ञ. स्थितिस्थापकता सिद्धांतावरील सुप्रसिद्ध ग्रंथाचे (१८९२–९३) कर्ते.
१८७५–१९५३	लूटव्हिख प्रांट्ल	सुप्रसिद्ध जर्मन शास्त्रज्ञ. स्थितिस्थापकता सिद्धांतातील घूर्णीय बलाच्या विश्लेषणाच्या साबण-पटल अनुरूपणाचे जनक वार्ताववर चाचण्यांचे जनक वायुगतिकीत संशोधन कार्य त्यांच्या हाताखालून पुढील शास्त्रज्ञ शिकून नावारूपास आले : थीओडोर फोन कार्मन-वायुगतिकी ए. नडाय व डब्ल्यू. प्रेगर-पदार्थांचा आकार्यता सिद्धांत फ्लीग-लाद्यांचे विश्लेषण जे. पी. डेनहारटॉग-पदार्थबलवित्रान एस्. पी. ट्यिमशेन्कॉ-संरचनांचे विश्लेषण व स्थितिस्थापकता सिद्धांत.
१९१५	जी. ए. मॅनी	अमेरिकन शास्त्रज्ञ. सुप्रसिद्ध उतार-विचलन पद्धती यांमधील पारस्परिक संबंधाची आधारभूत मीमांसा.
१९२४	ए. ऑस्टेनफिल्ड	जर्मन शास्त्रज्ञ. प्रेरणा पद्धती व विचलन पद्धती यांमधील पारस्परिक संबंधाची आधारभूत मीमांसा.
१९२५	एस्. पी. ट्यिमशेन्कॉ	रशियन शास्त्रज्ञ. अमेरिकेत स्थायिक होऊन कार्य. पदार्थबलविज्ञान व स्थितिस्थापकता सिद्धांत यांच्या इतिहासावर महत्वाचा ग्रंथ लिहिला संरचनाशास्त्रातील प्रत्येक क्षेत्रातील सिद्धांतावर अनेक प्रमाणभूत ग्रंथ या ग्रंथांचा आजही जगातील या विषयावरील जवळजवळ प्रत्येक संशोधन पत्रिकेत संदर्भ दिला जातो विश्लेषणातील श्रेढी पद्धतीचे पुरस्कर्ते.
१९३०	हार्डी क्रॉस	अमेरिकन शास्त्रज्ञ. आजच्या संगणक युगामध्ये सुद्धा संरचना विश्लेषणाची जी पद्धती सर्वांत जास्त वापरली जाते अशा परिबल-वितरण पद्धतीचे जनक.
१९४०	आर्. व्ही. साउथवेल	इंग्रज शास्त्रज्ञ. संरचना विश्लेषणाच्या संख्यात्मक पद्धतींपैकी प्रसरण पद्धतीचे जनक.
१९३०/४०	बी. जी. गॅलर्किन आणि एल्. व्ही. केंटरोव्हिच	सातत्यक यामिकीशास्त्रातील व चलनकलनातील काही महत्त्वाचे सिद्धांत मांडले.
१९४७	एस्. लेव्ही	आधुनिक आव्यूह प्रेरणा पद्धतीचा शोध.
१९५३	एस्. लेव्ही	आधुनिक आव्यूह विचलन पद्धतीचा शोध.
१९५७	गास्पर कानी	जर्मन शास्त्रज्ञ. संरचना विश्लेषणाच्या सुप्रसिद्ध परिवलीय अंशदान पद्धतीचे जनक. ही पद्धती ‘कानी पद्धती’ म्हणूनच ओळखली जाते.
१९५३–६५	आर. डब्ल्यू. क्लफ (अमेरिकन), एम्. जे. टर्नर (अमेरिकन), जे. एच्. आर्गरिस, (अमेरिकन), आर्. एच्. गॅलागर (अमेरिकन) बी. एफ्.इ. ह्युब्क (पोर्तुगीज) ओ.सी. झियकीविक्स (इंग्रज) सी. ए. फेलिपा (इटालियन).	एकोणिसाव्या व विसाव्या शतकांत पुढे आलेल्या व संरचना विश्लेषणात क्रांती करणाऱ्या परिमित घटक पद्धतीचा शोध लावून आणि या पद्धतीची सर्वांगीण प्रगती करून विश्लेषणाचे स्वतंत्र शास्त्र निर्माण करण्यास या सर्वांनी हातभार लावला.
[वरील कोष्टकातील संघांच्या स्पष्टीकरणासाठी व अधिक माहितीसाठी ‘यामिकी’, ‘स्थिति-स्थापकता’, ‘पदार्थोचे बल’, ‘वायुगतिकी’, ‘आकार्यता’, ‘वातविवर’, ‘अवकलन व समकलन’, ‘चलनकलन’, ‘फूर्ये श्रेढी’ इ. नोंदी व तसेच आर्किमिडीज, व्ही.ची, गॅलिलीओ, हुक, न्यूटन, बेर्नुली, ऑयलर, ॲलांबरो, माँझ, पॉस्ले, कोशी, फूर्ये, यंग, स्टोक्स, रॅकिन, प्रांट्ल, केल्व्हिन, मॅक्सवेल, रॅली इ. शास्त्रज्ञांच्या चरित्र नोंदी पहाव्यात कोष्टकात जेथे नुसते एकच साल दिलेले आहे तो त्या त्या व्यक्तीच्या कार्याचा काळ समजावा].

 

काँक्रीटसारखा पदार्थ पोलादाइतक्या मोठ्या प्रमाणावर आकार्य प्रवृत्ती दाखवीत नाही. आकार्यतेत फार मोठ्या प्रमाणावर प्रतिविकृती येऊनही पदार्थ भंग न पावण्याची प्रवृत्ती अपेक्षित असते. काँक्रीट मात्र फार थोड्या प्रतिविकृतीखाली भंग पावते पण प्रबलित काँक्रीटमध्ये प्रबलक सळ्या ह्या पोलादाच्या असल्याने पोलादाच्या आकार्यतेचा लाभ प्रबलित काँक्रीटमध्ये घेता येतो. परम भार पद्धतीत संरचनेचा भंग-भार हा परम भार धरून भंजनापासून सुरक्षिततेची माया ही परम भार/अनुज्ञात (कार्यकारी) भार या गुणोत्तरावरून ठरविली जाते. मात्र या पद्धतीत कार्यकारी भाराखालील संरचनेच्या विरूपणाचे विश्लेषण केले असता कित्येक वेळा ते स्थितीस्थापक पद्धतीत धरल्या जात असलेल्या मर्यादेपेक्षा जास्त होत असल्याचे ह्या पद्धतीची जागा नुकतीच स्थिती-सीमा पद्धतीने घेतली आहे. स्थिति-सीमा पद्धतीने घेतली आहे.

स्थिती-सीमा पद्धतीत संरचनची सुरक्षिततेची स्थिती व सेवायोग्यतेची स्थिती अशा दोन्ही स्थितींचा विचार करून दोन्ही स्थितींशी संबंधित भार व विरूपणाच्या मर्यादा निश्चित केल्या जातात. उदा., सुरक्षिततेच्या दृष्टीने संरचनेवरील भार तिच्या भंग-भारापेक्षा जास्त असता कामा नये ही अट संरचनेवरील भाराची सीमा वा मर्यादा आखून देते, तर सेवायोग्यतेच्या दृषअटीने संरचनेवर नेहमी येणाऱ्या कार्यकारी भारामुळे होणारी संरचनेची जी विरूपणे (वा विचलने) संरचना निकामी वा निरूपयोगी करतील ती विरूपणाची (वा विचलनाची) सीमा होय. अती विरूपणामुळे तर संरचना निकामी होऊ शकतेच पण त्या बरोबरच त्यामुळे मोठ्या भेगा पडूनही तडे जाऊन पाण्याच्या टाकीसारखी संरचना निकामी होऊ शकते. चल (बदलत्या) भारामुळे होणाऱ्या अती कंपनांमुळेही संरचना निकामी होऊ शकते. म्हणून सेवायोग्य स्थितीसाठी करावयाचे विरूपणाचे, विचलनाचे, कंपनांचे व भेगांच्या रूंदीचे गणन हे कार्यकारी भाराखालीच करावयाचे असते व या भाराखाली संरचना स्थितिस्थापक प्रवृत्ती दाखवीत असल्याने हे सर्व विश्लेषण स्थितिस्थापक पद्धतीने करावे लागते. त्याउलट सुरक्षिततेची सीमा म्हणजे भंजनाची स्थितीही परम भाराशी संबंधित असल्याने तिचे गणन परम भार वा आकार्य पद्धतीने केले जाते. अशा तऱ्हेने स्थिति-सीमा पद्धती ही स्थितिस्थापक पद्धती व परम भार पद्धती या दोहींमधील दोष टाळून त्यांचा सुयोग्य मेळ साधते. अस्थितिस्थापक पद्धती ही संरचनेच्या किंवा पदार्थांच्या अस्थितिस्थापक वर्तनावर आधारित असून ती खरीखुरी अवस्था प्रतिबिंबित करणारी असली, तरी गणीतीय विश्लेषणास अतिशय क्लिष्ट व कठीण असल्याने तिचा वापर विशेष होत नाही. अर्धदृढ सांध्यांनी युक्त संरचनांसाठी या पद्धतीचा वापर करण्यात येतो.

संरचनेवर येणाऱ्या भारांच्या अथवा क्रियांच्या प्रकारानुसार संरचना विश्लेषणाचे व अभिकल्पाचे पुढील प्रकार होत : (१) स्थितिकीय विश्लेषण, (२) गतिकीय विश्लेषण, (३) औष्णिक विश्लेषण, (४) स्थैर्यता विश्लेषण, (५) भूकंपरोधी अभिकल्प, (६) स्फोटरोधी अभिकल्प, (७) घूर्णवाती वादळ निरोधी [⟶ घूर्णवाती वादळ] अभिकल्प, (८) अणुकेद्रीय विक्रियारोधी अभिकल्प, (९) आंदोलन विश्लेषण, (१०) प्रतिकृती विश्लेषण.

स्थितिकीय विश्लेषणामध्ये फक्त संरचनेवर येणाऱ्या स्थिर भारांचा विचार केला जातो. हे विश्लेषण सर्वसाधारणपणे निवासी व कार्यालयीन इमारतींच्या बाबतीत केले जाते. पुलासारख्या वास्तूवर चल भार व कंपने येत असल्याने अशा भारांचा व त्यांच्या परिणामांचा विचार करणारे गतिकीय विश्लेषण करावे लागते. स्तंभ तन्वाकार असल्यास तो लपकण्याची शक्यता असते, त्यामुळे अशा स्तंभांनी युक्त संरचनांसाठी स्थितिस्थापक स्थैर्यता विश्लेषणही करावे लागते. औष्णिक पात्राच्या बाबतीत किंवा धुराड्याच्या अभिकल्पामध्ये तापमानातील फरकामुळे होणाऱ्या परिणामाचे विश्लेषण करावे लागते. यास औष्णिक क्रियेचे विश्लेषण म्हणतात. अणुशक्ती केंद्रातील धारक पात्रे व टाक्या अणुकेंद्रीय विक्रियेस किती रोध करू शकतात याचे विश्लेषण करून अणुकेंद्रीय विक्रियारोधी अभिकल्प करावा लागतो [⟶ अणुकेंद्रीय अभियांत्रिकी]. खाणींच्या जवळपास जेथे खाणकामासाठी वारंवार स्फोट केले जातात, अशा ठिकाणच्या आसपासच्या संरचनांसाठी स्फोटरोधी अभिकल्प करावा लागतो. ज्या प्रदेशात घूर्णवाती वादळे सारखी होत असतील अशा ठिकाणच्या संरचनांचा घूर्णवातविरोधी अभिकल्प करावा लागतो. वितळजोडकाम तंत्राने सांधलेल्या पोलादी संरचनांवर होणारा आवर्ती आघाती भाराच्या आंदोलनाचा परिणाम आंदोलन विश्लेषणात पाहिला जातो. जेव्हा एखाद्या संरचनेच्या विश्लेषणास गणितीय पद्धत, सूत्रे किंवा सिद्धांत उपलब्ध नसतील तेव्हा अशा संरचनेची प्रतिकृती (मॉडेल) तयार करून तिची चाचणी घेऊन संरचनेचा अभिकल्प करावा लागतो. ही प्रतिकृती विश्लेषणाता उपयोग होतो [⟶प्रतिकृति]. याशिवाय ज्या काही संरचनांचे (उदा., मोठ्या यंत्रांचे जोड, धरणाचे भाग इत्यादींचे) गणितीय विश्लेषण करणे शक्य नसते अशा संरचनांचे प्रायोगिक पद्धतींनी विश्लेषण केले जाते. विश्लेषणाच्या प्रायोगिक पद्धतीमध्ये प्रकाश स्थितिस्थापकता तंत्र, विद्युत् रोधमापन (विद्युत् प्रतिविकृतिमापन) तंत्र, ठिसूळ लेप तंत्र अशा विविध तंत्रांचा समावेश होतो [⟶ पदार्थांचे बल].

संरचनेवर येणारे भार व क्रिया : संरचनेचे विश्लेषण करण्यापूर्वी तिच्यावर येणाऱ्या भारांचे व क्रियांचे परिणाम ठरविणे व संरचनेवर अनिष्टतम परिणाम करणाऱ्या भारांचे वितरण व संयोग ठरविणे या गोष्टी कराव्या लागतात. संरचनेवर येणाऱ्या भारांमध्ये व क्रियांमध्ये संरचनेचे स्वतःचे वजन म्हणजे अचल भार किंवा जड भार, चल भार (म्हणजेच अस्थिर भार उदा., माणसे, प्राणी, वाहने, फर्निचरसारखे सामान, यंत्रसामग्री इत्यादींमुळे येणारा भार), हिम भार, वाऱ्याचा दाब किंवा चोषण (ओढून घेणे), पाण्याचा किंवा मातीच्या भरावाचा आडवा रेटा, लाटांचा परिणाम, वाहनामुळे व अन्य कारणांमुळे येणारा आघाती भार, भूकंप, यंत्राचे चलन, स्फोट किंवा अन्य कारणांनी येणारे भार, कंपने व हादरे, हवामानाचा, पाण्याचा व रसायनांचा होणारा परिणाम या सर्व गोष्टींचा समावेश होतो. अशा विविध संभाव्य भारांचा व क्रियांचा अलगपणे किंवा एकत्रितपणे होणाऱ्या परिणामांचा अंदाज विश्लेषणात करावा लागतो. हे सर्व भार विविध संबंधित संस्थांच्या (उदा., रेल्वे, नगरपालिका, सार्वजनिक किंवा राष्ट्रीय बांधकाम खाते), मानक संस्थांच्या संहितांनी अथवा नियमावलींनी सूत्रवृद्ध केलेले असतात व त्यांचा विश्लेषणात वापर केला जातो.

बांधकामाचे पदार्थ : गुणधर्म व निवड : बांधकामाच्या पदार्थासाठी बल, तन्यता(तार काढता येण्याची क्षमता), स्थितिस्थापकता, आकार्यता, लवचिकता, कठिणता, अग्निरोधकता, गंजरोधकता, टिकाऊपणा, कार्यसुकरता, अल्प खर्चीपणा व सहज उपलब्ध असणे हे सांरचनिक गुण मानले जातात. ह्यांतील बहुतांश गुण असलेले पदार्थ संरचनेत वापरले जातात. बांधकामाच्या रूढ सामग्रीत दगड, विटा, लाकूड, काँक्रीट (साधे, प्रबलित व पूर्वप्रतिबलित), लोखंड, पोलाद, ॲल्युमिनियम, इतर लघुभारी मिश्रधातू यांचा समावेश होतो. या पदार्थांच्या सर्वसाधारण गुणधर्मांसाठी ‘बांधकाम सामग्री’ ही नोंद पहावी. भाराखाली कमी अधिक प्रमाणात विरूपण वा विचलन अथवा विस्थापन होणे हा प्रत्येक पदार्थांछा मूलभूत गुणधर्म होय, तरी पण पदार्थाची निवड करताना त्या पदार्थांचे खास व विशिष्ट गुणधर्मही लक्षात घ्यावे लागतात. पोलाद व लाकूड ताण प्रेरणा व संकोची प्रेरणासारख्या प्रमाणात घेतात तर काँक्रीट, दगड व विटा यांचे बांधकाम ताण प्रेरणा घेऊ शकत नाहीत. त्यामुळे असे पदार्थ वापरावयाचे असल्यास या पदार्थाच्या घटकामध्ये ताण प्रेरणा येणार नाही अशी रचना (उदा., कमानी, घुमटी किंवा कवची रचना) तरी करावी लागते किंवा ताण घेण्यासाठी पोलादसारखे प्रबलक तरी वापरावे लागतात किंवा पूर्वप्रतिबलनाचे तंत्र वापरावे लागते. काँक्रीट हे मानवनिर्मित असल्याने त्यास जरूर तो आकार देता येतो, त्यात जरूर ते सामर्थ्यही आणता येते पण त्यात लवचिकता अजिबात नसल्याने कोसळण्यापूर्वी ते कोणतीच पूर्व सूचना देत नाही, हा एक मोठा धोका असतो. पोलादमध्ये भरपूर तन्यता असल्याने ते अचानक एकाएकी तुटत किंवा कोसळत नाही. वितळजोड सांध्यामुळे मात्र त्यात कित्येक वेळा ठिसूळपणा येतो. पोलादाचे बल त्याच्या वजनाच्या मानाने प्रचंड असले, तरी त्याचबरोबर पोलादाला पाहिजे तो आकार देता येत नाही. व पोलादी घटक दिसायला आकर्षत दिसत नाही हे त्याचे दोष होत.

तसेच पोलाद तितके अग्निरोधकही नाही. आगीच्या प्रखर उष्णतामानामुळे ते वाटेल तसे वाकडे-तिकडे होऊन संरचना मोडते म्हणून त्यास काँक्रीटचे आवरण देऊन त्याची अग्निरोधकता वाढवावी लागते. लाकडाचे बल व टिकाऊपणा कमी पण कापणी-जोडणी इत्यादींच्या दृष्टीने सोईचे असते म्हणून ते तात्पुरत्या कामचलाऊ हंगामी संरचनासाठी वापरले जाते. पदार्थांच्या सांरचनिक गुणधर्मांचा विचार करताना त्या पदार्थाचे बल वा सामर्थ्य फक्त विचारात न घेता शून्य भारापासून परम भारापर्यंत होणारे त्याचे वर्तन, वेगवेगळ्या प्रकारच्या भारांखाली होणारे विरूपण, आघात भाराखालील वर्तन, कंपनाचे त्यावर होणारे परिणाम, औष्णिक बदलाचे त्यावर होणारे परिणाम, व्युत्क्रमी व आवर्ती भारांचा होणारा परिणाम, दीर्घकाळ राहणाऱ्या भारामुळे होणारे विसर्पण व त्यात येणारा शिणवटा या सर्व गुणधर्मांचा व परिणामांचा साकल्याने विचार करावा लागतो.

संरचनेचे विश्लेषण : बाहेरील भारांचा अथवा क्रियांचा संरचनेवर होणाऱ्या परिणामांचा अभ्यास म्हणजे संरचनेचे विश्लेषण होय. हे परिणाम म्हणजे संरचनेच्या घटकांमध्ये अंतर्गत प्रतिबल निर्माण होणे, संरचनचे विरूपण, विचलन वा विस्थापन होणे, संरचनेचा आधार अथवा एखादा घटक खचणे, एखाद्या घटकाच्या व्याकुंचनामुळे (लपकण्यामुळे) संरचनेची स्थैर्यता नष्ट होणे, संरचनेत कंपने निर्माण होणे, अतिविरूपणामुळे संरचनेस तडा जाणे अशा विविध प्रकारचे असू शकतात. या सर्वांचा अभ्यास विश्लेषणात अभिप्रेत आहे. हा अभ्यास संरचनेची सुरक्षितता, स्थैर्य व सेवायोग्यता यांच्या दृष्टीने अत्यावश्यक होय. संरचनेच्या विश्लेषणाचे एकूण संरचनाशास्त्रातील स्थान आ. १ वरून लक्षात येईल.

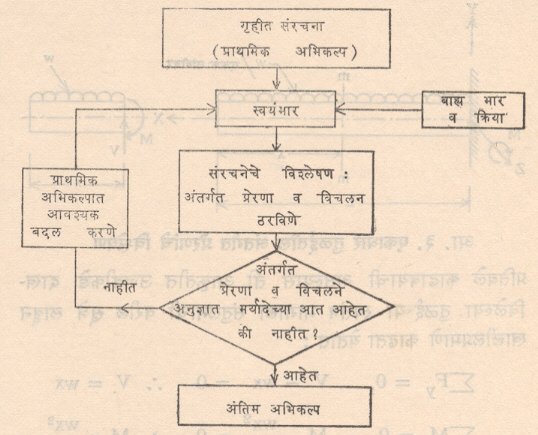
संरचनेच्या विश्लेषणाचे स्वरूप आ. २ वरून लक्षात येईल. यावरून हेही लक्षात येईल की, संरचनेचे भूमितीय व भौतिक गुणधर्म तसेच तिच्यावरील भार व क्रिया या विश्लेषणाच्या देयक (दिलेल्या) राशी होत, तर अंतर्गत प्रतिबले व विचलन ह्या परिणाम राशी होत. विश्लेषणाने देयक राशींवरून अंतर्गत प्रतिबले किंवा विचलने स्वतंत्रपणे काढता येतात. इतकेच नव्हे, तर प्रतिबल आणि विचलन यांतही पारस्परिक संबंध असल्याने सुरूवातीस दोन्हींपैकी कोणतीही एक राशी काढल्यास प्रतिबल-विचलन संबंधाचा उपयोग करून दुसरी राशी मिळू शकते.

 

 

 

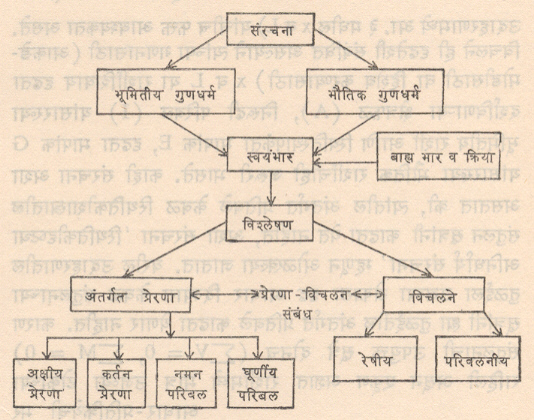
बाह्य भारांवरून अंतर्गत प्रतिबले काढण्यासाठी स्थितिकीशास्त्रातील संतुलनाच्या सूत्रांचा [⟶ यामिकी] उपयोग केला जातो. कोणतीही संरचना कोणत्याही परिस्थितीत स्थिर राहणे आवश्यक असल्याने तिला संतुलनाची सूत्रे लावता येतात. ही सूत्रे खालील प्रमाणे होत :

∑ F_x = 0, ∑ F_y = 0, ∑F_z = 0

∑ M_x = 0, ∑ M_y= 0 , ∑M_z = 0.

म्हणजेच तीनही प्रमुख अक्षांकडील एकूण प्रेरणांची बेरीज व तीनही अक्षांभोवतालच्या परिबलांची बेरीज शून्य होय. या सूत्रांचा उपयोग करून संरचनेतील अंतर्गत प्रतिबले काढता येतात.

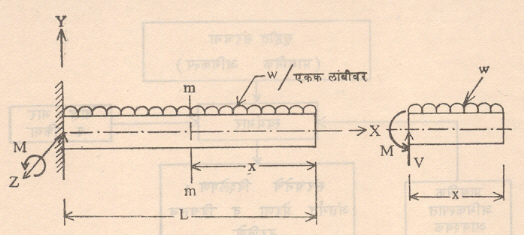
उदा., आ. ३ मधील एकाधार तुळईच्या m-m या काटच्छेदावर येणारी अंतर्गत प्रतिबले काढावयाची असल्यास ती आकृतीत उजवीकडे दाखविलेर्या तुळईच्या स्वतंत्र भागाला संतुलनाची वरील सूत्रे लावून खालीलप्रमाणे काढता येतात :

∑Fy = 0,		V –	wx	= 0		∴ V =	wx
∑Mz = 0,		M –	wx2	= 0		∴ M =	wx2
			2				2

 

यात x ला मूल्य देण्याने त्या त्या काटच्छेदावरील अंतर्गत प्रतिबले मिळू शकतात. ज्या संरचनांतील अंतर्गत प्रतिबले केवळ स्थितिकीशास्त्रातील संतुलन सूत्रांच्या आधारे मिळू शकतात, त्यांना ‘स्तिथिकीदृष्ट्या निर्धार्य संरचना’ म्हणतात. अशा संरचनांतील अंतर्गत प्रतिबले काढण्यासाठी बाह्य भाराबरोबर फक्त भूमितीय राशी (वरील उदाहरणामध्ये आ. ३ मधील x व L) यांचीच फक्त आवश्याकता असते. विचलने ही दृढतेशी संबंधित असल्याने त्यांच्या गणनासाठी (आकडेमोडीसाठी वा हिशेब करण्यासाठी) x व L या राशींशिवाय दृढता दर्शविणाऱ्या क्षेत्रफळ (A), निरूढी परिबल (I) यांसारख्या भूमितीय राशी आणि स्थितीस्थपकंता मापांक E, दृढता मापांक G यांसारख्या भौतिक राशींचीही जरूरी भासते. काही संरचना अशा असतात की, त्यांतील अंतर्गत प्रतिबले केवळ स्थितिकीशास्त्रातील संतुलन सूत्रांनी काढता येत नाहीत, अशा संरचना ‘स्तिथिकीदृष्ट्या अनिर्धार्य संरचना’ म्हणून ओळखल्या जातात. वरील उदाहरणातील तुळईला उजव्या टोकाला दृढ आधार दिल्यास केवळ संतुलनाच्या सूत्रांनी ह्या तुळईतील अंतर्गत प्रतिबले काढता येणार नाहीत. कारण संतुलनाची उपयुक्त सूत्रे दोनच (∑ V = 0, ∑M = 0) राहिली असून एकूण अज्ञात राशींमध्ये मात्र उजव्या टोकाच्या आधार-प्रतिक्रियेची भर पडली असून त्या दोनाएवजी तीन झाल्या आहेत (आ. ४).

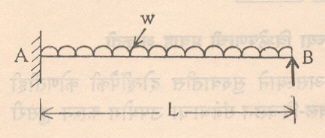
(या अगोदरच्या आ. ३ च्या उदाहरणात VA व MA एवढ्या दोनच अज्ञात राशी होत्या). तेव्हा अशा संरचनेच्या विश्लेषणासाठी आणखी समीकरणांची आवश्यकता असते. ही समीकरणे सुसंगत विचलानाच्या तत्त्वाच्या आधारे किंवा संरचनेच्या (विचलन वक्राच्या) अखंडतेच्या तत्त्वाच्या आधारे मिळविली जातात. वरील उदाहरणात दुसऱ्या टोकाला आधार दिल्यामुळे तो आधार नसताना तेथे होणारे तुळईचे रेषीय विचलन होऊ शकलेले नाही म्हणजेच आधारबिंदूचे रेषीय विचलन शून्य होय, ही सुसंगत विचलनाच्या तत्वावर आधारित अट आणखी एक समीकरण देते. म्हणजेच yB (= w मुळे येणारे B बिंदूचे रेषीय विचलन – VB मुळे होणारे तेथील रेषीय विचलन) =0

∴y =	wL4	–	VBL3	= 0		∴VB =	3	wL.
	8EI		3EI				8

या उदाहरणामध्येही संरचनेची L एवढीच भूमितीय राशी आवश्यक ठरते. आता याच उदाहरणातील B टोकाकडील आधार आ. ५ मध्ये दाखविल्याप्रमाणे एखाद्या स्थितिस्थापक तारेने दिल्यास B बिंदूचे रेषीय विचलन शून्य राहणार नाही.

सुसंगत विचलन तत्त्व किंवा अखंडतेच्या तत्त्वाच्या आधारे B हा बिंदू A B या तुळईवर तसेच BC या तारेवर असल्याने ह्या बिंदूचे रेषीय विचलन दोन्हा भागांसाठी सारखेच असले पाहिजे. म्हणजे तुळईचे B बिंदू येथील रेषीय विचलन = तारेचे त्याच बिंदूवरील त्याच दिशेने होणारे रेषीय विचलन.तारेत T एवढा ताण  असल्यास

	wL4I	‒	TL3I	=	TL2
	8E1 I1		3E1 I1		E2 A2

 

हे समीकरण होऊन त्यावरून T चे मूल्य मिळू शकते. एकदा T काढल्यानंत डाव्या टोकाकडील आधार राशी स्थितिकी सूत्रांवरून मिळू शकतात पण वरील उदाहरणात T ही परिणाम राशी काढण्यासाठी तुळई व तार यांचे E1, I1, L1 व E2, A2, L2 हे भूमितीय व भौतिक गुणधर्म माहीत असावे लागतात. वरील उदाहरणामध्येw भारामुळे B बिंदू होणारे विचलन

yB =	wL4
	8 E I

 

सूत्राने मिळते. हे सूत्र बाह्यभार-विचलन असा सरण संबंध दर्शविते. म्हणजे अंतर्गत प्रतिबले न काढताही बाह्यभारावरून सरळ स्वतंत्रपणेही विचलन काढता येते. हेच विचलन अंतर्गत प्रेरणांवरून काढावयाचे असल्यास

EI	d2 y	= M
	dx2

 

किंवा y = ∫∫ M ⁄ EI या ऑयलर-बेर्नुली यांच्या सिद्धांतावरून मिळते किंवा

Y=	dU
	dP

 

या कास्तिल्येनो यांच्या स्थितिस्थापक ऊर्जा प्रमेय किंवा आभासी कार्याचे तत्त्व ,अशाच इतर मुलभूत सिद्धांताद्वारे मिळते. या सिद्धांतांचे विवेचन प्रस्तुत नोंदीच्या पुढील भागात केले आहेच. वरील तिसऱ्या उदाहरणात तारेतील रेषीय विचलनासाठी δ = TL/AE या स्थितिस्थापकतेसंबंधीच्या हुक यांच्या नियमाचा आधार घेतला आहे. यात T ही अंतर्गत प्रेरणा होय म्हणजेच वरील सूत्र हे अंतर्गत प्रेरणा-विचलन संबंध दर्शविते. वरील सर्व विवेचनावरून लक्षात येईल की, विश्लेषणातील अंतर्गत प्रेरणा ठरविणे या भागांसाठी संतुलन तत्त्वाचा व अखंडता अथवा विचलानाची सुसंगतता या तत्त्वाचा उपयोग केला जातो, तर विचलने ठरविणे या भागांसाठी प्रेरणा-विचलन संबंधाचा वापर केला जातो.

आपण या पूर्वी पाहिले आहे की, विश्लेषणाच्या दृष्टीने स्थितिकीदृष्ट्या निर्धार्य व स्थितिकीदृष्ट्या अनिर्धार्य असे संरचनेचे दोन प्रकार होतात. संरचनेची ही स्थितिकीय अनिर्धार्यता संरचनेच्या संतुलनास लागणाऱ्या आधार-प्रतिक्रियांपेक्षा जास्त आधार-प्रतिक्रिया दिल्याने किंवा संरचनेत स्थैर्यतेस आवश्यक असणाऱ्या घटकांपेक्षा जास्त घटक समाविष्ट केल्यामुळे निर्माण होते. ह्या अतिरिक्त आधार प्रतिक्रिया किंवा हे अतिरिक्त घटक अतिरिक्त अज्ञात राशी निर्माण करतात. म्हणजेच संरचनेच्या अनिर्धार्यतेची मात्रा बरोबर अतिरिक्त आधार-प्रतिक्रिया व अतिरिक्त घटकांची संख्या होय. अतिरिक्त घटक हे सर्वसाधारणपणे कैच्यांमध्ये आढळतात. कोणत्याही कैचीचे मूळ स्वरूप तीन घटक व तीन सांधे यांनी युक्त असा त्रिकोण हो होय. या मूळ त्रिकोणास दोन घटक व एक सांधा वाढवून कैचीचे स्वरूप बदलता येते. म्हणून स्थिर कैचीमधील सांधे व घटक यांच्या संख्या एकमेंकीस m = 2j ‒ 3 या सूत्राने जोडलेल्या असतात. यात m ही घटकांची संख्या व j ही सांध्यांची संख्या होय. प्रत्यक्ष कैचीत n एवढे घटक असल्यास (n‒m) एवढे घटक अतिरिक्त होत. म्हणजे कैचीमध्ये अतिरिक्त अंतर्गत घटकांमुळे आलेल्या अनिर्धार्यतेची मात्रा ही (n-m) एवढी होय. उदा., आ. ६ (अ) मध्ये दाखविलेल्या कैचीमध्ये j = 4,

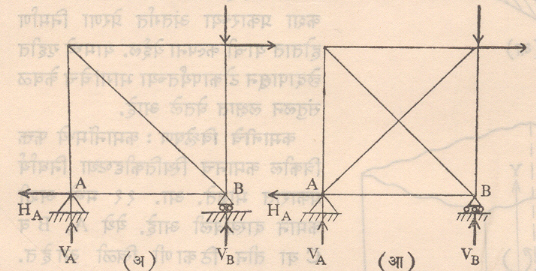
वरील सूत्रावरून स्थिरतेसाठी घटकांची संख्या (२ X ४) – ३ = ५ असायला हवी व तशी आहे त्यामुळे ही कैची अंतर्गत प्रतिबलाच्या दृष्टीने निर्धार्य होय. ह्याच कैचीत आ. ६ (आ) मध्ये दाखविल्याप्रमाणे दुसऱ्या कर्ण दिशेने आणखी एक घटक वाढविल्यास तो अतिरिक्त ठरतो. त्यामुळे ही कैची एका मात्रेने अनिर्धार्य होय. बहिर्गत आधार-प्रतिक्रियांचा विचार करता दोन्ही कैच्यांमध्ये आधार-प्रतिक्रिया तीनच आहेत. (HA, VA, VB) व संतुलन समीकरणेही तीन आहेत (∑Fx = 0, ∑Fy = 0, ∑Mz = 0). म्हणून त्या दृष्टीने ही निर्धार्य ठरते. पण याच कैचीच्या B ह्या टोकास रूळ-आधारऐवजी A बिंदूप्रमाणे खीळ-आधार दिल्यास एकूण आधार-प्रतिक्रियांची संख्या चार होते (H_A, V_A, H_B, V_B). या परिस्थितीत ही कैची बहिर्गत आधार-प्रतिक्रियांच्या दृष्टीने एका मात्रेने अनिर्धार्य होते आणि तिची एकूण अनिर्धार्यता मात्रा दोन होते. (एक अंतर्गत घटकाच्या अतिरिक्ततेमुळे आणि एक बहिर्गत आधार-प्रतिक्रियेच्या अतिरिक्ततेमुळे).

अंतर्गत प्रेरणांचे व विचलनांचे प्रकार : संरचनेच्या घटकांवर बाहेरून येणाऱ्या भाराच्या प्रकारावर अंतर्गत प्रेरणांचे आणि विचलनांचे प्रकार अवलंबून असतात. साध्या खीळ सांध्याच्या कैचीत बाहेरील भार हा फक्त सांध्यांवर म्हणजे घटकांच्या टोकांकडून येत असल्याने घटकामध्ये फक्त अक्षीय ताण प्रेरणा किंवा संकोची प्रेरणा येते (आ. ७ मध्ये AB व BC या घटकांत संकोची प्रेरणा, तर AC या घटकात ताण प्रेरणा येते).

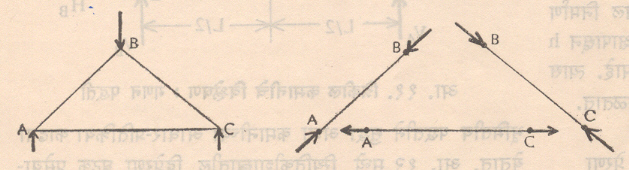
या घटकांमध्ये प्रेरणा अक्षीय दिशेने येत असल्याने त्यामध्ये अक्षीय दिशेनेच (रेषीय) विचलन होते. आ. ८ मध्ये दाखविलेल्या तुळईवर बाहेरून F हा भार टोकाकडे येत नसून मधल्या भागा तिरका येत असल्याने त्या भाराचा पार्श्विक अवयव (घटक) Fy यामुळे काटकोनी छेदांवर तुळईमध्ये कर्तन प्रतिबल व नमन परिबले येतात, तर Fx या अक्षीय अवयवामुळे अक्षीय प्रतिबल येते आणि त्यामुळे तुळईत अनुक्रमे कर्तरीय विचलन, आनमन व अक्षीय विचलन येते.

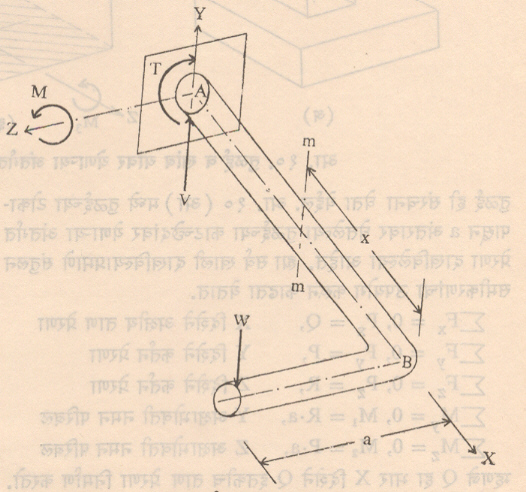
आ. ९ मध्ये दाखविलेल्या यंत्राच्या दांड्यावर बाहेरील भार W हा आ. ८ मधील तुळईप्रमाणे X‒Y या उभ्या प्रतलात येत नसल्याने या दांड्याच्या AB भागावरील कोणत्याही उभ्या m-m काटच्छेदावर कर्तन प्रेरणा (W), नमन परिबल (Mx = W.x) व घूर्णीय परिबल (T_x = W .a) अशा तीनही प्रकारच्या प्रेरणा आणि तदनुरूप विचलने येतात. नमन विचलनांमध्ये रेषीय विचलन आणि परिवलन अशा दोन्हींचा समावेश होतो.

 

स्थितिकीदृष्ट्या निर्धार्य संरचनांचे विश्लेषण : सांरचनिक विश्लेषणामध्ये बाहेरील भारामुळे संरचनेच्या घटकांमध्ये येणाऱ्या अंतर्गत प्रेरणांचे गणन व संरचनेच्या विचलनाचे गणन अशा दोन मुख्य गोष्टींचा समावेश होतो. स्थितिकीदृष्ट्या निर्धार्य संरचनांमध्ये घटकांत येणाऱ्या अंतर्गत प्रेरणा संरचनेच्या विचलनांवर अवलंबून नसल्याने त्या स्वतंत्रपणे काढता येतात. तसेच विचलनही स्वतंत्रपणे काढता येते प्रथम अंतर्गत प्रेरणांच्या विश्लेषणाचे व नंतर विचलनांच्या विश्लेषणाचे विवरण केलेले आहे.

 

स्थूलमानाने तुळई, खांब, कमान, कैची व चौकट हे संरचनेचे मुख्य प्रकार होत.

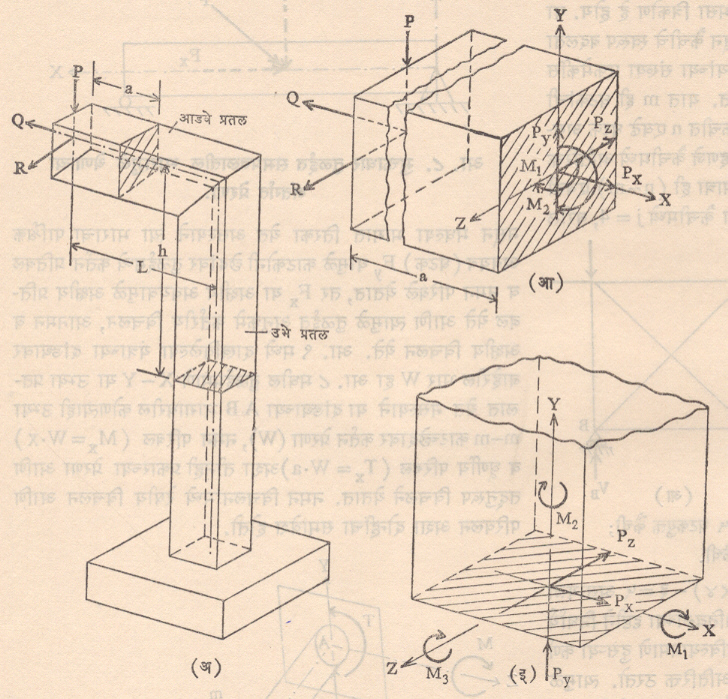तुळई व खांब यांचे विश्लेषण : ‘पदार्थाचे बल’ या नोंदीत हे विश्लेषण दिलेले आहेच. त्याचे एक सर्वसमावेशी उदाहरण म्हणून आ. १० (अ) मध्ये दर्शविलेली उभ्या खांबास जोडलेली आडवी तुळई ही संरचना घेता येईल. आ. १० (आ) मध्ये तुळईच्या टोकापासून a अंतरावर घेतलेल्या तुळईच्या काटच्छेदांवर येणाऱ्या अंतर्गत प्रेरणा दाखविलेल्या आहेत. ह्या सर्व खाली दाखविल्याप्रमाणे संतुलन समीकरणांचा उपयोग करून काढता येतात.

---

∑Fx = 0, Px = Q,	X दिशेने अक्षीय ताण प्रेरणा
∑Fy = 0, Py = P,	Y दिशेने कर्तन प्रेरणा
∑Fz = 0, Pz = R,	Z दिशेने कर्तन प्रेरणा
∑My = 0, M1 = R. a,	Y अक्षाभावती नमन परिबल
∑Mz = 0. M2 = P. a,	Z अक्षाभोवती नमन परिबल

म्हणजे Q हा भार X दिशेने Q इतकीच ताण प्रेरणा निर्माण करतो. P हा भार Y दिशेने P इतकीच कर्तन प्रेरणा व Z अक्षाभोवती P . a इतके नमन परिबल निर्माण करतो. R हा भार Z दिशेने R इतकीच कर्तन प्रेरणा व Y अक्षाभोवती R . a इतके नमन परिबल निर्माण करतो. त्याचप्रमाणे आ. १० (इ) मध्ये तुळईच्या X अक्षापासून h एवढ्या अंतरावर घेतलेला खांबाचा काटच्छेद दाखविला आहे. त्यास संतुलनाची समीकरणे लावल्याने खालीलप्रमाणे प्रतिबले मिळतात.

∑Fx = 0, Px = Q,	X दिशेने कर्तन प्रेरणा
∑Fy = 0, Py = P,	Y दिशेने अक्षीय संकोची प्रेरणा
∑Fz = 0, Pz = R,	Z दिशेने कर्तन प्रेरणा
∑Mx = 0, M1 = R. h,	X अक्षाभोवती नमन परिबल
∑My = 0, M2 = R. L,	Y अक्षाभोवती घूर्णीय परिबल
∑Mz = 0, M3 = (P.L + Qh),	Z अक्षाभोवती नमन परिबल

P च्या परिणामाने Y दिशेने P इतकी अक्षीय संकोची प्रेरणा व Z अक्षाभोवती PL इतके नमन परिबल येते.

Q च्या परिणामाने X दिशेने Q इतकी कर्तन प्रेरणा व अक्षाभोवती Q.h इतके नमन परिबल येते.

R च्या परिणामाने Z दिशेने R इतकी कर्तन प्रेरणा व X अक्षाभोवती R.h इतके नमन परिबल आणि Y अक्षाभोवती R.L इतके घूर्णीय परिबल येते.

या उदाहरणावरून संरचनेच्या घटकात कशा प्रकारच्या अंतर्गत प्रेरणा निर्माण होतात याची कल्पना येईल. यामध्ये गृहीत छेदापासून टोकापर्यंतच्या भागांचेच केवळ संतुलन लक्षात घेतले आहे.

---

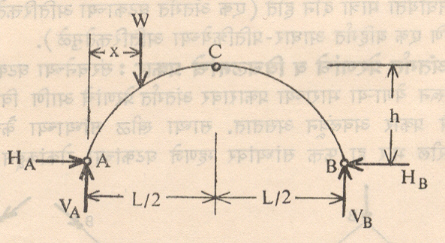
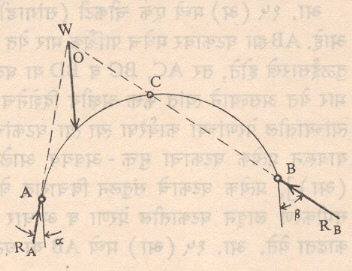
कमानीचे विश्लेषण : कमानींमध्ये फक्त त्रिकील कमानच स्थितिकीदृष्ट्या निर्धार्य प्रकारात मोडते. आ. ११ मध्ये अशी कमान दाखविली आहे. येथे A, B व C या तीन ठिकाणी खिळी आहेत. म्हणजे या ठिकाणी नमन परिबल शून्य असते. कमानीवर उभा भार येत असला, तरी आधाराकडे आडवी रेटा येत असल्याने दोन्ही आधार आडव्या प्रतिक्रिया देतात. एकूण आधार-प्रतिक्रिया चार होतात (HA, VA, VB, HB). संतुलनाच्या तीन समीकरणांशिवाय C बिंदू येथेही खीळ असल्याने तेथेही नमन परिबल शून्य असते व त्यामुळे ∑M_C = 0 हे आणखी एक समीकरण मिळून सर्व आधार-प्रतिक्रिया मिळतात. थोडक्यात यामध्ये कमानीच्या एका (AC किंवा BC) भागाचे संतुलन स्वतंत्रपणे लक्षात घेण्यात येते. एकदा आधार-प्रतिक्रिया मिळाल्यावर पुन्हा संतुलन समीकरणांच्याच साहाय्याने कमानीच्या कोणत्याही काटच्छेदावर येणाऱ्या अक्षीय प्रेरणा, कर्तन प्रेरणा व नमन परिबल काढता येते. भूमितीय पद्धतीने सुद्धा अशा कमानीच्या आधार-प्रतिक्रिया काढता येतात. आ. १२ मध्ये स्थितिकीशास्त्रातील द्विप्रेरणा घटक प्रमेयानुसार कमानीच्या BC ह्या घटकावर बाहेरून कोणताच भार येत नसून फक्त B व C या टोकांकडेच प्रेरणा येत असल्याने त्या BC या दिशेनेच कार्यान्वित होतात. म्हणजे B टोकाकडे आधार-प्रतिक्रिया R_B ही CB दिशेने येते. या प्रेरणेची कार्यरेषा बाहेरून येणाऱ्या w या भाराच्या कार्यरेषेस O या बिंदूत मिळते. पुन्हा एकदा स्थितिकीशास्त्रातीलच त्रिप्रेरणा संतुलन तत्त्वान्वये कमान RA, R_B व w या तीन प्रेरणांखाली संतुलित राहत असल्याने या तिन्ही प्रेरणा एककेंद्री असल्या पाहिजेत म्हणून R_A ह्या आधार-प्रतिक्रियेची कार्यरेषा ही O या बिंदूतून जायला हवी. म्हणजेच R_A ची दिशा AO ही होय. एकदा R_A व R_B यांच्या दिशा α व β या कोनांच्या रूपाने मिळाल्यावर प्रेरणा त्रिकोणाच्या साह्याने किंवा पुन्हा तीन संतुलन समीकरणांच्या साहाय्याने V_A, V_B व H काढता येतात.

कैचीचे विश्लेषण : हे विश्लेषण गणन पद्धती व भूमितीय आलेखन पद्धती अशा दोन्ही तऱ्हेने होऊ शकते.

गणन पद्धती : या पद्धतीचे सांधा विश्लेषण पद्धती व छेद पद्धती असे दोन प्रकार आहेत.

---

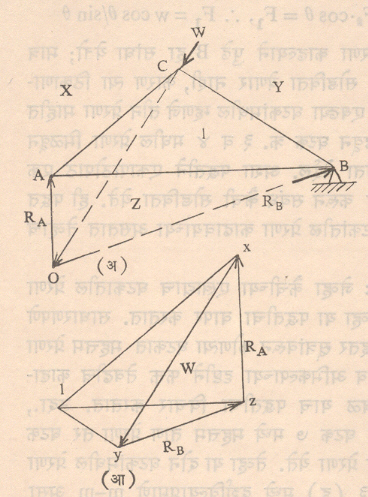
(१) सांधा विश्लेषण पद्धती : या पद्धतीमध्ये कैचीच्या सांध्यावर येणाऱ्या प्रेरणांच्या संतुलनाचा विचार केला जातो. सांध्यावर येणाऱ्या सर्व प्रेरणा एककेंद्री असल्याकारणाने संतुलनासाठी उपयुक्त अशी दोनच समीकरणे असतात (∑F_x = 0, ∑F_y=0). त्यामुळे ज्या सांध्यावर दोनपेक्षा जास्त घटकांतील प्रेरणा अज्ञात असणार नाहीत असाच सांधा या दोन समीकरणांच्या आधारे सोडवून दोन घटकांमधील अज्ञात प्रेरणा काढता येतात. ह्या प्रेरणा घटकांच्या अक्षीय दिशेनेच येतात. या पद्धतीत विश्लेषणाची सुरूवात अशा दोनच किंवा त्याहून कमी अज्ञात प्रेरणा असलेल्या सांध्याने करून प्रथम दोन घटकांतील प्रेरणा काढतात व पुढे याच पद्धतीने पुढील दोन किंवा कमी अज्ञात प्रेरणांनी युक्त सांध्यांचे एकापाठोपाठ एक असे विश्लेषण संतुलन समीकरणाच्या साहाय्याने करून संबंध कैची सोडवली जाते. आ. १३ (अ) मध्ये A हाच फक्त सांधा दोन अज्ञात प्रेरणा असलेला आहे. आ. १३ (आ) मध्ये दर्शविलेल्या A या साध्यावरील प्रेरणांना संतुलन समीकरणे लावून घटक क्र. १ व २ मधील प्रेरणा अगोदर काढल्या जातात.

∑Fy = 0 ⟶F2.sin θ = w,	∴ F2 = w/sin θ आणि
∑Fx = 0 ⟶ F2.cos θ = F1,	∴ F1 = w cos θ/sin θ

घटक क्र. २ मधील प्रेरणा काढल्याने पुढे B हा सांधा येतो मात्र C हा सांधा आताच सोडविता येणारे नाही, कारण त्या ठिकाणावरील क्र. ४,५ व ६ एवढ्या घटकांमधील म्हणजे तीन प्रेरणा माहीत नाहीत. B सांधा सोडवून घटक क्र. ३ व ४ मधील प्रेरणा मिळवून मग C सांध्याकडे जाता येईल. अशा पद्धतीने एकापाठोपाठ एक सर्व सांध्यांचे विश्लेषण करून संबंध कैची सोडविता येते. ही पद्धत जेव्हा कैचीच्या सर्व घटकांतील प्रेरणा काढावयाच्या असतात तेव्हाच वापरतात.

(२) छेद पद्धती : जेव्हा कैचीच्या एखाद्याच घटकातील प्रेरणा काढावयाची असते तेव्हा या पद्धतीचा वापर करतात. साधारणपणे संरचना सिद्धांतातील इतर सूत्रांवरून कोणत्या घटकात महत्तम प्रेरणा येते हे माहीत असता व अभिकल्पाच्या दृष्टीने फक्त तेवढीच काढावयाची असल्यास केवळ याच पद्धतीचा विचार करतात. उदा., आ. १३ (इ) मध्येच घटक ७ मध्ये महत्तम ताण प्रेरणा तर घटक ९ मध्ये महत्तम संकोची प्रेरणा येते. तेव्हा या दोन घटकांमधील प्रेरणा काढण्यासाठी आ. १३ (इ) मध्ये दर्शविल्याप्रमाणे m‒m असा छेद घेतला जातो. या छेदामध्ये कैचीचे दोन भाग होतात. व त्यांतील एका भागाच्या संतुलनाचा विचार करून त्यास संतुलन समीकरणे लावून छेद गेलेल्या घटकांमधील प्रेरणा काढता येतात (दोन्ही पद्धतींमध्ये मूलभूत दृष्ट्या संतुलनाचाच विचार आहे. फरक एवढाच की, पहितील सांध्याच्या संतुलनाचा, तर दुसरीत संरचनेच्या काही भागाच्या‒तुकड्याच्या‒संतुलनाचा विचार आहे). या पद्धतीत एका प्रतलात येणाऱ्या पण एककेंद्री नसलेल्या प्रेरणांचे संतुलन येत असल्याने संतुलाची तीन समीकरणे (∑F_x = 0, ∑F_y = 0, ∑M_z = 0) उपलब्ध असल्यामुळे छेद असा घ्यावा लागतो की, जो तीनपेक्षा जास्त घटकांना छेदून जाणार नाही (म्हणजेच संतुलनाचा विचार करता तीनपेक्षा जास्त अज्ञात राशी असणार नाहीत). आ. १३ (इ) मध्ये खाली दर्शविल्याप्रमाणे संतुलन समीकरणांचा वापर करून ७, ८ व ९ या घटकांतील प्रेरणा काढता येतात.

---

∑V	=	0,	F8.sin θ	=	w		∴ F8	=	w/sin θ
∑ ME	=	0,	F7.d	=	w.2a		∴ F7	=	w.2a/d
∑MF	=	0,	F9.d	=	w.3a		∴ F9	=	w.3a/d

भूमितीय आलेखन पद्धती : वरील गणितीय पद्धतीशिवाय कैचीच्या विश्लेषणासाठी मॅक्सवेल या शास्त्रज्ञांनी भूमितीय रचनेच्या साहाय्याने प्रेरणांचे आलेख काढून घटकातील अंतर्गत प्रेरणा काढण्याची पद्धती शोधून काढली. हे आलेख ‘मॅक्सवेल आलेख’ म्हणून ओळखले जातात. ही पद्धती संरचनेची आधार-प्रतिक्रिया (म्हणजे बाहेरील प्रेरणा) व संरचनेच्या घटकांमधील अंतर्गत प्रेरणा अशा दोन्हींसाठी वापरतात. आ. १४ (अ) मध्ये एक त्रिकोणी कैची दाखविली असून तिला A या ठिकाणी रूळ-आधार व B या ठिकाणी खीळ-आधार आहे. त्यामुळे A बिंदूवरील आधार-प्रतिक्रिया (R_A) OA या उभ्या दिशेनेच येऊ शकते. W या बाह्यभाराची कार्यरेषा वाढविली असता ती R_A च्या कार्यरेषेस O या बिंदूत मिळते. सबंध संरचनेवर w, R_A व R_B या फक्त तीन बहिर्गत प्रेरणा काम करीत असल्याने संतुलनासाठी त्या तीनही एककेंद्री असावयाला हव्यात, या स्थितिकीच्या तत्त्वानुसा B येथील आधार-प्रतिक्रियेची (R_B हिची) कार्यरेषासुद्धा O बिंदूमधून जायला हवी. यामुळे RB ची OB ही दिशा निश्चित होते. आता संरचनेवरील बाहेरील प्रेरणा (w, R_A व R_B) व संरचनेच्या (AB, BC, CA, या सर्व ) घटकांतील प्रेरणांच्या कार्यरेषा माहीत झाल्यावर दोन प्रेरणा-रेषांमधील जागेस अक्षराच्या किंवा आकड्यांच्या मदतीने संकेतन केले जाते. हे रॉबर्ट बोया शास्त्रज्ञांनी सुचविल्याने अशा संकेतनास ‘बो संकेतन’ म्हणतात. या संकेतनामुळे प्रत्येक प्रेरणा ही तिच्या दोन्ही बाजूंकडील संकेत चिन्हाने ओळखली जाऊ शकते (उदा., w म्हणजे xy, RB म्हणजे yz व RA म्हणजे zx तर AB, CB व CA या घटकांमधील प्रेरणा Z1 Y1 व X1 होतात ). हे संकेतन केल्यावर पहिल्यांदा बाहेरील प्रेरणांचा आलेख काढला जातो. त्यासाठी प्रेरणामूल्यांचे ठराविक प्रमाणमान घेऊन त्यानुसार एकेक प्रेरणेच्या दिशेने प्रमाणित रेषा एकीपुढे एक क्रमागत पद्धतीने काढून प्रेरणांचा बहुभुजाकृती आलेख काढला जातो. वरील उदाहरणात आ. १४ (आ) मध्ये xy ही रेषा w या प्रेरणेला समांतर व तिची लांबी w च्या मूल्याच्या प्रमाणमानात घेतली जाते. y बिंदूमधून RB ला समांतर रेषा व x बिंदूमधून R_A ला समांतर रेषा काढल्यास त्या z या बिंदूत मिळतात. त्यामुळे xyz हा प्रेरणा त्रिकोण तयार होतो. R_B चे मूल्य yz च्या लांबीच्या प्रमाणमानात व दिशा y कडून z कडे व RA चे मूल्य zx च्या लांबीच्या प्रमाणमानात व दिशा z कडून x कडे हे या त्रिकोणावरून ठरते. हा प्रेरणा त्रिकोण बाहेरील प्रेरणांसाठी काढलेला आहे. हीच कृती आ. १४ (अ) मधील A ह्या बिंदूवर येणाऱ्या R_A, AB ह्या घटकातील प्रेरणा व AC ह्या घटकातील प्रेरणा या प्रेरणांना लावून xIz हा प्रेरणा त्रिकोण काढला जातो, तर C बिंदूवरील w, AC या घटकातील प्रेरणा व BC ह्या घटकातील प्रेणा या प्रेरणांपासून xyl हा प्रेरणा त्रिकोण काढला जातो व त्यावरून AB, BC व AC यांमधील प्रेरणा अनुक्रमे zl, yl आणि xl च्या लांबीच्या प्रमाणमानात मिळतात. आ. १४ (आ) मधील तयार झालेल्या एकूण आकृतीस ‘मॅक्सवेल प्रेरणा आलेख’ म्हणतात. हा आलेख काढतानाही सांधा पद्धती प्रमाणे असे सांधे एकामागून एक घ्यावे लागतात की, जेथे दोनपेक्षा जास्त घटकांतील प्रेरणा अज्ञात असणार नाहीत, जेव्हा हे शक्य नसते तेव्हा घटक बदली पद्धतीचा वापर करतात.

चौकटीचे विश्लेषण : चौकटी संरचनेमध्ये काही घटकांच्या फक्त टोकांकजेच प्रेरणा येतात, असे घटक द्वि-प्रेरणा घटक म्हणून ओळखले जातात. अशा घटकांमध्ये कैचीतील घटकांप्रमाणे फक्त अक्षीय दिशेने प्रेरणा येते. यांशिवाय काही घटकांवर दोन टोकांशिवाय मधल्या भागावरही पार्श्विक प्रेरणा येतात. अशा वेळी अशा घटकाचा मुक्त-अवयव आलेख काढून प्रत्येक मुक्त-अवयवाचे संतुलन लक्षात घेऊन विश्लेषण केले जाते.

आ. १५ (अ) मध्ये एक चौकटी (सांगाडी) संरचना दाखविली आहे. AB ह्या घटकावर मधेच पार्श्विक भार येत असल्याने त्याचे वर्तन तुळईसारखे होते, तर AC, BC व BD या घटकांच्या फक्त टोकांकडे भार येत असल्याने त्यांत फक्त अक्षीय दिशेनेच प्रेरणा येतात. म्हणजे त्यांच्यातील प्रेरणांच्या कार्यरेषा त्या त्या घटकांच्याच दिशेने जातात. यावरून प्रत्येक घटकाचा मुक्त-अवयव आलेख काढून [आ. १५ (आ)], प्रत्येक घटकाचे संतुलन विचारात घेऊन व त्यास संतुलन समीकरणे लावून घटकातील प्रेरणा व आधार-प्रतिक्रिया असे सर्व काढता येते. आ. १५ (आ) मध्ये AB या घटकासाठी तर AC, BC व BD या घटकांमध्ये अनुक्रमे R₁, R₂ व R₃ एवढी अक्षीय संकोची प्रेरणा येतात.

---

∑Fx = 0,

R2sin β = W cos α,

∴R2 = W

cos α

…

…

(१)

sin β

∑MB = 0,

R1.L = W sin α (L‒a),

R1

=

W sin α.(L-a)

…

…

(२)

L

∑V = 0, R3 = Wsin α – R1 – R2.cos β =

…

…

(३)

आडव्या प्रतळातील वक्र तुळ्या : अशा तुळईवर येणाऱ्या उभ्या भारांमुळे तुळईच्या कोणत्याही काटच्छेदावर नमन परिबलाबरोबर घूर्णीय परिबल येते. आ. १६ मध्ये आडव्या प्रतलातील टोकाकडे बद्ध-आधार असलेला वर्तुलपाद वक्र तुळई दाखवली आहे. तिच्या वर टोकाकडे येणाऱ्या W ह्या उभ्या भारामुळे बद्ध-आधारवर

M_x = W.b इतके नमन परिबल X अक्षाभोवती

M_z = W.a इतके घूर्णीच परिबल Z अक्षाभोवती

व F_y = W इतकी कर्तन प्रेरणा Y दिशेने येते.

संरचनेवरील चल भारांचा परिणाम : अचल भारामुळे येणाऱ्या अंतर्गत प्रेरणा भार स्थिर असल्याने बदलत नाहीत पण चलभारांची जागा सारखी बदलत असल्याने त्यामुळे निर्माण होणाऱ्या संरचनेतील प्रेरणा व आधार-प्रतिक्रिया चल भारांच्या स्थानानुसार बदलत जातात. अशा वेळी प्रत्येक प्रकारच्या प्रेरणेसाठी चल भाराच्या स्थानानुसार निर्माण होणाऱ्या प्रेरणांचा वितरण आलेख काढला जातो. अशा आलेखास ‘प्रभाव रेषा’ किंवा ‘प्रभाव आलेख’ म्हणतात.

---

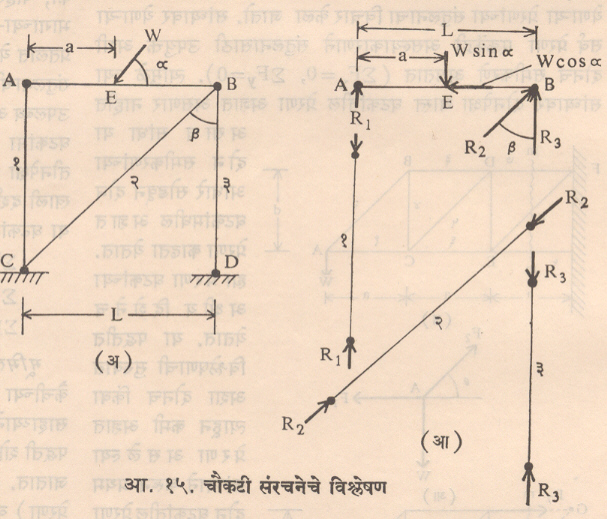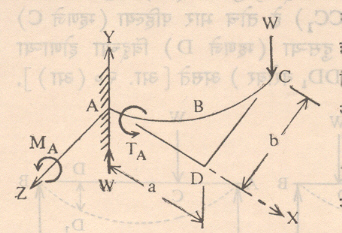आ. १७ (अ) मध्ये दर्शविलेल्या मुक्ताधार तुळईसाठी उजव्या टोकाकडील आधार-प्रतिक्रियेचा प्रभाव आलेख आ. १७ (आ) मध्ये, तुळईच्या मध्यभागी येणाऱ्या नमन परिवलाचा प्रभाव आलेख आ. १७ (इ) मध्ये, तर तुळईच्या एकचतुर्थांश गाळ्याच्या ठिकाणच्या कर्तन प्रेरणेचा प्रभाव आलेख आ. १७ (ई) मध्ये दाखविला आहे. कोणत्याही प्रेरणेचा प्रभाव आलेख काढताना बाहेरील भार एकक मूल्याचा धरला जातो व ज्या ठिकाणी ती प्रेरणा काढावयाची असेल त्या ठिकाणी हा एकक भार ठेवून (कार्यान्वित करून) त्या प्रेरणेचा तुळईवरील आलेख काढला जातो. हा आलेखच त्या प्रेरणेचा त्या ठिकाणचा प्रभाव आलेख ठरतो. या प्रभाव आलेखाची कोणत्याही जागोवरची कोटी (उभ्या सहनिर्देशकाची लांबी) एकक चल भार त्या जागी असताना आलेले या प्रेरणेचे मूल्य दर्शविते [म्हणजे वरील उदाहरणात आ. १७ (आ) मध्ये बिंदूवरील कोटीचे मूल्य x/L हे एकक चलभार E या ठिकाणी असता येणाऱ्या B येथील आधार-प्रतिक्रियेचे मूल्य होय किंवा आ. १७ (इ) मधील मध्यभागावरील नमन परिबलाच्या प्रभाव आलेखातील E बिंदूवरील कोटीचे मूल्य x/२ हे एकक भार E बिंदूवर असताना C बिंदूवर येणाऱ्या नमन परिबलाचे मूल्य होय]. एकक भाराचे डाव्या टोकाकडून असलेले अंतर x हे प्रभाव सूत्राचे चलपद होय. आ. १७ (आ) मध्ये R_B=x/L हे R_B च्या प्रभाव आलेखाचे सूत्र होय. भाराची जागा म्हणजेच R_B चे मूल्य माहित असता चे मूल्य वरील सूत्राने मिळते. R_B चा प्रभाव आलेख काढण्यासाठी एकक भार B या ठिकाणी ठेवून आलेख काढला आहे. मध्यबिंदू C वरील नमन परिबलाचा प्रभाव आलेख एकक भार C बिंदूवर ठेवला असता येणारा तुळईचा नमन परिबल आलेख होय. ज्या वेळेस एकक चल भार A व C यांच्या मध्ये x एवढ्या अंतरावर असेल (म्हणजे x &lt L/2) तेव्हा C बिंदूवरील परिबलाचे सूत्र खालीलप्रमाणे येते :

---

MC = RB. L/2 =	x	.	L	=	X
	L		2		2

हाच भार C व B यांच्यामध्ये असल्यास (म्हणजे x &gt L/2)

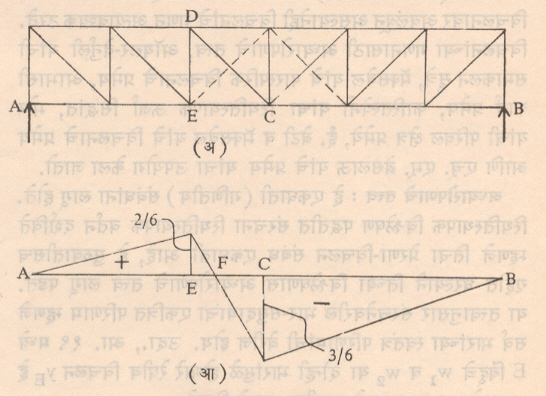MC = RA.	L	=	L – x	.	L	=	L – x
	2		L		2		L

---

याच पद्धतीने १/४ गाळ्याच्या ठिकाणच्या कर्तन प्रेरणेचा आलेख त्याच ठिकाणी एकक भार ठेवून आ. १७ (ई) मध्ये काढला आहे. या प्रभाव आलेखाच्या आधारे चल भार कोणत्या जागी असता प्रेरणेचे मूल्य महत्तम असेल हे कळू शकते. उदा., D बिंदूवरील महत्तम धन कर्तन प्रेरणा चल भार D बिंदूच्या जरा डावीकडे असता १/४ एवढ्या मूल्याची, तर महत्तम ऋण कर्तन प्रेरणा चल भार D बिंदूच्या जरा उजवी कडे असता ३/४ एवढ्या मूल्याची असेल. कोणत्याही भारामुळे येणारी प्रेरणा ही प्रभाव आलेखाच्या कोटीस त्या भाराच्या मूल्याचे गुणून मिळते. म्हणजे वरील उदाहरणात w भारामुळे C बिंदूवर येणारे नमन परिबल तो भार C बिंदूवर असता wL/4 इतके होते. समवितरित चल भारामुळे येणारी प्रेरणा ही तो बार जेवढ्या भागावर वितरित झालेला असेल तेवढ्या भागाच्या प्रभाव आलेखाच्या क्षेत्रफळास त्या चल भाराच्या वितरित भारमूल्याने गुणून मिळते. यावरून समावितरित भारामुळे येणारी महत्तम प्रेरणा काढावयाची असल्यास तो भार केवढ्या भागावर वितरित झालेला असावा की, ज्यामुळे प्रभाव आलेखाचे क्षेत्रफळ जास्तीत जास्त होईल हे ठरविता येते. उदा., आ. १७ (ई) मध्ये D बिंदूवरील महत्तम धन कर्तन प्रेरणेसाठी समवितरित भार हा AD एवढ्याच भागावर असायला हवा, तर महत्तम ऋण कर्तन प्रेरणेसाठी तोच भार DB एवढ्याच भागावर (त्यापेक्षा कमी नाही की जास्त नाही) असायला हवा.

याच पद्धतीने पुलांच्या कैच्यांच्या घटकांमध्ये येणाऱ्या अक्षीय प्रेरणांसाठी सुद्धा प्रभाव आलेख काढून त्यांतील महत्तम प्रेरणा व त्यासाठी तद्नुरूप चल भाराची जागा ठरविता येते. आ. १८ (अ) मध्ये दाखविलेल्या N प्रकारच्या कैचीच्या मधल्या चौकटीतील CD या कर्ण घटकामध्ये येणारी प्रेरणाही सुद्धा त्यातील CE भागामधील कर्तन प्रेरणेनुसार येत असल्याने या प्रेरणेचा प्रभाव आलेखही आ. १८ (आ) प्रमाणे येतो. त्यावरून लक्षात येईल की, चल भार AF एवढ्या भागावर असता त्यात धन प्रकारचे म्हणजे ताण प्रेरणा येईल, तर तोच चल भार FB या भागावर जाण्याचे त्यात ऋण प्रकारची (म्हणजे विरोधी प्रकारची) म्हणजेच संकोची प्रेरणा निर्माण होते. याचा अर्थ एकाच घटकामध्ये चल भार एका बाजूने दुसऱ्या बाजूस जात असता त्यात उलटसुलट प्रेरणा निर्माम होतात. प्रेरणांचे असे व्युत्क्रमण होणे शक्य तो टाळले जाते कारण एकतर तो घटक अशा दोन्ही प्रकारच्या प्रेरणांसाठी अभिकल्पित करावा लागतो आणि शिवाय सारख्या सामर्थ्य कमी होते. मधल्या दोन्ही चौकटींच्या कर्ण घटकांमध्ये व्युत्क्रमी भार येत असल्याने हे टाळण्यासाठी या दोन्ही चौकटींमध्ये दोन्ही कर्णांच्या दिशेने तील घातले जातात (हे आकृतीत तुटक रेषेने दाखविले आहेत). हे कर्णबंधक (अर्थात तीर) ताण प्रेरणा घेण्यासाठी अभिक्लपित करतात म्हणजे दोन्हीपैंकी ज्यात ताण प्रेरणा येईल तेवढाच कार्यकारी राहतो, म्हणजे चल भार एका बाजूस असेल तेव्हा एक कर्णबंधक कार्यकारी राहतो, तर तोच चल भार दुसऱ्या बाजूस गेला असता अकार्यकारी (वा सुप्त) राहून दुसरा कर्णबंधक कार्यकारी होतो. अशा कर्णबंधकास प्रत्यबंधक म्हणतात.

संरचनेचे स्थितिस्थापक विश्लेषण: संरचनेतील विचलनांचे गणन : संरचनेची सुरक्षितता पाहाण्यासाठी ज्याप्रमाणे संरचनेच्या घटकांतील प्रेरणा काढणे आवश्यक ठरते त्याचप्रमाणे संरचनेच्या कार्योपयुक्ततेच्या (सेवा-पात्रतेच्या) दृष्टीने संरचनेतील विचलने ही ठराविक मर्यादेत आहेत की नाहीत, हे पहाण्यासाठी विचलनांचे गणन करणे आवश्यक असते. इतकेच नव्हे, तर स्थितिकीदृष्ट्या अनिर्धार्य संरचनांच्या बाबतीत, तर संरचनेच्या घटकांमधील प्रेरणासुद्धा संरचनेच्या नम्यतेवर (लवचिकपणावर) अथवा दृढतेवर म्हणजेच संरचनेच्या विचलनावर अवलंबून असल्यानेही विचलनांचे गणन अत्यावश्यक ठरते. विचलनांच्या गणनासाठी अध्यारोपणाचे तत्त्व, ऑयलर-बेर्नुली यांची समाकलन सूत्रे, मॅक्सवेल यांचे पारस्परिक विचलानाचे प्रमेय, आभासी कार्य प्रमेय, कास्तिल्यंनो यांचा स्थितिस्थापक ऊर्जा सिद्धांत, मोर यांची परिबल क्षेत्र प्रमेये, ई. बेटी व मॅक्सवेल यांचे विचलनाचे प्रमेय आणि एच्.एम्.ब्रेसलाऊ यांचे प्रमेय यांचा उपयोग केला जातो.

अध्यारोपणाचे तत्त्व : हे एकघाती (गणितीय) संबंधांना लागू होते. स्थितिस्थापक विश्लेषण पद्धतीत संरचना स्थितिस्थापक वर्तन दर्शविते म्हणजे तिचा प्रेरणा-विचलन संबंध एकघाती आहे, हे सुरवातीसच गृहीत धरल्याने तिच्या विश्लेषणास अध्यारोपणाचे तत्त्व लागू पडते. या तत्त्वानुसार संरचनेवरील भार-समुदायाचा एकत्रित परिणाम म्हणजे सर्व भारांच्या स्वतंत्र परिणामांची बेरीज होय. उदा., आ. १९ मध्ये E बिंदूचे w1 व w2 या दोन्ही भारांमुळे होणारे रेषीय विचलन yE हे अध्यारोपणाच्या तत्त्वाने खालील सूत्राने मिळते :

y_E = y_E1 + y_E2

येथे y_E1 = फक्त w₁ मुळे होणारे E बिंदूचे विचलन व y_E2 = फक्त w₂ मुळे होणारे E बिंदूचे विचलन आहे.

पुढील भाग पाहण्यासाठी येथे क्लिक करा

“