मापव समाकलन : वक्राची लांबी, पृष्ठभागाचे क्षेत्रफळ, घनाकृतीचे घनफळ, वस्तूचे द्रव्यमान किंवा वजन, वस्तूवरील विद्युत् भार, एखाद्या यदृच्छ घटनेची संभाव्यता यांसारख्या प्रश्नांच्या संदर्भात माप ही संकल्पना रोजच्या व्यवहारात तसेच विज्ञानात नेहमी वापारण्यात येते. ही संकल्पना जरी इतिहासपूर्व काळापासून उपयोगात असली, तरी मापाची अमूर्त संकल्पना विसाव्या शतकापर्यंत मांडण्यात आलेली नव्हती. वर उल्लेखिलेले प्रश्न या अमूर्त संकल्पनेची केवळ विशिष्ट उदाहरणे आहेत. ⇨ एमील वॉरेल (१८७८–१९५६),⇨ कामीय झॉर्दा (१८३८–१९२२) व विशेषतः ⇨ आंरी लेआँ लबेग (१८७५–१९४१) या फ्रेंच गणितज्ञांनी या विषयात मूलभूत महत्त्वाचे कार्य केले आहे. प्रस्तुत नोंदीमध्ये वरील प्रश्नांचे व्यापकीकरण करून एकमितीय, द्विमितीय, त्रिमितीय, प-मितीय (प–पूर्णांक) अवकाशातील बिंदू संचांकरिता माप ही संकल्पना मांडलेली आहे. सुरुवातीस रेषेवरील बिंदू संचच अभिप्रेत आहेत.
पुढील विवेचनात ⇨ संच सिद्धांतातील काही संकल्पनांचा वापर करावयाचा असल्याने त्यांचे थोडक्यात विवरण येथे केले आहे. क्ष हा स या संचाचा घटक असेल, तर क्ष є स असे लिहितात. क्ष हा घटक नसेल, तर क्ष ¢ स असे लिहितात. स या संचाचे निदर्शन दोन प्रकारे करतात. पहिला प्रकार म्हणजे संचातील सर्व घटक महिरपी कसांमध्ये मांडून, जसे १० पेक्षा कमी असणाऱ्या विषम संख्यांचा संच {१, ३, ५, ७, ९} असा दर्शवितात किंवा संच बनविण्याचा नियम वापरून जसे स ={क्ष│0 < क्ष < ५}. दोन संचांचा संयोग U या चिन्हाने दर्शवितात व त्यांचा छेद ∩ या चिन्हाने दर्शवितात. संचातील एखाद्या बिंदूच्या परिसरातील सर्व बिंदू संचामध्ये असतील, तर त्या बिंदूला अंतर्बिंदू म्हणतात. संचाचे सर्व घटक अंतर्बिंदू असतील, तर त्या संचाला खुला संच म्हणतात. ज्या बिंदूच्या परिसरात अंतर्बिंदू व बाह्यबिंदू दोन्हीही असतील अशा बिंदूला सीमा बिंदू म्हणतात. संचाचे सीमा बिंदू संचामध्ये समाविष्ट असल्यास अशा संचाला बंद संच म्हणतात. रेषेवरील खुले अंतराल हा खुला संच असतो व बंद अंतराल हा बंद संच असतो. खुला संच हा खुल्या अंतरालानी तयार होतो, हे दाखविता येते. प-मितीय अवकाशात बिंदू (क्ष१, क्ष२, …..क्षप) या प सहनिर्देशकांनी मिळतो [→ भूमिती ]. प-मितीय अवकाशातील खुले अंतराल म्हणजे कर < क्षर < खर र = १, २, …, प. तसेच बंद अंतराल म्हणजे कर ⩽ क्षर ⩽ खर र = १, २, …, प. स संचाचा पूरक संच स पुढील व्याख्येने मिळतो : स′ ={क्ष │ क्ष ∉ स}. स आणि श हे दोन संच असतील, तर स – श ची व्याख्य़ा पुढीलप्रमाणे असते.
स — श ={क्ष │ क्ष є स, क्ष∉ श}.[→ संच सिद्धांत ].
मापाची व्याख्या : रेषेवरील अंतरालाची लांबी म्हणजेच त्या अंतरालाचे माप होय. माप हे योगशील फलन [→ फलन] होईल अशीच मापाची व्याख्या करावयाची आहे. म्हणजेच दोन वियुक्त (ज्यात एकही घटक समाईक नाही अशा) संचांच्या संयोगाचे माप हे त्या संचाच्या मापांची बेरीज असली पाहिजे. ख हा कोणताही खुला संच असेल, तर योगशीलतेची अट पुरी करण्याकरिता त्याचे माप म (ख) म्हणजे ज्या खुल्या अंतरालांच्या संयोगातून तो निर्माण झाला असेल त्या अंतरालांच्या मापांची बेरीज होय (ही बेरीज अभिसारी आहे म्हणजेच तिला सीमा आहे, हे गृहीत आहे). ख१ आणि ख२ हे दोन खुले संच असून त्यांमध्ये एकही बिंदू समाईक नसेल, तर
म (ख१ U ख२) = म (ख१)+ म (ख२)
जर ख१, आणि ख२ यांमध्ये समाईक बिंदू असतील, तर
म (ख१ U ख२) + म (ख१ ∩ ख२) = म (ख१) + म (ख२) हे सिद्ध करता येते. याचाच विस्तार करून असे म्हणता येईल की, ख१, ख२,….. ही वियुक्त खुल्या संचांची श्रेणी असेल, तर म (ख१ U ख२ U ख३….) = म (ख१) + म (ख२) + .. ज्या अंतरालांनी खुला संच निर्माण झाला त्यांच्या लांब्यांची श्रेढी अपसारी असेल, तर संचाचे माप = ∞ (अनंत) असे म्हणता येईल, परंतु माप सांत असणे विवरणाच्या दृष्टीने सोईस्कर असल्यामुळे पुढील विवेचनात माप सांतच आहे, असे गृहीत धरले आहे.
समजा, ब हा कोणताही बंद संच आहे आणि ख हा एक खुला संच असा आहे की, ब ⊂ ख. मग बच्या मापाची व्याख्या पुढीलप्रमाणे होईल.
म (ब) = म (ख) – म (ख – ब)
(ब बंद व ख खुला असल्या कारणाने ख – व खुला संच होईल). अर्थातच माप बंद संचांकरिता सुद्धा योगशील आहे. तसेच
ब ⊂ ख ⇒ म (ब) < म (ख)
आणि ख ⊂ब⇒ म (ख) < म (ब).
लबेग माप : स हा कोणताही संच असेल, तर त्याच्या म* (स) या बाहेरील मापाची व्याख्या पुढीलप्रमाणे:
म* (स) = स समाविष्ट करणाऱ्या खुल्या संचांच्या मापांचा निम्न बंध (खालची सीमा).
म* (स) या स च्या आतील मापाची व्याख्या पुढीलप्रमाणे :
म* (स) = स मध्ये समाविष्ट असणाऱ्या बंद संचांच्या मापांचा ऊर्ध्व बंध (वरची सीमा).
जर म* (स) = म* (स) असेल, तर स हा संच मापनीय आहे असे म्हणतात व त्याचे माप म (स) म्हणजे म* (स) आणि म* (स) यांचे समान मूल्य (यालाच ‘लबेग माप’ असे म्हणतात) होय.
वरील व्याख्यांवरून पुढील निष्कर्ष सहज मांडता येतात :
(१) स ⊂ (अ, ब) ⇒ म* (स) = व— अ— म* (स’),
(स’ हा सचा पूरक संच).
(२) म* (स) ⩾ म* (स).
(३) स१ स२ ⊃ म* (स१) ≥ म* (स२) आणि म* (स१) ≥ म* (स२).
येथे दिलेली मापाची व्याख्या खुल्या व बंद संचांकरिता वापरली असता पूर्वीप्रमाणेच मापे मिळतात. हे उघड आहे.
मापाच्या योगशीलतेसंबंधी बाहेरील व आतील मापांकरिता पुढील विधाने सिद्ध करता येतात.
(१) म* (स१ ⋃ स२) + म* (स१ ∩ स२) ⩽ म* (स१) + म* (स२).
(२) म* (स१ ⋃ स२) + म* (स१ ∩ स२) ≥ म* (स१) +म* (स२).
यावरून दोन संच वियुक्त व मापनीय असतील, तर त्यांचा संयोग संचही मापनीय असतो आणि
म (स१ + स२) = म (स१) + म (स२).
लबेग मापाच्या संकल्पनेचे वैशिष्ट्य म्हणजे योगशीलता गुणधर्म सांतच नव्हे, तर संचांच्या गणनीय अनंत संख्येकरिताही वापरता येतो, म्हणजेच स१, स२, … मापनीय असतील, तर
स१ U स२ U स३ … सुद्धा मापनीय असतो आणि
म (स१ Uस२…) = म (स१) + म (स२) +…..
एकच बिंदू असलेल्या संचाचे माप शून्य असते व म्हणून गणनीय बिंदू संचाचे माप शून्य असते. शून्य मापाच्या संचाचे दुसरे उदाहरण म्हणजे कँटर संच (गेओर्क कँटर या गणितज्ञांच्या नावावरून ओळखण्यात येणारा संच). हा संच [०, १] या बंद अंतरालातील एक तृतीयांश अंतराल काढून, नंतर राहिलेल्या प्रत्येक अंतरालातील एक तृतीयांश अंतराल काढून आणि हीच क्रिया अमर्यादपणे चालू ठेवून मिळतो. (काढून टाकलेली अंतराले खुली अंतराले असतात).
अमापनीय संचाचे उदाहरण पुढीलप्रमाणे : समजा, अ हे अंतराल [०, १] आहे. जर य є अ, तर श हा संच पुढीलप्रमाणे तयार केला आहे.
श= {य│ ० < क्ष < १ आणि क्ष — य परिमेय}.
क्ष ला अ मधील निरनिराळी मूल्ये दिली असता मिळणारे सर्व श वियुक्त संच असतील, हे उघड आहे. निवडीचे गृहीत वापरून सर्व श मधून एक एक बिंदू निवडून तयार झालेला संच स अमापनीय असतो, असे दाखविता येते.
मापाचे पुढील गुणधर्मही लक्षणीय आहेत.
(१) स१, स२ वियुक्त असल्यास
म* (स१ U स२) ≥ म* (स१) + म* (स२) ≥ म* (स१ U स२)
(२) श मापनीय व म* (स) सांत असेल, तर
म* (स) = म* (श ∩ स) + म* (स – श ∩ स)
(३) समजा, स१ ⊂ स२ ⊂ स३… आणि स = सीमा सन [→ अवकलन व समाकलन]. जर प्रत्येक सन मापनीय असेल, तर स मापनीय असतो
म (स) = सीमा म (सन)
न → ∞
(४) समजा, स१ ⊃ स२ ⊃ स३ .. ही एक संचांची उतरती श्रेणी आहे आणि श्रेणीतील सर्व संच मापनीय आहेत, तर
म (सीमा सन) = सीमा म (सन).
(५) जर सर्व सन मापनीय असतील आणि ते सर्व सांत मापाच्या संचामध्ये समाविष्ट असतील तर,
सीमा म (सन) ⩽ म (सीमा सन).
(६) सीमा म (सन) ≥ म (सीमा सन).
(७) स हा कोणताही संच असेल, तर श आणि ष असे मापनीय संच सापडतील की,
श ⊂ स ⊂ ष आणि
म (श) = म* (स),
म* (स) = म (ष).
बहुमितीय अवकाश : येथपर्यंत रेषीय संचांच्या मापाचा विचार केला आहे. बहुमितीय अवकाशातील संचांकरिता मापाची संकल्पना कशी मांडावयाची हे पुढील विवेचनात दर्शविले आहे. प-मितीय अवकाशात अंतरालाची व्याख्या पुढीलप्रमाणे :
अर < क्षर < बर, र = १, २, ….प (खुले अंतराल)
अर ⩽ क्षर ⩽ बर, र = १, २, …प (बंद अंतराल), हे वर आलेच आहे. प-मितीय अवकाशातील ख हे खुले अंतराल असेल, तर त्याच्या मापाची व्याख्या पुढीलप्रमाणे :
|
र=प |
|||
|
म (ख) |
= |
∏ |
(बर – अर), |
|
र=१ |
या व्याख्येचा उपयोग करून रेषीय संचाच्या मापाचे वर विवरण केलेले आहे त्या धर्तीवर प-मितीय अवकाशातील संचाच्या मापाचे विवरण करता येते.
कोटी संच :समजा, स हा क्ष अक्षावरील एक बिंदू संच आहे. स मधील प्रत्येक बिंदूतून उ उंचीचा कोटी [य सहनिर्देशक दर्शविणारी उभी रेषा→ भूमिति] काढला आहे व
को = {(क्ष, य) │क्ष є स, ० ⩽ य≤ उ},
तर म* (को) = उ म* (स) आणि म* (को) = उ म* (स)
जर स मापनीय असेल, तरच को मापनीय असतो व मग म (को) = उ म (स).
मापनीय फलने : समजा, स० या मापनीय संचावर व्याख्यात (व्याख्या केलेले) फ (क्ष) हे फलन आहे. स० संचातील ज्या बिंदूकरिता फ (क्ष)> अअसेल त्या बिंदूंचा संच स (फ> अ) ने दर्शवू. त्याचप्रमाणे स (फ< अ), स (फ ⩽ अ) वगैरे चिन्हे वापरू.
अ च्या मूल्यांकरिता स (फ > अ), स (फ < अ), स (फ ≥ अ) आणि स (फ ⩽ अ) यांपैकी कोणताही एक संच मापनीय असेल, तर फलन फ (क्ष) मापनीय आहे असे म्हणतात. वरीलपैकी कोणताही एक संच मापनीय असताना इतर सर्व संच मापनीय असतात, असे दाखविता येते.
मापनीय फलनांचे पुढील गुणधर्म महत्त्वाचे आहेत : (१) फ मापनीय फलन असेल व क हा स्थिरांक असेल, तर फ + क आणि क फ मापनीय असतात. (२) फ१ आणि फ२ मापनीय असतील, तर स (फ१ > फ२) हा संच मापनीय असतो. (३) फ१ आणि फ२ सांत असून मापनीय असतील, तर फ१ + फ२ आणि फ१ — फ२ मापनीय असतात. त्याचप्रमाणे फ१ फ२ हे सुद्धा मापनीय असते. (४) समजा, फ१, फ२… ही एक मापनीय फलनांची श्रेणी आहे. फ१, फ२…या फलनांच्या क्ष बिंदूतील मूल्यांचा ऊर्ध्वबंध ऊ (क्ष) ने दर्शविला, तर ऊ (क्ष) मापनीय असते. निम्न बंधाविषयी असेच विधान करता येते. (५) मापनीय फलनांच्या एकदिक् श्रेणीचे [→ श्रेढी] सीमा फलन मापनीय असते. (६) संतत फलन [→ फलन] मापनीय असते. (७) कोणतीही मापनीय फलन जवळ-जवळ संतत असते (एखादा गुणधर्म शून्य मापाचा उपसंच सोडून बाकीच्या संचावर सत्य असल्यास तो जवळ जवळ सर्व संचावर सत्य आहे असे म्हणतात). (८) शून्य मापाच्या संचावरील व्याख्यात फलन मापने य असते. (९) │फ│ हे फलन स संचावर मापनीय असेल, तर |फ| सुद्धा मापनीय असते.
येथपावेतो वर्णन केलेली आतील व बाहेरील मापावर आधारलेली मापाची संकल्पना प्रथमतः लबेग यांनी १९०२ मध्ये मांडली. त्यांनी डॉक्टरेट पदवीकरिता लिहिलेल्या प्रबंधामध्ये ती मांडली होती. सुरुवातीच्या काळामध्ये या प्रबंधावर प्रतिकूल टीका झाली परंतु जसजसा मापाचा व लबेग समाकलाचा [यासंबंधी खाली माहिती दिलेली आहे] उपयोग बहुसंख्य गणितज्ञ आपल्या लेखनामध्ये करू लागले तसतशी त्याची प्रतिष्ठा वाढत गेली व गणितीय विश्लेषणामध्ये त्याला महत्त्वाचे स्थान प्राप्त झाले.
लवेग समाकल : समजा, स हा एक क्ष – अक्षावरील बिंदू संच आहे व को हा प्रतलीय बिंदू संच पुढील व्याख्येने दिला आहे.
को= { (क्ष, य) │क्ष є स, ० ⩽ य ⩽ फ (क्ष) },
को ला फलन फ (क्ष) चा स संचावरील कोटी संच म्हणता येईल. जर को मापनीय असेल, तर फ (क्ष) लबेग समाकलनीय आहे असे म्हणतात व तो समाकल
∫स फ (क्ष) d क्ष अथवा L ∫स फ (क्ष) d क्ष या चिन्हांनी दर्शवितात. अर्थात समाकलाचे मूल्य = म (को).
वरील व्याख्येमध्ये फलन फ (क्ष) चे मूल्य धन आहे, हे गृहीत धरले आहे. तसे नसेल, तर फ (क्ष) ची फोड करून ते दोन धन फलनांची वजाबाकी म्हणून पुढीलप्रमाणे मांडता येते.
फ + (क्ष) = फ (क्ष), फ (क्ष) > ०}’
= ०, फ (क्ष) < ०
फ—(क्ष) = — फ (क्ष), फ (क्ष) < ०}
= ०, फ (क्ष) > ०
आणि फ (क्ष) फ+ (क्ष) – फ— (क्ष)
जर को+आणि को— हे फ+ व फ—यांचे कोटी संच असतील,
तर फ (क्ष) चा समाकल म (को+) – म (को—).
रीमान समाकलाची व्याख्या व त्याकरिता फ (क्ष) वर घालावी लागणारी बंधने सर्व परिचित आहेत [→ अवकलन व समाकलन]. लबेग समाकलाकरिता पुढील बंधने आवश्यक ठरतील. संच स मापनीय असला पाहिजे व कोटी संच को हाही मापनीय असला पाहिजे. पुढील विवेचनात समाकल म्हणजे लबेग समाकल अभिप्रेत आहे.
संकलन सीमेच्या भाषेत समाकल : समजा, फ (क्ष) मापनीय आहे आणि क ≤ फ (क्ष) ≤ ख.[क, ख] अंतरालाचे पुढीलप्रमाणे भाग पाडले आहेत,
क = ल१ < ल२…. लन = ख
समजा, सर = स [लर ⩽ फ (क्ष) < लर+१] आणि
|
न |
न |
||||||
|
ब |
= |
∑लर+१ |
म(सर) |
आणि |
भ |
= |
∑लरम(सर) |
|
१ |
१ |
जेव्हा सर्वांत मोठे उप-अंतराल [लर+१– ल२] शून्योपगामी होईल तेव्हा ब आणि भ या दोहोंची सीमा
∫स फ (क्ष) d क्ष होईल.
लबेग समाकलाची संकल्पना रीमान समाकलापेक्षा व्यापक आहे हे पुढील उदारहणावरून दिसून येईल.
फ (क्ष) = १, क्ष परिमेय }
= ०, क्ष अपरिमेय }
हे फलन रीमान व्याख्येप्रमाणे समाकलनीय नाही परंतु तेच फलन लबेग व्याख्येप्रमाणे समाकलनीय आहे. जे फलन रीमान व्याख्येप्रमाणे समाकलनीय आहे ते लबेग व्याख्येप्रमाणेसुद्धा समाकलनीय असते परंतु याचा व्यत्यास खरा नाही.
फ (क्ष) ही स वर समाकलनीय असेल, तर │फ (क्ष)│ ही समाकलनीय असते. फ (क्ष) मापनीय असेल, तर याचा व्यत्यासही खरा असतो (रीमान समाकलाकरिता व्यत्यास खरा नाही). अनंत श्रेढींची परिभाषा वापरून असे म्हणता येईल की, लबेग समाकल केवल अभिसारी असतो.
समाकलाचे गुणधर्म : (१) फ (क्ष) ≤ ग (क्ष) असेल, तर
![]()
(२) स हा स१, स२,…. वगैरे संचांचा सांत किंवा गणनीय अनंत संयोग असेल,
तर


संभाव्यता सिद्धांतातील उपयोग : संभाव्यता सिद्धांतामध्ये लबेग समाकलाचा पुष्कळ ठिकाणी वापर केला जातो, याची उदाहरणे खाली दिली आहेत.
(१) समजा नि निष्पत्तीचे फलन घ (नि) ने दर्शविले, तर
{नि घ (नि) ⩽ क्ष} हा संच एक घटना होईल, त्याची संभाव्यता सं {घ ⩽ क्ष} हे एक क्ष चे फलन होईल ते फप (क्ष) ने दर्शवू.
या फलनाला घ या यदृच्छ चलाचे वंटन फलन म्हणतात [→ संभाव्यता सिद्धांत]. या फलनाच्या अवकलजास [dफ/dक्ष = प (क्ष)] घ ची घनता किंवा वारंवारता फलन म्हणतात.{घ} चे अपेक्षित मूल्य अ {घ} ने दर्शविल्यास
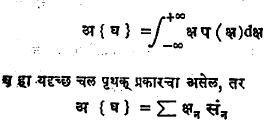

माप संकल्पनेतील नंतरची प्रगती : लबेग यांच्या कल्पनांची स्पष्टपणे मांडणी होण्यास त्यांचा प्रबंध प्रकाशित झाल्यानंतर सु. १५ वर्षे जावी लागली. या प्रक्रियेतून क्षेत्रफळे, द्रव्यमाने, संभाव्यता यांसारख्या प्रश्नांतील मापासंबंधीचे व्यापक उत्तर उपलब्ध झाले व शेवटी त्यातील संकल्पनात्मक तत्त्वार्थ नित्य वेगळा करण्यात आला. तथापि हे उत्तर व तत्त्वार्थ अनुभवातील संज्ञांपेक्षा फार अमूर्त अशा स्वरूपात मांडण्यात आले. या प्रक्रियेतील व्यापकीकरणाचे कार्य फ्रेंच गणितज्ञ टी. जे. स्टील्टजेस व जर्मन गणितज्ञ जे. के. ए. रेडॉन यांनी केले आणि अमूर्तीकरणाचे कार्य एम्. आर्. फ्रेशे व जर्मन गणितज्ञ कोन्स्टांटीन काराथेऑदॉरी यांनी केले. १९३० मध्ये बनाख अवकाशातील [→ फलनक विश्लेषण] मूल्ये असणारी फलने प्रचारात आली व तेव्हापासून माप या संकल्पनेचा पुढील अमूर्तीकरण प्रारंभ झाला. यात मापे व फलने (आणि त्यामुळे समाकल) वरीलप्रमाणे संख्यात्मक मूल्ये धारण करण्याऐवजी अधिकाधिक अमूर्त अवकाशांतील मूल्ये धारण करतात आणि अभिसरणाचे निरनिराळे प्रकारही यात वापरण्यात येतात. अशा प्रकारे माप व समाकलन सिद्धांतातील लक्षणांची निरनिराळी रूपे (संख्यात्मक प्रश्नांतसुद्धा) आढळतात. तथापि सारतः त्यांतील संकल्पनात्मक तत्त्वार्थ तोच आहे, मात्र त्याचे निरनिराळ्या पार्श्वभूमीवर वेगवेगळ्या दृष्टीकोनांतून विवरण केलेले दिसून येते. या संकल्पनांचे महत्त्व म्हणजे त्यांमुळे अवकलन सिद्धांत, मर्यादा मूल्य [→ अवकल समीकरणे], संभाव्यता सिद्धांत, ⇨ गट सिद्धांत, ⇨ वर्चस् सिद्धांत, ⇨ हरात्मक विश्लेषण यांसारख्या विषयांत प्रभावी गणितीय साधने उपलब्ध झालेली असून त्यांचा अधिकाधिक वापर होत आहे.
संदर्भ : 1. Asplund, E. Bungart. L. A. First Course in Integration,New York, 1966.
2. Halmos, P. R. Measure Theory, New Delhi, 1964.
3. Kolmogorov, A. N. Fomin, S. V. Trans. Brunswick, N. A. Jeffrey, A. Measure, Lebesgue Integralsand Hilbert Space, New York, 1961.
4. Saks, S. Trans.Young, L. C. Theory of Intergal, New York, 1964.
5.TayLor, A. E. General Theory of Functions and Intergration, New York, 1965.
ओक, स. ज.
“