संख्या

संख्या : गणितामध्ये अनेक भिन्न गोष्टींकरिता संख्यांचा वापर केला जातो : गणनक्रियेमध्ये वापरण्यात येणाऱ्या संख्या (धन पूर्णांक; १,२,३ या इत्यादी); आदर्श मापनांमध्ये मिळू शकणाऱ्या संख्या (उदा., २/३, ३…; सत् संख्या); असत् संख्या (उदा., -१) आणि गणिताच्या प्रगत शाखेत वापरण्यात येणाऱ्या इतर अधिक अमूर्त संकल्पना (उदा., सदसत् संख्या आणि सांतातीत संख्या). प्राथमिक अंकगणितामध्ये धन पूर्णांक आणि शून्य, अपूर्णांक यांचा, थोड्या प्रमाणात धन सत् संख्यांचा (उदा., ३) आणि कधी तरी ऋण सत् संख्यांचा वापर केला जातो. बीजगणितामध्ये ऋण संख्या आणि असत् संख्या असलेल्या गुंतागुंतीच्या आकडेमोडींचा सामान्यतः समावेश असतो. प्रस्तुत नोंदीत संख्या या संकल्पनेची प्रागैतिहासिक काळापासून आतापर्यंत कशी प्रगती होत गेली याचे वर्णन केले आहे.

नैसर्गिक संख्या : (अ) १, २, ३, ४,… या परिचित संख्यांना नैसर्गिक संख्या, मोजसंख्या, पूर्ण संख्या किंवा धन पूर्णांक संख्या असे म्हणतात. नैसर्गिक संख्यांचा संच (१, २, ३, ४,… न,… } असा लिहितात. नैसर्गिक संख्या न संपणाऱ्या असल्या तरी त्या लिहिण्यासाठी वापरण्याची चिन्हे १, २,…, ९ इतकीच आहेत. ९ पुढील संख्या स्थानमूल्याची कल्पना वापरून लिहितात. उदा., २७ या संख्येतील २ चिन्हाचे मूल्य दोन नसून स्थानानुसार ‘वीस’ असे आहे. स्थानमूल्याची कल्पना ही भारतीयांनी शोधून काढली.

नैसर्गिक संख्या क्रमाने येतात व पुढील संख्या मागील प्रत्येक संख्येहून मोठी असते. उदा., १७ ही संख्या ९ या संख्येहून मोठी आहे, कारण नैसर्गिक संख्यांच्याक्रमात १७ ही संख्या ९ नंतर येते. लघुगुरू-भाव हा नैसर्गिक संख्यांचा पहिला गुणधर्म होय. ब ही संख्या अ पेक्षा मोठी आहे, हे ब > अ असे दाखवितात.

(आ) नैसर्गिक संख्यांच्या संचात बेरीज (+) व गुणाकार (x) या दोन द्विपद-क्रिया करता येतात. बेरीज या क्रियेसाठी नैसर्गिक संख्यांतील अनुक्रमाचा उपयोग होतो.अ ही नैसर्गिक संख्या असेलतर अ+१ म्हणजे अ नंतर लगेच येणारी संख्या अ+ या चिन्हाने दाखवितात. अ + १ = अ+ आणि अ +(ब+)=(अ + ब)+ या दोन नियमांवरून कोणत्याही दोन नैसर्गिक संख्यांची बेरीज सांगता येते. बेरीज या क्रियेचे खालील दोन गुणधर्म व्याख्येच्या साहाय्याने सिद्ध करता येतात :

अ + ब = ब + अ ( क्रमनिरपेक्षता )

( अ + ब ) + क = अ + ( ब + क ) ( साहचर्य )

गुणाकार ही द्विपद क्रिया पुढील दोन नियमांनी केलेली आहे. अ x १ = अ आणि अ x (ब+) = अ x ब+अ. या नियमांच्या आधारे खालील गुणधर्म सिद्ध करता येतात :

अ x ब = ब x अ ( क्रमनिरपेक्षता )

अ x (ब x क) = (अ x ब) x क ( साहचर्य )

अ x (ब + क ) = अ x ब + अ x क ( गुणाकाराचे बेरजेवरील वितरण )

(इ) गुणाकार या क्रियेचा एक परिणाम म्हणजे घातांकाची कल्पना हा होय. अ या नैसर्गिक संख्येचा न वेळा स्वत:शीच गुणाकार केला, तर अ x अ x …. x अ ( न वेळा ) ही संख्या मिळते. ती अ न या चिन्हाने दर्शवितात. अ न ची ही व्याख्या वापरून खालील नियम सिद्घ होतात.

अ^म x अ^न= अ ^म+न 

(अ^म)^न=अ^मxन 

(अxब)^म=अ^म xब^म 

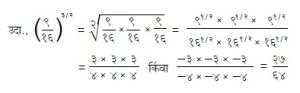
(ई) नैसर्गिक संख्यांच्या बाबतीत महत्त्वाचा नियम म्हणजे गणिती विगमनाचा नियम हा आहे. समजा, सर्व नैसर्गिक संख्यांच्या बाबतीत पहा गुणधर्म लागू होतो असे सिद्घ करावयाचे आहे. त्यासाठी पुढील दोन अटींची पूर्तता होणे पुरेसे असते : (१) १ या संख्येबद्दल प हा गुणधर्म खरा आहे (२) प हा गुणधर्म अ या नैसर्गिक संख्येबद्दल खरा असेल तर तो अ⁺या संख्येबद्दलही खरा आहे. उदा., सिद्ध करावयाचे आहे की,

(उ) नैसर्गिक संख्यांच्या संचाचा विस्तार‘शून्य’या संख्येचा नैसर्गिक संख्येत समावेश करून झाला. वर वर्णन आलेच आहे की, १, …., ९ या चिन्हांचा उपयोग करून कोणतीही संख्या स्थानमूल्याच्या आधाराने तयार होते. ‘वीस’ ही संख्या लिहिण्याची पूर्वीची पद्धती २l अशी होती. रेषेच्या एका बाजूला ‘२’ हे चिन्ह लिहिल्याने ‘२’ या चिन्हाचे स्थान मूल्य बदलते असे दाखविता येते. उजवीकडील जागा रिकामी न ठेवता कालांतराने तेथे ० हे चिन्ह वापरात आले. म्हणजे ‘वीस’ ही संख्या २० अशी लिहीत. पुढे मधली रेष काढून त्याला २० असे सुटसुटीत रूप आले. मुळात चिन्ह म्हणून आलेले ० नंतर एक नैसर्गिक संख्या म्हणून गणले जाऊ लागले. स्थान मूल्याच्या कल्पने प्रमाणेच ० ही कल्पना भारतीयांचीच आहे. [⟶शून्य].

‘०’ ही नैसर्गिक संख्या मानावयाची असेल तर बेरीज, गुणाकार व घातांक या क्रियाही ० ला झाल्या पाहिजेत. या क्रियांचा विस्तारही खालीलप्रमाणे करण्यात आला.

०+०=००x ० = ० अ+० = ० + अ = अ

अ x ० = ० x अ = ० अ ० = १ (अ = ०) ०^अ=०.

पूर्णांकसंख्या: {०,१,२,३,४,….} हा नैसर्गिक संख्यांचा संच असून बेरीज व गुणाकार या त्या संचातील दोन द्विपद-क्रिया आहेत.

बेरीज या क्रियेवर आधारित असा प्रश्नविचारता येतो की, अ या संख्येत कोणती नैसर्गिक संख्या मिळविली असता ब ही संख्या येईल ? या प्रश्नाचेच अधिक गणितीरूप असे की, अ + क्ष = ब. हे समीकरण सोडविता येईल का ?

ब > अ असे असेल तेव्हा अ+क्ष= ब हे समीकरण सोडविता येते. उदा., २ + क्ष = ५ याचे बीज क्ष=३ असे आहे परंतु ब < अ असेल तेव्हा अ + क्ष = ब या समीकरणाला नैसर्गिक संख्यांच्या संचात उत्तर नाही. उदा.,५ + क्ष = २ या समीकरणाचे बीज नैसर्गिक संख्यांच्या संचात सापडणार नाही.

अशी समीकरणे सोडविता यावीत यासाठी नैसर्गिक संख्यांच्या संचात -१, -२, -३,…. इ. ऋण पूर्णांकांची भर घालण्यात येऊन {….,-४, -३,-२,-१,०,१,२,३,….} असा पूर्णांक संख्यांचा संच तयार करण्यात आला. पूर्णांकाच्या संचात अ + क्ष = ब हे समीकरण कायमच सोडविता येते.

पूर्णांकांचा संच हा नैसर्गिक संख्यांच्या संचाचा युक्तिसंगत विस्तार असेल तर बेरीज, गुणाकार व घातांक या क्रिया या संचात ही करता येतात. धन पूर्णांकांची बेरीज व गुणाकार वर दिलेलेच आहेत. ऋण पूर्णांकांच्या बेरीज व गुणाकारासाठी पुढील नियम आहेत : (-अ) +(- ब) = -(अ + ब) येथे अ व ब हे धन पूर्णांक आहेत. तसेच (-अ) x(-ब) =अ x ब. –अ हा ऋण पूर्णांक असेल व ब हा धन पूर्णांक असेल तर (-अ)+ ब यांची व्याख्या अशी केली जाते : जर अ<ब आणि अ+ट= ब असेल तर (-अ) +ब = ब+(-अ) = ट. जर ब < अ आणि ब + ट = अ असेल तर (-अ) +ब = -ट त्याचप्रमाणे (-अ) xब = -(अ x ब).

समजा अ व ब हे धन पूर्णांक आहेत. अ ब या घातांकाची व्याख्या वर दिलीच आहे. (-अ) ब ची व्याख्या (-अ) चा स्वत:शी ब वेळा गुणाकार अशीच होते. म्हणजे (-अ)ब=(-अ) x….x (-अ) हा गुणाकार ब वेळा. पण अ ब ची व्याख्या मात्र १/अ ब अशी आहे.

जर अ व ब हे धन पूर्णांक असतील आणि अ < ब असेल, तर-अ आणि-ब यांच्यातील लघुगुरूत्व –ब < -अ असे असते. सर्व ऋण पूर्णांक हे शून्यापेक्षा लहान होत.

परिमेय संख्या : नैसर्गिक संख्यांच्या बाबतीत असा प्रश्न विचारता येतो की, १२ हा ३ च्या किती पट आहे ? म्हणजेच तिनाला कितीने गुणले असता १२ येतात ? किंवा ३ x क्ष = १२ या समीकरणाचे उत्तर किती ? क्ष = ४ हे याचे उत्तर आहे पण अ व ब ही कोणतीही पूर्णांकाची जोडी दिली तर याचे उत्तर पूर्णांकाच्या संचात मिळतेच असे नाही. उदा., ५ x क्ष = १२ या समीकरणास पूर्णांक संचात उत्तर नाही. यासाठी पूर्णांक संचाचा विस्तार करून परिमेय संख्यांचा संच तयार करण्यात आला. अ व ब हे पूर्णांक असतील आणि ब = ० तर अ/ब या संख्येला परिमेय संख्या किंवा गुणोत्तरीय संख्या असे म्हणतात. -३/२, २/३, -७/११ या परिमेय संख्या आहेत. सर्व पूर्णांक संख्यासुध्दा परिमेय संख्या आहेत.

उदा., -३ ही पूर्णांक संख्या -३/१ अशी लिहिता येते. परिमेय संख्या या गुणोत्तर स्वरूपाच्या असल्याने एकच परिमेय संख्या अनेक गुणोत्तरांनी दर्शविता येते. उदा., २/३ ही परिमेय संख्या -४/-६, ८/१२ अशा अनेक गुणोत्तरांनी दाखविता येते.

परिमेय संख्या अ/ब ही (अ,ब) अशा क्रमित जोडीच्या स्वरूपात बऱ्याचदा लिहितात. परिमेय संख्यांची बेरीज व गुणाकार क्रमित जोड्यांच्या साहाय्याने खालीलप्रमाणे करतात.

(अ, ब)+(क, ड)=(अड+बक, बड)

(अ, ब) x (क, ड)=(अक, बड)

परिमेय संख्या (अ, ब) ही (क, ड) या परिमेय संख्येपेक्षा मोठी आहे. याचा अर्थ (अ, ब) व (-क, ड) यांची बेरीज ही धन परिमेय संख्या आहे.

अ व ड या धन पूर्णांक संख्या असतील तर अ १/ ड याचा अर्थ, अशी संख्या की जिचा ड हा घातांक घेतल्यास अ हा पूर्णांक मिळतो, असा होतो. उदा., (८)१/३ = २ कारण २३=८. अ १/ ड ही संख्या ड √अ अशीही लिहितात. ही संख्या नेहमीच परिमेय संख्या असेल असे नाही. अ ^१/ड ची ही व्याख्या केल्या नंतर अ/ब आणि क/ड या परिमेय संख्या दिल्या असतील तर (अ/ब) ^क/ड याची व्याख्या करता येते.

सत्‌ संख्या : नैसर्गिक संख्यांबाबत करता येणारी तिसरी क्रिया म्हणजे घातांक घेणे ही होय. क्ष२=४ हे समीकरण नैसर्गिक संख्यांच्या संचात सोडविता येते व त्याचे उत्तर २ हे आहे. हेच समीकरण पूर्णांक संख्यांच्या संचातही सोडविता येते आणि त्याची उत्तरे +२ व -२ अशी येतात. क्ष२ = ४/९ हे समीकरण परिमेय संख्यांच्या संचात सोडविता येते आणि त्याची उत्तरे २/३,-२/३ अशी येतात. क्ष २=७ हे समीकरण मात्र परिमेय संख्यांच्या संचात सोडविता येत नाही. कारण अशी कोणतीच परिमेय संख्या नाही की, तिचा वर्ग ७ होईल. अशा तऱ्हेची समीकरणे सोडविण्याच्या प्रयत्नातून अ परिमेय संख्यांचा शोध लागला.

अपरिमेय संख्यांची कल्पना काही भौमितिक गुणोत्तरांवरूनही येते. लांबीचे कोणतेही परिमाण घेतले तरी वर्तुळाचा परीघ व व्यास यांचे गुणोत्तर (π) परिमेय संख्येत लिहिता येत नाही. कारण व्यासाची लांबी पूर्णांकात आली ( किंवा परिमेय संख्येत आली ) तर परिघाची लांबी परिमेय असत नाही. काटकोन त्रिकोणाच्या काटकोन करणाऱ्या बाजू १ मापाच्या घेतल्या, तर कर्णाची लांबी (√२) ही परिमेय संख्येत येत नाही.

सारांश, गणिती क्रिया करताना परिमेय संख्यांचा संच ही अपुरा पडतो, असे दिसून येते. यासाठी परिमेय संख्यांच्या संचाचा विस्तार अपरिमेय संख्यांची भर घालून करतात. विस्तारित संचाला सत्‌ संख्यांचा संच आणि त्यातील प्रत्येक सदस्याला सत्‌ संख्या असे म्हणतात.

⇨ यूलिउस डेडेकिंट (१८३१-१९१६) या गणितज्ञांनी सत्‌ संख्यांची उपपत्ती खालीलप्रमाणे तयार केली. क्ष ही एक सत्‌ संख्या असेल तर ती क्ष=(L, U)अशी लिहावी. उजवीकडील क्रमित जोडीत L व U हे परिमेय संख्यांचे संच आहेत. या संचांचे पुढील गुणधर्म आहेत : (१) L व U मिळून सर्व परिमेय संख्या होतात. (२) L व U हे संच अरिक्त आहेत. (३) L मधील प्रत्येक परिमेय संख्या ही U मधील कोणत्याही परिमेय संख्येपेक्षा लहान आहे.

उदा., √२ ही सत्‌ संख्या घेतली व L हा संच पुढीलप्रमाणे तयार केला. L मध्ये सर्व ऋण परिमेय संख्या व ० आहेत. या खेरीज L मध्ये अशा धन पूर्णांक संख्या आहेत की, ज्यांचे वर्ग २ पेक्षा लहान आहेत. उरलेल्या सर्व परिमेय संख्या U मध्ये घेतल्यास असा पडताळा घेता येतो की, L व U यांच्या ठिकाणी वर सांगितलेले गुणधर्म आहेत. म्हणून √२=(L,U).कोणतीही परिमेय संख्या (उदा., ७/११) हीदेखील याचप्रमाणे (L,U) अशा जोडीने दाखविता येईल.

डेडेकिंट यांनी सत्‌ संख्यांची बेरीज व गुणाकार या क्रिया तसेच लघु-गुरूत्व संबंध यांची मांडणी या व्याख्येच्या आधाराने करून दाखविली. ⇨गेओर्क कँटर (१८४५-१९१८) या गणित ज्ञांनी सत्‌ संख्यांची एक उपपत्ती परिमेय संख्यांच्या श्रेणींच्या आधाराने दिली. सत्‌ संख्यां विषयीच्या दोन्ही उपपत्ती प्रमाण मानल्या जातात.

अ_० +अ_१क्ष+…………..+अ_नक्ष^न=०.…….(1)

या समीकरणातील अ०, अ१, …..,अन हे सहगुणक पूर्णांक असतील तर त्या समीकरणाला पूर्णांक-सहगुणक-समीकरण असे म्हणतात. अशा समीकरणाची बीजे असलेल्या सत्‌ संख्यांना बैजिक सत्‌ संख्या असे म्हणतात. कोणतीही परिमेय संख्या अ/ब ही अ-बक्ष=० या समीकरणाचे बीज असल्याने, सर्व परिमेय संख्या बैजिक असतातच. काही अपरिमेय संख्याही बैजिक असतात. उदा., ही अपरिमेय संख्या क्ष २-२=० या समीकरणाचे बीज असल्याने बैजिक आहे. पण π, ३√३, e या संख्या अपरिमेय आहेत पण बैजिक नाहीत. यांना अबैजिक ( बीजातीत ) सत्‌ संख्या असे म्हणतात. [⟶ इ पाय् ].

एका सरळ रेषेवर ० हा आदि बिंदू घेतला. कोणतीही विशिष्ट लांबी हे मोजमापाचे एकक धरून आकृतीत दाखविल्याप्रमाणे मानरेषा तयार करता येते. असे गृहीत धरले आहे की, मानरेषेवरील प्रत्येक बिंदूशी एक व एकच सत्‌ संख्या संलग्न आहे आणि प्रत्येक सत्‌ संख्येचा दर्शक असा एक व एकच बिंदू मानरेषेवर आहे. मानरेषाही तुटक नसून संतत आहे. याचाच अर्थ सत्‌ संख्या याही संतत आहेत. कोणत्याही दोन सत्‌ संख्यांच्या दरम्यान तिसरी सत्‌ संख्या नक्कीच असते.

सदसत्‌ संख्या : संख्या या संकल्पनेचा जो विस्तार झाला त्याच्या प्रत्येक पायरीवर हाती असलेल्या संख्या संचात कोणते तरी समीकरण सोडविता न आल्याने विस्ताराची दुसरी पायरी निर्माण झालेली आहे. सत्‌ संख्यांच्या पायरीवरून असत् आणि सदसत्‌ संख्यांची पायरी गाठण्यामागेही हाच हेतू होता. कोणत्याही सत्‌ संख्येचा वर्ग ऋण सत्‌ संख्याअसू शकत नाही. ऋण संख्येचा वर्ग व धन संख्येचा वर्ग धनच असतो. त्यामुळे क्ष २ + १ = ० हे समीकरण सत्‌ संख्यांच्या संचात सोडविता येत नाही. त्यामुळे संख्येच्या संकल्पनेचा विस्तार करून असत्‌ संख्यांची भर घालण्यात आली.

√-१ ही संख्या मूळ असत्‌ संख्या मानली जाते व ती ‘ i ’ या चिन्हाने दर्शवितात. या चिन्हाचा उपयोग करून कोणत्याही ऋण सत्‌ संख्येचे वर्गमूळ दाखविता येते. उदा., √-५ = i √ ५

सदसत्‌ संख्या म्हणजे दोन सत्‌ संख्यांची जोडी असते. अ व ब या सत्‌ संख्या असतील तर ( अ, ब ) ही क्रमित जोडी सदसत्‌ संख्या असून ती अ + i ब अशीही लिहितात. यातील i =√-१ आहे  प्रत्येक  सत्‌ संख्याही सदसत्‌ संख्याच आहे. कारण अ ही सत्‌ संख्या ( अ, ० ) या क्रमित जोडीने दाखविता येते, तर i ब ही असत्‌ संख्या ( ०, ब ) या जोडीने दाखविता येते. अशा तऱ्हेने सत्‌ संख्यांचा संच हा सदसत्‌ संख्यांच्या संचाचा उपसंच आहे.

सदसत्‌ संख्यांची बेरीज व गुणाकार यांची व्याख्या खालील प्रमाणे करतात.

(अ, ब)+( क, ड)=(अ+क, ब+ड)

(अ, ब)x(क, ड)=(अक – बड, अड+बक)

या व्याख्येचा उपयोग करून दाखविता येते की,

(०,१)x(०,१)=(-१,०)

म्हणून √ (-१, ०) = (०, १)

सदसत्‌ संख्यांच्या बाबतीत मात्र लघुगुरू-संबंध शक्य होत नाही.

सत्‌ संख्या ज्याप्रमाणे सरळ रेषेवर दर्शविता येतात त्याप्रमाणे सदसत्‌ संख्या प्रतलावरील बिंदूंनी दर्शविता येतात. अ+i ब ही सदसत्‌ संख्या प (अ, ब) या (अ, ब) हे सहनिर्देशक असलेल्या बिंदूने दाखविली जाते.

सहनिर्देशक प्रतलाचा आ हा आदिबिदू असेल तर आप या रेषाखंडाची लांबी  √ अ२ + ब२ होते.  √अ२ + ब२ याला अ + i ब या सदसत्‌ संख्येचे ‘केवलमूल्य’असे म्हणतात. जर आपने क्ष-अक्षाशी केलेला कोन θ असेल तर tan θ= ब /अ असतो. θ ला अ+i ब या सदसत्‌ संख्येचा कोनांक असे म्हणतात.

सदसत्‌ संख्यांच्या संचात कोणतेही समीकरण सोडविता येते. अ०+अ१क्ष+….+ अ न क्ष न =० या समीकरणातील अ०, अ१, ….,अ न हे सहगुणक कोणत्याही संख्या असल्या तरी या समीकरणाची सर्व बीजे सदसत्‌ संख्यांच्या संचात असतात.

सांतातीत संख्या : एकोणिसाव्या शतकाच्या शेवटच्या चरणात कँटर यांनी सांतातीत संख्या ही नवीन संकल्पना प्रचारात आणली. या संकल्पनेची पहिली पायरी म्हणजे संचांक ही संकल्पना होय. A={अ, ब, क} हा संच असेल तर या संचाचे तीन सदस्य आहेत. म्हणून या संचाचा अंक ३ होय. B={१,२,३,} याचा संचांक ही तीनच होय. या दोन संचांत अ ↔ १, ब ↔ २, क ↔ ३ अशी एकास-एक संगती बसविता येते. उलट असेही म्हणता येते की, S1 ‘ व S2’या संचांत एकास-एक संगती बसविता येत असेल तर S1’ व S2’ यांचा संचांक एक असतो.

हाच युक्तिवाद पुढे नेऊन कँटर यांनी असा प्रश्न उपस्थित केला की, N = {१,२,३,….} या नैसर्गिक संख्या संचाचा अंक किती ? E = { २,४,६,…. } हा संच N चा उपसंच आहे. तरी N व E यांच्यात २ ↔ १, ४ ↔ २, ६ ↔ ३ अशी एकास-एक संगती बसविता येते. यावरून असे म्हणता येते की, N चा संचांक व त्याच्या E या उपसंचाचा अंक एकच आहेत. जेव्हा एखादया संचाचा व त्याच्या सुयोग्य उपसंचाचा अंक एकच असतो तेव्हा तो संचांक सांतातीत असतो, असे म्हणतात N या संचाच्या अंकाला कँटर यांनी N०(अलेफ नॉट किंवाअलेफ नल ) असे नाव दिले. नंतर त्यांनी असेही दाखविले की, परिमेय संख्यांचा संच Q याचा संचांक अलेफ नॉटच आहे.

समजा, A व B हे दोन संच असे आहेत की, A ची B शी एकास-एक संगती लावता येत नाही परंतु B चा सुयोग्य उपसंच B1 याच्याशी A ची एकास-एक संगती लावता येते. अशा स्थितीत B चा संचांक हा A च्या संचांकापेक्षा मोठा आहे, असे मानतात. सांतातीत संचांकांच्या बाबतीतही हे लघुगुरूत्व लावता येते.

कँटर यांनी असे दाखवून दिले की, अंतराल I हा ० व १ यांच्या दरम्यानच्या सर्व सत्‌ संख्यांचा संच घेतला तर I चा संचांक N० पेक्षा मोठा असतो. या संचांकास त्यांनी N1 (अलेफवन) असे नाव दिले. त्यांनी असेही सिद्घ केले की, कोणताही सांतातीत संचांक दिला असता त्याहून मोठा अंक असलेला संच मिळू शकतो. अशा रीतीने सांतातीत संख्यांची चढती श्रेणी नसंपणारी आहे.

संचांकांची बेरीज, गुणाकार यांच्याही व्याख्या कँटर यांनी दिल्या. त्यांच्यातील लघुगुरूत्व कसे मिळते ते वर दिले आहेच. संचांकांचे घातांकही काढता येतात. या सर्व व्याख्या अतिशय तांत्रिक असल्याने येथे दिलेल्या नाहीत.

१, २, ३, …. ह्या नैसर्गिक संख्यांकडे मोज अंक व संचांक म्हणून पाहता येते. त्याचप्रमाणे क्रमिक किंवा वस्तूंची क्रमवारी ठरविणारे अंक म्हणूनही पाहता येते. कँटर यांनी असा सिद्धांत मांडला की, १, २, ३, ४, …. ही क्रमांकांची श्रेणी वाढवीत नेता येते.

१, २, ३, …. ह्या नैसर्गिक संख्यांनी दर्शविलेली क्रमवारी संपल्यावर ω ही पहिली सांतातीत क्रमसंख्या येते. नंतर w + १, ω + २, …., २ ω ही क्रमिक संख्यांची श्रेणी मिळते. ही श्रेणी अशीच वाढवीत नेऊन ω२ + ω, ω२ + ω+१, …. अशा क्रमसंख्या मिळत जातात.

या क्रमसंख्यांची बेरीज व गुणाकार याक्रिया कँटर यांनी बसविल्या. यांचे लघुगुरूत्व क्रमवारीवरूनच ठरते.

पहा : अंक; अंकगणित; संख्या सिद्धांत; संच सिद्धांत.

संदर्भ : 1.Borevich, Z. I. Shefarevich, I. R. Number Theory, London, 1966.

2. Hunter, J. Number Theory, London, 1964.

3. Koch,Telmut, Introduction to Classical Mathematics (Vol. I),London, 1991.

4. Ni√en, Ivan Zuckerman, H. S. Montgomery, H. L. An Introduction to the Theory ofNumbers, 1991.

भावे, श्री. मा.