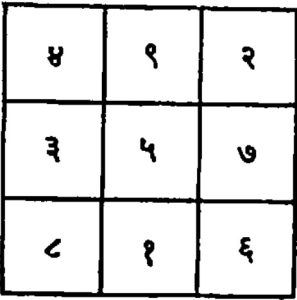
मनोरंजक चौरस : (मॅजिक स्केअर) प२ संख्या प स्तंभात व प रांगात अशा तर्हेने मांडल्या की, प्रत्येक स्तंभातील संख्याची, प्रत्येक रांगेतील संख्यांची व प्रत्येक कर्णातील संख्याची बेरीज तीच येत असेल, तर अशा मांडणीला मनोरंजक चौरस किंवा जादूचा चौरस म्हणतात. आ. १ मध्ये अशा तर्हेजचा १ ते ९ या संख्या वापरून रचलेला एक मनोरंजक चौरस दाखविला आहे .यातील स्तंभाची रांगांची व कर्णाची बेरीज प्रत्येकी १५ आहे. या संख्येला चौरसाचा स्थिरांक म्हणतात. प. या संख्येला चौरसाची कोटी म्हणतात.
|
४ |
९ |
२ |
|
३ |
५ |
७ |
|
८ |
१ |
६ |
आ. १. १ ते ९ संख्यांचा मनोरंजक चौरस ( बेरिज १५ ).
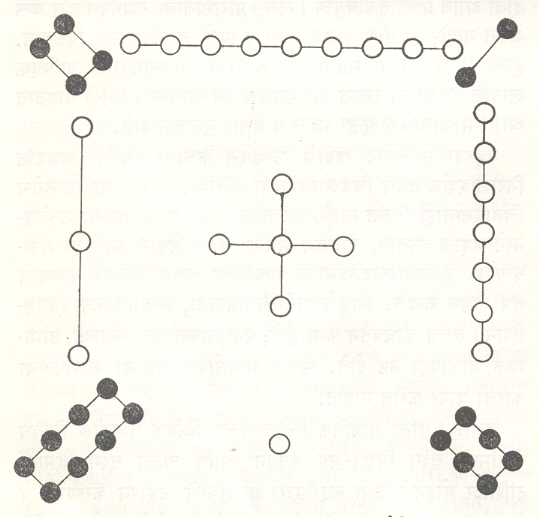
इतिहास : मनोरंजक चौरस रचण्याची सुरूवात सर्व प्रथम चीनमध्ये झालेली आढळून येते. आ.१ मधील तिसर्या् कोटीच्या चौरसाला चीन मध्ये लो-शू (Lo-Shu) हे नाव दिलेले होते. तो 1-King [ क्रमयचांविषयीचा ग्रंथ ⟶ समचयात्मक विश्लेषण] या नावाच्या ग्रंथात दिलेला आहे (मूळ स्वरूपातील चौरस आ. २ मध्ये दिला आहे.) हा ग्रंथ वॉन-वँग (इ.स.पू. ११८२-११३५) यांनी लिहिलेला असावा. अशी आख्यायिका प्रचलित आहे की ,यू बादशाह (इ.स.पू.सु. २२००) हे पीत नदीच्या (हवांग हो नदीच्या) काठावर उभे असताना त्यांना एका दैवी कासवाच्या पाठीवर दोन गूढ आकृत्या दिसल्या आणि त्यांपैकी लो-शू ही एक आकृती होती. लो-शू आकृती आ.२ मध्ये दर्शविल्याप्रमाणे I-King मध्ये दिलेली आढळून येते.
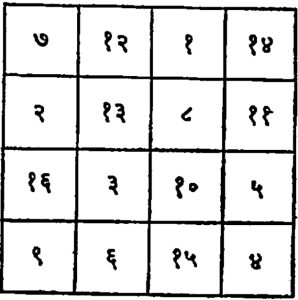
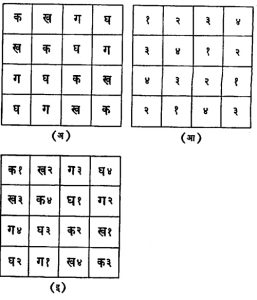
जपानमध्ये या विषयात सतराव्या शतकात लोकांनी विशेष रस घेतल्याचे दिसून येते. चीनमधून मनोरंजक चौरस भारतात आणि लगतच्या आशियातील इतर देशांमध्ये अवतरला परंतु तो चीनमधून सरळ भारतात आला की अरबस्तान व पर्शियामार्गे भारतात आला याबद्दल निश्चित माहिती उपलब्ध नाही. खजुराहो येथील जैन शिलालेखात चौथ्या कोटीचा चौरस आढळून येतो. त्याचा काल साधारणपणे अकराव्या किंवा बाराव्या शतकाचा असावा. हा चौरस आ.३ मध्ये दाखविला आहे. हा चौरस या विषय़ातील प्रगत अभ्यासाचा निदर्शक आहे. कारण एकतर हा चौरस कम कोटीचा आहे व त्याचे सुमारे उपचौरस आ. ४ मध्ये दाशविल्याप्रमाणे एकमेकांशी विशेष लक्षणीय संबंध (प्रत्येक उपचौरसातील दोन दोन घटकांची बेरीज) दाखवितात. भारतामध्ये मनोरंजक चौरसाची माहिती इतिहासपूर्व काळापासून होती, या काही लेखकांच्या मतामध्ये तथ्य आढळून येत नसले तरी तेराव्या शतकाच्या सुमारास भारतीयांनी या विषयात बरीच प्रगती केली होती. इ.स.१३५६ मध्ये नारायण पंडित यांनी आपल्या गणित कौमुदी या ग्रंथामध्ये मनोरंजक चौरसाची पुष्कळ उदाहरणे दिलेली आहेत. भारतीयांनी चौथ्या कोटीच्या चौरसामध्ये विशेष रस दाखविला होता.
|
७ |
१२ |
१ |
१४ |
|
२ |
१३ |
८ |
११ |
|
१६ |
३ |
१० |
५ |
|
९ |
६ |
१५ |
४ |
आ. ३. खजुराहो येथे आढळलेला चौरस.
|
१९ |
१५ |
||||
|
९ |
२५ |
९ |
२५ |
||
|
१५ |
१९ |
||||
|
१९ |
१५ |
||||
|
२५ |
९ |
२५ |
९ |
||
|
१५ |
१९ |
आ. ४. आ. ३ मधील चौरसातील उपचौरसांचे विशेष लक्षणीय संबंध.
मनोरंजक चौरस पुरातन काळापासून चीन, भारत ,तिबेट, मलाया वगैरे पौर्वात्य देशांमध्ये मंत्रतंत्र विद्येमध्ये वापरण्यात येत असे. आ. १ मध्ये दिलेला चौरस भविष्यकथानकरिता ज्योतिषी वापरीत असत. अशा चौरसात काही दैवी शक्ती आहे असे मानण्यात आल्यामुळे त्यांचा उपयोग औषधीपात्र, मंत्रसिध्द ताईत वगैरे वस्तूमध्ये करण्यात येत असे. काही चौरसांना अशुभ व काहींना शुभ मानण्यात येत असे. ज्यू लोकांनी लो शूचा धार्मिक चिन्ह म्हणून उपयोग केला. इ.स.९०० च्या सुमारास एका अरबी ग्रंथामध्ये तिसर्या कोटीचा मनोरंजक चौरस सुलभ प्रसूतीकरिता मांत्रिक तोडगा म्हणून दिलेला आहे. भारतीयांमध्ये चौथ्या कोटीचा मनोरंजक चौरस शुभ मानला जात असे व तो मंत्रसिध्द ताईतामध्ये वापरला जात असे. कला क्षेत्रामध्ये मनोरंजक चौरसमनोरंजक चौरसाचा पहिला वापर आलब्रेक्त ड्यूरर (१४७१-१५२८) यांच्या मेलँकोलिया नावाच्या प्रसिध्द उत्कीर्ण कलाकृतीत केलेला आढळून येतो.
मोठमोठ्या गणितज्ञांनी मनोरंजक चौरसामध्ये रस घेतला व त्यांच्या कामगिरीमुळे मनोरंजक चौरसांना ⇨गट सिध्दांत .जालक, लॅटिन चौरस.⇨निर्धारक वगैरे गणिताच्या विशेष शाखांमध्ये स्थान प्राप्त झाले. तरीही मनोरंजक चौरस रचण्यामध्ये हौशी मंडळीनी विशेष उत्साहाने भाग घेतला. फ्रँक्लिन चौरस या नावाने प्रसिध्द असलेला १६ कोटीचा चौरस बेंजामिन फ्रँक्लिन यांच्या मते आतापर्यंत जादूगारांनी निर्माण केलेल्या जादूच्या चौरसांमध्ये अत्युकृष्ट जादूंनी भरलेला जादूचा चौरस आहे. या चौरसाबद्दल पुष्कळच निबंध लिहिले गेले आहेत.
चौरसांची संख्या व काही संज्ञा : १ ते प२ या संख्या वापरून तयार केलेला मनोरंजक चौरस हा प कोटीचा प्रमाणित मनोरंजक चौरस होय. सर्व संख्यांच्या बेरजेला प ने भागून येणारी संख्या (म्हणजेच एका स्तंभातील किंवा रांगेतील किंवा कर्णातील संख्यांची बेरीज) ही त्या चौरसाचा स्थिरांक म्हणून ओळखली जाते. अर्थातच ही संख्या (प+प) एवढी असते. एखाद्या चौरसापासून परिभ्रमण व परावर्तन या क्रियांनी निर्माण केलेले चौरस भिन्न मानले जात नाहीत, हे लक्षात घेता तिसर्या कोटीचा प्रमाणित चौरस एकुलता एकच रचता येतो. चौथ्या कोटीच्या एकून चौरसांची संख्या ८८० आहे. ही गोष्ट बर्नार्ड फ्रेनिकल द बेसी यांनी १६९३ मध्ये नजरेस आणली. १९७३ मध्ये संगणकाच्या (गणक यंत्राच्या) साहाय्याने पाचव्या कोटीच्या चौरसांची संख्या २७,५३,०५,२२४ इतकी निर्धारित करण्यात आली आहे. मनोरंजक चौरसातील प्रत्येक संख्या प+१ मधून वजा करून नवीन चौरस तयार केला , तर त्याला पूरक चौरस म्हणतात. हाही चौरस मनोरंजक असतो. मनोरंजक चौरसामध्ये मध्य संख्येला सममित असणार्यार दोन संख्यांची बेरीज प+१ असेल तर त्या चौरसाला सहयोगी किंवा सममित मनोरंजक चौरस म्हणतात.
चौरसामध्ये जे लहान चौरस असतात त्यांना घरे म्हणतात. रांगांना वरून खाली १, २, ३ वगैरे क्रमांक देतात. तसेच स्तंभांना डावीकडून उजवीकडे क्रमांक देतात क आणि (प+१-क) क्रमांक असणार्यां रांगांना (स्तंभाना) पूरक म्हणतात. क क्रमांकाच्या रांगेतील ख वे घर आणि (प+१-क) या क्रमांकाच्या रांगेतील (प+१-ख) वे यांना वितलीय संबधित घरे म्हणतात.
रचना : मनोरंजक चौरसांची रचना, पुष्कळ प्रकारांनी करतात. त्यांतील एक सुलभ पध्दत खाली दिली आहे.मनोरंजक चौरसांच्या रचनेकरिता चौरसांचे तीन प्रकार विचारात घ्यावे लागतात. (१) विषम कोटीचे चौरस (२) २(२प+१) अशा समकोटीचे चौरस आणि (३) ४ प अशा सम कोटीचे चौरस. या तीन प्रकारांकरिता निरनिराळे नियम पुढे दिले आहेत.
|
१७ |
२४ |
१ |
८ |
१५ |
|
२३ |
५ |
७ |
१४ |
१६ |
|
४ |
६ |
१३ |
२० |
२२ |
|
१० |
१२ |
१९ |
२१ |
३ |
|
११ |
१८ |
२५ |
२ |
९ |
आ. ५. विषम कोटीच्या चौरसाची रचना.
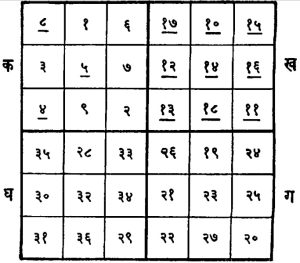
(१)विषम कोटीचा चौरस : असा चौरस रचण्याकरिता एस.दला ल्यूबे यांनी १६९३ च्या सुमारास एक नियम दिला आहे, तो असा. पहिल्या रांगेच्या मधल्या घरामध्ये १ ही संख्या ठेवा. यानंतरच्या संख्या क्रमवार ईशान्य दिशेने चढणार्या् कर्णरेषेमध्ये लिहाव्यात. हे करताना पुढील नियम पाळावेत (अ) उच्चतम रांगेमध्ये पोचल्यावर पुढची संख्या नीचतम रांगेमध्ये ती रांग उच्चतम रांगेच्या वर आहे असे मानून लिहावी. (आ) उजवीकडच्या शेवटच्या स्तंभापर्यंत पोचल्यावर नंतरची संख्या डावीकडच्या स्तंभामध्ये तो उजवीकडच्या स्तंभाच्या पलीकडे आहे असे मानून लिहावी. (इ) पूर्वी संख्या भरलेली आहे अशा घरात वा उजवीकडच्या वरच्या कोपर्या त पोचल्यावर पुढील संख्या लगतच्या खालच्या घरात भरावी. आ. ५ मध्ये पाचव्या कोटीचा चौरस दाखविला आहे. त्याचे निरीक्षण केल्यास वरीन नियम सहज समजून येईल.
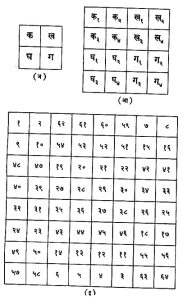
(२)प= २(२ ब+१) असा सम कोटीचा चौरस : असा चौरस रचण्यासाठी आ. ६ मध्ये दाखविल्याप्रमाणे चार भाग पाडा.त्यांना क, ख, ग, घ अशी नावे देऊ. क मध्ये वर दिलेल्या द ला ल्यूवे यांच्या नियमाप्रमाणे एका मनोरंजक चौरसाची १ ते या संख्या वापरून रचना करा. त्याच पध्दतीने ख,ग,आणि घ मध्ये अनुक्रमे क + १ ते २ फ, २फ+१ ते ३फ आणि ३फ +१ ते ४ फ अशा संख्या वापरून मनोरंजक चौरसांची रचना करा.तयार झालेल्या चौरसामध्ये स्तंभाची बेरीज तीच आहे हे सहज पडताळून पहाता येईल. क मधील मधल्या रांगेतील डावीकडील एक संख्या सोडून व संख्या घ्या, तसेच इतर रांगातील डावीकडून ब संख्या ध्या व या सर्व संख्यांची घ मधील डावीकडून ब+२ स्तंभांतील संख्यांची ग मधील संख्याबरोबर अदलाबदल करा. तयार होणारा नवीन चौरस हा इच्छित प =२ (२ब+१) कोटीचा मनोरंजक चौरस होय. आ. ६ मध्ये क व ख मधील ज्या संख्यांची बदली करावयाची आहे त्या अधोरेखित केल्या आहेत. वरील पध्दत रॅल्फ स्ट्रेची यांनी शोधून काढली.
|
८ – |
१ |
६ |
१७ – |
१० – |
१५ – |
|
३ |
५ – |
७ |
१२ – |
१४ – |
१६ – |
|
४ – |
९ |
२ |
१३ – |
१८ – |
११ – |
|
३५ |
२८ |
३३ |
२६ |
१९ |
२४ |
|
३० |
३२ |
३४ |
२१ |
२३ |
२५ |
|
३१ |
३६ |
२९ |
२२ |
२७ |
२० |
आ. ६. प = २ ( २ब + १ ) अशा सम कोटीच्या चौरसाची रचना.
(३) प = ४ व कोटीचा चौरस : अशा चौरसाच्या रचनेकरिता फर्थ यांनी १८८९ मध्ये पुढील पध्दत शोधून काढली. १ ते प२ या संख्या क्रमवार प्रत्येक रांगेमध्ये डावीकडून उजवीकडे आणि रांगा वरून खाली घेऊन लिहा. चौरस पूर्वीप्रमाणेच क,ख,ग आणि घ अशा चार भागांत विभागा. या चार भांगाचेही पुन्हा चार सारख्या भागांत विभाजन करा [आ.७ (अ) व (आ) ] आता क २ व क३ यांमधील संख्यांची त्यांच्य़ाशी वितलीय संबंधीत ग मधील संख्याबरोबर अदलाबदल करा. तसेच ख१ व ख४ यांमधील संख्याची त्यांच्याशी वितलीय संबंधित घ मधील संख्यांबरोबर अदलाबदल करा. तयार होणारा नवीन चौरस हा इच्छित मनोरंजक चौरस होय.आ. ७ (इ) मध्ये आठव्या कोटीचा मनोरंजक चौरस वरील नियम वापरून तयार केला आहे.
|
क १ |
क २ |
ख १ |
ख १ |
|
क ३ |
क ४ |
ख ३ |
ख ४ |
|
घ १ |
घ २ |
ग १ |
ग २ |
|
घ ३ |
घ ४ |
ग ३ |
ग ४ |
( अ )
|
क |
ख |
|
घ |
ग |
( आ )
|
१ |
२ |
६२ |
६१ |
६० |
५९ |
७ |
८ |
|
९ |
१० |
५४ |
५३ |
५२ |
५१ |
१५ |
१६ |
|
४८ |
४७ |
१९ |
२० |
२१ |
२२ |
४२ |
४१ |
|
४० |
३९ |
२७ |
२८ |
२९ |
३० |
३४ |
३३ |
|
३२ |
३१ |
३५ |
३६ |
३७ |
३८ |
२६ |
२५ |
|
२४ |
२३ |
४३ |
४४ |
४५ |
४६ |
१८ |
१७ |
|
४९ |
५० |
१४ |
१३ |
१२ |
११ |
५५ |
५६ |
|
५७ |
५८ |
६ |
५ |
४ |
३ |
६३ |
६४ |
( इ )
आ. ७. प = ४ ब या कोटीच्या चौरसाची रचना
परिवेष्टित चौरस : कोणत्याही प कोटीचा मनोरंजक चौरस रचण्याकरिता बी. फ्रेनिकस यांनी एक सर्वसाधारण पध्दत सुचविली आहे. प कोटीचा चौरस रचण्याकरिता प्रथम (प-२) कोटीचा चौरस रचावयाचा. या चौरसाच्या प्रत्येक घटकामध्ये (२प-२) ही संख्या मिळवावयाची आणि नंतर १,२ …. (२प-२) या न वापरलेल्या संख्या, तसेच त्यांच्या प२ प२-१ ….. (प२-२प+३) या पूरक संख्या सीमेवरील ४ (प-१) घरांमध्ये अशा तर्हेने भरा वयाच्या की, प्रत्येक रांगेची, स्तंभाची व कर्णाची बेरीज प एवढी होईल. आता फक्त सीमेवरील रांग व स्तंभ यांचीही बेरीज तेवढीच होईल हे पहावयास हवे. ही गोष्ट प्रयत्न-प्रमाद पध्दतीने साधावी लागते. सीमेवरील संख्या लिहिण्याकरिता काही नियमही तयार करण्यात आले आहेत. मात्र ते पुष्कळ गुंतागुंतीचे आहेत.आ. ८ मध्ये तिसर्या कोटीच्या चौरसापासून पाचव्या कोटीचा चौरस तयार करून दाखविला आहे.
|
२ |
२५ |
२३ |
७ |
८ |
|
४ |
१६ |
९ |
१४ |
२२ |
|
२१ |
११ |
१३ |
१५ |
५ |
|
२० |
१२ |
१७ |
१० |
६ |
|
१८ |
१ |
३ |
१९ |
२४ |
आ. ८. तिसऱ्या कोटीच्या चौरसापासून तयार केलेला पाचव्या कोटीचा परिवेष्टित चौरस.
व्यापक-कर्ण चौरस : ज्याचौरसामध्ये नेहमीच्या रांग, स्तंभ, कर्ण व यांच्या बेरजेव्यतिरिक्त खंडित कर्णाची (एक आंशिक कर्ण व त्याचा पूरक समोरच्या कोनातील आंशिक कर्ण मिळून खंडित कर्ण तयार होतो).बेरीजही तीच येते अशा चौरसांना व्यापक-कर्ण चौरस म्हणतात. याचौरसांना नासिक चौरस (ए.एच.फ्रॉस्ट या इंग्रज धर्मप्रसारकांना एकोणिसाव्या शतकात नासिक येथे आढळलेल्या अशा प्रकारच्या चौथ्या कोटीच्या चौरसांना त्यांनी दिलेल्या नावावरून) वा परिपूर्ण चौरस किंवा अघोरी (डायाबॉलिक) चौरस असेही म्हणतात. आ. ९ मध्ये चौथ्या कोटीचा व्यापक-कर्ण मनोरंजक चौरस दाखविला आहे. या चौरसामध्ये कोपर्या्तील संख्या व दुसर्या कर्णाच्या पलीकडील लगतच्या छोट्या कर्णावरील तीन संख्या यांची बेरीच तसेच कोपर्या शेजारील त्या कोपर्यातून जाणार्याो रांग व स्तंभ यांतील लगतच्या दोन संख्या व समोरील कोपर्याचतील अशाच तर्हेयच्या दोन संख्या यांची बेरीज चौरसाच्या स्थिरांकाबरोबर आहे. व्यापककर्ण, मनोरंजक चौरसाच्या व्याख्येवरून दिसून येईल की, अशा चौरसाचे दोन रांगांमधील किंवा दोन स्तंभामधील रेषेने दोन भाग पाडले व त्यांची अदलाबदल केली तर नवा चौरसही व्यापक कर्ण मनोरंजक चौरस होईल. यावरून स्पष्ट होईल की, एक उभी विभागणी व एक आडवी विभागणी करून कोणतीही संख्या एका इच्छित घरामध्ये आणता येईल. ३ किंवा त्याच्या कोणच्याही सम पटीच्या कोटीच्या व्यापक कर्ण मनोरंजक चौरसाची रचना करता येत नाही. तसेच २(३प+१) अशा कोटीच्या व्यापक कर्ण मनोरंजक चौरसाची रचना अशक्य आहे. लो-शू हा तिसर्या् कोटीचा मनोरंजक चौरस सहयोगी आहे. परंतु व्यापक-कर्ण चौरस नाही. चौथ्या कोटीचा मनोरंजक चौरस सहयोगी असू शकेल किंवा व्यापक-कर्ण असू शकले, परंतु त्यामध्ये एकाच वेळी हे दोन गुणधर्म असू शकणार नाहीत. पाचव्या कोटीचा मनोरंजक चौरस मध्यभागी १३ ही संख्या असल्यास (आ.५ ) त्यामध्ये दोन्ही गुणधर्म आढळून येतात.
|
१५ |
१० |
३ |
६ |
|
४ |
५ |
१६ |
९ |
|
१४१ |
११ |
२ |
७ |
|
८ |
१३ |
१२ |
आ. ९. चौथ्या कोटीचा व्यापक-कर्ण मनोरंजक चौरस.
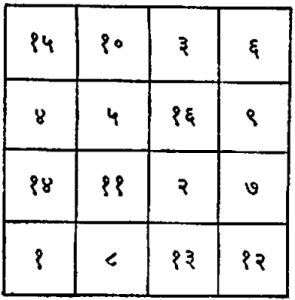
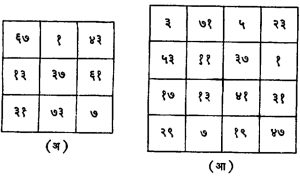
क्रमवार संख्या नसलेले चौरस : आतापर्यंत मनोरंजक चौरस रचण्याकरिता क्रमवार संख्यांचा वापर केला होता.क्रमवार नसलेल्या संख्या वापरून तयार करण्यात आलेल्या मनोरंजक चौरसामध्ये अविभाज्य संख्या वापरून रचलेल्या मनोरंजक चौरसाचे स्थान लक्षणीय आहे, अशा तर्हेनचे दोन चौरस आ. १० (अ) व (आ) मध्ये दाखविले आहेत. आ. १० (अ) मधील चौरस एच.ई.डूडनी व आ. १० (आ) मधील चौरस ई.जी.बी.बेर्घाल्ट व सी.डी शूल्यधाम यांनी तयार केले होते.
|
३ |
७१ |
५ |
२३ |
|
५३ |
११ |
३७ |
१ |
|
१७ |
१३ |
४१ |
३१ |
|
२९ |
७ |
१९ |
४७ |
( अ )
|
६७ |
१ |
४३ |
|
१३ |
३७ |
६१ |
|
३१ |
७३ |
७ |
( आ )
आ. १०. क्रमवार संख्या नसलेले चौरस
दुहेरी मनोरंजक चौरस : प च्या काही मूल्याना (>८) असे मनोरंजक चौरस रचता येतात की, प्रत्येक संख्येचा वर्ग केला, तर तयार होणारा नवीन चौरसही मनोरंजक असतो. अशा चौरसाना दुहेरी मनोरंजक चौरस असे म्हणतात.
मनोरंजक घन : मनोरंजक चौरसाच्या संकल्पनेचा विस्तार करून ती त्रिमिती अवकाशात वापरली, तर मनोरंजक घनाची कल्पना करता येईल. १ ते प संख्या प*प*प त्रिमती समुच्चयामध्ये अशा मांडल्या की, कोणत्याही सरळ रेषेतील प संख्यांची बेरीज तीच येईल, तर त्याला परिपूर्ण मनोंरजक घन म्हणतात. अर्थात अशा सरळ रेषामध्ये लांबी, रूंदी व उंची यांना समांतर रेषा तसेच घनाचे चार कर्ण व जात्य (लंब) छेदाचे कर्ण यांचा समावेश होईल. अशा घनाचा स्थिरांक (प४+प) होईल. तीन व चार कोटीचे मनोरंजक घन रचता येणार नाहीत, हे सिध्द झालेले आहे. ५,६,व ७ कोटीचे मनोरंजक घन आहेत किंवा नाहीत हे निश्चित सांगता येत नाही. आठव्या कोटीचा परिपूर्ण मनोरंजक घन रचता येतो, हे आर.एल. मायर यांनी १९७० मध्ये सिध्द केले. त्यांनी दिलेल्या पध्दतीने पुष्कळच मनोरंजक घन रचता येतात.
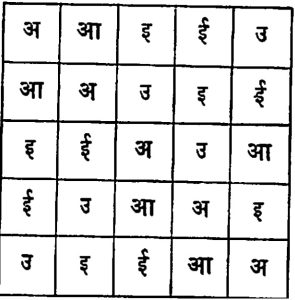
लॅटिन चौरस : वरील रूढ व्याख्येत हा चौरस बसत नसला तरी यामुळे मनोरंजन होत असल्याने या महत्वाच्या चौरसाचा येथे समावेश केलेला आहे.प कोटीच्या चौरसामध्ये प चिन्हे (वा अक्षरे) अशी लिहिली की, प्रत्येक स्तंभ व प्रत्येक रांग यांमध्ये सर्व चिन्हे भिन्न आहेत, तर अशा चौरसाला लॅटिन चौरस म्हणतात. सांख्यिकीमध्ये (संख्याशास्त्रामध्ये) ⇨ प्रयोगांचा अभिकल्प तयार करताना लॅटिन चौरसाचा उपयोग करतात. कोणत्याही कोटीचा लॅटिन चौरस रचणे फार कठीण काम आहे. एका विशिष्ट पध्दतीचे लॅटिन चौरस पुढिल पध्दतीने तयार करता येतील.तळातील रांगेमध्ये ० क, २ क………. (प – १)क या संख्या लिहा व डावीकडील स्तंभामध्ये ० ख,२ख,…..(प-१) ख या संख्या लिहा. आता प्रत्येक घरामध्ये त्याच्याशी संबंधित तळची रांग व डावीकडील स्तंभ यांतील संख्याची बेरीज (मापी प म्हणजे प ने भागून उरलेली बाकी) लिहा. येथे क व प तसेच ख व प यांना समान गुणक नाहीत असे गृहीत धरले आहे. आ. ११ मध्ये पाचव्या कोटीचा लॅटिन चौरस दाखविला आहे.
|
अ |
आ |
इ |
ई |
उ |
|
आ |
अ |
उ |
इ |
ई |
|
इ |
ई |
अ |
उ |
आ |
|
ई |
उ |
आ |
अ |
इ |
|
उ |
इ |
ई |
आ |
अ |
आ. ११. पाचव्या कोटीचा लॅटिन चौरस
दोन लॅटिन चौरस अध्यारोपित केले असता (एकावर दुसरा ठेवला असता) एका चौरसातील कोणतेही एक चिन्ह दुसर्यार चौरसातील प्रत्येक चिन्हाशी एकदाच निगडित होत असेल, तर अशा चौरसातील प्रत्येक चिन्हाशी एकदाच निगडित होत असेल, तर अशा चौरसांना जात्य लॅटिन चौरस म्हणतात. आ. १२ मध्ये चौथ्या कोटीचे दोन जात्य लॅटिन चौरस दाखविले आहेत.
|
क |
ख |
ग |
घ |
|
ख |
क |
घ |
ग |
|
ग |
घ |
क |
ख |
|
घ |
ग |
ख |
क |
|
१ |
२ |
३ |
४ |
|
३ |
४ |
१ |
२ |
|
४ |
३ |
२ |
१ |
|
२ |
१ |
४ |
३ |
( आ )
|
क१ |
ख२ |
ग३ |
घ४ |
|
ख३ |
क४ |
घ१ |
ग२ |
|
ग४ |
घ३ |
क२ |
ख१ |
|
घ२ |
ग१ |
ख४ |
क३ |
( ई )
आ. १२. जात्य लॅटिन चौरस ( अ ) व ( आ ) आणि अध्यारोपित चौरस ( इ ).
परस्पर जात्य लॅटिन चौरसांची रचना ही एक प्रयोगांच्या अभिकल्पातील महत्वाची समचयात्मक समस्या आहे. प्रसिध्द स्विस्व गणितज्ञ लेनई ऑयलर यांनी १७८२ मध्ये असे अनुमान मांडले होते की, ४त+२ (त कोणतीही पूर्णांक संख्या) या कोटीचे परस्पर जात्य लॅटिन चौरस अस्तित्वात असू शकणार नाहीत. राजचंद्र बोस व श.शं. श्रीखंडे या भारतीय गणितज्ञांनी १९६० मध्ये ऑयलर यांच्या अनुमानाशी विसंगत अशा बाबीसाव्या कोटीच्या दोन जात्य लॅटिन चौरसांची रचना केली आणि प =२ (मापी ४) अशा असंख्य मूल्यांना ऑयलर यांचे अनुमान टिकू शकत नाही, असे दाखवून दिले.
संदर्भ : 1. Ball, W.W.R. Mathermatical Recreations Essaus,London, 1959.
2. Smith, D.E. History of Mathematics, 2 Vols, New York, 1951.
ओक, स. अ.
“
