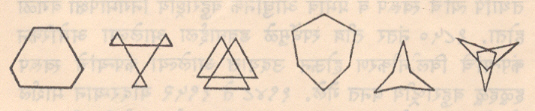बहुभुजाकृति : अवकाशात अ१, अ२ , …, अप हे कोणतेही प बिंदू, त्यांतील कोणतेही तीन बिंदू घेतले तरी ते एका रेषेत असणार नाहीत, अशा प्रकारे घेतले आणि ते अ१ अ२, अ२ अ३, …, अप-१ अप , अप अ१ या प रेषाखंडांनी जोडले, तर तयार होणाऱ्या आकृतीस ‘प-बहुभुजाकृती’ म्हणतात. त्या प बिंदूंना शिरोबिंदू आणि प रेषाखंडांना बाजू म्हणतात. हे सर्व बिंदू एकाच प्रतलात नसतील, तर वितलीय बहुभुजाकृती मिळते, पण जर ते एकाच प्रतलात असतील, तर एकतली बहुभुजाकृती मिळते, प चे मूल्य ३, ४, ५, ६, ….. असेल त्यानुसार अनुक्रमे त्रिकोण, चौकोन, पंचकोन, षट्कोन, … अशी नावे रूढ आहेत. एकतली बहुभुजाकृतीच्या बाजूंनी परिवेष्टित असलेल्या भागास प्रांत म्हणतात. अ१ अ२ अ३ .….. अप अ१ या मार्गाने गेल्यास प्रांत सतत डावीकडे राहत असेल, तर त्या मार्गाची दिशा धन आहे असे समजतात. एखाद्या एकतली बहुभुजाकृतीच्या प्रांतातील कोणतेही दोन बिंदू घेतले असता, त्यांना जोडणारा रेषाखंड पूर्णपणे प्रांतातच समाविष्ट असेल, तर ती बहिर्वक्र बहुभुजाकृती होय. बहुभुजाकृतीतील एक बाजू वगळल्यास, उरलेल्या बाजूंपासून बहुभुजी रेषा मिळते.
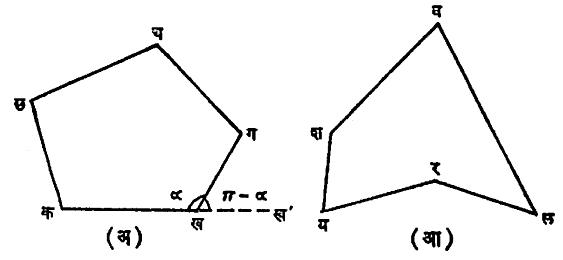
येथे एकतली बहुभुजाकृतीविषयीच फक्त विचार केलेला असल्याने, बहुभुजाकृती असे नुसते म्हटले असता ती एकतली आहे असे यापुढे समजावे. कखग ….बहुभुजाकृतीच्या शिरोबिंदू ख पाशी मिळणाऱ्या कख आणि खग या दोन बाजूंमधील जो कोन सर्वस्वी प्रांतात समाविष्ट असेल त्याला ख शी असलेला अंतर्कोन म्हणतात. याचप्रमाणे इतर शिरोबिंदूंशी असणारे अंतर्कोन मिळतील. बहुभुजाकृती जर बहिर्वक्र असेल, तर तिचा प्रत्येक अंतर्कोन Π पेक्षा (१८०० पेक्षा) कमी असतो पण ती जर बहिर्वक्र नसेल, तर मात्र तिचे काही अंतर्कोन Π हून जास्त असतात. बहिर्वक्र बहुभुजाकृतीची कख बाजू ख’ पर्यंत वाढविली, तर ख’ ख ग या कोनास ख शी असलेला बाह्यकोन म्हणतात. असेच इतर शिरोबिंदूंशी बाह्यकोन मिळतात. कोणत्याही शिरोबिंदूशी अंतर्कोन आणि बाह्यकोन यांची बेरीज Π असते (आ. १).
|
|
|
दोन क्रमागत नसलेल्या बाजू एकमेकींस छेदत नसतील, तर त्या आकृतीला ‘साधी’ बहुभुजाकृती म्हणतात. साधी नसलेली एक बहुभुजाकृती आ. २ मध्ये दाखविली आहे.
क्षेत्रफळ : अ१ अ२ …अप या प-बहुभुजाकृतीच्या प्रांतातील ब हा कोणताही एक बिंदू घेतला, तर बअ१ अ२ , बअ२ अ३, …, बअप-१ अप, बअप अ१ असे प त्रिकोण तयार होतील. या प्रत्येक त्रिकोणाचे योग्य चिन्हयुक्त क्षेत्रफळ काढून, सर्व प त्रिकोणांच्या क्षेत्रफळांची एकत्र बेरीज केली, तर बहुभुजाकृतीचे क्षेत्रफळ मिळते. या क्षेत्रफळांच्या बेरजेचे मूल्य ब च्या स्थानावर अवलंबून नसते, असे दाखविता येईल. बहुभुजाकृतीच्या अ१ , अ२ , … शिरोबिंदूंचे सहनिर्देशक (स्थानदर्शक संस्था) अनुक्रमे (क्ष१,य१), (क्ष२,य२), … असल्यास बहुभुजाकृतीचे क्षेत्रफळ = १/२ (क्ष१य२ – क्ष२य१) + (क्ष२य३ – क्ष३य२) + …..+ (क्षपय१ – क्ष१यप) या सूत्राने मिळते.
बहुभुजाकृतीय आसन्नीकरण : वक्राने परिवेष्टित असलेल्या भागाचे क्षेत्रफळ व वक्राची लांबी यांची आसन्न (अंदाजी) मूल्ये मिळविण्यासाठी बहुभुजाकृती व बहुभुजी रेषा यांचा फार उपयोग होतो. दिलेल्या बंद वक्राने परिवेष्टित भागाचे क्षेत्रफळ काढावयाचे असल्यास. या वक्रावर शिरोबिंदू असतील अशी अंतर्लिखित बहुभुजाकृती घेऊन तिचे क्षेत्रफळ काढावयाचे. या बहुभुजाकृतीच्या सर्वांत मोठ्या बाजूची लांबी क्ष असेल, तर बहुभुजाकृतीच्या बाजूंची संख्या अशी वाढवत न्यायची की, क्ष ⟶ ० होईल. पाहिजे असलेले बंद वक्र परिवेष्टित क्षेत्रफळ = सीमा (बहुभुजाकृतीचे क्षेत्रफळ) या
क्ष ⟶ ०
सूत्राने मिळते [⟶ अवकलन व समाकलन]. पुरातन काळी गणितज्ञांनी Π चे मूल्य मिळविण्यासाठी (वर्तुळाचे क्षेत्रफळ मिळविण्यासाठी) वर्तुळात अंतर्लिखित केलेल्या व वर्तुळाभोवती परिलिखित केलेल्या बहुभुजाकृतींचा उपयोग केला. याच कल्पनेच्या आधाराने क्षेत्रफळ काढण्याची समाकल पद्धती सिद्ध होते. तसेच एखाद्या वक्राची लांबी काढतानाही वक्रावर शिरोबिंदू असलेली बहुभुजी रेषा घेऊन लांबीचे आसन्न मूल्य काढता येते. प्रत्यक्ष लांबीचे सूत्र या आसन्न मूल्याची सीमा घेऊन सिद्ध करता येते. याच प्रकारे वक्राच्या लांबीसाठी समाकलनातील सूत्र सिद्ध होते. [⟶ अवकलन व समाकल].
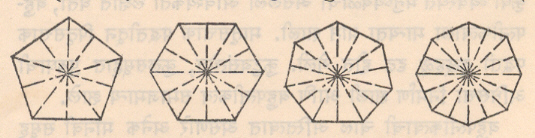
सुसम बहुभुजाकृती : बहुभुजाकृतीच्या सर्व बाजू समान लांबीच्या असून सर्व अंतर्कोन समान असतील, तर तिला सुसम बहुभुजाकृती म्हणतात (आ. ३). अशा बहिर्वक्र सुसम बहुभुजाकृतीचे सर्व शिरोबिंदू ज्या एकाच वर्तुळावर असतात, त्याला परिवर्तुळ म्हणतात. तसेच सुसम बहुभुजाकृतीच्या सर्व बाजू ज्या एकाच वर्तुळाला स्पर्श करतात, त्याला अंतर्वर्तुळ म्हणतात. ही वर्तुळे समकेंद्री असून त्यांच्या समान केद्रांला बहुभुजाकृतीचे केंद्र म्हणतात.
|
|
|
|
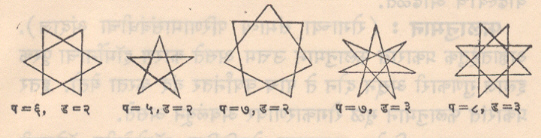
ज्या बहुभुजाकृती बहिर्वक्र नसून सुसम असतात, त्यांचा आकार ताऱ्याप्रमाणे दिसतो व त्यामुळे त्यांना ताराकृती म्हणतात. अशा आकृती (प > ४ असेल तरच) सुसम बहिर्वक्र प-बहुभुजाकृतीपासून पुढीलप्रमाणे तयार करता येतात.
अ१ अ२ … अप या सुसम बहिर्वक्र बहुभुजाकृतीचा अर शिरोबिंदू, अर+ड शिरोबिंदू जोडावयाचा (र = १, २,…), म्हणजे ताराकृती तयार होते. येथे ड हा पूर्णाक प/२ पेक्षा सहान असून ड आणि प यांमध्ये समान अवयव नसेल असा असला पाहिजे. ड ला ताराकृतीच्या दाटपणाचा निर्देशांक किंवा घनता म्हणतात (आ. ४).
वितलीय बहुभुजाकृतींसाठी ही सुसमतेची व्याख्या करता येते. वितलीय सुसम बहुभुजाकृतीच्या बाजूंची संख्या सम असते. अशा आकृतीत शिरोबिंदूचे दोन गट पडतात आणि एकाआड एक शिरोबिंदू एकाच गटात असतात. एका गटातील शिरोबिंदू एका प्रतलावरील वर्तुळावर असतात, तर दुसऱ्या गटातील शिरोबिंदू वरच्या प्रतलाला समांतर असणाऱ्या दुसऱ्या प्रतलावर वरील वर्तुळाला समांतर असलेल्या वर्तुळावर असतात. या दोन्ही प्रतलांना समांतर अशा प्रतलावर अशा वितलीय सुसम बहुभुजाकृतीचा प्रक्षेप केल्यास एकतली सुसम बहुभुजाकृती मिळते
सममिती : प्रतलीय सुसम बहुभुजाकृती पुढीलप्रमाणे स्थानांतरित केल्यास पुन्हा मूळ स्थितिप्रत येते. (१) केंद्रातून जाणाऱ्या व प्रतलाला लंब असणाऱ्या अशा अक्षाभोवती २Π/प च्या पटीतील कोणत्याही कोनातून धूर्णन (परिभ्रमण) केले असता किंवा (२) सममिती अक्षात दर्पण-प्रतिमा घेतली असता हा सममिती अक्ष दोन समोरासमोरचे शिरोबिंदू जोडून किंवा दोन समोरासमोरच्या बाजूंचे मध्यबिंदू जोडून किंवा शिरोबिंदू आणि त्याच्या समोरच्या बाजूचा मध्यबिंदू जोडून मिळविता येतो.
|
|
अर्ध-सुसम बहुभुजाकृती : काही वेळा बाजूंची संख्या सम असलेल्या बहुभुजाकृतीत (१) सर्व अंतर्कोन समान असतात, सर्व शिरोबिंदू एकाच वर्तुळावर असतात पण सर्व बाजू समान नसून एकाआड एक अशा बाजू मात्र समान लांबीच्या असतात किंवा (२) सर्व बाजू समान लांबीच्या असतात, त्या एका वर्तुळाला स्पर्श करतात पण सर्व अंतर्कोन समान नसून, एकाआड एक शिरोबिंदूशी असणारे अंतर्कोन समान मूल्याचे असतात. समान अंतर्कोन असलेल्या शिरोबिंदूचा एक गट एका वर्तुळावर आणि दुसरा गट दुसऱ्या समकेंद्री वर्तुळावर असतो. अशा बहुभुजाकृतींना अर्ध-सुसम बहुभुजाकृती म्हणतात (आ.५).
रचना : फक्त सरळ पट्टी आणि कंपास यांच्या साहाय्याने सुसम बहुभुजाकृती काढण्याची समस्या, पुरातन काळापासून गणितज्ञांनी हाताळली आहे. यूक्लिड यांनी समभुज त्रिकोण, चौरस आणि सुसम पंचकोन यांच्या रचनांविषयी चर्चा केली आहे. के. एन्. गौस यांनी या बाबतीत एक महत्त्वाचे प्रमेय सिद्ध केले, ते असे : प चे सर्व विषम अविभाज्य अवयव भिन्न असून ते २२र + १ या रूपाचे असतील (र हा धन पूर्णाक), तरच पट्टी-कंपास वापरून प-बहुभुजाकृतीची रचना शक्य आहे. अशा रूपातील पहिल्या पाच अविभाज्य संख्या ३, ५, १७, २५७ आणि ६५५३७ ह्या होत. यांखेरीज आणखी अशा संख्या अस्तित्वात नसाव्यात, असे मानण्यास पुरेशी जागा आहे.
संदर्भ : 1. Coxeter, H. S. M. Regular Polytopes, New York, 1963.
ओक, स. ज.
“