प्रेषण मार्ग :विद्युत् शक्तीचे किंवा संदेशाचे संवहन करणाऱ्या संवाहक प्रणालीला प्रेषण मार्ग म्हणतात. या प्रणालीच्या सर्वसाधारण स्वरूपात विद्युत् संकेत तिच्या दोन अग्रांवर आदान केला जातो, तर तिच्यामधून प्रदान दुसऱ्या दोन अग्रांद्वारे तो घेतला जातो. या प्रणालीचे सर्वांत सोपे उदाहरण म्हणजे दोन संवाहक समांतर तारा हे होय. यामध्ये आदान अग्राला प्रत्यावर्ती जनित्र (यांत्रिक शक्तीचे प्रत्यावर्ती म्हणजे ज्याचे मूल्य व दिशा दर सेकंदात वारंवार उलट सुलट बदलते, अशा विद्युत् प्रवाहात रूपांतर करणारे साधन) जोडलेले असते व प्रदान अग्राला विद्युत् भार जोडला जातो (पहा आ. ३). या प्रणालीमध्ये पुढील गोष्टी लक्षात घेण्याजोगत्या आहेत : (१) जनित्राने एका टोकास पुरविलेले विद्युत् वर्चस् (विद्युत् पातळी) एका ठराविक परिमित गतीने तारांवरून मार्गक्रमण करते. या गतीचे मूल्य निरोधित तारांकरिता जवळजवळ प्रकाशाच्या निर्वातातील गतीएवढे म्हणजे ३ X १०१० सेंमी./से. असते. हिचे मूल्य तारांभोवती असलेल्या माध्यमाच्या विद्युत् गुणधर्मांवर अवलंबून असते असे आढळते. या परिमित गतीमुळे प्रदान व आदान विद्युत् वर्चस् यांमध्ये विलंब निर्माण होतो. (२) तारांचा रोध अथवा संरोध [→ प्रत्यावर्ती विद्युत् प्रवाह]वितरित स्वरूपाचा असतो. नेहमीच्या विद्युत मंडलामध्ये प्रवर्तक, धारित्र व रोधक यांसारखे पिंडित (ज्यात विद्युत् वा चुंबकीय ऊर्जा केंद्रित झालेली आहे असे) वा मुख्य व अक्रिय (जे ऊर्जेचे उद्‌गम नाहीत असे) मंडलघटक एकमेकांशी तारांनी जोडलेले असतात. परिगणनासाठी या जोडणाऱ्या तारांचा रोध, प्रवर्तकता इ. नगण्य समजण्यात येतात. या उलट प्रेषक तारांकरीत रोध, प्रवर्तकता, क्षरण संवाहकता (जळून जाणारा अनिष्ट विद्युत् प्रवाह ज्यातून वाहतो अशा मंडलातील निरोधक भागाची विद्युत् प्रवाह वाहून नेण्याची क्षमता), धारणा इ. त्यांच्या सबंध लांबीभर सारख्या प्रमाणात वितरित केले गेले आहेत, हे लक्षात घ्यावे लागते. आदान व प्रदानामध्ये मिळणारा विलंब अथवा प्रेषण मार्गांच्या संरोधाचे वितरित स्वरूप या दोन्ही गोष्टी, प्रेषण मार्गाची लांबी कमी असेल व त्यावरील प्रयुक्त विद्युत् संकेताची कंप्रता (दर सेकंदास होणाऱ्या कंपनांची संख्या) जास्त असेल, तर परिगणनाकरिता आवश्यक ठरतात. याकरिता असा एक सर्वसाधारण निकष वापरण्यात येतो की, जर मार्गाची लांबी विद्युत् तरंगलांबीच्या एक चतुर्थांश भागापेक्षा कमी किंवा बरोबर असेल, तर हे परिणाम विचारात घेणे आवश्यक असते. अशा परिस्थितीत प्रेषण मार्ग विद्युत् दृष्ट्या ‘आखूड’ आहे असे म्हटले जाते व मार्गाच्या विद्युत् कार्याचे वर्णन करण्याकरिता पुढे वर्णन केलेली प्रेषण मार्ग मीमांसा वापरावी लागते. जर मार्गाची लांबी वरील मानकापेक्षा जास्त असेल, तर नेहेमीची प्रत्यावर्ती विद्युत् प्रवाह जालकाकरिता वापरण्यात येणारी मीमांसा चालू शकते. या रीतीमध्ये सबंध मार्गाकरिता रोध, धारणा, संरोध इ. विद्युत् प्रचल (विशिष्ट परिस्थितीत निरनिराळी मूल्ये देता येणाऱ्या स्थिर राशी) पिंडित स्वरूपाचे (मार्गातील त्याच प्रकारच्या एकूण वितरित प्रचलाशी विद्युत् दृष्ट्या तुल्य असलेल्या एकाच प्रचलाच्या वा स्थिरांकाच्या स्वरूपाचे) आहेत असे धरले तरी चालते. घरगुती विद्युत् पुरवठ्याची कंप्रता ५० हर्ट्‌झ धरली, तर त्यापासून मिळणाऱ्या विद्युत् तरंगाची तरंगलांबी सु. ६,००० किमी. एवढी होते. यावरूनही मीमांसा विशेषेकरून उच्च श्राव्य, रेडिओ व सूक्ष्मतरंग कंप्रतेच्या (म्हणजे सु. २०० हर्ट्‌झ ते १०० गिगॅहर्ट्‌झ कंप्रतेच्या) संदेशवहनाकरिता महत्त्वाची आहे हे स्पष्ट होते. (३) मार्गाच्या विद्युतीय गुणधर्मांमुळे आदान व प्रदान अग्री मिळणाऱ्या विद्युत् संकेत मूल्यांत जर लक्षणीय फरक पडत असेल, तरच त्या प्रेषण मार्गास ‘प्रेषण तारा’ ही संज्ञा दिली जाते. या व्याख्येप्रमाणे घरातील दिवा, स्विच व वीजपुरवठा यांना जोडणाऱ्या तारांना प्रेषण मार्ग म्हणता येणार नाही. या प्रणालीमध्ये दूरध्वनी, तारायंत्र संकेताकरिता वापरल्या जाणाऱ्या केबली, विद्युत् पुरवठा तारा, रेडिओ व सूक्ष्मतरंग दळणवळणासाठी वापरल्या जाणाऱ्या केबली, ⇨ तरंग मार्गदर्शक या सर्वांचा समावेश होतो. संवाहकांची संख्या, त्यांची मांडणी, त्याभोवती असणाऱ्या विद्युत् व चुंबकीय क्षेत्रांचा वितरण आकृतिबंध यांनुसार प्रेषण मार्गांचे वर्गीकरण केले जाते. त्यांतील मुख्य प्रकार खालीलप्रमाणे आहेत.
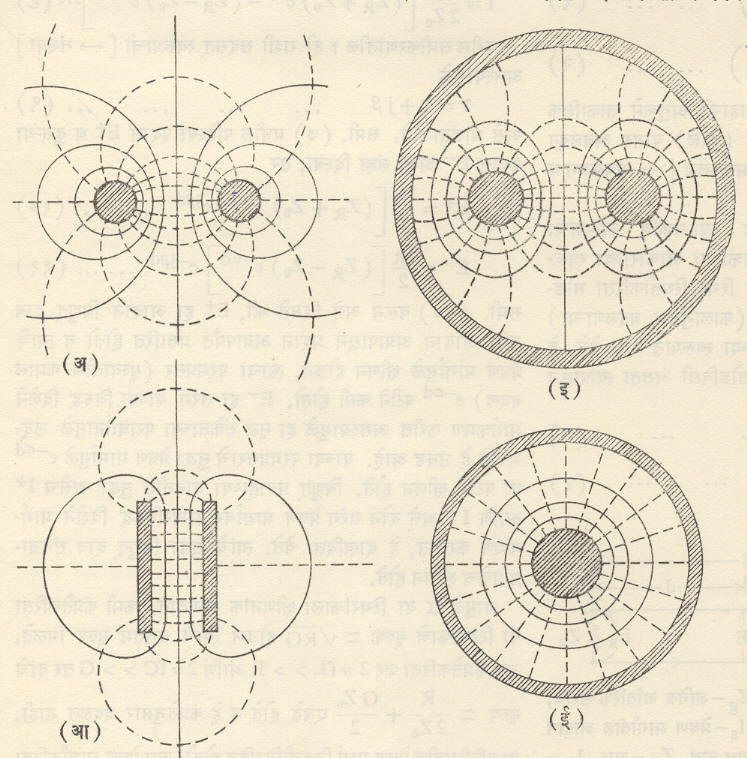प्रकार :अनावृत्त तार प्रेषण मार्ग : या प्रकारात दोन समांतर तारा सर्वसाधारपणे ठराविक अंतरावर निरोधित आधारावर बसविलेल्या असतात. या प्रकाराची योजना विद्युत् शक्ती संवहन अथवा दूरध्वनी, तारायंत्र यांसारख्या कमी कंप्रता संदेशवहनाकरिता वापरली जाते. असे प्रेषण मार्ग बांधण्यास व देखभाल करण्यास अल्प खर्चाचे असतात. यामध्ये नीच व मध्यम कंप्रतांकरिता क्षीणनाचे प्रमाण कमी असते. परस्पर परावर्ती व्यतिकरणामुळे यामध्ये संभाषण संकर (म्हणजे इष्ट संभाषणात इतर अनिष्ट संकेत मिसळल्यामुळे निर्माण होणारा अडथळा, उदा., दूरध्वनी केबलमधील लगतच्या तारांच्या दोन निरनिराळ्या जोड्यांमध्ये एकमेकांचे संभाषण ऐकू येणे) हा दोष निर्माण होतो. उच्च कंप्रता संकेताकरिता त्यापासून होणाऱ्या प्रारणक्षयाचे (तरंगरूपी ऊर्जेच्या क्षयाचे) प्रमाण मोठे असल्यामुळे या प्रकाराचा उपयोग उच्च कंप्रतेकरिता करीत नाहीत. आ. १ (अ) मध्ये या प्रकारच्या प्रेषण मार्गाची संरचना व त्याभोवती मिळणारे विद्युत् चुंबकीय क्षेत्रांचे वितरण दाखविले आहे.
समांतर पट्टिका व संरक्षित जोडी : यांपैकी पहिल्या प्रकारात [आ. १ (आ)] दोन संवाहक पट्टिका जवळ आणल्यामुळे त्यांमधील धारणा वाढून त्यांचा विशेषक संरोध (याचे स्पष्टीकरण पुढे दिले आहे) बराच कमी होतो. संरक्षित जोडी [आ. १ (इ)] मध्ये दोन्ही तारांभोवती एक संवाहक आवरण वापरलेले असते. यामुळे जवळजवळ बसविलेल्या दोन प्रेषण मार्गांमध्ये होणारे व्यतिकरण खूप कमी करता येते.
समाक्ष केबल :[आ. १ (ई)]. यामध्ये प्रेषणमार्गाला त्याच्या संरचनेमुळे संरक्षण मिळून व्यतिकरणाचे प्रमाण अत्यंत कमी असते. तिच्या बाहेर विद्युत् चुंबकीय क्षेत्राचे मूल्य नगण्य असल्यामुळे तिच्यापासून होणारा प्रारणक्षय अगदी कमी असतो या कारणामुळे हिचा उपयोग रेडिओ व सूक्ष्मतरंग कंप्रतेच्या विद्युत् तंरगांचे वहन करण्याकरिता होतो. [→समाक्ष केबल].
विद्युत् चुंबकीय क्षेत्र मीमांसा वापरून असे दाखविता येते की, समांतर प्रेषण तारांच्या द्वारा अनेक रीतींनी वहन होऊ शकते. आतापर्यंतच्या व पुढील वर्णनाकरिता हे वहन फक्त ‘प्रधान’ रीतीने होत आहे, असे गृहीत धरले आहे. या रीतीमध्ये विद्युत् व चुंबकीय क्षेत्र दिशा एकमेंकीशी व प्रेषण मार्गाच्या दिशेस लंबरूप असतात आणि तरंगाचे प्रेषण प्रेषण मार्गाच्या लांबीच्या दिशेत होते. या प्रकारच्या वहनाला ‘अनुप्रस्थ विद्युत् चुंबकीय रीत’ (Transverse electromagnetic, TEM) अशी संज्ञा आहे. प्रेषण तारांमध्ये, कमी कंप्रतेच्या संकेताकरिता याच रीतीचे वहन शक्य असते. जेव्हा संकेत कंप्रता इतकी उच्च असते की, त्याची तरंगलांबी तारांमधील अंतराशी समतुल्य होते, तेव्हा वहनाच्या इतर रीती शक्य होतात. याचा वितार तरंग मार्गदर्शकामध्ये विशेषेकरून केला जातो [→तरंग मार्गदर्शक].
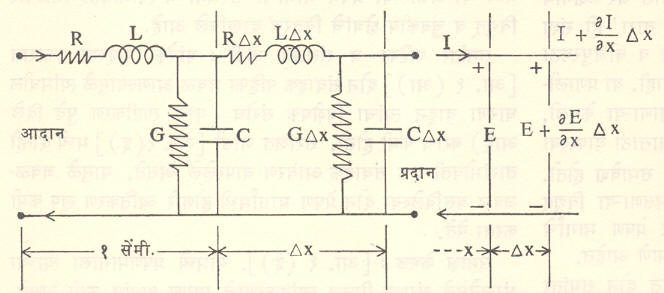प्रेषण मार्ग समीकरणे :‘प्रधान रीत’ वहनाकरिता ⇨अवकल समीकरणे मिळविण्याकरिता आ. २ मध्ये दाखविलेल्या एक सेंमी. व Δx लांबीच्या प्रेषण तारा विभागाकरिता त्यांना समतुल्य असणाऱ्या पिंडित प्रचल मंडलाचा उपयोग करता येतो. या कार्याकरिता प्रेषण मार्गाचे प्राथमिक विद्युतीय स्थिरांक R, L, G, C यांचा वापर केला जातो. R = प्रेषण तारांचा (दोन्ही) प्रती सेंमी. रोध, L= प्रेषण तारांची प्रती सेंमी. प्रवर्तकता, G = प्रेषण तारांमधील निरोधकातून काही क्षरण विद्युत् प्रवाह एका तारेपासून दुसऱ्या तारेपर्यंत येऊ शकतो, तो विचारात घेण्याकरिता हा प्रचल प्रेषण तारांची प्रती सेंमी. संवाहकता दाखवितो, C = दोन तारांमधील प्रती सेंमी. धारणा (हिचे मूल्यतारांमधील अंतर व त्यांमधील निरोधकाच्या विद्युतीय गुणधर्मांवर (अवलंबून राहते). आकृतीत Δx हा विभाग आदान अग्रापासून x अंतरावर आहे असे समजले आहे. येथे हे नमूद केले पाहिजे की, हे सर्व प्रचल खऱ्या अर्थाने स्थिरांक नसून ते विद्युत् संकेताच्या कंप्रतेनुसार थोड्या फार प्रमाणात बदलतात. उदा., रोध R याचे मूल्य ⇨ त्वक् परिणामामुळे कंप्रतेबरोबर वाढते. प्रवर्तकता नीच कंप्रतेच्या तुलनेने मध्यम कंप्रतेला थोडी घटते व यानंतर कंप्रता वाढविल्यास तिच्यामधील चलन महत्त्वाचे नसते.
मंडल सिद्धांताचा उपयोग करून खालील समीकरणे मिळतात.
| ∂E | = – | RI + L | ∂I | … … (१) | ||
| ∂x | ∂x | |||||
| ∂I | = – | GE + C | ∂E | … … (२) | ||
| ∂x | ∂t |
यांमध्ये E आणि I हे विद्युत् दाब व प्रवाहाची अनुक्रमे तत्कालिक मूल्ये दर्शवितात. ती x (अंतर) व t (काल) यांवर अवलंबून असल्यामुळे वरील समीकरणांत आंशिक अवकलज [→अवकलन व समाकलन] वापरलेले आहे.
परिगणनाकरिता विद्युत् दाब संकेत ज्या-वक्रीय स्वरूपाचा (त्रिकोणमितीतील ‘ज्या’ गुणोत्तराच्या वक्राच्या आकाराच्या स्वरूपाचा) आहे, असे समजून ही समीकरणे स्थिर स्थितीकरिता सोडविण्यात येतात. कोणत्याही कालपरिवर्ती (कालानुसार बदलणाऱ्या) प्रचलाचे वर्णन योग्य ज्या-वक्रीय घटकाच्या स्वरूपात देता येते, हे यामागील तत्त्व आहे. वरील समीकरणे सोडविली असता त्यांपासून खाली दिलेली सूत्रे मिळतात.
E=A1 e-rX + A2erx……(३)
| I= | 1 | (A1 e-rX – A2erx) … … (४) |
| Z0 |
येथे A1 आणि A2 हे स्थिरांक असून त्यांची मूल्ये आदान अग्राशी असलेल्या दाब (Es) व विद्युत् प्रवाह ( Is) या मूल्यांवरून ठरविता येतात. याकरिता प्रदान अग्रापाशी असलेल्या ER आणि IR या मूल्यांचा सुद्धा उपयोग करता येतो.
| येथे Z0 = | √ | R + j 2 π f L | … (५) |
| G + j 2 π f C |
f = विद्युत् संकेताची कंप्रता आणि j= √ -1.
Z0 या स्थिरांकाला मार्गाचा विशेषक संरोध म्हणतात. याचे मूल्य प्रेषण मार्गाची लांबी व तिला जोडलेला विद्युत् भार यांवर अवलंबून नसते, या गोष्टी लक्षात घेण्याजोगत्या आहेत.
समी. (३) व (४) मध्ये
r = √ (R + j 2 π f L) ( G + j 2 π f C) … (६)
असून e हा नैसर्गिक लॉगरिथमाचा आधारांक आहे [→ इ].
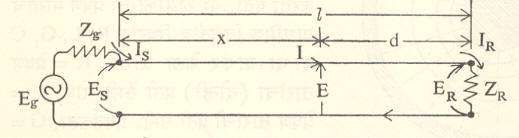
काही वेळा प्रेषण मार्गावरील अंतर आदान अग्रापासून न मोजता त्याच्या प्रदान अग्रापासून मोजणे जास्त सोयीस्कर होते (आ. ३). प्रेषण मार्गाची लांबी lएवढी असेल आणि हे अंतर d समजले, तर समी. (३) व (४) यांचे खालील रूपांतर होते.
| E = | IR | … (७) | |||
| 2 |
| I = | IR | … (८) | |||
| 2Z0 |
वरील समीकरणांतील rही राशी सदसत् स्वरूपाची [→संख्या] असल्यामुळे
r = α + j β … … … … (९)
असे मांडता येते. समी. (७) मधील पहिल्या पदास E+ व दुसऱ्या E–अशा संज्ञा दिल्या, तर
| E+ = |
IR |
[(ZR + Z0) eαd]ejβd |
… (१०) | |||
| 2 |
| E- = |
IR |
[(ZR + Z0) eαd]e-jβd |
… (११) | |||
| 2 |
समी. (१०) वरून असे दिसते की, E+ हा आदान विद्युत् दाब तरंग आदान अग्रापासून प्रदान अग्रापर्यंत प्रसारित होतो व त्याचे प्रेषण मार्गामुळे क्षीणन होऊन, त्याचा परमप्रसर (मूल्यातील कमाल बदल) e-αdपटीने कमी होतो. E– हा तरंग याच्या विरुद्ध दिशेने मार्गक्रमण करीत असल्यामुळे हा मूळ संकेताच्या परावर्तनामुळे उद्‌भवतो हे उघड आहे. याच्या परमप्रसराचे सुद्धा प्रेषण मार्गामुळे e-αd या पटीने क्षीणन होते. विद्युत् प्रवाहाच्या बाबतीत सुद्धा असेच I+ आणि I– असे दोन तरंग प्रेषण मार्गावर परस्परविरुद्ध दिशेने मार्गक्रमण करतात, हे दाखविता येते. त्यांचे सुद्धा विद्युत् दाब संकेताप्रमाणेच क्षीणन होते.
यामुळे αया स्थिरांकाला क्षीणनांक म्हणतात. कमी कंप्रतेकरिता या स्थिरांकाचे मूल्य ≈ √RG होऊन त्याचे लघुतम मूल्य मिळते. उच्च कंप्रतेकरिता जर 2 π f L >> R आणि 2p f C>> Gतर याचे मूल्य
| ≈ | R | + | G Z0 |
| 2 Z0 | 2 |
एवढे होते व हे कंप्रतेनुसार बदलत नाही. या परिस्थितीत प्रेषण मार्ग विकृतीविरहित होतो. ज्या प्रेषण मार्गांकरिता हवा निरोधक म्हणून वापरलेली असते, तेथे G या राशीचे मूल्य सर्वसाधारणपणे नगण्य असते. या कार्याकरिता जेथे रबरासारखे घन निरोधक वापरलेले असतात. तेथे या राशीचे मूल्य १०-५० पटींनीजास्त असते. ejβdया पदामुळे विद्युत् दाब कलेत (एखाद्या यदृच्छ संदर्भाच्या सापेक्ष मोजण्यात येणाऱ्या स्थितीत) पडणारा फरक अथवा विलंब दाखविला जातो. म्हणून βया राशीस ‘कला स्थिरांक’ म्हणतात. तरंगलांबी λ व तरंगवेग किंवा कलावेग (तरंगाबरोबर गतिमान होणाऱ्या व स्थिर कला स्थिती असलेल्या एखाद्या बिंदूचा वेग) v हे β या स्थिरांकापासून खालील सूत्रांवरून मिळतात.
| λ = 2 π / β v = | 2 π f | … … … (१२) |
| β |
प्रेषण मार्गाचा संरोध खालील सूत्रापासून मिळतो.
| Z = | Z0 (ZR + Z0) erd + (ZR – Z0) e-rd | … … … (१३) |
| (ZR + Z0)erd – (ZR – Z0) e-rd |
विद्युत् दाबाकरिता 
यास दाब परावर्तन गुणांक pEम्हणतात, कारण परावर्तित दाब तरंगाचा परमप्रसर आगत तरंगाच्या परमप्रसराच्या पटीत असतो. याचे मूल्य खालील सूत्राने दिले जाते.
| pE | ZR – Z0 | ... … … (१४) |
| ZR + Z0 |
विद्युत् प्रवाहाकरिता परावर्तन गुणांक 
याचे मूल्य 
एवढे असते, असे दाखविता येते. समी. (१४) वरून असे दिसते की, जर Z0 = ZR असेल, तर pE = 0, म्हणजे तरंगाचे प्रदान अग्रापाशी परावर्तन होत नाही. ज्या प्रेषण मार्गाचा शेवट विशेषक संरोधाएवढ्या भाराने होतो, त्यास अनुस्पंदनरहित [→अनुस्पंदन] प्रेषण मार्ग असे म्हणतात. अशा परिस्थितीत जनित्राने आदान अग्राद्वारे पुरविलेली विद्युत् ऊर्जा प्रेषण मार्गाने प्रगत होऊन तिचे भारात पूर्ण अवशोषण होते. अशा वेळी भार ‘सुजोड भार’ आहे असे म्हणतात.
समी. (१३) खालील स्वरूपात सुद्धा मांडता येते.
| Z = Z0 | ZR + Z0 tan h rd | … … (१५) |
| Z0 + ZR tan h rd |
यावरून असे दाखविता येते की, प्रेषण मार्गाचा प्रदान मंडल संक्षेप केला, तर मार्गाचा आदान संरोध Zsc खालील सूत्राने मिळतो.
Zsc = Z0 tan hrl … … (१६)
जर प्रदान अग्र खुले असेल, तर याचे मूल्य
| Z0c = | Z0 | एवढे होते. … … (१७) |
| tan hrl |
यावरून
Z0 = √ Zsc × Z0c … … (१८)
हे महत्त्वाचे सूत्र मिळते.
R, L, G, C यांना मागे नमूद केल्याप्रमाणे प्रेषण मार्गांचा प्राथमिक स्थिरांक म्हणतात, तर त्यांपासून मिळणाऱ्या Z0, α, β,vव λ यांना त्याचे द्वितीयक स्थिरांक म्हणतात.
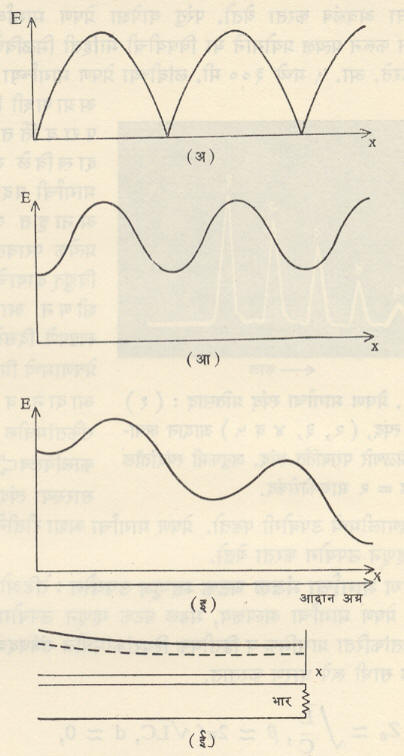
स्थिर तरंग:प्रेषण मार्गाच्या शेवटी सुजोड भार नसेल, तर प्रदान अग्रापाशी विद्युत् तरंगाचे परावर्तन होते. प्रदान अग्रापाशी येणाऱ्या सर्व ऊर्जेचे भार अवशोषण करू शकत नाही. उरलेली ऊर्जा परावर्तन तरंगाच्या स्वरूपात आदान अग्राकडे परत पाठविली जाते. या दोन तरंगांच्या अध्यारोपणामुळे (एकमेकांवर पडण्यामुळे) स्थिर तरंग निर्माण होतात. त्यामुळे (शिखर मूल्याने अथवा वर्ग माध्य मूळ मूल्याने म्हणजे सर्व मूल्यांचे वर्ग करून त्यांची सरासरी घेऊन मग तिचे वर्गमूळ काढून मिळणाऱ्या मूल्याने दर्शविलेल्या) विद्युत् दाबाची प्रेषण मार्गाच्यानिरनिराळ्या ठिकाणी निरनिराळी मूल्ये मिळतात. आ. ४ मध्ये काही ठराविक परिस्थितीत मिळणारे विद्युत् दाबाचे वितरण दाखविले आहे.
विद्युत् दाब स्थिर तरंग गुणोत्तर VSWR (Voltage Standing-Wave Ratio) ही राशी खालील सूत्राने दर्शविली जाते.
| VSWR= | ^ | = | ^ ^ | = | … (१९) | |
| E max | E+ + E– | 1 + pE | ||||
| ^ | ^ ^ | 1 – pE | ||||
| E min | E+ – E– |
येथे 
यांनी शिखर विद्युत् दाबाचे महत्तम व लघुतम मूल्य दर्शविले आहे.
VSWR या राशीला अर्थ प्राप्त होण्याकरिता प्रेषण मार्ग क्षीणन नगण्य असावे लागते, हे वरील आकृतीवरून स्पष्ट होते. याकरिता
2 π f L >> R आणि 2 π f C >> G …(२०)
या अटी पूर्ण होणे आवश्यक असते. व्यावहारिक प्रेषण मार्गाच्या बाबतीत या अटी सर्वसाधारणपणे रेडिओ कंप्रतेकरिता पुऱ्या केल्या जातात. त्यामुळे VSWR चे मापन या कंप्रतेच्या बाबतीतच महत्त्वाचे ठरते. ही सहज मोजण्याजोगी राशी असल्यामुळे तिच्यापासून परावर्तन गुणांकाचे मूल्य मिळवता येते.
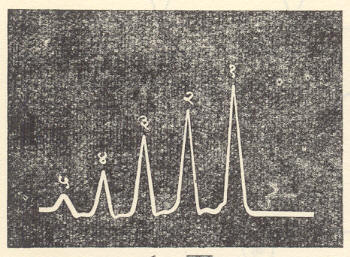अस्थायी स्पंद प्रसरण :(१) व (२) या समीकरणांचे अस्थायी निर्वाह (उत्तरे) गणितीय रीत्या काढण्याकरिता पायरी फलन प्रतिसाद पद्धतीचा अवलंब करता येतो. परंतु यापेक्षा प्रेषण मार्गावर स्पंद आदान करून प्रत्यक्ष प्रयोगाने या विषयीची माहिती मिळविणे जास्त सोपे ठरते. आ. ५ मध्ये ३०० मी. लांबीच्या प्रेषण मार्गाच्या आदान अग्रापाशी मिळणारे परावर्तीत स्पंद दाखविले आहेत. मार्गाची प्रदान अग्रे अनावृत आहेत. प्रत्येक परावर्तनानंतर विद्युत् दाबाचे होणारे क्षीणन आकृतीत स्पष्टपणे दिसते. स्पंद प्रेषणामध्ये मिळणारा आदान व प्रदान संकेतांमधील विशेषक कालविलंब ⇨रडारसारख्या स्पंद संदेशवहन प्रणालीमध्ये उपयोगी पडतो. प्रेषण मार्गाचा अशा रीतीने विलंब मार्ग म्हणून उपयोग करता येतो.
प्रेषण मार्गाचा मंडल घटक म्हणून उपयोग :रेडिओ कंप्रतांकरिता प्रेषण मार्गाचा अल्पक्षय, मंडल घटक म्हणून उपयोग होतो. या कंप्रतांकरिता प्राथमिक व द्वितीयक स्थिरांकांमधील संबंधदर्शक सूत्रे खालील साधी रूपे धारण करतात.
| Z0 ≈ | √ | L | , β ≈ 2 π f √ LC, d ≈ 0, v = | 1 | … (२१) |
| C | √ LC |
याचा अर्थ असा होतो की, प्रेषण मार्ग वापरल्यामुळे ZR या राशीचे ZS मध्ये रूपांतर होते. याकरिता काही प्रकार महत्त्वाचे आहेत.
मंडल संक्षेपित मार्गाकरिता 
म्हणजे Zs चा संरोध प्रवर्तनी स्वरूपाचा होतो.
मंडल खुले अथवा खंडित असल्यास 
म्हणजे Zsहा संरोध धारणी प्रकारचा होतो.
प्रेषण मार्गाची लांबी चतुर्थांश तरंग लांबीएवढी असल्यास
| Zs= | Z02 | … … … (२३) |
| ZR |
जर प्रेषण मार्गाचा मंडल संक्षेप केला असेल, तर Zs याचे मूल्यअती उच्च होते. अशा प्रेषण मार्गाचे गुणधर्म अनेकसरी अनुस्पंदन मंडलाप्रमाणे असतात. याकरिता R गुणांकाचे (साठणारी ऊर्जा व नष्ट होणारी ऊर्जा यांच्या गुणोत्तराचे) मूल्यही खूप उच्च प्रतीचे असते. या प्रेषण मार्गाचा संरोध हा मार्गाची लांबी तरंगलांबीपेक्षा कमी असेल, तर प्रवर्तनी व मार्ग लांबी तरंगलांबीपेक्षा जास्त असेल तर धारणी स्वरूपाचा असतो.
आंतरिक संरोध Zg असलेल्या जनित्राला ZR या शुद्ध रोधाला शक्ती पुरवायची असेल, तर सुजोडणीकरिता Z0 = √ Zg·ZRया विशेषक संरोधाचा प्रेषण मार्ग जोडावा असे दाखविता येते. या उदाहरणावरून चतुर्थांश तरंगलांबी प्रेषण मार्गाच्या विविध उपयोगांचे स्वरूप लक्षात येते.
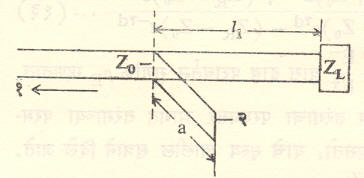संरोध सुजोडीकरण पद्धती : अती उच्च व सूक्ष्मतरंग कंप्रतांना संरोध सुजोडीकरणासाठी वापरण्यात येणारी खुंटयुक्त संरोध सुजोडीकरण पद्धत आ. ६ मध्ये दाखविली आहे. भारापासूनचे अंतर l1आणि खुंट लांबी a यांची मूल्ये अशा तऱ्हेने निवडली जातात की, मंडल संक्षेप करणाऱ्या खुंटाच्या संरोधामुळे निर्माण होणारे परावर्तित तरंग आणि भार संरोधामुळे निर्माण होणारे परावर्तित तरंग यांचे परमप्रसर समान मूल्याचे असतील पण त्यांच्या कला मात्र परस्पर
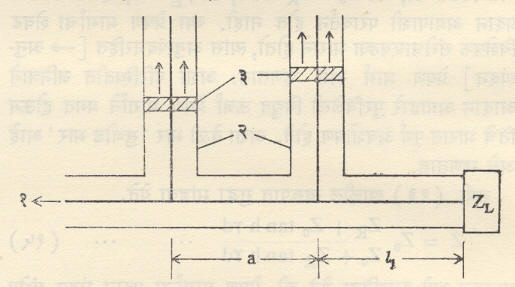विरुद्ध असतील. ही मूल्ये पी.एच्. स्मिथ यांनी तयार केलेल्या तक्त्यावरून सुलभतेने ठरविता येतात. दुसऱ्या प्रकारची दोन खुंटयुक्त संरोध सुजोडीकरण पद्धत आ. ७ मध्ये दाखविली आहे. यामध्ये दोन खुंटांच्या व दट्ट्यांच्या साहाय्याने प्रयत्न-प्रमाद पद्धतीने सुजोडीकरण करता येते. वरील दोन्ही पद्धती समाक्ष केबल मार्गांसाठीही वापरता येतात.
समाक्ष मार्गांसाठी संरोध सुजोडीकरणाकरिता वापरण्यात येणारी द्विखंड पद्धती आ.८ मध्ये दाखविली आहे. l2 हे खंडांमधील अंतर आहे.
असमांतर प्रेषण मार्ग : या प्रणालीमध्ये नेहमीच्या प्रेषण मार्गाप्रमाणे यातील तारा समांतर न ठेवता, त्यांमधील अंतर सारखे कमी किंवा जास्त केले जाते. याचा उपयोग अती उच्च कंप्रतेकरिता संरोध रोहित्र [→ रोहित्र] म्हणून किंवा मिलिसेकंद अवधिकाल असलेल्या स्पंदांकरिता स्पंद रोहित्र (ज्या – वक्रीय नसलेल्या स्पंदांचा विद्युत् दाब बदलण्याकरिता वापरण्यात येणारे रोहित्र) म्हणून करता येतो.
संदर्भ : 1. Johnson, W.C. Transmission Lines and Networks, Tokyo, 1950.
2. Konnully, G. J. Network Analysis and Transmission, Bombay, 1967.
3. Terman, F. E. Electronic and Radio Engineering, Tokyo, 1955.
शेंडे, अ. वा.; चिपळोणकर, व. त्रिं.