प्रक्षेपण, नकाशाचे

प्रक्षेपण, नकाशाचे : भूपृष्ठावर कल्पिलेल्या अक्षवृत्तांच्या व रेखावृत्तांच्या जाळीची कागदावरील प्रतिकृती किंवा चित्र म्हणजे प्रत्यालेख किंवा प्रक्षेपण होय. भू-गोलावरील म्हणजे पृथ्वीवरील कोणत्याही भूपृष्ठाचा आकार व त्याचे क्षेत्रफळ सपाट कागदावर नकाशाद्वारे दाखविण्यासाठी प्रक्षेपणाचे तंत्र वापरले जाते. मात्र प्रत्यक्ष छायाचित्राप्रमाणे भू-गोलावरील वृत्तांच्या जाळीचे चित्र कागदावर काढणे शक्य नसते तर त्यावरील वृत्तांचे प्रकाशाच्या साहाय्याने प्रक्षेपण केले असता त्यांचे चित्र सपाट पृष्ठभागावर कशा प्रकारे दिसेल, हे विचारात घेऊन तशा स्वरूपाची प्रतिकृती भूमितीच्या वा गणिताच्या आधारे कागदावर काढता येते. या प्रकारच्या प्रतिकृतीत भू-गोल हा त्रिमितीय (गोलाकृती) असल्याने व प्रक्षेपण हे द्विमितीय (सपाट) कागदावर काढावयाचे असल्याने त्यावरील वृत्तांची जाळी ही भू-गोलावरील वृत्तांच्या जाळीसारखी हुबेहुबे ठरु शकत नाही. प्रक्षेपणात अक्षवृत्ते व रेखावृत्ते यांच्या मूळ रचनेत फरक पडतो व त्यांची सापेक्ष दिशाही बदलते. प्रक्षेपणातील अक्षवृत्ते व रेखावृत्ते यांच्या मांडणीमुळे त्यात काही दोष निर्माण होतात. हे दोष कमीत कमी असावेत व भू-गोलावरील जास्तीत जास्त भाग सपाट पृष्ठभागावर शक्यतो बिनचूक व योग्य स्वरूपात दाखविता यावा, यासाठी भू-गोलाचे वेगवेगळ्या तुकड्यांत विभाजन करून प्रत्येक भागासाठी वेगवेगळी प्रक्षेपणे काढली जातात. ही प्रक्षेपणे काढण्यासाठी पृथ्वीचे आकारमान, त्रिज्या, अक्षांश व रेखांश यांच्या प्रामुख्याने विचार केला जातो. त्याचप्रमाणे भू-गोलावरील अक्षवृत्ते व रेखावृत्ते यांचा परस्परसंबंध, त्यांच्यामधील अंतर, ज्याचे प्रक्षेपणचित्र करावयाचे त्या प्रदेशाची आकृती, क्षेत्रफळ, वेगवेगळ्या स्थळांतील अंतरे, त्यांची सापेक्ष दिशा या गोष्टी प्रक्षेपण काढताना विशेष लक्षात घ्यावा लागतात. प्रक्षेपण काढताना त्यामागील हेतूलाही महत्त्व असते. संकल्पित प्रतिकृतीत एखाद्या प्रदेशाचे क्षेत्रफळ बिनचूक दाखविण्याचे उद्दिष्ट आहे की, त्याचा शुद्ध आकार दाखविणे अभिप्रेत आहे, हे लक्षात घ्यावे लागते व त्या दृष्टीने आवश्यक ते गुणधर्म असलेली प्रक्षेपणे वापरली जातात. उदा., ध्रुवावरील व ६०° ते ९०° अक्षांशांतील भागासाठी, हवाईमार्ग दाखविण्यासाठी खमध्य ध्रुवीय केंद्रीय (गोमुखी) प्रक्षेपण क्षेत्रफळाच्या दृष्टीने एक संबंध गोलार्ध नकाशात दाखविण्यासाठी खमध्य ध्रुवीय समक्षेत्र प्रक्षेपण निरनिराळ्या देशांच्या नकाशांसाठी शंकू प्रक्षेपण व उष्ण कटिबंधातील देश दाखविण्यासाठी दंडगोलप्रक्षेपणाचा वापर केला जातो. सागरी संचारासाठी मर्केटरचे प्रक्षेपण मार्गदर्शक ठरते.

 पृथ्वीविषयीच्या संशोधनानुसार तिचा आकार संपूर्ण वाटोळा नसून थोडासा अनियमित आहे. प्रक्षेपणासाठी पृथ्वीची विषुववृत्तीय त्रिज्या विचारात घेतली जाते. ती ६,३७८·२०६४ किमी. लांब आहे: परंतु सामान्यतः ही त्रिज्या ६,४०० किमी. किंवा ६४ कोटी सेंमी मानली जाते. भू-गोल ही पृथ्वीची लहान प्रतिकृती होय. या भू-गोलावरील अक्षवृत्ते आणि रेखावृत्ते एकमेकांना काटकोनात छेदतात. पृथ्वी वाटोळी असल्याने ह्या रेषाही वाटोळ्या आहेत. पृथ्वीच्या आसाला मद्यबिंदूशी काटकोनात छेदणारे प्रतल, पृथ्वीच्या पृष्ठभागाला ज्या बिंदूंत छेदते ते बिंदू जोडणारी रेषा म्हणजेच विषुववृत्त होय. या काल्पनिक वृत्ताने पृथ्वीचे उत्तर गोलार्ध आणि दक्षिण गोलार्ध असे दोन समान भाग पडतात. विषुववृत्ताच्या उत्तरेस ९० व दक्षिणेस ९० अक्षवृत्ते आहेत. ध्रुवाकडे गेल्यास यांची लांबी कमी कमी होत जाते. शेवटी ९०° उत्तर व दक्षिण ही दोन्ही अक्षवृत्ते बिंदुमात्रच असतात.

 पृथ्वीच्या दोन्ही ध्रुवांना जोडणाऱ्या व अक्षवृत्तांना काटकोनात छेदणाऱ्या काल्पनिक रेषांना रेखावृत्ते म्हणतात. रेखावृत्तांपैकी ग्रिनिचमधून जाणारे रेखावृत्त आंतरराष्ट्रीय संकेताने संदर्भ-वृत्त मानण्यात येते, त्याला ‘मूळ रेखावृत्त’ म्हणतात. पृथ्वीवरील कोणत्याही बिंदूचे स्थान त्याने या मूळ रेखावृत्ताच्या पूर्वेकडे अगर पश्चिमेकडे केलेल्या कोनावरून निश्चित होते. मूळ रेखावृत्त हे संदर्भ रेखावृत्त मानून रेखावृत्तांच्या मांडणीप्रमाणे त्याच्या पूर्वेस १८० व पश्चिमेस १८० अशी ३६० रेखावृत्ते आहेत. ही सर्व रेखावृत्ते लांबीने सारखी असतात. विषुववृत्तावर दोन रेखावृत्तांमधील अंतर १११·३२१ किमी. भरते. हे अंतर जसजसे ध्रुवबिंदूंकडे जावे तसतसे कमी होत जाते. स्थूलमानाने भूपृष्ठावर १° अंतरावरील कोणत्याही दोन अक्षवृत्तांमधील अंतर १११ किमी. असते. [⟶अक्षांश व रेखांश].

 नकाशात स्थाननिश्चितीसाठी अक्षवृत्ते व रेखावृत्ते यांचा उपयोग ख्रि. पू. काळातही केल्याचे दिसून येते. त्यातूनच प्रक्षेपणाची कल्पना पुढे आली असावी. नकाशे चित्रित करण्यासाठी प्रक्षेपणांचा उपयोग करण्याची कला ग्रीकांनी अवलंबिल्याचे तत्कालीन काही नकाशांवरून दिसून येते. इ. स. पू. सु. २७६ ते १९४ या काळात एराटॉस्थीनीझने ज्ञात असलेल्या जगाचा नकाशा काढताना ७ अक्षवृत्तांचा व ७ रेखावृत्तांचा उपयोग केल्याचे ग्रांथिक पुरावे आढळतात. त्यानंतर हिपार्कस आणि माराइनस यांनी अक्ष-रेखादी वृत्तांच्या जाळीचा उपयोग नकाशासाठी केला परंतु त्यांतील दोषांवर टॉलेमीने टीका करून आपल्या नकाशात अनुरूप अशी सुधारणा केली (इ. स. दुसरे शतक). त्याने अक्षवृत्ते आणि रेखावृत्ते यांच्या वर्तुळाकार जाळीवर जगाचा नकाशा तयार केला. टॉलेमीच्या काळापासून पंधराव्या शतकापर्यंत या क्षेत्रात फारशी प्रगती झाली नाही. रोमन काळातील नकाशांत अक्षांश-रेखांशांविषयीचा विचार केलेला आढळत नाही. टॉलेमीने तयार केलेल्या नकाशांत सध्याच्या साध्या शंकू प्रक्षेपणासारखी प्रक्षेपणे आढळतात. ग्रीक भूगोलवेत्ता बॉन याच्या प्रक्षेपणातील दोष दूर करून ते सुधारण्याचे प्रयत्न व्हाल्टझेम्यूलरने (१४७० ? ते १५२२ ?) १५०७ मध्ये केले. १४६६ मध्ये जर्मनांनी काढलेल्या ‘ट्रॅपीझफॉर्म’ नकाशांच्या आधारेच फ्लॅमस्टीड प्रक्षेपण तयार करण्यात आले. यानंतरच्या अर्धशतकात जर्मन भूगोलवेत्ता ग्लेरेनस याने खमध्य ध्रूवीय समांतर प्रक्षेपणाचा उपयोग केलेला पहिला नकाशा तयार केला. गेर्‌हार्ट मर्केटर (क्रेमर) (१५१२–९४) या फ्लेमिश भूगोलवेत्त्याने दोन प्रमाण अक्षवृत्ते असलेल्या शंकू प्रत्यालेखाच्या आधारे यूरोपचा नकाशा तयार केला व त्यानेच जगाचा नकाशा (मर्केटर्स वर्ल्ड मॅप) तयार केला. अठराव्या शतकात जर्मन गणिती योहान लँबर्टने (१७२८–७७) गणितीय प्रक्षेपणांत मोलाची भर घातली. एकोणिसाव्या व विसाव्या शतकांत विज्ञानाच्या प्रगतीबरोबरच नकाशाशास्त्रात खूपच प्रगती झाली व प्रक्षेपण तंत्राचा विकास घडून आला.

 प्रक्षेपणांचे वर्गीकरण हे स्थूल मानाने दोन दृष्टींनी केले जाते : (१) प्रक्षेपण काढण्याच्या पद्धतीनुसार, (२) प्रक्षेपणांच्या गुणधर्मांनुसार.

प्रक्षेपण काढण्याच्या पद्धतीनुसार प्रक्षेपणांचे पुढील प्रकार होतात: (अ) खमध्य प्रक्षेपणे : भू-गोलावर कोणत्याही एका ठिकाणी सपाट कागद स्पर्श करून ठेवला असता, प्रकाशक्षेपकाच्या साहाय्याने अगर इतर पद्धतींनी गोलावरील वृत्तांच्या जाळीचे चित्र वा प्रक्षेपण कागदावर काढता येते अशा प्रक्षेपणांना खमध्य प्रक्षेपणे म्हणतात. (आ) दंडगोलाकार प्रक्षेपणे : दंडगोलाकार कागदाचे वेष्टन भू-गोलावर ठेवून त्यावरील वृत्तांच्या जाळीचे प्रक्षेपण कागदावर टाकले असता, जे चित्र मिळेल व कागद सपाट पसल्यानंतर ते जसे दिसेल तशा प्रकारची वृत्तांची मांडणी केला असता, ही प्रक्षेपणे तयार होतात. (इ) शंकू प्रक्षेपणे : शंकाकृती कागद भू-गोलाच्या एखाद्या अक्षवृत्तावर टेकवून ठेवला असता ज्या स्वरूपाचे चित्र मिळेल ते सपाट  कागदावर जसे

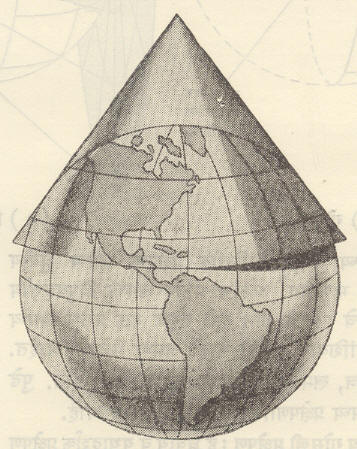दिसेल, त्याची कल्पना करून गोलावरील जाळीची मांडणी केला असता शंकू प्रक्षेपणे तयार होतात. (ई) सांकेतिक प्रक्षेपणे : काही प्रक्षेपणे केवळ विशिष्ट हेतू साध्य करण्यासाठी गणिताच्या आधाराने काढलेली असतात. त्यामुळे प्रक्षेपणांवरील उणिवांचे प्रमाण कमी करता येते व जी गोष्ट दाखवावयाची आहे, तिला उपयुक्त ठरणारे प्रक्षेपणे काढता येते. अशा प्रक्षेपणांस सांकेतिक प्रक्षेपणे म्हणतात.

 प्रक्षेपणांच्या गुणधर्मांनुसार पुढीलप्रमाणे वर्गीकरण केले जाते : (अ) समक्षेत्र प्रक्षेपणे : या प्रक्षेपणांच्या आधारे काढलेल्या नकाशांत प्रदेशांचे क्षेत्रफळ बरोबर दाखविता येते, तथापि प्रदेशांच्या आकारांत मात्र दोष निर्माण होतात. (आ) शुद्ध आकारदर्शक प्रक्षेपणे : या प्रक्षेपणांच्या साहाय्याने नकाशांतील लहान लहान प्रदेशांचा आकार बरोबर ठेवता येतो. मात्र नकाशांचे प्रमाण निरनिराळ्या अक्षवृत्तांवर बदलते. त्यामुळे प्रदेशांच्या क्षेत्रफळांत दोष निर्माण होतात. (इ) समांशीय प्रक्षेपणे : या प्रक्षेपणांच्या आधाराने काढलेल्या नकाशांत त्यांच्या केंद्रांपासून निरनिराळ्या स्थानांच्या दिशा बरोबर दाखविल्या जातात.

(अ) खमध्य प्रक्षेपणे : या प्रक्षेपणांचे प्रमुख तीन उपप्रकार आहेत. गोलावरील ध्रुव बिंदू, विषुववृत्त किंवा तिसऱ्याच एखाद्या बिंदूवर स्पर्शप्रतलाप्रमाणे सपाट कागद टेकवून वृत्तांची जाळी त्यावर प्रक्षेपित केली असता, जी प्रक्षेपणे मिळतात ती अनुक्रमे खमध्य ध्रुवीय, खमध्य विषुववृत्तीय आणि खमध्य तिर्यक असतात. या तीन उपप्रकारांचे प्रत्येकी अनेक उपप्रकार मिळतात. उदा., प्रकाशक्षेपक गोलाच्या केंद्रस्थानी आहे, असे गृहीत धरुन खमध्य ध्रुवीय प्रक्षेपणाचे जे स्वरूप असेल, ते प्रकाशक्षेपक गोलावर स्पर्शबिंदूच्या विरुद्ध टोकाला ठेवल्यास दिसणाऱ्या स्वरूपापेक्षा निराळे दिसेल. प्रकाशक्षेपक अनंत अंतरावर ठेवल्यास ते स्वरूप आणखी बदलेल. अशा रीतीने सपाट कागदाच्या सापेक्षतेने प्रकाशक्षेपकाच्या बदलत्या स्थानानुसार तीन उपप्रकार मिळतात. त्यांना अनुक्रमे खमध्य ध्रुवीय छायाशंकू किंवा त्रैज्य किंवा गोमुखी प्रक्षेपण, खमध्य ध्रुवीय

 समांशीय प्रक्षेपणांचे तीन प्रकार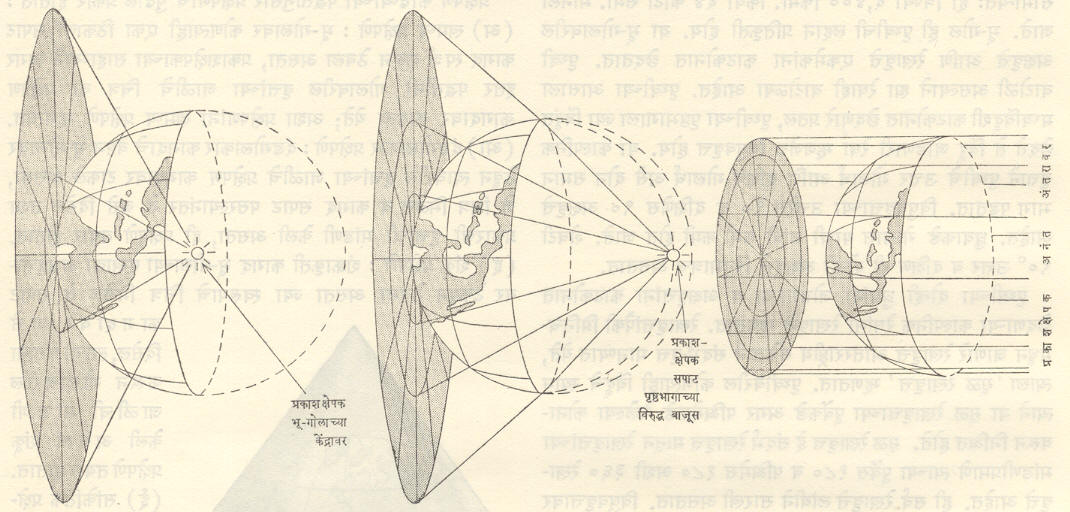

त्रिमितीय प्रक्षेपण, खमध्य ध्रुवीय लंबजन्य प्रक्षेपण असे म्हणतात. अशाच प्रकारे खमध्य विषुववृत्तीय व खमध्य तिर्यक यांचे प्रत्येकी तीन असे एकूण नऊ प्रकार खमध्य प्रक्षेपणांचे होतात. यांशिवाय इतरही काही खमध्य प्रक्षेपणे आहेत. त्यांमध्ये खमध्य समक्षेत्र, खमध्य समांतर प्रक्षेपण इ. मुख्य होत. पुढे काही वैशिष्ट्यपूर्ण खमध्य प्रक्षेपणांविषयी माहिती दिली आहे.

 (१) खमध्य ध्रुवीय गोमुखी प्रक्षेपण : हे ध्रुवीय व यथादर्शक प्रक्षेपण आहे. कागदाचा पृष्ठभाग उत्तर अगर दक्षिण ध्रुवबिंदूवर आणि प्रकाशक्षेपक गोलाच्या मध्यभागी ठेवल्यास कागदावर वृत्तांच्या जाळीचे जसे छायाचित्र मिळते, तसे ते या प्रक्षेपणात भूमितीच्या साहाय्याने काढले जाते. या प्रक्षेपणात विषुववृत्त दाखविता येत नाही, कारण त्याची छाया कागदावर अनंत अंतरावर मिळेल. सर्व अक्षवृत्ते समकेंद्रीय वर्तुळे असतात. रेखावृत्ते ही कोनमापकाच्या साहाय्याने काढल्याने व ती उत्तर ध्रुवबिंदूशी जोडली असल्याने हे एक समांशीय प्रक्षेपण तयार होते. प्रक्षेपणाच्या केंद्रभागापासून दिशा बरोबर दाखविली जाते. या प्रक्षेपणात अक्षवृत्ते व रेखावृत्ते यांची लांबी वाजवीपेक्षा अधिक वाढल्याने गोलावरील त्यांच्या प्रमाणापेक्षा प्रक्षेपणात त्यांचे प्रमाण वाढलेले दिसते. यामुळे प्रदेशाचे क्षेत्रफळ किंवा विस्तार अचूक दाखविणे शक्य होत नाही. याशिवाय अक्षवृत्ते व रेखावृत्ते यांच्या प्रमाणातील वाढही सारखी नसते त्यामुळे प्रक्षेपण समाकारदर्शकही ठरत नाही. मात्र गोलावरील कोणतेही बृहद्‌वृत्त या प्रक्षेपणात सरळ रेषेत मांडले जात असल्याने, कमीत कमी अंतराचे बृहद्‌वृत्तीय मार्ग सरळ रेषा काढून सहज दाखविता येतात. अशा रीतीने या प्रक्षेपणाच्या आधारे काढलेल्या नकाशाचा उपयोग ध्रुव प्रदेशातील मोहिमेसाठी किंवा आकाशमार्ग व नभोवाणीशी संबंधित गोष्टी दाखविण्यासाठी केला जातो.

(२) खमध्य विषुववृत्तीय गोमुखी प्रक्षेपण :हे प्रक्षेपण भूमितीच्या साहाय्याने काढणे जरा अवघड आहे. यात सर्वप्रथम पृथ्वीदर्शक गोल काढला जातो. वर उल्लेखिलेल्या ध्रुवीय गोमुखी प्रक्षेपणाप्रमाणे विषुववृत्तावरील स्पर्शबिंदूपासून रेखावृत्तांचे अंतर आणि स्पर्शबिंदूतूनजाणाऱ्या रेखावृत्तावरील अक्षवृत्तांचे अंतर ठरविण्यासाठी प्रकाशक्षेपकाचा उपयोग करता येतो. मध्य रेखावृत्त विषुववृत्ताला काटकोनात असते व त्यावरील अक्षवृत्तांची अंतरे विषुववृत्तावरील रेखावृत्तांच्या अंतराइतकीच असतात. या प्रक्षेपणाचा उपयोग विषुववृत्तीय भागात पसरलेल्या खंडांचे किंवा देशांचे नकाशे तयार करण्यासाठी होतो. मात्र मध्य रेखावृत्तासभोवती असणाऱ्या भागाचेच चित्र वास्तवतेशी जुळणारे असते.  

(३) खमध्य तिर्यक गोमुखी प्रक्षेपण :हे प्रक्षेपण गणिताच्या तसेच भूमितीच्या साहाय्याने तयार केले जाते. पण रचना बरीच अवघड असते. समशीतोष्ण कटिबंधातील प्रदेश दाखविण्यासाठी याचा उपयोग होतो.

 (४) खमध्य त्रिमितीय प्रक्षेपण : खमध्य त्रिमितीय प्रक्षेपणांचेही तीन उपप्रकार आहेत. गोलावरील ध्रुवबिंदू, विषुववृत्त किंवा त्यांदरम्यानचा कोणताही बिंदू यांवर नकाशाचे केंद्र ठेवले असता हे तीन भिन्न प्रकार मिळतात. प्रत्येक प्रक्षेपणात प्रकाशक्षेपकाचे स्थान गोलावरील स्पर्शबिंदूच्या अगदी उलट बाजूस म्हणजेच प्रतिध्रुवस्थाशी असते. खमध्य ध्रुवीय त्रिमितीय प्रक्षेपणात प्रकाशक्षेपकाचा उपयोग करून अक्षवृत्तांची ध्रुवापासून अंतरे ठरविणे सोपे जाते. त्यांचा उपयोग करून अक्षवृत्ते काढता येतात. या प्रक्षेपणातील रेखावृत्ते ध्रुवबिंदूशी वास्तव कोन करून काढता येतात. या प्रक्षेपणात नकाशाच्या केंद्रभागापासून अक्षवृत्तांमधील अंतर वाढत जाते. विषुववृत्ताचे ध्रुवापासूनचे अंतर गोलाच्या त्रिज्येच्या दुप्पट असते. अक्षवृत्तांची त्रिज्यादेखील गोलावरील त्यांच्या त्रिज्येच्या मानाने अधिक असते. अक्षवृत्तप्रमाण वाढत जाते आणि रेखावृत्तप्रमाणही त्याच प्रमाणात वाढत जाते त्यामुळे हे एक शुद्ध आकारदर्शक प्रक्षेपण बनते. विषुववृत्तीय आणि तिर्यक त्रिमितीय प्रक्षेपणे ही केवळ गणिताच्या आधाराने काढलेली असतात.

(५) खमध्य लंबजन्य प्रक्षेपणे :खमध्य प्रक्षेपणांचा हा तिसरा प्रकार होय. यात प्रकाशक्षेपक अनंत अंतरावर असतो. ध्रुवीय आणि विषुववृत्तीय लंबजन्य प्रक्षेपणे भूमितीच्या साहाय्याने सहज काढता येतात. ध्रुवीय प्रक्षेपणात अक्षवृत्ते समकेंद्र वर्तुळे असतात. केंद्रापासून दूर गेल्यास त्यांमधील अंतर कमी होत जाते. रेखावृत्ते विषुववृत्ताला लंबरूप व एकमेकांशी शुद्ध कोन करतात. रेखावृत्ते मागे दिल्याप्रमाणे खमध्य प्रक्षेपणानुसार काढलेली असतात. विषुववृत्तीय त्रिमितीय प्रक्षेपणाची रीत सोपी आहे. यात मध्य रेखावृत्तावरील अक्षवृत्तांमधील अंतरे आणि विषुववृत्तावरील रेखावृत्तांमधील अंतरे सारखी असतात. इतर अंतरे गणिताच्या साहाय्याने काढून अक्षवृत्ते आणि रेखावृत्ते यांची जाळी तयार करता येते. या प्रक्षेपणातील रेखावृत्ते वक्राकार व अक्षवृत्ते सरळ असतात. या प्रक्षेपणाचा उपयोग पृथ्वीचा गोलार्ध यथार्थपणे दाखविण्यासाठी चांगल्या रीतीने होतो. आफ्रिका, खंड, हिंदी महासागर इ. भूभाग आणि सागरी भाग या प्रक्षेपणाने चांगल्या रीतीने दाखविता येतात. आतापर्यंत वर्णन केलेल्या तीन यथादर्शक प्रकारांशिवाय भूमितीचा उपयोग करून खमध्य समक्षेत्र व समांतर प्रक्षेपणे काढता येतात. त्यांतील समक्षेत्र प्रक्षेपण निरनिराळ्या गोष्टींचे वितरण दाखविण्याच्या दृष्टीने फार उपयोगी पडते.

 (आ) दंडगोलाकार प्रक्षेपणे : गोलाभोवती कागदाचे दंडगोलाकार वेष्टन करून त्यावर वृत्तांच्या जाळीचे प्रक्षेपण केले असता, ज्या प्रकारची प्रक्षेपणे मिळू शकतात तशी किंवा त्यांत आवश्यक तो बदल करून

गणिताच्या साहाय्याने जी प्रक्षेपणे काढली जातात, त्यांना दंडगोलाकार प्रक्षेपणे म्हणतात.

(१) साधे दंडगोलाकार प्रक्षेपण : यालाच ‘प्लेट कारी’ असे म्हणतात. या प्रक्षेपणात विषुववृत्ताची लांबी त्याच्या गोलावरील लांबीबरोबर दाखविलेली असते. ही लांबी २ × π ×त्रिज्या अशी असते. नकाशाचे प्रमाण जर १ : ५०,००,००,००० आहे असे मानल्यास, गोलाची त्रिज्या अर्धा इंच = १·२७ सेंमी. भरते व विषुववृत्ताची लांबी  २ ×३·१४३ ×^१/_२ = ३·१४३ इंच = ७·९८ सेंमी. भरते. इतक्या लांबीची ही रेषा घेतल्यावर, रेखावृत्ते ३०° अंतरावर दाखवावयाची झाल्यास, तिचे सारखे १२ भाग (^३६०/_३० = १२) पाडतात. त्या भागांतून विषुववृत्तास लंबरेषा काढल्या असता, प्रत्येक रेखावृत्त ३०° अंतरावर तयार होते. ही रेखावृत्ते १८०° पश्चिमपासून १८०° पूर्व रेखावृत्तांपर्यंत दाखविली जातात. ०° रेखावृत्त हे संपूर्ण जगासाठी काढलेल्या प्रक्षेपणातील मध्यवर्ती रेखावृत्त असते. या प्रक्षेपणात अक्षवृत्तावरील ३०° रेखावृत्तांतील अंतरे आणि रेखावृत्तावरील ३०° अक्षवृत्तांमधील अंतरे सारखीच असल्याने, मध्यवर्ती रेखावृत्तावर अक्षवृत्तावरील एका विभागाचे अंतर घेऊन उत्तरेस आणि दक्षिणेस खुणा केल्या असता अक्षवृत्तांची स्थाने निश्चित होतात व त्यांतून विषुववृत्ताला समांतर रेषा काढल्या असता प्रक्षेपण तयार होते.

 या प्रक्षेपणात सर्व अक्षवृत्ते विषुववृत्ताइतकीच लांब दाखविली असल्याने विषुववृत्ताखेरीज इतर अक्षवृत्तांवर प्रमाणवाढ होते. ६०° अक्षवृत्तावर ती दुपटीने होते, तर ९०° अक्षवृत्तावर ती अनंत पटींनी होते. या प्रक्षेपणातील रेखावृत्ते सरळ रेषा असून ती अक्षवृत्तांना काटकोन करतात आणि त्यांचे प्रमाणही बरोबर असते. त्यामुळेच हे प्रक्षेपण समक्षेत्रही नाही व शुद्ध आकारदर्शकही नाही. विषुववृत्ताजवळचा प्रदेश या प्रक्षेपणावर चांगला दाखविता येतो. कधीकधी या प्रक्षेपणावर दक्षिण अमेरिका, आफ्रिका यांसारखी विषुववृत्ताभोवती पसरलेली खंडे दाखवितात.

(२) लँबर्टचे दंडगोलाकार समक्षेत्र प्रक्षेपण : प्रक्षेपणात विषुववृत्ताची लांबी २ ×π×त्रिज्या अशी असते. रेखावृत्ते साध्या दंडगोलाकार प्रक्षेपणासारखी काढलेली असतात. पण अक्षवृत्तांचे अंतर गोलावरील त्यांच्या व विषुववृत्ताच्या प्रतलांमधील अंतराइतके असते. विषुववृत्तापासून दूर गेल्यावर अक्षवृत्तांमधील अंतरे कमीकमी होत जातात. अर्थात रेखावृत्तांचे प्रमाणही कमीकमी होत जाते. सर्व रेखावृत्तांची लांबी गोलाच्या व्यासाबरोबर असते. या प्रक्षेपणात विषुववृत्तावर अक्षवृत्तांचे आणि रेखावृत्तांचे प्रमाण बरोबर असते. इतरत्र अक्षवृत्तांच्या प्रमाणात वाढ होते व रेखावृत्तांच्या प्रमाणात घट होते. प्रक्षेपणात कोणत्याही एका ठिकाणी अक्षवृत्तावर ज्या प्रमाणात वाढ होते, त्याच प्रमाणात रेखावृत्तावर घट होत असल्याने प्रदेशाचे क्षेत्रफळ कायम राहते. मात्र त्याचा आकार बिघडतो. तरीही या प्रक्षेपणात उष्ण कटिबंधीय प्रदेशांचा नकाशा, त्यांचा आकार विशेष न बिघडविता दाखविता येतो. या प्रक्षेपणात मध्य व उच्च कटिबंधातील प्रदेश मात्र त्यांच्या आकाराच्या दृष्टीने फार विचित्रपणे दाखविले जातात. म्हणून या प्रक्षेपणाचा उपयोग उष्ण कटिबंधीय वितरणे दाखविण्यासाठी करतात. उष्ण कटिबंधातील भात, ताग, रबर, मसाल्याचे पदार्थ, चहा, कॉफी इत्यादींची क्षेत्रे दाखविण्यासाठी या प्रक्षेपणाचा चांगला उपयोग होतो.

(३) मर्केटरचे प्रक्षेपण : सोळाव्या शतकात गेर्‌हार्ट मर्केटर हा फ्लेमिश भूगोलवेत्ता व नकाशातज्ञ होऊन गेला. त्याने १५३८ मध्ये जगाचा एक नकाशा प्रसिद्ध केला १५४१ मध्ये पृथ्वीचा गोल व १५५४ मध्ये यूरोप खंडाचा नकाशा तयार केला. १५८५ ते १५९० या काळात त्याने तयार केलेले नकाशे प्रसिद्ध आहेत. १५६९ मध्ये जगाचा नकाशा काढण्यासाठी त्याने एक प्रक्षेपण सुचविले. १५९९ मध्ये ब्रिटिश नकाशातज्ञ एडवर्ड राइट याने त्यात थोडी सुधारणा केली. हे प्रक्षेपण ‘मर्केटरचे प्रक्षेपण’ म्हणून प्रसिद्ध आहे. या प्रक्षेपणात आणि दंडगोलाकार समक्षेत्र प्रक्षेपणात पुढील बाबतींत साम्य आहे : (१) विषुववृत्ताची लांबी सारखी आणि शुद्ध असते. (२) सर्व अक्षवृत्ते विषुववृत्ताइतकीच लांब व विषुववृत्ताला समांतर असतात. त्यामुळे विषुववृत्तापासून वाढत्या अंतराबरोबर अक्षवृत्तप्रमाणात वाढ होतजाते. (३) रेखावृत्ते सरळ रेषा असून ती अक्षवृत्तांना काटकोन करतात. विषुववृत्तावर ती सारख्या व शुद्ध अंतरावर असतात.

 मर्केटरचे प्रक्षेपण एका महत्त्वाच्या बाबतीत समक्षेत्र प्रक्षेपणापासून निराळे आहे. या प्रक्षेपणामध्ये कोणत्याही ठिकाणी अक्षवृत्तप्रमाणातव रेखावृत्तप्रमाणात होणारी वाढ सारखी असावी, अशा दृष्टीने अक्षवृत्तांचे विषुववृत्तापासून अंतर ठरविण्यात येते. प्रक्षेपणाच्या या विशिष्ट गुणामुळे कोणत्याही एका ठिकाणी प्रदेशाच्या क्षेत्रफळात जरी वाढ होत असली, तरी त्या प्रदेशाचा आकार कायम राहतो. या प्रक्षेपणात अक्षवृत्तांची विषुववृत्तापासूनची अंतरे गणिताच्या साहाय्याने निश्चित केलेली असतात. शेजारी दिलेल्या कोष्टकाच्या आधारे ती काढता येतात. या प्रक्षेपणात प्रदेशांच्या आकाराच्या शुद्धतेकडे लक्ष दिल्यामुळे नकाशातील कोणतीही सरळ रेषा नेहमी एकच आणि खरी दिशा दाखविते. अशा तऱ्हेने प्रक्षेपणात सतत एकच दिशा कायम दाखविणाऱ्या रेषेस ⇨ऱ्हंब रेषा वा ‘एकदिशनौपथ’(लोक्झोड्रोम) असे म्हणतात. त्यामुळेच या प्रक्षेपणाचा उपयोग वारे, सागरी प्रवाह, व जलमार्ग यांच्या दिशा दाखविणाऱ्या नकाशांसाठी केला जातो.

 कमीत कमी लांबीच्या मार्गाने प्रवास करणे केव्हाही हितकर असते. कोणत्याही दोन बिंदूंमधील कमीत कमी लांबीचा मार्ग म्हणजे त्या दोन बिंदूंमधून जाणारे बृहत्‌ वर्तुळ हे होय. बृहत्‌ वर्तुळाचा मार्ग या प्रक्षेपणात दाखविल्याने असे आढळून येते की, उत्तर आणि दक्षिण गोलार्धांत हा मार्ग वक्राकार दाखविला जाऊन त्या वक्ररेषेची बहिर्वक्र बाजू उ. व द. गोलार्धांत अनुक्रमे उत्तरेकडे आणि दक्षिणेकडे असते. त्यामुळे प्रक्षेपणात कमी अंतर दाखविणाऱ्या या वक्ररेषेच्या मार्गावरून जहाजांनी प्रवास करावयाचे ठरविले, तर त्या जहाजास आपली दिशा पदोपदी बदलावी लागते. प्रवासमार्गाची लांबी कमीच असावी व त्याचबरोबर जहाजास शक्य तितक्या कमी वेळा दिशा बदलावयास लागावी, म्हणून प्रक्षेपणातील दोन बिंदूंमधील बृहत्‌ वर्तुळाचा मार्ग आणि ऱ्हंब रेषेचा मार्ग यांचा समन्वय करण्यात येतो. म्हणजेचबृहत्‌ वर्तुळाच्या मार्गाचे आवश्यक तितके भाग पाडण्यात येतात व ते स्वतंत्र अशा ऱ्हंब रेषांनी जोडण्यात येतात.

  नकाशातील दिशा हा या प्रक्षेपणातील विशेष गुण सोडल्यास हे प्रक्षेपण इतर बाबतींत दिशाभूल करणारे आहे. उच्च अक्षवृत्तांतील प्रदेशाचे क्षेत्रफळ या प्रक्षेपणावर फारच चुकीचे मिळते. प्रत्यक्षात ग्रीनलंड हे क्षेत्रफळाने दक्षिण अमेरिकेच्या एक-दशांश आहे. पण या प्रक्षेपणात मात्र त्याचा विस्तार दक्षिण अमेरिकेपेक्षाही मोठा दिसतो. अलास्का हे राज्य क्षेत्रफळाने अमेरिकेच्या संयुक्त संस्थानांच्या एक-पंचमांश असून या प्रक्षेपणात मात्र ते संयुक्त संस्थानांइतकेच मोठे दिसते. या प्रक्षेपणात ९०° अक्षवृत्त दाखविता येत नाही. कारण त्याचे विषुववृत्तापासून अंतर अनंत असते.

(४) गॉलचे प्रक्षेपण : हे एक सुधारलेले दंडगोलाकार प्रक्षेपण आहे. यात कागदाचा दंडगोल भू-गोलावरील ४५° उ. व ४५° द. या अक्षवृत्तांना स्पर्श करीत आहे, अशी कल्पना केलेली असते. अर्थातच या दोन अक्षवृत्तांमधील गोलाचा भाग दंडगोल कागदाच्या बाहेर आहे, हे ओघानेच स्पष्ट होते.

 या प्रक्षेपणात विषुववृत्ताची लांबी ४५° अक्षवृत्ताच्या परिघाइतकी असते. इतर दंडगोलाकार प्रक्षेपणांसारखे यातही विषुववृत्ताचे पाहिजे तितके भाग पाडून मिळणाऱ्या बिंदूंतून रेखावृत्ते काढतात. त्रिमितीय प्रक्षेपणाप्रमाणे विषुववृत्तावर कोणत्याही एका ठिकाणी प्रकाशक्षेपक ठेवून त्याच्या प्रतिध्रुवस्थ बिंदूंतून जाणाऱ्या रेखावृत्तावर गोलीवरील अक्षवृत्ते प्रक्षेपित केली जातात.

या प्रक्षेपणात ४५° अक्षवृत्ताची लांबी बरोबर दाखविली असल्याने ते प्रमाण-अक्षवृत्त असते. दोन प्रमाण-अक्षवृत्तांच्या (४५° उ. व ४५° द.) मधील अक्षवृत्तांची लांबी वाजवीपेक्षा कमी असल्याने त्यांवरील अक्षवृत्तप्रमाण कमी होते. याउलट प्रमाण-अक्षवृत्तांच्या पलीकडील अक्षवृत्ते वाजवीपेक्षा जास्त मोठी दाखविल्याने त्यांच्यावर प्रमाणवाढ होते.

या प्रक्षेपणात अक्षवृत्ते सारख्या अंतरावर काढली जात नाहीत. त्यांच्यामधील अंतर ध्रुव प्रदेशाकडे वाढत जाते. अर्थात मर्केटरच्या प्रक्षेपणातील वाढत्या अंतराप्रमाणे हे अंतर वाढत नाही. दोन प्रमाण-अक्षवृत्तांमध्ये रेखावृत्तप्रमाण घटते, व प्रमाण-अक्षवृत्तांपलीकडे ध्रुवबिंदूंकडे ते वाढत जाते. प्रक्षेपणातील या वैशिष्ट्यांमुळे हे समक्षेत्र आणि शुद्ध आकारदर्शक प्रक्षेपण होत नाही. खरे म्हणजे दंडगोलाकार समक्षेत्र प्रक्षेपण व मर्केटरचे प्रक्षेपण या दोघांचा समन्वय या प्रक्षेपणात साधला जातो. म्हणून यात असलेले दोष विचारात घेऊनही जगाचे सर्वसाधारण नकाशे तयार करण्याकडे या प्रक्षेपणाचा उपयोग होतो.

(५) मर्केटरचे (आडवे) किंवा गौसचे प्रक्षेपण : या प्रक्षेपणात कागदाचा दंडगोल गोलावरील कोणत्याही बृहत्‌ वर्तुळाला स्पर्श करीत आहे, अशी कल्पना करून आडवे प्रक्षेपण काढले जाते. ईजिप्तसारख्या पूर्व-पश्चिम विस्तार कमी असलेल्या देशांचा शुद्ध आकार दर्शविणाऱ्या नकाशांसाठी या प्रक्षेपणाचा फार उपयोग होतो. ज्या बृहत्‌ वर्तुळाला कागदाचा दंडगोल स्पर्श करीत असतो, ते वर्तुळ या प्रक्षेपणात मध्य रेखावृत्त असते. यात मध्यवर्ती रेखावृत्त व विषुववृत्त ही सरळ रेषांनी व इतर सर्व वृत्ते वक्ररेषांनी दाखविलेली असतात. अक्षवृत्ते व रेखावृत्ते परस्परांना काटकोन करतात. नकाशाच्या केंद्र भागापासून पूर्व-पश्चिमेस तसेच दक्षिण-उत्तरेस प्रमाण वाढत जाते. म्हणून मध्यवर्ती रेखावृत्ताला लागून असलेल्या लहान प्रदेशांचेच क्षेत्रफळ या प्रक्षेपणाच्या मदतीने समाधानकारक दाखविता येते. मध्यवर्ती रेखावृत्तापासून दूर गेल्यास क्षेत्रफळात मोठ्या प्रमाणावर दोष उत्पन्न होतात. मोठ्या प्रमाणावर लहान प्रदेशांचे नकाशे या प्रक्षेपणावर काढावयाचे झाल्यास वृत्तांमधील प्रदेशाचा आकारआयताकार होतो. १ इंचास १ मैल या प्रमाणावर या प्रक्षेपणाच्या आधारे सैनिकी सर्वेक्षण नकाशे काढले गेले आहेत.

 (इ) शंकू प्रक्षेपणे : पूर्व-पश्चिम विस्तार बराच मोठा असलेल्या यूरोप, आशिया, उत्तर अमेरिका आणि ऑस्ट्रेलिया खंडांचे नकाशे काढण्यासाठी या प्रक्षेपणाच्या निरनिराळ्या प्रकारांचा उपयोग करतात. पण खरे म्हणजे समशीतोष्ण कटिबंधातील लहान देशच या प्रक्षेपणावर चांगल्या रीतीने रेखांकित केले जातात.

 (१) एक प्रमाण-अक्षवृत्त असलेले साधे शंकू प्रक्षेपण : या प्रत्यालेखाच्या रचनेत कागदाचा शंकू प्रक्षेपीय भू-गोलावर अशा प्रकारे ठेवला जातो की, शंकूचा शिरोबिंदू हा भू-गोलाच्या ध्रुवबिंदूवर राहील व त्याच वेळी शंकू प्रक्षेपीय भू-गोलावरील एखाद्या अक्षवृत्ताला स्पर्श करील. शंकू ज्या अक्षवृत्ताला स्पर्श करतो त्या अक्षवृत्ताला प्रमाण-अक्षवृत्त म्हणतात. या आधारभूत कल्पनेचा विचार करूनच हे प्रक्षेपण काढले जाते. या प्रक्षेपणात रेखावृत्तप्रमाण बरोबर असते अक्षवृत्तप्रमाण फक्त प्रमाण-अक्षवृत्तावर बरोबर असते. प्रमाण-अक्षवृत्तापासून जसजसे दक्षिणोत्तर अंतर वाढते, तसतशी अक्षवृत्तप्रमाणात वाढ होत जाते कारण यामध्ये प्रमाण-अक्षवृत्त सोडल्यास शंक्वाकृती कागदावरील इतर अक्षवृत्तांची लांबी गोलावरील त्याच अक्षवृत्तांच्या लांबीपेक्षा जास्त भरते. म्हणून हे प्रक्षेपण समक्षेत्रदर्शक नाही किंवा शुद्ध आकारदर्शकही नाही. मात्र प्रमाण-अक्षवृत्ताच्या शेजारील भागातील प्रदेश त्यात बऱ्यापैकी दाखविले जातात.

 या प्रक्षेपणात रेखावृत्ते सरळ रेषा असून ती ९०° अक्षवृत्ताच्या पलीकडून म्हणजेच शंक्वाकृती कागदाच्या शिरोबिंदूतून काढलेली असतात. अक्षवृत्ते समकेंद्रीय वर्तुळाचे चाप असून ती सारख्या अंतरावर काढलेली असतात. निवडलेले प्रमाण-अक्षवृत्त जितके विषुववृत्ताजवळ असते, तितकाच शिरोबिंदूचा कोन कमी होत जातो. रेखावृत्ते जवळजवळ एकमेकांना समांतर होत जातात, अक्षवृत्तांची वक्रता कमी होत जाते आणि ज्या बिंदूतून रेखावृत्ते बाहेर पडतात, तो बिंदू कागदापासून दूर दूर जाऊ लागतो. जेव्हा विषुववृत्त हेच प्रमाण-अक्षवृत्ते असते तेव्हा शंक्वाकृती कागदाचे रूपांतर दंडगोलात होते आणि तदनंतर दंडगोलाकार समांतरित प्रक्षेपण तयार होते. या प्रक्षेपणात गोलाचा सबंध पृष्ठभाग दाखविला जाऊन त्याची लांबी २×π×त्रिज्या आणि रुंदी π×त्रिज्या अशी असते. त्या प्रक्षेपणात रेखावृत्ते उभ्या सरळ रेषा असतात आणि अक्षवृत्ते आडव्या सरळ रेषा असतात. सर्व अक्षवृत्ते समान लांबीची (विषुववृत्ताइतकी लांब) आणि समान अंतरावर असतात. प्रमाण-अक्षवृत्त जसजसे ध्रुवबिंदूजवळ नेण्यात येते, तसतसा कागदाच्या शंकूचा कोन अधिकाधिक मोठा होत जातो आणि जेव्हा प्रमाण-अक्षवृत्त हे ध्रुववृत्तच गृहीत धरले जाते, तेव्हा तो ध्रुवावर स्पर्शरेषेप्रमाणे स्पर्श करतो. त्यावेळी खमध्य ध्रुवीय समांतरित प्रक्षेपण तयार होते.

 (२) दोन प्रमाण-अक्षवृत्तांचे साधे शंकू प्रक्षेपण : या प्रक्षेपणात दोन प्रमाण-अक्षवृत्ते कल्पिलेली असतात. या दोन प्रमाण-अक्षवृत्तांच्या दरम्यानचा प्रदेश बरोबर दाखविला जातो परंतु जसजसे या अक्षवृत्तांपासून दूर जावे, तसतशी प्रदेशाच्या आकारात विकृती निर्माण होऊ लागते. त्यामुळे ज्या प्रदेशाचा नकाशा या प्रक्षेपणाद्वारे काढावयाचा असतो, तेथील प्रमाण-अक्षवृत्तांची निवड अशा दृष्टीनेच केली जाते की, त्या प्रदेशाचा दोन-तृतीयांश भाग हा त्यांच्या दरम्यान असेल. एक-षष्ठांश भाग हा त्या प्रत्येक अक्षवृत्ताच्या बाहेर असेल. उदा., जपानचा विस्तार ३०° उ. ते ४५° उ. आहे. तेव्हा त्याच्या नकाशासाठी दोन प्रमाण-अक्षवृत्त असलेले प्रक्षेपण काढताना ३३° उ. व ४२° उ. ही दोन प्रमाण-अक्षवृत्ते मानल्यास जपानचा नकाशा योग्य प्रकारे तयार होईल.

या प्रक्षेपणात रेखावृत्तांची लांबी अचूक असल्याने रेखावृत्तप्रमाण बरोबर असते. दोन प्रमाण-अक्षवृत्तांची लांबी बरोबर असल्याने त्यांच्यावरील अक्षवृत्तप्रमाण बरोबर असते. पण त्यांच्या बाहेरच्या बाजूंस वाढत्या अंतराबरोबर इतर अक्षवृत्तांवर प्रमाणवाढ झपाट्याने होते. दोन अक्षवृत्तांमध्ये अक्षवृत्तप्रमाणात घट होते. या प्रक्षेपणाच्या द्वारे ज्या प्रदेशांचा दक्षिणोत्तर विस्तार कमी आहे, अशा लहान प्रदेशांचे (विशेषतः समशीतोष्ण कटिबंधातील) नकाशे चांगले काढता येतात. अशा प्रदेशाचे दक्षिणोत्तर सहा सारखे भाग पाडल्यास पहिल्या आणि पाचव्या भागांतून जाणारी अक्षवृत्ते प्रमाण-अक्षवृत्ते म्हणून निश्चित केली जातात त्यामुळे त्यांच्या दरम्यानच्या बाहेरील प्रदेशात अक्षवृत्तप्रमाणात जरी वाढ होत असली, तरी त्यात चुकीचे प्रमाण कमी असते. हीच गोष्ट प्रमाण-अक्षवृत्तांच्या विरुद्ध विभागाकडील घटत्या प्रमाणाच्या बाबतीत लागू पडते. हे प्रक्षेपण समक्षेत्रही नाही किंवा शुद्ध आकारदर्शकही नाही. तरीही यूरोप, आशिया, उत्तर अमेरिका आणि ऑस्ट्रेलिया यांचे नकाशे काढण्यासाठी त्याचा चांगला उपयोग होतो.

(३) शंक्वाकृती समक्षेत्र प्रक्षेपण : वर वर्णिलेल्या दोन प्रक्षेपणांत आवश्यक तो बदल केल्यास हे प्रक्षेपण तयार होते. या प्रक्षेपणात अक्षवृत्तातील अंतर कमी-जास्त करण्यात येऊन रेखावृत्तांची लांबी प्रक्षेपणातील अक्षवृत्तांच्या लांबीच्या प्रमाणात कायम करण्यात येते. कागदाच्या शिरोबिंदूच्या ठिकाणी ध्रुवबिंदूचे स्थान असते. रेखावृत्त-प्रमाण ध्रुवबिंदूकडे वाढत जाते. या प्रक्षेपणालाच लँबर्टचे प्रक्षेपण म्हणतात.

 (४) शंक्वाकृती शुद्ध आकारदर्शक प्रक्षेपण : प्रक्षेपणातील रेखावृत्तांची लांबी ठरविताना त्यांच्यावरील प्रमाणात होणारी वाढ किंवा घट ही त्यांच्या आनुषंगिक अक्षवृत्तांवरील प्रमाणात होणाऱ्या तशाच बदलासारखीच राहिली, तर ते शुद्ध आकारदर्शक प्रक्षेपण तयार होईल. या प्रक्षेपणात ९०° अक्षवृत्त म्हणजे शंकूचा शिरोबिंदू होय. प्रमाण-अक्षवृत्ताच्या दोन्ही बाजूंस प्रमाणवाढ होते. दोन प्रमाण-अक्षवृत्ते असल्यास त्यांच्यामधील भागात प्रमाण घटते. या प्रक्षेपणात कोणत्याही एका बिंदूशी अक्षवृत्तप्रमाण आणि रेखावृत्तप्रमाण सारखेच असते. लँबर्टचे हे दुसरे प्रक्षेपण होय.

 (५) बॉनचे समक्षेत्र प्रक्षेपण : हे फेरफार केलेले एक प्रमाण-अक्षवृत्त प्रक्षेपण आहे. शंक्वाकृती कागदाचा पृष्ठभाग गोलावरील प्रमाण अक्षवृत्ताला स्पर्श करील अशा रीतीने शंकूवर ठेवण्यात येते. साध्या शंक्वाकृती प्रक्षेपणाप्रमाणेच या प्रक्षेपणातही मूळ रेखावृत्तावर सारखे भाग पाडून अक्षवृत्तांसाठी समकेंद्रीय वर्तुळाचे चाप काढण्यात येतात. त्यामुळे रेखावृत्तप्रमाण सर्व ठिकाणी बरोबर असते. प्रक्षेपणातील प्रत्येक अक्षवृत्ताची लांबी तिच्या गोलावरील लांबीशी प्रमाणित करण्यात येते. नंतर तिचे सारखे भाग पाडून अक्षवृत्तांवरील योग्य बिंदू जोडून रेखावृत्ते काढण्यात येतात. त्यामुळे अक्षवृत्तप्रमाणदेखील सर्व ठिकाणी बरोबर असते व हे प्रक्षेपण समक्षेत्रीय असते. प्रक्षेपणात मध्यवर्ती रेखावृत्त सोडल्यास इतर रेखावृत्ते वक्राकार असतात व मूळ रेखावृत्तापासून वाढत्या अंतराबरोबर त्यांच्या वक्रतेचे प्रमाण वाढत जाते. ती अक्षवृत्तांना काटकोन करत नाहीत. म्हणून हे प्रक्षेपण शुद्ध आकारदर्शक नसते. ज्या प्रदेशांचा पूर्व-पश्चिम विस्तार कमी असतो, अशा उपोष्ण आणि समशीतोष्ण कटिबंधातील प्रदेशांचे नकाशे या प्रक्षेपणाने चांगल्या रीतीने काढले जातात.

(६) सॅन्सन-फ्लॅमस्टीड (ज्या वक्रीय) प्रक्षेपण : या प्रक्षेपणात व बॉनच्या प्रक्षेपणात बरेच साम्य आहे. विषुववृत्त हे प्रमाण-अक्षवृत्त धरून जेव्हा वरील प्रक्षेपणासारखी वृत्तांची जाळी काढण्यात येते, तेव्हा हे प्रक्षेपण तयार होते. विषुववृत्तावर उभ्या केलेल्या शंकूचे साहजिकच दंडगोलात रूपांतर होते व विषुववृत्ताचे अनंत त्रिज्येच्या वर्तुळात अगर सरळ रेषेत रूपांतर होते. इतर अक्षवृत्ते याला समकेंद्रीय म्हणजे समांतर रेषाच असतात. ती सारख्या अंतरावर काढलेली असतात, त्यामुळे रेखावृत्तप्रमाण बदलत नाही व त्यांची लांबी गोलावरील त्यांच्या लांबीइतकीच असते. प्रक्षेपणातील मूळ रेखावृत्त अक्षवृत्तांना लंबरूप असते. इतर रेखावृत्ते मात्र वक्राकार असतात. त्यामुळे हे प्रक्षेपण समक्षेत्र असले, तरी शुद्ध आकारदर्शक नसते. प्रदेशांचा आकार, विशेषतः प्रक्षेपणाच्या कडेला, अतिशय विकृत होतो. आफ्रिका आणि दक्षिण अमेरिका या खंडांचे भिंतीवरचे नकाशे व नकाशासंग्रहातील नकाशे या प्रक्षेपणावर काढले जातात. ऑस्ट्रेलिया व पॉलिनीशिया यांचे नकाशेही या प्रक्षेपणाच्या आधाराने काढले गेले आहेत, अर्थात या प्रक्षेपणावर संपूर्ण जगदेखील दाखविता येते. त्यामुळे याचा जागतिक वितरणे दाखविण्यासाठी उपयोग केला जातो.

 (७) बहुशंकू प्रक्षेपण : या प्रक्षेपणात सर्व अक्षवृत्तांची लांबी प्रमाणबद्ध असते. म्हणजेच त्यांच्यातील अक्षवृत्तप्रमाण शुद्ध असते. मध्यवर्ती रेखावृत्तावरही प्रमाण बरोबर असते. अक्षवृत्ते वर्तुळांचे चाप असतात. पण ही वर्तुळे समकेंद्रीय नसतात. प्रत्येक अक्षवृत्त हे प्रमाण-अक्षवृत्त आहे असे मानले जाते. या अक्षवृत्तावरील स्पर्शरेषा व गोलाचा वर वाढविलेला काल्पनिक आस ज्या ठिकाणी छेदतात, त्या बिंदूपासून साध्या शंकू प्रक्षेपणात दाखविल्याप्रमाणे प्रत्येक अक्षवृत्त काढले जाते. अशा रीतीने गोलावरील आसावर निरनिराळ्या अक्षवृत्तांसाठी निरनिराळे बिंदू मिळतात व त्या बिंदूंपासून त्या त्या अक्षवृत्तांचे चाप प्रक्षेपणात काढले जातात. मध्यवर्ती रेखावृत्तावर दोन अक्षवृत्तांतील अंतर सारखे असते. त्याच्या दोन्ही बाजूंना मात्र अक्षवृत्तांमधील अंतर वाढत जाते. म्हणजेच मध्यवर्ती रेखावृत्तावर अचूक असणारे रेखावृत्तीय प्रमाण दोन्ही बाजूंस वाढते. त्यामुळे हे प्रक्षेपण समक्षेत्र किंवा शुद्ध आकारदर्शक नसते.

 प्रक्षेपणाची मर्यादा उत्तर ध्रुवबिंदू आणि विषुववृत्तापर्यंत वाढविता येते, हे या प्रक्षेपणातील तुटक रेषा दाखविते. दक्षिण गोलार्धासाठी प्रक्षेपण तयार करण्याचे झाल्यास त्याच प्रकारचे दुसरे प्रक्षेपण काढावे लागेल. प्रक्षेपण समक्षेत्र अगर शुद्ध आकारदर्शक नसले, तरी प्रत्येक अक्षवृत्त प्रमाण-अक्षवृत्त मानल्याने प्रक्षेपण मध्यवर्ती रेखावृत्त कायम ठेवून तुकड्यातुकड्यांनी काढल्यास असे अनेक तुकडे अक्षवृत्तावर उत्तर-दक्षिण दिशेत सहज जोडले जाऊ शकतात. त्यामुळे मोठ्या प्रमाणावरील नकाशे काढून त्यांची जुळणी करण्याची आवश्यकता भासल्यास अशा प्रक्षेपणाचा उपयोग करणे योग्य ठरते.

 बहुशंकू प्रक्षेपणाचा उपयोग १ : १०,००,००० या प्रमाणावर आंतरराष्ट्रीय नकाशा तयार करण्यासाठी करण्यात यावा अशी शिफारस सुरुवातीस नकाशातज्ञांनी केली होती. तथापि १९०९ मध्ये त्यासाठी नेमलेल्या समितीने या प्रक्षेपणात सुधारणा करून नवीन प्रक्षेपण सुचविले. या सुधारित प्रक्षेपणात दोन स्वतंत्र नकाशांच्या उत्तर-दक्षिण कडादेखील एकमेकींना जुळाव्या म्हणून प्रक्षेपणातील रेखावृत्ते सरळ करण्यासाठी योग्य ती उपाययोजना करण्यात आली. त्यामुळे मोठ्या प्रमाणावर काढलेले स्थलवर्णनात्मक नकाशे अभ्यासासाठी एकत्र जोडता येणे शक्य झाले. 

बहुशंकू प्रक्षेपणात मध्यवर्ती रेखावृत्ताच्या पूर्वेस आणि पश्चिमेस रेखावृत्तप्रमाण वाढत जाते. आंतरराष्ट्रीय नकाशात नकाशाचे क्षेत्र ४° अक्षांश आणि ६° रेखांश एवढे मर्यादित असते. बहुशंकू प्रक्षेपणाच्या तुलनेत या प्रक्षेपणातील अतिटोकाकडील अक्षवृत्ते एकमेकांना जरा अधिक जवळ काढलेली असतात. त्यामुळे मध्यवर्ती रेखावृत्ताच्या पूर्वेस २° आणि पश्चिमेस २° या दोन रेखावृत्तांदरम्यानच्याअक्षवृत्तांमधील अंतर अचूक असते. रेखावृत्तांचे समान भाग पाडून त्या विभाजन बिंदूंना जोडणारी अक्षवृत्ते काढली जातात.

(ई) संकेतात्मक किंवा गणितीय प्रक्षेपणे : (१) मॉलवाइडचे समक्षेत्र प्रक्षेपण : हे प्रक्षेपण गणितावर आधारलेले आहे. यात प्रमाणित पृथ्वीच्या गोलाच्या पृष्ठभागाचे निम्मे क्षेत्रफळ (२π×  त्रिज्या^२) एक वर्तुळ काढून दाखविलेले असते.   

साध्या वर्तुळाचे क्षेत्रफळ = πत्रिज्या^२ 

अर्धगोलाचे क्षेत्रफळ = २ πत्रिज्या^२ 

अर्धगोलाचे क्षेत्रफळ वर्तुळाने दाखवावयाचे झाल्यास त्या वर्तुळाच्या त्रिज्येची लांबी वाढवावी लागेल. 

πत्रिज्या^२ = किंवा त्रिज्या = √२ त्रिज्या  

नकाशाचे प्रमाण जर १ : २५,००,००,००० असेल, तर ह्या प्रमाणावर अर्धगोलाची त्रिज्या १”भरेल व वर्तुळाची त्रिज्या = √२ ×१ʺ = १·४१४ इंच किंवा ३·६ सेंमी. भरेल. ही त्रिज्या घेऊन वर्तुळ काढले असता, त्या वर्तुळाचे क्षेत्रफळ प्रमाणित पृथ्वीच्या अर्धगोलाच्या क्षेत्रफळाबरोबर भरते.

 अर्थात प्रक्षेपण संपूर्ण जगासाठी काढल्यास त्याचा सर्वोच्च बिंदू उ. ध्रुव व सर्वांत खालचा बिंदू द. ध्रुव दाखवील. त्यांना जोडणारी  अर्धवर्तुळे अनुक्रमे ९०° पश्चिम आणि ९०° पूर्व रेखावृत्ते असतील. दोन्ही ध्रुव

जोडणारी सरळ रेषा मध्यवर्ती रेखावृत्त असेल. सबंध गोलाचे प्रक्षेपण काढण्यासाठी अक्षवृत्तांची विषुववृत्तापासूनची अंतरे मूळ रेखावृत्तावर शेजारील कोष्टकाप्रमाणे निर्धारित करावयाची असतात. अक्षवृत्तांच्या वर्तुळातील लांबीचे दोन सारखे भाग करून येणारे अंतर घेऊन अक्षवृत्ते वर्तुळाबाहेर वाढविली जातात. नंतर सर्व अक्षवृत्ते सारख्याच भागांत विभागण्यात येऊन विभजान-बिंदूला जोडणाऱ्या रेषा काढल्यावर रेखावृत्ते पूर्ण होतात.  

सबंध गोलाचा पृष्ठभाग या प्रक्षेपणात दाखविता येतो. या प्रक्षेपणात अक्षवृत्ते सरळ रेषा असतात. पण मध्यवर्ती रेखावृत्तावर ती समान अंतरावर काढली जात नाहीत. मध्यवर्ती रेखावृत्त सरळ रेषा असते. ९०° रेखावृत्ते अर्धवर्तुळे असतात. इतर रेखावृत्ते गोलाकार असतात. हे एक समक्षेत्र प्रक्षेपण आहे. नकाशासंग्रहातील जगाचे बरेचसे नकाशे या प्रक्षेपणावर काढले जातात. याची ज्या वक्रीय प्रक्षेपणाशी तुलना करता आकार विकृती कमी करण्याच्या दृष्टीने हे प्रक्षेपण सरस ठरते. 

मॉलवाइड प्रक्षेपणात अनेक सुधारणा करून निरनिराळी प्रक्षेपणे काढण्यात आली आहेत. त्यांपैकीच एक खंडित प्रक्षेपण होय. या खंडित प्रक्षेपणात सरहद्दीवरील प्रदेशांच्या आकारात संभवणाऱ्या दोषांचे प्रमाण बरेच कमी करण्यात येते. 

 (२) गोलाकार प्रक्षेपण : हे प्रक्षेपण फार लोकप्रिय आहे. नकाशासंग्रहामधील दोन गोलार्धांचे नकाशे या प्रक्षेपणावर काढलेले असतात. या प्रक्षेपणातील वर्तुळाचे क्षेत्रफळ गोलार्धाच्या क्षेत्रफळाबरोबर दाखविले असल्याने या वर्तुळाची त्रिज्या √२×गोलाची त्रिज्या एवढी असते. प्रक्षेपणात विषुववृत्त आणि मध्यवर्ती रेखावृत्त सोडल्यास इतर वृत्ते वक्राकार असतात. अक्षवृत्ते ही चापाप्रमाणे काढण्यात येऊन त्या चापांची बहिर्वक्र बाजू विषुववृत्ताकडे असते. रेखावृत्तांची अंतर्वक्र बाजू मध्यवर्ती रेखावृत्ताकडे असते. अक्षवृत्ते मध्यवर्ती रेखावृत्तावर सारख्या अंतरांवर काढलेली असतात. तसेच रेखावृत्ते विषुववृत्तावर समान अंतरांवर काढलेली असतात. विषुववृत्ताखेरीज इतर अक्षवृत्ते रेखावृत्तांना काटकोन करीत नाहीत. त्यामुळे मूळ रेखावृत्त सोडल्यास इतर वृत्तांवरील प्रमाण कमीजास्त होऊन आकारात दोष निर्माण होतो. हा दोष प्रक्षेपणाच्या कडेला मोठ्या प्रमाणात होतो म्हणून हे प्रक्षेपण समक्षेत्रही नाही आणि शुद्ध आकारदर्शकही नाही. पण ते काढण्यास फार सोपे आहे.  

वरील प्रक्षेपणांशिवाय अलीकडच्या काळात जगाचे नकाशे काढण्यासाठी अनेक प्रक्षेपणे निघाली आहेत. त्यांत ऐतॉफचे प्रक्षेपण, कासीनीचे प्रक्षेपण, सॅन्सन–फ्लॅमस्टीडचे खंडित प्रक्षेपण इ. प्रक्षेपणांचा उल्लेख करणे जरूरीचे आहे.  

योग्य प्रक्षेपणाची निवड :कोणत्याही देशाच्या नकाशासाठी योग्य ते प्रक्षेपण निवडण्यासाठी दोन गोष्टींचा विचार करावा लागतो. त्या म्हणजे त्या देशाचा पूर्व-पश्चिम आणि दक्षिणोत्तर विस्तार आणि नकाशा काढण्याचा हेतू, या होत. यांशिवाय प्रक्षेपण काढण्याची सुलभता ध्यानात घेणेदेखील आवश्यक असते.

 सर्वसाधारणपणे ध्रुवीय प्रदेश दाखविण्यासाठी खमध्य ध्रुवीय, उष्ण कटिबंधातील प्रदेश दाखविण्यासाठी दंडगोलाकार व समशीतोष्ण कटिबंधातील भाग दाखविण्यासाठी शंकू प्रक्षेपणाचा उपयोग करणे सोयीस्कर ठरते. अर्थात ज्या ठिकाणी विशिष्ट गुणधर्म प्रक्षेपणात असणे आवश्यक ठरते, त्यावेळी विषुववृत्तीय व खमध्य तिर्यक प्रक्षेपणे काढण्यास कठीण असूनही उपयोगात आणणे जरूरीचे ठरते. उदा., आफ्रिकेसारख्या उष्ण कटिबंधातील प्रदेशात विमानमार्ग आखावयाचे झाल्यास, ते खमध्य विषुववृत्तीय गोमुखी प्रक्षेपणाच्या साहाय्याने आखणेच सोयीस्कर ठरेल. अशा वेळी दंडगोलाकार प्रक्षेपण उपयोगी पडणार नाही. तसेच ज्या ठिकाणी अचूक दिशा दाखविणे अतिशय आवश्यक असेल, त्या ठिकाणी मर्केटर प्रक्षेपणाला पर्याय नाही. स्थलवर्णनात्मक नकाशांसारखे मोठ्या प्रमाणावरील अनेक तुकडे तयार करावयाचे झाल्यास सुधारित बहुशंकू प्रक्षेपण योग्य ठरते. 

नकाशावर लोकसंख्या, पिके, वनस्पती यांचे वितरण बिंदूंच्या साहाय्याने दाखवावयाचे असल्यास समक्षेत्र प्रक्षेपण वापरणे योग्य ठरते कारण त्यामुळेच वितरणाच्या घनतेची योग्य कल्पना आपल्याला येऊ शकेल. याउलट नकाशासंग्रहामध्ये राजकीय नकाशे काढावयाचे झाल्यास शुद्ध आकारदर्शक प्रक्षेपणे वापरणे उचित ठरते. ज्यावेळी एखाद्या शहरापासून निरनिराळ्या शहरांचे बृहत्‌ वृत्तीय अंतर (कमीत कमी) नकाशावर सरळ मिळावे अशी अपेक्षा असेल, त्यावेळी त्या शहरावर केंद्रित झालेले खमध्य तिर्यक समांतर प्रक्षेपण वापरणे इष्ट ठरते. ध्रुवीय प्रदेशातील मोहिमांतील प्रगती अजमावण्यासाठी खमध्य ध्रुवीय समांतर प्रक्षेपण योग्य होईल. 

जागतिक वितरण दाखविण्यासाठी संपूर्ण जग दाखविणाऱ्या ज्या वक्रीय आणि मॉलवाइड या प्रक्षेपणांचा उपयोग करणे उपयुक्त ठरते. मात्र ज्या वक्रीय प्रक्षेपणात कडेला आकार फारच बिघडतो. म्हणून मॉलवाइडचे प्रक्षेपण अधिक समर्पक ठरते.  

वाघ, दि. मु. फडके, वि. शं.

“