प्रतिकृती

प्रतिकृती : (मॉडेल) कोणत्याही मूर्त किंवा अमूर्त स्वरूपातील वस्तूचे किंवा वस्तूंच्या प्रणालींचे व त्यांच्या वैशिष्ट्यांचे काही मर्यादेपर्यंत दिग्दर्शन करू शकणाऱ्या वस्तूला, वस्तूंच्या प्रणालीला किंवा गणितीय प्रणालीला मूळ गोष्टीची प्रतिकृती (किंवा प्रतिरूप) असे म्हणतात. इमारत, जहाज, रेल्वे एंजिन यांसारख्या मूर्त वस्तूंच्या प्रतिकृती तयार केल्या जातात. जैव प्रणाली (उदा. रक्ताभिसरण संस्था), सामाजिक किंवा आर्थिक प्रणाली [उदा., अर्थमितीय प्रतिकृती ⟶ अर्थमिती] यांच्याही प्रतिकृती तयार केल्या जातात. जिची प्रतिकृती तयार करावयाची ती मूळ वस्तू प्रत्यक्षात असेल अगर नसेलही, उदा., एखाद्या नवीन यंत्राचा किंवा विमानासारख्या प्रणालीचा प्रथम फक्त आराखडाच उपलब्ध असतो व त्यावरून त्याची प्रतिकृतीच प्रथम तयार केली जाते.

गणितीय प्रतिकृती : भौतिकीय प्रणाली ही मूर्त स्वरूपात असते परंतु गणितीय प्रतिकृती ही अमूर्त असते. ती एखाद्या  ⇨अवकल समीकरणाच्या किंवा ⇨फलनाच्या स्वरूपात मांडली जाते. मूळ प्रणालीतील परिणामकारी घटक या फलनात किंवा समीकरणात काही प्रचलांच्या (ज्यांना निरनिराळी मूल्ये दिली असता दिलेल्या प्रणालीचे वा आविष्काराचे निरनिराळे प्रकार निर्देशित होतात अशा स्वेच्छ स्थिरांकांच्या किंवा चलांच्या) स्वरूपात व्यक्त केलेले असतात. या गणितीय प्रतिकृतींचा अभ्यास करून उपयुक्त निष्कर्ष काढता येतात. यासाठी कित्येकदा संगणकाचा (गणकयंत्राचा) उपयोग करणे आवश्यक होते. मूळ प्रणालीतील कोणते घटक जास्त महत्त्वाचे, कोणते घटक कसे बदलले, तर प्रणाली जास्त कार्यक्षम होईल, कोणते घटक दुर्लक्षणीय मानता येतील अशा प्रश्नांची उत्तरे त्यावरून मिळू शकतात. उदा., हृदयाच्या कार्याची गणितीय प्रतिकृती तयार करून तिचा संगणकाच्या साहाय्याने अभ्यास केला असता त्यावरून हृदयाच्या कार्याबद्दल महत्त्वाची माहिती मिळू शकते. आधुनिक उद्योगधंद्यातील व्यवस्थापनाच्या समस्या सोडविण्याकरिता, त्यांची गणितीय प्रतिकृती मांडून तिच्या निर्वाहावरून (समीकरण सोडवून मिळालेल्या उत्तरावरून) त्या समस्या सोडविण्यासाठी विविध पर्याय उपलब्ध होऊ शकतात.[⟶ संक्रियात्मक अन्वेषण].

परंतु अभियांत्रिकीच्या विविध शाखा, स्थापत्यशास्त्र यांसारख्या शास्त्रशाखांतील कित्येक समस्या अशा स्वरूपाच्या असतात की, त्यांच्या सुयोग्य गणितीय प्रतिकृती मांडताच येत नाहीत किंवा मांडल्या तरी त्यांचे निर्वाह काढता येत नाहीत. अशा परिस्थितीत इष्ट प्रणालीची भौतिकीय प्रतिकृती तयार करून तिच्यावर प्रयोग करून समस्यांची सोडवणूक करावी लागते.

‘चुंबकीय सूची दक्षिण-उत्तर दिशेने स्थिर राहते याचे कारण पृथ्वी हाच एक लोहचुंबक आहे.’ हा सिद्धांत प्रस्थापित करण्यासाठी विल्यम गिल्बर्ट (१५४४-१६०३) यांनी पृथ्वीच्या गोलाच्या प्रतिकृतीचा उपयोग केला होता. त्याचप्रमाणे पृथ्वीच्या गाभ्यात एक प्रकारचे स्वयंउत्तेजित विद्युत् जनित्र (डायनामो) कार्य करीत असते ही ⇨ भूचुंबकत्वासंबंधीची आधुनिक कल्पना मान्य होण्यापूर्वी त्याच्या प्रतिकृती करून पडताळा पहाण्यात आला होता. 

कित्येक शास्त्रीय सिद्धांतही प्रतिकृतीच्या स्वरूपात व्यक्त केले जातात. अशा प्रतिकृतींना ‘प्रतिमान’ हे नाव देतात. उदा., अणूची संरचना किंवा अणुकेंद्राची संरचना यांबद्दलची प्रतिमाने सुचविली गेली आहेत. [⟶ अणु व आणवीय संरचना].

मापप्रमाण : प्रतिकृतीचे (लांबी, रुंदी यांसारखे) विशिष्ट परिणाम व मूळ वस्तूचे तेच परिणाम यांच्या गुणोत्तराला मापप्रमाण असे म्हणतात. उदा., प्रतिकृतीतील १ मिमी. अंतर मूळ वस्तूतील १ मीटर ( = १००० मिमी.) अंतर दिग्दर्शित करीत असेल, तर मापप्रमाण n = ^१/_१००० होईल. अनेकदा प्रतिकृतीचे आकारमान मूळ वस्तूपेक्षा लहान असते (n &lt १) परंतु कित्येकदा मूळ वस्तू व प्रतिकृती सारख्याच आकारमानाच्या असू शकतात. (n = १). मूळ वस्तू फारच लहान असेल, तर तिची प्रतिकृती तिच्यापेक्षा मोठी करणेच उपयुक्त होते (उदा., कानाची अंतर्रचना दर्शविणारी प्रतिकृती). मापप्रमाणाचे मूल्य हे शेवटी प्रतिकृतीकडून कोणते उद्दिष्ट साधावयाचे आहे, त्याच्यावर अवलंबून असते.

ऐतिहासिक पार्श्वभूमी : प्रतिकृतीची कल्पना अती प्राचीन काळापासून चालत आलेली असावी असे दिसते. पुराणात विश्वामित्रांनी प्रतिसृष्टी निर्माण केल्याचा उल्लेख आहे. आदिम लोक पूजाविधीसाठी पूजनीय वस्तूंची शिल्पे, कोरीव आकृत्या इत्यादींची निर्मिती करीत असत. त्यांच्यामध्ये काही अलौकिक शक्ती वास करीत असावी असा त्यांचा समज होता. आफ्रिकन जमातींमध्ये वन्य पशू, प्राणी, व्यक्ती यांच्या प्रतिकृती केल्या जात असत. पूजाविधीप्रमाणेच जादूटोणा, चेटूक, रोगनिवारण अशा हेतूंसाठीही प्रतिकृती घडविल्या जात. इ. स. पू. सु. ४००० वर्षे या काळात ईजिप्तमध्ये पिरॅमिड ही प्रचंड थडगी बांधण्यात आली. ईजिप्शियन सम्राटांच्या या थडग्यांतून अनेक वस्तूंच्या व माणसांच्या प्रतिकृती सापडल्या आहेत. त्या काळी असा समज होता की, मृत व्यक्तीचा आत्मा पुन्हा त्याच्या शरीरात प्रवेश करतो. त्यानुसार सम्राट जिवंत झाल्यावर त्याच्या सेवेसाठी व उपभोगासाठी दासदासी, सैनिक, कारागीर, पाळीव पशू, वाहने, भांडीकुंडी वगैरे नित्याच्या वस्तू यांच्या प्रतिकृती अशा थडग्यांतून ठेवल्या जात. छोट्या आकारमानाच्या या प्रतिकृती लाकडातून मोठ्या कौशल्याने कोरलेल्या असत. इ. स. पू. २५००० वर्षांच्या जहाजांच्या प्रतिकृतीही त्यात मिळाल्या आहेत. या प्रतिकृतींवरून तत्कालीन ईजिप्शियन लोकांच्या रीतीभाती व जीवनपद्धतीबद्दल माहिती मिळते. जगातील अनेक वस्तुसंग्रहालयांतून यांपैकी प्रतिकृती पहावयास मिळतात. 

अशाच प्रकारच्या काही चिनी मातीच्या प्रतिकृती प्राचीन चिनी थडग्यांमधून सापडल्या आहेत. प्राचीन ग्रीक संस्कृतीतील काही उपलब्ध प्रतिकृतींवरून तत्कालीन ग्रीक जीवनाची कल्पना येऊ शकते. 

सतराव्या शतकांत जे. बी. कॉलबेअर (१६१९-४३) या फ्रान्सच्या जलवाहतूक मंत्र्यांनी प्रथम प्रमाणबद्ध प्रतिकृती तयार करून मग तीनुसार प्रत्यक्ष जहाज बांधावे असा आदेश काढला व एक नवीनच प्रथा सुरू केली. एकोणिसाव्या शतकात फ्रेंच सरकारने अशा सर्व प्रतिकृतींचे एक संग्रहालय बनविले. या प्रतिकृतींवरून वेगवेगळ्या जहाजांतील सोयी-गैरसोयींची व गुणदोषांची आधीच कल्पना येऊन त्यानुसार नव्या जहाजाच्या अभिकल्पात योग्य त्या दुरुस्त्या करणे शक्य होऊ लागले. 

उद्दिष्टे : प्रतिकृतीची उद्दिष्टे अगदी वेगवेगळ्या प्रकारांची असू शकतात. त्यानुसार निर्माण केलेल्या प्रतिकृतीच्या स्वरूपात व ती करण्याच्या पद्धतीत आणि त्यासाठी खर्च केलेले कौशल्य आणि पैसा यांमध्ये प्रचंड फरक पडू शकतो. 

(१) केवळ मनोरंजन किंवा खेळ म्हणून मोठ्या प्रमाणावर प्रतिकृती बनविल्या जातात. लहान मुलींची चूल-बोळकी-बाहुल्या, दिवाळीत मुले बांधतात ते किल्ले, मोटारी, आगगाड्या, रॉकेटे यांसारखी मुलांची खेळणी ही या प्रकारच्या प्रतिकृतींची उदाहरणे आहेत. या प्रतिकृतीमध्ये प्रमाणबद्धता किंवा यथातथ्यता या गुणांवर फार भर दिला नाही तरी चालू शकते. सर्वसामान्यपणे साम्य असले म्हणजे झाले. मूळ वस्तूप्रमाणे कमी-अधिक प्रमाणात कार्य करू शकणारी खेळणी (उदा., स्प्रिंगची मोटार) हे या प्रकारच्या प्रतिकृतीचे काहीसे वरच्या दर्जाचे स्वरूप होय. 

---

(२) छंद म्हणून कित्येकदा आगगाड्या, विमाने, धरणे इत्यादींच्या प्रतिकृती तयार केल्या जातात. त्यांमध्ये मूळ वस्तूचे जास्तीत जास्त यथातथ्य दिग्दर्शन करण्याची कोशीस केली जाते. या प्रतिकृती मूळ वस्तूपेक्षा आकारमानाने लहान असल्या, तरी त्यांमध्ये मूळ वस्तूचे जास्तीत जास्त तपशील व्यक्त करण्याचा प्रयत्न केला जातो. अशा प्रतिकृती अनेकदा प्रत्यक्ष कार्यकारीही असतात (उदा., विमानाची प्रतिकृती प्रत्यक्ष उड्डाणही करू शकते). अशा प्रतिकृतीसाठी जरूर ती उपकरणे, साधने व कच्चा माल पुरविणाऱ्या मोठमोठ्या  संस्था पुढारलेल्या देशांत प्रस्थापित झालेल्या आहेत. या प्रकारच्या प्रतिकृती निर्माण करण्यामध्ये मुलांची संशोधक बुद्धी, कौशल्य व शास्त्रीय दृष्टी यांची वाढ होत असल्यामुळे त्या तयार करण्यास सर्वतोपरीने उत्तेजन देण्यात येते.

(३) धार्मिक कारणासाठी किंवा जादूटोणा इत्यादींकरिता फार पूर्वीपासून प्रतिकृती केल्या जात आहेत. महाराष्ट्रात मातीचे नाग (नागपंचमीच्या दिवशी) तयार करण्याची प्रथा आहे. गणपतीसारख्या देवादिकांच्या मूर्ती हासुद्धा प्रतिकृतीचा एक खास प्रकार समजला पाहिजे परंतु तेथे मूळ देवाचे स्वरूप कोणीच पाहिलेले नसल्याने केवळ काल्पनिक वर्णनावरूनच या मूर्ती साकार केल्या जातात. आफ्रिकेतील काही जमातींत ज्या व्यक्तींवर ‘करणी’ करावयाची असेल तिची प्रतिकृती करून तिच्यावर जादूटोण्याची क्रिया केली जाते.

(४) वस्तूची किंवा लोकांची व त्यांच्या जीवन पद्धतीची माहिती देण्यासाठीही प्रतिकृती केल्या जातात. दिल्ली येथील बाहुल्यांच्या आंतरराष्ट्रीय संग्रहालयात भारतातील विविध प्रांतांतील व देशांतील लोकांचे पेहराव, विवाह पद्धती यांचे बाहुल्यांच्या द्वारे दिग्दर्शन केले आहे. हे या प्रकारच्या प्रतिकृतीचे उदाहरण आहे. स्वीडनमध्ये स्कान्सेन येथे उभारलेल्या शेती व ग्रामीण प्रदर्शनात सोळाव्या व सतराव्या शतकांतील ग्रामीण इमारती व कृषिविषयक अवजारे जशीच्या तशी ठेवली असून तत्कालीन पेहेराव वापरून तेथील कर्मचारी त्याकाळच्या पद्धतीनुसार कृषिकर्मे करीत असतात. प्रतिकृतींचा हा एक आगळाच नमुना होय. 

(५) जाहिरातीसाठी अनकेदा प्रतिकृतींचा वापर केला जातो. घड्याळे, पादत्राणे यांच्या मोठ्या  आकारमानाच्या प्रतिकृती दुकानांबाहेर लावलेल्या अनेकांच्या पाहण्यात असतील. अशा तऱ्हेने प्रतिकृतींचा वापर करताना कित्येकदा पराकाष्ठेची कल्पकता दाखविली जाते. फिरत्या मंचावर ठेवून प्रतिकृतींचे वेगवेगळ्या दिशांनी दर्शन व्हावे अशी योजनाही केव्हा केव्हा करतात. केव्हा केव्हा या प्रतिकृती हालचालीही करू शकतात. 

(६) चित्रपट, दूरचित्रवाणी यांसारख्या मनोरंजन प्रकारांत विशेषतः ऐतिहासिक प्रसंग, विमान पडणे, मोठी आग लागणे यांसारखे भयंकर प्रसंग, यांचे चित्रण करताना प्रतिकृतींचा उपयोग फार मोठ्या प्रमाणावर केला जातो. सामान्यतः मूळ वस्तूपेक्षा लहान आकारमानाच्या प्रतिकृती घेतात व छायाचित्रणातील खुब्यांचा वापर करून प्रत्यक्ष प्रसंगाचा आभास उत्पन्न केला जातो. नव्या नाटकाचे व चित्रपटाचे नेपथ्य करण्यापूर्वी प्रथम तिच्या छोट्या प्रतिकृती तयार करून त्यांचा अभ्यास करतात व शेवटी नेपथ्याची निवड करतात. पात्रांच्या वेशभूषा निवडण्यासाठीही हे तंत्र वापरले जाते. 

(७) शैक्षणिक क्षेत्रात प्रतिकृतींचा उपयोग फार मोठ्या प्रमाणावर केला जातो. रसायनशास्त्रात रेणूंची संरचना समजून देण्यासाठी प्रतिकृतींचा वापर फारच उपयुक्त होतो. यामध्ये वेगवेगळ्या मूलद्रव्यांचे अणू वेगवगळ्या रंगांच्या गोट्यांनी दर्शविले जातात. या गोट्यांमधील भोकांतून खुंट्या बसवून त्या इष्ट आकारात जोडता येतात व अशा तऱ्हेने रेणूच्या संरचनेचे त्रिमितीय चित्र उभे करता येते (खंड ८ मधील चित्रपत्र क्र. ५२ वरील डीऑक्सिरिबोन्यूक्लिइक अम्लाची प्रतिकृती पहा). वैद्यकशास्त्रात शरीरातील वेगवेगळ्या अवयवांचे कार्य त्यांच्या प्रतिकृतींच्या साहाय्याने समजून देता येते. संपूर्ण मानवी शरीराची मोठी पारदर्शक प्रतिकृती तयार करून तीमध्ये शरीरातील अस्थिसंस्था, रक्ताभिसरणसंस्था, तंत्रिका (मज्जा) संस्था इत्यादींचे उत्कृष्टपणे दिग्दर्शन करता येते.

अभियांत्रिकीत विविध स्वरूपांच्या प्रतिकृती वापरल्या जातात. काही प्रतिकृती विशिष्ट यंत्रांच्या रचना स्पष्ट करण्याकरिता बनविलेल्या असतात. छेदात्मक प्रतिकृती विशिष्ट प्रतलात (पातळीत) यंत्राचा काटच्छेद कसा दिसेल ते दाखवितात. कार्यकारी प्रतिकृती प्रत्यक्ष चालविता येतात व त्यांवरून मूळ यंत्रातील विविध भागांचे कार्य कसे चालते ते पाहता येते. अणुकेंद्रीय विक्रियकासारख्या (अणुभट्टीसारख्या) उपकरणाची प्रतिकृती अशा प्रकारे तयार करतात की, ती उघडून तिच्यावर वेगवेगळ्या स्तरांवर असलेल्या रचना दाखविता येतात. 

उठावाचे नकाशे हा एक प्रतिकृतीचा विशेष प्रकार असून त्याच्या साहाय्याने नद्या, डोंगर, पाणलोटाची क्षेत्रे इत्यादींचे चांगले दिग्दर्शन करता येते.

विमान चालविण्याच्या प्रशिक्षणासाठी वैमानिकाची बसण्याची जागा, नियंत्रण उपकरण फलक इत्यादींची हुबेहूब प्रतिकृती वापरतात. संगणकाच्या साहाय्याने शिक्षक विमानोड्डाणात तोंड द्याव्या लागणाऱ्या विविध परिस्थितींचे दिग्दर्शन करतो व त्यानुसार प्रशिक्षणार्थीला अनुरूप कार्यवाही करावयाचा सराव देतो. या योजनेमुळे शिक्षणासाठी विमान व चालक यांना धोका पत्करावा लागत नाही आणि त्याचप्रमाणे भारी किंमतीचे विमानही शिक्षणासाठी गुंतून पडत नाही.

(८) देशोदेशींची प्रसिद्ध शिल्पे, पुराण वस्तू इत्यादींचे प्रतिकृतींच्या द्वारे संग्रहालयांतून व राष्ट्रीय वा आंतरराष्ट्रीय प्रदर्शनांतून दर्शन घडविता येते. नवीन वसाहती किंवा घरे यांची प्रत्यक्ष बांधणी करण्याआधी त्यांच्या प्रमाणबद्ध प्रतिकृती करून त्यांचे संपूर्ण चित्र उभे करता येते. 

(९) अधिकाऱ्यांना लष्करी डावपेचांचे शिक्षण देण्यासाठी वालुका प्रतिकृतीवर लुटपुटीच्या मोहिमा खेळल्या जातात. त्यांना ट्यूट (TEWT) असे म्हणतात. यामध्ये डोंगराळ, रेताड, जंगली असे विविध प्रकारचे भूभाग थोड्या जागेत दाखविता येतात. त्यांना अनुरूप विविध पर्यायी डावपेच योजनांचा तौलनिक अभ्यास करता येतो. ट्यूट हा लष्करी अधिकाऱ्यांच्या प्रशिक्षणातील एक अविभाज्य घटक झालेला आहे. त्याचप्रमाणे सैनिकांना शत्रूच्या व आपल्या विमानांची व लढाऊ जहाजांची ओळख सहज पटावी यासाठी त्यांच्या प्रतिकृतींचा उपयोग केला जातो. 

दुसऱ्या महायुद्धात प्रतिकृतींचे काही आश्चर्यकारक उपयोग केले गेले. जर्मन लोकांनी फ्रान्सचा पाडाव केला तेव्हा वाटेतील एक मोक्याचा व अभेद्य किल्ला झटपट जिंकता यावा यासाठी एका जंगलात त्या किल्ल्याची पूर्णाकृती प्रतिकृती करून तिच्यावर हल्ला करण्याचा सराव जर्मन सैनिकांना देण्यात आला होता. त्याचप्रमाणे पुढे नॉर्मंडीमध्ये दोस्त सैन्य प्रत्यक्ष उतरविण्याआधी त्याला प्रतिकृतींच्या साहाय्याने या कार्याचा कित्येक दिवस सराव देण्यात येत होता. त्यामुळेच हा अवघड कार्यक्रम बऱ्याच प्रमाणात सुरळीतपणे पार पडू शकला. ब्रिटनवरील जर्मनांच्या हवाई हल्ल्याच्या वेळी हल्ला करणारी विमाने किती संख्येने येतात व कोठे जात आहेत, हे एका मोठ्या नकाशावर एकसारखे दाखविले जाई. त्यानुसार ब्रिटिश अधिकारी योग्य त्या ठिकाणी आपली लढाऊ विमाने केंद्रित करून हल्लेखोरांचा उत्तम प्रकारे मुकाबला करू शकत. 

---

सर्वसामान्य प्रतिकृतींसाठी लागणारे साहित्य : सर्वसामान्य प्रतिकृती बनविण्याकरिता विविध प्रकारचे साहित्य व साधने लागतात. निरनिराळ्या प्रकारचे कागद व पुठ्ठे, लाकूड, धातूचे पत्रे, सेल्युलॉइड, प्लॅस्टिक इ. पृष्ठभागांकरिता आणि गोंद, सरस, खळ, संश्लिष्ट (कृत्रिम) रेझीन वगैरे जोडकामासाठी वापरतात. माती, मेण, प्लॅस्टर, कागदाचा लगदा किंवा लाकडाचा भुस्सा यांचा साचेकामाकरिता उपयोग करतात. यांशिवाय अनेकदा कापड, चामडे, रेशीम, काच यांचाही उपयोग करणे आवश्यक असते. कोणत्या प्रतिकृतीकरिता कोणते साहित्य व कोणती हत्यारे लागतील हे त्या त्या प्रतिकृतीच्या स्वरूपावर अवलंबून असते. साधारणतः सुरी, चाकू, कात्री, सुईदोरा, तसेच सुतारकामाची हत्यारे इ. लागतात. आधुनिक उपकरणांमध्ये विद्युत् शक्तींवर चालणारी विविध हत्यारे व डाखकाम करण्याचे साधन यांचाही अंतर्भाव होतो. प्रतिकृती पूर्ण झाल्यावर तिचा हुबेहूबपणा, तीवरील पोत व इतर तपशील दर्शविण्यासाठी रंगकामाची आवश्यकता असते.

अभियांत्रिकीतील उपयोग : आतापर्यंत वर्णन केलेल्या प्रतिकृतींकडून ‘मूळ वस्तूच्या स्वरूपाचे कमीअधिक प्रमाणांत हुबेहूब दर्शन घडविणे’ यापेक्षा जास्त अपेक्षा नसते परंतु अभियांत्रिकीमध्ये प्रत्यक्ष वस्तू तयार करण्यापूर्वीच प्रथम आराखड्यानुसार तिची प्रतिकृती तयार करण्यात येते. या प्रतिकृतीवर विविध चाचण्या घेऊन त्यांवरून इष्ट वस्तू जास्तीत जास्त कार्यक्षम व कमी खर्चाची होण्यासाठी कोणते फेरफार करणे आवश्यक आहे याचा अभ्यास केला जातो व त्यानुसार शेवटी वस्तू बनविली जाते. एखादे धरण किंवा विमान बांधणे हे इतके प्रचंड खर्चाचे व वेळ घेणारे काम असते की, ते बांधण्याच्या आधी त्याचा सर्वांगीण अभ्यास करून जास्तीत जास्त निर्दोष अभिकल्प (आराखडा) करणे आवश्यक असते. याकरिता लागणाऱ्या प्रतिकृती तयार करताना कित्येक जादा बंधने पाळावी लागतात. अशा प्रकारच्या प्रतिकृतींची निर्मिती व त्यांचा उपयोग करून मार्गदर्शक निष्कर्ष काढणे जे एक स्वतंत्र शास्त्रच बनले आहे.

प्रतिकृती आवश्यकता : प्रचंड खर्चाची धरणे, पूल, पूर नियंत्रण योजना, बंदरांची आखणी यांसारखे स्थापत्य प्रकल्प किंवा विमान, मोटार, जहाज यांसारख्या एखाद्या वाहनासारखे द्रायुयामिकीय अभिकल्प [⟶ द्रायुयामिकी] तयार करताना उपलब्ध गणितीय सूत्रांचा वापर करून वस्तूवर पडणारे दाब, कर्षण (मागे ओढून धरणारी) प्रेरणा इत्यादींचे गणन करतात व त्यानुसार व पूर्वानुभवाचा उपयोग करून वस्तूचा सुयोग्य आकार व परिमाणे निश्चित करण्याचा प्रयत्न करतात परंतु या बाबतीत कित्येक परिणाम इतके गुंतागुंतीचे असतात की, संबंधित समीकरणांचे गणिती निर्वाह काढता येत नाहीत आणि त्यामुळे त्यासंबंधीची सूत्रेही अस्तित्वात नाहीत. म्हणून इष्ट वस्तूंच्या प्रतिकृतीवर प्रयोग करून त्यावरूनच इष्टतम अभिकल्प तयार करणे भाग पडते.

द्रायुयामिकीय प्रतिकृती : उद्दिष्टे : द्रायुयामिकीय प्रणालींच्या (उदा., धरणे, पूर नियंत्रण योजना, बंदरे, कालवे, पूल, जहाजे, विमाने, टरबाइने इत्यादींच्या) प्रत्यक्ष निर्मितीपूर्वी त्यांच्या वैशिष्ट्यांची कल्पना येण्यासाठी प्रतिकृतींचा फार उपयोग होतो. या प्रतिकृती मूळ प्रकल्पापेक्षा बनविण्यास स्वस्त असतात. जरूर वाटेल त्याप्रमाणे त्यांत फेरफार करणे सहज शक्य होते, त्याचप्रमाणे त्यांची निर्मितीही थोड्या वेळात व सहज करता येते. अशा प्रतिकृतींचा अभ्यास करण्यामागे सामान्यतः पुढील (एक किंवा अधिक) हेतू असतात : (१) प्रत्यक्ष प्रणाली पूर्ण झाल्यानंतर कशी दिसेल, तिच्या वेगवेगळ्या भागांची परस्पर प्रमाणे काय असतील इ. वैशिष्ट्यांचे दिग्दर्शन करणे (२) प्रणालीच्या विविध भागांतून किंवा वरून वहाणाऱ्या प्रवाहाचे वेगवेगळ्या  ठिकाणी वेग, प्रवेग आणि त्यांच्या दिशा यांचे दिग्दर्शन करणे (३) प्रणालीतील वस्तूंवरील व त्यांच्या विविध भागांवरील दाब व तज्जन्य प्रेरणा यांचे वितरण दिग्दर्शित करणे (४) वेगवेगळी रंध्रे, द्वारे, नाली यांच्या वहनक्षमतेचा अंदाज घेणे (५) द्रायुगतिकीय यंत्रांची कार्यक्षमता अजमावणे (६) जहाजे, विमाने इत्यादींच्या गतीला वेगवेगळ्या कारणांमुळे होणाऱ्या रोधांचे मापन करणे व त्यामुळे होणारा ऊर्जा व्यय निश्चित करणे (७) अंतिम प्रणालीचे किंवा तिच्या एखाद्या भागाचे कार्य पूर्व योजनेनुसार होईल की नाही, याचा अभ्यास करणे (८) अंतिम प्रणाली जास्तीत जास्त कार्यक्षम कशी करता येईल याचे उपाय शोधून काढणे आणि (९) अंतिम प्रणालीची कार्यक्षमता कमी न होऊ देता तिच्या उत्पादनाचा खर्च कमी व्हावा यासाठी तिच्या रचनेत किंवा उत्पादन पद्धतीत कोणते फरक करता येतील त्यांचा मागोवा घेणे. 

 प्रतिकृतींचा उपयोग करून विशिष्ट द्रायुयामिकीय प्रकल्प किंवा प्रणालीची उद्दिष्टे जास्त जलद सुलभतेने, काटकसरीने साध्य करणे शक्य होते परंतु केव्हा केव्हा अंतिम प्रणाली व प्रतिकृती यांच्यामध्ये संपूर्णपणे एकसारखेपणा (साधर्म्य) प्रस्थापित करता येत नाही. अशा वेळी प्रतिकृतीच्या अभ्यासावरून मिळणारे निर्वाह प्रणालीला संपूर्णपणे लागू पडत नाही व त्यामुळे मिळणारे मार्गदर्शन अगदी बिनचूक किंवा संपूर्ण असत नाही, ही प्रतिकृतीच्या उपयुक्ततेतील एक महत्त्वाची उणीव आहे.

द्रायुगतिकीय प्रकल्पासाठी प्रतिकृतींचा उपयोग करण्याच्या कल्पनेचे जनक विल्यम फ्रूड हे इंग्रज नाविक वास्तुशिल्पज्ञ होत. प्रकल्पित जहाज बांधण्यापूर्वी त्याच्यासारख्या आकृतीच्या प्रतिकृतीवर प्रयोग करून त्यांवरून जहाजाच्या गतीला विरोध करणाऱ्या विविध प्रकारच्या कर्षण प्रेरणांचा अभ्यास करण्याची पद्धती त्यांनी प्रथम सुरू केली. या कामासाठी एक प्रायोगिक तलाव बांधण्यासाठी त्यांना १८७० मध्ये सरकारी अनुदानही देण्यात आले. प्रतिकृतीवर केलेल्या प्रयोगांवरून मिळणारे निष्कर्ष प्रत्यक्ष जहाजाला कसे लागू करावेत याबद्दलही त्यांनीच प्रथम काही नियम बसविले. ही पद्धत आता इतकी सर्वमान्य झाली आहे की, प्रतिकृतीवर प्रयोग करून पाहिल्याखेरीज कोणत्याही मोठ्या जहाजाचे बांधकाम हल्ली हाती घेत नाहीत. इतकेच नाही तर अशीच पद्धत आता विमाने, क्षेपणास्त्रे इत्यादींच्या बाबतीतही वापरली जाते.

परिणामकारी व गैरलागू घटक : प्रतिकृतीवरील प्रयोगांवरून अपेक्षित राशींची (उदा., दाब, प्रेरणा, कर्षण रोध इत्यादींची) विश्वसनीय मूल्ये मिळावी यासाठी प्रतिकृती तयार करताना काही संकेत पाळले जाणे आवश्यक आहे. यासाठी अगदी प्रथमच प्रकल्पित प्रणालीतील ज्या राशींचा किंवा परिणामांचा अभ्यास करावयाचा असेल, त्यांच्या संदर्भात कोणते घटक वा प्रचल गैरलागू आहेत आणि कोणते परिणामकारी आहेत त्याची स्पष्ट जाणीव ठेवली पाहिजे. प्रतिकृतीत फक्त परिणामकारी घटक वा प्रचल प्रतिबिंबित करणे आवश्यक असते. गैरलागू घटक वा प्रचल प्रतिकृतीत प्रतिबिंबित केले नाहीत, तरी मिळणाऱ्या निष्कर्षात काही कमतरता येत नाही. उलट त्यामुळे प्रतिकृती तयार करण्याचे काम जास्त सोपे होते.

उदा., नदीच्या पुरात तिच्यावरील पुलाच्या स्तंभावर ते उखडले जाण्याची क्रिया होत असते पण या क्रियेत स्तंभाची उंची किंवा स्तंभाची एकूण संख्या यांचा काहीच परिणाम होणार नाही व म्हणून हे दोन प्रचल येथे गैरलागू आहेत. पण स्तंभाचा आकार, त्याच्या पायाचा आकार व खोली, त्याच्याजवळील पाण्याचा वेग आणि त्याची दिशा या गोष्टी हे या समस्येतील परिणामकारक घटक आहेत. प्रतिकृतीत फक्त त्यांचीच दखल घ्यावी लागेल.

साधर्म्याचे तत्त्व : प्रतिकृतीच्या अभ्यासावरून निघणारे निष्कर्ष विशिष्ट परिणामाच्या बाबतीत अंतिम अभिकल्पालाही लागू पडले, तरच प्रतिकृतीवर केलेले प्रयोग उपयुक्त ठरतील. यासाठी अभिकल्पित वस्तू व तिची प्रतिकृती यांच्या गुणधर्मांत विवक्षित बाबींमध्ये एकसारखेपणा म्हणजेच साधर्म्य प्रस्थापित झाले पाहिजे, हेच साधर्म्याचे तत्त्व होय.

द्रायुयामिकीय प्रतिकृती पुढील दोन प्रकारची साधर्म्ये प्रस्थापित होणे आवश्यक असते. ती म्हणजे (१) भूमितीय साधर्म्य व (२) गतिकीय साधर्म्य ही होत.

---

 

भूमितीय साधर्म्य : हे साधण्यासाठी प्रतिकृती व अभिकल्पित वस्तू यांचे आकार सारखेच असून शिवाय त्या दोहोंमध्ये लांबी, रुंदी, उंची इ. परिमाणांची गुणोत्तरे समान असली पाहिजेत. म्हणजेच त्यांची मापप्रमाणे समान असली पाहिजेत परंतु काही परिस्थितीत ही सर्वच गुणोत्तरे समान करता येत नाहीत. उदा., नदी, बंदर, कालवा इत्यादींच्या प्रतिकृतीत सर्व गुणोत्तरे सारखी ठेवू गेल्यास प्रतिकृतीची खोली इतकी कमी होईल की, त्यावरून काही उपयुक्त माहिती मिळू शकणार नाही. प्रतिकृतीची खोली जास्त ठेवू गेल्यास  व इतर मापप्रमाणे समान ठेवली, तर प्रतिकृती मर्यादित जागेत मावणार नाही. अशा परिस्थितीत लांबी-रुंदीसाठी वेगळे (^१/_१०० ते ^१/_१०००) व खोली-उंचीसाठी वेगळे ( ^१/_२० ते  ^१/_१००) मापप्रमाणे ठेवणे भाग पडते.

द्रायुयामिकीय प्रयोगामध्ये प्रकल्पाधीन वस्तूचे (उदा., जहाजाचे) किंवा वास्तूचे (उदा., धरणाचे) आकारमान फारच मोठे असते. त्याची प्रतिकृती आटोपशीर आकारमानाची करणे जरूर असते. म्हणजेच प्रत्यक्ष वस्तूपेक्षा प्रतिकृती आकारमानाने खूपच लहान असते.

गतिकीय साधर्म्य : हे साधर्म्य प्रस्थापित केले, तर मग (मूळ प्रणाली किंवा) अभिकल्पित वस्तूवरील  वेगवेगळ्या बिंदूंवर लागू होणाऱ्या प्रेरणा या प्रतिकृतीवरील अनुरूप बिंदूंवर कार्य करणाऱ्या प्रेरणांच्या ठराविक पटीत येतात. यामुळे प्रतिकृतीवरील प्रेरणांचे प्रयोगात मापन करून त्यावरून अभिकल्पित वस्तूवर लागू होणाऱ्या प्रेरणांची मूल्ये काढता येतात. 

प्रतिकृतीत वरील दोन्ही साधर्म्ये मिळविली असतील, तर मग अभिकल्पित वस्तू व तिची प्रतिकृती यांच्या भोवतीचे प्रवाहविन्यासही (प्रवाहाची रचनाही) एकसारखेच होतात. पूर नियंत्रण योजना, बंदरे यांसारख्या अभिकल्पांच्या बाबतीत या प्रवाहविन्यासाचा अभ्यास महत्त्वाचा असतो.

शास्त्रीय बैठक : ही साधर्म्ये साध्य करण्याची पद्धत ⇨परिमाणात्मक विश्लेषणातील सुप्रसिद्ध पाय् (π) सिद्धांतावर आधारलेली आहे. (येथे या सिद्धांताच्या तात्त्विक तपशीलात न शिरता त्याचा उपयोग कसा होतो याचीच फक्त चर्चा केली आहे). समजा की, एका विशिष्ट प्रणालीबद्दलच्या भौतिकीय प्रचलांमधील परस्परसंबंध एका (ज्ञात किंवा अज्ञात) फलनाच्या स्वरूपात व्यक्त करता येत आहे. मग तोच संबंध आपणाला त्या प्रचलांपासून बनविलेल्या काही मितिहीन समूहांच्या [उदा., ओ. रेनल्ड्झ या शास्त्रज्ञांच्या नावाने ओळखण्यात येणारा रेनल्ड्झ अंक ⟶ द्रायुयामिकी] फलनाच्या स्वरूपातही व्यक्त करता येईल. यातील मितिहीन समूहांना ‘पाय् पदे’ असे म्हणतात. समजा की, विशिष्ट प्रणालीतील प्रचलांची π₁, π₂, …π_s अशी s पायपदे तयार होतात व त्या प्रचलाचे मूल्य प्रतिकृतीवर केलेल्या प्रयोगावरून काढावयाचे आहे तो फक्त π ₁ या पदात येतो. मग पाय् सिद्धांतानुसार आपणाला पुढील समीकरणासारखे समीकरण मांडता येईल. 

π₁ =f (π₂, π₃ … …, π_s)   …   …   …   …   …   …   …   …   …  (१)

(येथे f या फलनाचे स्वरूप आपणास माहीत असेलच असे नाही). या समीकरणाला त्या प्रणालीचे अभिलक्षण समीकरण असे म्हणतात. 

प्रतिकृतीवरील प्रयोगात बरोबर तशाच घटना कार्यान्वित होत असल्याने, तिच्याबद्दलचा तद्नुरूप पाय् पदांच्याबद्दलही असेच अभिलक्षण समीकरण लागू पडेल. प्रतिकृतीची पाय् पदे अनुक्रमे π₁’, π₂’, … π_s’ यांनी व्यक्त केल्यास

π₁’ = f ( π₂’, π₃’,… … π_s’)   …   …   …   …   …   …   …   …   …    (२)

π1	=	f (π2, π3,… …, πs)	…   …   … (३)
π1’		f (π2’, π3’,… …, πs’)

 प्रतिकृती तयार करताना अशी योजना केली की,

 π₂ = π₂’, π₃ = π₃’, … , π_s = π_s’   …   …   …   …   …   …   …   …   (४)

तर मग वरील समी. (३) मधील उजव्या बाजूचे मूल्य एक होईल व मग π₁ = π₁’ असे समीकरण मिळेल. π₁’ चे मूल्य प्रतिकृतीवर केलेल्या प्रयोगावरून मिळते. तेच π₁ चेही मूल्य होय. त्यावरून π₁ मधील इच्छित प्रचलाचेही मूल्य काढता येईल. यावरून हे उघड होते की, प्रतिकृतीवर केलेल्या प्रयोगावरून मिळणारे निष्कर्ष अभिकल्पित प्रणालीला लागू पडावेत यासाठी वरील समी. (४) ची पूर्ती होणे ही आवश्यक अट आहे. ही अट शब्दांत पुढीलप्रमाणे व्यक्त करता येईल. ‘प्रतिकृती अशा तऱ्हेने बनविली व वापरली पाहिजे की, विशिष्ट घटनेत प्रभावी असणाऱ्या तिच्याबद्दलच्या विविध पाय् पदांची म्हणजेच मितिहीन समूहांची मूल्ये, अभिकल्पित प्रणालीच्या त्या त्या मितिहीन समूहांच्या मूल्याबरोबर असली पाहिजेत’.

या अटीवरून प्रतिकृती तयार करताना तिची लांबी, रुंदी यांसारखी परिमाणे व तापमान, घनता, स्थितिस्थापकता गुणांक [⟶ स्थितिस्थापकता]  इ. राशींची मूल्ये, प्रकल्पित प्रणालीच्या तुलनेने किती प्रमाणात कमी (किंवा जास्त) केली असता साधर्म्य प्रस्थापित होईल ते समजते आणि त्यानुसार सुयोग्य प्रतिकृती बनविणे शक्य होते. 

द्रायूतून वस्तूची गती : हवेतून जाणारे विमान, तोफगोळा किंवा क्षेपणास्त्र त्याचप्रमाणे पाण्यातून जाणारे जहाज, पाणबुडी किंवा पाणतीर यांची गती या प्रकारात येते. या आविष्कारांचा अभ्यास करताना वस्तूची प्रतिकृती स्थिर ठेवून द्रायू तिच्याभोवती तशाच सापेक्ष गतीने सोडल्यास प्रतिकृतीवर लागू होणाऱ्या प्रेरणांचे वितरण मूळातल्याप्रमाणेच होते. अशा तऱ्हेने प्रतिकृतीचा अभ्यास करणे पुष्कळदा जास्त सोयीचे होते. ⇨वातविवर (ज्यात वस्तूंवरून जाणाऱ्या वायुप्रवाहांचे परिणाम निर्धारित करता येतात असा बंदिस्त मार्ग) व जलविवर यांचे उपयोग याच तत्त्वावर आधारलेले आहेत.  

अशा वस्तूवर लागू होणाऱ्या कर्षण प्रेरणांच्या दृष्टीने पुढील प्रचल परिणामकारक असतात : (१) वस्तूची अभिलक्षण लांबी (d), (२) द्रायूची घनता (p), (३) त्याचा शुद्ध गतिकीय श्यानता गुणांक (μ ⟶ श्यानता), (४) पृष्ठताण (σ), (५) वस्तूचा द्रायुसापेक्ष वेग (v), (६) हा वेग सदिश (वेगाचे परिमाण व त्याची दिशा निर्देशित करणारी रेषा) व वस्तू यांच्यामधील कोन (α). हवेसारख्या संकोच्य (दाब देऊन आकारमान कमी करता येणाऱ्या) द्रायूमधून जाणाऱ्या वस्तूचा वेग हा द्रायूतील ध्वनिवेगाच्या तुलनेने कमी नसेल, तर ध्वनिवेग (C) हा आणखी एक घटक कार्यकारी होतो.

गतीमुळे फारशी उष्णता उत्पन्न होत नसेल, तर गतिकीय साधर्म्यासाठी सामान्यतः कोष्टक क्र. १ मधील पाय् पदे म्हणजेच मितिहीन समूह विचारात घ्यावे लागतात. 

---

कोष्टक क्र१. गतिकीय साधर्म्यासाठी विचारात घ्यावे लागणारे मितिहीन समूह.
मितीहीन समूह		खास नाव	संबंधित भौतिकीय परिणाम
pvd	=R	रेनल्ड्झ अंक	श्यानता
μ
v	=M	माख अंक	(द्रायूची) संकोच्यता
C
v2	= F	फ्रूड अंक (पहिला)	गुरुत्वाकर्षण
dg
pv2d	= W	वेबर अंक (पहिला)	पृष्ठताण
σ
Cpμ	= P	प्रांट्ल अंक	उष्णता संवहन
k
[Cp= स्थिर दाबाखालील वायूची विशिष्ट उष्णता k = उष्णता संवाहकता (⟶ उष्णता उष्णता संवहन) वरील मितिहीन समूह अनुक्रमे ओ. रेनल्ड्झ, ई. माख, डब्ल्यू. फ्रूड, डब्ल्यू. ई. वेबर आणि एल्. प्रांट्ल या शास्त्रज्ञांच्या नावांवरून ओळखण्यात येतात].

परंतु हाती घेतलेल्या समस्येत यांपैकी कोणते परिणाम जास्त जोरदार ठरतील, कोणते कमी जोरदार होतील व कोणते दुर्लक्षणीय मानता येतील याचा अंदाज आधीच करता आला, तर काम जास्त सोपे होते. अनेकदा या परिणामांबद्दलची गणितीय सूत्रे उपलब्ध असतात. त्यांच्यावरून अचूक मार्गदर्शन मिळू शकते. याखेरीज प्रयोग करणाऱ्याची कल्पकता व त्या विषयातील पूर्वानुभव यांचे तर अमोल साहाय्य होतेच.

एक उदाहरण : पाय् सिद्धांताचा उपयोग स्पष्ट करण्यासाठी येथे एक उदाहण विचारात घेऊ. समजा की, हवेतून (ध्वनिवेगापेक्षा बऱ्याच) कमी वेगाने जाणाऱ्या विमानाच्या पंखावरील प्रेरणेचा (F चा) प्रतिकृतीच्या साहाय्याने अभ्यास करावयाचा आहे. या समस्येत पृष्ठताण व संकोच्यता हे परिणाम वगळता येतील, हे प्रथम दर्शनीच उघड होते. म्हणून F हा फक्त d, p, v, μ, व α यांचेच फलन होईल. पाय् सिद्धांतानुसार या प्रचलांपासून मिळणारे α (कोन हा मितीहीन असतो),  

R व	F	हे तीनच मितिहीन समूह होऊ शकतील (यांपैकी	F
	pd2v2		pd2v2

हा समूह प्रमाण मितिहीन समूह नसून प्रचलित समस्येसाठी मितिहीन होईल अशा रीतीने तो बनवून घेतला आहे). मग या समस्येचे अभिलक्षण समीकरण 

F	= f ( R, α) …     …..    …..   ….. (५)
pd2v2

असे मांडता येईल. 

 α च्या दृष्टीने साधर्म्य प्रस्थापित करण्यात काहीच अडचण येत नाही परंतु प्रतिकृतीच्या R चे मूल्य प्रकल्पित विमानाइतके करताना अडचण होते

	(	R =	pv d	).	प्रतिकृतीच्याd चे मूल्य खूप कमीअसते म्हणूनR चे
			μ

मूल्य तेच येण्यासाठी त्याच प्रमाणात p वाढविला पाहिजे. यासाठी प्रतिकृतीवर वातविवरात प्रयोग करताना जास्त दाबाखालील हवा वापरून तिच्या p चे मूल्य इष्ट प्रमाणात वाढविले जाते. R व α यांच्या मूल्यांसाठी प्रयोगावरून F चे मूल्य काढता येते व त्यावरून विमानाच्या पंखावर पडणाऱ्या प्रेरणांची मूल्ये काढता येतात.

अंशतः साधर्म्य : वरील उदाहरणात विमानाचा वेग ध्वनिवेगाइतका किंवा त्याहून जास्त होणार असेल, तर त्याला होणाऱ्या प्रतिरोधात श्यानता, उष्णतेचे संवहन व दाबामुळे होणारा वायूचा संकोच या सर्वांचा वाटा असतो आणि α, R, P, M व γ[वायूच्या दोन विशिष्ट उष्णता C_P व C_V यांचे गुणोत्तर ⟶ उष्णता]  या पाच मितिहीन समूहांचा अंतर्भाव करावा लागेल. मग अभिलक्षण समीकरण

F	= f (α, R, P, M, γ) …   …   …. (६)
pv2d2

असे लिहावे लागेल. गणित करता असे दिसून येते की, R व M या दोघांची सममूल्यता एकाच वेळी साधावयाची असेल, तर त्यासाठी प्रतिकृतीचे आकारमान प्रकल्पित विमानाएवढे मोठे करावे लागेल आणि हे तर अव्यवहार्य आहे.

येथे एक मार्ग असा अनुसरतात की, प्रतिरोधात जास्त मोठा वाटा ज्या परिणामाचा असेल त्याच्याशी संबंधित असलेला मितिहीन समूह बरोबर सममूल्य करावयाचा व दुसरा जास्तीत जास्त सममूल्यतेप्रत आणण्याचा प्रयत्न करावयाचा. वरील विमानाच्या उदाहरणात M बरोबर सममूल्य करून घेतात व R च्या बाबतीत अंशतःच सममूल्यता शक्य होते. या परिस्थितीत मिळणारे निष्कर्ष पूर्णपणे बरोबर येणार नाहीत व त्यांना काही शुद्धी लावल्याशिवाय ते प्रत्यक्ष विमानाला लागू होणार नाहीत, हे उघड आहे.

नद्या, बंदरे इत्यादींच्या प्रतिकृती : भारतात नद्यांच्या प्रतिकृती बनविण्याचे तंत्र १९१६ सालापासून वापरले जात आहे. यासाठी त्या वेळच्या मुंबई सरकारने पुण्याजवळ हडपसर येथे पहिले संशोधन केंद्र सुरू केले. खडकवासला (पुणे) येथील ⇨सेंट्रल वॉटर अँड पॉवर रिसर्च स्टेशन या संशोधन केंद्रामध्ये आतापर्यंत अनेक नद्यांच्या प्रतिकृती बनविण्यात आल्या आहेत. हे केंद्र भारत सरकारने आपल्या ताब्यात घेऊन त्याची फार मोठी वाढ केली आहे. अशीच केंद्रे काही राज्य सरकारांनी व विद्यापीठांनीही चालविली आहेत. त्यांत पंजाब, उत्तर प्रदेश व पश्चिम बंगाल या राज्यांची केंद्रे आणि रुडकी व बंगलोर येथील विद्यापीठीय केंद्रे विशेष उल्लेखनीय आहेत. पूर योजनांचा अभ्यास करण्यासाठी अमेरिकेत जॅक्सन येथे बनविलेली मिसिसिपी नदीची प्रतिकृती व हॉलंडमध्ये बनविलेली ⇨झाइडर झीची प्रतिकृती या जगप्रसिद्ध आहेत.  

अशा तऱ्हेच्या अभ्यासावर काही मर्यादा पडतात व त्या लक्षात घेऊनच हे कार्य करावे लागते. उदा., ३०० किमी. लांबीच्या नदीची प्रतिकृती १०० मी. लांबीची बनविली आहे. याच प्रमाणात प्रतिकृतीतील नदीची खोली ठेवू गेल्यास ती ३ सेंमी. पेक्षाही कमी येईल. म्हणजेच खोलीसाठी घ्यावयाचे मापप्रमाण लांबीच्या मापप्रमाणापेक्षा मोठे घेणे आवश्यक आहे. मूळ नदीच्या ठिकाणची सर्वच परिस्थिती काटेकोरपणे प्रतिकृतीत आणणे केवळ अशक्य आहे.  

वाहत्या पाण्यासंबंधीच्या समस्येत बांधावरील प्रवाह, जलद्वारांतील प्रवाह, कालव्यातील प्रक्षुब्ध प्रवाह, प्रवाहाच्या काठावरील जमिनीची धूप, वाळू व गाळ यांचे प्रवाहामुळे वहन इ. अनेक गोष्टींचा विचार करावा लागतो. नदीच्या प्रतिकृतीत गुरुत्वाकर्षण प्रेरणा प्रमुख असल्याने त्या प्रतिकृतीची मापप्रमाणे फ्रूड यांच्या नियमानुसार ठरविण्यात येतात.

प्रतिकृतीतील नद्यांचे तळ जरूरीप्रमाणे वाळूचे किंवा पक्के काँक्रीटचे बनवावे लागतात. उदा., पुलाच्या खांबाभोवतालच्या वाळूची धूप, नदी सुधारणा अशा प्रकल्पांच्या प्रतिकृतींत तळ वाळूचे, तर धरणातील पाण्याच्या नियंत्रणासारख्या अभ्यासात पक्के तळ वापरणे योग्य ठरते. या दोन प्रकारांनुसार रुंदीचे उंचीच्या मापाशी प्रमाणही वेगळे वापरावे लागते.

---

प्रतिकृतीमधून पाणी सोडावयाचे ते अगदी नियमित वेगाने सोडावे लागते. मूळ ठिकाणी कोठे गाळ जमणे, कोठे वाळूची बेटे तयार होणे, तर इतर कोठे काठाची धूप होणे असे प्रकार घडत असतात. प्रतिकृतीतही ते तसेच त्या त्या ठिकाणी घडतात असे दिसेतो पाण्याचा वेग इ. प्रचल योग्य त्या दिशेने बदलत न्यावे लागतात. अशा तऱ्हेने सुयोग्य प्रतिकृती तयार झाली आहे, याची खातरजमा झाल्यानंतरच इष्ट समस्या सोडविण्याच्या दृष्टीने प्रयोग हाती घेतात. मगच या प्रयोगांच्या निष्कर्षाचा अभिकल्पात उपयोग होईल असा विश्वास बाळगता येतो.

अनुरूपता : जेव्हा भौतिकीच्या एका शाखेतील एखादा (अ हा) प्रचल विशिष्ट मर्यादेपर्यंत दुसऱ्या शाखेतील (आ या) एखाद्या प्रचलासारखा वागतो (म्हणजे त्या संबंधीची गणितीय समीकरणे सारख्याच स्वरूपाची असतात) तेव्हा ते दोन प्रचल परस्परांचे अनुरूप प्रचल आहेत, असे म्हटले जाते. उदा., उष्णतेच्या संवहनात तापमान T याला विद्युत् संवहनात विद्युत् दाब V हा अनुरूप प्रचल आहे.

अनुरूप प्रतिकृती : ध्वनी, द्रायुयामिकी, यामिकी अशा कित्येक क्षेत्रांत अशा समस्यांना तोंड द्यावे लागते की, त्यांमध्ये परस्परांवर कमी-अधिक परिणाम करणारे अनेक घटक अंतर्भूत झालेले असतात. अशा अनेक घटकांची मिळून एक प्रणाली बनते. अशा प्रणालीची त्याच शाखेतील प्रतिकृती बनवून व तिच्यावर प्रयोग करून समस्येची सोडवणूक करणे अशक्यप्राय होते. अशा वेळी मूळ प्रणालीमधील घटकांना अनुरूप अशी दुसऱ्या शास्त्र शाखेतील अनुरूप अशी मूळच्यासारखीच प्रणाली बनवितात. तिला अनुरूप प्रणाली असे म्हणतात. अर्थात ही अनुरूप प्रणाली तयार करण्यास सुकर व कमी खर्चाची असून तिच्यात फेरफार करणे, तिच्यावर प्रयोग करणे व तिच्यात येणारी विविध प्रचलांची मूल्ये मोजणे हे सहज शक्य झाले पाहिजे, तरच ती उपयुक्त ठरू शकेल.

विद्युत् क्षेत्रातील रोधक, धारित्र (विद्युत् भार साठवून ठेवणारे साधन) यांसारखे घटक सहज उपलब्ध होतात. त्यांची विद्युत् मंडले म्हणजेच प्रणाली बनविणे व त्यात फेरफार करणे सोपे असते आणि विद्युत् राशींची सूक्ष्ममापने करणारी उपकरणेही सहज मिळू शकतात. म्हणून प्रयोगासाठी अनुरूप प्रतिकृती ही विद्युत् मंडलाच्या स्वरूपातच प्रायः बनविली जाते. द्रायुयामिकीय, ध्वनिकीय व अभियांत्रिकीय प्रणालींच्या अनुरूप विद्युतीय प्रतिकृतींचा प्रयोगासाठी अनेक ठिकाणी उपयोग होतो.

विद्युत् प्रवाहासंबंधी गणित करताना जी. एस्. ओहम यांचे सूत्र  

विद्युत् प्रवाह (i) =	विद्युत् दाब (V)
	विद्युत् रोध (R)

= k x	विद्युत् दाब (V) x संवाहकाच्या काटच्छेदाचे क्षेत्रफळ (A)
	संवाहकाची लांबी (l)

∴ i =	k V A
	l

 वापरले जाते. येथे k या स्थिरांकाचे मूल्य संवाहकाच्या गुणधर्मावर अवलंबून असते.

मातीची धरणे बांधताना बंधाऱ्याखालून किती प्रमाणात पाणी झिरपेल यांचा आगाऊ अंदाज करणे आवश्यक असते. सच्छिद्र माध्यमातून प्रती सेकंदाला झिरपून वाहणाऱ्या पाण्याचे वस्तुमान Q काढण्यासाठी एच्. पी. जी. डार्सी या फ्रेंच अभियंत्यांचे सूत्र Q = k’iA वापरले जाते. येथे i हे दोन बाजूच्या पाण्याच्या दाबातील फरक व वहनमार्गाची लांबी यांचे गुणोत्तर व A हा वाहकाचा लंबछेद आहे. k’ या गुणांकाचे मूल्य जागेवरच्या परिस्थितीनुसार बदलते. या दोन समीकरणांमधील पराकाष्ठेच्या साम्यावरून विद्युतीय अनुरूप प्रतिकृतीची कल्पना पुढे आली. प्रकल्पित धरणाच्या नमुन्यानुसार विद्युत् मंडल तयार करून त्यात ठिकठिकाणी विद्युत् दाब, विद्युत् प्रवाह व रोध यांची मापने करतात आणि त्यावरून डार्सी यांच्या समीकरणातील अनुरूप राशींची मूल्ये सुलभतेने निश्चित करता येतात.

कोष्टक क्र. २ मध्ये काही गतिकीय राशी व तदनुरूप विद्युतीय राशी दिलेल्या आहेत. त्यावरून राशींची अनुरूपता स्पष्ट होईल. 

कोष्टक क्र.२काही गतिकीय व अनुरूप विद्युतीय राशी

गतिकीय प्रणालीतील राशी

अनुरूप विद्युतीय राशी

वस्तुमानm

प्रवर्तकत्वL

स्प्रिंगेचा गुणांकk

धारकतेचा व्यस्तांक

1

C

संदमन गुणांकb

रोधR

स्थानांतरx

विद्युत् भारq

dq

वेग

dx

विद्युत् प्रवाहi =

dt

dt

प्रेरणाF

विद्युत् दाबV

कंप्रताω

(प्रत्यावर्ती प्रवाह) कंप्रताω

गतीचे समीकरण :

विद्युत् दाबाचे समीकरण :

m d2x

+b

dx

+ kx

Ld2q

+ R

dq

+

q

dt2

dt

dt2

dt

C

= F0sin pt

= V0sin pt

 

[स्प्रिंगेचा गुणांक म्हणजे स्प्रिंगेला लावलेली प्रेरणा व तीमुळे स्प्रिंगेचे होणारे प्रसरण यांचे गुणोत्तर संदमन गुणांक म्हणजे पदार्थाच्या गतीला विरोध करणारी घर्षणजन्य प्रेरणा व पदार्थाचा वेग यांचे गुणोत्तर कंप्रता म्हणजे एका सेकंदात होणाऱ्या आंदोलनांची संख्या संवाहकातीन विद्युत् प्रवाह  ^di/_dt या त्वरेने बदलत असेल व त्यामुळे संवाहकास V हा वर्चोभेद (विद्युत् पातळ्यांतील फरक) प्रवर्तित होत असेल, तर ^V / _{di / dt} = L विद्युत् प्रवर्तकत्व विद्युत् घटकाला q हा विद्युत् भार दिल्यामुळे त्याचे विद्युत् वर्चस् V ने वाढत असेल, तर ^V / _q = C धारकता प्रत्यावर्ती प्रवाह म्हणजे ठराविक कालाने ज्याचे मूल्य व दिशा एकसारखी बदलत असतात असा विद्युत् प्रवाह p = कोनीय कंप्रता =  2π x कंप्रता t – काल F₀ व V₀ ही F व V या राशींची कमाल मूल्ये]

येथे हे नमूद करणे जरूर आहे की, यामिकीय प्रणालीत जेव्हा प्रेरणा एकसरीत असतात तेव्हा अनुरूप विद्युतीय प्रणालीत वर्चोभेद अनेकसरीत घ्यावे लागतात. अनेक यामिकीय प्रणालींमधील घटकांची प्रेरित कंपने कशी नियंत्रित करावीत ही एक महत्त्वाची समस्या असते. तिची सोडवणूक करण्यासाठी अनुरूप विद्युतीय प्रणालीचा चांगला उपयोग होतो. उदा., मोटारगाडीत बसणाऱ्या माणसांना बसणारे धक्के कमीत कमी होण्यासाठी कोठे कोठे व किती ताकदीच्या स्प्रिंगा बसवाव्यात, मोटारीच्या सांगाड्यात वस्तुमानाचे वितरण कसे करावे हे निश्चित करण्यासाठी अनुरूप विद्युतीय प्रणालीचा उपयोग करतात. या संबंधीची विद्युत् प्रणाली इतकी जटिल होते की, तिची उकल करण्यासाठी संगणकाची मदत घ्यावी लागते.

---

ध्वनिकीय-विद्युतीय अनुरूपता : ध्वनिकीय प्रणालीतील मूलभूत राशी व त्यांच्या अनुरूप विद्युतीय राशी कोष्टक क्र. ३ मध्ये दिल्या आहेत.

कोष्टक क्र. ३. मूलभूत ध्वनिकीय राशी व अनुरूप विद्युतीय राशी
ध्वनिकीय राशी	अनुरूप विद्युतीय राशी
(ध्वनिकीय) दाब p	विद्युत् दाब V
आयतन प्रवाह = ध्वनि-आंदोलनजन्य	विद्युत् प्रवाह i
कणवेग U x तेथील काटच्छेदाचे क्षेत्रफळ S
ध्वनिकीय प्रवर्तकत्व La	विद्युत् प्रवर्तकत्व L
ध्वनिकीय धारकता Ca	विद्युत् धारकता C
ध्वनिकीय रोध Ra	विद्युत् रोध R

ध्वनिकीय प्रणालीत लहान व्यासाच्या नळ्या, मोठ्या व्यासाच्या कोठ्या, तबकडीतील छिद्रे अशा घटकांचा वापर होतो. छिद्रे व लहान नळ्या प्रवर्तकाप्रमाणे कार्य करतात नळीची परिणामी लांबी l_e, तिच्या काटच्छेदाचे क्षेत्रफळ S व हवेची घनता p असल्यास तिचे ध्वनिकीय प्रवर्तकत्व 

La	=	ple	किग्रॅ./मी. इतके असते.
		S

रुंद कोठीचे आयतन (घनफळ) V व हवेतील ध्वनिवेग c असल्यास तिची ध्वनिकीय धारकता

Ca =	V	मी.४ से.४ / किग्रॅ. असते.
	p c2

ध्वनीमुळे होणाऱ्या वायुकणांच्या आंदोलनांना श्यानतेमुळे विरोध होतो व त्यामुळे काही ध्वनिऊर्जेचा (उष्णतेत रूपांतर होऊन) ऱ्हास होतो. हा विरोध विद्युत् रोधासारखेच कार्य करतो म्हणून त्याला ध्वनिकीय रोध असे म्हणतात.  

ग्रामोफोनची ध्वनिमंजुषा, तिला जोडणारी नळी व पुढील कर्णा, ध्वनिक्षेपकाची पेटी, सनईसारख्या वाद्याची नळी, मोटारीच्या ध्वनिशामक इ. अनेक साधने इतर कार्याबरोबरच ध्वनिकीय गाळणी म्हणून कार्य करीत असतात. त्यांचे कार्य पर्याप्त करण्यासाठी अनुरूप विद्युत् प्रणालीवर प्रयोग करून त्यांची व त्यांच्या घटकांची मापे, आकार ठरविली जातात. या पद्धतीने मिळणारे निष्कर्ष बरेचसे ढोबळ स्वरूपाचे असतात.

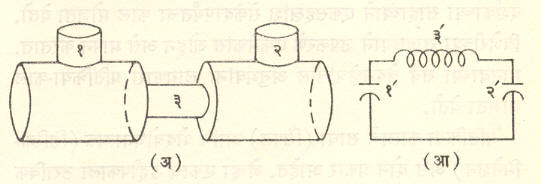
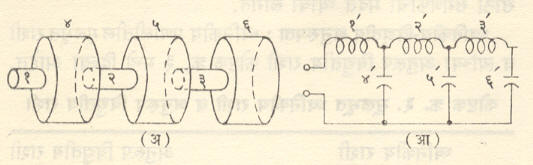
मोटार किंवा फटफटी यांच्या एंजिनाच्या आवाजात उच्च कंप्रतांच्या ध्वनींचे प्राबल्य असते. हा आवाज परिणामकारकपणे कमी करावयाचा म्हटल्यास या उच्च कंप्रतांचे ध्वनीच बाहेर येऊ देता कामा नयेत. अशा गाळणीला निम्नपारक गाळणी म्हणतात. आ. १ (अ) मध्ये अशा गाळणीची मूलभूत रचना व १ (आ) मध्ये अनुरूप विद्युत् मंडल दाखविले आहे. अशा अनेक मूलभूत गाळण्या एकीपुढे एक जोडून मोटारीचा ध्वनिशामक तयार करतात. त्यामुळे बाहेर येणाऱ्या ध्वनीची तीव्रता मोठ्या प्रमाणावर कमी होते. [आ. २ (अ) व (आ)].

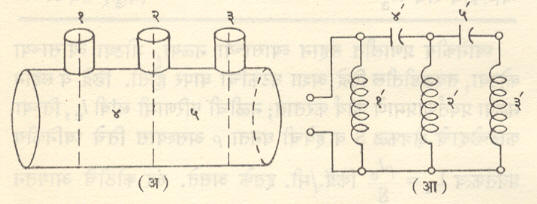
विशिष्ट कंप्रतेच्या वरच्या कंप्रता पार जाऊ देणाऱ्या गाळणीला उच्चपारक गाळणी (आ. ३) म्हणतात. (चित्रपत्र १४, १५).

.

पहा : द्रायुयामिकी वातविवर वायुयामिकी सदृशीकरणत. 

संदर्भ : 1. Bayley, Thomas, Model Making in Cardboard, Leicester, 1964.

           2. Central Board of Irrigation, Manual of River Behaviour Control and Training, New Delhi.

           3. Eves, John, Model Making in Schools, London, 1961.

           4. Hopwood, R. R. Science Model Making, London, 1963.

           5. Kline, S. J. Similitude and Approximation Theory, New York, 1965.

           6. Machol, R. E., Ed. Systems Engineering Handbook, New York, 1965.

           7. Pankhurts, R. C. Dimensional Analysis and Scale Factors, New York, 1964.

           8. Raghunath H. M. Dimensional Analysis and Hydraulic Model Testing, Bombay, 1968.

           9. Streeter, V. L., Ed. Handbook of Fluid Dynamics, New York, 1961.

  

शहाणे, शा. वि आपटे, ज. पां. सप्रे, गो. वि.

पुरोहित, वा. ल. गुप्ते, रा. द.

---

                               

---

                        

“