प्रकाशीय व्यूहांतील विपथन

प्रकाशीय व्यूहांतील विपथन : विविध प्रकारचे आरसे, भिंगे, लोलक व तत्सम प्रयुक्तींच्या काही विशिष्ट प्रकारे केलेल्या मांडणीमुळे तिच्यावर पडणाऱ्या, प्रकाशावर परावर्तन, प्रणमन, प्रकीर्णन, शोषण, ध्रुवण इ. क्रिया [⟶ प्रकाशकी] घडून येतात. अशा मांडणीला प्रकाशीय व्यूह म्हणतात. अशा व्यूहाच्या काही अंगभूत गुणधर्मांमुळे त्यांच्याद्वारे मिळणाऱ्या प्रतिमेमध्ये विविध प्रकारचे दोष उत्पत्र होतात. या दोषांना विपथने असे म्हणतात.

प्रकाशविज्ञानाच्या तत्त्वानुसार आदर्श प्रकाशीय व्यूहामुळे बिंदुमात्र वस्तूची प्रतिमा बिंदुमात्रच यावयास हवी. त्याचप्रमाणे व्यूहाच्या अक्षाला लंब ठेवलेल्या लहान आकारमानाच्या वस्तूची प्रतिमा आकारमानाने तंतोतंत वस्तूसारखीच असावयास पाहिजे. भिंग (किंवा भिंग-समुच्चय) अथवा आरसा यांच्यावर आपाती होणारे किरण जर त्याच्या अक्षाभोवतालच्या अगदी छोट्या भागावर पडत असतील, तर त्या किरणांना उपाक्षीय किरण असे म्हणतात. भिंगाच्या अथवा आरशाच्या बाबतची गणितीय सूत्रे, फक्त उपाक्षीय किरणांनी प्रतिमा तयार होत असेल, तरच लागू पडतात परंतु प्रत्यक्ष उपयोगात आरशाचा वा भिंगाचा बराच मोठा भाग कार्यवाहीत येत असतो व त्यामुळे तयार होणाऱ्या या प्रतिमेत काही दोष म्हणजेच विपथने उत्पन्न होतात. ही विपथने एकवर्णी (ज्यातील तंरगलांबी अतिशय अरुंद पल्ल्यात निबद्ध आहेत असा एकाच रंगाचा) प्रकाश वापरला तरीही टाळता येत नाहीत. त्यामुळे त्यांना एकवर्णी विपथने असेही संबोधण्यात येते. प्रकाशीय प्रयुक्तींमध्ये आरशांपेक्षा भिंगांचाच मुख्यत्वे करून वापर केला जातो म्हणून पुढील विवेचन प्रामुख्याने भिंग-प्रणालींच्या (भिंग-समुच्चयांच्या) संदर्भातच केलेले आहे.

विपथनांचे प्रकार : असे समजा की, भिंगाच्या अक्षावर ठेवलेल्या बिंदुमात्र वस्तूपासून तिरक्या दिशेने निघून भिंगाच्या परिघावर आपाती होणारा किरण भिंगाच्या मुख्य अक्षाशी θ हा कोन करतो. 

 परंतु θ अतिशय लहान असल्यास आपाती होणारे सर्व किरण उपाक्षीय होतील व वरील अनंत श्रेढीमध्ये b³,θ⁵ वगैरे θ ची उच्च घातयुक्त पदे θ च्या मानाने उपेक्षणीय ठरतील म्हणून sin θ = θ मानता येईल. असे मानून प्रतिमेबद्दल मांडलेल्या सिद्धांताला प्रथम क्रम सिद्धांत असे म्हणतात. समजा, θ वाढता वाढता इतका मोठा झाला की b³ चे पद उपेक्षणीय नाही परंतु θ⁵ व त्यापेक्षा उच्च घातांकांची पदे उपेक्षणीय आहेत. या गृहीतावर आधारलेल्या सिद्धांताला तृतीय क्रम सिद्धांत असे म्हणतात. या सिद्धांताचे विवरण १८५५ मध्ये एल्. पी. सिडेल यांनी केले, म्हणून त्याला सिडेल सिद्धांत असेही म्हणतात.

या सिद्धांतानुसार, जास्त तिरके किरण आपाती होत असल्यास, व्यूहातून निर्गत होणारे तरंगमुख [⟶ तरंग गति] पूर्णपणे गोलीय असत नाही. आदर्श परिस्थितीत ते पूर्णपणे गोलीय असते. गोलीय आकारापासून तरंगमुखाचा होणारा हा भ्रंश सर्व विपथनांना कारणीभूत आहे. सिडेल यांनी असे दाखवून दिले की, प्रथम क्रमाच्या सिद्धांताच्या समीकरणात पाच जादा पदे अंतर्भूत केल्यास तृतीय क्रम क्रम सिद्धांताचे समीकरण मिळते. आदर्श परिस्थितीत ही पाचही पदे शून्यप्राय असतात. त्या पाचांपैकी प्रत्येक पद एका वेगळ्या विपथनाचे निदर्शक असते. ही पाच विपथने म्हणजे (१) गोलीय विपथन, (२) प्रतिमा-विकार, (३) दृष्टिवैषम्य, (४) वक्रता, (५) विकृती ही होत.

प्रकाशीय व्यूहाचा छिद्रव्यास (व्यूहाच्या अक्षास समांतर असलेली किरण शलाका व्यूहाच्या जेवढ्या पृष्ठभागातून आत जाऊन प्रतिमा पाडू शकते तेवढ्या पृष्ठभागाचा व्यास) अधिकच मोठा असल्यास θ⁵ ची पदे किंवा त्याहूनही उच्च घातांकांची पदे विचारात घ्यावी लागतील परंतु नेहमीच्या व्यूहासाठी तृतीय घातापर्यंतच्या पदांचा अंतर्भाव करणे पुरेसे असते, असे दिसून आले आहे.

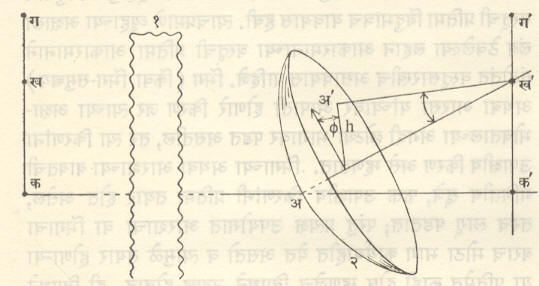
विपथनांच्या तपशीलवार चर्चेत फार क्लिष्ट गणितकृत्ये करणे जरूर पडते. ती टाळून फक्त विपथनांच्या बद्दलची सर्वसामान्य रूपरेषा तरंग सिद्धांतानुसार [⟶ प्रकाश] पुढे दिली आहे. समजा कखग

(आ. १) या वस्तूची एका विशिष्ट प्रकाशीय व्यूहामुळे (एक किंवा अधिक भिंगांनी बनलेल्या प्रणालीमुळे) उपाक्षीय किरणांनी तयार झालेली क’ख’ग’ ही प्रतिमा आहे. ख पासून ख’ कडे जाणारा किरण निर्गत तरंगमुखाला अ’ मध्ये छेदतो.

अ’ख’क’ आणि कक’ख’ या प्रतलांमधील कोन ϕ आहे

येथे h हे अ’ चे अख’ पासूनचे अंतर h₀ हे h चे कमाल मूल्य आहे. मग विपथन फलन W हे r, σ व ϕ यांचे फलन असते. छिद्रव्यास व प्रतिमेची उंची फार नसेल, तर W हे फलन घात श्रेढीच्या स्वरूपात लिहिता येईल. सममितीच्या अनुरोधाने या श्रेढीतील काही पदे गाळता येतील. संदर्भ गोलाचा मध्य सोयीस्कर ठिकाणी आहे असे मानल्यास विपथन फलन पुढीलप्रमाणे लिहिता येईल.

W = (_oC₄,_or⁴ + ₁C₃,₁ σr³ cos ϕ +₂C₂,₂ σ²r²cos²ϕ

                               + ₂C₂, _oσ²r² + ₃C₁,₁σ³r cos ϕ) + ₀C⁶,₀r⁶ +…                                   (१)

या समीकरण C या सहगुणकांचे पादांक अनुक्रमे σ, r आणि cos ϕ  यांचे घातांक आहेत. 

गोलीय विपथन : समी. (१) मध्ये σ = 0 असल्यास (म्हणजेच प्रतिमेवरील बिंदू ख’ चे अक्षापासूनचे अंतर शून्यप्राय असल्यास)

W = ₀C₄, ₀r⁴ + ₀C₆, ₀r⁶ +  …    …   …   (१ अ)

या समीकरणाने दिल्या जाणाऱ्या विपथनास गोलीय विपथन असे म्हणतात. छिद्रव्यासानुसार भिंगाच्या केंद्रांतरात होणारा बदल म्हणजेच गोलीय विपथन. छिद्रव्यास लहान असल्यास यातील पहिले पद (₀C₄,₀r⁴) दुसऱ्या पदाच्या मानाने खूपच मोठे असते आणि त्याला प्राथमिक किंवा सिडेल यांचे गोलीय विपथन असे म्हणतात. ₀C₆,₀r⁶ या पदाला दुय्यम गोलीय विपथन असे म्हणतात. नेहमीच्या प्रकाशीय व्यूहांच्या बाबतीत फक्त प्राथमिक गोलीय विपथन लक्षात घेणे पुरेसे ठरते.

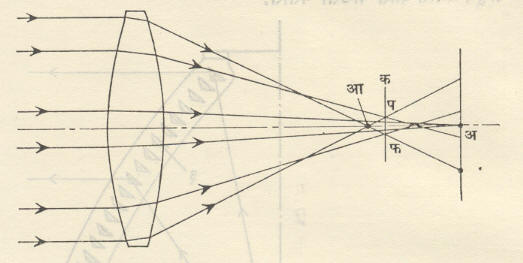
गोलीय विपथनामुळे (आरशाचे किंवा) भिंगाचे परिघीय किरणांसाठी असणारे केंद्रांतर उपाक्षीय किरणांच्या केंद्रांतरापेक्षा कमी असते. आ. २ मध्ये आ हे परिघीय केंद्र व आहे त्या भिंगाचे उपाक्षीय केंद्र आहे. अआ या अंतराला अन्वायाम गोलीय विपथन असे म्हणतात. या विपथनामुळे वस्तुबिंदूपासून निघालेले व भिंगातून बाहेर येणारे सर्वच्या सर्व किरण कोणत्याही एका बिंदूत केंद्रित होऊ शकत नाहीत. त्यामुळे प्रतिमेचा रेखीवपणा कमी होतो. आकृतीत क या ठिकाणी पडदा ठेवल्यास त्याला सर्व किरण पफ या व्यासाच्या वर्तुळात छेदतील. येथे या वर्तुळाचा व्यास किमान होतो व म्हणून प्रतिमेचा रेखीवपणा जास्तीत जास्त असतो. या वर्तुळाला ‘किमान संकरवृत्त’ असे म्हणतात.

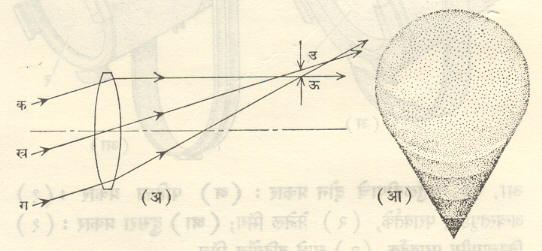
प्रतिमा-विकार : समी. (१) मधील ₁C₃,_1 σr³cos ϕ या पदाने व्यक्त होणाऱ्या विपथनाला प्राथमिक प्रतिमा-विकार असे म्हणतात. थोडक्यात प्रतिमा-विकार म्हणजे छिद्रव्यासानुसार होणारा प्रतिमेच्या विवर्धनातील बदल होय. cos ϕ च्या ३, ५ अशा विषम घातांकयुक्त पदांनी दुय्यम, तिय्यम वगैरे प्रतिमा-विकार व्यक्त होतात. मुख्य अक्षापासून जरा दूर असणाऱ्या वस्तुबिंदूच्या बाबतीतच प्रतिमा-विकार संभवतो [आ. ३ (अ)]. या विपथनामुळे बिंदुमात्र वस्तूची प्रतिमा काहीशी धूमकेतूच्या आकृतीसारखी मिळते [आ. ३ (आ)]. या विपथनाचे विवरण करण्यासाठी आपण असे मानू की, प्रकाशीय व्यूह म्हणजे फक्त एक भिंग असून त्यामध्ये प्रतिमा-विकाराशिवाय इतर कोणतेही विपथन नाही. भिंगावर त्याच्या मध्याभोवती लागोपाठ एकमध्य (एकच मध्य परंतु निरनिराळी त्रिज्या असलेली) वर्तुळे काढली, तर सबंध भिंगाची अनेक वलयाकृती पट्ट्यांमध्ये विभागणी करता येईल. यांपैकी प्रत्येक पट्ट्याचे परिणामी केंद्रांतर

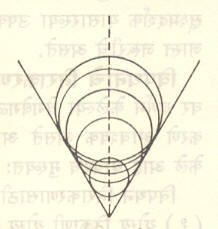
वेगळे असते. त्यामुळे वेगवेगळ्या पट्ट्यांतून जाणाऱ्या किरणांमुळे एकाच वस्तुबिंदूच्या पडद्यावर मिळणाऱ्या प्रतिमा म्हणजे वेगवेगळ्या त्रिज्यांची व वेगवेगळ्या ठिकाणी मध्य असलेली वर्तुळे (आ. ४) असतात. ती एकमेकांवर पडून त्यामुळे शेवटी धूमकेतू सदृश आकाराची प्रतिमा मिळते.

प्रतिमा-विकार हा असममित असल्यामुळे दूरदर्शक किंवा सूक्ष्मदर्शकातील लंघक तंतू (वस्तुभिंगामुळे जेथे प्रतिमा निर्माण होते अशा एकमेकांना लंब असलेल्या आणि ज्यांचा छेदबिंदू दूरदर्शकांच्या-वा सूक्ष्मदर्शकाच्या-अक्षावर आहे अशा घातूच्या सूक्ष्म तारा, कोळ्याच्या जाळ्याचे धागे वा तत्सम सूक्ष्म तंतू) प्रतिमेच्या नक्की कोणत्या बिंदूवर संपाती करावे हे समजणे अवघड होते. ही अडचण गोलीय विपथनाच्या बाबतीत येत नाही.

 दृष्टिवैषम्य व क्षेत्र-वक्रता : समी. (१) मधील ₂C₂,₂ σ²r²cos² ϕ या पदाने व्यक्त होणाऱ्या विपथनाला प्राथमिक दृष्टिवैषम्य हे नाव असून cos ϕ चे समघातांक असणारी इतर पदे अधिक उच्च क्रमाचे दृष्टिवैषम्य दिग्दर्शित करतात. हे विपथनही अक्षापासून अधिक दूर असणाऱ्या वस्तुबिंदूच्या बाबतीतच आढळून येते. 

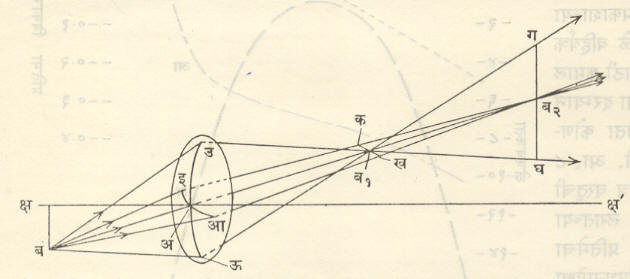
 एकंदरीत पाहता दृष्टिवैषम्ययुक्त निर्गत तरंगमुखाची वक्रता सर्वत्र सारखी असत नाही. त्यामुळे अक्षापासून दूर असणाऱ्या बिंदुमात्र वस्तूची प्रतिमा ही दोन वेगवेगळ्या ठिकाणी असलेल्या परस्पर लंब अशा दोन रेषाच असते. या दोन रेषांचे दरम्यान कोठेही पडदा ठेवल्यास त्यावर मिळणारी प्रतिमा एक अस्पष्ट वर्तुळ किंवा लंबवर्तुळ असते. एका विशिष्ट ठिकाणी पडदा ठेवल्यास हे वर्तुळ किमान व्यासाचे असते व त्याला किमान अस्पष्टतेचे वर्तुळ असे म्हणतात. हीच सर्वांत समाधानकारक प्रतिमा होय. आ. ५ मध्ये ब हा वस्तूवरील अक्षापासून दूर असलेला बिंदू असून अ हा भिंगाचा प्रकाशीय मध्य आहे. बअ या किरणाला प्रमुख किरण म्हणतात आणि बअ व भिंगाचा मुख्य अक्ष क्षअक्ष’ यांनी निश्चित केलेल्या बउअऊ या प्रतलाला स्पर्शीय प्रतल असे म्हणतात. त्याचप्रमाणे स्पर्शीय प्रतलाला लंब आणि बअ या प्रमुख किरणामधून जाणाऱ्या बआअइ प्रतलाला अरीय प्रतल असे म्हणतात. निर्गत तरंगमुख पूर्णपणे गोलीय नसल्याने स्पर्शीय प्रतलातील सर्व किरण ब_१ येथे केंद्रित होतात, तर अरीय प्रतलातील किरण ब_२ येथे केंद्रित होतात. सर्वच्या सर्व निर्गत किरणांचा विचार केल्यास असे दिसते की, यांचे दोन गट कख व गघ या दोन रेषांमधून जातात. यांतील गघ ही रेषा स्पर्शीय प्रतलात असून कख अरीय प्रतलात आहे व प्रमुख किरणाला लंब आहे. अशा तऱ्हेने ब या एका वस्तुबिंदूच्या दोन रेषात्मक प्रतिमा मिळतात, यालाच दृष्टिवैषम्य म्हणतात. कख या रेषेला प्राथमिक प्रतिमा व गघ ला दुय्यम प्रतिमा असे म्हणतात आणि या दोन रेषांमधील (प्रमुख किरणानुसारी) अंतराला दृष्टिवैषम्य-फरक असे म्हणतात. ब हा वस्तुबिंदू अक्षापासून जितका जास्त दूर जाईल तितका दृष्टिवैषम्य-फरक वाढत जातो.

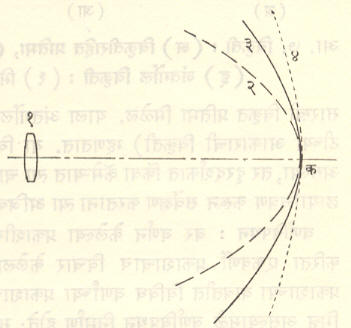
वर उल्लेखिलेला ब हा वस्तुबिंदू भिंगाच्या अक्षावरच असल्यास त्याची प्राथमिक प्रतिमा, दुय्यम प्रतिमा व किमान अस्पष्टतेचे वर्तुळ ही सर्व अक्षावर एकाच ठिकाणी क येथे पडतात. आता वस्तुबिंदू अक्षापासून व त्याला लंब दिशेने दूर दूर नेत गेल्यास या तिन्हींची स्थाने परस्परांपासून जास्त जास्त अलग होत जातात व त्याच बरोबर अक्षापासूनही जास्त जास्त दूर जातात. आ. ६ मध्ये दाखविलेल्या बिंदुपथावरून या बदलांचे एकूण स्वरूप लक्षात येईल. हे सर्व बिंदुपथ अन्वस्तीय (त्रिमितीमध्ये अन्वस्तपृष्ठीय म्हणजे अन्वस्त आपल्या अक्षाभोवती फिरविल्यास निर्माण होणाऱ्या पृष्ठीय आकाराचे) असतात. किमान संकर वृत्ताच्या जागी प्रतिमा जास्तीत जास्त रेखीव असते. म्हणून त्या ठिकाणच्या आलेखाला कमाल रेखीवतेचे  पृष्ठ किंवा जे. पेट्झवेल या शास्त्रज्ञांच्या नावावरून पेट्झवेल पृष्ठ असे म्हणतात.

दृष्टिवैषम्य-फरक हा एकाच भिंगाच्या बाबतीत भिंगाचा प्रणमनांक [⟶ प्रकाशकी] व त्याच्या पृष्ठांची वक्रता आणि भिंग समुच्चयाच्या बाबतीत यांखेरीज त्यांच्यामधील अंतरावरही अवलंबून असतो.

प्रणमनांक वक्रता व भिंगांमधील अंतरे हे प्रचल (विशिष्ट परिस्थितीत स्थिर असणाऱ्या राशी) योग्य त्या तऱ्हेने निवडल्यास अरीय व स्पर्शीय वक्र पेट्झवेल वक्राशी संपाती करता येतात म्हणजेच दृष्टिवैषम्य शून्य होते. मग प्रकाशीय व्यूहाच्या अक्षाला लंब अशा ठेवलेल्या रेखीय वस्तूची प्रतिमा पेट्झवेल पृष्ठावर केंद्रित होईल, म्हणजे एखाद्या सपाट पडद्यावर प्रतिमेचे सर्व भाग एकाच वेळी केंद्रित होऊ शकणार नाहीत. पेट्झवेल पृष्ठाचा आकार लक्षात घेता हे स्पष्ट होईल की, पडदा प्रथम क येथे (आ. ६) ठेवल्यास वस्तूच्या अक्षावरील भागाचीच प्रतिमा सुस्पष्ट दिसेल. पडदा जसजसा भिंगाकडे न्यावा तसतसे अक्षापासून अधिकाधिक दूरच्या भागांची प्रतिमा स्पष्ट होत जाईल. सपाट पडद्यावर संपूर्ण प्रतिमा एकाच वेळी सुस्पष्ट न मिळण्याच्या या दोषाला क्षेत्र-वक्रता असे म्हणतात.

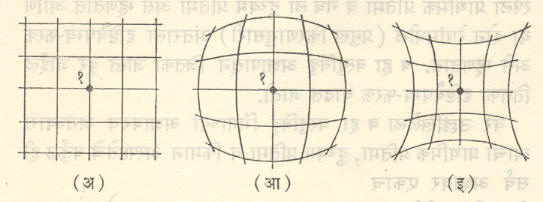
विकृती : समी. (१) मधील ₃C₁,₁σ³r cos ϕ  हे पद विकृती (विपथन) दर्शविते. कल्पना करा की, विकृतीखेरीज बाकीची सर्व विपथने शून्य आहेत व वस्तू म्हणून अक्षाला लंब अशी चौरसांची जाळी ठेवली आहे [आ. ७ (अ)]. विकृतींमुळे वस्तूमधील वेगवेगळ्या भागांचे वर्धन वेगवेगळे होते. अक्षापासून जो जो दूर जावे तो तो वर्धन कमी होत गेल्यास आ. ७ (आ) सारख्या आकाराची प्रतिमा मिळेल. याला बहिर्गोल विकृती (किंवा पिंपाच्या आकाराची विकृती) असे म्हणतात. याउलट परिस्थिती असल्यास आ. ७ (इ) सारखी विकृती प्रतिमा मिळेल. याला अंतर्गोल विकृती (किंवा सोंगटीच्या आकाराची विकृती) म्हणतात. या विकृती थोड्या प्रमाणात असल्या, तर दूरदर्शकात किंवा कॅमेऱ्यात त्या चालू शकतात परंतु हवाई छायाचित्रण करून सर्वेक्षण करताना त्या अजिबात असता कामा नयेत.

 वर्णविपथन : वर वर्णन केलेल्या प्रकाशीय व्यूहातील विपथनांकरिता एकवर्णी प्रकाशाचाच विचार केलेला होता परंतु बहुवर्णी प्रकाशाच्या बाबतीत विविध वर्णांच्या प्रकाशाच्या प्रणमनांकांची मूल्ये भिन्न असल्यामुळे वर्णविपथन निर्माण होते म्हणून ते फक्त भिंगांच्या बाबतीतच शक्य आहे. आरशाने निर्माण होणाऱ्या प्रतिमांत वर्णविपथन संभवतच नाही.

भिंगासाठी केंद्रांतराचे सूत्र पुढीलप्रमाणे आहे.

 येथे f भिंगाचे केंद्रांतर, R₁, R₂ भिंगाच्या दोन पृष्ठांच्या वक्रता त्रिज्या व μ भिंगाच्या द्रव्याचा प्रणमनांक आहे परंतु प्रणमनांक प्रकाशाच्या तरंगलांबीनुसार (स्थूलमानाने रंगानुसार) बदलतो. त्यामुळे बहिर्वक्र भिंगाचे केंद्रांतर निळ्या रंगासाठी किमान व तांबड्या रंगासाठी कमाल मूल्याचे असते. वर्णपटातील इतर रंगांची केंद्रांतरे या दोहोंच्या दरम्यान असतात (आ. ८). यामुळे पांढरा प्रकाश वापरला असता कोणत्याही बिंदुमात्र वस्तूची बिंदुमात्र प्रतिमा मिळू शकत नाही. आ. ८ मध्ये इ या बिंदूच्या ठायी पडदा ठेवल्यास त्यावर बिंदुमात्र वस्तूची प्रतिमा किमान व्यासाचे वर्तुळ (किमान संकरवृत्त) असते. लगतच्या वस्तुबिंदूंची अशी प्रतिमा वर्तुळे परस्परांवर पडल्यामुळे प्रतिमेचा रेखीवपणा कमी होतो. याबबतीत सामान्यतः गोलीय विपथनापेक्षा वर्णविपथन जास्त प्रभावी असते. म्हणून अगदी साध्या प्रकाशीय उपकरणात सुद्धा वर्णविपथनाचे निराकरण करण्याला प्राधान्य दिले जाते.

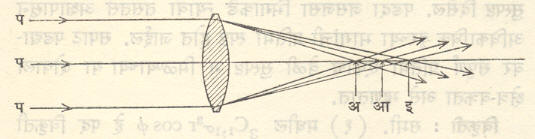
तांबड्या व निळ्या किरणांच्या केंद्रबिंदूंमधील अंतराला ‘अन्वायाम वर्णविपथन’ असे म्हणतात. कॅमेऱ्यासारख्या साधनातील भिंगाच्या बाबतीत हे अन्वायाम वर्णविपथन कमी करणे विशेष जरूरीचे असते.

तांबड्या व निळ्या किरणांनी बनलेल्या (विशिष्ट वस्तूंच्या) दोन प्रतिमांच्या उंचीमधील फरकाला ‘अनुप्रस्थ वर्णविपथन’ असे म्हणतात. या विपथनामुळे प्रतिमेच्या कडा रंगीत दिसतात. दूरदर्शक किंवा सूक्ष्मदर्शक यासारख्या उपकरणामध्ये या विपथनाचे निराकरण करणे जास्त जरूरीचे असते.

विपथनांचे निराकरण : उच्च दर्जाच्या प्रकाशीय उपकरणातून वर वर्णन केलेल्या वेगवेगळ्या विपथनांचे जास्तीत जास्त निराकरण करणे आवश्यक असते आणि विपथनांचे किती प्रमाणात निर्मूलन केले आहे यावरच मुख्यतः त्या उपकरणाची गुणवत्ता व किंमत ठरते.

विपथन निराकरणासाठी सामान्यतः पुढील उपाय योजले जातात : (१) योग्य ठिकाणी योग्य आकाराचे अटकाव वापरणे, (२) भिंगपृष्ठांच्या वक्रता योग्य तऱ्हेने बदलणे, (३) भिंगे तयार करण्यासाठी खास प्रकारच्या काचांचा उपयोग करणे, (४) एका भिंगाऐवजी अनेक भिंगांची प्रणाली वापरणे.

वरील उपाय अलग अलगपणे किंवा एकत्रित रीत्या वापरता येतात.

योग्य व्यासाचे द्वार असलेला अटकाव भिंगांच्या मागे किंवा पुढे ठेवून त्याचे भिंगापासूनचे अंतर बदलत गेल्यास विकृती, प्रतिमा-विकार, दृष्टिवैषम्य व क्षेत्र-वक्रता हे दोष कमीजास्त होतात परंतु गोलीय विपथन किंवा अन्वायाम वर्णविपथन याच्यावर त्याचा काहीच परिणाम होऊ शकत नाही. आ. ९ मधील आलेखांत हे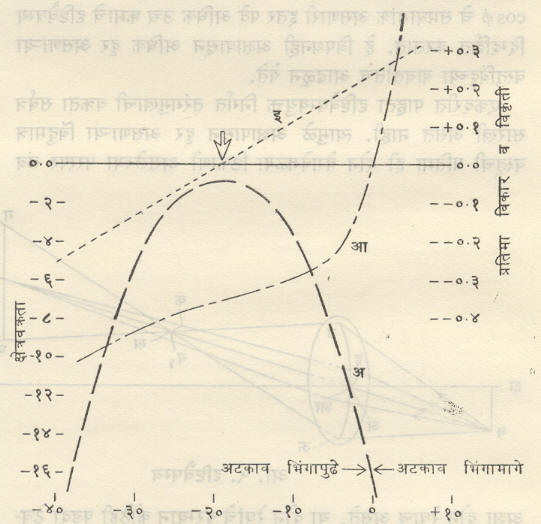 

फेरफार कसे होतात ते एका विशिष्ट भिंगाच्या बाबतीत दाखविले आहे. या वक्रांवरून हे दोष किमान होण्यासाठी अटकाव कोठे ठेवावा हे ठरविता येते.

विशिष्ट केंद्रांतर असलेल्या भिंगाच्या दोन्ही बाजूंच्या वक्रता-त्रिज्या बदलल्या असता, प्रतिमा-विकार व गोलीय विपथन कसकसे बदलतात, त्याचेही याचप्रमाणे वक्र काढून त्यावरून हे दोष किमान करण्याकरिता योग्य अशा वक्रता-त्रिज्या निवडता येतात.

भिंगासाठी वेगवेगळ्या खास प्रकारच्या काचा तयार करण्यात आल्या आहेत. परिदर्शकत्व, अपस्करणशीलता (दोन रंगांचे किरण परस्परांपासून अलग करण्याची क्षमता), परावर्तकत्व गुणांचा येथे मुख्‍यतः विचार करावा लागतो. त्‍यावरून इतर दोष दूर करता येतात.

एका भिंगाने निर्माण होणारे एक विशिष्ट विपथन धन असून दुसऱ्यामुळे ते विपथन ऋण होत असेल, तर त्‍या दोन भिंगांच्‍या एकत्र उपयोगाने त्‍या विपथनाचे अंशतः किंवा संपूर्ण निराकरण करता येईल. भिंग-प्रणाली वापरण्‍यातील मुख्‍य तत्त्व हेच आहे.

वर्णविपथनाचे निराकरण : या विपथनाच्‍या निराकरणासाठी हायड्रोजनाची C रेषा (तांबडी), सोडियमाची D रेषा (पिवळी) व हायड्रोजनाची F रेषा (निळी) या प्रमाण तरंगलांब्या घेतल्‍या जातात. त्‍यांच्‍याकरिता भिंगद्रव्‍याचे प्रणमनांक अनुक्रमे μ_C, μ_D व μ_F आणि केंद्रांतरे f_C , f_D व f_F या चिन्‍हांनी व्‍यक्‍त केली जातात. एकूण दृश्‍य वर्णपटात D रेषेचे स्‍थान मध्‍यवर्ती असते. त्‍यामुळे f_D हे भिंगाचे सरासरी केंद्रांतर येते.

वर्णविपथनाचे निराकरण करण्‍यासाठी सामान्‍यतः भिंगाची f_C व f_F ही दोन केंद्रांतरे सममूल्‍य करावी लागतात. ही गोष्ट एकाच भिंगाच्‍या बाबतीत शक्‍य नसल्‍याने त्‍यासाठी दोन भिंगे एकत्र करून त्‍यांचे जोडभिंग बनवितात. जोडीतील दोन भिंगे वेगवेगळ्या द्रव्‍यांची असून त्‍यांपैकी एक अभिसारी (किरण एका बिंदूकडे केंद्रित करू शकणारे) व दुसरे अपसारी (किरण परस्‍परांपासून दूर नेऊ पाहणारे) असावे लागते. वर्णविपथनरहित अशा भिंगजोडीला ‘विवर्ण भिंग’ किंवा ‘विवर्ण भिंगजोडी’ असे म्‍हणतात. विवर्ण भिंगापासून मिळणारे निराकरण अनेक प्रकाशीय उपकरणांत पुरेसे असते परंतु जास्‍त उच्‍च दर्जाच्‍या निराकरणासाठी तीन भिंगांपासून तयार केलेले जोडभिंग वापरतात. अशा जोडभिंगात वर्णविपथन व गोलीय विपथन या दोहोंचेही एकदमच निर्मूलन साधता येते. अशा जोडभिंगाला विवर्णिक (किंवा गोलीय व वर्णविपथनविरहित) भिंग असे म्‍हणतात. विवर्ण किंवा विवर्णिक जोडभिंगातील घटक भिंगे एकमेकांस अडकविलेली असतात.

एकाच प्रकारच्‍या काचेची दोन अभिसारी भिंगे घेऊनही विवर्ण भिंगजोडी तयार करता येते. अशा दोन भिंगांमध्‍ये त्‍यांच्‍या केंद्रांतरांच्‍या सरासरीइतके अंतर ठेवून ती एखाद्या नळीत पक्‍की बसविलेली असतात. दूरदर्शकात वापरण्‍यात येणाऱ्या रॅम्‍सडेन नेत्रभिंगसमूहात या तत्त्‍वाचा उपयोग केला आहे [⟶ दूरदर्शक].

विवर्ण भिंगाचे गणित : विवर्ण भिंगजोडी अभिसारी हवी असल्‍यास क्राउन काचेचे f या केंद्रांतराचे बहिर्वक्र भिंग व f ’ या केंद्रांतराचे फ्लिंट काचेचे भिंग यांची जुळणी केली जाते. त्‍यात f ⋞ f ’. ω व ω’ या त्‍या भिंगांच्‍या अपस्‍करणशीलता असल्‍यास विवर्ण जोडी होण्‍यासाठी,

अशा तऱ्हेने f_D व f_D’ यांची मूल्‍ये घ्‍यावी लागतात. या जोडीचे निष्‍पन्‍न केंद्रांतर F_D पुढील समीकरणाने दिले जाते.

दुय्यम वर्णपट : विवर्ण भिंगजोडीमध्‍ये निळा व तांबडा या दोन रंगांच्‍या बाबतीतच वर्णविपथनाचे निराकरण साधलेले असते. त्‍यातून शिल्‍लक राहणाऱ्या  वर्णविपथनाला दुय्यम वर्णपट हे नाव देतात. दुय्यम वर्णपटही नाहीसा करण्‍यासाठी तीन घटकांचे विवर्णिक जोडभिंग करण्‍याच्‍या पद्धतीचा वर उल्‍लेख केला आहे. अशा जोडभिंगात तीन रंगांच्‍यासाठी केंद्रांतरमूल्‍य एकच होईल अशी रचना केलेली असते. साधी काच व फ्ल्युओराइट या दोन द्रव्‍यांपासून बनविलेल्‍या जोडभिंगातही तीन रंगांसाठीविर्णविपथनाचे निराकरण होऊ शकते. एम्. जे. हर्झबर्गर यांनी विकसित केलेल्या तंत्रानुसार तीन द्रव्‍यांच्‍या तीन सुयोग्‍य भिंगांपासून बनविलेल्‍या जोडभिंगात चार रंगांसाठी वर्णविपथनाचे निराकरण होते. अशा संयुक्‍त भिंगाला ‘अती वि‍वर्णिक’ भिंग असे म्‍हणतात. या रचनेत गोलीय विपथनाचेही मोठ्या प्रमाणात निराकरण झालेले असते. सूक्ष्‍मदर्शकाच्‍या साहाय्याने छायाचित्रे घेतात तेव्‍हा सूक्ष्‍मदर्शकाचे वस्‍तुभिंग या प्रकारचे वापरणे श्रेयस्‍कर असते.

प्रकाशीय व्‍यूहाचे तंत्र : विशिष्‍ट उपयोगासाठी प्रकाशीय व्‍यूह तयार करण्‍याची पहिली पायरी म्‍हणजे व्‍यूहाचा अपेक्षित छिद्रव्‍यास, केंद्रांतर, क्षेत्र वगैरे गोष्‍टी निश्चित करणे. नंतर या अपेक्षा पूर्ण करणारी परंपरेने व पूर्वानुभवामुळे ज्ञात झालेली एक भिंग-प्रणाली नियुक्त्त केली जाते आणि वर वर्णन केलेल्या पद्धतीनुसार या भागातील प्राथमिक दोष किमान केले जातात. विविध दोष गणितकृत्‍याने काढणे (व नंतर त्‍यांचे निराकरण करणे) हे काम फार जि‍किरीचे असते, म्‍हणून यासाठी हल्‍ली संगणकाचाच (गणकयंत्राचाच) उपयोग करतात. त्‍यासाठी उपयुक्त अशी खास सूत्रेही आता काढण्‍यात आलेली आहेत. विविध विपथनांचे निराकरण करताना त्‍यामध्‍ये एक प्रकारचा समतोल साधणे आवश्‍यक असते. नाहीतर एक विपथन पूर्णपणे नष्‍ट होऊनही प्रतिमेच्‍या रेखीवपणात पुरेशी वाढ होणार नाही.

पहा : कॅमेरा दूरदर्शक प्रकाशकी भिंग सूक्ष्‍मदर्शक.

संदर्भ :  1. Ditchburn, R. W. Light, London, 1963.

            2. Jenkins, F. A. White, H. E. Fundamentals of Optics, New York, 1957.

            3. Morgan, J. Introduction to Geometrical and Physical Optics, New York, 1953.

            4. Smith, W. J. Modern Optical Engineering, New York, 1966.                

पुरोहित, वा. ल.

“