प्रकाशकी

प्रकाशकी : (ऑप्टिक्स). प्रस्तुत नोंदीसाठी प्रकाशकी म्हणजे प्रकाशाचे शास्त्र अशी व्याख्या स्वीकारलेली असून तीत प्रकाशाच्या विविध अविष्कारांचे विवेचन चार भागांत केले आहे.

(१) भूमितीय प्रकाशकी : या भागात प्रकाश हा बरोबर सरळ रेषेत जातो (रेखीय प्रसारण) या कल्पनेच्या आधारे ज्या आविष्कारांचा उलगडा करता येतो त्यांचाच फक्त विचार केला आहे. प्रकाशाचे तरंगात्मक स्वरूप आणि त्यामुळे होणारे विवर्तनासारखे परिणाम येथे दुर्लक्षणीय मानले आहेत.

(२) भौतिकीय प्रकाशकी : या भागात प्रकाशाच्या ज्या अविष्कारांचा उलगडा करण्यासाठी प्रकाशाचे तरंगात्मक स्वरूप लक्षात घेणे आवश्यक असते त्यांचा ऊहापोह केलेला आहे.

(३) विद्युत् प्रकाशकी व (४) चुंबकीय प्रकाशकी : या भागांमध्ये प्रकाशावर होणाऱ्या विद्युत् व चुंबकीय क्षेत्रांच्या परिणामांचा संक्षिप्त आढावा दिलेला आहे.

केव्हा केव्हा ‘पूंज प्रकाशकी’ हा एक प्रकाशकीचा स्वतंत्र भाग मानतात. त्यात प्रकाश व अणू किंवा त्याहूनही लहान द्रव्यकण यांमधील परस्परक्रियांचा विचार केला जातो. विविध आविष्कारांत प्रकाश ऊर्जेच्या प्रमाणात द्रव्याचा प्रतिसाद होतो असे गृहीत धरून केलेल्या प्रकाशाच्या अभ्यासाला ‘रेषीय प्रकाशकी’ असे म्हणतात. सामान्यतः प्रकाश व द्रव्य यांच्यातील परस्परक्रिया रेषीय असतात (म्हणजे ही परस्परक्रिया दर्शविणारा गणितीय संबंध एक घाती स्वरूपाचा असतो) परंतु काही खास परिस्थितीत [उदा., उच्च ऊर्जेच्या लेसर किरणांचा द्रव्यावर होणारा परिणाम → लेसर] या परस्पर क्रिया नैकरेषीयही (अरेषीय) असू शकतात. अशा आविष्कारांच्या अभ्यासाला ‘नैकरेषीय प्रकाशकी’असे म्हणतात. [→ नैकरेषीय आविष्कार].  

वातावरणामधील वायू, धूळ, जलबाष्प इत्यादींमुळे तसेच हवेच्या थरांच्या तापमान, दाब गुणधर्मात होणाऱ्या बदलामुंळे मृगजळ, प्रभामंडळ यांसारखे विविध आविष्कार अनुभवास येतात. या आविष्कारांच्या अभ्यासाला ⇨वातावरणीय प्रकाशकी असे म्हणतात.

प्रकाश उद्‌गम : सूर्य हा मनुष्याला अनेक प्रकारे उपयोगी पडणारा प्रकाश उद्‌गम आहे. आपल्या विविध व्यापारांसाठी उपयुक्त व बिनखर्चाचे प्रदीपन सूर्यप्रकाशाने होते. जेथे सूर्यप्रकाश प्रत्यक्षपणे पडू शकत नाही अशा ठिकाणी (उदा., इमारतींतून) हवेतील धूलिकणांवरून प्रकीर्णित झालेल्या (विखुरलेल्या) सूर्यप्रकाशामुळे प्रदीपन होते. सूर्यप्रकाशाला नैसर्गिक प्रकाश असे नाव देतात. याउलट वेगवेगळ्या प्रकारच्या दिव्यांपासून मिळणाऱ्या प्रकाशाला कृत्रिम प्रकाश असे म्हणतात.

पृथ्वीच्या पृष्ठभागावर पडणाऱ्या सूर्यप्रकाशातील तरंगलांब्या सु. ०·३μ (μ = मायक्रॉन = १०^–६ मीटर) ते ३μ यांच्या दरम्यान असतात. वनस्पतींची वाढ व वारा, पाऊस यांसारखे नैसर्गिक आविष्कार सूर्यप्रकाशामुळेच शक्य होतात. सूर्यप्रकाशाद्वारे पृथ्वीला प्रचंड प्रमाणावर ऊर्जेचा पुरवठा होत असतो. [→ सूर्यप्रकाश].

सूर्यप्रकाश उपलब्ध नसेल तेव्हा प्रदीपनासाठी विविध प्रकारच्या कृत्रिम प्रकाश उद्‌गमांची मदत घेतली जाते. प्रागैतिहासिक काळापासून इंधन म्हणून वेगवेगळी तेले व चरबी यांचा उपयोग करणारे चुडी, मशाली व अनेक प्रकारचे ⇨ दिवे यांचा वापर व विकास होत गेला आहे.

एकोणिसाव्या शतकाच्या अखेरीला विजेच्या दिव्याचा शोध लागल्यानंतर प्रदीपनाच्या क्षेत्रात मोठीच क्रांती झाली. तप्त तंतूचे दिवे, विद्युत् प्रज्योती, विद्युत् विसर्जन नलिका, अनुस्फुरक पद्धतीचे दिवे असे त्यांचे प्रमुख प्रकार सांगता येतील. [→विद्युत् दिवे].

 

भूमितीय प्रकाशकी 

प्रकाशकीच्या या शाखेचा मुख्य हेतू भिंग प्रणाली, कॅमेरे, सूक्ष्मदर्शक, दूरदर्शक यांसारखी प्रकाशीय उपकरणे तयार करणाऱ्या कारागिरांना उपयुक्त होतील अशी सूत्रे सिद्ध करणे हा असतो. भिंगे किंवा आरसे तयार करताना या सूत्रांनुसार काचा घासून त्यांच्या पृष्ठांना योग्य तो आकार देता येतो.

प्रकाश सरळ रेषेत जातो असे म्हणतात व हे सिद्ध करण्यासाठी पाठ्यपुस्तकांत काही प्रयोगही दिलेले असतात. परंतु मुळात सरळ रेषेच्या व्याख्येतच प्रकाश सरळ रेषेत जातो ही कल्पना अध्याहृत असते. त्यामुळे हे प्रयोग अर्थशून्य आहेत.

किरण व किरण-शलाका : दीप्त वस्तूवरील एका बिंदूपासून दुसऱ्या कोठल्याही बिंदूपर्यंत जाण्याचा प्रकाशाचा मार्ग म्हणजे किरण होय. एकाच बिंदूपासून निघणाऱ्या (किंवा एकाच बिंदूत येऊन मिळणाऱ्या) किरण समुच्चयाला किरण-शलाका किंवा किरणावली असे म्हणतात.

दिव्याच्या ज्योतीवरील एखाद्या बिंदूपासून निघणारे किरण सर्व दिशांना जातात व असे जाताना परस्परांपासून अधिकाधिक दूरदूर जात राहतात. अशा शलाकेला केंद्रापसारी शलाका असे म्हणतात. सूर्यकिरण बहिर्वक्र भिंगातून पलिकडे गेले असता तो सर्व किरणसमुच्चय एका बिंदूत येऊन मिळतो. एका बिंदूत केंद्रित होऊ पाहणाऱ्या अशा शलाकेला केंद्राभिसारी शलाका असे म्हणतात. अतिदूरच्या बिंदुमात्र उद्‌गमापासून येणारे किरण परस्परांना समांतर असतात. अशा किरण-शलाकेला समांतर शलाका असे म्हणतात. बिंदुमात्र उद्‌गम म्हणजे जो संबंधित उपकरणाजवळ किंवा डोळ्याशी अत्यंत लहान कोन अंतरित करतो तो उद्‌गम होय. या दृष्टीने ताऱ्यांचे प्रत्यक्ष आकारमान जरी पृथ्वीपेक्षा हजारो पटींनी मोठे असले,तरी पृथ्वीवरील निरीक्षकाच्या संदर्भात तारे हे बिंदुमात्र उद्‌गम मानता येतात.

छाया : एखाद्या विशिष्ट प्रदेशात (भागात) जेव्हा काही अपारदर्शक अडथळ्यामुळे एका विशिष्ट उद्‌गमापासून एकही प्रकाशकिरण पोहोचू शकत नाही तेव्हा तो प्रदेश (त्या उद्‌गमाच्या संदर्भात) त्या अडथळ्याची प्रच्छाया किंवा पूर्ण छाया आहे असे म्हणतात. प्रकाश उद्‌गमाचा आकार अडथळ्याच्या तुलनेने मोठा असल्यास काही प्रदेश असा मिळतो की, तेथे त्या उद्‌गमाच्या काही भागापासून निघणारे किरण पोहोचू शकतात, तर बाकीच्या भागापासून निघणारे किरण तेथे पोहोचू शकत नाहीत अशा प्रदेशाला उपच्छाया किंवा अंशच्छाया असे म्हणतात. बिंदुमात्रे उद्‌गमामुळे एकच रेखीय छाया मिळते, तर विस्तृत उद्‌गमामुळे प्रच्छाया व उपच्छाया अशा दोन छाया मिळू शकतात.

आ. १ मध्ये बिंदुमात्र उद्‌गमामुळे रेखीव छाया कशी तयार होते ते स्पष्ट केले आहे (आकृतीमध्ये बिंदुमात्र उद्‌गम विजेच्या दिव्याच्या गोळ्यावर काळा कागद चिकटवून त्यावर पाडलेल्या एका बिंदुरूप छिद्राच्या स्वरूपात दाखविला आहे). बिंदुमात्र उद्‌गमापासून निघून अडथळ्याच्या कडांवर स्पर्श करणाऱ्या किरणांचा एक शंकू बनतो. या शंकूच्या अडथळ्यापलीकडच्या भागात कोठूनही प्रकाशकिरण येऊ शकत नाहीत. याला छायाशंकू असे म्हणतात. पलीकडे ठेवलेल्या पडद्यावरील व या शंकूचा छेद म्हणजे पडद्यावरील छाया होय. पडदा जितका दूर न्यावा तितकी छाया आकारमानाने मोठी होईल हे उघड आहे.

आ. २(अ) मध्ये विस्तृत प्रकाश उद्‌गमामुळे प्रच्छाया आणि उपच्छाया कशा उत्पन्न होतात ते दाखविले असून आ. २(आ) मध्ये पडद्यावर या छाया कशा दिसतात ते दिग्दर्शित केले आहे. उद्‌गमाच्या कडेपासून अडथळ्याच्या त्याच बाजूच्या कडांना स्पर्श करून जाणाऱ्या किरणांमध्ये एक शंकू बनतो. त्याला प्रच्छायाशंकू (३)असे म्हणतात. उद्‌गम व अडथळा यांमधील अंतर कमी केल्यास किंवा उद्‌गमाचा आकार वाढविल्यास या शंकूचा शिरोबिंदू अडथळ्याच्या अधिक जवळ येईल. हा शिरोबिंदू व अडथळा यांच्या दरम्यान कोठेही पडदा (६)ठेवल्यास त्यावर आ. २(आ) मध्ये दाखविल्याप्रमाणे प्रच्छाया व उपच्छाया मिळतील. पडदा (४)येथे ठेवल्यास प्रच्छाया बिंदुमात्र मिळेल पण पडदा (४)च्या पलीकडे ठेवल्यास प्रच्छाया अजिबात मिळणार नाही. आकृतीवरून उपच्छाया शंकू व उपच्छाया यांची निर्मिती स्पष्ट होईल.

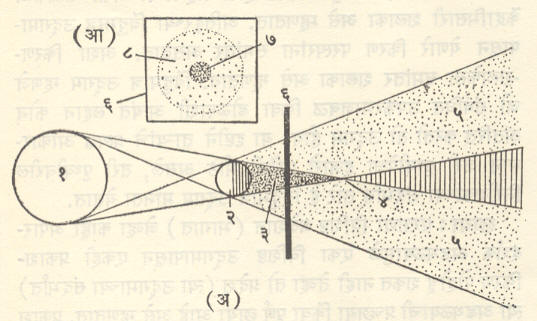
अमावस्येला सूर्य व पृथ्वी यांच्या दरम्यान चंद्र आल्यास पृथ्वीच्या ज्या भागावर प्रच्छाया पडते तेथे खग्रास व जेथे उपच्छाया पडते तेथे खंडग्रास सूर्यग्रहण दिसते. [→ग्रहण].

सूचिछिद्र कॅमेरा : सर्व बाजूंनी बंद असलेल्या पेटीच्या एका बाजूच्या मध्यावर सूक्ष्म (सूईच्या इतपत व्यासाचे) छिद्र पाडतात. या छिद्रासमोरच्या बाजूवर छायाचित्रण फिल्म ठेवल्यास तिच्यावर वस्तूचे छायाचित्र उमटू शकते. म्हणून या रचनेला सूचिछिद्र कॅमेरा असे म्हणतात. आ. ३ मध्ये १, २, ३ ही (मेणबत्तीची ज्योत) प्रकाशित वस्तू (४) या सूचिछिद्रासमोर ठेवली आहे. १, २, ३ यासारख्या प्रत्येक बिंदूपासून निघणाऱ्या लहान किरण-शलाका सूचिछिद्रातून जाऊन (अनुक्रमे १’, २’, ३’ येथे छिद्राच्या आकारानुसार प्रकाशित छिद्रांच्या रूपात) समारोल पडद्यावर पडतात व अशा तऱ्हेने पडद्यावर त्या वस्तूची प्रतिमा उमटते. ही प्रतिमा आकृतीत दाखविल्याप्रमाणे उलटी असते. (४) व (६) यांमधील अंतर वाढविल्यास प्रतिमेचे आकारमान वाढते. छिद्राचे आकारमान मोठे केल्यास प्रतिमा जास्त तेजस्वी परंतु अस्पष्ट होते. छिद्र व वस्तू यांमधील अंतर (u)आणि छिद्र व प्रतिमा यांमधील अंतर (v)असल्यास पुढील समीकरण लागू पडते.

प्रतिमेची उंची	=	v
वस्तूची उंची		u

या कॅमेऱ्यासाठी वस्तू स्वयंप्रकाशितच असण्याची आवश्यकता नाही. (६)या ठिकाणी घासलेल्या काचेचा पडदा ठेवल्यास त्यावर रंगीत वस्तू व इकडे तिकडे जाणारे प्राणी इत्यादींचा एक प्रकारचा रंगीत चलच्चित्रपटच दिसू शकतो. प्रकाशाच्या रेखीय प्रसारणाच्या गुणाचा सूचिछिद्र कॅमेरा हे एक आकर्षक प्रात्यक्षिकच आहे. मात्र भिंगयुक्त कॅमेऱ्याच्या तुलनेने पाहता या कॅमेऱ्यापासून मिळणारी छायाचित्रे फारच कमी रेखीव असतात व त्यांना उद्‌भासन कालही (प्रकाशाचा फिल्मवर परिणाम होण्यासाठी फिल्म उघडी ठेवण्याचा कालही) खूपच लागतो. त्यामुळे हल्ली त्यांचा छायाचित्रणासाठी उपयोग केला जात नाही.

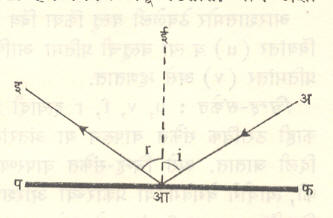
परावर्तन : आरशासारख्या चकचकीत पृष्ठावर उन्हाचा कवडसा पडल्यास तो आरशापासून परत मूळच्या बाजूलाच फेकला जातो. या आविष्काराला प्रकाशाचे परावर्तन असे म्हणतात. पाण्याच्या पृष्ठभागात आपणाला प्रतिबिंबे दिसतात (त्याच बरोबर पाणी स्वच्छ असल्यास डबक्याच्या तळच्या वस्तूही दिसतात). आरशातील प्रतिबिबांइतकी ही प्रतिबिंबे तेजस्वी दिसत नाहीत. कारण येथे पडलेल्या प्रकाशापैकी फारच थोड्या अंशाचे परावर्तन (अंशतः परावर्तन) होत असते. आ. ४ मध्ये समतल (सपाट) पृष्ठावरून होणारे एका किरणाचे परावर्तन दाखविले आहे. आईं हा आपाती बिंदूतून पृष्ठाला काढलेला लंब आहे. लंबाशी आपाती किरणाने केलेल्या कोनाला आपाती कोन (i) व परावर्तीत किरणाने केलेल्या कोनाला परावर्तन कोन (r)असे म्हणतात. अनेक प्रयोगान्ती असे दिसून आले आहे की, (१)आपाती किरण, परावर्तित किरण व आपाती बिंदूच्या ठायीचा पृष्ठलंब हे तिन्ही एकाच प्रतलात असतात. (२)आपाती किरण व परावर्तित किरण हे पृष्ठलंबाशी समान मूल्याचे कोन करतात म्हणजेच ∠ i = ∠ r. यांना परावर्तनाचे नियम असे म्हणतात.

परावर्तन पृष्ठ वक्र किंवा कोणत्याही आकाराचे असले, तरी त्याच्यापासून होणाऱ्या परावर्तनाला हेच नियम लागू पडतात. मात्र अशा वेळी वेगवेगळ्या आपात बिंदूंतून काढलेले पृष्ठलंब सामान्यतः परस्परांना समांतर असणार नाहीत. त्यामुळे सबंध पृष्ठापासून होणाऱ्या परावर्तनाचे एकूण स्वरूप काहीसे वेगळे दिसेल.

घर्षित काच किंवा टीपकागद यासारख्या पृष्ठापासून प्रकाशाचे सर्वच दिशांना परावर्तन होते, याला विसरित परावर्तन असे म्हणतात. स्वयंप्रकाशी नसलेल्या वस्तू आपणाला दिसू शकतात त्या त्यांच्याकडून आलेल्या विसरित परावर्तनामुळेच. विसरित परावर्तनालाही वरील परावर्तनाचे नियमच लागू पडतात. मात्र अशा पृष्ठावर ठायीठायी त्याचे सूक्ष्म भाग वेगवेगळ्या दिशांना वळलेले असतात. त्यामुळे अशा प्रत्येक भागावर आपाती कोनांची मूल्ये वेगवेगळी येतात व एकंदरीत पहाता सबंध पृष्ठावरून मिळून सर्व दिशांनी प्रकाश परावर्तित झाला आहे असे वाटते. चांगल्या आरशाच्या परावर्तक पृष्ठापासूनही अल्पसे विसरित परावर्तन होतेच आणि त्यामुळे आपणाला तो पृष्ठभाग दिसू शकतो.

सपाट आरशातील प्रतिमा : आ. ५ मध्ये सपाट आरशात वस्तूची प्रतिमा कशी व कोठे तयार होते ते दाखविले आहे.

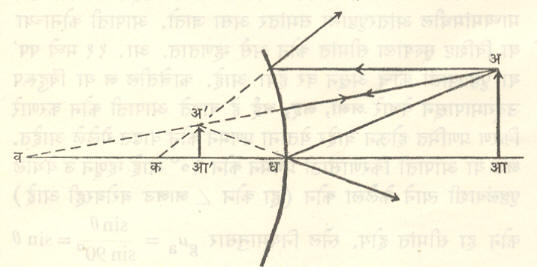
पफ या सपाट आरशासमोर व ही एक वस्तू ठेवली असून तिची आरशातील प्र ही प्रतिमा कोठे तयार होते व ड या निरीक्षकाला ती कशी काय दिसू शकते हे पाहण्यासाठी व वरील कोणत्याही अ या बिंदूपासून निघणारे कोणतेही दोन किरण (अब आणि अक) असे घेतले की, आरशावरून परावर्तन झाल्यानंतर ते निरीक्षकाच्या डोळ्यात शिरतील (येथेही परावर्तनाचे नियम लागू पडतात). हे परावर्तित  किरण केंद्रापसारी आहेत. आरशाच्या मागील बाजूला (तुटक रेषांनी दाखविल्याप्रमाणे) वाढविल्यास ते आ येथे परस्परांस मिळतात म्हणून निरीक्षकाला ते आ पासून येत आहेत असे वाटते म्हणजेच अ ची प्रतिमा आ येथे दिसते. ही प्रतिमा अर्धपर्यस्त (म्हणजे डाव्या व उजव्या बाजूंची अदलाबदल झालेली) असते. मापन करून पाहता असे दिसून येते की, अ आणि आ यांची आरशापासूनची लंब अंतरे समान असतात.

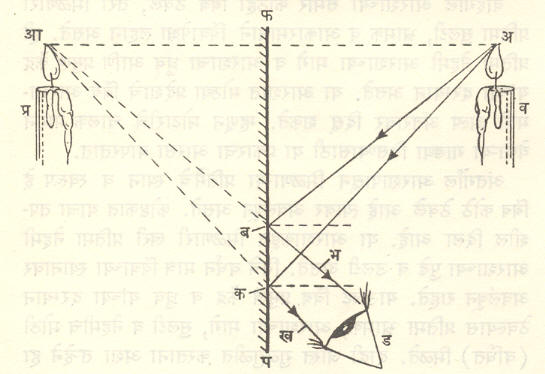
भ्रामक प्रतिमा व खरी प्रतिमा :आ. ४ मध्ये आ येथे प्रत्यक्षात परावर्तित किरण परस्परांना मिळत नाहीत म्हणून तेथे एखादा पडदा ठेवून त्यावर ही प्रतिमा पाडता येणार नाही. म्हणून अशा प्रतिमेला भ्रामक (किंवा आभासी) प्रतिमा असे म्हणतात.

अंतर्गोल आरसे (किंवा बहिर्गोल भिंगे) यांच्या साहाय्याने निर्माण होणाऱ्या प्रतिमा (अनेकदा) पडद्यावर पाडता येतात (उदा., चित्रपटगृहात). त्या प्रतिमा जेथे तयार होतात तेथे परावर्तित (किंवा प्रणमित) किरण प्रत्यक्षच एकमेकांना मिळतात. अशा प्रतिमांना खऱ्या (किंवा वास्तव) प्रतिमा असे म्हणतात.

गुणित परावर्तन : दोन आरशांत काही (θ हा) कोन करून त्यांच्या दरम्यान एखादी वस्तू ठेवल्यास त्या वस्तूच्या दोन आरशांत प्रतिमा तयार होतातच पण पुढे त्या प्रतिमांच्या पुन्हा प्रतिमा, त्यांच्याही पुन्हा प्रतिमा तयार होऊन अनेक प्रतिमांची एक मालिका तयार होते. आरशांतील कोन θ असल्यास तयार होणाऱ्या प्रतिमांची संख्या n = ³⁶⁰/_θ –१ या समीकरणाने दिली जाते. बहुरूपदर्शक या उपकरणाचे कार्य याच तत्त्वावर चालते.

---

बहुरूपदर्शक : या उपकरणात समान लांबीच्या व रुदींच्या तीन समतल आरशाच्या पट्ट्या एका नळीत अशा बसवितात की, त्यांचा एक समभुज त्रिकोणी ‘लोलक’ बनेल. सर्व पट्ट्यांची परावर्तक पृष्ठे या ‘लोलका’च्या आतल्या बाजूचा येतात (आ. ६). नळीच्या एका तोंडावर दोन काचेच्या तबकड्या बसविलेल्या असून त्यांच्यामध्ये रंगीत मणी किंवा काचेचे तुकडे टाकलेले असतात. बाहेरची तबकडी घर्षित काचेची व आतली पारदर्शक असते. नळीच्या दुसऱ्या तोंडावर मध्यभागी लहान भोक असलेली अपारदर्शक तबकडी बसविलेली  असते. या भोकातून पाहिले असता त्या रंगीत तुकड्यांची तीन आरशांत गुणित परावर्तने होऊन सुंदर सममित आकृत्या दिसतात. बहुरूपदर्शक आपल्या अक्षाभोवती फिरविल्यास काचेच्या तुकड्यांची स्थाने बदलतात व त्यामुळे आकृत्याही बदलतात. अशा तऱ्हेच्या अनंत आकृत्या मिळू शकतात. खेळणे म्हणून लहान मुलेही हे उपकरण घरी बनवू शकतात. आरशाऐवजी साध्या तावदानाच्या काचेच्या पट्ट्याही वापरता येतात. कित्येकदा तीन पट्ट्यांऐवजी दोनच पट्ट्या, त्यांच्यामध्ये ६०° चा कोन करून वापरतात. 

आरशाचे विचलन : समजा की, एका आरशावर एका ठराविक दिशेने प्रकाशकिरण आपाती होत आहे व त्यामुळे परावर्तित किरण एका विशिष्ट दिशेने जात आहे. आपाती किरणाची दिशा न बदलता, फक्त आरसा α या कोनातून फिरविला, तर असे दिसून येते की, परावर्तित किरणाच्या दिशेत २ α इतका बदल होतो. म्हणजे आरशाच्या भ्रमणकोनाचे दुप्पट विवर्धन होते. सूक्ष्म भ्रमणकोन मोजण्यासाठी या तत्त्वाचा उपयोग करतात.

वक्र आरसे : आरशांचे परावर्तक पृष्ठभाग शंक्वाकार, वृत्तचित्त्याकार (दंडगोलाकार), विवृत्तपृष्ठीय (ज्याचा परावर्तक पृष्ठभाग विवृत्त म्हणजे लंबवर्तुळ अक्षामोवती फिरवून तयार होणाऱ्या पृष्ठाचा एक भाग आहे अशा आकाराचा), अन्वस्तपृष्ठीय, अपास्तपृष्ठीय किंवा गोलाकार अशा वेगवेगळ्या आकारांचे असू शकतात. विवृत्तपृष्ठीय, अपास्तपृष्ठीय आणि अन्वस्तपृष्ठीय आरशांचा ज्योतिषशास्त्रीय दूरदर्शकांमध्ये उपयोग करतात. दूरवर पोहोचू शकणारी समांतर किरण-शलाका मिळविण्यासाठी मोटारीच्या पुढच्या दिव्यांच्या मागे अन्वस्तपृष्ठीय आरसे बसविलेले असतात. इतर आरशांतून वस्तूची प्रतिमा विवक्षितपणे विकृत झालेली अशी मिळते. करमणुकीसाठी म्हणून त्यांचा केव्हा केव्हा उपयोग केला जातो. वक्र आरशांपैकी गोलीय आरसेच म्हणजे ज्या आरशाचा परावर्तक पृष्ठभाग हा एखाद्या गोलाचा एक भाग आहे असे आरसेच जास्त करून वापरले जातात.

काही व्याख्या :गोलीय आरशांच्या संदर्भात वापरल्या जाणाऱ्या काही संज्ञांच्या व्याख्या पुढीलप्रमाणे आहेत : (१)गोलीय आरसा हा ज्या संपूर्ण गोलाच्या पृष्ठभागाचा एक भाग असतो त्या गोलाच्या मध्यबिंदूला त्या आरशाचा वक्रता मध्य व त्रिज्येला आरशाची वक्रता त्रिज्या (r) असे म्हणतात.

(२)गोलीय आरशापासून होणारे परावर्तन वक्रता मध्याच्या बाजूकडे होत असल्यास त्या आरशाला अंतर्गोल आरसा व वक्रता मध्याच्या विरुद्ध बाजूकडे होत असल्यास त्या आरशाला बहिर्गोल आरसा असे म्हणतात.

(३)आरशाच्या परावर्तक पृष्ठभागाच्या मध्यबिंदूला आरशाचा ध्रुव असे म्हणतात.

(४)आरशाचा ध्रुव आणि वक्रता मध्य यांच्यामधून जाणाऱ्या सरळ रेषेला आरशाचा मुख्य अक्ष असे म्हणतात.

(५)मुख्य अक्षातून जाणाऱ्या प्रतलाने आरशाचा घेतलेला छेद म्हणजे आरशाचा मुख्य छेद होय.

(६)आरशाच्या वर्तुळाकार कडेच्या व्यासाला आरशाचा छिद्र व्यास (ॲपर्चर) असे म्हणतात. पुढे येणाऱ्या सर्व सूत्रांत आरशाचा छिद्र व्यास फार कमी आहे असे अध्याहृत असते.

(७)आरशावर समांतर किरण-शलाका पडली असता परावर्तनानंतर सर्व किरण ज्या एका बिंदूत केंद्रित होतात (किंवा होतात असा भास होतो) त्या बिंदूला आरशाचा प्रमुख केंद्रबिंदू किंवा केंद्र असे म्हणतात. अंतर्गोल आरशाच्या बाबतीत परावर्तित किरण खरोखरीच एका बिंदूत केंद्रित होतात. म्हणून त्याला खरा केंद्र बिंदू (व आरशाला केंद्राभिसारी आरसा) असे म्हणतात. बहिर्गोल आरशांच्या बाबतीत, परावर्तित किरणांच्या केवळ दिशा मागे वाढविल्या असता एका बिंदूत मिळतात. म्हणून त्याला भ्रामक केंद्रबिंदू (व आरशाला केंद्रापसारी आरसा) असे म्हणतात.

(८)आरशाचा ध्रुव व केंद्रबिंदू यांच्यामधील (अक्ष समांतर अंतराला आरशाचे केंद्रांतर (f)असे म्हणतात.

आरशासमोर ठेवलेली वस्तू किंवा बिंब व ध्रुव यांमधील अंतराला बिंबांतर (u) व त्या वस्तूची प्रतिमा आणि ध्रुव यांमधील अंतराला प्रतिमांतर (v) असे म्हणतात.

चिन्ह-संकेत : u, v, f, r इत्यादी प्रकाशीय अंतरे मोजताना काही ठराविक संकेत वापरून या अंतरांना धन किंवा ऋण चिन्हे दिली जातात. असे चिन्ह-संकेत वापरण्यामागील मुख्य उद्देश्य हा की, त्यायोगे वेगवेगळ्या प्रकारच्या आरशांसाठी व वेगवेगळ्या परिस्थितींत u, v व f यांना जोडणारे एकच सूत्र लागू पडावे. सध्या असे सु. सहा चिन्ह-संकेत प्रचारात आहेत. चिन्ह-संकेत बदलला, तर लागू पडणारे सूत्रही बदलू शकते. म्हणून विशिष्ट चिन्ह-संकेताला अनुरूप असेच सूत्र त्या वेळी वापरणे आवश्यक आहे.

सर्व चिन्ह-संकेतांत खरा-धन व खोटा (भ्रामक)-ऋण हा संकेत-संच वापरण्यास सोपा असल्याने त्याचा येथे वापर केला आहे. हा संकेत-संच सूत्ररूपाने पुढीलप्रमाणे सांगता येईल.

(१) खरी प्रतिमा व खरे बिंब यांची अंतरे धन मानावी.

(२)भ्रामक प्रतिमा व भ्रामक बिंब यांची अंतरे ऋण मानावी.

(३)केंद्राभिसारी पृष्ठाचे केंद्रांतर व वक्रता त्रिज्या धन मानावी.

(४)केंद्रापसारी पृष्ठाचे केंद्रांतर व वक्रता त्रिज्या ऋण मानावी. यानुसार अंतर्गोल आरशाचे केंद्रांतर व वक्रता त्रिज्या धन आणि बहिर्गोल आरशाचे केंद्रांतर व वक्रता त्रिज्या ऋण येतात.

(५)खऱ्या प्रतिमेची (वा खऱ्या बिंबाची) उंची व वर्धन धन आणि भ्रामक प्रतिमेची (वा भ्रामक बिंबाची) उंची व वर्धन ऋण समजावे. याचबरोबर हेही लक्षात ठेवावे की, सामान्यतः खरी प्रतिमा ही पर्यस्त म्हणजे उलटी व भ्रामक प्रतिमा सुलटी असते.

गोलीय आरशामुळे मिळणाऱ्या प्रतिमा :अंतर्गोल व बहिर्गोल या दोन्ही प्रकारच्या आरशांच्या बाबतीत छिद्र व्यास लहान असून बिंब बिंदू अक्षावर असल्यास पुढील सूत्र लागू पडते.

1	+	1	=	2	=	1
u		v		r		f

बहिर्गोल आरशाच्या समोर कोठेही बिंब ठेवले, तरी मिळणारी प्रतिमा सुलटी, भ्रामक व आकारमानाने बिंबापेक्षा लहान असते. ही प्रतिमा नेहमी आरशाच्या मागे व आरशाचा ध्रुव आणि प्रमुख केंद्र यांच्या दरम्यान असते. या आरशात मोठ्या प्रदेशाचे बिंब आरशामागे अल्प अंतरावर दिसू शकते. म्हणून मोटारीचे चालक मागून येणाऱ्या गाड्या दिसण्यासाठी या प्रकारचा आरसा वापरतात.

अंतर्गोल आरशापासून मिळणाऱ्या प्रतिमेचे स्थान व स्वरूप हे बिंब कोठे ठेवले आहे त्यावर अवलंबून असते. कोष्टकात याचा तपशील दिला आहे. या आरशाकडून मिळणारी खरी प्रतिमा नेहमी आरशाच्या पुढे व उलटी असते. तिचे वर्धन मात्र बिंबाच्या स्थानावर अवलंबून राहते. याउलट बिंब प्रमुख केंद्र व ध्रुव यांच्या दरम्यान ठेवल्यास प्रतिमा भ्रामक, आरशाच्या मागे, सुलटी व नेहमीच मोठी (वर्धित) मिळते. दाढी जास्त गुळगुळीत करताना अशा तऱ्हेने हा आरसा वापरल्यास अगदी लहान खुंटही दिसू शकतात.

किरण आकृती  : किरणांच्या आकृती काढून त्यांवरून प्रतिमेचे स्थान व स्वरूप निश्चित करता येते. यासाठी कोणतेही दोन आपाती किरण घेऊन परावर्तनानंतर ते परस्परांना जेथे छेदतील तेथे प्रतिमा बिंदू असतो या नियमाचा उपयोग करतात. पुढील किरण यासाठी विशेष सोयीचे आहेत.

अंतर्गोल आरशासाठी बिंब (वस्तू) व प्रतिमा यांच्या स्थिती 

बिंबाचे स्थान	प्रतिमेचे स्थान	प्रतिमेचे स्वरूप
अनंत अंतराव (u→ ∞) वक्रता मध्याच्या पलीकडे (r &lt u &lt ∞)	प्रमुख केंद्रावर (v = f) प्रमुख केंद्र व वक्रता मध्य यांच्या दरम्यान (f &lt v &lt r)	उलटी, खरी व लहान. उलटी, खरी व लहान.
वक्रता मध्यावर (u = r)	वक्रता मध्यावर (v = r)	उलटी, खरी व बिंबाएवढ्याच आकाराची.
वक्रता मध्य व प्रमुख केंद्र यांच्या दरम्यान (f &lt u &lt r)	वक्रता मध्यापलीकडे (r &lt v &lt ∞)	उलटी, खरी व वर्धित.
प्रमुख केंद्रावर (u = f)	फार दूर (v → ∞)	उलटी, खरी व वर्धीत.
प्रमुख केंद्र व ध्रुव यांच्या दरम्यान (o &lt u &lt f)	आरशाच्यामागे (v ऋण)	सुलटी, भ्रामक व वर्धित.

(१) आपाती किरण प्रमुख अक्षाला समांतर असेल,तर परावर्तित किरण परावर्तनानंतर (अंतर्गोल आरशाच्या बाबतीत) मुख्य केंद्रातून जातो किंवा (बहिर्गोल आरशाच्या बाबतीत) त्याची दिशा मागे वाढविल्यास प्रमुख केंद्रातून जाते.

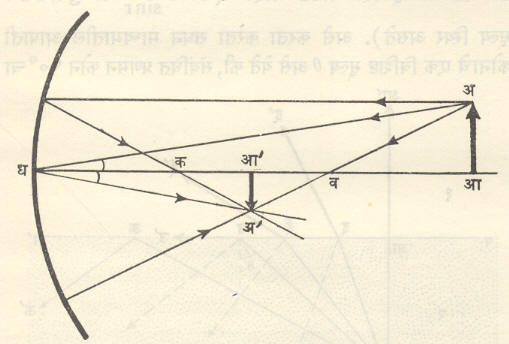
(२)आपाती किरणाची दिशा वक्रता मध्यातून जात असल्यास परावर्तित किरणाची दिशा उलट परंतु आपाती किरणाशी संपाती असते.

(३)आपाती किरण आरशाच्या ध्रुवावर पडल्यास परावर्तित किरण अक्षाशी तेवढाच कोन करून पण विरुद्ध बाजूला जातो. आ. ७ व आ. ८ मध्ये अंतर्गोल व बहिर्गोल आरशांच्या बाबतीत या नियमाचा उपयोग करून प्रतिमा कशी निश्चित होते ते दाखविले आहे. आकृतीत प्रत्यक्ष किरण अखंड रेषांनी व किरणांच्या वाढविलेल्या दिशा तुटक रेषांनी दाखविल्या आहेत.

आरशांची निर्मिती  :उच्च परावर्तनशीलतेसाठी आरशाचा पृष्ठभाग धातूचा असणे इष्ट असते. सामान्यतः काचेवर चांदी किंवा ॲल्युमिनियम या धातूच्या पातळ थराचे विलेपन करून आरसे तयार केले जातात. सर्वसामान्य उपयोगात हे विलेपन काचेच्या मागल्या बाजूवर करतात. त्यामुळे परावर्तक पृष्ठ हवेच्या दुष्परिणामापासून आपोआपच सुरक्षित राहते परंतु अशा आरशात काचेच्या पुढच्या पृष्ठापासूनही होणारे अल्प परावर्तन काही घोटाळे निर्माण करते. म्हणून उच्च दर्जाच्या उपकरणासाठी काचेच्या पुढच्या पृष्ठावरच विलेपन करतात. हे विलेपन करण्याआधी घासून त्या काच पृष्ठाला इष्ट तो आकार दिलेला असतो. अवरक्त किरणांच्या (दृश्य वर्णपटातील तांबड्या रंगाच्या पलीकडील अदृश्य किरणांच्या) परावर्तनासाठी सोने किंवा त्यापेक्षाही प्लॅटिनम धातूचे विलेपन जास्त प्रभावी ठरते. [→आरसा].

प्रणमन : प्रकाशकिरण जेथे एका पारदर्शक माध्यमातून दुसऱ्या माध्यमात प्रवेश करतो तेथे सामान्यतः किरणाच्या दिशेत एकदम बदल होतो. या दिशाबदलाला प्रणमन असे म्हणतात. प्रणमनाबरोबरच आपाती किरणाचे मूळच्या माध्यमात अंशतः परावर्तनही होत असतेच. आपात बिंदूवरून दोन माध्यमांमधील आंतरपृष्ठाला काढलेल्या पृष्ठलंबाशी आपाती किरण जो कोन करतो त्याला आपाती कोन (i)असे म्हणतात, तर त्याच पृष्ठलंबाशी (दुसऱ्या माध्यमातील) प्रणमित किरणाने केलेल्या कोनाला प्रणमन कोन (r)असे म्हणतात. आपाती कोनापेक्षा प्रणमन कोन लहान असल्यास (r &lt i) दुसरे माध्यम पहिल्यापेक्षा (प्रकाशीय दृष्ट्या) सघन आहे असे म्हणतात. याउलट r &gt i असल्यास दुसरे माध्यम (प्रकाशीय दृष्ट्या) विरल आहे असे म्हणतात. या सघनता-विरलतेचा वस्तूंच्या घनतेशी काहीही संबंध नाही, हे लक्षात घ्यावे.’

प्रणमनाचे नियम : पुढील दोन नियमांचे प्रणमनामध्ये पालन होते,असे प्रयोगांवरून दिसून आले आहे.

(१) आपाती किरण, प्रणमित किरण आणि आपात बिंदूच्या ठायीचा पृष्ठलंब हे तीनही एकाच प्रतलात असतात.

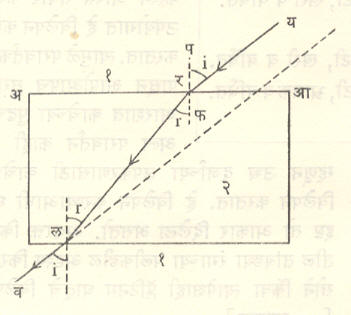
(२) एका विशिष्ट (१ या) माध्यमातून दुसऱ्या (२ या) माध्यमात प्रकाश प्रणमित होतो तेव्हा विशिष्ट तरंगलांबीच्या प्रकाशासाठी ^{sin i}/_{sin r} = μ = एक स्थिरांक असतो, असे आढळून येते. याला स्नेल नियम (व्हिलेब्रॉर्ट स्नेल या डच शास्त्रज्ञांच्या नावावरून) असे म्हणतात.μया स्थिरांकाला दुसऱ्या (२ या) माध्यमाचा पहिल्या माध्यमाच्या संदर्भात प्रणमनांक असे म्हणतात व हे स्पष्ट करण्यासाठी हा प्रणमनांक _१^μ_२ अशा तऱ्हेने लिहितात. बहुतेक प्रयोगांत पहिले माध्यम १ हे हवा असते. नुसते μ_२ असे लिहिल्यास २ या माध्यमाचा हवेच्या संदर्भातील प्रणमनांक असा अर्थ होतो. पदार्थाचा निर्वाताच्या संदर्भात प्रणमनांक बहुधा n किंवा μ या अक्षराने व्यक्त केला जातो. सामान्यतः खास उल्लेख केला नसेल, तर μ म्हणजे पिवळ्या रंगासाठी प्रणमनांक मानला जातो. १ पेक्षा २ सघन असल्यास r &lt i आणि _१μ_२ &gt १, उलट २ विरल असल्यास _१μ_२ &lt१. आ. ९ मध्ये प्रकाशकिरण हवेतून (१) काचेत (२) जाताना होणारे प्रणमन दाखविले आहे.

प्रकाशमार्ग व्युत्क्रमी असतात या तत्त्वाचा उपयोग केल्यास या आकृतीवरून हे लक्षात येईल की, २ या माध्यमातून लर या मार्गाने किरण आपाती झाल्यास प्रणमित किरणाचा मार्ग रय हा होईल. या परिस्थितीत आपाती कोन = r, प्रणमन कोन = i म्हणून

२μ१ =	sin r	यावरून १μ२ =	१	हा सामान्य नियम मिळतो.
	sin i		२μ१

आ. ९ मध्ये २ हा काचेचा आयताकार ठोकळा असल्यास रल हा किरण विरुद्ध बाजूने परत १ या माध्यमात (लव असा) बाहेर येईल तेव्हा तो मूळच्या (यर या) आपाती किरणाला समांतर असेल, हेही प्रकाशमार्गाच्या व्युत्क्रमीपणाच्या तत्त्वानुसार सिद्ध करता येईल.

२, ३, ४, …, १० इ. अनेक पारदर्शक माध्यमांचे समांतर बाजू असलेले ठोकळे एकापुढे एक असे परस्परांना चिकटवून ठेवले आणि त्यांच्याभोवती १ हे माध्यम असेल, तर आपाती किरण प्रथम १ मधून २ मध्ये, मग २ मधून ३ मध्ये याप्रमाणे विविध माध्यमांतून जात जात शेवटच्या १० माध्यमातून पुन्हा १ मध्येच बाहेर येईल. अशा परिस्थितीत पहिला आपाती किरण व शेवटचा बाहेर येणारा किरण हे परस्परांना समांतर असतात. त्याचप्रमाणे _१μ_२X _२μ_३X_३μ_४X… X_१०μ_१= १ हे सिद्ध करता येते.

प्रणमनांक मोजण्यासाठी वापरण्यात येणाऱ्या विविध पद्धती व उपकरणे यांचे वर्णन ‘प्रणमनांकमापन’या नोंदीत दिलेले आहे. 

प्रणमनामुले प्रतिमेचे उन्नतीकरण : पाण्यासारख्या सघन माध्यमातून प्रणमन होऊन जे किरण बाहेर येतात त्यांच्या साहाय्याने पाण्याच्या तळातील वस्तू पहिल्या असता त्या काहीशा वर उचलच्या गेलेल्या दिसतात. त्यामुळे एखाद्या डबक्याची खोली वास्तविक असते तीपेक्षा कमी दिसते. आ. १० मध्ये ही घटना कशी घडून येते, ते स्पष्ट केले आहे. निरीक्षकाची दृष्टिरेषा पाण्याच्या पृष्ठभागाला (जवळजवळ) लंब असल्यास,

डबक्याची खरी खोली	=	पाण्याचा प्रणमनांक
डबक्याची भासमान खोली

हे सूत्र सिद्ध करता येते.

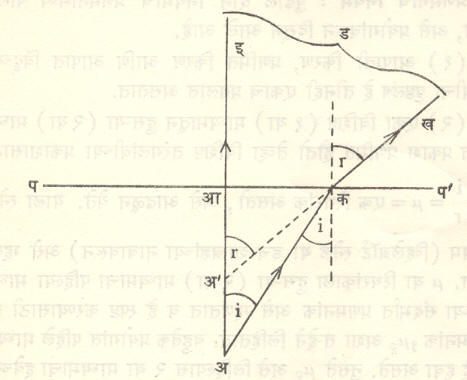
आइ व कख हे दोन बाहेर आलेले किरण निरीक्षकाच्या डोळ्यात शिरतात. ते मागे वाढविले असता अ‘या बिंदूत मिळतात म्हणजेच अ‘पासून येतात, असा भास होतो. म्हणून अ‘येथे वस्तूची भ्रामक प्रतिमा तयार होते. याउलट पाण्यातील निरीक्षक आकाशात उडणाऱ्या पक्ष्याकडे पाहील तेव्हा पक्ष्याची उंची वाढल्याचा निरीक्षकाला भास होईल. याच आविष्कारामुळे पाण्यात अर्धवट बुडविलेली काठी पृष्ठभागापाशी वाकडी झाल्यासारखी भासते.

संपूर्ण अंतर्गत परावर्तन : सघन माध्यमातून आपाती होऊन विरल माध्यमात किरण प्रवेश करतो तेव्हा ∠r &gt ∠i म्हणजेच प्रणमित किरण पृष्ठलंबापासून दूर वळतो. जसजसे ∠i चे मूल्य वाढवावे तसतसे ∠r चे मूल्यही वाढल जाईल (कारण ^{sin i}/_{sin r} या गुणोत्तराचे मूल्य स्थिर असते). असे करता करता सघन माध्यमातील आपाती कोनाचे एक विशिष्ट मूल्य θ असे येते की, संबंधित प्रणमन कोन ९०° चा येतो. अशा वेळी प्रणमित किरण विरल माध्यमामधून पण त्या दोन माध्यमांमधील आंतरपृष्ठाला समांतर असा जातो. आपाती कोनाच्या या विशिष्ट मूल्याला सीमांत कोन असे म्हणतात. आ. ११ मध्ये पप’या पृष्ठाखाली काच असून वर हवा आहे. काचेतील अ या बिंदुरूप उद्‌गमापासून येणारे अआ, अइ, अई हे वाढते आपाती कोन करणारे किरण प्रणमित होताना प्रणमन कोन वाढत गेलेले आहेत. अउ या आपाती किरणासाठी प्रणमन कोन ९०° आहे म्हणून उ येथील पृष्ठलंबाशी त्याने केलेला कोन (हा कोन ∠ आअउ बरोबरही आहे) कोन हा सीमांत होय. स्नेल नियमानुसार

gμa =	sin θ	= sin θ [g-काच, a-हवा] म्हणून aμg =	1	या सूत्राचा वापर करून
	sin 90°		sin θ

प्रणमनांकाचे मूल्य काढता येते. काचेसाठी सीमांत कोन सु. ४२° व पाण्यासाठी सु. ४८°· येतो.

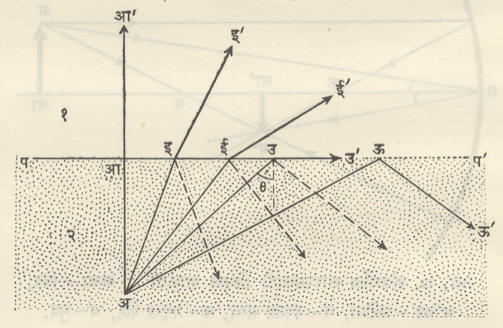
आकृतीत अऊ या किरणाचा आपाती कोन θ पेक्षाही मोठा असल्याने तदनुरूप प्रणमन कोनांच्या sine चे मूल्य १ पेक्षाही अधिक यावयास हवे (नाही तर स्नेल नियमाचे पालन होणार नाही) परंतु हे शक्यच नाही. त्यामुळे या किरणांचे प्रणमन होतच नाही व तो संपूर्णपणे परत काचेतच परावर्तित होतो. या आविष्काराला ‘संपूर्ण अंतर्गत परावर्तन’असे म्हणतात, कारण यात आपाती प्रकाशापैकी जवळजवळ १०० टक्के ऊर्जा परावर्तित होते. इतर कोठल्याही परावर्तनात इतकी कार्यक्षमता मिळत नाही, म्हणून अतिशय प्रभावी परावर्तन इष्ट असेल तेव्हा संपूर्ण अंतर्गत परावर्तनाचा अवलंब केला जातो. 

आ. ११ मध्ये इ, ई, उ या बिंदूंतून निघणाऱ्या तुटक रेषांनी तेथे होणारे अंशतः परावर्तन दाखविले आहे. आपाती कोनाचे मूल्य वाढत जाते त्याबरोबर परावर्तित ऊर्जेचे प्रमाण प्रथम हळूहळू वाढत जाते व सीमांत कोनाजवळ (θ जवळ) ते एकदम १०० टक्क्यांवर जाते (आ. १२ मधील आलेख पहा).

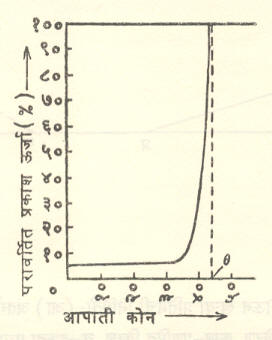
मृगजळ हा सृष्टिचमत्कार एकप्रकारे संपूर्ण अंतर्गत परावर्तनामुळेच घडून येतो [→ वातावरणीय प्रकाशकी].

लोलकातील अंतर्गत परावर्तन : तीन समतल पृष्ठांनी सीमित केलेल्या प्रणमनी माध्यमाकृतीला त्रिधारी (किंवा त्रिकोणी) लोलक असे म्हणतात. या पृष्ठांच्या परस्परांना छेदाणाऱ्या रेषा (धारा) परस्परांना समांतर असतात. या रेषांना लंब दिशेने लोलकाचा छेद घेतल्यास त्याला लोलकाचा मुख्य छेद असे म्हणतात. हा लंब छेद समद्विभुज काटकोन त्रिकोण (आ. १३)असल्यास त्या लोलकाला संपूर्ण अंतर्गत परावर्तनी लोलक असे म्हणतात. आ. १३(अ) मध्ये लोलकाच्या कख या बाजूवर लंब दिशेने आपाती झालेले १-२ हे किरण सरळ आत जाऊन कग या बाजूवर ४५ अंशांचा आपाती कोन करतात. हा कोन सीमांत कोनापेक्षा (४२° पेक्षा) मोठा असल्याने हे किरण हवेत बाहेर न येता त्यांचे संपूर्ण अंतर्गत परावर्तन होऊन ते १’-२’ यांनी दर्शविलेल्या दिशेने खग या बाजूतून बाहेर पडतात. अशा तऱ्हेने प्रकाश तीव्रवेत (विशेष) कमतरता न येता किरणाचे ९०° मधून विचलन करता येते. ⇨ परिदर्शकात अशा प्रकारे लोलकाचा उपयोग करतात.

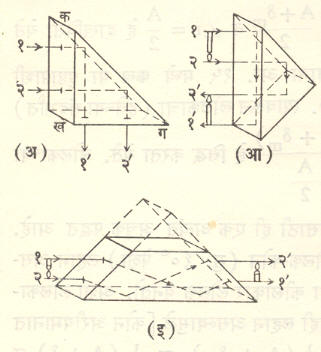
उलटी प्रतिमा सुलटी करण्यासाठी द्विनेत्री दूरदर्शकात [बायनॉक्युलरमध्ये →दूरदर्शक] दोन पॉरो लोलक (आय्. पॉरो या इटालियन अभियंत्यांच्या नावावरून ओळखण्यात येणारे लोलक) वापरतात. पॉरो लोलक वरीलप्रमाणेच असतात पण त्यांत किरणांचे १८०° मधून विचलन होते. परावर्तनाने मिळणारी प्रतिमा अर्धपर्यस्त (म्हणजे अर्धवट उलटी) असते. आरसा व वस्तू यांच्या परस्पर संदर्भ स्थितीनुसार प्रतिमेत डावी बाजू उजवीकडे (बाजू अर्धपर्यसन) किंवा खालची बाजू वर (वर-खाली अर्धपर्यसन) असा फरक पडतो. आरशात पाहून आपण डावीकडे भांग पाडतो तेव्हा प्रतिबिंबात तो उजवीकडे दिसतो, ही गोष्ट सर्वांच्या परिचयाची आहे. दूरदर्शकाच्या वस्तुभिंगामुळे तयार होणारी प्रतिमा संपूर्णपणे उलटी असल्याने ती पूर्णपणे सरळ करण्यासाठी दोन पॉरो लोलक लागतात. आ. १३(आ) मध्ये पॉरो लोलकाडून वर-खाली अर्धपर्यसनाचे निराकरण कसे केले जाते, ते दाखविले आहे.

आ. १३(इ) मध्ये या लोलकाच्या वापराचा तिसरा प्रकार दाखविला आहे. याला डोव्हे लोलक (एच्. डब्ल्यू. डोव्हे या जर्मन भौतिकीविज्ञांच्या नावावरून) असे म्हणतात. यात आपाती किरणांची मूळ दिशा कायम राहून फक्त वर-खाली अर्धपर्यसनाचे निराकरण होते. आपाती प्रकाशाच्या दिशेभोवती हा लोलक फिरविल्यास प्रतिमा दुप्पट कोनातून फिरते. पाणबुडीमधील परिदर्शकात या लोलकाचा विशेष उपयोग होतो.

संपूर्ण अंतर्गत परावर्तनाच्या तत्त्वाचा उपयोग करणाऱ्या वर वर्णन केलेल्या लोलकांच्या प्रकारांखेरीज खास उपयोगांकरिता इतर विशिष्ट प्रकारचे व याच तत्त्वाचा उपयोग करणारे लोलक योजण्यात आलेले आहेत. उदा., लुमर-ब्रोडहुन प्रकाशमापकात वापरण्यात येणारा लोलक [→प्रकाशमापन].

---

गोलीय पृष्ठावर प्रणमन : दोन पारदर्शक माध्यमांमधील आंतरपृष्ठ गोलीय असल्यास त्यामधून प्रकाशकिरण जाताना होणाऱ्या प्रणमनाला वर आलेले प्रणमनाचे नियमच लागू पडतात परंतु पृष्ठाच्या विशिष्ट आकारामुळे काही खास परिणाम घडून येतात. अशा गोलीय पृष्ठांच्या संयोगापासून ⇨ भिंगे बनत असल्याने त्यांच्या अभ्यासाला विशेष महत्त्व आहे. प्रणमनी गोलीय पृष्ठांच्या संदर्भात वक्रता त्रिज्या, मुख्य छेद, मुख्य अक्ष, छिद्रव्यास, ध्रुव इ. संज्ञांचे अर्थ गोलीय आरशांच्या संदर्भात दिल्यानुसारच आहेत. येथेही सूत्रांची सिद्धता करताना ‘छिद्रव्यास लहान आहे’असे गृहीत धरलेले असते. या सूत्रांमध्ये एकरूपता येण्यासाठी येथेही चिन्ह-संकेतांचा वापर करावा लागतो. पूर्वी दिलेल्या चिन्ह-संचाला येथे दोन जादा संकेतांची जोड द्यावी लागते.

(१) जे गोलीय पृष्ठ विरल माध्यमातून पाहता बहिर्गोल दिसते त्याची वक्रता त्रिज्या धन व जे अंतर्गोल दिसते त्याची वक्रता त्रिज्या ऋण मानावी.

(२) दोन माध्यमांच्या प्रणमनांकांमधील वजाबाकी येईल तेव्हा नेहमी मोठ्या मूल्याच्या प्रणमनांकांतून कमी मूल्याचा प्रणमनांक वजा करून येणारी धन वजाबाकीच घ्यावी (म्हणजेच वजाबाकीचे केवळमूल्य घ्यावे).

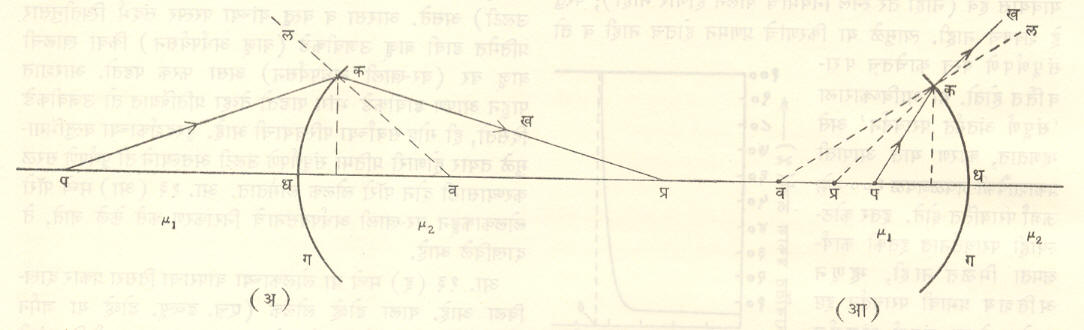
आ. १४(अ) मध्ये बहिर्गोल व १४(आ) मध्ये अंतर्गोल पृष्ठावरून प्रकाशाचे प्रणमन झालेले दाखविले आहे. आपाती किरण ज्यातून येतात त्या माध्यमाचा प्रणमनांक μ₁ व ज्यात प्रणमन होते त्या माध्यमाचा प्रणमनांक μ₂ (μ₂ &gt μ₁) आहे. आ. १४(अ) मध्ये प्रणमनामुळे खरी प्रतिमा व १४(आ) मध्ये भ्रामक प्रतिमा तयार होते.

u, v, r या अक्षरांचे पूर्वीप्रमाणेच अर्थ मानून व चिन्ह-संकेत वापरून गोलीय पृष्ठावरून होणाऱ्या प्रणमनासाठी सर्व परिस्थितीत

μ2	+	μ1	=	।μ2 — μ1।
V		u		r

हे सामान्य सूत्र सिद्ध करता येते.

---

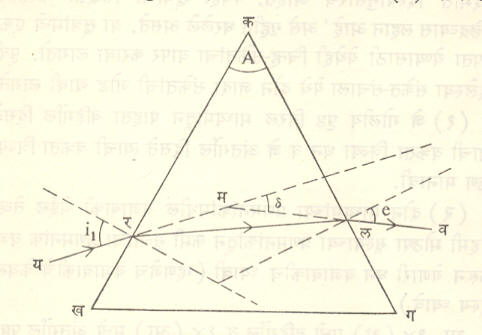
लोलक : लोलकातून होणारे विचलन : आ. १५ मध्ये त्रिकोणी लोलकाचा मुख्य छेद दाखविला असून

∠ खकग = A हा लोलक-कोन आहे. त्याच्या समारेची बाजू (खग) ही लोलकाचा पाया होय. यर हा किरण i₁हा आपाती कोन करून कख या बाजूवर आपाती होतो व प्रणमन होऊन रल या मार्गे लोलकातून जातो. ल येथे परत हवेत बाहेर येताना प्रणमन होते व तेथील पृष्ठलंबाशी e हा निर्गत कोन करून तो लव या मार्गे बाहेर पडतो. आपाती किरण पुढे व निर्गत किरण मागे वाढविल्यास ते म या बिंदूमध्ये परस्परांना छेदतात आणि तेथे त्या दोहोंमध्ये δहा कोन होतो. याचा अर्थ असा की, या लोलकामधून गेल्याचा परिणाम म्हणून मूळ किरण δया कोनातून वळतो. या δकोनाला विचलन कोन असे म्हणतात. र आणि ल या दोन्ही ठिकाणी प्रणमन होते तेव्हा अर्थातच प्रणमनाच्या दोनही नियमांचे पालन होते.

आपाती कोनाचे (i₁) मूल्य प्रथम अगदी कमी घेऊन ते हळूहळू वाढवीत न्यावे व प्रत्येक i₁च्या मूल्यासाठी विचलन कोन (δ)मोजावा. याप्रमाणे प्रयोग करून आपाती कोन व विचलन कोन यांचा आलेख काढल्यास आ. १६ मध्ये दाखविल्याप्रमाणे विचलन वक्र मिळतो. या वक्रावरून असे दिसते की, जसजसा आपाती कोन वाढत जातो तसतसा विचलन कोन प्रथम कमी होत जातो व शेवटी आपाती कोनाच्या i या विशिष्ट मूल्यासाठी विचलन कोन किमान (δ_m) होतो. यापुढे i₁वाढवीत गेल्यास विचलन कोन पुन्हा वाढू लागतो.

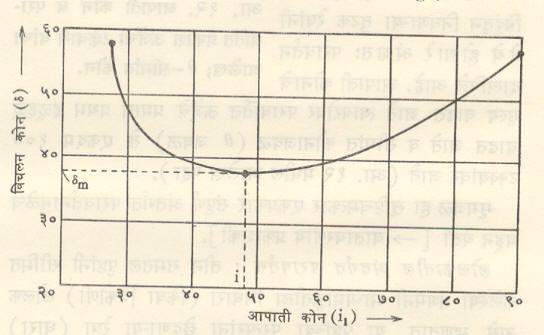
प्रकाशाच्या व्युत्क्रमतेच्या नियमानुसार किमान विचलनाच्या वेळी ∠i = ∠ e हे सिद्ध करता येते (∠e = निर्गत कोन). यावरून साध्या भूमितीवरून

∠i =	A + δm	व∠  r =	A
	2		2

हे दाखविता येते (∠r हा δ = δ_m असताना आ. १५ मध्ये कख या पृष्ठापाशीहोणारा प्रणमन कोन आहे). त्यावरून लोलकाचा (हवेच्या संदर्भात) प्रणमनांक

μ =	sin ½ (A + δm)	हे सिद्ध करता येते.
	sin A/2

लोलकाच्या द्रव्याचा प्रणमनांक काढण्यासाठी ही एक अत्यंत अचूक पद्धत आहे.

कीलाकार लोलक : लोलक-कोन (सु. १०° पेक्षा) लहान असल्यास पाचरीच्या आकाराचा कीलाकार लोलक बनतो. अशा लोलकामुळे मिळणारा विचलन कोनही लहान असल्यामुळे [कोन अरीयमानात दिल्यास→ कोन] sin ½ (A + δ_m) ≈  ½ ( A + δ) व

sin	A	≈	A
	2		2

ही आसन्न (अंदाजी) समीकरण वापरता येतात. मग

µ =	sin ½ (A + δm)	≈	A + δ
	sin A/2		A

ही आसन्न समीकरण मिळते (असा लोलक नेहमी किमान विचलनासाठी वापरला जात असल्यामुळे δ_mऐवजी δ हेच अक्षर वापरतात).

यावरून δ ≈ ‌(μ – 1) A या समीकरणाप्रत आपण येतो. वावरून असे दिसते की , विचलन कोन लोलक-कोनाच्या सम प्रमाणात व त्याचप्रमाणे लोलक-द्रव्याच्या प्रणमनत्वाच्या (μ –1या राशीला प्रणमनत्व असे म्हणतात) सम प्रमाणात असतो.दोन सारखे कीलाकार लोलक जोडून ठेवून एकाच्या संदर्भात दुसरा फिरविता येण्याची व्यवस्था केल्यास या जोडीमुळे मिळणारे विचलन फिरविण्याच्या कोनानुसार कमी-अधिक होते,या रचनेला रिझ्ली लोलक किंवा हर्शेल लोलक असे म्हणतात.अनेक प्रकाशकीय उपकरणांत त्याचा वापर केला जातो.

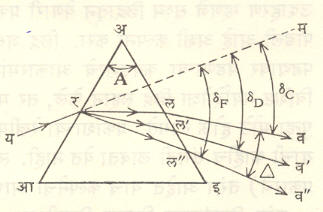
लोलकीय अपस्करण : प्रकाशाच्या रंगानुसार प्रणमनांक वेगळा असतो. पांढरा प्रकाश हा सप्तरंगांचे मिश्रण असून त्याच्या वर्णपटात एका टोकाला तांबडा, दुसऱ्या टोकाला जंबू (जांभळा) व साधारण मध्यावर पिवळा रंग येतो परंतु जंबू रंगाच्या प्रकाशासाठी डोळ्याची संवेदनशीलता फारच कमी असल्याने त्याच्या ऐवजी निळा रंग हाच वर्णपटाचे दुसरे टोक मानण्याचा प्रघात आहे. सामान्यतः खास रंगाचा निर्देश न केल्यास प्रणमनांक म्हणजे माध्य रंगासाठी म्हणजे पिवळ्या रंगासाठी दिला आहे, असे समजण्यात येते, बिनचूक निर्देशनासाठी तांबडा रंग म्हणजे हायड्रोजन वर्णपटातील (C) रेषेची तरंगलांबी, निळा म्हणजे त्याच वर्णपटातील F या रेषेची तरंगलांबी व पिवळा रंग म्हणजे सोडियमाच्या वर्णपटातील D या रेषेची तरंगलांबी समजण्यात येते [→ वर्णपटविज्ञान] व त्यांच्यासाठी विशिष्ट माध्यमाचे (हवेच्या संदर्भात) प्रणमनांक μ_C, μ_F या μ_D या चिन्हांनी व्यक्त केले जातात. प्रयोगांवरून असे दिसते की, कोणत्याही माध्यमाच्या बाबतीत μ_C &lt μ_D &lt μ_F कीलाकार लोलकाच्या विचलनाचे सूत्र या तीन तरंगलांब्यांसाठी वापरतात. δ_C = (μ_C – 1) A, δD = (μ_D – 1) A व δ_F = (μ_F – 1) A ही समीकरणे मिळतात यावरून δ_F &gt δ_D&gt δ_C हे स्पष्ट होते. अशा तऱ्हेने पांढरा प्रकाश लोलकावर पडल्यास त्यातील वेगवेगळ्या तरंगलांब्यांच्या किरणांचे वेगवेगळ्या मूल्याच्या कोनांमधून विचलन होऊन वेगवेगळे रंग परस्परांपासून अलग होतात, या आविष्काराला अपस्करण असे म्हणतात, लोलकामधून बाहेर येणाऱ्या कोणत्याही दोन वेगळ्या रंगाच्या किरणांमधील कोनाला त्या रंगांमधील कोनीय अपस्करण असे म्हणतात. खास करून C व F वर्णरेषांच्या रंगांमधील कोनाला लोलकाचे कोनीय अपस्करण (Δ) असे म्हणतात (आ. १७). आवृतीवरून हे स्पष्ट होईल की, Δ = δ_F —δ_C = (μ_F — 1) A — (μ_C — 1)A Δ = A (μ_F—μ_C). μ_F — μ_C या राशीचे मूल्य वेगवेगळ्या माध्यमांकरिता वेगवेगळे असते. यावरून असे म्हणता येते की, लोलकापासून मिळणारे अपस्करण लोलकाच्या माध्यमावर त्याचप्रमाणे लोलक-कोनाच्या मूल्यावर अवलंबन असते.

लोलकाचे कोनीय अपस्करण (Δ)	= माध्यमाची अपस्करणशीलता (ω).
लोलकामुळे माध्य रंगाचे होणारे विचलन (δD)

या समीकरणने अपस्करणशीलतेची व्याख्या दिली जाते. वर दिलेल्या कीलाकार लोलकासाठीही d_D व Δ यांची समीकरणे वापल्यास…..

Δ	=	A (μF—μC)	=	μF—μC
δD		A (μD—1)		μD—1

हे समीकरण मिळते. वावरून हे स्पष्ट होते की, अपस्करणशीलता लोलक-कोनावर अवलंबून नसून ती केवळ त्याच्या द्रव्यावर अवलंबून असते. ही समीकरणे कीलाकार लोलकासाठीच पूर्णपणे लागू आहेत. लोलक-कोन मोठा असल्यास ही समीकरणे गुणात्मक रीत्या लागू पडतात.

वर्णपटाची अपरिमेयता : लोलक, भिंगे यांसारखी प्रकाशीय उपकरणांत वापरावयाची साधने बनविण्यासाठी विविध खास घटक द्रव्यांपासून बनविलेल्या काचा किंवा प्लॅस्टिके वापरतात [→ भिंग]. या वेगवेगळ्या प्रकारच्या काचांच्या अपस्करणशीलतेची मूल्ये वेगळी असतात. दोन वेगळ्या प्रकारच्या काचांपासून सुयोग्य लोलक-कोन घेऊन असे दोन लोलक आपणास बनविता येतील की, त्यांपासून मिळणारे कोनीय अपस्करण समान मूल्याचे असेल, तरीही या दोन लोलकांपासून मिळणाऱ्या वर्णपटांतील इतर वर्णरेषांची स्थाने तंतोतंत एकसारखी येत नाहीत. लोलकांपासून मिळणाऱ्या वर्णपटांच्या या वैशिष्ट्याला वर्णपटांची अपरिमेयता असे म्हणतात. या वैशिष्ट्यामुळेच विवर्ण लोलक किंवा विवर्ण भिंगे बनविणे शक्य होते.

विवर्ण लोलकयुग्म : ज्या लोलकामधून पांढरा प्रकाशकिरण जाऊ दिला असता अपस्करण होणार नाही पण फक्त (माध्य किरणाचे) विचलन होईल त्याला विवर्ण लोलक असे म्हणतात. एकच लोलक विवर्ण होऊ शकणारच नाही, हे वरील विवेचनावरून लक्षात आलेच असेल, पण सुयोग्य लोलक-कोनांची मूल्ये असणारे दोन वेगवेगळ्या द्रव्यांचे लोलक एकमेकांना विरोधी दिक्‌स्थितीत ठेवले असता त्याच्यामुळे निष्पन्न अपस्करण शून्य मूल्याचे होईल परंतु काही विचलन अवशिष्ट राहील अशी रचना करणे शक्य होते. या रचनेला विवर्ण लोलकयुग्म असे म्हणतात. यासाठी सामान्यतः क्राउन व फ्लिंट या दोन प्रकारच्या काचांचे लोलक वापरतात. आ. १८ मध्ये असे विवर्ण लोलकयुग्म दाखविले आहे. विरुद्ध दिक्‌स्थितीमुळे दोन घटक लोलकांची व्यक्तिगत उपस्करणे व विचलने परस्परांविरुद्ध दिशांनी होतात परंतु अपस्करणांची मूल्ये समान येतील अशा तऱ्हेने A व A’ हे लोलक-कोन घेतल्यामुळे परिणामी अपस्करण शून्य होते परंतु वैयक्तिक विचलने δ व δ’ ही असमान असल्याने (δ’—δ) इतके परिणामी विचलन मिळू शकते.

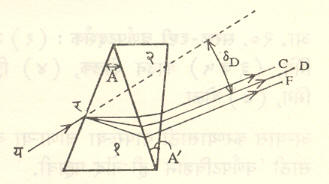
सरळ- दृष्टि लोलक : वरीलप्रमाणेच लोलकांची मांडणी करून त्यांचे लोलक-कोन A व A’ असे निवडता येतात की, त्यामुळे होणारी वैयक्तिक विचलने δ व δ’ सममूल्य परंतु उलट दिशेने व्हावीत, त्यामुळे परिणामी विचलन शून्य होते परंतु Δ’—Δ एवढे परिणामी अपस्करण शिल्लक राहते, आ. १९ मध्ये हे स्पष्ट केले आहे, D रेषेच्या तरंगलांबीचा निर्गत किरण आपाती किरणाला समांतर आहे (δ—δ’ = 0) परंतु C व F किरणांमध्ये काही कोन (Δ—Δ’ एवढा) होतो.

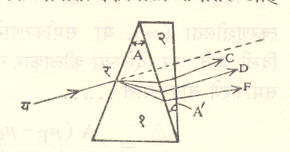
सरळ-दृष्टी वर्णपटदर्शक : या उपकणातून सरळ प्रकाश उद्‌गमाकडे पाहून त्या उद्‌गमाचा वर्णपट दिसू शकतो, त्यामुळे हा वापरण्यास जास्त सोपा असतो परंतु त्याने मिळणारे अपस्करण कमी असते, म्हणून तो वर्णपटांच्या गुणात्मक परीक्षणासाठीच मुख्यतः वापरला जातो, हे उपकरण सरळ-दृष्टि लोककावरच आधारलेले आहे. आ. २० मध्ये (१) ही फट उद्‌गमाकडे रोखली असता तिच्यामधून निघणारे किरण (२) या विवर्ण भिंगांकडून (परस्परांना) समांतर केले जातात, ही समांतर किरण-शलाका मग (३—४—५) या सरळ-दृष्टी लोलकावर पडून तिचे विचलनरहित अपस्करण होते. यासाठी एकूण लोलकांची संख्या ३ (किंवा ५) अशी विषम असून क्राउन आणि फ्लिंट लोलक एकाआड एक असे परस्परांना जोडून वसविलेले असतात. (६) व (७) या भिंगांचा मिळून एक दूरदर्शक बनतो व त्यातून निष्पन्न वर्णपटाचे अवलोकन केले जाते. (६) या भिंगाकडून तांबडे व निळे किरण अलग अलग केंद्रित होतात. अधिक बारकाईने वर्णपटांचा अभ्यास करण्यासाठी वापरल्या जाणाऱ्या वर्णपटमापकांच्या तपशीलासाठी ‘वर्णपटविज्ञान’ ही नोंद पहावी.

---

भिंगे : दोन्ही पृष्ठे वक्र किंवा एक पृष्ठ वक्र आणि दुसरे सपाट यांनी सीमित केलेल्या प्रणमनी माध्यमाला भिंग असे म्हणतात. भिंगांबद्दलच्या सविस्तर माहितीसाठी ‘भिंग’ ही नोंद पहावी. विवर्ण भिंगाची माहिती ‘दूरदर्शक’ या नोंदीत आली असून ‘प्रकाशीय व्यूहातील विपथन’ या नोंदीत भिंगांमुळे तयार होणाऱ्या प्रतिमांमधील विविध दोष व त्यांचे निराकरण यांची चर्चा केली आहे, कॅमेऱ्याकरिता वापरण्यात येणाऱ्या विविध भिंग प्रणालींचे वर्णन ‘कॅमेरा’ या नोंदीत दिले आहे.

तंतु-प्रकाशकी : जॉन टिंड्ल या भौतिकीविज्ञांनी १८७० मध्ये संपूर्ण अंतर्गत परावर्तनाचा उपयोग करून काचेच्या वक्र दंडातून प्रकाशाचे संवहन करता येते, असे दाखविले होते, काचेच्या वा पारदर्शक प्लॅस्टिकच्या एकाच जाड दंडातून प्रकाशाचे संवहन करण्याऐवजी त्याच द्रव्याच्या सूक्ष्म तंतूंचा जुडगा वापरला, तर त्याच्या एका टोकाकडून दुसऱ्या टोकापाशी प्रतिमेचे प्रेषण करता येते, कारण त्यात जुडग्यातील प्रत्येक तंतू प्रतिमेचा काही भाग दुसऱ्या टोकाला जशाचा तसा पोहचवितो व पूर्ण प्रतिमा मिळू शकते. या गुणधर्माच्या अभ्यासामुळे प्रकाशकीची ‘तंतु-प्रकाशकी’ ही नवीनच शाखा निर्माण झालेली असून तिचा प्रतिमा प्रेषण, संदेशवाहन इ, विविध क्षेत्रांत उपयोग होत आहे.

या पद्धतीत पारदर्शक तंतूमध्ये संपूर्ण अंतर्गत परावर्तनाद्वारे प्रकाशाचे संवहन होत असल्याने प्रकाश शलाका त्याच माध्यमात परावर्तित होते. त्यामुळे तंतूंच्या एका बाजूकडून दुसऱ्या बाजूकडे प्रकाश शलाकेचे परावर्तन होऊन तिचे नागमोडी मार्गानेसुद्धा संवहन केले जाते. तसेच या पद्धतीत साध्या परावर्तनापेक्षा प्रकाशाचा व्यय अत्यल्प होत असल्याने प्रतिमेचे खूप दूरवर प्रेषण होऊ शकते, तंतु-प्रकाशतीत वापरण्यात येणारे सूक्ष्म अरुंद संवाहक तंतू सामान्यतः अधिक प्रणमनांक असलेल्या काचेच्या दंडगोलाकार तंतूभोवती सापेक्षतः कमी प्रणमनांक असलेल्या काचेचा पाताळ थर देऊन तयार करतात. या दोन प्रकारच्या काचांच्या विभाजक पृष्ठभागावर संपूर्ण अंतर्गत परावर्तन होते. थरांमुळे आतील परावर्तक पृष्ठभागाचे संरक्षण होण्याबरोबरच जुडग्यातील तंतू एकमेकांपासून अलग राहतात. हे तंतू विविध आकारांचे व आकारमानांचे तयार करता येतात. विकृत प्रतिमा मिळू नये म्हणून जुडग्यातील तंतू योग्य प्रकारे जुळविलेले असणे अत्यावश्यक असते.

प्रकाशकीय तंतू जरूर तसे वाकविता येत असल्याने शरीरातील अंतर्गत अवयवांची अथवा यंत्रामधील प्रत्यक्ष तपासणी करणे अडचणीचे असते, अशा भागांची तपासणी करण्याकरिता अशा तंतूंच्या जुडग्याचा वापर करणारे तंतुदर्शक नावाचे उपकरण तयार करण्यात आले आहे. या उपकरणात तंतूंच्या जुडग्याभोवतील आवरणात बाह्य दिव्याचाही समावेश केलेला असल्याने पोटात वा इतरत्र तो सोडून अंतर्गत अवयवांची वा यंत्रभागांची छायाचित्रे घेता येतात. लेसर किरणांचा उपयोग करून प्रकाशीय तंतूंच्या साहाय्याने दूरध्वनी आणि प्रदत्त (माहिती) संदेशवहन करण्याची पद्धत प्रत्यक्ष व्यवहारातही आलेली आहे. [→ प्रकाशीय संदेशवहन लेसर].

 

भौतिकीय प्रकाशकी

प्रकाशाच्या ज्या आविष्कारांची उकल तरंग सिद्धांताशिवाय करता येत नाही, त्यांची चर्चा या विभागात केली आहे. याचे अत्यंत सोपे उदाहरण म्हणजे सूक्ष्म छिद्रातून येणारी प्रकाश शलाका एका पडद्यावर पाडली आहे अशी कल्पना करा. छिद्र जसजसे लहान करावे तसतसे पडद्यावर पडणाऱ्या कवडशाचे आकारमान लहान होत जाते परंतु विशिष्ट मर्यादेपेक्षा छिद्र लहान केले, तर मग कवडशाचे आकारमान पुन्हा मोठे होऊ लागते. प्रकाशाच्या रेखीय प्रसारणाच्या दृष्टिकोनातून वाची काहीच संगती लावता येत नाही. त्यासाठी प्रकाश हे (विशिष्ट प्रकारचे) तरंग आहेत याच कल्पनेचा आधार घ्यावा लागतो.

तरंग सिद्धांताचा विकास क्रिस्तीआन हायगेन्झ (१६२९—९५), टॉमस यंग (१७७३—१८२९) व ऑग्यूस्तीन झां फ्रेनेल (१७८८—१८२७) यांनी केला [→ प्रकाश]. तरंग सिद्धांतानुसार भूमितीय प्रकाशकीतील सर्व आविष्कारांचेही यथायोग्य स्पष्टीकरण करता येते. मूळ कल्पनेनुसार हे तरंग ईथर या काल्पनिक माध्यमाच्या [→ ईथर—२] कणांच्या आंदोलनाच्या स्वरूपाचे असतात, असे मानले होते. जे. सी. मॅक्सवेल (१९३१—७९), यांच्या सिद्धांतानुसार प्रकाश म्हणजे विद्युत् चुंबकीय तरंग आहे हीच तरंग सिद्धांताची भूमिका आता मान्यता पावली आहे परंतु विद्युत् चुंबकीय तरंगांची गणितकृत्ये फारच क्लिष्ट आहेत. ओ. वायनर यांनी केलेल्या प्रयोगावरून हे स्पष्ट झाले की, फ्रेनेल यॉनी कल्पिलेली ईथर-कणांची आंदोलने विद्युत् चुंबकीय तरंगातील विद्युत् क्षेत्र सदिशाच्या (दिशा व परिमाण दर्शविणाऱ्या राशीच्या) आंदोलनाशी बरोबर जुळतात. विविध आविष्कारांची चर्चा फ्रेनेल यांच्या कल्पनेनुसार सुलभतेने करता येते, म्हणून प्रस्तुत नोंदीतील बहुतेक चर्चा फक्त ईथर-कणांच्या आंदोलनाऐवजी विद्युत् क्षेत्र सदिशाची आंदोलने एवढा फरक करून हायगेन्झ व फ्रेनेल यांच्या पद्धतीनुसारच केली आहे.

तरंग गतीबद्दल मुख्य संज्ञा व संकल्पना : तरंग गतीसंबंधीच्या प्रमुख संकल्पनांचा व संज्ञांचा येथे थोडक्यात आढावा घेतला आहे (अधिक माहितीसाठी ‘तरंग गति’ ही नोंद पहावी). तरंग गतीचे दोन मुख्य प्रकार अनुतरंग व अवतरंग हे आहेत. प्रकाश तरंग हे अवतरंग या प्रकारात मोडतात. ताणलेल्या तारेवरील तरंग याच प्रकारात मोडतात. या तरंग प्रकारात माध्यमांच्या कणांची आंदोलने तरंगांच्या प्रसारणाच्या दिशेला लंब दिशेने होतात. अशा (ज्या-वक्रीय) तरंगाचे दिग्दर्शन आ. २१ मध्ये केले आहे.

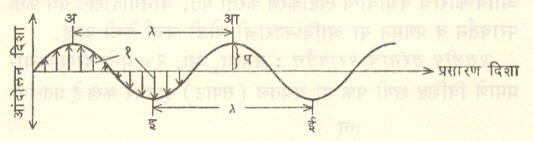
प्रकाश तरंगात कणांच्या आंदोलनाऐवजी विद्युत् क्षेत्र तीव्रता सदिशात आवर्ती बदल होत असतात. विशिष्ट क्षणी काही बिंदूंच्या ठिकाणचे विद्युत् क्षेत्र तीव्रता सदिश आकृतीत बाणयुक्त उभ्या रेषांनी दाखविले आहे. सर्वसामान्य अवतरंगाच्या बाबतीत हे बाण त्या त्या बिंदूचे स्थानांतरण दिग्दर्शित करतील.

दोलायमान कणाची आंदोलन स्थिती म्हणजेच त्या बिंदूच्या ठिकाणची कला (एखाद्या संदर्भाच्या सापेक्ष असणारी स्थिती) होय. आंदोलन स्थितीमध्ये कणाचे स्थानांतरण व वेग या दोन (सदिश) राशींचा अंतर्भाव होत असतो. आ. २१ मध्ये अ व आ या बिंदूंची आंदोलन स्थिती एकसारखीच आहे (तशीच ही इ व ई या बिदूंचीही एकसारखी आहे). अशा एकसारखी आंदोलन स्थिती असणाऱ्या दोन लागोपाठच्या बिंदूंमधील कलांतर २ π (अरीयमान) असते. अ व इ किंवा आ व ई यांच्या कला परस्परांविरुद्ध आहेत. विरुद्ध कला असणाऱ्या दोन लगतच्या बिंदूंमधील कलांतर π असते. २ π कलांतर असणाऱ्या कोणत्याही दोन बिंदूंमधील (सरळ रेषेत मोजलेले) अंतर तरंगलांबी (λ) इतके असते, तर π कलांतर असणाऱ्या बिंदूंमधील अंतर अर्ध तरंगलांबी ( ^λ/₂) इतके असते.

आंदोलनात होणाऱ्या कमाल स्थानांतरणाला तरंगाचा परमप्रसर असे म्हणतात. प्रकाशाचे दीप्तिमान त्याच्या तरंगांच्या परमप्रसराच्या वर्णाच्या सम प्रमाणात असते. तरंगामुळे एका सेकंदात होणाऱ्या आंदोलनांच्या संख्येला कंप्रता (ν) असे म्हणतात. प्रकाश तरंगांच्या बाबतीत, विशिष्ट माध्यमातील प्रकाशवेग v = νλ व λ = ^v/_ν ही समीकरणे मिळतात. विशिष्ट प्रकाशाची कंप्रता कोणत्याही माध्यमात स्थिर मूल्यी राहते परंतु वेगवेगळ्या माध्यमांत प्रकाशवेग वेगळी मूल्ये धारण करतो, त्यामुळे (वरील समीकरणानुसार) माध्यम बदलले की, सामान्यतः तरंगलांबी बदलते.

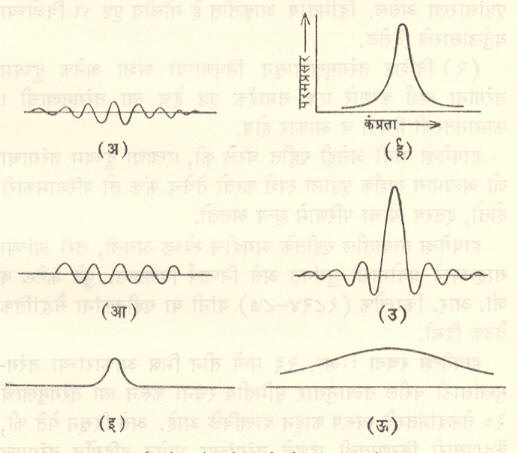
विशिष्ट प्रकाश तरंगाची कंप्रता (किंवा तरंगलांबी) एकाच निश्चित मूल्याची असेल, तर त्या प्रकाशाला एकवर्णी प्रकाश असे म्हणतात. खराखुरा एकवर्णी प्रकाश मिळण्यासाठी प्रकाश उद्‌गमापासून अनंत लांबीची अखंड तरंगमाला निर्माण झाली पाहिजे परंतु अणूमधील मूलभूत ‘आंदोलन’ फक्त मर्यादित लांबीच्याच तरंगमाला निर्माण करू शकतात. त्यामुळे तज्‍जन्य प्रकाशाची कंप्रता काही Δν या मर्यादेत बदलते म्हणजे आदर्श एकवर्णी प्रकाश मिळूच शकत नाही. आ. २२ मध्ये काही आकारांच्या तरंगमाला आणि त्यांमधील कंप्रता वितरणाचे आलेख दाखविले आहेत. अणूमधुन उत्सर्जित होणाऱ्या वर्णरेषेची तरंगमाला आ. २२ (अ) मध्ये दाखविली असून तिच्यामधीन कंप्रता वितरण आ. २२ (ई) मध्ये दाखविले आहे. एखाद्या अत्यल्प काळाकरिता उघडणाऱ्या झडपेच्या साहाय्याने मिळणारा व सर्वत्र तारखा परमप्रसर असलेला आदर्श एकवर्णी तरंगमालाखंड आ. २२ (आ) मध्ये व त्यातीत कंप्रता वितरण आ. २२ (उ) मध्ये दाखविली आहेत. आ. २२ (इ) हा एक स्पंद असून त्यातील कंप्रता वितरण आ. २२ (ऊ) मध्ये दाखविले आहेत. अती उष्ण पदार्थापासून उत्सर्जित होणारा पांढरा प्रकाश अशा स्पंदांच्या स्वरूपात असतो. तो प्रकाश लोलकातून [किंवा विवर्तन जालकातून → विवर्तन जालक] गेला असता सप्तरंगी वर्णपट मिळतो. यावरून हे सप्तरंग पांढऱ्या प्रकाशाचे घटक आहेत, असा निष्कर्ष न्यूटन यांनी काढला होता परंतु वरील विवेचनाच्या अनुरोधाने असे दिसते की, न्यूटन यांच्या प्रयोगात लोलक हा फूर्ये विश्लेषकाचे [→ हरात्मक विश्लेषण] कार्य करतो व या अर्थाने हे रंग लोलकातच तयार होतात. ए. गाय व इतर शास्त्रज्ञांनी या दृष्टिकोनावर भर दिला आहे. [आ. २२ (अ), (आ), (इ) मध्ये दाखविलेल्या तरंगमालांचे (ई), (उ), (ऊ) ही ‘फूर्ये रूपांतरे’ आहेत → समाकल समीकरणे व रूपांतरे].

तरंग-वेग व समूह-वेग : कोणत्याही प्रकारच्या तरंगांच्या प्रसारणात माध्यमाच्या कणांचे प्रसारण होत नसून आंदोलन स्थिती किंवा कला पुढे पुढे जात असते व त्यामुळे ऊर्जेचे प्रसारण होते, ज्या वेगाने एकाच कंप्रतेच्या तरंगाची कला प्रसारित होईल त्या वेगाला तरंग-वेग किंवा कला-वेग (v) असे म्हणतात परंतु सामान्यतः प्रकाश म्हणजे अनेक कंप्रतांच्या (किंवा तरंगलांब्यांच्या) तरंगांचा समूह किंवा तरंगपुंज असतो. अशा तरंग-समूहाच्या वेगाला समूह-वेग (u) असे म्हणतात. ज्या माध्यमात सर्व तरंगलांब्यांचा तरंग-वेग समान असतो त्यामध्ये त्या तरंगांचा समूह-वेग व तरंग-वेग सारखेच येतील उदा., निर्वातात ही परिस्थिती असते परंतु वास्तव माध्यमात (उदा., काचेत) तरंग-वेग हा तरंगलांबीनुसार बदलतो. अशा वेळी समूह-वेग हा तरंग-वेगापेक्षा वेगळा येतो आणि त्यांमधील संबंध पुढील समीकरणाने मिळतो.

u = v – λ.	dv
	dλ

येथे λ ही प्रकाशाची त्या माध्यमातील तरंगलांबी आहे. प्रकाश ऊर्जा या समूह-वेगानेच प्रसारित होते व म्हणून प्रकाशवेगाचे मापन करण्याच्या प्रयोगात आपण या समूह-वेगाचे मापन करतो, हे लक्षात घेणे महत्त्वाचे आहे.

हायगेन्झ तत्त्व : तरंगांचे प्रसारण रेखीय नसते तेव्हा तरंग सिद्धांतानुसार विविध प्रकाशीय आविष्कारांचे स्पष्टीकरण करताना किरणांची कल्पना अग्राह्य ठरते. विशिष्ट तरंगमुखाचे (सर्व दिशांत तारख्याच वेगाने प्रसारित होणारा तरंग ज्या ज्या ठिकणी पोहोचला असेल ते सर्व बिंदू जोडून तयार होणाऱ्या कल्पित पृष्ठाचे) t या कालानंतरचे स्थान व आकार काढता येण्यासाठी हायगेन्झ यांनी एक उपयुक्त अभिकल्पना मांडली, तिलाच हायगेन्झ तत्त्व अतें म्हणतात. हे तत्त्व पुढीलप्रमाणे मांडता येईल.

(१) कोणत्याही तरंगमुखावरील प्रत्येक बिंदु एका दुय्यम स्वतंत्र प्रकाश उद्‌गमासारखे कार्य करतो व सर्व दिशांना दुय्यम तरंग उत्सर्जित करतो. विशिष्ट एकविध माध्यमात प्रकाश वेग v असल्यास t कालानंतर या दुय्यम तरंगांचा आकार vt या त्रिज्येच्या गोलीय पृष्ठांसारखा असेल, द्विमितीय आकृतीत हे गोलीय पृष्ठ vt त्रिज्येच्या वर्तुळासारखे दिसेल.

(२) विशिष्ट तरंगमुखपासून निघणाऱ्या अशा अनेक दुय्यम तरंगांना स्पर्श करणारे एक समाईक पृष्ठ हेच त्या तरंगमुखाची t कालानंतरची स्थिती व आकार होय.

हायगेन्झ यांनी असेही गृहीत धरले की, एखाद्य दुय्यम तरंगाचा जो अल्पभाग स्पर्शक पृष्ठाला स्पर्श करतो तेथेच फक्त तो परिणामकारी होतो, इतरत्र त्याचा परिणाम शून्य असतो.

हायगेन्झ तत्त्वातील गृहीतके अगदीच स्वेच्छ असली, तरी त्यांच्या साहाय्याने प्रयोगाशी सुसंगत असे निष्कर्ष मिळतात. पुढे फ्रेनेल व जी. आर्. किरखोफ (१८२४—८७) यांनी या गृहीतकांना सैद्धांतिक बैठक दिली.

हायगेन्झ रचना : आ. २३ मध्ये तीन भिन्न आकारांच्या तरंग-मुखांसाठी वरील तत्त्वानुसार भूमितीय रचना करून त्या तरंगमुखाचे ३० सेकंदांनंतरचे स्वरूप काढून दाखविले आहे. असे दिसून येते की, केंद्राभिसारी किरणावली म्हणजे तरंगांच्या भाषेत बहिर्गोल तरंगमुख व केंद्राभिसारी किरणावली म्हणचे अंतर्गोल तरंगमुख आणि समांतर किरणावली म्हणजे प्रतलीय तरंगमुख होय.

आकृतीवरून हायगेन्झ रचना समजून येईल. तीवरून हेही समजेल की, बहिर्गोल तरंगमुख उत्तरोत्तर मोठे होत जाऊन मूळची ऊर्जा अधिकाधिक मोठ्या पृष्ठभागावर वाटली जाईल. या उलट अंतर्गोल तरंगमुख उत्तरोत्तर लहान होत जाऊन शेवटी जेथे बिंदुरूप होईल तेथे सर्व ऊर्जा केंद्रित होईल.

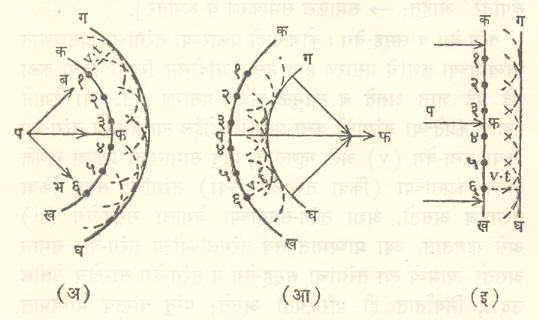
हायगेन्झ रचनेच्या साहाय्याने परावर्तन, प्रणमन आणि भिंगे व सपाट किंवा वक्र आरसे यांच्यामुळे मिळणाऱ्या प्रतिमा इ. सर्व आविष्कारांचे यथायोग्य स्पष्टीकरण करता येते. वानगीदाखल येथे फक्त परावर्तन व प्रणमन या आविष्कारांची थोडी चर्चा केली आहे.

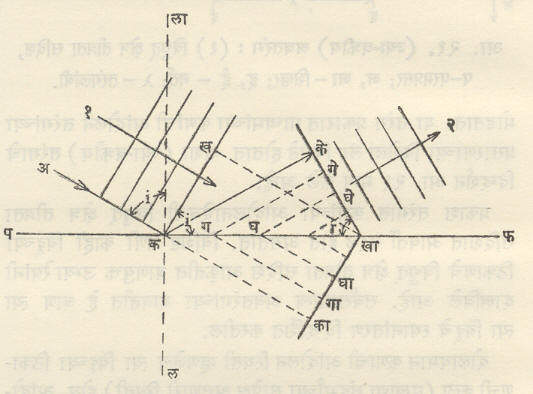
प्रतलीय तरंगाचे परावर्तन : समजा, आ. २४ मध्ये दाखविल्याप्रमाणे विशिष्ट क्षणी पफ या समतल (सपाट) पृष्ठावर कख हे प्रतलीय तरंगमुख आपाती झाले असून त्या दोहोंमधील आपाती कोन i आहे. ख येथील (तरंगजन्य) विक्षोभ पफ वर खा येथे पोहोचण्यासाठी t से. काल लागेल असे समजल्यास t या काली खा या बिंदूपासून शून्य लांबीच्या त्रिज्येचा वर्तुळाकार दुय्यम तरंग निघेल, परावर्तकाच्या अभावी याच वेळी क येथील विक्षोभ का येथे पोहोचला असता पण क हा बिंदू परावर्तक पृष्ठावर असल्याने क पासून निघणारा दुय्यम तरंग कका (= vt v – माध्यमातील तरंग-वेग) एवढ्या त्रिज्येचे वर्तुळ होईल, पण हा दुय्यम तरंग मूळच्याच माध्यमात (पफ च्या वरच्या बाजूला) प्रसारित होईल. क मध्य व कका त्रिज्या घेऊन वर्तुळाचा चाप काढल्यास खा मधून त्याला स्पर्शिका खाके ही होईल. हेच परावर्तित तरंगमुख होय. हे सहज दाखविता येते की, मध्यंतरीच्या ग, घ यांसारख्या बिंदूंपासून गगा, घघा इत्यादी लांबीच्या त्रिज्या असलेले दुय्यम तरंग निघून पफ च्या वरच्या बाजूस जातील व त्या सर्वांना खाके ही रेषा स्पर्श करते. भूमितीच्या साहाय्याने परावर्तित तरंगमुख खाके आणि पफ यांमधील कोन (= r परावर्तन कोन) हा आपाती कोनाशी सममूल्य आहे, हे सिद्ध करता येते.

प्रतलीय तरंगाचे समतल पृष्ठावरून प्रणमन : आ. २५ मध्ये पफ हे दोन माध्यमांमधील आंतरपृष्ठ असून त्याच्या वरच्या माध्यमात प्रकाशवेग v₁ व खालच्या माध्यमात तो v₂ आहे. ख पासून खा येथे पोहोचण्यास विक्षोभाला t काल लागत असल्यास खखा = v₁t येईल व माध्यम बदलले नसते, तर t या काली कखची स्थिती काखा ही झाली असती परंतु पफ च्या खालच्या माध्यमात प्रकाशवेग v₂ असल्याने t या काली क पासून v₂t या त्रिज्येचा दुय्यम तरंग प्रसारित होईल. क हा मध्य घेऊन v₂t या त्रिज्येचा चाप काढून त्याला खाके ही

स्पर्शिका काढल्यास खाके हेच प्रणमित तरंगमुख होय. हे सहज दाखविता येते की, ग, घ यांसारख्या दरम्यानच्या बिंदूंपासून निघणाऱ्या सर्व दुय्यम तरंगांची खाके ही समाईक स्पर्शिका आहे.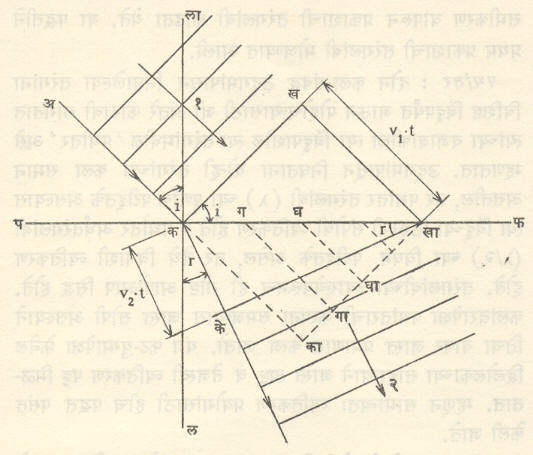

आवृतीवरून असे दिसते की,

sin i	=	v1t	=	v1	= μ = एक स्थिरांक.
Sin r		V2t		v2

अशा तऱ्हेने स्नेल नियम सिद्ध होतो परंतु त्यापुढे जर sin i &gt Sin r असेल, तर v₁ &gt v₂ म्हणजेच या विवेचनानुसार विरल माध्यमातील प्रकाशवेगापेक्षा सधन माध्यमातील प्रकाशाचा वेग कमी असावयास पाहिजे. जे. बी. एल्. फूको यांच्या प्रयोगावरून याची सत्यता सिद्ध झाली. [→ प्रकाशवेग].

व्यतिकरण : आ. २१ मध्ये अवतरंगांचे सर्वोच्च भाग म्हणजे शिखरे व सर्वांत खोल भाग म्हणजे गर्त दाखविले आहेत. एका तरंगाचे शिखर दुसऱ्या तरंगांच्या गर्तावर बरोबर पडले, तर गर्त व शिखर परस्परांना नाहीसे करतील. एक गर्त व एक शिखर यांमध्ये कलांतर (2n + 1) π (म्हणजे π च्या विषम पूर्णांकी पटीत) असते. यावरून व्यापकीकरण करून असा नियम देता येतो की, विशिष्ट ठिकाणी संपाती होणाऱ्या दोन तरंगांमधील कलांतर π (किंवा त्याच्या विषम पूर्णांकी पट) असेल, तर ते तरंग तेथे परस्परांचे निराकरण करतात. यामुळे प्रकाश तरंगांच्या बाबतीत त्या ठिकाणी अंधार निर्माण होईल. याला विनाशी व्यतिकरण असे म्हणतात. याउलट दोन प्रकाश तरंग 2 π किंवा त्याच्या पूर्णपटीच्या कलांतराने एकत्र आल्यास ते परस्परांना पोषक होऊन तेथे जास्त तीव्र प्रकाश तयार होईल, अशा आविष्काराला संपोषी व्यक्तिकरण असे म्हणतात.

व्यतिकरणाच्या अटी : पाण्यावरील तरंगांच्या बाबतीत व्यतिकरण होते, हे प्रयोगाने सहज दाखविता येते परंतु प्रकाशाच्या बाबतीत प्रारंभी केलेले सर्व प्रयोग याबाबतीत अयशस्वी ठरले (आणि त्यामुळे तरंग सिद्धांताच्या सत्यतेबद्दलच शंका उत्पन्न झाली). याचे कारण म्हणजे या प्रयोगांतून त्यासाठी आवश्यक त्या अटींची पूर्ती झालेली नव्हती. किंबहुना या अटींची नीटशी कल्पनाच त्या काळी नव्हती. व्यतिकरणाचा पहिला यशस्वी प्रयोग यंग यांनी इ. स. १८०० मध्ये केला व त्यामुळेच त्यासाठी आवश्यक असलेल्या अटींची नीट कल्पना विकसित झाली. त्या अटी अशा : (१) यासाठी एकवर्णकल्प (जवळजवळ एकवर्णी) प्रकाश वापरला पाहिजे. (२) वापरावयाचे दोनही प्रकाश उद्‌गम अल्प विस्ताराचे किंवा अरुंद असावेत. (३) त्या दोन उद्‌गमांमधील अंतर अगदी थोडे (फार तर काही मिमी.) असावे. (४) शेवटची व सर्वांत महत्त्वाची अट म्हणजे ते उद्‌गम कला-संबद्ध असले पाहिजेत (त्यांच्या कलांमध्ये कायम काही निश्चित अंतर–कलांतर–असले पाहिजे).

कला-संबद्ध उद्‌गम ही कल्पना थोडी जास्त स्पष्ट करणे जरूर आहे. एखादी ज्योत किंवा तात तंतू यासारख्या उद्‌गमात प्रत्यक्षात असंख्य अणू तरंगमालांचे अगदी स्वेच्छ तऱ्हेने उत्सर्जन करीत असतात आणि अशा प्रत्येक उत्सर्जनात तरंगाची प्रारंभीची कला अत्यंत अनियमितपणे एकसारखी बदलत असते. हे बदल प्रती सेकंदाला सु. १० कोटी वेळा होत असतात. या बदलांचे आपणाला काहीही नियंत्रण करता येत नाही . यामुळे दोन स्वतंत्र उद्‌गमांपासून निघणाऱ्या तरंगांमधील कलांतर क्षणोक्षणी बदलत असते. म्हणून दोन स्वतंत्र उद्‌गम (उदा., दोन ज्योती किंवा दोन विद्युत् दिवे) कधीच कला-संबद्ध होऊ शकत नाहीत. यासाठी दोन कला-संबद्ध उद्‌गम हे एकाच स्वतंत्र उद्‌गमापासून कोणत्यातरी पद्धतीने सिद्ध करावे लागतात. या पद्धती पुढे दिल्या आहेत.

कला-संबद्धतेची अनिवार्यता : समजा की, दोन कला-संबद्ध नसलेल्या उद्‌गमांपासून निघणारे प्रकाश तरंग एका पडद्यावर एका बिंदूच्या ठायी एकत्र येत असून त्यांच्या मधील कलांतर एका विशिष्ट क्षणी तेथे अंधार उत्पन्न करते आहे परंतु पुढच्याच क्षणी हे कलांतर आपोआप बदलून तेथे अंधाराऐवजी तीव्र दीपन होईल. पडद्यावरील प्रत्येक बिंदूवर अशा तऱ्हेने दीपनात होणारे बदल अती त्वरेने होत असल्याने मानवी नेत्राला त्यांचा मागोवा घेताच येत नाही व पडद्यावर सर्वत्र सरासरी दीप्तीचे प्रकाशन झाले आहे असे प्रतीत होते.

कला-संबद्ध उद्‌गम : असे उद्‌गम मिळविण्याच्या प्रमुख पद्धती म्हणजे (१) यंग यांचे फट-युग्म, (२) फ्रेनेल यांचा द्विलोलक, (३) हंफ्री लॉइड यांचा आरसा, (४) फेलीक्स बिलेत यांचे दुभंगित भिंग इत्यादी. आ. २६ मध्ये या पद्धती दाखविल्या आहेत. या सर्व पद्धतींत एकवर्णी प्रकाशाने दीप्त केलेली एक अरुंद फट ही

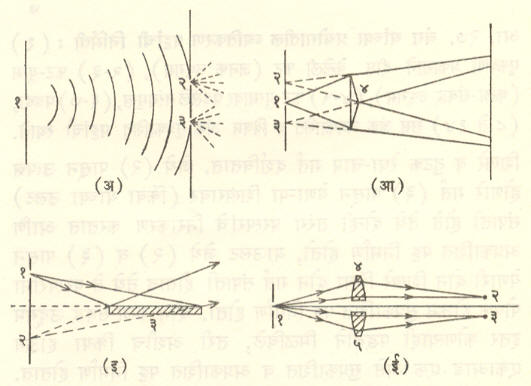
मुख्य किंवा जनक उद्‌गम म्हणून वापरली जाते. तिच्यापासून निघणारा प्रकाश वरीलपैकी एखाद्या साधनावर पडून दोन कला-संबद्ध उद्‌गम मिळविले जातात.

यंग यांच्या पद्धतीत एकाच तरंगमुखाने प्रकाशित झालेल्या दोन फटी या कला-संबद्ध उद्‌गम म्हणून वापरल्या जातात. फ्रेनेल द्विलोलकाच्या दोन भागांमधून होणाऱ्या विचलनाने जनक उद्‌गमाच्या तयार होणाऱ्या दोन (भ्रामक) प्रतिमा या कला-संबद्ध उद्‌गम म्हणून वापरल्या जातात. लॉइड आरशाच्या पद्धतीत खुद्द जनक उद्‌गम व त्याची सपाट आरशातील भ्रामक प्रतिमा या दोहोंचा कला-संबद्ध उद्‌गम म्हणून उपयोग केला जातो. बिलेत पद्धतीत भिंगाच्या दोन भागांनी बनविलेल्या दोन खऱ्या प्रतिमा कला-संबद्ध उद्‌गम म्हणून कार्य करतात.

यंग यांचा प्रयोग : आ. २७ मध्ये यंग यांच्या प्रयोगात व्यतिकरणाने पडद्यावर सुप्रकाशित व अप्रकाशित पट्टे (व्यतिकरण पट्टे) कसे तयार होतात, हे दाखविले आहे.

या आकृतीत गोलाकार चापांनी (२) व (३) या कला-संबद्ध उद्‌गमांपासून निघणारे दुय्यम तरंग दाखविले असून अखंड रेषा-चाप शिखरे व तुटक रेशा-चाप गर्त दर्शवितात. जेथे (२) पासून उत्पन्न होणारे गर्त (३) पासून येणाऱ्या शिखरावर (किंवा याच्या उलट) संपाती होते तेथे दोन्ही तरंग परस्परांचे निराकरण करतात आणि अप्रकाशित पट्ट निर्माण होतो, याउलट जेथे (२) व (३) पासून येणारी दोन शिखरे किंवा दोन गर्त संपाती होतात तेथे ते परस्परांना पोषक होऊन सुप्रकाशित पट्ट निर्माण होतो. दोन कला-संबद्ध उद्‌गम इतर कोणत्याही पद्धतीने मिळविले, तरी अशीच क्रिया होऊन एकाआड एक असे सुप्रकाशित व अप्रकाशित पट्ट निर्माण होतात. (चित्रपत्र ३८).

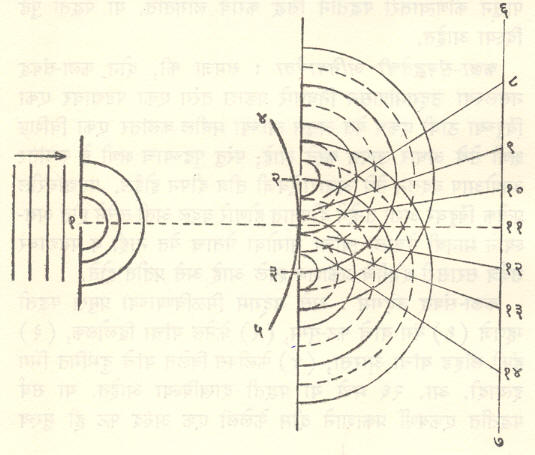
हे पट्ट परस्परांना समांतर असतात. दोन लागोपाठच्या सुप्रकाशित (किंवा अप्रकाशित) पट्टांमधील अंतर z असल्यास z = ^λD/d हे सहज सिद्ध करता येते (येथे d हे दोन कला-संबद्ध उद्‌गमांमधील अंतर, D हे उद्‌गमांपासून पडद्याचे अंतर व λ ही प्रकाशाची तरंगलांबी होय). प्रयोगात z, d व D यांची मूल्ये मोजून त्यावरून वरील समीकरण वापरून प्रकाशाची तरंगलांबी काढता येते. या पद्धतीने प्रथम प्रकाशाची तरंगलांबी मोजण्यात आली.

पथांतर : दोन कला-संबद्ध उद्‌गमांपासून निघालेल्या तरंगांना विशिष्ट बिंदूपर्यंत जाऊन पोहोचण्यासाठी जी अंतरे काटावी लागतात त्यांच्या वजाबाकीला त्या बिंदूपाशील त्या तरंगांमधील ‘पथांतर’ असे म्हणतात. उद्‌गमांपासून निघताना दोन्ही तरंगांच्या कला समान असतील, तर पथांतर तरंगलांबी (λ) च्या पूर्णांक पटीइतके असल्यास त्या बिंदूच्या ठिकाणी संपोषी व्यतिकरण होते व पथांतर अर्धतरंगलांबी (λ/२) च्या विषम पटीइतके असेल, तर तेथे विनाशी व्यतिकरण होते. तरंगलांबीच्या व्याख्येवरूनच ही गोष्ट आपोआप सिद्ध होते. कलांतरापेक्षा पथांतराची कल्पना समजण्यास जास्त सोपी असल्याने तिचा वापर जास्त प्रमाणात केला जोता. यंग फट-युग्मापेक्ष फ्रेनेल द्विलोलकाच्या साहाय्याने जास्त स्पष्ट व तेजस्वी व्यतिकरण पट्ट मिळतात. म्हणून सामान्यतः व्यतिकरण प्रयोगांसाठी हीच पद्धत पसंत केली जाते.

पातळ पटलामुळे होणारे व्यतिकरण : आ. २८ मध्ये दाखविल्याप्रमाणे समजा की, पफ व बभ या एका पातळ पटलाच्या दोन समांतर बाजू असून त्यांच्यावर कच हा एकवर्णी प्रकाशकिरण आपाती झाला आहे. येथे त्याचे अंशतः परावर्तन (च-१ या दिशेने) व अंशतः प्रणमन (चट या दिशेने) होईल. ट येथेही पुन्हा अंशतः प्रणमन (ट-१ या दिशेने) व परावर्तन (टछ या दिशेने) होईल. याप्रमाणे छ, ज, झ आणि ठ, ड इत्यादी ठिकाणी अंशतः प्रणमने व परावर्तने होऊन पफ च्या वरच्या बाजूला १, २, ३,…. इ. अनंत समांतर किरणांचा समूह मिळेल. या किरणांची तीव्रता उत्तरोत्तर कमी कमी होत जाईल.

सघन माध्यमाच्या पृष्ठावरून होणाऱ्या परावर्तनात आपोआपच π इतके कलांतर म्हणजेच λ/२ इतके पथांतर होते परंतु जेव्हा विरल माध्यमाच्या पृष्ठापासून परावर्तन होते, तेव्हा असा प्रकार होत नाही (हे सैद्धांतिक व प्रायोगिक अशा दोन्ही पद्धतींनी सिद्ध करता येते). वरील पटलाचे माध्यम हवेपेक्षा सघन असून पटल हवेमध्ये आहे असे गृहीत धरल्यास थोडे गणितकृत्य करता असे सिद्ध करता येते की, (१) लागोपाठच्या

दोन किरणांतील पथांतर हे पटलाची जाडी व प्रणमनांक यांच्या सम प्रमाणात असून ते आपाती कोनावरही अवलंबून असते. (२) एखाद्या भिंगाच्या साहाय्याने १, २, ३, … इ. सर्व किरण एकत्र आणल्यास त्यांचे संपोषी किंवा विनाशी व्यतिकरण होईल त्यानुसार परावर्तित प्रकाशाने पटल सुप्रकाशित किंवा अप्रकाशित दिसेल, याचा निर्णय करण्यासाठी फक्त १ व २ या किरणांमधील पथांतर लक्षात घेणे पुरेसे असते.

समांतर पटलावर एखाद्या विस्तृत प्रकाश उद्‌गमापासून प्रकाश पडत असल्यास त्याच्यावर वेगवेगळे आपाती कोन करणारे किरण आपाती होतात. पटलाच्या वरून त्याच्याकडे विशिष्ट दिशेने पाहिल्यास काही ठराविक आपाती कोन मूल्यासाठी संपोषी व्यतिकरणाच्या अटीची पूर्तता होते व सुप्रकाशित पट्ट निर्माण होतात, याउलट विनाशी व्यतिकरणाच्या अटीची पूर्तता होते तेथे अप्रकाशित पट्ट दिसतात. फाब्री-पेरॉ, मायकेलसन, लुमर-गेरके इ. व्यतिकरणमापकांचे [→ व्यतिकरणमापन] कार्य या तत्त्वावर आधारलेले आहे.

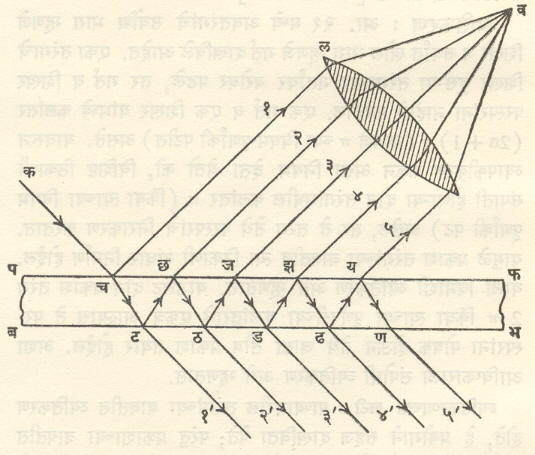
पटल पृष्ठे असमांतर असून त्याच्यावर विस्तृत प्रकाश उद्‌गमापासून प्रकाश आपाती झल्यास होणारी परिस्थिती आ. २९ मध्ये दाखविली आहे.

क या बिंदूपासून निघणारा १ हा किरण च येथे आपाती होऊन पफ पासून १’ या दिशेने परावर्तित होऊन डोळ्यात शिरतो. त्याचप्रमाणे २ हा किरण ट येथे अंशतः परावर्तन होऊन २’ या मार्गे डोळ्यात शिरतो, हे दोन किरण डोळ्याच्या भिंगाकरवी चा येथे एकत्र आणले जातात (त्याचप्रमाणे ख पासून निघालेले किरण छा येथे एकत्र येतील) आणि त्यांच्यामधील परिणामी पथांतर λ/२ च्या विषम पटीइतके असल्यास त्या विशिष्ट रंगाच्या संदर्भात च हा पटलाचा भाग अप्रकाशित दिसेल. आपाती प्रकाश पांढरा असल्यास चचा रंग पांढरा उणे λ चा रंग असा दिसेल, उदा., λ हा पिवळा रंग असेल, तर पांढरा उणे पिवळा = निळा. म्हणजे च हा भाग निळा दिसेल (अशा दोन रंगांना परस्परांचे पूरक रंग असे म्हणतात). याचप्रमाणे पटलाच्या वेगवेगळ्या बिंदूंवर (उदा., छ) वेगवेगळ्या तरंगलांब्यांसाठी विनाशी व्यतिकरणाची अट पूर्ण होऊन तेथे त्या त्या तरंगलांब्यांचे पूरक रंग दिसतील, पावसाळ्यात डबक्यावर तरंगणाऱ्या तेलाच्या तवंगावर मनोहर रंग दिसतात, ते या प्रकारे उत्पन्न होतात.

न्यूटन वर्तुळे : एका सपाट पृष्ठावर बहिर्गोल भिंग ठेवले असता त्या दोहोंच्या मध्ये एक हवेचा स्तर होतो. या स्तराची जाडी मध्यभागी शून्य असून मध्यापासून दूर जावे तशी ती जाडी वाढत जाते. या स्तराच्या दोन पृष्ठांवरून वरीलप्रमाणे प्रकाशाचे अंशतः परावर्तन/प्रणमन होऊन व्यतिकरणामुळे सुप्रकाशित व अप्रकाशित वर्तुळमालिका दिसू शकते. तिला न्यूटन यांची वर्तुळे असे म्हणतात. पांढऱ्या प्रकाशात पाहिले असता ही वर्तुळे रंगीत दिसतात (चित्रपत्र ३८). एकवर्णी प्रकाशात ती अधिक स्पष्ट दिसतात व त्यांचे मापन करून त्यावरून प्रकाशाची तरंगलांबी काढता येते.

व्यतिकरण व ऊर्जेचे अक्षय्यत्व : जेथे विनाशी व्यतिकरण होऊन अप्रकाशित पट्ट निर्माण होतात, तेथे प्रकाश ऊर्जेचा नाश झाला असे सकृद्दर्शनी वाटेल परंतु तेथे ऊर्जेचा नाश होत नसून तेथील प्रकाश ऊर्जा सुप्रकाशित पट्टांच्या ठायी संक्रमित होऊन तेथील प्रकाश तीव्रता एरवीच्या दुप्पट होत असते. म्हणजेच व्यतिकरणामुळे प्रकाश ऊर्जेचे केवळ पुनर्वितरण होते व ऊर्जेच्या अक्षय्यत्वाच्या सिद्धांताला बाध येत नाही.

व्यतिकरणाचे उपयोग : (१) व्यतिकरणाचा उपयोग करून प्रकाशाची तरंगलांबी मोजता येते, हे वर आलेच आहे. (२) तरंगलांबी ज्ञात असल्यास व्यतिकरणाचा उपयोग करून लांबीचे अत्यंत अचूक मापन करता येते. याचा उपयोग अनेक ठिकाणी केला जातो. (३) भिंगे, आरसे इत्यादींच्या पृष्ठभागांचे आकार बरोबर तयार झाले आहेत की नाही, त्याची परीक्षा करण्याची पद्धती व्यतिकरणावरच आधारलेली आहे. (४) व्यतिकरणाच्या उपयोगाने कॅमेरा वा दूरदर्शक यांच्या भिंगांच्या पृष्ठावरून परावर्तनामुळे होणारा प्रकाश तीव्रतेतील व्यय खूप कमी करता येतो. (५) व्यतिकरणावर आधारलेल्या प्रकाशीय गाळण्या अत्यंत कार्यक्षम असतात. (६) व्यतिकरणाचा उपयोग करून वायूंचे प्रणमनांक मोजता येतात. (७) वर्णरेषांच्या सूक्ष्म रचनेचा अभ्यास करता येतो. [→ व्यतिकरणमापन].

वायनर यांचा प्रयोग : ध्वनीप्रमाणे प्रकाशही तरंगस्वरूपी असल्याने आपाती व परावर्तित प्रकाश तरंगांमध्ये व्यतिकरण होऊन अप्रगामी प्रकाश तरंग बनले पाहिजेत. या अप्रगामी तरंगांमध्ये प्रस्पंद व निस्पंद बिंदूही तयार झाले पाहिजेत [→ तरंग गति]. या अप्रगामी तरंगांचे अस्तित्व सिद्ध करण्यासाठी वायनर यांनी पुढील प्रयोग केला.

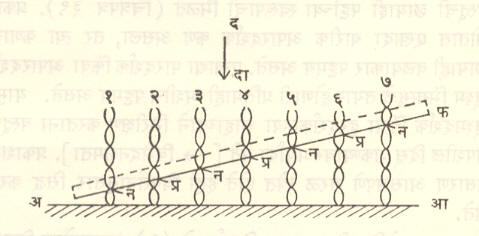
एक आरसा क्षितिज समांतर ठेवून त्याच्यावर त्याच्याशी लहानसा कोन करून एक छायाचित्रण फिल्म ठेवली. या रचनेवर उदग्र दिशेने एकवर्णी प्रकाश तरंग आपाती केल्यास आपाती व परावर्तित तरंगांमध्ये व्यतिकरण होऊन अप्रगामी तरंग तयार होतात. त्यांच्यामुळे निर्माण होणारे प्रस्पंद जेथे छायाचित्रण फिल्मला छेदतात तेथे प्रकाशीय विक्षोभ महत्तम झाल्यामुळे फिल्म काळी होते व जेथे निस्पंद पडतात तेथे कहीच क्रिया होत नाही. अशा रीतीने त्या फिल्मचे विकाशन (प्रकाशन केलेल्या फिल्मवरील अदृश्य चित्राचे दृश्य चित्रात रूपांतर करण्यासाठी करण्यात येणारी रासायनिक प्रक्रिया) केल्यानंतर तिच्यावर समांतर काळे पट्टे आढळून आले व अप्रगामी तरंगांची निर्मिती सिद्ध झाली.

प्रकाशाच्या विद्युत् चुंबकीय तरंग सिद्धांतानुसार आरशाच्या पृष्ठभागावर विद्युत् क्षेत्र तीव्रता-सदिशाच्या दृष्टीने निस्पंद पण चुंबकीय क्षेत्र तीव्रता-सदिशाच्या दृष्टीने प्रस्पंद निर्माण होतो. फिल्मवर तयार झालेले काळे पट्टे विद्युत् क्षेत्र तीव्रता-सदिशाच्या प्रस्पंदांशी बरोबर जुळतात. यावरून छायाचित्रण पायसाचे (प्रकाशाला संवेदनशील असणाऱ्या रासायनिक द्रव्याचे) काळे होणे व त्याचप्रमाणे इतर प्रकाशीय आविष्कारांत फक्त विद्युत् क्षेत्र तीव्रता-सदिशच प्रभावी असतो, हे सिद्ध झाले.

अप्रगामी प्रकाश तरंगांच्या उपयोगाने रंगीत छायाचित्र काढण्याची एक पद्धत गाब्रिएल लीपमान यांनी १८९१ साली शोधून काढली होती परंतु ती वापरण्यास कठीण असल्यामुळे आता वापरली जात नाही.

विवर्तन : प्रकाशाचे प्रसारण संपूर्णपणे रेखीय होत नाही. यामुळे घडून येणाऱ्या आविष्कारांना विवर्तन असे म्हणतात. जेव्हा प्रकाश झोताचा विस्तार एखादी फट किंवा छिद्र यामुळे मर्यादित होतो तेव्हा विवर्तन घडून येते. त्याचप्रमाणे एखाद्या अडथळ्याजवळून (प्रकाश) तरंग जातात तेव्हाही विवर्तनाचा आविष्कार उत्पन्न होतो. विवर्तन सर्वच प्रकारच्या तरंगांच्या बाबतीत घडून येऊ शकते. इतकेच नव्हे, तर फक्त तरंग सिद्धांतानुसारच विवर्तनाचे स्पष्टीकरण देता येते. सामान्यतः असे म्हणता येईल की, एकाच तरंगमुखाच्या वेगवेगळ्या भागांपासून निघणाऱ्या व विशिष्ट बिंदूपाशी एकत्र येणाऱ्या दुय्यम तरंगांमधील व्यतिकरणामुळे विवर्तनाचे आविष्कार सिद्ध होतात.

काही परिणाम : प्रकाशाचा झोत जेव्हा एखाद्या ऋजुधारेला (सुरीच्या तीक्ष्ण पात्यासारख्या सरळ कडेला) लागून जाऊन पलीकडे पडद्यावर पडतो तेव्हा त्या धारेच्या छाया विभागात काही प्रकाश प्रवेश करतो, असे सूक्ष्म निरीक्षण केल्यास दिसून येते. त्यामुळे धारेच्या छायेची कडा रेखीव मिळत नाही. त्याचबरोबर पडद्यावरील प्रकाशित भागात छायेच्या कडेलगत काही सुप्रकाशित व अल्प प्रकाशित पट्ट (तुलनेने हे पट्टे काळे) दिसतात (चित्रपत्र ३९). खूप अरुंद फटीमधून प्रकाश पलीकडे जाऊन पडद्यावर पडला असताही असेच पट्ट मिळतात. सूक्ष्म छिद्रातून जाऊन प्रकाश पलीकडील पडद्यावर पडल्यास तेथे एका आड एक सुप्रकाशित व अप्रकाशित वलये मिळतात. सुईसारख्या बारीक वस्तूची छायाही पट्टांच्या स्वरूपाची मिळते (चित्रपत्र ३९). प्रकाश झोतात एखादा बारीक अपारदर्शक कण असला, तर त्या कणाची छायाही वलयाकार पट्टमय असते. एखाद्या पारदर्शक किंवा अपारदर्शक सूक्ष्म भिंगामुळे तयार होणारी प्रतिमाही अशीच पट्टमय असते. यामुळे सूक्ष्मदर्शक किंवा दूरदर्शकांच्या साहाय्याने निरीक्षण करताना वस्तूचा तपशील दिसू शकण्यावर मर्यादा येते [→ विभेदनक्षमता]. प्रकाशाचे प्रसारण आसन्नपणे सरळ रेषेत होते हेही विवर्तनानुसार सिद्ध करता येते.

प्रकार : ऐतिहासिक दृष्ट्या विवर्तनाचे (१) फ्राउनहोफर विवर्तन (योझेप फोन फ्राउनहोफर या भौतिकीविज्ञांच्या नावाने ओळखले जाणारे) व (२) फ्रेनले विवर्तन (ऑग्यूस्तीन झां फ्रेनेल या भौतिकीविज्ञांच्या नावाने ओळखले जाणारे) असे दोन प्रकार मानले जातात. जेव्हा विवर्तन होणारे तरंगमुख प्रतलीय असते (म्हणजेच परिणामतः प्रकाश उद्‌गम विवर्तनकारक अडथळ्यापासून वा रंध्रापासून अनंत अंतरावत असतो) व विवर्तनाचे परिणाम ज्या पडद्यावर पहावयाचे तोही अनंत अंतरावर असतो, म्हणजेच निरीक्षणसाठी दूरदर्शक किंवा भिंग वापरावे लागते, तेव्हा त्याला फ्राउनहोफर विवर्तन असे म्हणतात. या प्रकाराची उपपत्ती त्यामानाने सोपी असते. याउलट जेव्हा प्रकाश उद्‌गम व पडदा हे दोन्ही विवर्तनकारक अडथळ्यापासून किंवा रंध्रापासून जवळ असतात तेव्हा त्याला फ्रेनेल विवर्तन असे म्हणतात. या प्रकारात तरंगामुखे बहिर्गोल असतात. त्यामुळे याचे गणिती विश्लेषण बरेच कठीण होते. तत्त्वतः या दोन प्रकारांत काहीच भेद नाही.

विश्लेषण : विवर्तनाचे विश्लेषण करण्याच्या पद्धतीची सर्वसामान्य रूपरेषा पुढीलप्रमाणे सांगता येईल : (१) ज्याचे विवर्तन व्हावयाचे असेल त्या तरंगामुखावरील प्रत्येक बिंदू हायगेन्झ तत्त्वानुसार सर्व दिशांनी एकाच कलेमध्ये असणारे दुय्यम तरंग निर्माण करतो. (२) त्या तरंगमुखाचे अनेक पट्टांत विभाजन करावयाचे, ते अशा तऱ्हेने की, लागोपाठच्या दोन पट्टांमधून निधून विशिष्ट इष्ट बिंदूला पोहोचणाऱ्या दुय्यम तरंगांमधील सरासरी पथांतर λ/2 असेल. या पट्टांना ‘अर्धआवर्तकाल पट्ट’ असे म्हणतात. (३) प्रत्येक अर्ध-आवर्तकाल पट्टापासून निघून इष्ट बिंदूला पोहोचणाऱ्या दुय्यम तरंगाचा परमप्रसर काढावयाचा. (४) नंतर या सर्व परमप्रसरांची बीजगणितीय बेरीज (जास्त अचूक म्हणजे सदिश बेरीज) घेतली असता त्यावरून इष्ट बिंदूच्या ठायी विवर्तित तरंगाचा परिणामी परमप्रसर मिळेल. कोणत्याही दोन लागोपाठच्या पट्टांपासून निघणाऱ्या दुय्यम तरंगांमध्ये λ/2 हे पथांतर असल्याने विषम क्रमांकाच्या पट्टांमुळे निर्माण होणारे परमप्रसर धन घेतल्यास सम क्रमांकांपासून निर्माण होणारे परमप्रसर ऋण होतील हे लक्षात येईल. (५) परिणामी परमप्रसराचा वर्ग हा इष्ट बिंदूच्या ठायीची प्रकाश तीव्रता देईल. पडद्यावरील प्रत्येक बिंदूच्या बाबतीत ही कृती करून पडद्यावरील प्रकाशाचे वितरण काढता येईल. म्हणजेच पडद्यावरील विवर्तनाचा आकृतिबंध निश्चित करता येईल.

अर्ध-आवर्तकाल पट्टांची कल्पना फ्रेनेल यांनी मांडली. फ्रेनेल विवर्तनाच्या अभ्यासाला ती अत्यंत उपयुक्त असून ती कशी वापरली जाते हे फक्त एका उदाहरणाच्या साहाय्याने पुढे दाखविले आहे. फ्राउनहोफर विवर्तनाच्या बाबतीत या पट्टांचा उपयोग करण्याची आवश्यकता नसल्याने त्याचे विश्लेषण होपे होते, हे पुढील एका उदाहरणावरून स्पष्ट होईल.

फ्राउनहोफर विवर्तन-एकाकी फटीमधून : आ. ३१ मध्ये अआ ही एक a रुंदीची व अनंत लांबीची फट असून तिच्यावर λ तरंगलांबीचे प्रतलीय तरंगमुख डावीकडून आपाती होत आहे. फटीतून वेगवेगळ्या दिशांनी विवर्तन झालेले प्रकाश तरंग भ या भिंगाने कख या (भिंगाच्या केंद्रीय प्रतलात ठेवलेल्या) पडद्यावर केंद्रित केले जातात. अआ या फटीवरील प्रत्येक बिंदू सर्व दिशांना शून्य कलांतर असलेले दुय्यम तरंग प्रसारित करतो. आपाती किरणाच्याच (म्हणजे मप या) दिशेने जाणारे किरण पडद्यावर प येथे केंद्रित होऊन तेथे तेजस्वी बिंदू तयार होईल. या दिशेला विवर्तन कोन शून्य मूल्याचा आहे. फट व पडदा आकृतीच्या प्रतलाला लंब आहेत. म्हणून वरीलप्रमाणे पडद्यावर प मधून जाणारी व फटीला समांतर अशी सुप्रकाशित रेषा मिळेल.

आपाती किरणाशी θ हा कोन करणारे (म्हणजेच विवर्तन कोन θ असणारे) सर्व किरण परस्परांना समांतर असतील व ते फ येथे केंद्रित होतील. फ येथील प्रकाशनाची तीव्रता निश्चित करण्यासाठी आ मधून θ या दिशेने विवर्तन झालेल्या किरणावर अइ हा लंब काढा. अइ पासून पुढे फ पर्यंत सर्व किरणांमधील प्रकाशीय पथांतर शून्य आहे (कारण अइ हे θ या दिशेने विवर्तन झालेले तरंगमुख आहे). अआ पासून अइपर्यंत या किरणांत विविध पथांतरे उत्पन्न होतील. आकृतीवरून हे उघड आहे की, फटीच्या दोन टोकांपासून निघणाऱ्या किरणामधील पथांतर आइ = a sin θ आहे. समजा की, a sin θ = λ. मग फ येथे सर्व किरणांचे विनाशी व्यतिकरण होऊन अप्रकाशित (म्हणजेच तुलनेने काळा) पट्ट तयार होईल. हे सिद्ध करण्यासाठी फटीचे म येथे दोन सारखे भाग केले अशी कल्पना करा व फटीच्या वरच्या अर्धातील बिंदूंना अ पासून खाली म पर्यंत १, २, ३… असे क्रमांक द्या. त्याचप्रमाणे खालच्या अर्धातील बिंदूंनाही म पासून खाली क्रमांक द्या. हे उघड आहे की, वरचा पहिला व खालचा पहिला या दोन बिंदूंपासून निघणाऱ्या किरणांमधील पथांतर ½ a sin θ = ½ λ होईल व म्हणून फ येथे त्यांचे विनाशी व्यतिकरण होईल. याचप्रमाणे या दोन अर्धांमधील संगत बिंदूंच्या जोड्या घेतल्या, तर त्यांचेही विनाशी व्यतिकरण होईल व फ येथे प्रकाश-तीव्रता शून्य होईल. फ हा बिंदू प पासून दूर नेत गेल्यास, म्हणजेच θ वाढवत गेल्यास पुन्हा अशी स्थिती येईल की, a sin θ = 2 λ त्या वेळी पुन्हा पडद्यावर अप्रकाशित पट्ट मिळेल. व्यापकीकरण करता, a sin θ = n λ (n = १, २, ३, ४ ….. इत्यादी पूर्णांक) हे समीकरण लागू पडेल त्या त्या बिंदूपाशी अप्रकाशित पट्ट मिळतील परंतु दोन अप्रकाशित पट्टांच्या मधे एक सुप्रकाशित पट्ट असलाच पाहिजे, म्हणून पडद्यावर एकाआड एक सुप्रकाशित व अप्रकाशित पट्टांची मालिका दिसेल (चित्रपत्र ३९) परंतु प पासून दूर जावे तसतशी सुप्रकाशित पट्टांची प्रकाश-तीव्रता उत्तरोत्तर कमी होत जाते. पडद्यावरील प्रकाश-तीव्रतेचे वितरण आ. ३२ मध्ये आलेखरूपाने दाखविले आहे. हे पट्ट आ. ३० मध्ये प च्या वर तसेच खालीही सममित (दोन्हीकडे सारखे) मिळतात. पट्टांच्या प्रकाश-तीव्रता काढण्याचे गणित बरेच गुंतागुंतीचे असल्याने येथे गाळले आहे.

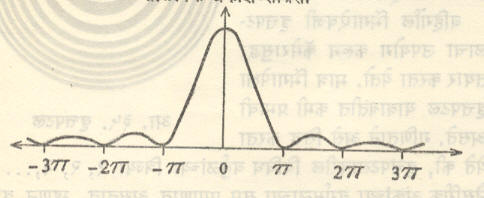
प येथील सुप्रकाशित पट्टाला प्रधान महत्तम व इतर सुप्रकाशित असलेल्या पट्टांना दुय्यम महत्तम असे म्हणतात. प्रधान महत्तमाची प्रकाशन-तीव्रता १ मानल्यास दुय्यम महत्तमाच्या तीव्रता अनुक्रमे

4	,	4	,	4	,………………………..अशा येतात.
9π2		25π2		49π2

वरील विश्लेषणात पडद्याच्या विशिष्ट भागावर फटीच्या त्याच्या समोरील भागावरूनच प्रकाश येतो असे मानले आहे. प्रत्यक्षात असे घडत नाही. आयताकार रंध्रातून मिळणारा विवर्तन आकृतिबंध चित्रपत्र ३९ मध्ये दाखविला आहे. दोन फटी शेजारी शेजारी ठेवल्यास प्रत्येक फटीच्या विवर्तन पट्टाबरोबरच त्याच्या व्यतिकरणाचेही पट्ट तयार होतात (चित्रपत्र ३९). अनेक फटींची मालिका ठेवल्यास त्या रचनेला ⇨ विवर्तन जालक असे म्हणतात. त्याच्या साहाय्याने वर्णपट मिळू शकतात (चित्रपत्र ३९). सूक्ष्म रंध्रातून विवर्तन झाल्यास समकेंद्री अप्रकाशित व सुप्रकाशित वलये मिळतात. (चित्रपत्र ३९).

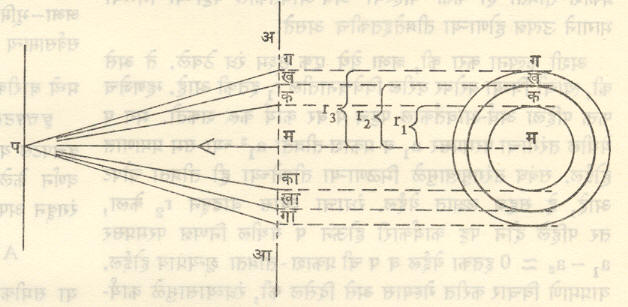
अर्ध-आवर्तकाल पट्ट : फ्रेनेल यांच्या अर्ध-आवर्तकाल पट्टांची रचना व उपयोग समजण्यासाठी आ. ३३ मध्ये दर्शविल्याप्रमाणे अशी कल्पना करा की, एक प्रतलीय तरंगमुख (अआ) उजवीकडून डावीकडे जात असून त्यामुळे प या बिंदूवर उत्पन्न होणारी प्रकाश-तीव्रता अभ्यासावयाची आहे. पम हा प पासून अआ वर टाकलेला लंब आहे (म ला प चा ध्रुव असे म्हणतात). समजा की, पम = b आणि प्रकाशाची तरंगलांबी λ आहे. प हा मध्य व अनुक्रमे

b+	λ	, b+	2λ	, b+	3λ	,……, b+	mλ
	2		2		2		2

अशा त्रिज्या घेऊन गोलपृष्ठे काढा. ही पृष्ठे अआ ला अनुक्रमे r1, r2, r3,……., r_m इ. त्रिज्यांच्या वर्तुळांत छेदतील. अशा दोन लोगोपाठच्या वर्तुळांच्या परिघांमध्ये आंतरछेदित झालेल्या कंकणाकृती पट्टांना अर्ध-आवर्तकाल पट्ट असे म्हणतात.

या पट्टांच्या त्रिज्या b व λ यांच्या मूल्यांवर अवलंबून असतात (आसन्नतः r_m=√mbλ). b= ३२ सेंमी. व λ = ५ X १०^-५ सेंमी. असल्यास पहिल्या वर्तुळाची त्रिज्या अवधी ०·००५ सेंमी. येते. यावरून आ. ३२ मध्ये दाखविलेली वर्तुळे खूपच मोठी केलेली आहेत, हे लक्षात येईल. लागोपाठच्या दोन पट्टांपासून प प्रत जाणाऱ्या तरंगांतील सरासरी पथांतर ^λ/₂ येते. त्याचप्रमाणे कोणत्याही पट्टामुळे प येथे निर्माण होणाऱ्या तरंगाचा परमप्रसर, त्या पट्टच्या क्षेत्रफळाच्या सम प्रमाणात व त्याच्या प पासूनच्या सरासरी अंतराच्या व्यस्त प्रमाणात असतो, हेही सहज दाखविता येते. त्याचप्रमाणे लागोपाठच्या पट्टांपासून येणाऱ्या तरंगांमधील पथांतर λ/2 असल्याने, सर्व विषम क्रमांकांच्या पट्टांमुळे प येथे उत्पन्न होणारा परमप्रसर धन घेतल्यास सम क्रमांकांच्या पट्टांमुळे उत्पन्न होणारे परमप्रसर ऋण चिन्हांकित घ्यावे लागतील. या परमप्रसरांची मूल्ये अनुक्रमे a₁, —a₂, a₃, —a₄,……. अशी दाखविल्यास प येथील निष्पन्न परमाप्रसराचे मूल्य

A= a₁ —a₂ + a₃, — a₄ + a₅ —…. a_m या समीकरणाने दिले जाईल, m विषम किंवा सम असेल त्यानुसार A= ^a₁/₂ ± ^a_m /₂ हे सिद्ध करता येते. पट्टांची एकूण संख्या m मोठी असल्यास ^a_m/₂ दुर्लक्षणीय होते व A= ^a₁/₂ असे आसन्न समीकरण मिळते. प्रकाश-तीव्रता परमप्रसराच्या वर्गाच्या सम प्रमाणात असते. त्यामुळे प येथील प्रकाश-तीव्रता I α a₁²/₄, असा निष्कर्ष निघतो. याचा अर्थ असा की, सबंध मोठ्या तरंगमुखामुळे प येथे उत्पन्न होणारी प्रकाश-तीव्रता ही फक्त पहिल्या अर्ध-आवर्तकाल पट्टाच्या निम्म्या भागाने उत्पन्न होणाऱ्या तीव्रतेइतकीच असते.

अशी कल्पना करा की, अआ येथे एक सूक्ष्म रंध्र ठेवले. ते असे की, त्याची त्रिज्या बरोबर वरील विवेचनातील r₁ इतकी आहे. म्हणजेच फक्त पहिला अर्ध-आवर्तकाल पट्टच प वर कार्य करू शकतो. मग प येथील तरंगाचा परमप्रसर a₁ व प्रकाश-तीव्रता a₁² च्या सम प्रमाणात होईल. सबंध तरंगमुखामुळे मिळणाऱ्या तीव्रतेच्या ही तीव्रता चीपट आहे, हे सहज लक्षात येईल. रंध्राचा व्यास वाढवून r₂ केला, तर पहिले दोन पट्ट कार्यकारी होऊन प येथील निष्पन्न परमप्रसर a₁ — a ₂ ≈ 0 इतका येईल व प ची प्रकाश-तीव्रता शून्यप्राय होईल. याप्रमाणे विचार करीत गेल्यास असे दिसेल की, रंध्रव्यासामुळे कार्यकारी होणाऱ्या एकूण अर्ध-आवर्तकाल पट्टांची संख्या विषम झाल्यास प सुप्रकाशित होईल व सम झाल्यास अप्रकाशित होईल. (चित्रपत्र ३९).

आता असे समजा की, म येथे अशा त्रिज्येची अपारदर्शक तबकडी ठेवली की, तिच्यामुळे पहिले k अर्ध-आवर्तकाल पट्ट झाकले जातील. मग प येथील निष्पन्न परमप्रसर

Ak = ak+1 — ak+2 ………. am ≈	ak+1
	2

k चे मूल्य बरेच जास्त असेल, तर a_k+1 दुर्लक्षणीय असेल व प येथे अंधार दिसेल म्हणजेच तबकडीच्या छायेचा मध्य बिंदूही अंधःकारमय असेल, हे प्रकाशाच्या रेखीय प्रसारणाशी सुसंगत आहे परंतु k चे मूल्य अल्प असल्यास, म्हणजेच तबकडीची त्रिज्या लहान असल्यास, a_k+1 दुर्लक्षणीय होणार नाही व छायेचा मध्य बिंदू सुप्रकाशित दिसेल (चित्रपत्र ३९). हे रेखीय प्रसारणाशी विसंगत आहे, कारण येथे अडथळ्यावरून वळून प्रकाश छाया भागात गेला असे दिसते. थोडक्यात म्हणजे अडथळे व रंध्रे यांची आकारमाने प्रकाशाच्या तरंगलांबीच्या मानाने मोठी असतील, तर रेखीय प्रसारण अनुभवाला येते, नाहीपेक्षा विवर्तनाचा आविष्कार दृष्टीला पडतो. विशिष्ट बिंदूपाशी प्रकाशन निर्माण करण्यामध्ये (त्या बिंदूशी निगडित असे) पहिले काही थोडे (२५ से ३०) अर्थ-आवर्तकाल पट्टच सक्षम असतात. रंध्राचे किंवा अडथळ्याचे आकारमान यापेक्षा मोठे असेल, तर विवर्तन अनुभवाला न येता प्रकाशाचे रेखीय प्रसारणच होत आहे असे वाटते.

वरील विवेचनात आपाती तरंगमुख प्रतलीय आहे असे मानले आहे. म्हणजेच प्रकाश उद्‌गम अनंत अंतरावर आहे असे गृहीत धरले आहे. बिंदुमात्र प्रकाश उद्‌गम परिमित अंतरावर असेल, तर मिळणारे तरंगमुख गोलीय असेल. उद्‌गम अरुंद फटीच्या स्वरूपाचा असेल, तर मिळणारे तरंगमुख वृत्तचित्याकार असेल परंतु या परिस्थितीतही त्या तरंगमुखाचे अर्ध-आवर्तकाल पट्टांमध्ये वरीलप्रमाणेच विभाजन करून पडद्यावरील प्रकाश-तीव्रता काढता येते. फरक इतकाच होतो की, तरंगमुख वक्र असल्यामुळे पट्टांचे आकार वेगळे येतात व एकूण गणित जास्त गुंतागुंतीचे होते.

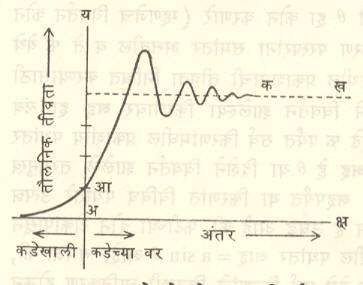
ऋजुधारेमुळे निर्माण होणारे विवर्तन पट्ट चित्रपत्र ३९ मध्ये दाखविले असून त्यामधील प्रकाश-तीव्रता वितरण आ. ३४ मधील आलेखाने व्यक्त केले आहे. अआ ही रेषा धारेच्या भूमितीय छायेची कडा दर्शविते. चित्रपत्र ३९ मध्ये बारीक तारेमुळे झालेला विवर्तन आकृतिबंध दाखविला आहे.

वृत्तपटल : फ्रेनेल यांच्या अर्ध-आवर्तकाल पट्टांच्या कल्पनेला वृत्तपटल या साधनाच्या गुणधर्मावरून आश्चर्यकारक पुष्टी मिळते. वर वर्णन केलेल्या पट्टांपैकी सर्व सम क्रमांकांचे पट्ट काळ्या रंगाने रंगवून अपारदर्शक केल्यास प येथील (आ. ३३) परिणामी परमप्रसर

A’ = a₁ + a₃ + a₅ + a₇ + …………… +a_m

या समीकरणाने दिला जाईल. यातील उजवीकडची सर्वच पदे धन असल्यामुळे A’ हा सबंध तरंगमुखामुळे निष्पन्न होणाऱ्या A या परमप्रसरापेक्षा खूपच मोठा असणार म्हणजेच आपाती प्रतलीय तरंगामुळे प येथे अत्यंत तीव्र प्रकाशबिंदू तयार होईल. अशा रचनेला वृत्तपटल (आ. ३५) असे म्हणतात. सम क्रमांकाच्या पट्टावर λ/2 जादा पथांतर करील अशा जाडीचा पारदर्शक थर दिल्यास प येथील परिणामी परमप्रसर दुप्पट होईल व प्रकाश-तीव्रता चौपट होईल. हे कार्य बहिर्गोल भिंगासारखेच आहे. भिंगाच्या भागांची जाडी अशी साधलेली असते की, तिच्यातून बाहेर येणाऱ्या (व प येथे पडणाऱ्या) सर्व किरणांमधील प्रकाशीय पथांतर λ च्या पूर्ण पटीत असते.

बहिर्गोल भिंगाऐवजी वृत्तपटलाचा उपयोग करून कॅमेरासुद्धा तयार करता येतो. मात्र भिंगापेक्षा वृत्तपटल याबाबतीत कमी प्रभावी असते. गणिताने असे सिद्ध करता येते की, वृत्तपटलावरील विविध वर्तृळांच्या त्रिज्या १, २, ३, …… इ. नैसर्गिक अंकांच्या वर्गमूळाच्या सम प्रमाणात असतात. म्हणून वृत्तपटल तयार करताना प्रथम एका कागदावर अशा त्रिज्यांची समकेंद्री वर्तुळे काढतात. नंतर त्यांमधील एकाआड एक पट्ट काळे करून त्याचे न्यूनीकृत छायाचित्र काढतात. हे (पारदर्शक काचेवर काढलेले) छायाचित्र म्हणजेच वृत्तपटल होय.

शोषण, प्रकीर्णन व अपस्करण : वायुरूप, द्रवरूप किंवा घनरूप अशा कोणत्याही पारदर्शक माध्यमातून प्रकाश जातो, तेव्हा पारगमनाच्या अंतराबरोबर प्रकाशाची तीव्रता कमी होत जाते. याला कारणीभूत म्हणजे शोषण व प्रकीर्णन या दोनही क्रिया असतात. द्रव्यामधून प्रकाश जातो तेव्हा त्याचा वेगही कमी होतो. वेगात पडणारा हा फरक प्रकाशाच्या तरंगलांबीवर अवलंबून असतो. त्यामुळे तरंगलांबीनुसार प्रकाशाचा प्रणमनांकही बदलतो.

शोषण : विशिष्ट माध्यमात प्रवेश करताना एका प्रकाश-शलाकेची तीव्रता I₀ असून माध्यमातून X इतके अंतर गेल्यावर तिची तीव्रता I होते असे समजू. प्रयोगावरून असे दिसून येते की,

I = I₀ e^-αx

येथे e हा स्वाभाविक लॉगरिथमाचा आधारांक आहे [→ लॉगरिथम] आणि α हा त्या विशिष्ट माध्यमाचा एक स्थिरांक असून त्याला माध्यमाचा शोषण गुणांक असे म्हणतात. हे समीकरण प्रथम पी. बूगेअर (१६९८—१७५८) यांनी शोधून काढले व जे. एच्. लँबर्ट (१७२८—७७) यांनीही पुढे ते स्वतंत्रपणे शोधून काढले. म्हणून ते बूगेअर नियम किंवा लँबर्ट नियम या नावाने ओळखले जाते. I/I₀ गुणोत्तराला त्या (x या) जाडीसाठी माध्यमाची पारदर्शकता असे म्हणतात.

दोन प्रकार : सर्वसामान्य शोषण आणि विवेचक शोषण असे शोषणाचे दोन प्रकार पडतात. जेव्हा विविध तरंगलांब्यांच्या प्रकाश तरंगांचे एकसारखेच शोषण होते तेव्हा त्याला सर्वसामान्य शोषण असे म्हणतात. उदा., दिव्याच्या काजळीचे कण या प्रकारचे शोषण करतात. त्यांचा पृष्ठभागावर सूक्ष्म छिद्रे असतात. त्यामुळे त्यांवर पडलेल्या किरणांची छिद्रांच्या आत पुनःपुन्हा परावर्तने होऊन प्रत्येक परावर्तनात अंशतः शोषण होत जाते. शोषित ऊर्जेचे शेवटी उष्णतेत रूपांतर होते असे पृष्ठभाग कृष्णवर्ण दिसतात.

प्रकाशापैकी जेव्हा काही निवडक तरंगलांब्यांचे प्रकर्षाने शोषण होते व उरलेल्या प्रकाशाचे पारगमन (किंवा परावर्तन) होते तेव्हा त्याला विवेचक शोषण असे म्हणतात. असे पदार्थ प्रकाशापैकी काही विशिष्ट रंगांचे तीव्र शोषण करतात म्हणून ते रंगीत दिसतात. फुले, भिंतींचे रंग, रंगीत कपडे हे सर्व विवेचक शोषणामुळे रंगीत दिसतात.

उच्च दर्जाच्या चष्म्याच्या काचांत जंबुपार व अवरक्त (दृश्य वर्णपटातील अनुक्रमे जांभळ्या रंगाच्या पलीकडील व तांबड्याच्या अलीकडील अदृश्य) किरणांचे विवेचक शोषण होऊन दृश्य प्रकाशाचे पारगमन होते. यामुळे अपायकारी किरणांपासून डोळ्यांना संरक्षण मिळते व वस्तू पहाण्यात काही अंतराय येत नाही. वर्णपटविज्ञानात वर्णपटाच्या विविध भागांसाठी खास द्रव्यांची भिंगे व लोलक वापरावे लागतात. कारण इष्ट तरंगलांब्यांचे त्यांमध्ये शोषण न होणे जरूर असते. [→ वर्णपटविज्ञान].

अनुस्फुरण व प्रस्फुरण : खऱ्याखुऱ्या शोषणात शोषित प्रकाश ऊर्जेचे उष्णतेत रूपांतर होते परंतु काही पदार्थ विशिष्ट तरंगलांब्यांच्या प्रकाशाचे शोषण करतात व त्याहून अधिक तरंगलांबीच्या प्रकाशाचे उत्सर्जन करतात. आपाती किरण पडणे बंद झाल्याबरोबर जेव्हा उत्सर्जनाची क्रिया थांबते तेव्हा त्याला अनुस्फुरण आणि आपाती किरण पडणे बंद झाल्यानंतरही काही कालपर्यंत जेव्हा उत्सर्जन चालू राहते तेव्हा त्याला प्रस्फुरण असे म्हणतात. अत्यंत कमी दाबाच्या काही वायुरूप पदार्थांकडून शोषित तरंगलांबीच्याच प्रकाशाचे उत्सर्जन होते. याला अनुस्पंदन प्रारण असे म्हणतात. [→ संदीप्ति].

प्रकीर्णन : प्रकाशाच्या मार्गात आलेल्या द्रव्याच्या कणांकडून प्रकाश ऊर्जेचे शोषण होते व नंतर त्या कणांकडून पुन्हा प्रकाशाचे सर्व दिशांनी वेगवेगळ्या प्रमाणात प्रेषण होते. याला प्रकीर्णन असे म्हणतात. साध्या शोषणाप्रमाणे प्रकीर्णनात शोषित ऊर्जेचे उष्णतेत रूपांतर होत नाही हा मुख्य फरक आहे.

पदार्थीय माध्यमातून प्रकाशाचे प्रसारण होत असताना प्रसारण दिशेने प्रकाश-तीव्रतेत जी घट झालेली दिसते ती दोन भागांत झालेली असते. एक भाग निखळ शोषणामुळे व दुसरा भाग या प्रकीर्णनामुळे. बूगेअर समीकरणात आलेला α हा शोषण गुणांक α_a व α_s या दोन घटकांचा मिळून बनलेला असतो (α = α_a + α_s). α_a हा निखळ शोषण गुणांक व α_s हा प्रकीर्णन गुणांक होय.

वेगवेगळ्या दिशांना प्रकीर्णित होणाऱ्या प्रकाशाचे प्रमाण वेगवेगळे असते. मूळ प्रकाशाच्या प्रसारणाच्या दिशेला लंब दिशेने प्रकीर्णनाचे प्रमाण कमाल असते. त्याचप्रमाणे तुलनेने पहाता कमी तरंगलांबीच्या प्रकाशाचे प्रकीर्णन जास्त प्रमाणात होते. प्रकीर्णित प्रकाश रेखीय ध्रुवित (याचे स्पष्टीकरण ‘ध्रुवण’ ह्या उपशीर्षकाखाली पहावे) असतो, हाही प्रकीर्णनाचा एक विशेष आहे.

उपपत्ती : विद्युत् चुंबकीय तरंग सिद्धांतानुसार प्रकाश किरणाच्या प्रसारण दिशेला लंब अशी प्रत्यावर्ती (दिशा उलटसुलट होत असलेली) विद्युत् व चुंबकीय क्षेत्रे प्रसारित होत असतात आणि वायनर यांच्या प्रयोगावरून हे दिसून येते की, सर्व प्रकाशीय परिणामांच्या संदर्भात त्यातील फक्त विद्युत् क्षेत्राचेच परिणाम कारणीभूत असतात. द्रव्याच्या अणु-रेणूंमध्ये इलेक्ट्रॉन बद्ध झालेले असतात. आपाती प्रत्यावर्ती विद्युत् क्षेत्रामुळे अशा बद्ध इलेक्ट्रॉनांची प्रेरित कंपने सुरू होतात व म्हणून (विद्युत् चुंबकीय सिद्धांतानुसार) त्यांच्यापासून प्रकाशाचे प्रेषण सुरू होते. हा प्रेषित प्रकाशच प्रकीर्णित प्रकाश होय. आ. ३६ मध्ये क येथील (विद्युत् निरोधक पदार्थाच्या) रेणूवर अक या दिशेने अध्रुवित प्रकाश आपाती होत असून त्याच्यामुळे क वर अक ला लंब दिशेने कार्य करणारे E_x व E_z हे विद्युत् क्षेत्राचे परस्परांना लंब असे घटक आहेत. त्यांच्यामुळे क येथील इलेक्ट्रॉनाची अनुक्रमे आई ला व इउ ला समांतर आंदोलने होतील व प्रेषित तरंगात याच दिशेने आंदोलने असतील. प्रकाश अवतरंगरूपी असल्याने या आंदोलनांमुळे अनुक्रमे कइ (व कउ) आणि कआ (व कई) या दिशेने रेखाध्रुवित प्रकाश दिसेल.

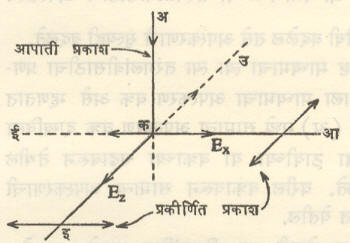
प्रकीर्णक पदार्थाच्या एकक घनफळातून प्रकीर्णित होणारा प्रकाश भागिले आपाती प्रकाशाची तीव्रता या गुणोत्तराला प्रकीर्णनक्षमता असे म्हणतात. विद्युत् चुंबकीय सिद्धांतानुसार असे सिद्ध करता येते की,

प्रकीर्णनक्षमता =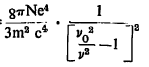

येथे e = इलेक्ट्रॉनीय विद्युत् भार, m = इलेक्ट्रॉनाचे वस्तुमान, c = प्रकाशवेग, N = एकक घनफळातील प्रकीर्णक अणू वा रेणू, v = आपाती प्रकाशाची कंप्रता, v₀ = बद्ध इलेक्ट्रॉनांची नैसर्गिक कंप्रता.

नेहमीच्या स्थितीमधील अणूवर दृश्य प्रकाश पडत असेल, तर (v₀ / v)² &gt &gt 1 म्हणून वरील समीकरण,

प्रकीर्णनक्षमता =	8 π Ne4
	3m2 v04λ4

(λ = आपती प्रकाशाची तरंगलांबी) असे लिहिता येते. यावरून प्रकीर्णनक्षमता तरंगलांबीच्या चतुर्थ घाताच्या व्यस्त प्रमाणात असते, हे लक्षात येईल. या सूत्राला रॅली सूत्र (जॉन विल्यम स्ट्रट—लॉर्ड रॅली यांच्या नावावरून) असे म्हणतात. [→ आकाषवर्ण].

क्ष – किरण आपाती होत असल्या (v₀/ v)² &lt &lt 1 या परिस्थितीत

प्रकीर्णनक्षमता =	8 π Ne4
	3m2 c4

असे सूत्र मिळते. याला टॉमसन सूत्र (जी. पी. टॉमसन यांच्या नावावरून) असे म्हणतात. v = v₀ असल्यास अनुस्पंदनी प्रकीर्णन होते. v व v₀ जवळजवळ सारख्या मूल्याचे झाल्यास प्रकीर्णन फार मोठ्या प्रमाणात होते. या दोन्ही प्रकारांत वरील सूत्रात संदमनाच्या परिणामाचा अंतर्भाव करावा लागतो.

वरील विवेचनात आपाती प्रकाशाच्या तरंगलांबीच्या तुलनेने प्रकीर्णक कणाचे आकारमान अगदी लहान आहे, असे गृहीत धरले आहे. कणांचे आकारमान मोठे असल्यास सर्वच तरंगलांब्यांचे सु. सारखेच प्रकीर्णन होते व प्रकीर्णित प्रकाश पांढरा दिसतो.

अपस्करण : प्रकाश तरंगातील प्रत्यावर्ती विद्युत् क्षेत्र आणि द्रव्याच्या अणूंमधील बद्ध इलेक्ट्रॉन यांच्यामधील परस्परक्रियेमुळे हा आविष्कार घडून येतो. प्रकाशाच्या मूळ तरंगलांबीमध्ये (λ मध्ये) dλ हा अल्प बदल केल्यास त्यामुळे माध्यमाचा प्रणमनांक dμ इतका बदलला, तर ^dμ/_dλ या अवकलजाला माध्यमाचे λ या तरंगलांबीसाठीचे अपस्करण असे म्हणतात. तरंगलांबी बदलेल तसे अपस्करणाचे मूल्यही बदलते.

तरंगलांबी व विशिष्ट माध्यमाचा त्या त्या तरंगलांबीसाठीचा प्रणमनांक यांच्या आलेखाला माध्यमाचा अपस्करण वक्र असे म्हणतात (आ. ३७). आ. ३७ (अ) मध्ये सामान्य अपस्करण वक्र दाखविला आहे. विशिष्ट बिंदूच्या ठायीच्या या वक्राच्या चढावरून तेथील अपस्करण मूल्य मिळते. वरील वक्रावरून सामान्य अपस्करणाची खालील वैशिष्ट्ये लक्षात येतील.

(१) अपस्करण मूल्य नेहमी ऋण चिन्हांकित असते. म्हणजेच तरंगलांबीत वाढ झाली की, प्रणमनांकाचे मूल्य कमी होते.

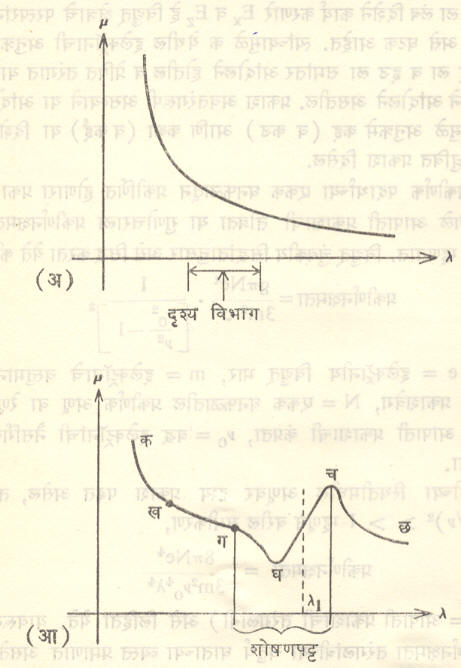
(२) तरंगलांबी वाढेल त्याबरोबर अपस्करणाचे केवळ मूल्य कमी होते. भिंगे, लोलक इ. प्रकाशीय साधने तयार करण्यासाठी वापरल्या जाणाऱ्या काचा, पाणी इत्यादींच्या अपस्करण वक्रांचा आकार सर्वसामान्यपणे आ. ३७ (अ) सारखा असतो. म्हणजेच त्यांच्यामध्ये सामान्य अपस्करण प्रत्ययाला येते. ए. एल्. कोशी (१७८९—१८५७) यांनी सामान्य अपस्करण वक्रासाठी पुढील अनुभवसिद्ध सूत्र दिले आहे.

μ = A +	B	+	C
	λ2		λ4

येथे A, B, C हे स्थिरांक असून त्यांची मूल्ये वेगवेगळ्या माध्यमासाठी वेगवेगळी असतात व ती प्रयोगाने काढावी लागतात.

परंतु जेव्हा माध्यम विशिष्ट (λ₁ या) तरंगलांबीच्या

प्रकाशाचे विवेचक शोषण करते तेव्हा त्या तरंगलांबीच्या आसपास अपस्करण वक्राचा आकार फारच वेगळा येतो [आ. ३७ (आ)] आणि मग या ठिकाणी असामान्य अपस्करण झाले असे म्हणतात. आ. ३७ (आ) मध्ये वक्राच्या कखग या भागाचा आकार सामान्य अपस्करण वक्रासारखाच आहे. तसाच चछ या भागातही आहे परंतु गघ या भागात वक्राचा उतार एकदम वाढलेला आहे, तर घच या भागात अपस्करणाचे मूल्य घन चिन्हांकित आहे.

अपस्करणाचा सिद्धांत : असामान्य अपस्करणाची उपपत्ती देण्याचा डब्ल्यू. सेलमायर यांनी १८७१ मध्ये प्रयत्न केला परंतु त्याला मर्यादितच यश मिळाले. एच्. एल्. एफ्. हेल्महोल्ट्स, एच्. ए. लोरेन्ट्स आणि पी. ड्रूडे यांनी विद्युत् चुंबकीय सिद्धांतानुसार दिलेली उपपत्ती या आविष्काराला चांगली लागू पडते. या उपपत्तीनुसार अपस्करणकारक माध्यमातील इलेक्ट्रॉन, त्याच्यावर प्रकाश आपाती झाला की, प्रकाशांतर्गत प्रत्यावर्ती विद्युत् क्षेत्रामुळे प्रेरित कंपने करू लगतात. या इलेक्ट्रॉनांना पूर्व स्थितीला आणू पहाणाऱ्या प्रेरणा रेखीय असतात. त्याचप्रमाणे त्यांच्या कंपनगतीला विरोध करणाऱ्या प्रेरणाही अस्तित्वात येतात व त्यांची मूल्ये इलेक्ट्रॉनांच्या (कंपनजन्य) वेगाच्या सम प्रमाणात असतात. अशा या इलेक्ट्रॉनांच्या कंपनांचे ⇨ अवकल समीकरण मांडून त्याचे निर्वाह काढल्यास पुढील समीकरण मिळते.

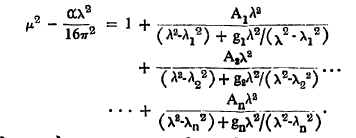
येथे α हा शोषण गुणांक असून λ आपाती प्रकाशाची तरंगलांबी व λ₁, λ₂,……. λ_n या माध्यमाच्या विवेचक शोषणाच्या तरंगलांब्या आहेत.g₁, g₂, …… g_n हे गुणक संबंधिक कंपनातील विरोधी प्रेरणांचे निदर्शक असून A₁, A₂ ……..A_n हे स्थिरांक आहेत.

ध्रुवण : अध्रुवित व रेखीय ध्रुवित प्रकाश : नैसर्गिक किंवा अध्रुवित प्रकाशात प्रकाश आंदोलने किरणाला लंब अशा प्रतलात कोणत्याही दिशेने होत असतात व ही दिशा एकसारखी बदलत असते. काही उपायाने ही सर्व आंदोलने एका निश्चित दिशेनेच होतील, असे करता येते. अशा प्रकाशाला रेखीय ध्रुवित वा प्रतलीय ध्रुवित प्रकाश असे म्हणतात व त्या प्रकाशाचे ध्रुवण झाले आहे, असे म्हटले जाते.

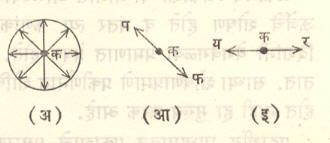
आ. ३८ मध्ये प्रकाशकिरण क या बिंदूमधून आकृतीच्या प्रतलाला लंब दिशेने निरीक्षकाकडे येत आहे, असे मानले आहे आणि बाणांकित रेषांनी आंदोलन दिशा दाखविल्या आहेत. आ. ३८ (अ) मध्ये आकृतीच्या प्रतलात ही आंदोलने सर्व दिशांनी होतात असे दाखविले आहे. म्हणजे ही अध्रुवित प्रकाश किरणाची परिस्थिती आहे. आ. ३८ (आ) व ३८ (इ) मध्ये आंदोलने फक्त पफ किंवा यर या एका निश्चित दिशेनेच होत आहेत. या दोन्ही आकृती रेखीय ध्रुवित किरणाच्या आहेत.

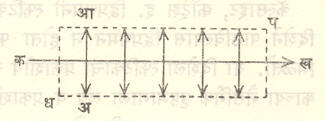
आंदोलनाची दिशा व किरणाच्या प्रसारणाची दिशा यांनी निश्चित होणाऱ्या प्रतलाला आंदोलन प्रतल (कंपन प्रतल किंवा ध्रुवण प्रतल) असे म्हणतात (आ. ३९).

रेखीय ध्रुवित प्रकाशकिरणावरील सर्व बिंदूंच्या ठायीची आंदोलने फक्त या एकाच प्रतलात होत असतात. म्हणून अशा किरणाला प्रतलीय ध्रुवित प्रकाश असेही म्हणतात.

वृत्तीय ध्रुवित व विवृत्तीय ध्रुवित प्रकाश : प्रकाश-आंदोलनदर्शक सदिश म्हणजेच ‘प्रकाश सदिश’ म्हणजे विद्युत् चुंबकीय तरंग सिद्धांतातील विद्युत् क्षेत्र तीव्रता सदिशच होय. काही परिस्थितींत प्रकाश सदिशांची लांबी स्थिरमूल्यी राहते पण तो सदिश किरणाच्या दिशेभोवती घड्याळाच्या काट्याप्रमाणे (किंवा त्याच्या उलट दिशेने) भ्रमण करीत असतो. अशा प्रकाशाला वृत्तीय ध्रुवित (किंवा वर्तुलीय ध्रुवित) प्रकाश असे म्हणतात. केव्हा केव्हा प्रकाश सदिशाच्या भ्रमणाबरोबर त्याची लांबी अशा प्रकारे कमीजास्त होत असते कि, त्या सदिशाचे टोक एक विवृत्त (दीर्घवर्तुळ) आरेखित करते. अशा प्रकाशाला विवृत्तीय ध्रुवित प्रकाश असे म्हणतात. महत्त्वाची गोष्ट ही आहे की, अध्रुवित व वेगवेगळ्या प्रकार ध्रुवित झालेले प्रकाश हे आपणाला सर्व सारखेच दिसतात. खास उपकरणाच्या साहाय्याशिवाय त्यांच्या ध्रुवण स्थितीची ओळख पटू शकत नाही.

तोलमल्ली: (टुर्मलीन). या खनिजाच्या [→ तोरमल्ली] स्फटिकाच्या पातळ षट्‌कोनी पट्ट्या काढता येतात. या षट्‌कोनाचा एक कर्ण [आ. ४० (अ)] इतर कर्णापेक्षा जास्त लांब असतो, त्याला तोरमल्लीचा अक्ष असे म्हणतात.

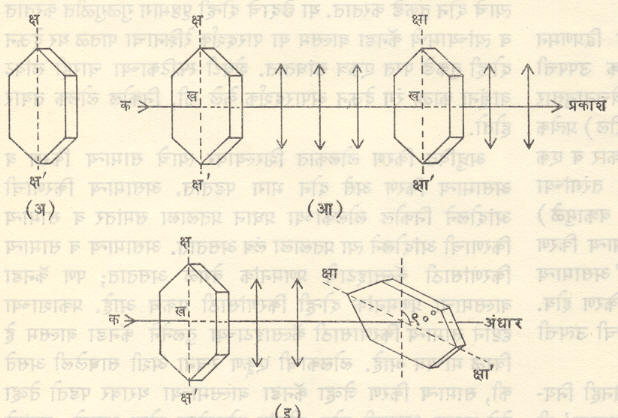
तोरमल्लीच्या दोन पट्ट्यांचे अक्ष परस्परांना समांतर ठेवून त्यांवर लंब दिशेने प्रकाश पाडल्यास [आ. ४० (आ)] तो त्यांमधून बाहेर येतो म्हणजेच या पट्ट्या पारदर्शक आहेत परंतु यांतील एक पट्टी स्थिर ठेवून दुसरीचा अक्ष आपाती प्रकाशाच्या दिशेभोवती फिरवत गेल्यास बाहेर येण्याऱ्या प्रकाशाची तीव्रता उत्तरोत्तर कमी होत जाते व शेवटी जेव्हा त्या दोघांच्या अक्षांमध्ये ९० अंशांचा कोन होतो तेव्हा दोहोंमधून मिळून काहीही प्रकाश बाहेर येत नाही. या वेळी बाहेर येणाऱ्या प्रकाशाचे विलोपन झाले असे म्हणतात व तोरमल्लीच्या त्या दोन पट्ट्या जात्य आहेत असे म्हणतात [आ. ४० (इ)]. म्हणजे या स्थितीत दुसरी पट्टी प्रकाशाला अपारदर्शक आहे असे दिसते. तोरमल्लीच्या फक्त एकाच पट्टीवर प्रकाश पाडून ती फिरविण्याचा प्रयोग केल्यास तिच्या कोणत्याही स्थितीत बाहेर येणाऱ्या प्रकाशाच्या तीव्रतेत काहीही फरक पडत नाही असेही दिसून येते.

या प्रयोगावरून पुढील निष्कर्ष निघतात : (१) नैसर्गिक (अध्रुवित) प्रकाश तोरमल्लीच्या पट्टीवर पाडल्यास तिच्या कोणत्याही स्थितीत ती त्या प्रकाशाला सारखीच पारदर्शक असते. (२) परंतु एका पट्टीतून बाहेर आलेला प्रकाश दुसऱ्या पट्टीवर पडत असल्यास, विशिष्ट स्थितीतच ही दुसरी पट्टी पारदर्शक असते व एका विशिष्ट स्थितीत ती पूर्णपणे अपारदर्शक होते. यावरून पहिल्या पट्टीतून बाहेर आलेल्या प्रकाशाला काही दिशाविषयक खास गुण प्राप्त झालेले आहेत असे दिसते. अशा प्रकाशाला रेखीय ध्रुवित प्रकाश असे नाव दिले आहे.

वरील निष्कर्षांची संगती लावण्यासाठी (फक्त) पुढील गृहीतकेच उपयोगी पड शकतात : (१) प्रकाश तरंगातील आंदोलने प्रसारण दिशेला लंब असली पाहिजेत म्हणजेच प्रकाश तरंग हे अवतरंग आहेत. (२) तोरमल्लीमधून प्रकाश जाताना फक्त तोरमल्लीच्या अक्षाला समांतर अशीच आंदोलने आरपार जाऊ शकतात. (३) आपाती होणाऱ्या रेखीय ध्रुवित प्रकाशाच्या आंदोलनाची दिशा तोरमल्लीच्या अक्षाला लंब असल्यास तिच्यातून काहीही प्रकाश बाहेर येऊ शकत नाही. (४) सर्वसामान्यतः आपाती रेखीय ध्रुवित प्रकाशाच्या आंदोलनाची दिशा व तोरमल्लीचा अक्ष यांच्यामधील कोन θ असल्यास बाहेर येणाऱ्या प्रकाशाची तीव्रता cos² θ च्या सम प्रमाणात असते.

हा तोरमल्लीच्या दोन पट्ट्यांचा प्रयोग प्रकाशाचे अवतरंगत्व सिद्ध करणारा निर्णायक प्रयोग आहे. या प्रयोगातील पहिली पट्टी प्रकाशाचे रेखीय ध्रुवण करण्याचे कार्य करते. हे कार्ये करणाऱ्या साधनाला ध्रुवक असे म्हणतात. दुसरी पट्टी आपाती प्रकाशाच्या ध्रुवणाचे परीक्षण करते. असे कार्य करणाऱ्या साधनाला विश्लेषक असे म्हणतात. ही दोन्ही कार्ये करण्यासाठी इतर जास्त प्रभावी साधने उपलब्ध आहेत. त्यांची माहिती पुढे दिली आहे.

विशिष्ट प्रकाश झोत रेखीय ध्रुवित आहे की नाही याचा निर्णय विश्लेषकाच्या साहाय्याने पुढीलप्रमाणे करता येतो : (१) तो प्रकाश झोत विश्लेषकावर पाडून विश्लेषक हळूहळू (वर वर्णन केल्याप्रमाणे) फिरवत गेल्यास बाहेर येणाऱ्या प्रकाशाच्या तीव्रतेत काहीही फरक न पडल्यास आपाती प्रकाश अध्रुवित (किंवा वृत्तीय ध्रुवित) असला पाहिजे. (२) बाहेर येणाऱ्या प्रकाशाची तीव्रता कमीजास्त होत विश्लेषकाच्या एका विशिष्ट स्थितीत तीव्रता शून्य झाल्यास आपाती प्रकाश रेखीय ध्रुवित असला पाहिजे. (३) बाहेर येणाऱ्या प्रकाशाची तीव्रता एका कमाल मूल्यापासून किमान मूल्यापर्यंत बदलत जात असेल (परंतु शून्य होत नसेल), तर आपाती प्रकाश अंशतः रेखीय ध्रुवित (किंवा विवृत्तीय ध्रुवित) असला पाहिजे.

अध्रुवित व वृत्तीय ध्रुवित प्रकाश किंवा अंशतः रेखीय ध्रुवित किंवा विवृत्तीय ध्रुवित प्रकाश यांची ओळख पटण्यासाठी विश्लेषकाला चतुर्थांश-तरंग-पट्टिकेची जोड द्यावी लागते. या पट्टिकेची माहिती पुढे दिली आहे.

परावर्तनामुळे होणारे ध्रुवण : असंवाहक पृष्ठापासून परावर्तित झालेला प्रकाश अंशतः रेखीय ध्रुवित झालेला असतो. १८०८ साली ई. माल्यूस यांनी असा शोध लावला की, समतल काचपृष्ठावर ५७°·५ आपाती कोन केला असता मिळणारा परावर्तित प्रकाश पूर्णपणे रेखीय ध्रुवित असतो. त्याचबरोबर त्या काचेतून पलीकडे बाहेर येणारा (पारगत) प्रकाश अंशतः रेखीय ध्रुवित असतो परंतु त्यात अध्रुवित प्रकाशाचेच प्रमाण फार असते. अशा (सु. २०) समांतर काच पट्टिकांचा संच करून ठेवला असता त्यामधून पारगत होणारा प्रकाश जवळजवळ पूर्णपणे रेखीय ध्रुवित असतो. या रचनेचाही ध्रुवक किंवा विश्लेषक म्हणून उपयोग करता येतो.

द्विप्रणमन : आइसलँड स्पार म्हणजेच शुद्ध स्वरूपातील ⇨ कॅल्साइट या खनिजाचे स्फटिक पारदर्शक असतात. या स्फटिकावर एक किरण आपाती झाला असता त्याच्यापासून दोन प्रणमित किरण उपलब्ध होतात, असे १६६९ मध्ये ई. बार्थोलिनस या शास्त्रज्ञांना आढळून आले (आ. ४१).

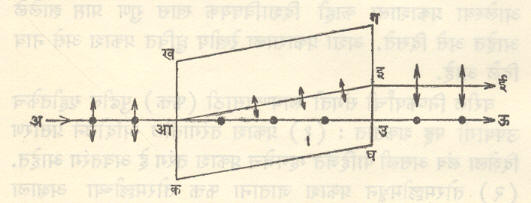
कॅल्साइटाप्रमाणेच इतर कित्येक पारदर्शक स्फटिकांत द्विप्रणमन होऊ शकते. या विलक्षण आविष्काराची समाधानकारक उपपत्ती तरंग सिद्धांतानुसार हायगेन्झ यांनी दिली. त्यांच्या विवेचनानुसार कॅल्साइटासारख्या असममित माध्यमातील (प्रकाश तरंगावरील) प्रत्येक बिंदूपासून एकाच वेळी (द्विमितीय आकृतीत) एक वर्तुळाकार व एक विवृत्ताकार असे दोन दुय्यम तरंग निघतात. वर्तुळाकार तरंगांच्या अन्वालोपामुळे (सर्व तरंगांच्या अग्रबिंदूतून काढलेल्या वक्रामुळे) सामान्य तरंग मिळतो व त्याच्याशी संबंधित किरण हा सामान्य किरण होय. त्याचप्रमाणे विवृत्ताकार तरंगांचा अन्वालोप म्हणजे ‘असामान्य तरंग’ आणि त्याच्याशी निगडित किरण हा असामान्य किरण होय. हायगेन्झ यांच्या रचनेचा उपयोग करून या दोन्ही किरणांची उत्पत्ती समाधानकारकपणे देता येते.

या दोन किरणांपैकी सामान्य किरण हा प्रणमनाच्या दोनही नियमांचे पालन करतो, असे दिसून येते (म्हणूनच त्याला ‘सामान्य’ ही उपाधी दिली आहे). असामान्य किरणाला साधारणतः प्रणमनाचे दोनही नियम लागू पडत नाहीत. तोरमल्लीसारख्या विश्लेषकाचा उपयोग करता हे दोनही किरण रेखीय ध्रुवित झालेले असतात असे आढळते. आ. ४१ मध्ये आपाती किरण स्फटिकावर लंब दिशेने पडला आहे. अशा वेळी प्रणमन कोन शून्य असला पाहिजे. त्यानुसार जाणारा आउऊ हा किरण सामान्य किरण होय. आइ हा किरण असामान्य किरण होय. असामान्य किरणाचे आंदोलन प्रतल आकृतीच्या प्रतलाशी अनुपाती असते, तर सामान्य किरणाचे त्याला लंब असते. या दोन्ही किरणांची प्रकाश-तीव्रता आपाती किरणाच्या बरोबर निम्मी असते.

कॅल्साइट, क्वॉर्ट्‌झ इ. द्विप्रणमनी स्फटिकांतून प्रकाश एका विशिष्ट दिशेने पाठविल्यास द्विप्रणमन न होता फक्त एकच प्रणमित किरण मिळतो. या दिशेला स्फटिकाचा प्रकाशीय अक्ष असे म्हणतात. स्फटिकाच्या नैसर्गिक पृष्ठभागाला लंब व प्रकाशीय अक्षाला समांतर असे प्रतल काढल्यास त्याला स्फटिकाचे प्रधान प्रतल असे म्हणतात. प्रधान प्रतलाच्या योगे स्फटिकाच्या घेतलेल्या छेदाला स्फटिकाचा प्रधान छेद असे म्हणतात.

कॅल्साइट, क्वॉर्ट्‌झ यांसारख्या स्फटिकांना एकच प्रकाशीय अक्ष असतो म्हणून त्यांना एक-अक्षीय स्फटिक असे म्हणतात. बर्फ, नॅप्थॅलीन यांसारख्या स्फटिकांना दोन प्रकाशीय अक्ष असतात म्हणून त्यांना द्वि-अक्षीय स्फटिक असे म्हणतात.

निकोल लोलक : ध्रुवक व विश्लेषक या दोन्ही उपयोगांसाठी निकोल लोलक हे सर्वांत जास्त कार्यक्षम साधन असून सर्व अचूक प्रयोगांत त्याचा उपयोग केला जातो. हे लोलक कॅल्साइटापासून बनविले जातात. याचे तत्त्व थोडक्यात असे सांगता येईल की, द्विप्रणमनामुळे मिळणाऱ्या दोन किरणांपैकी सामान्य किरणाचे संपूर्ण अंतर्गत परावर्तनाच्या साहाय्याने निराकरण करून फक्त असामान्य किरण यातून बाहेर पडू शकेल, अशी याची रचना केलेली असते. या लोलकाचा शोध विल्यम निकोल (१७६८—१८५१) यांनी लावला म्हणून त्याला त्यांचे नाव देण्यात आले आहे. या लोलकाचा उल्लेख नुसता ‘निकोल’ असाही करण्यात येतो.

निकोल लोलक तयार करण्यासाठी कॅल्साइटाचा निर्दोष असा स्फटिक निवडतात. त्याची लांबी जाडीच्या सु. तिप्पट घेतात (आ. ४२). त्याच्या अरुंद बाजूंचे फलक समचतुर्भुज घेतात. या दोन्ही अरुंद बाजूंचे कखखा आणि गघघा हे (पाचरीच्या आकाराचे) भाग घासून काढून टाकतात. ते इतपत की, आकृतीतील क आणि ग येथील लघुकोनाचे मूल्य मूळ ७१° असते ते ६८° होते. नंतर आकृतीच्या प्रतलाला लंब व खाघा या रेषेतून जाणाऱ्या प्रतलावर स्फटिक कापून त्याचे दोन तुकडे करतात. या छेदाचे दोन्ही पृष्ठभाग गुळगुळीत करतात व त्यांच्यामध्ये कॅनडा बाल्सम या पारदर्शक रेझिनाचा पातळ थर देऊन दोन्ही तुकडे परत एकत्र सांधतात. शेवटी स्फटिकाच्या चारही लांबट बाजूंना काळा रंग देऊन अपारदर्शक केले की, निकोल लोलक तयार होतो.

अध्रुवित किरण लोलकात शिरल्यावर त्याचे सामान्य किरण व असामान्य किरण असे दोन भाग पडतात. असामान्य किरणाची आंदोलने निकोल लोलकाच्या प्रधान प्रतलाला समांतर व सामान्य किरणाची आंदोलने त्या प्रतलाला लंब असतात. असामान्य व सामान्य किरणांसाठी कॅल्साइटाचे प्रणमनांक वेगळे असतात पण कॅनडा बाल्समाचा प्रणमनांक दोन्ही किरणांसाठी एकच आहे. प्रकाशाच्या दृष्टीने सामान्य किरणासाठी कॅल्साइटाच्या तुलनेने कॅनडा बाल्सम हे विरळ माध्यम आहे. लोलकाची एकूण रचना अशी साधलेली असते की, सामान्य किरण जेव्हा कॅनडा बाल्समाच्या थरावर पडतो तेव्हा तेथे त्याचा आपाती कोन सीमांत कोनापेक्षा मोठा असतो. त्यामुळे त्याचे संपूर्ण अंतर्गत परावर्तन होऊन तो लोलकाच्या काळ्या केलेल्या लांबट बाजूवर पडतो व तेथे शोषला जातो परंतु असामान्य किरणाच्या बाबतीत असे घडत नसल्याने तो लोलकातून सरळ बाहेर येतो. अशा तऱ्हेने निकोल लोलकाचा ध्रुवक म्हणून उपयोग करता येतो.

लोलकावर आपाती होणारा किरण रेखीय ध्रुवित असून त्याचे आंदोलन प्रतल लोलकाच्या प्रधान छेदाशी θ हा कोन करीत असल्यास लोलकात प्रवेश केल्यावर त्याचीही असामान्य किरण व सामान्य किरण अशा दोन किरणांत विभागणी होते. आपाती किरणाचा परमप्रसर a असल्यास असामान्य किरणाचा परमप्रसर a cos θ व सामान्य किरणाचा a sin θ असतो. मग वरीलप्रमाणेच क्रिया होऊन फक्त असामान्य किरण बाहेर पडतो. आता आपाती किरण हा अक्ष कल्पून त्याच्या भोवती θ वाढेल अशा तऱ्हेने लोलक फिरवत गेल्यास a cos θ कमी होत जातो व लोलकातून बाहेर येणाऱ्या प्रकाशाची तीव्रता (=a² cos² θ ) त्यामुळे कमी होत जाते. शेवटी जेव्हा θ = 90° होतो, तेव्हा a cos θ = 0 व बाहेर येणाऱ्या प्रकाशाची तीव्रता शून्य होते. अशा तऱ्हेने निकोल लोलकाचा विश्लेषक म्हणूनही उपयोग करता येतो. कारण वरीलप्रमाणे निकोल लोलक फिरवून त्याच्या विशिष्ट स्थितीत बाहेर येणाऱ्या प्रकाशाची तीव्रता शून्य होत असेल, तर आपाती प्रकाश रेखीय ध्रुवित असला पाहिजे, असा निष्कर्ष काढता येतो.

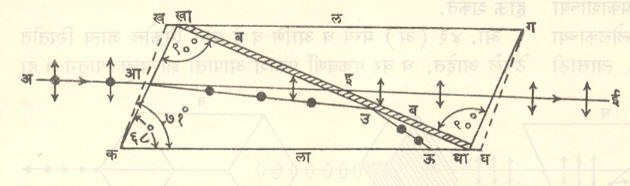
काही विशिष्ट पदार्थांतून रेखीव ध्रुवित प्रकाश जाऊ दिल्यास त्या प्रकाशाचे आंदोलन प्रतल विशिष्ट कोनातून फिरते असे आढळून येते. पदार्थाच्या या गुणधर्माला ध्रुवण घूर्णकता (किंवा प्रकाशीय चलन) असे म्हणतात. एक निकोल ध्रुवक व दुसरा विश्लेषक म्हणून वापरून त्यांच्या मधल्या जागेत ध्रुवक घूर्णक पदार्थ ठेवल्यास त्या पदार्थाची ध्रुवण घूर्णकता मोजता येते. अशी रचना ज्यात केलेली असते त्या उपकरणाला ध्रुवणमापक म्हणतात व त्याचा उपयोग विद्रावातील साखर (शर्करामापक), अल्कलॉइडे, स्टेरॉइडे, औषधी कार्बनी संयुगे इत्यादींचे प्रमाण काढण्यासाठी होतो. [→ ध्रुवणमिति].

द्विवर्णिकता : काही द्विप्रणमनी स्फटिकांतून जाताना सामान्य किंवा असामान्य किरणांपैकी कोणत्यातरी एकाचे विवेचनात्मक जादा शोषण होते. स्फटिकाची जाडी पुरेशी असल्यास त्यात एका किरणाचे संपूर्ण शोषण होऊन फक्त एकच रेखीय ध्रुवित किरण बाहेर येईल. अशा स्फटिकांना द्विवर्णिक स्फटिक असे म्हणतात. तोरमल्लीचा याच प्रकारात समावेश होतो.

पोलरॉइड : मानवनिर्मित द्विवर्णिक तबकड्यांना पोलरॉइड असे म्हणतात. रेखीय ध्रुवित प्रकाशाच्या व्यावहारिक उपयोगामध्ये जेथे मोठ्या क्षेत्रफळाचे ध्रुवक व विश्लेषक वापरावे लागतात तेथे फक्त पोलरॉइडच उपयोगी पडू शकते.

इ. स. १८५२ मध्ये डब्ल्यू. बी. हिरापाथ यांनी क्विनीन आयडोसल्फेट या कार्बनी संयुगाचे (याला हिरापाथाइट असे आता म्हणतात) लहान स्फटिक बनविले. हे स्फटिक उत्तम द्विवर्णिक असल्याचे दिसून आले. एका प्रकारच्या पोलरॉइडात या द्रव्याचा उपयोग करण्यात येतो. १९३२ मध्ये ई. एच्. लँड यांनी पोलरॉइड फिल्मचा शोध लावला. पॉलिव्हिनिल अल्कोहॉलाची पातळ पट्टी ताणून तिचे रेणू परस्परांना समांतर केले जातात व मग तीत आयोडिनाचे शोषण करून ही फिल्म बनविली जाते. ही फिल्म निर्जलीकारकाच्या संसर्गात गरम केली म्हणजे द्विवर्णिक बनते. ध्रुवक व विश्लेषक या दोन्ही तऱ्हांनी पोलरॉइड वापरता येते.

उपयोग : रस्त्याच्या पृष्ठभागावरून विशेषतः पावसाळ्यात परावर्तित झालेल्या प्रकाशात आपाती प्रतलाला लंब असणारी आंदोलने जास्त प्रमाणात असतात. प्रकाशीय अक्ष उदग्र असलेल्या पोलरॉइडाचा चष्मा वापरल्यास त्यात ही आंदोलने पूर्णपणे रोधली जातात व फक्त उपयुक्त अशा विसरित प्रकाशामुळे वस्तू अधिक चांगल्या दिसू शकतात. कॅमेऱ्यापुढे पोलरॉइड गाळणी वापरल्यास याच क्रियेमुळे छायाचित्रे अधिक स्पष्ट येतात. मोटारींचे अग्रदीप व वातरोधक (विंडशिल्ड) यावर प्रकाशीय अक्ष उदग्र दिशेशी ४५° कोन करणारे पोलरॉइड बसविल्यास समोरून येणाऱ्या मोटारीच्या दिव्यांचा प्रकाश वातरोधकाकडून पूर्णपणे रोधला जातो परंतु चालकाला स्वतःच्या मोटारीच्या दिव्यांच्या प्रकाशामुळे सर्व काही दिसू शकते. आगगाडीचे डबे व विमाने यांच्या खिडक्यांवर एक स्थिर व एक फिरवता येईल असे दोन पोलरॉइडाचे पत्रे बसवितात आणि त्यामुळे आत येणाऱ्या प्रकाशाची तीव्रता इच्छेनुसार कमीजास्त करता येते. त्रिमितीय चित्रे व चित्रपट पहाण्यासाठीही पोलरॉइड चष्मे वापरले जातात.

चतुर्थांश-तरंग-पट्टिका : ही पट्टिका करण्यासाठी कॅल्साइट, क्वॉर्ट्‌झ किंवा अभ्रक यांसारख्या द्विप्रणमनी पदार्थाची पातळ पट्टी घेतात. तिचा प्रकाशीय अक्ष तिच्या पृष्ठभागाला समांतर राहील अशा रीतीने ती कापलेली असते. या पट्टीवर लंब दिशेने अध्रुवित प्रकाश आपाती झाल्यास पट्टीत गेल्यानंतर त्याचे असामान्य व सामान्य अशा दोन किरणांत विभाजन होते परंतु दोन्ही किरण पट्टीतून एकाच दिशेने (पृष्ठभागाला लंब अशा) मार्गक्रमण करतात. या दोन किरणांसाठी पट्टीच्या प्रणमनांकांची मूल्ये वेगवेगळी असतात. पट्टीची जाडी t आणि असामान्य व सामान्य किरणांसाठी प्रणमनांक अनुक्रमे μ_e व μ_o असलेल्या पट्टीतून बाहेर पडते वेळी त्या दोन किरणांत t (μ_e ~ μ_o)इतके प्रकाशीय पथांतर उत्पन्न होते व त्यामुळे त्यांच्यामध्ये

2 π	t (μe ~ μo)इतके कालांतर उत्पन्न होते. हे प्रकाशीय पथांतर	λ	(4n + 1)
λ		4

इतके होईल अशी त्या पट्टीची जाडी साधल्यास त्या पट्टीला चतुर्थांश-तरंग-पट्टिका असे म्हणतात (येथे λ प्रकाशाची तरंगलांबी व n कोणताही पूर्णांक). अशा पट्टिकेमुळे तीमधून बाहेर येणाऱ्या दोन किरणांमध्ये π/2 इतके परिणामी कलांतर उत्पन्न होते.

या दोन किरणांमधील प्रकाशीय आंदोलने परस्परांना लंब असून त्यांचे परमप्रसर समान मूल्यांचे असतात. त्यांच्यामध्ये π/2 हे कलांतर असल्यामुळे ⇨ सरळ हरात्मक गतीच्या सिद्धांतानुसार त्यांच्या संयोगामुळे वर्तुळाकार गती निष्पन्न होते. म्हणून बाहेर पडणारा प्रकाश वृत्तीय ध्रुवित असतो.

या पट्टिकेवर रेखीय ध्रुवित प्रकाश आपाती केल्यास सामान्यतः तिच्यातून बाहेर येणारा प्रकाश विवृत्तीय ध्रुवित असतो परंतु आपाती किरणाचे आंदोलन प्रतल व पट्टिकेचा प्रकाशीय अक्ष यांच्यामध्ये ४५° चा कोन होत असल्यास तो प्रकाश वृत्तीय ध्रुवित असतो. अशा तऱ्हेने या पट्टिकेच्या साहाय्याने वृत्तीय ध्रुवित किंवा विवृत्तीय ध्रुवित प्रकाश मिळविता येतो.

अध्रुवित व वृत्तीय ध्रुवित प्रकाशांतील फरक ओळखणे : या दोन्ही प्रकारच्या प्रकाशांच्या मार्गात निकोल लोलक ठेवून तो (किरणाच्या दिशेला अक्ष कल्पून) कसाही फिरविला, तरी बाहेर येणाऱ्या प्रकाशाच्या तीव्रतेत काहीही फरक पडत नाही. त्यामुळे केवळ निकोल लोलकाच्या साहाय्याने त्यांच्यामधील फरक ओळखणे अशक्य होते. त्यासाठी चतुर्थांश-तरंग-पट्टिका उपयोगी पडते.

परीक्षा करावयाचा प्रकाश प्रथम लंब दिशेने पट्टिकेतून जाऊ द्यावा व नंतर त्याच्या मार्गात निकोल लोलक ठेवून तो फिरवावा. निकोलामधून बाहेर येणाऱ्या प्रकाशाच्या तीव्रतेत निकोल फिरविण्याने काहीच फरक पडत नसेल, तर मूळचा प्रकाश अध्रुवित असला पाहिजे कारण अध्रुवित प्रकाश चतुर्थांश-तरंग-पट्टिकेतून जाऊ दिला असता बाहेर येणारा प्रकाश वृत्तीय ध्रुवीत असतो व वृत्तीय ध्रुवित प्रकाश निकोलामधून जात असेल, तर निकोल फिरविल्याने बाहेर येणाऱ्या प्रकाशाच्या तीव्रतेत काहीच फरक पडत नाही.

परंतु वरील प्रयोगात निकोल फिरवून त्याच्या एका कोणत्या तरी स्थितीत बाहेर येणाऱ्या प्रकाशाची तीव्रता शून्य झाली, तर मग मूळचा प्रकाश वृत्तीय ध्रुवित असला पाहिजे कारण वृत्तीय ध्रुवित प्रकाश चतुर्थांश-तरंग-पट्टिकेतून जाताना त्याचे दोन रेखीय ध्रुवित किरणांत विभाजन होते व त्या दोहोंच्या आंदोलनात π/2 हे कलांतर असते. पट्टिकेतून बाहेर येणाऱ्या दोन आंदोलनांत ± π/2 हे जादा कलांतर उत्पन्न केले जाते. त्यामुळे निष्पन्न कलांतर 0 किंवा π होते. हे कलांतर असणाऱ्या परस्परांना लंब असणाऱ्या दोन सरळ हरात्मक गतींचा संयोग होऊन त्यामुळे एक सरळ रेषीय हरात्मक गती तयार होते. त्यामुळे हा प्रकाश रेखीय ध्रुवित असतो व योग्य स्थितीत निकोल लोलक ठेवल्यास तो थांबविला जातो.

अंशतः रेखीय ध्रुवित किंवा विवृतीय ध्रुवित प्रकाश निकोलामधून जाऊ देऊन निकोल फिरवत गेले असता बाहेर येणाऱ्या प्रकाशाची तीव्रता एका विशिष्ट स्थितीत कमाल होते व त्या स्थितीला लंब अशा स्थितीत किमान होते. म्हणजेच फक्त निकोलाचा उपयोग करून या दोन प्रकारच्या प्रकाशांमधील फरक ओळखता येत नाही परंतु असा प्रकाश प्रथम चतुर्थांश-तरंग-पट्टिकेमधून जाऊ देऊन नंतर त्यातून पारगत होणाऱ्या प्रकाशाची निकोलाच्या साहाय्याने परीक्षा केल्यास मूळचा विवृत्तीय ध्रुवित प्रकाश निकोलाच्या एका स्थितीत पूर्णपणे अडविला जातो परंतु अंशतः ध्रुवित प्रकाश असा अडविला जात नाही (याचे स्पष्टीकरण वरील वृत्तीय ध्रुवित व अध्रुवित प्रकाशांच्या स्पष्टीकरणाप्रमाणेच आहे). अशा तऱ्हेने त्या दोहोंमधील फरक समजू शकतो.

ध्रुवित प्रकाशाचे व्यतिकरण : यंग यांचे फट-युग्म उपकरण वापरून फ्रेनेल, डी. एफ्. ॲरागो (१७८६—१८५३) इ. शास्त्रज्ञांनी ध्रुवित प्रकाशाच्या व्यतिकरणाचा अभ्यास केला व पुढील निष्कर्ष काढले : (१) दोन रेखीय ध्रुवित किरणांची आंदोलन प्रतले एकमेकांना लंब असतील, तर त्यांच्यामध्ये व्यतिकरण होऊ शकत नाही. (२) एकाच उद्‌गमापासून निघालेल्या दोन रेखीय ध्रुवित किरणांची आंदोलन प्रतले अनुपाती (जुळती) केल्यानंतरच त्या किरणांमध्ये व्यतिकरण होऊ शकते.

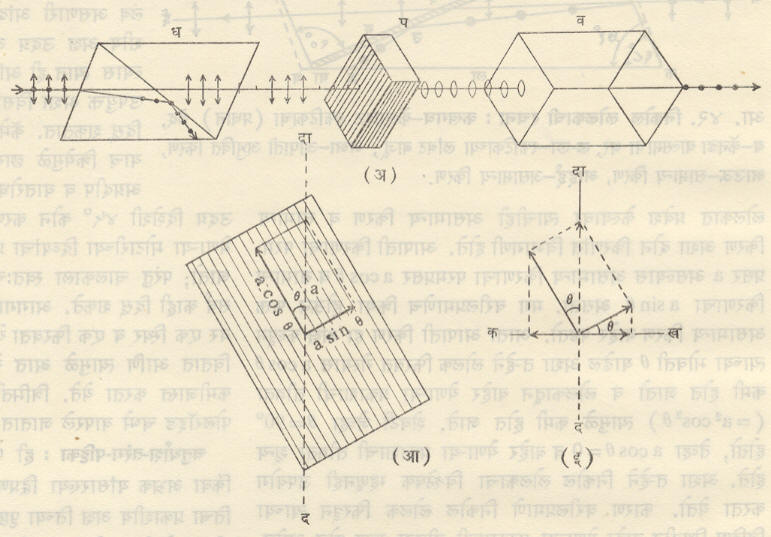
आ. ४३ (अ) मध्ये ध आणि व हे दोन निकोल जात्य स्थितीत ठेवले आहेत. ध वर एकवर्णी प्रकाश आपाती झाल्यास त्यातून a हा परमप्रसर असलेला रेखीय ध्रुवित प्रकाश बाहेर येतो व त्याची आंदोलने ध च्या प्रधान छेदाला (ददा ला) समांतर असतात. व हा विश्लेषक निकोल जात्य आहे म्हणजेच त्याचा प्रधान छेद (कख) ध च्या प्रधान छेदाला लंब आहे. म्हणून व मधून काहीही प्रकाश बाहेर येत नाही.

प ही द्विप्रणमनी स्फटिकाची पातळ पट्टी असून तिचा प्रकाशीय अक्ष (ददा) तिच्या पृष्ठांना समांतर आहे. ददा शी θ हा काही कोन करून प ही पट्टी या दोन निकालांच्यामध्ये आकृतीत दाखविल्याप्रमाणे घातल्यास सामान्यतः काही प्रकाश व मधून बाहेर येतो.

ध मधून बाहेर येणारा प्रकाश प वर पडल्यावर त्याचे a cos θ व a sin θ या परमप्रसराच्या दोन घटकांत विभाजन होते व ते प मधून अनुक्रमे असामान्य व सामान्य किरण म्हणून एकाच दिशेने मार्गक्रमण करतात [आ. ४३ (आ)]. हे दोन किरण व वर पडल्यानंतर त्यांचे (व च्या संदर्भात) सामान्य आणि असामान्य अशा प्रत्येकी दोन किरणांत विभाजन होते. त्यांपैकी सामान्य किरण ध मधून बाहेर येऊ शकत नाही. दोन असामान्य किरणांचे परमप्रसर समान मूल्यांचे (= a cos θ·sin θ) असून त्यांचे सदिश परस्परांना विरुद्ध दिशेला असतात [आ. ४३ (इ)].

परंतु प ची जाडी t असल्यास प मध्येच त्या दोघांत

δ =	2 π	t (μe-μo )
	λ

इतके कलांतर उत्पन्न झालेले असते. δ = 0, 2 π, 4 π ….. इत्यादी असल्यास या दोन किरणांचे विनाशी व्यतिकरण होऊन काहीच प्रकाश बाहेर येणार नाही परंतु δ चे मूल्य यापेक्षा भिन्न असल्यास काही प्रकाश बाहेर येईल.

प ही पट्टी पाचरीच्या आकाराची असल्यास t चे मूल्य ठिकठिकाणी बदलत जाईल. जेथे t चे मूल्य δ = ०, 2π, 4π, …. इत्यादी मूल्ये येण्यास योग्य असेल तेथे अप्रकाशित कृष्ण पट्ट व इतर ठिकाणी प्रकाशित पट्ट तयार होतील अणि व पलीकडे पडदा ठेवल्यास त्यावर समांतर व्यतिकरण पट्ट मिळतील.

प वर आपाती होणारे किरण अभिसारी असल्यास (प च्या बाजू समांतर असल्या तरीही) किरणांची प मधील प्रकाशीय पथांची लांबी त्यांच्या तिरकसपणानुसार बदलत जाईल व त्यामुळे समकेंद्री वर्तुळाकार व्यतिकरण पट्टांची मालिका मिळेल. आपाती प्रकाश पांढरा असल्यास हे पट्ट रंगीत दिसतील (चित्रपत्र ३८).

अनुप्रयोग : खनिजविज्ञानात खनिजांचे अभिनिर्धारण (निश्चिती) करण्यासाठी या व्यतिकरण आकृतिबंधांचा खूप उपयोग होतो [→ खनिजविज्ञान]. काच किंवा पारदर्शक प्लॅस्टिकावर प्रतिबल (बाह्य प्रेरणांमुळे निर्माण होणाऱ्या अलगीकरण, आकुंचन वा सरकणे या क्रियांना रोध करणारी घन पदार्थातील प्रेरणा) उत्पन्न झाले असता त्या पदार्थात तात्पुरते द्विप्रणमनत्व उत्पन्न होते. मग तो पदार्थ जात्य निकोलांमध्ये ठेवून वरीलप्रमाणे निरीक्षण केल्यास व्यतिकरण पट्ट मिळतात (चित्रपत्र ३८). त्यांच्यावरून पट्टीतील ताणाचे वितरण समजू शकते. पूल, मोठ्या इमारती यांच्या अभिकल्पात (आराखड्यात) वापरावयाच्या तुळयांचे (गर्डरांचे) काचेचे नमुने तयार करून त्यांमधील ताणांच्या वितरणाचा अशा तऱ्हेने अभ्यास करतात व त्यानुसार तुळयांचे आकारमान ठरवितात. काचेच्या वस्तू थंड होताना त्यांच्या आत अंतर्गत ताण निर्माण होतात. त्यामुळे त्या सहज तडकू शकतात. हे टाळण्यासाठी मंद शीतलन करून त्यांच्यामधील ताण कमी करावे लागतात व ताण पुरेसे कमी झाले की नाही, याची वरील पद्धतीने तपासणी करता येते.

 

चुंबकीय प्रकाशकी

तीव्र चुंबकीय क्षेत्राच्या प्रकाशावर होणाऱ्या विविध परिणामांचा अभ्यास चुंबकीय प्रकाशकीमध्ये अंतर्भूत होतो. प्रकाश हे जरी विद्युत् चुंबकीय प्रारण असले, तरी ज्ञात चुंबकीय प्रकाशकीय परिणाम हे चुंबकीय क्षेत्र व प्रकाश यांच्यातील प्रत्यक्ष परस्परक्रियेमुळे निर्माण होत नाहीत, तर जे द्रव्य प्रकाशाचे उत्सर्जन किंवा शोषण करण्याच्या अवस्थेत आहे त्यावरील चुंबकीय क्षेत्राच्या प्रभावामुळे घडून येतात.

झीमान परिणाम : प्रकाश उद्‌गम तीव्र चुंबकीय क्षेत्रात ठेवला असता त्या उद्‌गमाच्या वर्णपटातील वर्णरेषांचे दोन किंवा अधिक रेषांमध्ये विभाजन होते. हा शोध पीटर झीमान (१८६५—१९४३) यांनी लावला म्हणून त्याला झीमान परिणाम असे म्हणतात [→ अणुकेंद्रीय व आणवीय परिबले]. या रेषांच्या अभ्यासाचा अणुरचना समजण्यास चांगला उपयोग होतो. अशाच प्रकारे शोषण रेषांचेही विभाजन होते, त्याला नियमविरुद्ध (किंवा व्युत्क्रमी) झीमान परिणाम असे म्हणतात.

फोख्ट परिणाम किंवा चुंबकीय द्विप्रणमन : एखाद्या बाष्पाला तीव्र चुंबकीय क्षेत्र लावून त्या बाष्पातून चुंबकीय क्षेत्ररेषांना लंब दिशेने प्रकाशकिरण पाठविल्यास त्याचे द्विप्रणमन होते. या परिणामाचा शोध डब्ल्यू. फोख्ट (१८५०—१९१९) यांनी लावला.

फॅराडे परिणाम : एखाद्या काचेच्या ठोकळ्याला तीव्र चुंबकीय क्षेत्र लावल्यास तो ठोकळा ध्रुवण घूर्णक बनतो. असाच परिणाम इतर घन, द्रव व वायुरूप पदार्थांतही आढळून येतो. याला मायकेल फॅराडे (१७९१—१८६७) यांच्या नावावरून फॅराडे परिणाम असे म्हणतात.

कॉटाँ—मूटाँ परिणाम : तीव्र चुंबकीय क्षेत्रात ठेवलेल्या द्रवातून चुंबकीय क्षेत्ररेषांना लंब दिशेने प्रकाशकिरण सोडला असता त्याचे द्विप्रणमन होते. या परिणामाचा शोध एमे ऑग्यूस्त कॉटाँ व एच्. मूटाँ यांनी १९०५ मध्ये लावला.

कर चुंबक-प्रकाशीय परिणाम : चुंबकाच्या ध्रुवाच्या पृष्ठभागावरून रेखीय ध्रुवित प्रकाशाचे लंब दिशेने परावर्तन झाल्यास परावर्तित प्रकाश विवृत्तीय ध्रुवित झालेला आढळतो. या परिणामाचा शोध १८७५ मध्ये जॉन कर (१८२४—१९०७) यांनी लावला. [→ कर परिणाम].

 

विद्युत् प्रकाशकी

विद्युत् क्षेत्राचे प्रकाशावर किंवा माध्यमाच्या प्रकाशीय गुणधर्मावर होणारे परिणाम विद्युत् प्रकाशकीत अभ्यासले जातात. हे परिणाम प्रकाशाचे उत्सर्जन, शोषण वा प्रेषण करणाऱ्या द्रव्यावरील विद्युत् क्षेत्राच्या प्रभावामुळे घडून येतात.

श्टार्क परिणाम : प्रकाश उद्‌गम तीव्र विद्युत् क्षेत्रात ठेवला असता त्याच्या वर्णपटातील वर्णरेषा रुंदावतात किंवा त्यांचे (काहीसे झीमान परिणामाप्रमाणे) विभाजन होते. याला ⇨ श्टार्क परिणाम असे योहानेस श्टार्क (१८७४—१९५७) या शास्त्रज्ञांच्या नावावरून म्हणतात. अणूची संरचना समजण्यासाठी याचा उपयोग होतो. शोषण रेषांचे अशाच प्रकारे रुंदावणे किंवा विभाजन होणे याला व्युत्क्रमी श्टार्क परिणाम असे म्हणतात.

कर विद्युत् प्रकाशीय परिणाम : कित्येक समदिक् पदार्थ (उदा., काच) तीव्र विद्युत् क्षेत्रात ठेवले असता त्यांना एक-अक्षीय द्विप्रणमनी स्फटिकासारखे गुणधर्म प्राप्त होतात. याला कर विद्युत्‌ प्रकाशीय परिणाम असे म्हणतात. प्रकाशवेग मोजण्याच्या कर-घट पद्धतीत वापरण्यात येणाऱ्या प्रकाशीय झडपेचे कार्य या परिणामावर आधारलेले आहे [→ प्रकाषवेग].

पोकेल्स परिणाम : काही द्विप्रणमनी स्फटिक तीव्र विद्युत् क्षेत्रात ठेवले असता त्यांच्या द्विप्रणमनविषयक गुणधर्मांत फेरफार होतात. या परिणामाचा शोध एफ्. पोकेल्स यॉनी लावला.

संदर्भ : 1. Ditchburn, R. W. Light, London, 1963.

2. Jenkins, F. A. White, H. E. Fundamentals of Optics, New York, 1957.

3. Monk, G. S. Light : Principles and Experiment, New York, 1963.

4. Morgan, y3wuoeph, Geometrical and Physical Optics, New York, 1953.

5. Robertson, J. K. Introduction to Optics, New Delhi, 1965.

6. Rosi, Bruno, Optics, London, 1962.

7. Smith, C. J. A Degree Physics, Part III : Optics, London, 1960.

8. Wood, R. W. Physical Optics, New York, 1959.

परांजपे, य. रा.; पुरोहित, वा. ल.