अवगम सिद्धांत

अवगम सिद्धांत : (इन्फर्मेशन थिअरी). संकेतनासंबंधीचा (संदेश धाडताना त्यातील शब्दांकित किंवा अक्षरांकित अवगमाचे दुसऱ्‍या संज्ञेत किंवा चिन्हात रूपांतर करण्यासंबंधीचा) संदेशवहनशास्त्रातील एक महत्त्वाचा सिद्धांत. अवगम म्हणजे ज्ञान अथवा माहिती. ही माहिती संदेशाच्या स्वरूपात प्राप्त होते. कोणत्याही संदेशाचे प्रेषण माहितीच्या मूळ रूपात करता येत नाही. संदेशवहनाच्या कोणत्याही पद्धतीमध्ये संदेशाचे प्रथम सांकेतिक स्वरूपात रूपांतर करावे लागते आणि नंतर इष्टस्थानी त्याचे मूळ रूपांतर होते.

रेडिओ, दूरचित्रवाणी, दूरध्वनी यांसारख्या नवनवीन संदेशवहन माध्यमांचा विकास हे विसाव्या शतकातील तंत्रविद्येचे एक मोठे वैशिष्ट्य होय. या संदेशवहन पद्धतींना मूलभूत असणाऱ्‍या गणितीय नियमांचा तसेच संकेतन, निःसंकेतन (संकेतनापासून अवगम परत मिळविणे) व इतर प्रक्रिया यांचा मुख्यत्वे विचार अवगम सिद्धांतात होतो. या सिद्धांताच्या आधारे अवगमाचे तसेच निरनिराळ्या संदेशवहन प्रणालींतील (व्यूहांतील) संदेश प्रेषण करण्याच्या, साठविण्याच्या अथवा इतर संस्करण करण्याच्या क्षमतेचे मापन करता येते.

अवगम सिद्धांताचा उपयोग मुख्यत्वे पुढील हेतूंसाठी करण्यात येतो. (१) उपलब्ध संदेशवहन क्रिया जास्तीत जास्त कार्यक्षम करण्याचे मार्ग शोधून काढणे. (२) गोंगाट (अनिष्ट विद्युत् विक्षोभ) अस्तित्वात असतानाही इष्ट संदेश बिनचूक पोचविण्यासाठी अनुकूलतम प्रणाली शोधून काढणे. (३) संदेश ज्या परिवाहातून (अवगम नेणाऱ्‍या मार्गातून) जातो त्या परिवाहाच्या कमाल मर्यादा निश्चित करणे. अवगम सिद्धांतातील मूलभूत तत्त्वांचा जरी संदेशवहनशास्त्रातच अधिक महत्त्वाचा उपयोग होत असला, तरी त्यांतील काही संकल्पना मानसशास्त्र व भाषाशास्त्र यांसारख्या शास्त्रांतही उपयुक्त असल्याचे आढळले आहे.

रेडिओ, तारायंत्र, दूरचित्रवाणी, इलेक्ट्रॉनीय संगणक (गणितकृत्ये करणारे यंत्र) इ. प्रणालींतून निर्माण होणाऱ्या विविध प्रकारच्या संदेशांबरोबरच मानव व इतर प्राणी यांच्या तंत्रिकांतून (मज्जातंतूंतून) जाणाऱ्‍या संदेशांचाही अवगम सिद्धांतात विचार होतो. या सिद्धांताच्या दृष्टीने संदेशातील अवगमाचा सामान्य भाषेतील प्रचलित अर्थ महत्त्वाचा नसतो, हे येथे लक्षात ठेवण्यासारखे आहे.

पूर्वेतिहास : १९२० च्या सुमारास हार्टली व नायक्विस्ट यांनी भिन्न संदेशवहन प्रणालींच्या कार्यक्षमतेचे तौलनिक मूल्यमापन केले. या संदर्भात अवगमाचे मापन होऊ शकते व त्याचा तारायंत्राच्या संकेत वेगाशी निकटचा संबंध आहे असे आढळले. शॅनन यांनी १९४८ मध्ये अवगम सिद्धांतातील मूलभूत कल्पनांचे प्रथम गणितीय रूपात विवेचन केले. त्यापूर्वी काही वर्षे वीनर यांनी ‘सायबरनेटिक्स’(मानवी शरीरातील नियंत्रण तंत्राचा व त्यास अनुसरून तयार केलेल्या यांत्रिक व विद्युत् नियंत्रण तंत्रांचा अभ्यास) या शीर्षकाखाली संदेशवहनाच्या सामान्य तत्त्वांचा विचार केला होता. त्या तत्त्वांचा शॅनन यांनी उपयोग करून घेतला. हॅमिंग, रलेपिअन, होफमान यांनी तसेच आर. सी. बोस व डी. के. रे-चौधरी या भारतीय शास्त्रज्ञांनीही अवगम सिद्धांताच्या प्रगतीस हातभार लावला आहे.

संदेशवहनातील मूलभूत घटक : व्यापक दृष्टीने कोणत्याही संदेशवहन प्रणालीमध्ये असणारे मूलभूत घटक आ. १ मध्ये दाखविले आहेत.

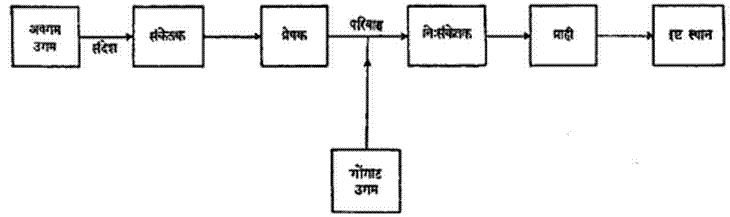
अवगम उगमापासून निघालेल्या संदेशाचे परिवाहास अनुकूल अशा स्वरूपात संकेतन होऊन तो प्रेषकाकडे जातो. तेथून तो परिवाहाद्वारे निःसंकेतकात परत रूपांतरित होऊन ग्राहीला मिळतो. अशा रीतीने आदान संदेशाचे इष्ट स्थानी प्रदान होते. संकेत परिवाहातून जात असताना त्यामध्ये बऱ्याच वेळा विक्षोभ निर्माण होतो. हा विक्षोभ गोंगाटामुळे होतो असे मानले जाते. हा परिणाम दाखविण्याकरिता आ. १ मध्ये गोंगाट उगमाचा अंतर्भाव केला आहे.

संदेशवहन प्रणालीचा अभिकल्प (योजना) करताना संदेशाच्या प्रेषणाची वेगराशी R (म्हणजे प्रति-सेकंदास धाडल्या जाणाऱ्‍या संकेतांची संख्या) व ते वाहून नेण्याची परिवाहाची धारकता C (म्हणजे प्रतिसेकंदास वाहून नेलेल्या संकेतांची संख्या) या दोन महत्त्वाच्या राशींचा विचार करावा लागतो. या सैद्धांतिक विचाराकरिता ‘अवगम’ हा वस्तुमान, लांबी, ऊर्जा इ. भौतिकीय राशींप्रमाणेच एक राशी आहे असे मानता येते. आ. १ मधील योजनेची मालवाहतूक योजनेशी तुलना केल्यास वरील गोष्टींची बरीचशी कल्पना येईल. काही कारखान्यांत ज्या ठिकाणी वस्तू तयार होतात, तेथून त्या दुसरीकडे वाहकपट्ट्यावरून नेल्या जातात. पट्ट्याच्या एका टोकाला R वस्तूंचा पुरवठा प्रति-सेकंदास होत असतो असे समजू आणि जर वाहकपट्ट्यामुळे C वस्तू प्रति-सेकंदास दुसऱ्‍या टोकास जात असतील, तर R = C असल्यास वाहतूक योजनेची कार्यक्षमता महत्तम होईल, हे उघड आहे. जर R हा C पेक्षा जास्त असेल तर R-C एवढ्या वस्तू प्रतिसेकंदास एका टोकास साचत राहतील. त्यामुळे वाहतूक योजना कार्यक्षम होणार नाही. याउलट R हा Cपेक्षा कमी असेल, तर वाहकपट्ट्याच्या धारकतेचा पुरेपूर फायदा घेतला जात नाही असे होईल म्हणजे याही दृष्टीने योजना कार्यक्षम ठरणार नाही. पण संदेशवहन प्रणालीमध्ये अवगमाची वेगराशी R ही जर परिवाह धारकता C पेक्षा जास्त नसेल, तरच अवगमाचे प्रेषण शक्य होईल. अवगम R = C इतक्या वेगराशीने पाठवणे फार कठीण असते. परंतु अवगम सिद्धांताची तत्त्वे वापरून सुयोग्य संकेतन पद्धती योजल्यास जवळजवळ Cइतक्याच वेगराशीने अवगम पाठवणे शक्य होते.

अवगम उगमाचे पृथक् व अखंड प्रकार : वर्णमालेतून निवडलेल्या अक्षरांपासून तयार केलेल्या शब्दांना ‘पृथक संदेश’म्हणतात.असा संदेश ज्या उगमापासून निघतो त्यास ‘पृथक् उगम’असे म्हणतात. या ठिकाणी ‘विशिष्ट चिन्हांचा संच’, या अर्थी ‘वर्णमाला’आणि ‘संचातील प्रत्येक चिन्ह’या अर्थी ‘अक्षर’असे म्हटले आहे. कोणत्याही भाषेतील लिपिबद्ध संदेश वा अंकबद्ध संदेश ही पृथक् संदेशाची उदाहरणे आहेत. याच्या उलट भाषण व संगीत यांचे उगम ही अखंड उगमाची उदाहरणे आहेत. वहन करण्यात येणाऱ्या संकेताच्या प्रकारानुसार परिवाहाचे पृथक् परिवाह व अखंड परिवाह असे वर्गीकरण करण्यात येते.

गोंगाटरहित व गोंगाटदूषित परिवाहांचे प्रकार : परिवाहातून ग्राहीस मिळालेला प्रदान संदेश आणि परिवाहास प्रेषकापासून मिळालेला आदान संदेश हे दोन्ही एकमेकांस समसमान असतातच असे नाही. या असमानतेचे कारण गोंगाट होय. आदान संदेशावरून प्रदान संदेशाचे निःसंदिग्धपणे आकलन करता आले तर‘तो परिवाह गोंगाटरहित आहे’असे म्हणतात. परंतु बहुधा परिवाहामध्ये गोंगाटाचा प्रवेश होतोच. त्यामुळे संदेशामध्ये विक्षोभ निर्माण होतो व संदेशवहनात अनेक दोष उत्पन्न होतात. ज्या परिवाहापासून मिळालेल्या प्रदान संदेशापासून आदान संदेशाविषयी निश्चित ज्ञान मिळत नाही त्या परिवाहास ‘गोंगाटदूषित परिवाह’म्हणतात व त्याची कार्यक्षमता गोंगाटामुळे कमी होते.

अवगममापन : अनेक प्रकारच्या संभाव्य संदेशांच्या संचातून एका विशिष्ट संदेशाची निवड करणे म्हणजेच अवगम होय. निवडलेल्या संदेशाचे विशिष्ट वर्णन प्रेषित केल्यास त्यापासून ग्राहीला मूळ संदेशाची निःसंदिग्धपणे पुनर्रचना करणे शक्य होते. वरील विधानाचे मर्म लक्षात येण्याकरिता व्यवहारातील एक सोपे उदाहरण घेऊ. अनेक घरांमध्ये विद्युत् घंटी बसविलेली असते व तिचा स्विच दाराजवळ बसविलेला असतो. बाहेर असणाऱ्या माणसाला स्विच दाबून तो आल्याची सूचना घरातील माणासांना देता येते. संदेशवहनातील ही सर्वांत सोपी योजना आहे. या प्रकारात फक्त दोनच प्रकारचे संदेश संभवतात : (१) घंटी वाजते, (२) घंटी वाजत नाही. ज्या प्रकारात दोन प्रकारचे संदेश संभवतात त्या पद्धतीला ‘द्विमान पद्धत’म्हणतात.

या दोन संदेशांची संभाव्यता समसमान असेल, तर अशा पद्धतीतून मिळणाऱ्या अवगमाचे मान हे log₂ 2= 1 एवढे धरण्यात येते. अवगमाचे मान दर्शविणारे पद लॉगरिथमाच्या स्वरूपात असल्यामुळे त्यामध्ये योगशील (बेरीज करता येण्याचा) गुणधर्म अभिप्रेत आहे. log₂2 याला ‘अवगम-कण’(इंग्रजीमध्ये ‘bit’) असे म्हणतात. अवगममापनाचे हे एकक आहे. जर एखाद्या प्रणालीत समसंभाव्यतेचे N संदेश असतील, तर त्यामधील  अवगममान log₂N एवढे असते. जर संभाव्यता असमान असून त्यांची मूल्ये p₁, p₂, …, p_Nअसतील, तर त्यातील अवगमाचे मान खालील समीकरणाने मिळते.

E = -(p₁log₂p₁+p₂log₂p₂+ … +p_Nlog₂p_N) …(१) या समीकरणावरून अवगमाचे मान शून्यापासून ते log₂N या महत्तम मूल्यापर्यंत असते असे दिसून येईल. एखाद्या घटकाची संभाव्यता जेव्हा १ होते, म्हणजे हा घटक निश्चितपणे मिळतो (म्हणजे इतर घटक मिळण्याची जेव्हा संभाव्यता नसते), तेव्हा अवगममूल्य शून्य असते.

याउलट जेव्हा सर्व घटकांची संभाव्यता समान (= ¹/_N) असते, तेव्हा अवगममूल्य महत्तम होते.

संकेतन पद्धती : संकेतन पद्धतीचे विवेचन करण्याकरिता तारायंत्र-संदेशवहन-पद्धती विचारात घेणे सोपे ठरते. या पद्धतीचा आराखडा आ. २ मध्ये दिला आहे. यापुढील विवेचन या पद्धतीच्या संदर्भात केले आहे. यामध्ये इंग्रजी वर्णमालेतील अक्षरे व इतर काही चिन्हे हेच घटक संदेश असतात. प्रत्येक अक्षर हे संकेतनक्रियेकरिता एका खंडासमान असते, असे समजले आहे. या घटक संदेशाचे सांकेतिक विद्युत् संदेशात (कट्ट व कड अथवा टिंब व प्रास) रूपांतर करण्याच्या अनेक पद्धती आहेत. 0,1 या आकड्यांनी दर्शविलेल्या द्विमान पद्धतीत २, ३ किंवा ५ स्थानांचे संच वापरून संदेश पाठविण्याचे तीन संभाव्य प्रकार खाली दाखविले आहेत. यांमध्ये इंग्रजी वर्णमालेतील X,W,Y,Z हीच चार अक्षरे उदाहरणादाखल घेतली आहेत.

वरील कोणत्याही पद्धतीत चुका होणारच हे गृहीत धरून त्यांचे अभिज्ञान व नंतर निरास कसा करता येतो, हे वरील तक्त्यावरून कळून येते. पहिल्या पद्धतीमधील X च्या अनुरूप सांकेतिक संदेशात चूक होऊन 11 च्या ऐवजी 10,01 धाडले गेले, तर W आणि Y या अक्षरांचे ज्ञान होईल. दुसऱ्या पद्धतीमध्ये अशा प्रकारची X मध्ये एकच चूक झाली तर पाठविलेला संकेत संदेश 111,100,010 असू शकेल. या संकेत समुच्चयाला कोणतेच अनुरूप अक्षर नसल्यामुळे चूक झाली आहे, हे लक्षात येते. तिसऱ्या पद्धतीत दोनपर्यंत चुका झाल्यास कळून येतात व एकीचा निरासही करता येतो. मिळालेल्या चुकीच्या सांकेतिक संदेशातील अंकसमुच्चय संकेत तक्त्यातील कोणत्या अक्षराच्या अंकसमुच्चयाशी सगळ्यात मिळता-जुळता आहे हे पाहिले असता चुकीचा निरास करता येतो, हे हॅमिंग यांनी दाखविले. यावरून असे दिसते की, संकेतन क्रियेमध्ये अंकसमुच्चयातील स्थाने वाढवीत गेल्यास चुका निदर्शनास येऊन त्यांचा निरास करण्याची संभाव्यता वाढते, तसेच अवगममान वाढते. तथापि असे करण्याने संदेश प्रेषणाची वेगराशी कमी होईल हे उघड आहे. वेगराशी कमी होऊ नये यासाठी एक युक्ती म्हणून इंग्रजी भाषेतील E,T,A,O ही अक्षरे व दोन शब्दांमधील मोकळी जागा यासाठीच फक्त चार स्थानी अंकसमुच्चय चिन्हे वापरण्यात येतात. व्यापक संकेतन पद्धतीमध्ये वर्णमालेतील निरनिराळ्या प्रत्येक अक्षराला भिन्न स्थानांक असलेले अंकसमुच्चय वापरतात. वर्णमालेतील i क्रमांकाच्या अक्षराकरिता जर L(i) स्थानांक वापरले आणि त्या अक्षराची संभाव्यता p(i) असली, तर प्रत्येक अक्षराकरिता लागणारे सरासरी स्थानांक L हे पुढील समीकरणाने मिळतात.

L=p(1) L(1)+p(2) L(2)+ … +p(N) L(N)… (२)

अनुकूलतम संकेतन पद्धती L चे मूल्य लघुतम करील. पण सांकेतिक संदेशाचे जर नीटपणे आकलन व्हायचे असेल, तर मॅकमिलन यांनी दाखविल्याप्रमाणे स्थानांकांनी एक अट पूर्ण करणे आवश्यक होते. या दोन अटींमुळे L चे लघुतम मूल्य खालील सूत्राने मिळते.

H = – ∑ p (i) log₂ p(i)                                          ….(३)

i

एकाहून अधिक अक्षरांचे खंड कल्पून संकेतन केल्यास अक्षरागणिक लागणारे सरासरी स्थानांक वरील H पेक्षा आणखीही कमी होतात. दोनदोन अक्षरांच्या समूहांच्या सापेक्ष वारंवारता व व्यवहारात असलेल्या अक्षर समूहावरील मर्यादा विचारत घेतल्या असता L चे मूल्य सु. १ ते १·५ पर्यंत खाली येते.

समीकरण (३) मधील उजव्या बाजूचे पद हे ऊष्मागतिकीतील ‘एंट्रॉपी’ राशी (उष्णतेच्या यांत्रिक व इतर स्वरूपाच्या ऊर्जांशी असलेल्या संबंधांचे गणितीय विवरण करणाऱ्या शास्त्रातील एक महत्त्वाची राशी,→एंट्रॉपी) व संभाव्यता यांतील संबंध दाखविणाऱ्या सूत्रासारखे आहे. वर विवेचन केल्याप्रमाणे अथवा संकेतन क्रियेकरिता जास्त मोठमोठे खंड केल्याने L च्या मूल्याला सीमित लघुतम मूल्य L_० येते. L_० ला अवगम उगमाची एंट्रॉपी म्हणतात. निराळ्या शब्दांत हे सांगावयाचे झाल्यास ‘उगम अक्षरागणिक L_० अवगम-कण या वेगराशीने अवगम निर्माण करतो ’असे म्हणता येते. जर उगमातून प्रति-सेकंदास सरासरीने n अक्षरे R या निश्चित वेगराशीने निर्माण होत असतील, तर एंट्रॉपीला n ने गुणले असता त्यापासून उगमाच्या अवगम वेगराशीचे मूल्य (अवगम-कण प्रति-सेकंदास या एककात) मिळते. उगमापासून मिळणाऱ्या पर्यायी संदेशांची संख्या व त्यांच्या संभाव्यता या दोन गोष्टी माहीत झाल्या, तर गणितीय पद्धतीचे एंट्रॉपीचे मूल्य काढता येते.

अवगम उगमापासून संभवणारी सगळी अक्षरे जेव्हा समसंभाव्य नसतात, तेव्हा उगमाच्या अवगम वेगराशीचे मूल्य शक्य असणाऱ्या महत्तम मूल्याहून (हे महत्तम मूल्य अक्षरे समसंभाव्य असतात तेव्हाच मिळत असते) कमी असते. अशा उगमास ‘अतिरिक्त उगम’असे म्हणतात. त्याच संदेशाचे वारंवार प्रेषण हे अतिरिक्ततेचे सोपे उदाहरण आहे. एखाद्या संदेशातील चूक तशीच राहण्याची संभाव्यता जास्त अतिरिक्त अवगम पाठवून कमी होईल. गोंगाटामुळे होणाऱ्या अवगमक्षयाच्या मूल्याचा अतिरिक्त अवगम पाठवून इष्ट स्थानी संदेशातील चुकीची संभाव्यता कमी करता येते. शॅनन यांनी लिपिबद्ध इंग्रजी भाषेची एंट्रॉपी अंदाजे अक्षरागणिक एक अवगम-कण असते असे दाखवले आहे. या भाषेची जर २७ समसंभाव्य संदेश पाठविणाऱ्या उगमाशी (ज्याची एंट्रॉपी नियमाप्रमाणे log₂27 = 4·8 एवढी असते) तुलना केली, तर इंग्रजी भाषा ८०%अतिरिक्त आहे असे म्हणता येते.

परिवाह धारकता : परिवाह म्हणजे एका ठिकाणाहून दुसऱ्या ठिकाणी संदेश नेण्यासाठी वापरलेले माध्यम होय. यासाठी परिवाहाला योग्य अशी संकेतन पद्धती वापरावी लागते. परिवाहाकरिता विशिष्ट सांकेतिक संदेश वापरावे लागतात आणि या प्रत्येक संदेशाला एक विशिष्ट कालावधी लागत असतो. माध्यमाच्या भौतिक गुणधर्मामुळे संकेतन-पद्धतीवरसुद्धा मर्यादा येतात. उदा.,∆f पट्टविस्तार (दर सेकंदास होणाऱ्या कंपनसंख्यांच्या म्हणजे कंप्रतांच्या अखंड पट्ट्याच्या दोन मर्यादांपाशी असलेल्या कंप्रतांतील फरक) असलेली तार माध्यम म्हणून वापरल्यास कोणत्याही सांकेतिक संदेशाकरिता Δt = ¹/_Δfयाहून कमी कालावधीची योजना करता येणार नाही.

परिवाहास योग्य अशी संकेत वर्णमाला ठरली म्हणजे परिवाहाचे गुणधर्म निश्चित होतात. अर्थातच एका ठराविक वेगराशीनेच संदेशवहन होत असते. शॅनन यांनी या वेगराशीचे महत्तम मूल्य काही मर्यादेपुढे जाऊ शकत नाही असे सिद्ध केले आहे. प्रत्येक अक्षराची संभाव्यता आणि त्याला लागणारा कालावधी यांवर हे महत्तम मूल्य अवलंबून असते.

पृथक् व गोंगाटरहित परिवाहाद्वारे ज्या महत्तम वेगराशीने अवगमवहन (अवगम-कण प्रति-सेकंद) शक्य असेल, त्यास ‘परिवाहाची धारकता C’ असे म्हणतात.

गोंगाटदूषित पृथक् परिवाह वापरताना गोंगाटाचा अनिष्ट परिणाम होऊन प्रेषित अक्षर इष्ट स्थानी वेगळ्या अक्षराच्या रूपात प्राप्त होण्याची शक्यता असते, याचा विचार मागे केलाच आहे. गोंगाटामुळे प्रत्येक संकेताक्षरावर होणारा परिणाम जर स्वतंत्रपणे होत असले आणि जर प्रेषित केलेल्या 0,1 या चिन्हातील pअंशाचे 1, 0 या चुकीच्या चिन्हात परिवर्तन होत असेल, तर अशा गोंगाटदूषित परिवाहाची धारकता पुढील सूत्राने मिळते :

C=m[1+p log₂p+(1-p)log₂(1-p)] … (४)

यात m= प्रतिसेकंदास पाठविलेल्या संकेताक्षरांची अथवा चिन्हांची संख्या.

या सूत्रावरून गोंगाटदूषित परिवाहामधून ज्या वेगराशीने अवगमवहन होऊ शकेल तिचे सैद्धांतिक महत्तम मूल्य कळते.

दूरचित्रवाणी आणि रेडिओ : यांतील संदेश अखंड स्वरूपाचे असतात व त्यांचे वहन करण्याकरिता योजलेले परिवाह अखंडच असतात. व्यवहारातील अशा सर्व परिवाहांत गोंगाट असतोच. म्हणून गोंगाटदूषित परिवाहाच्या धारकतेसंबंधी थोडे विवेचन पुढे केले आहे. शॅनन यांनी असे सिद्ध केले की, पट्टसीमित परिवाहाची धारकता खालील सूत्राने मिळते :

C = B log₂ [1 + S/A ] हर्ट्‌‌‌‌‌‌‌‌‌झ                                   ….. (५)

येथे B म्हणजे परिवाहाचा पट्टविस्तार, A= गौस सिद्धांताप्रमाणे येणारी परिवाहातील गोंगाट शक्ती, S= प्रेषित विद्युत्‌संदेशाची सरासरी महत्तम शक्ती. S आणि A हे एकाच एककात मोजतात. यावरून असे दिसते की, परिवाह-धारकतेइतक्या वेगराशीने अवगम-प्रेषण करतानासुद्धा सुयोग्य संकेतन-पद्धती वापरून पट्टविस्तार आणि संदेश/गोंगाट हे गुणोत्तर यांच्यात देवघेव करता येते. प्रत्यक्षात वापरल्या जाणाऱ्या परिवाहापासून किती धारकता मिळते याची कल्पना पुढील काही उदाहरणांवरून येईल. दूरध्वनी व दूरचित्रवाणीकरिता अनुक्रमे २० हजार व ५ कोटी अवगमकण प्रतिसेकंद इतकी धारकता लागते. भाषण किंवा दूरचित्रवाणी यासाठी वापरल्या जाणाऱ्या संदेशात अवगममानाच्या दृष्टीने बरीच अतिरिक्तता असते. म्हणून सुयोग्य पण जटिल अशा संकेतन-पद्धतीचा वापर केल्यास याहून कमी धारकतेच्या परिवाहाद्वारे हे संदेश पाठविणे शक्य होते. बऱ्याच वेळा अंतिम ग्राहीस्थानी माणूसच असतो. माणसाला दृष्टिश्रवणादी इंद्रियांद्वारा सु. ५० अवगमकण प्रतिसेकंद याहून अधिक वेगराशीने अवगमाचे ग्रहण करता येत नाही, असे प्रयोगांवरून आढळून आले आहे.

अनुप्रयोग : आतापर्यंतचे विवेचन जरी संदेशवहन-पद्धतींच्या अनुषंगाने केलेले असले तरी अवगम-सिद्धांताचे उपयोग इतर अनेक शास्त्रांतही होतात. अशा काही अनुप्रयोगांची उदाहरणे खाली दिलेली आहेत.

(१)संदेशांच्या भविष्यकालातील संभाव्य मूल्याचे पूर्वानुमान करणे, उदा., युद्धकाळात गतिमान लक्ष्याचे ठराविक वेळी असणारे संभाव्य स्थान सूचित करणे (२) सर्वांत कार्यक्षम अशी गुप्त संकेत-लिपी शोधणे (३) भाषाशास्त्रामध्ये शब्दांची वारंवारता आणि त्यांचे वितरण यांविषयीचे गणितीय नियम मांडणे (४) मानसशास्त्रामध्ये उत्तेजकातील अवगमाचे मान व प्रतिसादकाल यांसंबंधीचे गणितीय विश्लेषण करणे (५) जीवविज्ञानामध्ये एका पिढीपासून दुसऱ्या पिढीकडे जननविषयक वैशिष्ट्यांचे संक्रमण व नियंत्रण करणारे नियम शोधून काढणे (६) उत्तेजकाविषयी कल्पना, त्याला मिळणारा प्रतिसाद अथवा तंत्रिका-संदेश व त्यामुळे घडून येणारे स्‍नायूंतील चलनवलन अथवा जीववस्तूंचे स्थूलमानाने दृष्टोत्पत्तीस येणारे वर्तन यासंबंधी संशोधन इत्यादी.

संदर्भ : 1. Brillouin, L. Science and Information Theory, New York, 1956.

2. Cherry, C. On Human Communication, New York, 1957.

3. Jagjit Singh, Great Ideas in Information Theory, Language and Cybernetics, London, 1967.

4. Ramkrishna, B. S. Principles of Information Theory, Journal of the Scientific and Industrial Research India, Vol. 20, 1961.

5. Shannon, C. E. Weaver, W. The Mathematical Theory of Communication, Urbana, 1959.

चिपळूणकर, व. ना.