अणुकेंद्रीय व आणवीय परिबले

अणुकेंद्रीय व आणवीय परिबले : आणवीय भौतिकीत ‘परिबल’ (एखाद्या अक्षाभोवती वस्तू फिरविण्याची प्रेरणेची क्षमता) ही संज्ञा मुख्यतः पुढील चार गोष्टींच्या संदर्भात वापरतात. (१) परिवलन परिबल, (२) चुंबकीय द्विध्रुवी परिबल (μ), (३) चतुर्ध्रुवी परिबल, (४) इतर चुंबकीय वा विद्युत् अनेकध्रुवी परिबले. यातील फक्त पहिल्या तिनांचा परिणाम प्रायोगिकरीत्या मोजतात.

बोर-प्रणीत अणुप्रतिमानानुसार इलेक्ट्रॉन हे अणुकेंद्राभोवती फिरत असतात. या गतीमुळे प्रत्येक इलेक्ट्रॉनाला जो कोनीय संवेग (निरूढी परिबल × कोनीय वेग) प्राप्त होतो, त्याला त्या इलेक्ट्रॉनाचे कक्षीय परिभ्रमण परिबल असे म्हणतात. केंद्राभोवती फिरताफिरता इलेक्ट्रॉन आपल्या स्वतःच्या अक्षाभोवतीही परिभ्रमण करीत असतो, असे मानल्यास आणवीय वर्णपटातील काही कूट प्रश्नांचा समाधानकारक उलगडा करता येतो. या गतीमुळे प्रत्येक इलेक्ट्रॉनाला प्राप्त होणाऱ्या कोनीय संवेगाला ‘इलेक्ट्रॉनाचे अंगभूत परिवलन परिबल’ असे म्हणतात. कोणत्याही इलेक्ट्रॉन किंवा न्यूक्लिऑन (प्रामुख्याने प्रोटॉन किंवा न्यूट्रॉन) यांच्या परिवलन-परिबलाचे मूल्य ¹/₂ ^h/_2π = ¹/₂  ħ (h=प्लांक स्थिरांक) इतके असते. सर्वांनाच नाही तरी बहुतेक इतर मूलकण व अणुकेंद्रे यांनाही परिवलन परिबल व चुंबकीय परिबलही असते. इलेक्ट्रॉनाच्या परिवलनाची कल्पना प्रथम पाउली यांनी सुचविली व त्यानंतर ऊलेनबेक व गूट्‌श्मिट यांनी ती अणूतील इलेक्ट्रॉनांना लावली. यामुळे वर्णपट-रेषांची सूक्ष्मरचना आणि झीमान परिणाम यांची संगती लावता आली. अणुकेंद्रातील मूलकणांच्या परिवलन परिबलांचा सदिश (दिशा आणि परिमाण असे दोन्ही गुण असलेल्या राशी) पद्धतीने संयोग होऊन त्यामुळे संपूर्ण अणुकेंद्राला परिणामी असे परिवलन परिबल प्राप्त होते. इलेक्ट्रॉनाचे कक्षीय परिभ्रमण परिबल नेहमी ħ  च्या पूर्ण पटीत असते. त्याचा इलेक्ट्रॉनाच्या परिवलन परिबलाशी संयोग होऊन एकत्रित आणवीय कोनीय संवेग उत्पन्न होतो. तो नेहमी ħ/₂ च्या पूर्ण पटीत असतो.

परिवलन परिबलाचा परिणाम म्हणून कणांना अंगभूत चुंबकीय द्विध्रुव परिबल (μ) प्राप्त होते. अशा प्रकारे अणुकेंद्रीय व आणवीय चुंबकीय परिबले उत्पन्न होतात.

याशिवाय अणुकेंद्रीय विद्युत् भाराच्या असममित विनिमयामुळे अणुकेंद्राला व अणूला चतुर्ध्रुवी किंवा अनेकध्रुवी परिबले प्राप्त होतात. दोन विरुद्ध चिन्हांचे परंतु सममूल्य विद्युत् भार एकमेकांपासून काही अंतरावर ठेवले असता विद्युत् द्विध्रुव तयार झाला, असे म्हणतात. असे सम परिबल असलेले द्विध्रुवांचे मध्यबिंदू एकमेकांपासून काही अंतरावर असून त्यांच्या परिबलाच्या दिशा एकमेकांच्या विरुद्ध असतील, तर त्या रचनेस विद्युत चतुर्ध्रुव असे म्हणतात. याचप्रमाणे दोन  चतुर्ध्रुवांपासून एक अष्टध्रुव, दोन अष्टध्रुवांपासून एक षोडशध्रुव वगैरे बहुध्रुव बनू शकतात. याच तत्वावर चुंबकीय चतुर्ध्रुव व इतर बहुध्रुवांची रचना असते.

वरीलपैकी प्रत्येक परिबलाशी संलग्न असे पुंजांक (पृथक् मूल्ये घेणाऱ्या म्हणजेच पुंजरूप असलेल्या राशीच्या निरनिराळ्या मूल्यांपैकी एक मूल्यदर्शक अंक म्हणजे पुंजांक होय) असतात. नव्या ⇨पुंजयामिकीनुसार, कण समूहांच्या समीकरणांची उकल केली असता मिळणाऱ्या निर्वाहात (समीकरण सोडवून मिळणाऱ्या उत्तरात) हे पुंजांक आपोआपच येतात. तर जुन्या पुंजयामिकीनुसार ‘विशिष्ट परिबल = पुंजांक × तद्विशिष्ट किमान मूल्यांचे परिबल’ असे असले, तरीही ही परिबले बहुधा त्यांच्यात्यांच्याशी संलग्न पुंजांकांनीच व्यक्त करण्याचा शिरस्ता आहे. ही सर्व परिबले सदिश असल्याने त्यांचे संयोग सदिश-संयोग-नियमानुसार करावे लागतात. यावरूनच अणूचे सदिश प्रतिमान (मॉडेल) उदयाला आले. प्रकाशवर्णपट-विज्ञानामध्ये हे प्रतिमान पूर्वीपासून फारच उपयोगी ठरले आहे.

कोष्टक क्र.१ मध्ये कणांचे गुणधर्म व कोष्टक क्रं.२ मध्ये वेगवेगळ्या पुंजांकांची चिन्हे व अर्थ दिले आहेत. लहान अक्षरे सुट्या कणांसाठी व मोठी कण-समुहांसाठी म्हणजे अणुकेंद्र किंवा अणु-रेणूसाठी वापरतात.

n= प्रमुख पुंजांक = १, २, ३,  …

 ι= कक्षीय परिभ्रमण पुंजांक = ०, १, २,  …

ι *h=परिभ्रमण-कोनीय संवेग 

m_ι =चुंबकीय परिभ्रमण पुंजांक ι, ι-१, ι-२…, (-ι+1),-ι

S=परिवलन परिबलांक= १/२,परिवलन परिबल= s*h 

µ_s=चुंबकीय परिवलन परिबलांक= १/२,-१/२ 

j = ι ±s = सुट्या कणांचा एकत्रित कोनीय सवेंगांक=१/२, ३/२, ५/२… 

m_j=सुट्या कणांचा एकत्रित चुंबकीय परिबलांक= j, j-1,…., 

(-j+1), -j. 

I=अणूकेंद्राचा एकत्रित कोनीय सेवेगांक 

J=अणूतील सर्व इलेक्ट्रॉनांचा एकत्रित कोनीय संवेगांक 

F=I+J,…,I-J=संकलित कोनीय संवेगांक (संपूर्ण अणूचा) 

µ_B=बोर-प्रणीत चुंबकीय परिवलाचे एकक 

µ_B=eħ     =९·२७×१०^-२४जूल मीटर^२ 

          2m_o                                     वेबर 

µ_M=अणुकेंद्रीय चुंबकीय परिबलाचे एकक. 

µ_M=µ_Bµ_o=५·०५×१०^-२७जूल मीटर^२ 

               M_o                                    वेबर 

चुंबकीय परिबलµ=mj·µ_Bकिंवाm_j.µ_M 

आणवीय परिबले: १९१३–१५ मध्ये बोर यांनी प्रसृत केलेल्या आणवीय वर्णपटाच्या उपपत्तीप्रमाणे[→ वर्णपटविज्ञान]सर्वसाधारण स्थितीत, अणूमधील इलेक्ट्रॉन काही निश्चित अशा स्थिर ऊर्जा-पातळ्यांत असतात. अशा स्थितीत कोणत्याही प्रकारचे प्रारण होत नाही. या पातळ्यांशी संबंधित असलेले इलेक्ट्रॉनीय कोनीय संवेगp=nħ इतके असले पाहिजेत. अशा एखाद्या पातळीतून इलेक्ट्रॉनाचे दुसऱ्या पातळीत संक्रमण झाले, तरच प्रकाशाचे प्रारण किंवा शोषण होते आणि त्या प्रकाशाची कंप्रता (प्रतिसेकंदास होणारी तरंग संख्या) νहीhν = W₁-W₂या सूत्राने मिळते (W = पातळीशी संलग्न इलेक्ट्रॉनाचे ऊर्जा-मूल्य W₁&gtW₂तर प्रारण वW₁&ltW₂तर शोषण). 

कित्येक आणवीय वर्णपटांतील रेषा एकाकी व सुट्या सुट्या असतात. पण अनेकदा एक एक रेषा म्हणजे दोन किंवा अधिक रेषांचा समूह आहे असे सूक्ष्म परीक्षणाने दिसून येते. यालाच ‘रेषांची सूक्ष्म रचना’असे म्हणतात.सूक्ष्म रचनेत रेषांचे द्विक, त्रिक, चतुष्क इ. समूह आढळतात. यावरून, प्रत्येक ऊर्जा-पातळी ही एकमेकानजीक अशा अनेक ऊर्जा-पातळ्यांचा समूह असली पाहिजे, असे मानणे भाग पडते. क्षार (अल्कली) मूलद्रव्यांच्या (उदा., सोडियम, पोटॅशियम इ.) वर्णपटात रेषा-द्विके आढळतात. म्हणून त्यांच्या अणूंत ऊर्जा-पातळ्या दुहेरी असल्या पाहिजेत. रेषांच्या या सूक्ष्म रचनेचा संबंध इलेक्ट्रॉनाचे अंगभूत परिवलन परिबल व तज्जन्य चुंबकीय परिबल यांच्याशी असतो. 

प्रत्येक ऊर्जा-पातळीचे निदर्शक पुंजांक(n, l, m_l, m_s)असतात. क्षुब्धताकारक बाह्य चुंबकीय क्षेत्रात अणू ठेवलेला नसेल, तर पातळ्यांचे पुंजांक वेगवेगळ्या मूल्यांचे असूनही त्या पातळ्यांची ऊर्जा-मूल्ये समान असणे शक्य होते. अशा वेळी ऊर्जा-पातळ्या अपभ्रष्ट स्थितीत आहेत. असे म्हटले जाते. 

झीमान परिणाम :प्रकाशाचा उगम चुंबकीय क्षेत्रात ठेवला असता किंवा विद्युत् क्षेत्रात ठेवला असता एक वर्णपटरेषा भंग पावून अनेक रेषा उत्पन्न झालेल्या दिसतात. याला अनुक्रमे‘झीमान परिणाम’व ‘स्टार्क परिणाम’असे म्हणतात. झीमान परिणामाचा शोध १८९६ मध्ये डच शास्त्रज्ञ झीमान यांनी लावला. 

प्रकाशाचे प्रारण करणाऱ्या अणूंभोवती चुंबकीय क्षेत्र प्रस्थापित केल्यास त्या अणूंतील अपभ्रष्ट पातळ्यांचे निरनिराळ्या ऊर्जा-पातळ्यांत विभाजन होते, हे झीमान परिणामाचे कारण आहे. चुंबकीय क्षेत्राला लंब दिशेने पाहिले असता, मूळ एका वर्णपटरेषेचे तीन रेषांत विभाजन झालेले दिसले, तर त्याला सामान्य परंतु खऱ्या अर्थाने‘ढोबळ’किंवा‘स्थूल’झीमान परिणाम म्हणतात. अणूचे एकत्रित परिवलन परिबलS*= 0 असल्यास सामान्य झीमान परिणाम मिळतो. परंतुS*चे मूल्य शून्य नसल्यास एका रेषेचे तिनाहून अधिक रेषांत विभाजन झालेले आढळते. याला नियमविरुद्ध (पण खऱ्या अर्थाने सूक्ष्म) झीमान परिणाम म्हणतात. सामान्य परिणाम हा खरोखर अपवादात्मक असून नियमविरुद्ध परिणाम हाच जास्त सार्वत्रिक स्वरूपाचा आहे. झीमान परिणामात विभाजन झालेल्या रेषांतील कंप्रतांतर व रेषांची संख्या यांवरून आणवीय परिबले निश्चित करता येतात. याची गणितीय बैठक संक्षिप्तपणे पुढीलप्रमाणे आहे:  

सामान्यपणेµचुंबकीय परिबल असलेला कोणत्याही चुंबकीय द्विध्रुवBतीव्रतेच्या चुंबकीय क्षेत्रात, क्षेत्ररेषांशीθ हा कोन करून ठेवला तर द्विध्रुवाच्या स्थितिज ऊर्जेत पडणारा फरकΔW=-Bµcosθया समीकरणाने दिला जातो. येथेµcosθहाµचा B च्या दिशेवरील प्रक्षेप आहे. हा नियम आणवीय चुंबकांना लावल्यास चुंबकीय क्षेत्रामुळे अणूतील ऊर्जा-पातळ्यांची मूल्येही अशीच बदलतील हे उघड आहे. परंतु आणवीय परस्परक्रियांत पुंजसिद्धांत लागू करावे लागतात. त्यामुळे वरील समीकरणातील cosθ=m_jहीच मूल्ये घेऊ                                                                                                                                        j*

शकतो. येथेm_j = J, J-1, J-2, …, (-J+1)किंवा-Jहीच मूल्ये धारण करू शकतो. त्या चुंबकीय क्षेत्रामुळे होणारा ऊर्जा-पातळीतील ऊर्जा-बदल पुढील सूत्राने दिला जातो. 

Δ W=-m_j·g_j ×   eh          B 

                       4∏m_o 

g_j‘ला लांडे’गुणक असे म्हणतात. त्याच्या मूल्याचे सूत्रg_j=+1J*²+S*²-L*²असे आहे.अणुकेंद्रीय

                                                                                                     2J*²…(A)

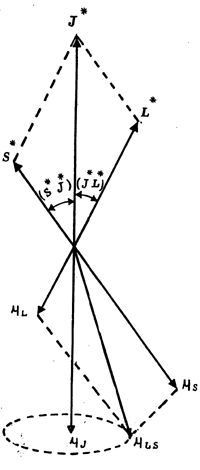
परिबल वगळता, राहिलेल्या अणूचेJ*च्या दिशेने परिणामी चुंबकीय परिबलµ_j= g_jµ_B·J*असते.g_j हा गुणक येण्याचे कारण सामान्यत:µ_SL हाJ*ला समांतर नसतो, हे आहे. ही गोष्ट आ. १ वरून स्पष्ट होईल. आ. १ मध्ये 

µ_L=  ħL*e 

               2m_o 

µ_s= 2ħS*e 

                 2m_o 

परिणामी चुंबकीय परिबल µ_j = g_j·J*ħ  e    g_j·J*·µ_B

                                                                 2m_o

J* = L*

∴ S* = 0 असल्यास g_{j =}1 या A समीकरणवरून सहज स्पष्ट होईल परंतु Δmj = ±1 हा नियम पाळला जातो. म्हणून या परिस्थितीत, मूळ रेषेच्या कंप्रतेत पडणारा फरक, Δν पुढील समीकरणाने मिळेल : 

hΔν = ± eh     .B

                      4πm₀

∴hΔν = ± eB 

                        4πm₀

अशा तऱ्हेने मूळ रेषांची कंप्रता ν असल्यास ν, ν + Δν व ν-Δν अशा कंप्रतांच्या ३ रेषा दिसतील (सामान्य परिणाम). या Δν ला ‘लारमर कंप्रता’ असे म्हणतात. रूढ यमिकीनुसार, अणूचा चुंबकीय परिबल सदिश या कंप्रतेने चुंबकीय क्षेत्राच्या दिशेभोवती परांचन (परिभ्रमण अक्षाची म्हणजे चुबंकीय परिबल सदिशाची गती शंक्काकार निर्माण करते) करू लागतो व त्यामुळे रेषेचे विभाजन होते.

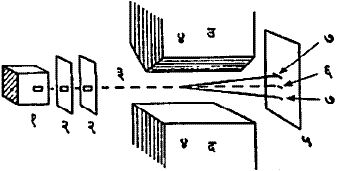स्टर्न-गेर्लाख प्रयोग : ओटो स्टर्न व वॉल्टर गेर्लाख यांनी १९२२ मध्ये प्रथम केलेल्या या प्रयोगाने लांडे गुणकाचे प्रत्यक्ष मापन करता येते. नैकविध (एकासारखे नसलेल्या ) बाह्य चुंबकीय क्षेत्रात आणवीय चुंबक ठेवल्यास त्यावर 

इतकी प्रेरणा लागू होते.  dB

                                      dz   हा क्षेत्राचा चढ सु. २५०० वेबर/मीटर³ इतका असावा लागतो. अशा क्षेत्रातून अणूंची शलाका जाऊ दिल्यास क्षेत्र रेषेच्या दिशेभोवती अणुचुंबक परांचन करू लागतील. पुंजयामिकीनुसार अणूंचे चुंबकीय परिबल सदिश, क्षेत्र रेषांशी काही ठराविक कोन करूनच परांचन करू शकतील, तर रूढ यामिकीनुसार या कोनाचे मूल्य काहीही असू शकेल. प्रयोगांती असे दिसून आले की, अणुशलाकेचे दोन वा अधिक भागांत विभाजन होते. यावरून वरील सूत्रांतील m_j काही ठराविक मूल्येच धारण करू शकतो हे सिद्ध झाले व पुंजयामिकीची सत्यता प्रस्थापित झाली.

या प्रयोगाचे संपूर्ण उपकरण निर्वात पात्रात ठेवलेले असते. प्रथमच्या प्रयोगात चांदीच्या (Ag) अणूंचा उपयोग केला होता. परंतु आता इतर कित्येक अणूंचाही या पद्धतीने अभ्यास केला गेला आहे. एका तप्त भट्टीत धातूंची वाफ करून त्यांच्या अणूंची शलाका दोन सूक्ष्म फटींच्या साहाय्याने केली जाते. ही शलाका अतितीव्र व नैकविध चुंबकीय क्षेत्रातून पलीकडे जाते व एका पडद्यावर पडते. पडद्यावर ती सारखी न पसरता काही पद्धतशीर रेषांची रचना दाखविते. या रेषांची संख्या 2J+1 असते. या रेषांमधील अंतरे मोजून त्यावरून g_j व     -m_j यांची मूल्ये काढता येतात. यासंबंधी माहिती कोष्टक क्र. ३ मध्ये दिली आहे.

अणुकेंद्रीय परिबले : अणुकेंद्रातील मूलकणांच्या परिभ्रमण व प्रामुख्याने अंगभूत परिवलनामुळे संपूर्ण अणुकेंद्राला जो कोनीय संवेग प्राप्त होतो त्याला अणुकेंद्राचे परिवलन परिवलन (I) म्हणतात. त्या संवेगामुळे अणुकेंद्राला µ हे चुंबकीय परिबल प्राप्त होते. I व J यांचा संयोग पुंज-नियमानुसार होऊन संपूर्ण अणूचा एकत्रित कोनीय संवेग F मिळतो. I चे मूल्य शून्य नसेल तर त्यामुळे अणूतील ऊर्जा-पातळ्यांच्या ऊजर्‍ांमध्ये अतिसूक्ष्म फरक पडतो. म्हणून वर्णपट-रेषांना अतिसूक्ष्म रचना प्राप्त होते. म्हणजेच, सकृद्दर्शनी एकेरी दिसणारी रेषा खरोखर अत्यंत जवळजवळ असलेल्या अनेक रेषांचा समुच्चय असतो. अतिसूक्ष्म रचनेतील रेषांची संख्या मोजून त्यावरून I काढता येतो व त्या रेषांमधील कंप्रतांतरांवरून (Δν) वरील सूत्राच्या साहाय्याने g व त्यावरून

µ चे मूल्य काढता येते. पण ही कंप्रतांतरे प्रकाशीय वर्णपटलेखकाने मोजणे मुष्किल असते. कारण त्यांची मूल्ये रेडिओ तरंगांच्या कंप्रतामूल्यांइतकी असतात. म्हणून रेडिओ तरंगांच्या ⇨ अनुस्पंदनाचा उपयोग करून g व I यांची मापने फार अचूकपणे करता येतात.

अणुकेंद्रीय चुंबकीय अनुस्पंदन : स्थिर चुंबकीय क्षेत्रात अणुकेंद्रीय चुंबक क्षेत्ररेषांभोवती विशिष्ट लारमर कंप्रतेने परांचन करीत असतो. अशा अणुकेंद्र-चुंबकावर उच्च कंप्रतेचे परंतु अल्प तीव्रतेचे प्रत्यावर्ती (आलटून पालटून दिशा बदलणारे) चुंबकीय क्षेत्र मूळच्या क्षेत्राच्या लंब दिशेने लागू केले व प्रत्यावर्ती क्षेत्राची कंप्रता हळूहळू बदलत जाऊन ती लारमर कंप्रतेइतकी झाली की, अणुकेंद्राच्या µ या सदिशाची दिशा एकदम बदलते आणि त्यासाठी लागणाऱ्या ऊर्जेचे शोषण होते. या आविष्काराला ‘अणुकेंद्रीय चुंबकीय अनुस्पंदन’ (NMR) असे म्हणतात. या तत्त्वावर आधारलेल्या प्रयोगांनी सुटे इलेक्ट्रॉन, प्रोटॉन, न्यूट्रॉन व वेगवेगळी अणुकेंद्रे या सर्वांची चुंबकीय परिबले काढता येतात. 

अणुकेंद्रीय परिवलन परिबल I व चुंबकीय परिबल µ असलेले अणुकेंद्र B तीव्रतेच्या चुंबकीय क्षेत्रात ठेवल्यास, ते B च्या दिशेभोवती

ν_L = g e  B

                4πM  

या लारमर कंप्रतेने परांचन करू लागते. अशा वेळी चुंबकीय अनुस्पंदन होण्यासाठी लावलेल्या प्रत्यावर्ती चुंबकीय क्षेत्राची कंपता f= ν_L= g e        B

                                                   4πM          असावी लागते. या सूत्रातील f व B ची मूल्ये माहीत असतील तर g चे मूल्य काढता येईल. सूत्रावरून हेही दिसते की f, B च्या समप्रमाणात असते. तेव्हा कोणतीही एक सोईस्कर f स्थिर ठेवून B चे मूल्य वाढवीत गेल्यास अनुस्पंदन मिळवता येईल. अचूक मापनाच्या दृष्टीने हीच पद्धत वापरली जाते.

रेणुशलाका-चुंबकीय अनुस्पंदन राबी-पद्धती : या पद्धतीने केवळ १०^-९ ग्रॅम इतके अल्प द्रव्य घेऊनही gचे मूल्य (०·०१ टक्के त्रुटीपर्यंत) अचूकपणे काढता येते.सर्व उपकरण (आ.३) निर्वात केलेले असते.

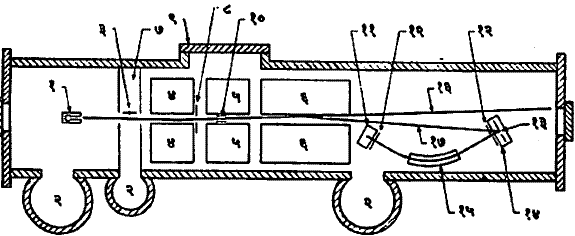तप्त भट्टीतून औष्णिक वेगाने (१०^३ ते १०^५ सेंमी. प्रतिसेकंद) विसरण पावणारे (एकमेकात मिसळणारे) अणू वा रेणू बारीक फटीतून शलाकेच्या स्वरूपात बाहेर पडतात व (४), (५), (६) या तीन चुंबकीय क्षेत्रांतून जाऊन अभिज्ञातकावर (कणाचे अस्तित्व ओळखणाऱ्या उपकरणावर) पडतात. (४) आणि (६) या दोन नैकविध क्षेत्रांची योजना अशी केलेली असते की, त्यांच्यामुळे रेणुशलाकेचे होणारे विचलन सममूल्य पण उलटसुलट असल्याने शलाका बरोबर आयनीकारक अभिज्ञातकावर केंद्रित होते. (५) हे परांचनकारक एकविध क्षेत्र असून तेथेच (१०) या तारेच्या साहाय्याने उच्च कंप्रतेचे पण अल्पमूल्य क्षेत्र, (५) ला लंबदिशेने उत्पन्न केले जाते व त्याची कंप्रता स्थिर ठेवून, (५) या क्षेत्राची तीव्रता हळूहळू वाढवत जाता शेवटी अभिज्ञातकावर पडणारी कणसंख्या किमान होते. हीच अनुस्पंदन झाल्याची खूण होय. या वेळचे (५) चे मूल्य B व ƒ यांवरून g चे मूल्य काढतात व त्यावरून Ι व μ काढली जातात, तसेच विद्युत् चतुर्ध्रुवी परिबलांचेही मापन करता येते.

घन, द्रव किंवा वायुरूप स्थितीतील पदार्थांचे अनुस्पंदन-पद्धतीने g गुणक काढण्यासाठी दोन पद्धती शोधून काढण्यात आलेल्या आहेत. पर्सेल टोरी व पाउंड यांच्या समचुंबकीय अनुस्पंदन-शोषण-पद्धतीत, अनुस्पंदनामुळे पदार्थाकडून सूक्ष्मतरंगांच्या ऊर्जेच्या होणाऱ्या शोषणावरून अनुस्पंदन झाल्याचे समजते. ब्लॉक, हानसेन व पॅकर्ड यांच्या अणुकेंद्रीय अनुस्पंदन प्रवर्तन-पद्धतीत विद्युत् प्रवर्तनामुळे उत्पन्न होणाऱ्या विद्युत् प्रेरक ऊर्जेवरून अनुस्पंदन झाल्याचे ओळखता येते.

प्रकाशीय वर्णपट-पद्धती : दोन एकविध अणूंपासून बनलेल्या रेणूंच्या वर्णपटातील रेषांच्या तीव्रतेवरूनही Ι काढता येतो.

अतिसूक्ष्म रचनेतील रेषांची सैद्धांतिक नियमांपासून होणारी च्युती (विचलन) मोजून त्यावरून विद्युत् चतुर्ध्रुवी परिबल काढता येते.

पहा: अणुकेंद्रीय भौतिकी अणु व आणवीय संरचना.

संदर्भ : 1. Evans, R. D. The Atoµic Nucleus, New York, 1955.

           2. Segre, E. G. Ed. Experiµental Nuclear Physics, Vol. I, New York, 1953.

           3.  Shankland, R. S. Atoµic and Nuclear Physics, New York, 1960.

गोडबोले, रा. द.

“