सापेक्षता सिद्धांत

सापेक्षता सिद्घांत : अवकाश व काल या दोन संकल्पनांचा एकत्रितपणे विचार करुन ⇨ॲल्बर्ट आइन्स्टाइन (१८७९–१९५५) या भौतिकीविज्ञांनी निर्माण केलेली भौतिकीची एक व्यापक उपपत्ती म्हणजे सापेक्षता सिद्घांत होय. या सिद्घांतामुळे भौतिकीतील नियमांना व्यापकत्त्व प्राप्त झाले आणि त्यामुळे भौतिकी व ⇨विश्वस्थितिशास्त्र  या ज्ञानशाखांतील महत्त्वाच्या विषयांचे विश्लेषण करणाऱ्या मूलभूत संकल्पनांवर दूरगामी परिणाम झाले.

सापेक्षता सिद्घांतांतर्गत मुख्यतः दोन उपपत्ती असून त्या आधुनिक भौतिकीचा सैद्घांतिक पाया बनल्या आहेत एक विशिष्ट ( किंवा मर्यादित) सापेक्षता सिद्घांत आणि दुसरी सर्वसाधारण (किंवा व्यापक) सापेक्षता सिद्घांत. या दोन उपपत्ती आइन्स्टाइन यांनी अनुक्रमे १९०५ व १९१५ मध्ये मांडल्या. त्यापूर्वी अस्तित्वात असलेला भौतिकी हा विषय ज्या गृहीतकांवर आधारलेला होता, त्यांपैकी अनेक गृहीतकांना आइन्स्टाइन यांनी या नव्या उपपत्तीद्वारा बाद ठरविले. त्याचबरोबर त्यांनी अवकाश, काल, द्रव्य (मॅटर), ऊर्जा, गुरुत्वाकर्षण इ. मूलभूत संकल्पनांना नव्या व्याख्या दिल्या. विशेषतः वैश्विक प्रक्रिया व सृष्टीची भूमिती समजण्यासाठी आवश्यक असा नवा पाया सापेक्षता सिद्घांतामुळे तयार झाला. या दोन्ही उपपत्तींनी भौतिकी व मानवी जीवन या दोहोंवर, मुख्यतः अणुऊर्जा व क्षेपणास्त्रे यांच्या वापराद्वारा, दूरगामी परिणाम घडवून आणला आहे.

निरनिराळे निरीक्षक निरनिराळ्या गतींनी जात असताना, त्यांचा परस्पर संदर्भात विचार केल्यास नैसर्गिक भौतिक नियम आणि मोजमापे बदलतात का व बदलत असल्यास ती कशा प्रकारे बदलतात, या प्रश्नांची उत्तरे सापेक्षता सिद्घांताद्वारा देता येतात. सापेक्षता सिद्घांताच्या स्पष्टीकरणासाठी धावणाऱ्या आगगाडीचे उदाहरण नेहमीच वापरले जाते. जमिनीवर एक बिंदू घेऊन त्याच्या संदर्भात एक आगगाडी सरळ रेषेत ताशी ७० किमी. वेगाने धावत असून त्याच धावणाऱ्या आगगाडीतील एक प्रवासी, आगगाडी जात असलेल्या दिशेनेच, आगगाडीच्या संदर्भात ताशी २ किमी. वेगाने चालत आहे असे समजा, तर त्या प्रवाशाचा जमिनीवरील त्या बिंदूच्या संदर्भात वेग काय असेल, या प्रश्नाचे उत्स्फूर्तपणे मिळणारे सरळ व स्वाभाविक उत्तर ताशी ७२ किमी. हे आहे. रुढ यामिकीमध्ये याप्रमाणे, संदर्भ-चौकटी  [⟶ संदर्भ-व्यूह] एकमेकींच्या संदर्भात एकविध गतीने प्रवास करीत असतील, तर वेग व अंतर यांची मूल्ये देणाऱ्या संख्या एका संदर्भ-चौकटीतून दुसऱ्या संदर्भ-चौकटीत बदली करता येतात. विद्युत् गतिकीमध्ये (गतिशास्त्रात) तसे करता येत नाही. वरील उदाहरणात प्रवाशाऐवजी प्रकाशाचा किरण आगगाडीतून प्रवास करीत असल्याचे समजले, तर जमिनीवर घेतलेल्या बिंदूच्या संदर्भात त्या प्रकाशकिरणाचा वेग, वरीलप्रमाणे त्या बिंदू-संदर्भातील आगगाडीचा वेग व आगगाडी-संदर्भातील प्रकाशकिरणाचा वेग यांच्या बेरजेएवढा नसतो. किंबहुना, दोन्ही संदर्भ-चौकटींसाठी तो सारखाच असतो. अमेरिकन भौतिकीविज्ञ ⇨आल्बेर्ट आब्राहाम मायकेलसन व अमेरिकन रसायनशास्त्रज्ञ ⇨एडवर्ड विल्यम्स मॉर्ली (मोर्ले) यांनी १८८७ मध्ये याबाबतीत महत्त्वाचे प्रयोग करुन वरील विधानासाठी पहिला निरीक्षणात्मक पुरावा दिलेला होता. प्रकाशाचा वेग कोणत्याही दिशेत व भ्रमणाच्या कोणत्याही अवस्थेत असलेल्या कोणत्याही संदर्भ-चौकटीसाठी एकच असतो, हे या प्रयोगाने दाखवून दिले होते – [⟶ अवकाश-काल].

पूर्वी भौतिकीमध्ये न्यूटनीय यामिकीचे जे स्थान होते, तेच स्थान आधुनिक भौतिकीमध्ये ⇨पुंजयामिकी व सापेक्षता सिद्घांत या दोन विषयांचे आहे. ज्या वेळी माफक आकारमानाच्या वस्तू माफक वेगाने फिरतात, त्या वेळी त्यांच्या गतीसंबंधी निष्कर्ष काढण्यासाठी न्यूटनीय यामिकीचा चांगला उपयोग होतो परंतु अणू व त्यांचे उपभाग यांसारख्या अतिसूक्ष्म वस्तू आणि विश्वकिरणांच्या (अवकाशातून पृथ्वीवर येणाऱ्या भेदक किरणांच्या ) कणांसारख्या अतिवेगवान वस्तू यांच्या बाबतीत निष्कर्ष काढण्यासाठी न्यूटनीय यामिकी पुरेशी पडत नाही. विसाव्या शतकाच्या सुरुवातीस या परिस्थितीचा प्रत्यय आला. निश्चितपणा ही न्यूटनीय यामिकीला केंद्रीभूत असलेली संकल्पना अतिसूक्ष्म वस्तूंच्या संदर्भात लागू पडणाऱ्या पुंजयामिकीत मानीत नाहीत आणि अतिवेगाने धावणाऱ्या वस्तूंच्या बाबतीत उपयोगी पडणारा विशिष्ट सापेक्षता सिद्घांत न्यूटनीय अभ्यासात मानलेल्या निरपेक्ष काल या संकल्पनेचा त्याग करतो.

⇨सर आयझॅक न्यूटन (१६४२–१७२७) यांनी गतिविषयक नियम व गुरुत्वाकर्षणाचा सिद्घांत मांडला आणि त्यांचा वापर करुन विश्वाचे स्वरुप कसे आहे, याची मांडणी केली. ते स्वरुप स्थिर, ठराविक व यंत्रवत होते. पुढील उदाहरणाने हे अधिक स्पष्ट होते : दोन वेगवेगळ्या घटना ( उदा., दोन भूकंप ) विचारात घ्या. त्या घटना एकमेकींपासून S अंतराने दूर असणाऱ्या ठिकाणी झाल्या असून त्यांच्या घडण्याच्या वेळेत t एवढा फरक आहे असे समजा. ‘एकविध वेगाने जाणाऱ्या प्रत्येक निरीक्षकाला (त्या प्रत्येकाच्या गतीची दिशा व वेग कोणतेही निरनिराळे असले तरी)  वरील दोन घटनांतील अंतर S व दोन घटनांतील वेळेचा फरक t हे सारखेच आढळून येतील’, या गृहीतकावर संपूर्ण न्यूटनीय भौतिकी आधारलेली आहे. अशा प्रकारे न्यूटनीय यामिकीत निरपेक्ष अवकाश व निरपेक्ष काल हे गतीचे निश्चल आहेत. विशिष्ट सापेक्षता सिद्घांताने या दृष्टिकोनात व विचारसरणीत बदल घडवून आणला.

एकोणिसाव्या शतकाच्या शेवटी न्यूटनीय यामिकी व ⇨जेम्स क्लार्क मॅक्सवेल  यांची विद्युत् चुंबकीय उपपत्ती यांच्यात वैज्ञानिक संघर्ष निर्माण झाला आणि या संघर्षात सापेक्षता सिद्घांताची बीजे आढळून येतात. विशिष्ट सापेक्षता सिद्घांताद्वारे या संघर्षाचे निराकरण करण्यात आइन्स्टाइन यांच्याप्रमाणेच डच भौतिकीविज्ञ ⇨हेंड्रिक आंटोन लोरेन्टस, ऑस्ट्रियाचे ⇨एर्न्स्ट माख आणि फ्रें च गणिती ⇨झ्यूल आंरी प्वँकारे यांचाही हातभार लागला. काही प्रमाणात लोरेन्ट्स व प्वँकारे यांचे संशोधन आइन्स्टाइन यांच्या आधीचे आहे मात्र आइन्स्टाइन यांना ते माहीत नव्हते. विशिष्ट सापेक्षता सिद्घांताचा बराचसा गणिती गाभा लोरेन्ट्स व प्वँकारे यांच्याकडून तयार झाला होता परंतु त्याला लागणारी सखोल भौतिकीय दृष्टी आइन्स्टाइन यांच्याकडून प्राप्त झाली व त्यामुळेच या सिद्घांताला त्या मानाने चटकन व सर्वदूर मान्यता मिळू शकली. प्वँकारे यांच्या दृष्टीने हा प्रश्न केवळ गणिती स्वरुपाचा होता. या नव्या सापेक्षता सिद्घांताचे श्रेय अनेकदा केवळ आइन्स्टाइन यांनाच दिले जाते परंतु प्वँकारे यांचेही नाव त्यातील महत्त्वाच्या भागाशी जोडले गेले आहे. या सिद्घांतासंबंधीच्या ज्ञानात हेर्मान मिन्कोवस्की (१८६४–१९०९) यांनीही भर घातली. त्यांनी चतुर्मितीय अवकाश-काल अखंडत्वाची (4 D स्पेस टाइम कन्टिन्युअम ) विस्तारित संकल्पना उपयोगात आणली त्यात काल-निर्देशांक व अवकाश-निर्देशांक यांना एकाच पातळीवर मानून त्यांच्या वापरात एकसारखेपणा आणला. त्यांनी विशिष्ट सापेक्षता सिद्घांताच्या समीकरणांना सुगम्य असे भूमितीय स्पष्टीकरण दिले.

व्यापक सापेक्षता सिद्घांताची मूळ मांडणी मात्र सर्वस्वी आइन्स्टाइन यांची आहे. त्यासाठी त्या वेळी नवीनच असलेल्या ⇨गेगॉऱ्यो रीत्ची-कूर्बास्त्रो  व ⇨तूल्यो लेअव्हि-चीव्हिता  यांनी निर्माण केलेल्या प्रदिश कलनशास्त्र या गणितातील विषयाला त्यांनी भौतिकीत आणले  [⟶ कलन प्रदिश]. हा गणिती विषय त्या वेळेपर्यंत पूर्ण विकसित झालेला होता व फक्त त्याचा योग्य उपयोग करणे बाकी होते. असे असले तरी त्या वेळी हा गणिती विषय तांत्रिक दृष्ट्या बराचसा कठीण, त्याचे व्यावहारिक उपयोग अतिशय कमी आणि त्याच्यावर आधारित निष्कर्षांचा पडताळा निरीक्षणातून होणे अवघड, अशा स्वरुपाचा होता.

या सर्व विवेचनाचा अर्थ असा नव्हे, की न्यूटनीय यामिकीचा आता काहीच उपयोग नाही. अभियांत्रिकी अथवा खगोलशास्त्रातील समस्या सोडविण्यासाठी उदा., मोटारगाड्या, विमाने व ग्रह यांसारख्या पुरेशा मोठ्या आकारमानाच्या वस्तू जेव्हा प्रकाशाच्या वेगाच्या तुलनेत कमी वेगाने जातात, तेव्हा त्या वस्तूंच्या संबंधातील समस्या हाताळण्यासाठी न्यूटनीय यामिकीचा चांगला व्यावहारिक उपयोग होतो. ताशी सु. ४०० किमी. वेगाने उडणाऱ्या विमानाच्या भमंतीचा अभ्यास करताना विशिष्ट सापेक्षता सिद्घांत विचारात न घेता काढलेल्या निष्कर्षात साधारणतः सु. एक टक्क्याच्या एक कोटीएवढ्या भागाइतकीच चूक होते परंतु अणुकेंद्रीय भौतिकीचा अभ्यास संपूर्णपणे पुंजयामिकी व सापेक्षता सिद्घांत यांच्यावर आधारलेला आहे.

विशिष्ट सापेक्षता सिद्घांत : ह्या उपपत्तीत गुरुत्वाकर्षण विचारात घेतले जात नाही. ही उपपत्ती निरुढीय संदर्भ-चौकटींनाच, म्हणजे ज्या संदर्भ-चौकटी एकाच ठराविक समान वेगाने सरळ रेषेत प्रवास करणाऱ्या असतात व ज्यांना प्रवेग नसतो, त्यांनाच लागू होते. निरुढीय (इनर्शिअल) चौकटीत जिच्यावर कोणतीही प्रेरणा काम करीत नाही, अशी कोणतीही वस्तू एकाच समान वेगाने एकाच सरळ रेषेत जात राहते. [ ⟶ निरुढि]. अतिवेगाने भ्रमण करणाऱ्या कणांच्या गतीचे वर्णन व इतर संबंधित प्रश्नांचा अभ्यास करण्यासाठी विशिष्ट सापेक्षता सिद्घांताचा उपयोग होतो. न्यूटनीय अभ्यासात अवकाश, काल, वस्तुमान व अंतर या संकल्पना निरपेक्ष असल्याचे मानतात. विशिष्ट सापेक्षता सिद्घांताने (१) या संकल्पना सापेक्ष असून त्या वस्तू व निरीक्षक यांच्यानुसार बदलतात, (२) वस्तूची निरपेक्ष गती ठरविणे शक्य नाही आणि (३) विश्वाच्या वर्णनासाठी अवकाश व काल यांचा एकत्रित विचार करुन मिळणाऱ्या चार-मितींची आवश्यकता आहे, हे दाखविले. या उपपत्तीनुसार प्रकाशाचा (विद्युत् चुंबकीय ऊर्जेचा) वेग तेवढा सर्व स्थितींतील व सर्व गतींतील निरीक्षकांना एकच असतो. प्रकाशाच्या वेगाशी तुलना करता गतीशी संबंधित असलेले वेग जेव्हा कमी असतात तेव्हा विशिष्ट सापेक्षता सिद्घांत आणि न्यूटनीय यामिकी या दोन्ही उपपत्ती स्वतंत्रपणे वापरुन केलेली आकडेमोड मिळतीजुळती असते.

विश्वाचे स्वरुप समजून घेण्यासाठी आइन्स्टाइन यांनी काल्पनिक (जे प्रत्यक्षात करता येतीलच असे नाही) प्रयोगांचा (इंग्रजी भाषेत थॉट एक्स्परिमेंट, जर्मन भाषेत गेडांकेन एक्स्परिमेंट) मार्ग अवलंबिला. त्यांनी हे जे ‘काल्पनिक प्रयोग’ केले, त्यांतील एक ते स्वतः सोळा वर्षांचे असताना त्यांनी आपल्या अंतःचक्षूंनी निरीक्षल्याचे म्हटले आहे. आइन्स्टाइन जाणत होते की, ⇨मॅक्सवेल विद्युत् चुंबकीय समीकरणां-नुसार निर्वात पोकळीमध्ये प्रकाशाचा वेग दर सेकंदाला ३× १०८ मी. (≈ तीन लाख किमी. = १,८६,४५१ मैल) इतकाच असतो तो कधीही व कोठेही शून्य असू शकत नाही. याचाच अर्थ असा की विद्युत् चुंबकीय नियम निरीक्षकावर अवलंबून नसतात परंतु रुढ यामिकी-नुसार सर्व निरीक्षकांना तेच नियम लागू होतात. आइन्स्टाइन यांना वाटत होते की, विद्युत् चुंबकीय उपपत्तीचे नियम सर्व परिस्थितींत सारखेच असले पाहिजेत.

वर उल्लेखिल्याप्रमाणे मायकेलसन व मॉर्ली या शास्त्रज्ञांनी क्लीव्हलँड येथील केस स्कूल ऑफ ॲप्लाइड सायन्स या संस्थेत १८८७ साली प्रयोग करुन अत्यंत काटेकोरपणे मोजमापे घेतली होती. पृथ्वीच्या भ्रमणाचा प्रकाशाच्या वेगाच्या मोजणीवर काय परिणाम होतो हे शोधण्यासाठी त्यांनी हा प्रयोग केला होता. पृथ्वीच्या गतीच्या दिशेने व त्या गतीच्या काटकोनात त्यांनी प्रकाशाचा वेग तुलनात्मक रीत्या मोजला ते दोन्ही वेग समान होते. रुढ यामिकीनुसार पृथ्वीच्या भ्रमणामुळे प्रकाशाचा वेग कमी अथवा जास्त झाला असता परंतु या प्रयोगात केलेल्या मोजणीतून असे आढळून आले की, पृथ्वीच्या भ्रमणामुळे प्रकाशाच्या वेगात काहीही बदल होत नाही तो नेहमी एकच राहतो. शिवाय दिशा कोणती आहे यावर प्रकाशाचा वेग अवलंबून नसतो तो कोणत्याही दिशेला एकच असतो. संदर्भ-चौकटीच्या गतीची स्थिती कोणतीही असली, तरी प्रकाशाचा वेग एकच राहतो हे या प्रयोगाने दाखवून दिले. या प्रयोगाचा अर्थ असाही होतो की, ‘ तत्पूर्वी मानले गेलेले प्रकाशतरंग ईथर नामक काल्पनिक माध्यमातून प्रवास करतात व त्यांची गती ही ईथरच्या संदर्भात असते’. हे गृहीतक अर्थशून्य असून प्रकाश ही संकल्पना रुढ भौतिकीने विशद करता येत नाही.

विशिष्ट सापेक्षता सिद्घांत पुढील दोन गृहीततत्त्वांवर आधारित आहे : (अ) सापेक्षतेचे तत्त्व : सर्व निरुढीय (ज्यावर कोणतीही बाह्य प्रेरणा काम करीत नाही अशा) निरीक्षकांना भौतिकीचे नियम समान असतात, म्हणजेच भौतिकीचे नियम निरनिराळ्या निरुढीय निरीक्षकांत फरक करीत नाहीत. याचाच अर्थ असा की, क व ख या निरनिराळ्या निरीक्षकांनी, मोजता येऊ शकणाऱ्या वस्तूंना लागू होणाऱ्या भौतिकीच्या नियमांसंदर्भात, आपापल्या निरुढीय सहनिर्देशक प्रणाली वापरुन लिहिलेल्या समीकरणांचे स्वरुप समान असेल. (आ) प्रकाशाच्या वेगाचे सर्वव्यापकत्त्व : सर्व निरुढीय निरीक्षकांना प्रकाशाचा वेग सगळीकडे एकच असतो. म्हणजेच कोणत्याही वेगाने गतिमान असलेल्या निरीक्षकाला निर्वात पोकळीतील प्रकाशाचा वेग समान आढळेल.

विशिष्ट सापेक्षता सिद्घांतावर आधारित काही परिणाम खालीलप्रमाणे आहेत. त्यांतील काही निष्कर्ष रोजच्या सर्वसाधारण अनुभवांना शह देणारे वाटले, तरी प्रयोगांनी ते खरे असल्याचे दाखविले गेले आहे.

(१) प्रकाशाची गती ही विश्वातील ज्ञात असलेली सर्वाधिक व निरपेक्ष गती आहे इतर कोणत्याही वस्तूला ती गती प्राप्त करता येत नाही. इतर सर्व गती सापेक्ष आहेत. मानव, बस, बंदुकीची गोळी, चंद्र, ग्रह, सूर्य, तारे इत्यादींच्या गती कोणाच्या तरी संदर्भात सापेक्ष आहेत. वस्तूची गती ठराविक गतीने जाणाऱ्या दुसऱ्या कोणत्याही वस्तूच्या सापेक्ष ठरविली गेली, तरीदेखील त्या दोघांना एकच सिद्घांत लागू पडतो (बदलत्या गतीत असलेल्या वस्तूंसाठी सर्वसाधारण सापेक्षता सिद्घांत उपयोगाला येतो).

(२) एकसामायिकता ही संकल्पना निरपेक्ष नाही. एका निरुढीय संदर्भ-चौकटीत एकसामायिक असणाऱ्या भौतिक घटना, पहिल्या चौकटीशी सापेक्ष गती असणाऱ्या दुसऱ्या निरुढीय संदर्भ-चौकटीत एकसामायिक असतातच असे नाही. म्हणजे निरीक्षकाशी निगडित नसलेली एकसामायिकता ही संकल्पना विशिष्ट सापेक्षता सिद्घांताने खरी नसल्याचे दाखविले आहे. दोन निरीक्षक एकमेकांसापेक्ष स्थिर असतील, तर त्यांची घड्याळे एकच वेळ दाखवतील परंतु त्या निरीक्षकांना एक-मेकांसापेक्ष काही गती प्राप्त झालेली असेल, तर त्यांच्या

येथे दुसऱ्याची गती पहिल्याच्या सापेक्ष x-अक्षाच्या दिशेने आहे आणि x ने दुसऱ्याचे पहिल्यापासूनचे (पहिल्याच्या संदर्भात) अंतर दाखविले आहे.

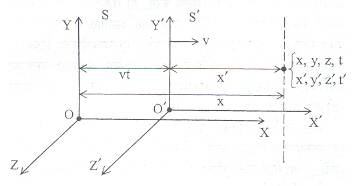
(3) कोणत्याही स्थानाचे सहनिर्देशक दोन निरुढीय संदर्भ-चौकटीत अनुक्रमे (x,y,z,) आणि (x’y’z’) असतील, तर या सहनिर्देशकांचे संबंध पुढीलप्रमाणे असतात : x’ = γ (x– vt) y’= y z’ = z.

येथे x आणि x’ अक्ष दुसऱ्या चौकटीच्या (पहिल्या चौकटीच्या सापेक्ष) गतीच्या दिशेने घेतले आहेत तर Y आणि Y’ , तसेच Z आणि Z’ या अनुक्रमे x व x ‘ दिशेला लंब असलेल्या दिशा आहेत. v ने दुसऱ्या चौकटीचा, पहिलीच्या सापेक्ष वेग दाखविला आहे γ काय आहे हे वर आले आहे t आणि t’ हे अनुक्रमे पहिल्या आणि दुसऱ्या चौकटीत स्थिर असणाऱ्या घड्याळाने दाखविलेले काल आहेत t आणि t’ यांच्यातील संबंध वर परिणाम (२) मध्ये दिलेला आहे. ही (चार) सूत्रे एका निरुढीय संदर्भ-चौकटीतून दुसऱ्या निरुढीय संदर्भ-चौकटीत सहनिर्देशकांचे रुपांतरण कसे करायचे हे दाखवितात (येथे t = t’ = 0 या काळी दोन्ही सहनिर्देशक प्रणाली एकमेकांशी तंतोतंत जुळतात असे सोयीसाठी घेतलेले आहे ). विशिष्ट सापेक्षता सिद्घांतातील वरील सहनिर्देशक रुपांतरण (लोरेन्ट्स रुपांतरण) न्यूटनीय यामिकीतील सहनिर्देशक रुपांतरणापेक्षा (गॅलिलीय रुपांतरण) वेगळे आहे.

(४) अवकाश-काल या एकत्रित संकल्पनेच्या संदर्भात निरनिराळ्या निरीक्षकांच्या बाबतीतील मोजमापांमधील संबंध रुढ (भौतिकीत घेतल्या जाणाऱ्या) संबंधापेक्षा निराळे होतात. उदा., (अ) सळईवर दोन खुणा करुन व त्यांतील एक खूण निरीक्षकाच्या संदर्भात स्थिर आहे असे समजून त्या दोन खुणांवरुन जायला लागणारा वेळ म्हणजे लांबी असे मानले, तर गती प्राप्त झालेल्या सळयांच्या गतीच्या दिशेतील लांबी कमी होते. (हे विधान कोणत्याही वस्तूंच्या सर्व आकारमानाला म्हणजेच वस्तूच्या लांबी, रुंदी, जाडी किंवा खोली या सर्वांनाच लागू पडते). (आ) निरीक्षकांच्या संदर्भात स्थिर असणाऱ्या घड्या ळांपेक्षा निरीक्षकाच्या संदर्भात ठराविक गतीने जाणारी घड्याळे हळू चालत असल्याचे जाणवते.

(५) विश्व हे अवकाश व काल यांचे एकत्रित अखंडत्व आहे. हेच वेगळ्या शब्दात मांडायचे तर दोन घटनांमधील केवळ अवकाश संदर्भातील अंतर ही कल्पना संदिग्ध आहे निरनिराळ्या निरीक्षकांच्या मोजण्यातून हे अंतर निरनिराळे मिळेल. त्याचप्रमाणे दोन घटनांमधील वेळ ही निरीक्षकाच्या गतीवर अवलंबून असेल सर्व निरीक्षकांसाठी ही वेळ एकच असणार नाही. अवकाश व काल या दोन्हींवर एकत्रितपणे आधारित दोन घटनांमधील अंतराल या संकल्पनेचे मूल्य, गती निरनिराळ्या असूनही सर्व निरीक्षकांना एकच आढळेल.

(६) वेगांच्या बेरजेचा नियम बदलतो : सुरुवातीला घेतलेल्या उदाहरणातील आगगाडी c या प्रकाशवेगाने व त्याच आगगाडीतील प्रवाशी आगगाडी जात आहे त्याच दिशेने आगगाडीच्या संदर्भात v या वेगाने जात असेल, तर आगगाडीबाहेरील एका स्थिर बिंदूच्या संदर्भात त्या प्रवाशाचा वेग न्यूटनीय यामिकीनुसार (c + v) असेल. या नियमा-नुसार v = 0 असल्याशिवाय c + v = c होणार नाही परंतु आइन्स्टाइन यांच्या उपपत्तीनुसार v = 0 नसतानाही c + v = c असते किंबहुना त्यांच्या उपपत्तीनुसार c + c = c असते. गणितात असे फक्त ∞, c, N० अशा चिन्हांनी दाखविलेल्या अनंत असलेल्या संख्यांच्या बाबतीतच घडू शकते. जसे N० + N० + N० = N० N० + c = c इत्यादी.

(७) कोणत्याही वस्तूचे ती ज्या चौकटीत स्थिर आहे त्या चौकटीत मोजले असता मिळणारे वस्तुमान वस्तुविशिष्ट अचल असते. या वस्तुमानाला वस्तूचे स्थिर वस्तुमान म्हणतात. मात्र वस्तू ज्या (निरुढीय) संदर्भ-चौकटीत स्थिर नाही त्या चौकटीमध्ये मोजले असता मिळणारे वस्तुमान चल असते आणि ते वस्तूच्या वेगानुसार वाढत जाते. याचे सूत्र m’= mγ. असे आहे. येथे m हे वस्तूचे स्थिर वस्तुमान, तर mहे ज्या चौकटीत त्या वस्तूचा वेग v आहे, तीत मोजलेले वस्तुमान असून γ ची व्याख्या वर दिलेली आहे. वस्तूचा वेग वाढून प्रकाशाच्या वेगाएवढा जसजसा होत जाईल तसतसे त्या वस्तूचे वस्तुमान अमर्यादपणे वाढत जाते  

 सापेक्षता सिद्घांतानुसार कोणत्याही भौतिक वस्तूला प्रकाशाचा वेग गाठणे शक्य नाही.  

(८) आइन्स्टाइन यांनी मांडायला सोपा, परंतु अतिमहत्त्वाचा काढलेला निष्कर्ष म्हणजे E = mc2 हे सूत्र. या सूत्रामुळे पदार्थाचे वस्तुमान किंवा द्रव्यमान (m) व त्यात दडलेली ऊर्जा (E) यांच्यातील द्वैत संपून त्यांच्यातील समतुल्यता जगापुढे आली (येथे c म्हणजे प्रकाशाचा वेग आहे). पदार्थाचे वस्तुमान व त्यातील ऊर्जा या एकाच नाण्याच्या दोन बाजू आहेत, म्हणून वस्तुमान व ऊर्जा यांचे एकमेकांत रुपांतर होऊ शकते, हे समजले. याच सूत्रामुळे अणुकेंद्राच्या विभाजनातून प्रचंड ऊर्जा बाहेर पडेल हे स्पष्ट झाले, परिणामी अणुकेंद्रीय विक्रियक आणि अणुबाँब यांची निर्मिती शक्य झाली.

 तसेच गतीला ऊर्जेची व्याख्या देणारे T = mv2 हे न्यूटनीय सूत्र T = mc2 (γ –1) असे बदलते.

आइन्स्टाइन यांनी वयाच्या सोळाव्या वर्षापासून संशोधनास सुरुवात केली, दहा वर्षांनंतर त्यांना सापेक्षता सिद्घांताची उकल झाली. त्यांच्या विशिष्ट सापेक्षता सिद्घांतामुळे शास्त्रीय जगतात खळबळ निर्माण झाली.

सर्वसाधारण सापेक्षता सिद्घांत : गुरुत्वाकर्षण कार्यरत आहे व नेहमी एकच स्थिर गती लागू नाही (म्हणजे प्रवेग काम करीत आहे) अशा परिस्थितीतील प्रश्न सर्वसाधारण सापेक्षता सिद्घांतात येतात. विशिष्ट सापेक्षता सिद्घांतात लादलेली (१) गुरुत्वाकर्षण विचारात घ्यायचे नाही व (२) निरुढीय संदर्भ-चौकट ही दोन्ही बंधने आइन्स्टाइन यांनी सर्वसाधारण सापेक्षता सिद्घांतात उठविली. अशा परिस्थितीशी संबंधित जे ‘काल्पनिक प्रयोग’ आइन्स्टाइन यांनी केले त्यांत त्यांनी असे दाखवून दिले की, ‘गुरुत्वाकर्षण क्षेत्रातील निरुढीय संदर्भ-चौकट’ व ‘प्रवेग कार्यरत असतानाची संदर्भ-चौकट’ या दोघींत फरक करणे शक्य नाही. म्हणजे एखाद्या बंदिस्त अवकाश कुपीमधील निरीक्षकाचा जेव्हा आपल्या खालील बैठकीवर दाब येतो, तेव्हा त्या दाबाचे कारण ‘तो व त्याची कुपी गुरुत्वाकर्षण क्षेत्रात स्थिर आहे ’ की ‘ त्याच्यावर व कुपीवर प्रवेग कार्य करीत आहे ’ यांपैकी कोणते हे तो सांगू शकत नाही.

विशिष्ट सापेक्षता सिद्घांतानुसार, ज्यावर कोणतीही प्रेरणा काम करीत नाही असा कण एका सरळ रेषेमध्ये त्याच ठराविक समान वेगाने पुढे पुढे जात राहतो परंतु व्यावहारिक जगात गुरुत्वाकर्षण सर्व बाजूंना असल्याने व ते सतत कार्यान्वित असल्याने प्रेरणारहित स्थिती निर्माण करता येत नाही. कोणत्याही वस्तूला, त्या वस्तूवरील इतर कोणत्याही प्रेरणेपासून परिरक्षित करता येईल परंतु गुरुत्वाकर्षणाबाबत तसे करणे अशक्य आहे. विशिष्ट सापेक्षता सिद्घांताशी निरुढीय संदर्भ-चौकट मूलभूतपणे व अविभाज्यपणे जोडलेली असून ती गुरुत्वाकर्षणाच्या अस्तित्वाशी विसंगत असल्याचे दिसून आले. विशिष्ट सापेक्षता सिद्घांत मांडून झाल्यानंतर, त्याचे गुरुत्वाकर्षण सामावून घेणाऱ्या व्यापकीकरणाची, म्हणजे सर्वसाधारण सापेक्षता सिद्घांताची मांडणी आइन्स्टाइन यांनी सुरु केली.

गुरुत्वाकर्षणाचे अस्तित्व सर्वदूर पसरलेले आणि सर्वकाळ कार्यवाहीत असल्याने ते सर्व द्रव्यांवर (वस्तुमानावर) कार्य तर करतेच, परंतु वस्तुमान आणि ऊर्जा एकच आहेत याचा अर्थ ते प्रकाशकिरणांसह सर्व ऊर्जांवरही कार्य करते. प्रकाशाच्या वेगाचे मूल्य कायम तेच असल्याने ते कधी बदलणार नाही. तेव्हा गुरुत्वाकर्षण व प्रकाश यांच्यात परस्परक्रिया कशी घडून येते हा महत्त्वाचा मुद्दा आहे. निरुढीय संदर्भ-चौकटी-मध्ये कणाच्या वेगात (म्हणजे वेगाच्या मूल्यात किंवा दिशेत) बदल झाल्याविना त्या कणावर क्रिया करणाऱ्या प्रेरणेचे अस्तित्व जाणवत नाही. म्हणजेच ‘ज्या कणावर एखादी प्रेरणा कार्य करते त्या कणाची दिशा किंवा वेग बदलतो’ या एकाच पद्घतीने प्रेरणेच्या अस्तित्वाची जाणीव होऊ शकते. गुरुत्वाकर्षणाचा प्रकाशावर असा कोणता परिणाम होतो की ज्यामुळे त्या गुरुत्वाकर्षणाची जाणीव होते. ज्या वेळी प्रकाश जड वस्तूच्या बाजूने जाईल तेव्हा त्या वस्तूच्या गुरुत्वाकर्षणामुळे तो वाकला पाहिजे. प्रकाशाच्या वेगात बदल न होता हे घडून येणे शक्य असते का? नदीच्या पाण्यात तरंगत राहून वाहत जाणारा लाकडाचा तुकडा, नदी वळण घेते त्या वेळी तुकड्याच्या आकारमानात किंवा वजनात बदल न होता तो वळण घेतो. प्रकाशाच्या बाबतीत असे घडणे शक्य असते का? प्रकाश अवकाशात पुढेपुढे जात असतो. अवकाश वाकला, म्हणजेच अवकाशाने वळण घेतले तरच प्रकाश वाकू शकेल. याचा अर्थ असा की, अतिशय जड वस्तूच्या गुरुत्वाकर्षणामुळे आजूबाजूस असलेल्या अवकाशाने वक्रता घ्यायला हवी, म्हणजे त्यामुळे प्रकाश आपोआप वळेल. सापेक्षता सिद्घांताने अवकाश व काल यांचे एकत्रीकरण केले असल्याने, गुरुत्वाकर्षणाने नुसत्या अवकाशालाच नव्हे तर अवकाश आणि काल यांच्या संयोगाला म्हणजे अवकाश-कालाला वळविले पाहिजे, अर्थात वक्रता प्राप्त करुन द्यायला पाहिजे. आइन्स्टाइन यांनी हा दृष्टिकोन विचारात घेतला. गुरुत्वाकर्षण सतत व सर्व बाजूंना अस्तित्वात असते. त्याचा प्रभाव आपल्याला पाहिजे तेव्हा थांबविणे वा सुरु करणे शक्य नसते, हे लक्षात घेऊन आइन्स्टाइन यांनी गुरुत्वाकर्षणाकडे भूमितीच्या दृष्टिकोनातून पाहून त्याला भूमितीय अर्थ दिला. त्यांनी गुरुत्वाकर्षणाचे अस्तित्व अवकाश-काल यांच्याशी संबंधित अयूक्लिडीय भूमितीशी जोडले. त्यानुसार गुरुत्वाकर्षण आता प्रेरणा मानली जात नसून ती संकल्पना अवकाश-काल या एकत्रित संकल्पनेच्या भूमितीशी एकजीव झाली आहे. वस्तुमान किंवा समतुल्य एकवटलेली ऊर्जा अवकाश-काल अखंडत्वात स्थानिक वक्रता निर्माण करते. या वक्र तेचा परिणाम म्हणून वस्तूंचे निरुढी मार्ग हे सरळरेषा नसून वक्र असतात व यासंबंधातील प्रवेग म्हणजेच गुरुत्वाकर्षण होय. म्हणजेच गुरुत्वाकर्षणाचा नियम हा आता अवकाश-कालाच्या वक्रतेपासून मिळविता येतो. अवकाश-कालाच्या वक्रतेच्या माध्यमातून गुरुत्वाकर्षणाचा अभ्यास म्हणजे सर्वसाधारण सापेक्षता सिद्घांत होय.

अशा तऱ्हेने व्यापक सापेक्षता सिद्घांत हा तत्त्वत : प्रामुख्याने गुरुत्वाकर्षणाचा सिद्घांत आहे. ‘निसर्गाचे नियम हे सर्व संदर्भ-चौकटींसाठी – त्या वेगवेगळ्या संदर्भ-चौकटींची गती कशीही असली तरी–तेच असले पाहिजेत ’ या मूलभूत गृहीततत्त्वाच्या आधारावर आइन्स्टाइन यांनी आपला विशिष्ट सापेक्षता सिद्घांत सर्वसाधारण सापेक्षता सिद्घांतात विस्तारित केला. या गृहीततत्त्वापासून सुरुवात करुन आइन्स्टाइन यांनी असे म्हटले की, ‘ संदर्भ-चौकटीच्या गतीतील बदल ( म्हणजे त्या संदर्भ-चौकटीचा प्रवेग ) कोणत्याही निरीक्षकाच्या दृष्टीने गुरुत्वाकर्षण क्षेत्राच्या त्यावर होणाऱ्या परिणामाशी समतुल्य असतो’ यालाच ‘समऐतुल्यता तत्त्व’ म्हणतात. गुरुत्वाकर्षण क्षेत्राच्या अस्तित्वामुळे मुक्तपणे खाली पडणाऱ्या वस्तू कशा खाली येतात, याचे निरीक्षण प्रथम गॅलिलीओ यांनी केले. या निरीक्षणाचा समतुल्यता तत्त्वाला पाठिंबाच मिळतो. गुरुत्वाकर्षण क्षेत्राच्या एकाच बिंदूपासून (म्हणजेच पृथ्वीच्या पृष्ठभागावरील एकाच उंचीपासून ) वातरहित वातावरणात खाली येणाऱ्या सर्व वस्तूंना त्यांचे वस्तुमान काहीही असले तरी, तोच प्रवेग अनुभवास येतो. तसे पाहता ‘ वस्तूचे वजन हे त्या वस्तूवरील गुरुत्वाकर्षणाची ओढ (प्रेरणा)’ असल्यास गॅलिलीओ यांचे वरील निरीक्षण छेद देणारे ठरते. न्यूटन यांच्या गतीच्या नियमानुसार वस्तूला मिळणारा प्रवेग त्या वस्तूवर कार्य करणाऱ्या प्रेरणेच्या प्रमाणात असतो. त्यामुळे अधिक वजनदार वस्तूवर गुरुत्वाकर्षणाची ओढ अधिक असावयास पाहिजे, म्हणून अधिक वजनदार वस्तू कमी वजनदार वस्तूहून अधिक प्रवेगाने खाली यावयास पाहिजेत असे वाटू शकते. निरनिराळ्या वजनांच्या वस्तू समान प्रवेगाने खाली येतात या निरीक्षणाने आइन्स्टाइन यांच्या लक्षात आले की, गुरुत्वाकर्षण ही प्रेरणा नसून विश्वातील द्रव्यामुळे चतुर्मितीय अवकाश-काल अखंडत्वात निर्माण झालेली विकृती आहे. मुक्तपणे खाली येणाऱ्या सर्व वस्तूंना चतुर्मितीय अवकाश-काल अखंडतेत होणारी विकृती सारख्याच प्रकारे अनुभवास येते व त्यामुळेच सर्व प्रकारच्या वस्तू सारख्याच प्रकारे खाली येत असतात. अयूक्लिडीय भूमितीच फक्त अवकाश-काल अखंडतेत होणारी विकृती सुयोग्य प्रकारे विचारात घेऊन तिचा गुरुत्वाकर्षण प्रेरणेशी संबंध प्रस्थापित करु शकते.

सर्वसाधारण सापेक्षता सिद्घांत हा आइन्स्टाइन यांच्या कल्पनाशक्तीचा व पखर बुद्घीमत्तेचा अत्युच्च आविष्कार ठरतो. सर्वसाधारण सापेक्षता सिद्घांत ही त्यासंबंधी काही पूर्वेतिहास नसताना एका व्यक्तीने निर्माण केलेली ज्ञानशाखा असून विज्ञानातील अशा प्रकारचे हे एकमेवाद्वितीय उदाहरण आहे. ज्या ज्या ठिकाणी गुरुत्वाकर्षण कार्य करते त्या त्या ठिकाणी भूमिती बदलते, हे आइन्स्टाइन यांनी दाखवून दिले. हे देखील आइन्स्टाइन यांचे विद्वत्तापूर्ण संशोधन आहे.

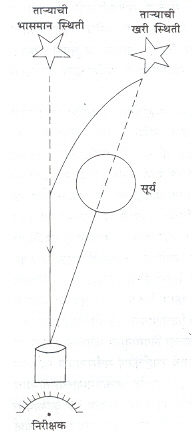
सर्वसाधारण सापेक्षता सिद्घांत जर्मन इयरबुक ऑफ फिजिक्समध्ये १९१६ मध्ये प्रसिद्घ झाला. त्याच्या असाधारणत्वामुळे साऱ्या शास्त्रीय जगाचे त्याकडे लक्ष गेले. त्या वेळी यूरोपात पहिल्या महायुद्घाचा भडका उडालेला होता. तरीदेखील लंडनच्या रॉयल सोसायटी व रॉयल ॲस्ट्रॉनॉमिकल सोसायटी या दोन विश्वविख्यात शास्त्रीय संस्थांनी आइन्स्टाइन यांच्या या दूरगामी परिणाम करणाऱ्या सिद्घांताचा पडताळा घेऊन तो खरा की खोटा (योग्य की अयोग्य) हे बघायचे ठरविले. यासाठी २९ मे १९१९ या दिवशी होणाऱ्या व उत्तर ब्राझील ते पश्चिम आफ्रिका या पट्ट्यात बराच काळ दिसू शकणाऱ्या खग्रा स सूर्यग्रहणाच्या वेळी शास्त्रशुद्घ निरीक्षण करण्यासाठी सर आर्थर स्टॅन्ली एडिंग्टन या इंग्रज खगोलशास्त्रज्ञाच्या पुढाकाराने योजना आखण्यात आली. त्या वेळेस ग्रहण लागणाऱ्या सूर्याच्या आसपास रोहिणी नक्षत्रातील ताऱ्यांचा तेजस्वी पुंजका असणार होता, हे लक्षात घेण्यात आले होते. दोन स्वतंत्र तुकड्या निरीक्षणासाठी दोन वेगवेगळ्या ठिकाणी रवाना झाल्या. एक तुकडी एडिंग्टन यांच्या नेतृत्वाखाली पश्चिम आफ्रिकेतील प्रिन्सिपी बंदरात गेली व दुसरी रॉयल ॲस्ट्रॉनॉमिकल सोसायटीचे ॲर्न्ड्यू  क्रोमेलिअन यांच्या नेतृत्वाखाली उत्तर ब्राझीलच्या समुद्रकिनाऱ्यावरील सोब्रा या बंदरावर गेली. त्यांनी ग्रहण लागलेल्या सूर्याभोवतीच्या ताऱ्यांची छायाचित्रे घेतली. त्यातून सूर्याच्या कडेने येणाऱ्या ताऱ्यांचा प्रकाश सूर्याकडे ओढला जात असल्याचे दिसून आले (आ. २). शास्त्रज्ञांनी सूर्याच्या गुरुत्वाकर्षणामुळे निर्माण झालेली सूर्याभोवतीच्या अवकाश-कालाची वक्रता मोजली. साधर्म्य दाखवून सांगायचे तर हा प्रकार असा आहे : व्यवहारात आपल्याला सूर्य पृथ्वीभोवती फिरतो असे दिसते परंतु पृथ्वी सूर्याभोवती फिरत असते हे सत्य असल्याचे आता माहीत झाले आहे. त्याचप्रमाणे प्रकाशाला वक्रता आलेली दिसते परंतु गुरुत्वाकर्षणामुळे अवकाश-कालात वक्रता निर्माण होते, हे सत्य आहे. २९ मे १९१९ या दिवशी शास्त्रज्ञांनी ही अवकाश-कालाची वक्रता मोजल्यामुळे आइन्स्टाइन यांच्या सर्वसाधारण सापेक्षता सिद्घांताला भक्कम आधार प्राप्त झाला. ६ नोव्हेंबर १९१९ या दिवशी रॉयल सोसायटीने एक जाहीर सभा घेऊन आइन्स्टाइन यांचा सिद्घांत शास्त्रीय दृष्ट्या सत्य असल्याचे जाहीर केले. आइन्स्टाइन यांनी आपल्या नव्या सिद्घांताद्वारा न्यूटन यांचे सिद्घांत पूर्णपणे बाद न ठरविता विश्वाच्या स्वरुपाची खरी ओळख होण्यासाठी त्यात कांतिकारक सुधारणा मात्र नक्कीच केल्या होत्या. १९१९ मधील वर उल्लेखिलेल्या एडिंग्टन यांच्या मोहिमेच्या यशानंतर सर्वसाधारण सापेक्षता सिद्घांत भौतिकीविद व सर्वसाधारण जनता या दोन्ही स्तरांवर लोकप्रिय झाला.

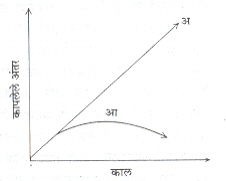
सर्वसाधारण सापेक्षता सिद्घांत हा विशिष्ट सापेक्षता सिद्घांताचे व्यापकीकरण असून अभ्यासासाठी घेतलेल्या परिस्थितीतील वेगांची मूल्ये प्रकाशाच्या वेगाच्या तुलनेत कमी असतात, तेव्हा न्यूटन यांच्या अभिजात गुरुत्वाकर्षण सिद्घांताचा त्यात सीमा-स्थितीच्या स्वरुपात अंतर्भाव होतो. गुरुत्वाकर्षण कार्य करीत असतानाच्या परिस्थितीत, सर्वसाधारण सापेक्षता सिद्घांतानुसार त्या गुरुत्वाकर्षणाचे परिणाम बाहेरुन स्वतंत्र रीत्या कार्य करणारी प्रेरणा अशा स्वरुपात न दाखविता, अवकाश-काल एकत्रितपणे घेऊन मांडलेल्या भूमितीतून येणारे अयूक्लिडीय गुणधर्म म्हणून दाखविले जातात. शिवाय सर्वसाधारण सापेक्षता सिद्घांत फार दुर्बल गुरुत्वाकर्षण कार्यरत असताना विशिष्ट सापेक्षता सिद्घांतापेक्षा वेगळा राहत नाही. उदा., समजा एक कण v वेगाने पृथ्वीच्या पृष्ठभागाला काटकोन करुन वर फेकला. पृथ्वीची गुरुत्वाकर्षण शक्ती कार्यरत नसल्याचे मानल्यास व त्या कणावर इतर कोणतीही प्रेरणा कार्य करीत नसल्यास न्यूटन यांच्या पहिल्या गतिनियमानुसार तो कण v या वेगाने सरळ रेषेत सारखा वरवर जात राहील. त्यामुळे त्या कणाने t कालानंतर गाठलेली उंची h = vt असेल परंतु g मूल्य असलेली गुरुत्वाकर्षण शक्ती तो  कण पृथ्वीच्या केंद्राकडे ओढत राहिली, तर t काळानंतर त्या कणाने गाठलेली उंची h = vt – 1/2 gt2 या सूत्राने मिळेल. त्या कणाशी संबंधित काल विरुद्घ कापलेले अंतर (= गाठलेली उंची) यांचा आलेख अन्वस्त असेल. हा अन्वस्त आइन्स्टाइन यांच्या उपपत्तीनुसार अयूक्लिडीय भूमि-तीतील सरळ रेषाच ठरतो व त्या भूमितीत हा अन्वस्त सरळ रेषेतील एकविध गती दाखवितो (आ. ३).   

न्यूटन यांच्या सिद्घांतानुसार गुरुत्वाकर्षणामुळे दोन वस्तू एकमेकींना आकर्षित करतात परंतु आइन्स्टाइन यांच्या सिद्धांतानुसार अवकाशकालाच्या वक्रतेमुळे दोन वस्तू एकमेकांकडे आकर्षित झाल्याचे वाटते.  

अशा तऱ्हेने आइन्स्टाइन यांचा सर्वऐसाधारण सापेक्षता सिद्घांत गुरुत्वाकर्षणाच्या खऱ्या अर्थावर प्रकाश टाकणारा सिद्घांत आहे. त्यानुसार (१) गुरुत्वाकर्षण ही प्रेरणा नसून ती विश्वाला आकार देणारी शक्ती ठरते. म्हणूनच असे म्हणता येईल की, न्यूटन यांनी गुरुत्वाकर्षणाचा शोध लावला आणि आइन्स्टाइन यांनी त्याचा खरा अर्थ उलगडून दाखविला. (२) यूक्लिडीय भूमितीत असलेली वक्ररेषा ही अवकाश-कालाच्या अयूक्लिडीय भूमितीत सरळरेषा ठरु शकते.

ताऱ्यांचा जन्म व मृत्यू, कृष्णविवरे आणि ग्रहांची गतिकी यांसारख्या मोठ्या प्रमाणावरच्या खगोलीय घटनांचे विश्लेषण करताना सर्वसाधारण सापेक्षता सिद्घांत वापरावा लागतो. उदा., विविध ग्रहमाला व त्यांच्याहून वरच्या दर्जाच्या ( पातळीच्या ) संरचना यांच्याविषयी भौतिकी व खगोलशास्त्र यांच्या दृष्टिकोनातून चर्चा करताना, तसेच संपूर्ण विश्वाचा जेव्हा प्रामुख्याने गुरुत्वाकर्षण व निरुढी यांच्या अनुषंगाने सम्यक् अभ्यास होतो, तेव्हा न्यूटनीय सिद्घांताऐवजी सर्वसाधारण सापेक्षता सिद्घांत उपयोगी पडतो.

गणिताचा वापर करुन सापेक्षता सिद्घांतावर आधारित काढलेल्या निष्कर्षांपैकी काही पुढे उद्धृत केले आहेत : (१) विश्वाचा सतत विस्तार होत असतो. आइन्स्टाइन यांच्या या निष्कर्षाचा पडताळा ⇨एडविन पॉवेल हबल यांनी १९१९ मध्ये प्रयोगाद्वारे घेतला. आपल्या ⇨ आकाशगंगा या दीर्घिकेच्या (तारामंडळाच्या) विस्ताराचा वेग दर सेकंदाला साधारण ९,६०० किमी. असल्याचे त्यांनी दाखवून दिले. (२) जेव्हा दूरवर असलेल्या ताऱ्यापासून निघणारा प्रकाशकिरण सूर्याच्या जवळून जातो तेव्हा तो सूर्याच्या गुरुत्वाकर्षणामुळे वाकतो. यामुळे त्या किरणाची मूळची आणि नंतरची दिशा यांच्यात १·७५ विकला = (१·७५/३६००) अंश इतका फरक पडतो. (३) बुध या गहाच्या नीचस्थानामध्ये दर शंभर वर्षांनी वर्तुळचापाच्या ४३ मिनिटांइतका फरक पडतो. बुधाची प्रत्यक्ष गती न्यूटन यांच्या नियमानुसार गणिताने काढलेल्या गतीशी जुळत नाही, त्याच्या या गतीचे स्पष्टीकरण सर्वसाधारण सापेक्षता सिद्घांतामुळे मिळाले. [⟶ बुध]. (४) प्रचंड आकारमानाच्या ताऱ्यांचे अतिशय लहान घट्ट वस्तूत पतन होते. या नव्या वस्तूला ⇨कृष्णविवर म्हणतात. त्याचे गुरुत्वाकर्षण क्षेत्र इतके प्रचंड तीव्र असते की, त्यात गेलेला प्रकाशदेखील तिथेच अडकून पडतो. (५) आइन्स्टाइन यांनी अवकाश-कालाला वक्रता असल्याचे व आपले विश्व चतुर्मितीय असल्याचे दाखवून पुढील प्रत्येक जोडीतील संकल्पनांमध्ये एकात्मता आणली : अवकाश व काल वस्तुमान व ऊर्जा ऊर्जा व संवेग भूमिती व गतिकी. आइन्स्टाइन यांनी १९१५ मध्ये रिक्त नसलेल्या अवकाश-काल संरचनेसाठी गुरुत्वाकर्षण संबंधात पुढील क्षेत्रसमीकरण मांडले :

या समीकरणाची डावी बाजू ‘अवकाश-कालाची’ भूमिती तर उजवी बाजू ‘गतिकीय भाग’ म्हणून संबोधिली जाते. या एका क्षेत्रसमीकरणात एकूण दहा द्वितीय श्रेणीच्या अरेषीय आंशिक ⇨अवकल समीकरणांचा समावेश आहे. हे समीकरण ‘आइन्स्टाइन यांचा गुरुत्वाकर्षणाचा सिद्घांत’ म्हणून ओळखले जाते. हे क्षेत्रसमीकरण अवकाश-काल एकत्रित अखंडत्वाच्या कोणत्याही बिंदूपाशी निगडित ऊर्जा अथवा वस्तुमान व अवकाश-कालाची वक्रता यांचा संबंध देते. हे समीकरण तयार करण्यासाठी आइन्स्टाइन यांनी अशा प्रत्येक बिंदूशी अवकाश-कालाच्या वक्रतेसहित भूमितीय गुणधर्मांशी संबंधित दहा फलांचा एक संच (मेट्रिक प्रदिश) आणि भौतिक गुणधर्मांशी संबंधित दहा फलांचा दुसरा संच (ऊर्जा प्रतिबल प्रदिश) जोडला.

‘कोणत्याही प्रेरणेचा परिणाम नसताना स्वतंत्रपणे खाली पडणारी वस्तू अल्पांतरी मार्ग घेते’ (हा मार्ग दोन बिंदूंतील कमीत कमी अंतर असते. अवकाश-काल जेव्हा वक्र असतो तेव्हा हे अंतर सरळरेषा नसते). हा नियम व वरील क्षेत्रसमीकरण मिळून सर्वसाधारण सापेक्षता सिद्घांत बनतो.

योग्य अशी काही गृहीतके घेतल्यावर आइन्स्टाइन यांच्या या क्षेत्रसमीकरणावरुन न्यूटन यांचा गुरुत्वाकर्षणाचा नियम मिळतो. म्हणजेच कमी वेग व दुर्बल क्षेत्र कार्यरत असताना न्यूटन यांचा गुरुत्वाकर्षणाचा नियम हा आइन्स्टाइन यांच्या सर्वसाधारण सापेक्षता सिद्घांताचा विशिष्ट प्रकार होतो. एका अर्थाने आइन्स्टाइन यांनी निरुढी व गुरुत्वाकर्षण या दोन संकल्पनांमध्ये दडलेल्या, परंतु अभिप्रेत असलेल्या समतुल्यतेचा शोध घेऊन सापेक्षतेचा सर्वसाधारण सिद्घांत मांडला. म्हणून त्याला न्यूटन यांच्या गुरुत्वाकर्षण सिद्घांताचे सापेक्षता संकल्पनेवर आधारित व्यापकीकरण असे काहीजण मानतात.

पहा : अवकाश-काल ईथर–२ गुरुत्वाकर्षण गुरुत्वीय अवपात निरुढि पुंजयामिकी पुंज सिद्घांत पुंजक्षेत्र सिद्घांत प्रकाशवेग भौतिकी.

संदर्भ : 1. Narlikar, Jayant, A Cosmic Adventure, pune, 2000.

         2. Narlikar, Jayant,General Relativity and cosmology, new Delhi 1978.  

         3. Resnik, Robert,Introduction to special Theory of Relativity, Wiley Eastern, 1979.

टिकेकर, व. ग.

“