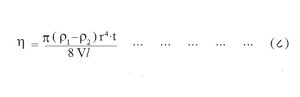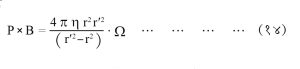श्यानता

श्यानता : (व्हिस्कॉसिटी). कोणताही द्रायू (द्रव किंवा वायू) क्षितिजसमांतर पातळीत एखादया पृष्ठभागावरून स्थिर वेगाने वाहत असेल तर त्या द्रायूच्या विविध थरांमधील अंतर्गत घर्षण प्रेरणा त्या गतीला विरोध करू लागतात. या अंतर्गत घर्षण प्रेरणेलाच द्रायूची श्यानता असे म्हणतात. श्यानतेच्या व्यस्तांकाला प्रवाहिता (फ्ल्यूइडिटी) असे म्हणतात.

द्रव स्थिर वेगाने वाहत असताना त्याच्यातील वेगवेगळ्या थरांचे वेग वेगवेगळे असतात. गतिमान द्रवातील अ आणि आ हे लगतचे दोन थर आ. १ मध्ये सुटे करून दाखविले आहेत. अ हा आ पेक्षा जास्त वेगाने वाहत असल्याने त्यांच्यातील घर्षणजन्य प्रेरणा अच्या गतीला विरोध करू लागते. आ च्या पुढील लगतचा थर त्याच्यातील अशाच प्रेरणेने आ च्या गतीला विरोध करतो. अशा प्रकारे अंतर्गत घर्षणजन्य प्रेरणा द्रवाच्या गतीला विरोध करते. श्यान प्रेरणा (घर्षणजन्य प्रेरणा) निर्माण होण्यासाठी द्रवाच्या दोन लगतच्या थरांमध्ये सापेक्ष गती असणे आवश्यक असते.

द्रवामध्ये आंतर-रेणवीय समाकर्षण प्रेरणेमुळे श्यानतेची निर्मिती होते. या प्रेरणा बाह्य रीतीने द्रवाला गती देणाऱ्या कोणत्याही प्रेरणेला विरोध करतात व त्यातून श्यानतेचा आविष्कार होतो. वायूमध्ये वेगवेगळ्या वेगाने गतिमान असलेल्या वायूंच्या भागातील रेणूंची देवाणघेवाण प्रवाहास विरोध करण्याला म्हणजे श्यानतेला कारणीभूत ठरते.

प्रतल आणि संक्षुब्ध प्रवाह : द्रव किंवा वायू रूपातील पदार्थांमध्ये दोन प्रकारचे प्रवाह असतात : (१) प्रतल किंवा प्रवाहरेखानुसारी प्रवाह, (२) संक्षुब्ध प्रवाह. प्रतल प्रवाहात थरांच्या श्रेणीच्या स्वरूपात द्रायू गतिमान असतात. प्रत्येक थर त्याच्या लगतच्या थरापेक्षा अधिक अगर कमी वेगाने वाहतो, म्हणजेच दोन थरांमध्ये वेग विक्षेपक असतो आणि द्रायू सुव्यवस्थित प्रकारे गतिमान राहतो. द्रायूचे कण ज्या मार्गांनी वाहत जातात, त्या मार्गांना प्रवाहरेखा म्हणतात. प्रवाहरेखेच्या स्पर्शिका प्रवाहाची दिशा दाखवितात. प्रतल प्रवाहाच्या प्रवाहरेखा एकमेकीस समांतर असतात. म्हणून प्रतल प्रवाहाला प्रवाहरेखानुसारी प्रवाह असेही म्हणतात. प्रतल प्रवाहाचा वेग क्रांतिक मर्यादेहून जास्त वाढल्यास प्रवाहरेखा विस्कळीत होतात. अशा प्रवाहाला संक्षुब्ध प्रवाह म्हणतात. ही वेगमर्यादा स्वरूपावर विशेषत: श्यानतेवर अवलंबून असते.

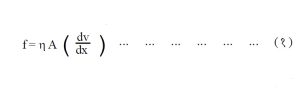
न्यूटन यांचे श्यानता सूत्र : प्रतल प्रवाही द्रवातील अंतर्गत घर्षणजन्य प्रेरणेचे मूल्य निर्धारित करण्याचे सूत्र आयझॅक न्यूटन यांनी सुचविले. त्यांच्या गृहिताप्रमाणे द्रवाच्या पृष्ठभागाचे क्षेत्रफळ, वेगप्रवणता आणि श्यानता गुणांक यांच्या गुणाकाराइतके घर्षणजन्य प्रेरणेचे मूल्य असते.

प्रतल प्रवाही द्रवाच्या A क्षेत्रफळांच्या दोन थरांमध्ये (किंवा पातळ्यांमध्ये) वेगप्रवणता राखण्यासाठी लागणारे कर्षण बल न्यूटन यांच्या समीकरणातून व्यक्त होते. (आ. १).

η या समानुपाती स्थिरांकाला श्यानता गुणांक अथवा गुणक म्हणतात. त्याचे परिमाण वस्तुमान x (लांबी) ^-१ (काल) ^-१ असून सेंमी.-ग्रॅम-सेकंद प्रणालीतील श्यानतेचे एकक पॉईज (१ ग्रॅ.से.मी. ^-१ से. ^१) आहे. याच्या आधारे श्यानता गुणांकाची सोपी व्याख्या पुढीलप्रमाणे करता येईल : द्रव अथवा वायू पदार्थाच्या एक एकक अंतरावरील दोन थरांमध्ये एक एकक सापेक्ष वेग राखण्यासाठी लागणाऱ्या दर एकक क्षेत्रफळावरील स्पर्शरेखीय बलास त्या द्रवाचा अथवा वायू पदार्थाचा श्यानता गुणांक म्हणतात. आंतरराष्ट्रीय SI परिमाण प्रणालीत श्यानतेचे एकक १० पॉईज बरोबर आहे.

प्रमाणित तापमान आणि दाबाखाली (२७३ के., १ वातावरणीय दाब) नायट्रोजन, ऑक्सिजन इ. साध्या वायूंची श्यानता १०० ते २०० मायक्रोपॉईज असते. या तुलनेत २०º से. तापमानाला पाणी, एथिल अल्कोहॉल, पारा इ. साध्या द्रवांची श्यानता १०० पट असते.

साधे वायू आणि द्रवामधील प्रतल आणि प्रवाहरेखीय प्रवाहाची वैशिष्टये समी. (१) शी तंतोतंत जुळत असल्याने त्यांना न्यूटनीय द्रायू असे म्हणतात. यांच्यात बाह्यप्रेरणा लावताच लगेच प्रवाह सुरू होतो. चिकण-माती, जिलेटीन, आगर, रक्त, शाई अथवा द्रव स्फटिक इ. पदार्थांची श्यानता व वैशिष्ट्ये न्यूटन सूत्राद्वारे वर्णन करता येत नसल्याने त्यांना अन्यूटनीय द्रायू म्हणतात. या प्रकारच्या द्रायूंना एका विशिष्ट किमान मूल्याची बाह्यप्रेरणा लावल्यानंतरच त्यांचा प्रवाह सुरू होतो.

स्टोक्स यांचा श्यानता नियम : ⇨सर जॉर्ज गेब्रिएल स्टोक्स यांनीअसे दाखवून दिले की, श्यानता गुणधर्म दर्शविणाऱ्या स्थिर माध्यमातून (द्रायूतून) एखादया पदार्थाचे चलन होत असेल, तर त्याच्या सभोवतालच्या द्रायूचेही त्यामुळे चलन होते. त्या पदार्थापासून दूर असणाऱ्या द्रायूचे विविध थर मात्र स्थिर अवस्थेतच राहतात. याचाच अर्थ स्थिर द्रायूतून एखादया पदार्थाचे चलन होते, तेव्हा त्या पदार्थाच्या लगतच्या थरामध्ये सापेक्ष गती निर्माण होते आणि द्रायूच्या श्यानतेमुळे त्या पदार्थावर विरोधी प्रेरणा कार्य करू लागते. स्टोक्स यांनी कर्षण बलाचे मूल्य देणारे खालील गणितीय सूत्र मांडले.

f = 6 π η r.v …    …    ….    ….   (२)

या सूत्रास स्टोक्स नियम असे म्हणतात. वरील सूत्रामध्ये f = ऋण-प्रवेगीय बल (विरोधी प्रेरणा), η = श्यानता गुणक, r = द्रवातून चलन होणाऱ्या पदार्थाची त्रिज्या, v = अंतिम वेग दर्शवितात.

वायूच्या श्यानतेचा रेणवीय मूलाधार : वायूमधील समांतर पातळीतील थर वेगवेगळ्या वेगाने प्रवाहित असतात. या थरांमध्ये होणाऱ्या संवेग संकमणामुळे अंतर्गत घर्षण प्रेरणा अर्थात ‘श्यानता ‘ निर्माण होते. या प्रकियेमध्ये दिशायुक्त ऊर्जेचे अवतरण होऊन तिचे यदृच्छ ऊष्मीय ऊर्जेत रूपांतर होते.

वायूंचे रेणू टणक गोलकाप्रमाणे आहेत, असे मानून वायुविषयक चलत्-रेणू-सिद्धांताव्दारे रेणूंचा सरासरी वेग व वायूची श्यानता यांच्यातील संबंध गणितीय समीकरणाव्दारे मांडता येतो. या पद्धतीमध्ये वायूतील रेणूंचा माध्य मुक्त पथ λ हा आ. १ मध्ये दर्शविल्याप्रमाणे x बरोबर असून A क्षेत्रफळाचे दोन परिकल्पित थर  v आणि v’ या वेगाने प्रवाहित आहेत. दोन थरांतील रेणूंच्या देवाणघेवाणीमुळे

¹/₃ Anc (mv-mv’ ) …    …    …    (३)

इतका नक्त संवेग दर सेकंदाला संक्रमित होतो. या ठिकाणी n ही रेणूंची संख्या आणि m हे त्यांचे वस्तुमान गृहीत धरले असून mv आणि mv’ हे

येथे d हा रेणूचा सरासरी व्यास आहे. वरीलपेक्षा जास्त अचूक गणित केल्यास समी. (६) मधील ^१/_३ संख्येबद्दल ०.४९९ संख्या येते. तथापि फलन स्वरूपी इतर रूप बदलत नाही. समी. (६) वरून वायूची श्यानता वायूवरील दाबाशी निरवलंबी व निरपेक्ष तापमानाच्या वर्गमूळाच्या समानुपाती असते. अर्थात हे अनुमान मर्यादित तापमान व दाब या बाबतीत सुसंगत आहे, असे प्रयोगाने सिद्घ झाले आहे. समी. (६) चा उपयोग करून वायूची श्यानता माहीत असल्यास रेणूच्या व्यासाचे विगणन करता येते.

साध्या द्रवांची श्यान वैशिष्ट्ये : साध्या द्रवांतदेखील कर्षण थरामधील संवेग संकमणामुळे श्यान वैशिष्ट्ये दिसून येतात.द्रवामध्ये माध्य मुक्त पथाला विशेष अर्थ नसल्याने त्यांच्यासाठी समी. (६) प्रमाणे सुलभ समीकरण अस्तित्वात नाही. द्रवाची श्यानता वाढत्या तापमानाला मोठया प्रमाणात घटते. साध्या द्रवाच्या श्यानतेचे व तापमानाचे परस्परावलंबन वायुविषयक ‘चलत् – रेणू’ सिद्धांताशी संबंधित नसून समी. (७) मध्ये दर्शविल्याप्रमाणे घातीय स्वरूपाचे असते.

वरील समीकरणामध्ये A आणि B द्रवाचे विशिष्ट प्रचल असून त्याचे मूल्य तापमानाच्या मर्यादित पल्ल्यात स्थिर असते. R =८.३१४ ज्यूल मोल हा वायू स्थिरांक आहे. द्रवांमधील विसरण प्रकियेप्रमाणेच श्यान प्रवाह ही गुंतागुंतीची प्रकिया असून तीत अनेक रेणू भाग घेतात.

द्रवावरील दाब आणि श्यानता या दोहोंमधील संबंध वायूमधील तशा संबंधापेक्षा खूपच वेगळ्या प्रकारचा असतो. कमी घनतेला वायूमध्ये हा संबंध जवळजवळ नसतोच. उच्च् जलस्थित प्रेरणेला द्रवाची श्यानता सर्वसाधारणपणे वाढते. प्रतल प्रवाहाला मात्र न्यूटन समीकरण अचूकपणे लागू पडते. यावरून असे अनुमान काढता येते की, कर्षण थरामध्ये संवेग संकमण होताना रेणूंच्या गतीमध्ये उच्च् श्रेणीचा परस्परान्वय असतो. दिलेल्या त्रिज्येच्या नळीमध्ये जेव्हा द्रवाच्या प्रवाहाचा वेग सीमित मूल्यापेक्षा वाढतो, तेव्हा प्रवाहरेखीय प्रवाहाचे संक्षुब्ध प्रवाहात रूपांतर होते. ‘r’ त्रिज्येच्या नळीत संक्षुब्ध प्रवाहाची सुरूवात होण्याचा निकष म्हणजे

‘रेनॉल्ड संख्या ‘ (2 rpv/η) सीमित मूल्यापेक्षा जास्त होते.

श्यानता आणि तापमान : द्रवाची श्यानता तापमानावर अवलंबून असते. तापमान वाढविले, तर श्यानता वाढते व कमी केल्यास ती कमी होते. अत्यंत कमी तापमानाला द्रवाची श्यानता शून्य असते. द्रवाचा प्रवाह घर्षणमुक्त असल्यास त्यास अतिप्रवाहिता म्हणतात. वातावरणाच्या दाबाखाली ४.२१६ के. तापमानाला हीलियम वायूचे द्रवात (हीलियम-I ) रूपांतर होते. त्याच्यापुढे जर द्रवरूप हीलियमाचे तापमान कमी केले, तर २.१८६ के. (लँब्डा पॉइंट) तापमानाला त्याचे रूपांतर द्रवरूप हीलियम-II मध्ये होते. द्रवरूप हीलियम-II याचे गुणधर्म असाधारण आणि चित्रविचित्र आढळतात यामध्ये अतिप्रवाहिता आढळते व जसजसे त्याचे तापमान वाढत जाईल, तसतसे त्याचे रूपांतर साधारण द्रवरूप हीलियम-I मध्ये होते.

श्यानतेचे मापन : नळीतून द्रव वाहताना नळीच्या कडांच्या संपर्कातील द्रव स्थिर राहतो आणि नळीच्या मध्यावर प्रवाहाचा वेग महत्तम असतो. या गृहिताचा उपयोग करून अरूंद नळीतून प्रतल प्रवाहाने वाहणाऱ्या द्रवाची श्यानता काढण्याचे सूत्र फ्रेंच क्रियावैज्ञानिक झां ल्‌वी मारी प्वाझय (पॉयसुली) यांनी शोधून काढले. पुरेशा लांबीच्या अरूंद नळीतून वाहणाऱ्या द्रवाची प्रतल प्रवाहाची वैशिष्ट्ये प्वाझय यांनी मांडलेल्या पुढील समीकरणातून व्यक्त होतात :

या समीकरणात η - द्रव पदार्थाची श्यानता (पॉईज किंवा किग्रॅ. मी.-१ से.^-१₎, r – नळीची त्रिज्या (सेंमी. किंवा मी.), l  – नळीची लांबी (सेंमी. किंवा मी.), (p₁ – p₂)  नळीच्या टोकांमधील दाबांतर (डाईन सेंमी.^-२ किंवा पास्कल) आणि V – नळीतून t सेकंदात वाहणाऱ्या द्रवाचे घनफळ आहे. या समीकरणाचा वापर करून द्रव किंवा वायू पदार्थाच्या श्यानतेचे निरपेक्ष मापन करता येते.

द्रवाची सापेक्ष श्यानता मोजण्यासाठी ‘ओस्टव्हाल्ट श्यानतामापक’ किंवा गोलक पतन श्यानतामापकाचा उपयोग करतात.

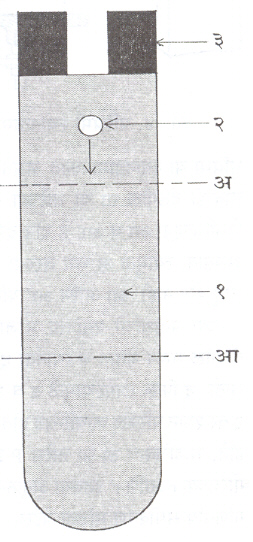
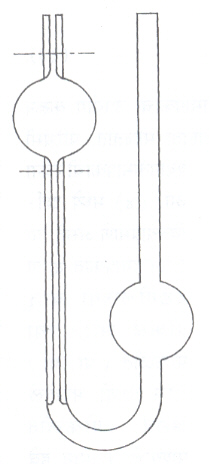ओस्टव्हाल्ट श्यानतामापक : यात पुरेशा लांबीच्या केशनलिकेने जोडलेले दोन काचेचे फुगे असलेली नळी असते (आ.२). उंच फुग्यात दोन खुणांमधील रिक्त जागेत मावेल एवढाच द्रव भरतात व त्याची पातळी खुणांबरोबर अचूकपणे ठेवतात. प्रयोगमापन सुरू करताना गुरूत्वाकर्षणामुळे द्रव केशनलिकेतून वाहू लागतो व त्याची वरील पातळी खाली येऊ लागते. ती पातळी खालच्या खुणेपर्यंत येण्यास लागणारा वेळ (t₁) मोजतात. नंतर श्यानता माहीत असलेला द्रव उंच फुग्यात भरून हाच प्रयोग पुन्हा करतात व लागणारा वेळ (t₂) मोजतात. खालील सूत्र वापरून माहीत नसलेल्या द्रवाची श्यानता मोजतात.

या सूत्रात p₁ आणि p₂ या दोन्ही द्रवाच्या घनता गृहीत धरल्या असून t₁आणि t₂ म्हणजे त्यांना अनुकमे लागणारा वेळ आहे.

गोलक पतन श्यानतामापक : या श्यानता-मापकाचे कार्य हे स्टोक्स यांच्या नियमावर आधारित आहे. कोणत्याही पदार्थाचे श्यान द्रवात मुक्त पतन होत असताना पदार्थ प्रथम प्रवेगित होतो. पदार्थावरील गुरूत्वाकर्षणाला ऊर्ध्व दिशेतील श्यान बल आणि उत्प्रणोदन तोलून धरतात. त्यामुळे नंतर पदार्थाचे पतन स्थिर वेगाने होऊ लागते. या स्थिर वेगाला ‘अंतिम वेग ‘ म्हणतात. अंतिम वेगावरून द्रवाची श्यानता ठरविता येते.

r त्रिज्या असणाऱ्या गोलकाचे v या स्थिर वेगाने η श्यानतेच्या द्रवाच्या पुरेशा उंचीच्या उभ्या स्तंभातून (आ. ३) पतन होताना गोलकावरील घर्षणजन्य प्रेरणा स्टोक्स नियमाप्रमाणे पुढील सूत्राने व्यक्त होते :

f = 6 π η v. r …    …   …  (१०)

त्याचप्रमाणे गोलकाचे पतन होत असताना त्याच्यावरील गुरूत्वाकर्षण प्रेरणा पुढील समीकरणाव्दारे निश्चित करता येते :

f¹ = ⁴/₃ π r³ (p-p’) g …  …  (११)

गोलकाचे जेव्हा स्थिर वेगाने पतन सुरू होईल, तेव्हा वरील दोन्ही प्रेरणांचे मूल्य सारखे होऊन ते परस्परविरोधी राहील. तेव्हा अशा वेळी समीकरणे (१०) आणि (११) यांचा वापर करून द्रवाची निरपेक्ष श्यानता पुढील समीकरणाव्दारे काढता येईल :

याच पद्धतीचा वापर करून सापेक्ष श्यानता काढण्यासाठी ज्याची श्यानता काढावयाची आहे असा एक द्रव आणि श्यानता माहीत असलेला दुसरा संदर्भ द्रव घेतात. या दोन्ही द्रवांच्या स्तंभांतून तंतोतंत सारख्या दोन गोलकांना समान अंतरातून पतन होण्यास लागणारा वेळ अचूकपणे मोजल्यास ओस्टव्हाल्ट यांच्या श्यानतामापकाप्रमाणे पुढील समीकरणाचा वापर करून सापेक्ष श्यानता काढता येते :

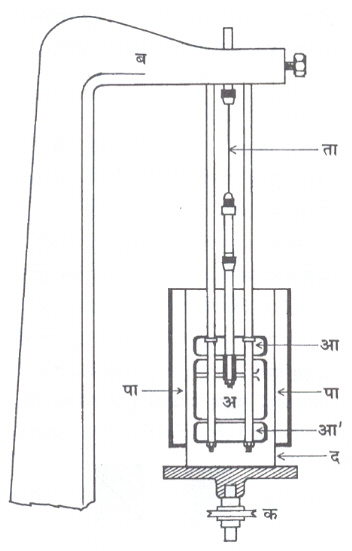
परिभ्रमी श्यानतामापक : परिभ्रमी श्यानतामापकाचा उपयोग करून विविध तापमानाला द्रव व वायू पदार्थाची श्यानता मोजतात. परिभ्रमी श्यानतामापकाची रचना आ. (४) मध्ये दर्शविल्याप्रमाणे असते. या श्यानतामापकात द या दंडगोलाच्या बाजू पोकळ असून त्या पोकळीत (पा, पा) गरम पाणी भरलेले असते. पोकळीत पाण्याचे तापमान हवे त्या प्रमाणात कमी-जास्त करता येते. द हा क या कप्पीस घट्टपणे जोडलेला असतो. द हा दंडगोल विद्युत् चलित्राच्या साह्याने इष्ट त्या कोनीय वेगाने फिरविण्याची सोय आणि कोनीय वेग मोजण्याची सुविधा या श्यानतामापकात असते. द दंडगोलाच्या आतमध्ये अ हा एक लाकडी दंडगोल ता या तारेच्या साहाय्याने टांगलेला असतो. त्याच्या दोन्हीबाजूंना आ व आ’ हे दोन दंडगोल अ च्या अगदी लगत बसविलेले असतात. त्यामुळे अ च्या वरच्या व खालच्या पृष्ठभागावर श्यान परिबल लागू होत नाही. आ आणि आ’ यांना संरक्षण दंडगोल असे म्हणतात.

ज्या पदार्थाची श्यानता मोजावयाची असेल, त्या पदार्थाने द हा दंडगोल भरून घेतात व त्यानंतर द हा ‘ Ω’ या कोनीय वेगाने फिरविला जातो. द फिरू लागल्यामुळे द व अ यांमधील पदार्थ प्रवाही होतो आणि द वर श्यान परिबल कार्यान्वित होते. त्यामुळे झ या कोनातून अ चे विचलन होते. साहजिकच ता या तारेस P इतका पीळ बसतो. अ व द या दंडगोलाच्या r आणि r’ इतक्या अनुकमे त्रिज्या असतील, तर खालील प्रकारचे गणितीय समीकरण मांडता येईल.

या समीकरणामध्ये B हा ता या तारेचा  स्थिरांक असून त्याचे मूल्य तारेची दृढता, लांबी तसेच त्या तारेची त्रिज्या इ. गोष्टींवर अवलंबून असते. अशा रीतीने समी. (१४) चा वापर करून परिभ्रमी श्यानतामापकाने एखादया द्रवाची श्यानता मोजता येते.

जटिल द्रवांच्या प्रवाह प्रवृत्ती : न्यूटनीय द्रायूंच्या प्रवाह गुणधर्माहून खूप भिन्न प्रवाह गुणधर्म असणारे पुष्कळ द्रव पदार्थ आहेत. त्यांचा अभ्यास साधारणपणे स्रोतशास्त्रात केला जातो. एकनताक्ष गंधकाच्या रेणूमध्ये आठ अणूंचे गोल कडे असते. हा रेणू ९५.५º से. तापमानाला वितळून त्याचे साध्या द्रवात रूपांतर होते. त्याची श्यानता ही साध्या (न्यूटनीय) द्रवाप्रमाणे कमी असते. तापमान वाढविल्यावर श्यानता घटते हे गुणधर्म साध्या द्रवांमध्ये असतात परंतु १६०º ते १८०º से. तापमानांदरम्यान या पदार्थाची श्यानता विलक्षण नाट्यपूर्ण रीत्या कित्येक पटींनी वाढते. या तापमानांदरम्यान रेणूतील अणूंचे गोलकडे उलगडून त्यावर लांब साखळीच्या बहुवारिकांची रचना तयार होते. तापमान १८०º से.पेक्षा जास्त झाल्यावर श्यानता पुन्हा कमी होते. कारण ऊष्मीय ऊर्जेमुळे लांब साखळी भंगून तिचे लहान भाग बनतात. ही किया अपरिवर्तनीय असल्याने गंधकाची वाफ थंड करूनच स्फटिकी गंधक मिळविता येतो.

तैलीय किंवा जलीय माध्यमातील घन पदार्थाच्या कलिली विकरणाची श्यानता जास्त असते परंतु स्थिर तापमानाला ढवळत ठेवल्यावर ती कमी होते आणि कर्तन बल कमी केल्यावर पुन्हा जास्त श्यानतेच्या पूर्वस्थितीवर जाते. हा आविष्कार प्रामुख्याने घन स्वरूपातील रंगद्रव्ये असणाऱ्या रंगामध्ये प्रामुख्याने आढळतो.

सस्तन प्राण्यांच्या शरीरातील रक्तवाहिन्यांमधील रक्ताचा प्रवाह अन्यूटनीय असतो आणि त्याला प्वाझय समी. (८) लागू पडत नाही. रक्तातील तांबड्या पेशी आणि इतर निलंबित द्रव्यांमुळे काहीसा हा गुणधर्म येत असला तरी हा आविष्कार फार गुंतागुंतीचा आहे.

काच हा अस्फटिकी घन पदार्थ असून रचनात्मक दृष्ट्या स्फटिकापेक्षा द्रवाला जवळचा आहे. दीर्घकाळ दाबाखाली ठेवल्यास सामान्य तापमानालादेखील काचेचा आकार बदलता येतो. तापमान मृदूकरण बिंदूपर्यंत वाढविल्यास तिची श्यानता कित्येक पटींनी बदलते. साधे द्रव साधारणपणे कर्तन बलाला समांतर दिशेत वाहतात, परंतु कर्तन बलाला असमांतर दिशेत प्रवाहित होणारे काही असंगत द्रव पदार्थ अस्तित्वात आहेत. असे द्रव विषमदिक् (अनआयसोट्रॉपिक) असून त्यांचे प्रवाही गुणधर्म प्रदिश (टेन्सॉर) असतात.

पहा : द्रायुयामिकी.

संदर्भ : 1. Acheson, D. J. Elementary Fluid Dynamics, 1990.

2. Curle, N. Davis, H. J. Modern Fluid Dynamics, Vol. 1., Incompressible Flow, 1968.

3. Massey, B. S. Mechanics of Fluids, 1983.

4. Mathur, D. S. Elements of Properties of Matters, 1982.

5. Sen Gupta, R Chatterjee, H. A Treatise on General Properties of Matter, Vol. I &amp II., Calcutta, 1981.

पुरोहित, वा. ल.; बोटे, शशिकांत रा.