उष्णता

उष्णता : उष्णतेची जाणीव स्पर्शाने होऊ शकते; उष्णतेमुळे पदार्थात होणाऱ्या रंगातील व आकारातील फेरबदलामुळे तिच्या तीव्रतेचा अंदाज करता येतो.

पाण्यास हळूहळू उष्णता दिली म्हणजे त्याचा कढतपणा वाढत जातो किंवा त्यातून उष्णता काढीत गेल्यास त्याचा थंडपणा वाढत जातो, हा अगदी नेहेमीचा अनुभव आहे. कढतपणाचा किंवा थंडपणाचा अंदाज स्थूलमानाने स्पर्शाने ठरवता येतो, हा अंदाज म्हणजे पाण्याच्या निरनिराळ्या वेळी असणाऱ्या औष्णिक स्थितींतील फरक होय. कढतपणाची किंवा थंडपणाची कल्पना अगदी मूलभूत आहे; किंबहुना कढतपणाची किंवा थंडपणाची स्थिती म्हणजेच तापमान अशी व्याख्या करतात. तापलेला पदार्थ थंड पदार्थावर ठेवला असता काही वेळाने दोन्हीही पदार्थांचे तापमान सारखेच होते, पण पाहिल्या पदार्थाच्या तापमानापेक्षा कमी झालेले आढळते; यावरून उष्णता, तापलेल्या पदार्थातून म्हणजे उच्च तापमानातून, थंड असलेल्या पदार्थाकडे म्हणजे नीच तापमानाकडे वाहते असा निष्कर्ष निघतो. यावरून तापमान हे उष्णता वहनाचे गमक आहे असे म्हणता येईल.

दोन पदार्थ एकमेकांस चिकटवून ठेवल्यास त्यांची औष्णिक स्थिती (तापमान) कालांतराने एकसारखी होते; म्हणजेच त्यांचे तापमान एकसारखे होते. तसेच एकाच औष्णिक स्थितीतील दोन पदार्थ तिसऱ्या पदार्थाच्या सान्निध्यात ठेवल्यावर त्या सर्वांची औष्णिक स्थिती एकसारखी असल्याचे आढळून आल्यास तिन्ही पदार्थांचे तापमान एकच आहे, असे ठरवता येते. या गृहीतावर व प्रायोगिक आधारावर तापमापकाची उभारणी झाली आहे.

सारख्याच तापमानाचे पदार्थ सारखीच उष्णता धारण करतील असे मात्र नाही. उदा., कढत पाण्याच्या भांड्यातून थोडे चमचाभर पाणी काढल्यास, भांड्यातील व चमच्यातील पाण्याचे तापमान सुरुवातीस सारखेच असले, तरी भांड्यातील पाण्याच्या उष्णतेचा साठा चमच्यातील पाण्याच्या उष्णतेच्या साठ्यापेक्षा केव्हाही निःसंशय जास्त आहे. पदार्थातील उष्णता संचय त्याच्या वस्तुमानावर, विशिष्ट उष्णतेवर (वि. उ. वर) तसेच तापमानावर अवलंबून असतो, हे प्रस्तुत नोंदीत पुढे योग्य ठिकाणी दाखविले आहे.

सूऱ्यापासून प्रारणाने (निर्वातातून तरंगरूपाने होणाऱ्या ऊर्जेच्या उत्सर्जनाने) उष्णता मिळते खरी पण सूर्य व पृथ्वी यांमधील प्रचंड अंतरात उष्णता नसते. पृथ्वीवरील पदार्थाकडून तसेच तिच्या वातावरणाकडून प्रारणाचे जेव्हा शोषण होते तेव्हाच पदार्थात उष्णता निर्माण होते. अशा रीतीने मिळालेली ही उष्णता सूऱ्यापासून निघालेल्या प्रारण-ऊर्जेच्या पदार्थांकडून झालेल्या शोषणामुळे मिळते. शोषित उष्णता ही प्रारण-ऊर्जेच्या एककातच मोजली जाते.

तापमापके : कोणत्याही शुद्ध पदार्थाचे घन अवस्थेतून द्रव अवस्थेत रूपांतर होत असताना विशिष्ट वातावरणीय दाबात एक ठराविक तापमान असते तसेच द्रव अवस्थेतून बाष्प अवस्थेतील रूपांतरही त्याच विशिष्ट दाबात, ठराविक तापमानासच होत असते. घन व द्रव तसेच द्रव व बाष्प या रूपांतरामध्ये समतोल असताना, पहिल्या तापमानास वितळबिंदू (किंवा गोठणबिंदू) व दुसऱ्यास उकळबिंदू अशी नावे आहेत. साधारणतः या दोन निश्चित बिंदूंतील फरक सांगण्यासाठी मानक (प्रमाणित) पदार्थ म्हणून पाणी वापरतात. पाण्याच्या गोठणबिंदूस बर्फबिंदू व उकळबिंदूस वाफबिंदू अशा संज्ञा देऊन व त्या बिंदूंची निश्चिती योग्य व प्रमाण शर्तीस अनुसरून केल्यावर, त्या दोन बिंदूंमधील अंतरास ‘मूलभूत अंतर’ असे मानतात.

ज्याचा एखादा गुणधर्म तापमानानुसार क्रमशः बदलतो असा कोणताही पदार्थ घेऊन, त्याच्या बदलत्या गुणधर्मावर आधारित असा तापक्रम वरील मूलभूत अंतराशी तुलना करून रचता येतो. निरनिराळ्या उच्च-नीच तापमानांसाठी निरनिराळ्या गुणधर्मांवर आधारित अशी तापमापके तयार करण्यात आली आहेत [→ तापमापन].

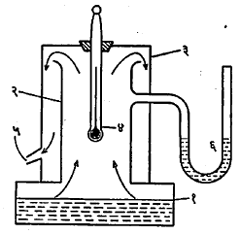
साधारणतः ०^० से. ते ३००^० से. तापमान मोजणारे तापमापक एका विशिष्ट काचेच्या केशनलिकेचे (केसासारख्या बारीक व्यासाच्या गाभ्याच्या नलिकेचे) बनविलेले असून, त्यात शुद्ध पारा वापरतात. अशा तापमापकाच्या बुडाशी असलेल्या पातळ काचेच्या लहानश्या फुग्यात पारा घालून, त्याला बाहेरून जाड पण लांबीभर सारखाच व्यास असलेली केशनलिका जोडतात व त्यातील हवा काढून दुसरे टोक वितळवून बंद करतात. ह्या केशनलिकेवर बर्फबिंदूची नोंद करण्यासाठी तापमापकाचा फुगा शुद्ध बर्फाचे बारीक तुकडे व थोडे शुद्ध पाणी असलेल्या नरसाळ्यात ठेवतात. केशनलिका तीतून पारा दिसेल अशी उभी ठेवतात. बऱ्याच वेळानंतर फुग्यातील पाऱ्याचे तापमान बर्फबिंदूइतके होते व केशनलिकेत बहिर्वक्र दिसणारे पाऱ्याचे पृष्ठ जेथे स्थिर झालेले दिसते तेथे केशनलिकेवर खूण करतात. समजा, फुग्यापासून ती खूण ल. सेंमी. उंच आहे. नंतर आ. १ मध्ये दाखविलेल्या उपकरणात तो तापमापक ठेवतात. या उपकरणास बाष्पबिंदुमापित्र असे नाव आहे. उपकरणाच्या खालच्या भागातील रुंद बुडाच्या व कमी उंचीच्या तांब्याच्या भांड्याला खालून उष्णता देऊन त्यातील पाणी उकळते ठेवतात. भांड्याच्या मधील भागावर ५-६ सेंमी. व्यासाचे भोक असून त्यावर तेवढ्याच व्यासाची सु. ३० सेमी. उंचीची तांब्याची नळी डाख देऊन पक्की व उभी जोडलेली असते. ह्या नळीवर दुसरी मोठ्या व्यासाची व त्याच धातूची, उपडी व घालता-काढता येण्यासारखी नळी ठेवलेली असते. तिच्या वरच्या बंद भागावर मधोमध एक भोक असून त्यात घट्ट बसणाऱ्या बुचातून तापमापक घालून तो आतल्या नळीच्या साधारण मध्यावर राहील असा ठेवतात. ह्या नळीच्या एका बाजूला निमुळती आखूड नळी वाफ किंवा वाफेचे पाणी जाण्यासाठी लावलेली असते व दुसऱ्या बाजूला दाबमापकाची नळी जाण्यासाठी भोक असते. सुमारे १० मिनिटे तापमापक कोरड्या वाफेत ठेवल्यावर केशनलिकेतील वर चढलेल्या व स्थिर झालेल्या पाऱ्याच्या पृष्ठाची केशनलिकेवर खूण करतात व दाबमापकाची नोंद घेतात. दाबमापकाच्या नोंदीवरून वाफबिंदूचे मूल्य निश्चित करता येते. यासाठी पाण्याचा वाफबिंदू व दाब या आलेखाचा उपयोग करतात. समजा, नोंद केलेल्या दाबाला आलेखावरून आलेला वाफबिंदू ९९·६^० से. आहे, या खूणेची फुग्यापासूनची उंची ल_९९._६ सेंमी. आहे, तर ल_९९·६- ल_० ही उंची ९९·६^० से. इतक्या तापमान अंतराबरोबर आहे, असे मानले जाते.

अवस्थांतर : द्रव्याच्या तीन अवस्था (घन, द्रव व वायू) असतात. घनावस्थेतील कोणताही पदार्थ तापवीत राहिल्यास काही वेळाने त्याचे रूपांतर द्रवावस्थेत होते व त्या द्रवाचे अखेर बाष्प किंवा वायू अवस्थेत रूपांतर होते. काही अपवाद सोडल्यास सर्व पदार्थांचे ठराविक तापमान व दाबात, घन अवस्थेतून द्रव व नंतर वायू अवस्थेत, रूपांतर होते. वातावरणीय प्रमाण दाबाखाली घन पदार्थाचा द्रव अवस्थेत होणारा बदल एका निश्चित तापमानातच होतो. विशेषतः स्फटिकवत अशा शुद्ध पदार्थाचे असे अवस्थांतर निश्चित तापमानातच होत असल्यामुळे त्यांच्या वितळबिंदू व वाफबिंदू यांमधील मूलभूत अंतराचा उपयोग तापमापकात करतात. एका अवस्थेतून दुसऱ्या अवस्थेत जाताना प्रत्येक पदार्थाला एका निश्चित मूल्याची उष्णता घ्यावी लागते किंवा त्यातून काढून घ्यावी लागते. याचे नेहेमीच्या अनुभवाचे उदाहरण म्हणजे बर्फ-पाणी-वाफ हा अवस्था बदल होय. एक वातावरणीय दाबात (७६ सेंमी. पाऱ्याच्या स्तंभाच्या दाबात) व ०^० सें. तापमानात, तापमान न वाढता, १ ग्रॅम बर्फाचे पाणी करण्यासाठी द्याव्या लागणाऱ्या उष्णतेस वितळण्याची (किंवा गोठण्याची) सुप्त उष्णता म्हणतात. त्याचप्रमाणे एक वातावरणीय दाबात व १००^० से. तापमानात, तापमान न वाढता, १ ग्रॅम पाण्याची वाफ करण्यास लागणाऱ्या उष्णतेस बाष्पीभवनाची सुप्त उष्णता म्हणतात. साधारणपणे प्रत्येक पदार्थासाठी अशा दोन प्रकारच्या सुप्त उष्णता असतात.

कित्येक प्रसंगी एकच पदार्थ तिन्हीही – घन, द्रव व बाष्प – अवस्थांत एकमेकांशी संलग्‍न राहू शकतात. उदा., बर्फ, पाणी व त्यावरील वाफ एका विशिष्ट तापमानात व दाबात एकत्रित आढळतात. या उदाहरणात तिन्ही अवस्थांत मूळ पदार्थ एकच म्हणजे पाणी असल्यामुळे या समूहावस्थेस ‘एक घटक समूहावस्था’ म्हणतात. दोन किंवा तीन घटक असणाऱ्या समूहावस्थाही असतात. अशा अनेक घटक असणाऱ्या समूहावस्थेतील विद्रावास उष्णता दिली (किंवा त्यातून काढून घेतली), तर त्यातल्या एका घटकाचे अवस्थांतर होऊ शकते. काही पदार्थ (उदा., आयोडीन) उष्णता दिल्यावर घन अवस्थेतून द्रव अवस्थेत न जाता एकदम बाष्प अवस्थेत जातात. अशा अवस्थांतराला संप्लवन म्हणतात व त्यासाठी लागणाऱ्या उष्णतेस संप्लवनाची सुप्त उष्णता म्हणतात. हे पदार्थ द्रव अवस्थेत न जाता एकदम बाष्प अवस्थेत जाण्याचे कारण म्हणजे घन अवस्थेत ह्या पदार्थाचा बाष्प-दाब वातावरणीय दाबापेक्षा मोठा असतो, हे होय. द्रव अवस्थेतून घन अवस्थेत जाताना ज्यांचे आयतन (घनफळ) वाढते, अशाच पदार्थांच्या बाबतीत, बाष्पाच्या दाबापेक्षा बाह्य दाब मोठा ठेवल्यास, घन पदार्थांना द्रव अवस्थेत नेता येते. आर्सेनिक हा घन पदार्थ अशा गुणधर्माचा असल्यामुळे, वातावरणीय दाब आवश्यक तेवढा मोठा ठेवल्यास, तो द्रव अवस्थेत मिळतो.

पदार्थाचे घन, द्रव व बाष्प या क्रमाने अवस्थांतर करताना आवश्यक ती सुप्त उष्णता द्यावी लागते, याच्या उलट क्रमाने बदल (बाष्प, द्रव व घन या क्रमाने) करताना तितक्याच प्रमाणात सुप्त उष्णता बाहेर पडते.

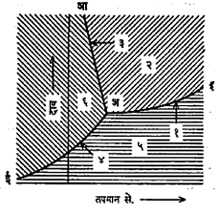
कोणताही पदार्थ एका विशिष्ट अवस्थेत राहण्याला, आवश्यक ते तापमान आणि त्याच्या सभोवतालचा दाब, ह्या गोष्टी प्रमुखतः कारणीभूत असतात. यामुळे पुष्कळ वेळा कोणता पदार्थ, कोणत्या तापमान-दाब यांखाली, कोणत्या अवस्थेत राहू शकतो, हे कळण्यासाठी तापमान-दाब याचा आलेख काढणे जरूर असते. अशा तापमान-दाब आलेखावरून अवस्थांतर कसे होऊ शकेल हेही कळते.

आकृती २ मध्ये बर्फ, पाणी व वाफ यांचा तापमान-दाब हा एकत्रित आलेख दाखवला आहे. दाब वाढविल्यास बर्फाचा वितळबिंदू कमी होतो. हा बदल अआ ही रेषा दाखवते. हिला हिम रेषा (३) म्हणतात. पाण्याचा उकळबिंदू दाब वाढविल्यास वाढत जातो. हा बदल अइ ही रेषा दाखवते, तिला वाफ रेषा (१) म्हणतात. त्याचप्रमाणे बर्फ व वाफ यांचा दाब-तापमान आलेख अई ही रेषा दाखवते, तिला हिम-दव रेषा (४) म्हणतात. अई वरील बिंदू हिम अवस्था दर्शवितात. तसेच अआच्या उजव्या बाजूस आणि अइ च्या वरच्या बाजूस पाणीच असते. अइ व अई या रेषांच्या खालच्या बाजूस बाष्पच असते. प्रयोगाने या रेषा अलग अलग काढतात. पण वरील आलेखात त्या एकत्रित दाखविण्याचे कारण म्हणजे तिन्ही रेषा एका बिंदूतच (आ.२ मधील अ बिंदू) छेदतात हे दिसते.  या बिंदूस ‘त्रिकबिंदू’ म्हणतात. प्रत्येकी दोन रेषा एकमेकींस छेदल्याने तीन छेदन बिंदू मिळणे शक्य आहे. असे भूमितीय दृष्टीने वाटले, तरी ते भौतिकीय दृष्टीने शक्य असत नाही, हे सिद्ध झाले आहे. अ बिंदूचे वैशिष्ट्य हे की, त्याने दर्शविलेल्या तापमानात व दाबात बर्फ, पाणी व वाफ या तीन अवस्था समतोलात असतात, म्हणून हा बिंदू ‘एकमेव’ आहे.

वितळण्याचे (अथवा गोठण्याचे ) व्यापक प्रकार : पदार्थाचे वितळणे (अथवा गोठणे) हे दोन प्रकारांनी होते एक प्रकार स्फटिकी व दुसरा अस्फटिकी. वर उल्लेख केलेले बर्फाचे वितळणे हे पहिल्या प्रकारात मोडते. शुद्ध पदार्थाचे – म्हणजे स्फटिकी पदार्थाचे –वितळबिंदू व गोठणबिंदू हे एकच असतात. घन अवस्थेतून द्रव अवस्थेत (वितळबिंदू) किंवा द्रव अवस्थेतून घन अवस्थेत (गोठणबिंदू) रूपांतरण एका निश्चित तापमानात होते. दुसऱ्या प्रकारात मोडणारे पदार्थ म्हणजे मेण, काच, गंधकाचा एक अस्फटिकी प्रकार, डांबर हे सांगता येतील. यांतील मेण, काच वगैरे पदार्थ अस्फटिकी असल्यामुळे त्यांचे वितळबिंदू एकमेकांपासून थोडे भिन्न असतात. हे दोन्ही बिंदू पहिल्या प्रकाराप्रमाणे निश्चित नसतात. द्रव अवस्थेतील अशा पदार्थांचे तापमान कमी करीत असताना ते घट्ट घट्ट होत जातात व त्यातील प्रवाहीपणा कमी होत जातो आणि शेवटी घन अवस्थेसारखे जरी ते झाले तरी त्या अवस्थेत निश्चित तापमान नसते, निश्चित सुप्त उष्णताही नसते आणि त्यांच्या आयतनात कोणत्याही तापमानात एकदम फरक झालेला आढळत नाही. पहिल्या प्रकारातील वितळणे हे निश्चित तापमान व निश्चित सुप्त उष्णता या दोहोंनी इतके नियमबद्ध झालेले आढळते की, त्यात बदल झाल्यास त्यात दुसऱ्या पदार्थाची भेसळ झाली असली पाहिजे असा निष्कर्ष काढता येतो.

नेहमीच्या व्यवहारात वापरल्या जाणाऱ्या काही धातूंचे वितळबिंदू किंवा गोठणबिंदू कोष्टक क्र. १ मध्ये दिले आहेत.

कोष्टक क्र. १. काही धातूंचे वितळबिंदू व गोठणबिंदू
धातू	वितळ-वा गोठण-बिंदू० से.	धातू	वितळ-वा गोठण-बिंदू० से.	धातू	वितळ-वा गोठण-बिंदू० से.
पारा	–३८·९	जस्त	४१९·५	सोने	१,०६३·०
कथिल	२३१·९	ॲल्युमिनियम	६६०·०	तांबे	१,०८३·०
शिसे	३२७·४	चांदी	९६०·८	निकेल	१,४५५·०

अतिशीतलीकरण : काही योग्य अटी संभाळल्यास शून्य अंश से.च्या खालील तापमानात पाणी न गोठता द्रव अवस्थेत राहू शकते, अशा स्थितीतील पाण्याला ‘अतिशीत पाणी’ असे म्हणतात. पाण्याच्या पृष्ठभागावर तेलाचा तवंग पसरवून गे-ल्युसॅक यांनी –१२^० से. इतक्या तापमानापर्यंत, बर्फ होऊ न देता, पाणी थंड केले होते. अशा ह्या अतिशीत केलेल्या पाण्यात, बर्फाचा अगदी लहान तुकडा टाकल्या बरोबर, पाण्याचे बर्फ होण्यास सुरुवात होऊन तापमान ०^० सें. पर्यंत चढत जाते. याप्रमाणे इतर पुष्कळ द्रवही त्यांच्या गोठणबिंदूखाली द्रव अवस्थेत ठेवता येतात. उदा., U अक्षराच्या आकारासारख्या काचेच्या नळीत फॉस्फरस वितळवून व त्याच्या मोकळ्या पृष्ठभागावर पाणी घालून थंड करीत गेल्यास फॉस्फरस घन अवस्थेत न येता तो द्रव अवस्थेत राहू शकतो. ४४^० से. हा त्याचा गोठणबिंदू आहे खरा पण त्या तापमानाखाली देखील फॉस्फरस द्रव अवस्थेत राहू शकतो. पिवळ्या प्रकारच्या घन फॉस्फरसाचा लहान तुकडा जर नळीत टाकला, तर लगेच आतील द्रव फॉस्फरसाचे घनीकरण सुरू होते व तापमान ४४^० से. पर्यंत चढावयास सुरुवात होते. कारण घनीभवनाचा वेग शीतलीकरणापेक्षा अधिक असतो. पण अस्फटिकी तांबड्या फॉस्फरसाने ही क्रिया सुरू होत नाही.

अतिपरिप्‍लुतता : बाष्प अवस्थेतून द्रव अवस्थेत बदल होताना, प्रथम योग्य तापमानाला बाष्प परिप्‍लुत (अधिकात अधिक प्रमाण) व्हावे लागते. हे तापमान म्हणजे असलेल्या दाबातला द्रवाचा उकळबिंदू होय. या परिप्‍लुत स्थितीत, बाष्प व तिचा द्रव यांमध्ये समतोल असतो. बदल होत असताना वरील तापमान व दाब (बाष्पाचा परिप्‍लुत दाब) स्थिर राहतात व सुप्त उष्णता बाहेर फेकली जाऊन बाष्पाचे द्रवात रूपांतर होऊ लागते. वाफेचे उदाहरण घेतल्यास वाफ प्रथम परिप्‍लुत होते व तिचे पाण्याच्या बारीक थेंबांत रूपांतर होते. थेंब फारच सूक्ष्म असल्यास समतोल रहात नाही व थेंबाची वाढ न होता त्याची पुन्हा वाफ बनते. या दृष्टीने धूलीकण वा धूम्रकण याचे महत्त्व असते, कारण त्याच्याभोवती वाफेच्या रूपांतर झालेल्या पाण्याचे थर बसतात व समतोल राहील अशा प्रकारे पाण्याचे थेंब तयार होतात. पण हे धूलीकण वा धूम्रकण नसतील, तर अवस्थांतर न होता वाफेची परिप्‍लुतता व त्याबरोबर परिप्‍लुत दाब ही वाढतात व वाफेचे पाण्यात अवस्थांतर न होता वाफ अतिपरिप्‍लुत बनते. ही अतिपरिप्‍लुतता सर्व बाष्पांच्या बाबतीत आढळते.

विद्रावांचे व मिश्रधातूंचे गोठणे : पाण्यात साखर किंवा लवण विरघळविल्यास या विद्रावाचा गोठणबिंदू पाण्याच्या गोठणबिंदूंच्या खाली जातो म्हणजे अशुद्धतेमुळे किंवा विद्रुतामुळे (विरघळलेल्या पदार्थामुळे) शुद्ध विद्रावकाचा (विरघळविणाऱ्या पदार्थाचा) गोठणबिंदू खाली उतरलेला आढळतो. गोठणबिंदूचे हे अवनमन (खाली जाणे) विद्रावाच्या सांद्रतेच्या (विरघळलेल्या विद्रुताच्या परिमाणाच्या) प्रमाणात असते. जेव्हा विद्रावाचे गोठण सुरू होते तेव्हा विद्रावक शुद्ध स्थितीत बाहेर पडू लागतो आणि ह्यामुळे राहिलेल्या विद्रावाची सांद्रता वाढत रहाते म्हणून ही गोठण क्रिया चालू असताना तापमान कायम न रहाता खाली खाली जात रहाते.

उकळत्या पाण्यात स्फटिकी सोडियम सल्फेटाचा परिप्‍लुत विद्राव तयार करून त्याचे तापमान बाहेरील तापमानाइतके उतरविल्यास अतिपरिप्‍लुत विद्राव तयार होईल त्यास लहान सहान देखील हादरे बसणार नाहीत व तो पूर्ण स्थिर राहील, अशी दक्षता घेतल्यावर स्फटिकीकरण न होता तो तसाच ठेवता येतो. पण त्यात बाहेरून त्याच विद्रुताचा एक बारीक तुकडा जरी टाकला, तरी स्फटिकीकरणास सुरुवात होऊन, ती क्रिया विद्रावाच्या परिप्‍लुत स्थितीच्या तापमानापर्यंत चालू राहते व सुप्त उष्णता बाहेर पडते.

सोडियम सल्फेटाच्या अतिपरिप्‍लुत विद्रावातून वर उल्लेख केल्याप्रमाणे स्फटिकीकरण होत असताना बरीच उष्णता बाहेर पडते या उलट हे लवण पाण्यात विरघळविल्यास उष्णतेचे शोषण होते व पाण्याचे तापमान कमी कमी होत जाते. ह्या लवणाची पूड ०^० से. तापमानाच्या पाण्यात विरघळवीत गेल्यास –१५^० से. इतके तापमान मिळू शकते. बर्फ व मीठ यांच्या मिश्रणानेही पाण्याचे तापमान –२२^० से. इतके कमी करता येते. ४ भार कॅल्शियम क्लोराइड व ३ भार बर्फ या मिश्रणाने तर –५५^० से. इतके तापमान आणता येते.

मिश्रधातू वितळवून थंड करीत गेल्यास ज्या घटक धातूचा वितळबिंदू दुसऱ्या घटकाच्या वितळबिंदूपेक्षा मोठा असतो, त्या वितळबिंदूस तो वितळलेला रस स्थिर राहून काही वेळाने तापमान हळूहळू उतरत जाऊन, दुसऱ्या घटकाच्या वितळबिंदूपाशी स्थिर होतो. काही मिश्रधातूंचे वितळबिंदू स्फटिकी पदार्थासारखे निश्चित असतात. अशा मिश्रधातूचा एक विशिष्ट गुणधर्म असा की, तिचा वितळबिंदू तिच्या घटक धातूंपेक्षा पुष्कळच कमी असतो. रोझ नावाची मिश्रधातू पुढील धातूंची बनविलेली असते : २ भाग बिस्मथ (वितळबिंदू २६९^० से.), १ भाग शिसे (वितळबिंदू ३२७^० से.) आणि १ भाग कथिल (वितळबिंदू २३२^० से.). पण ह्या दोन मिश्र धातूचा वितळबिंदू मात्र ९४^० से. आहे.

कोष्टक क्र. २. उष्णता संचयाची विविध मापन पद्धतींतील एकके
एकक	पाण्याचे वस्तुमान	तापमान फरक	प्रमाणित तापमान फरक	संज्ञा	पद्धती
कॅलरी – ग्रॅम कॅलरी	१ ग्रॅम	१० से.	१४.५० ते १५·५० से.	कॅलरी	सेंटिमीटर-ग्रॅम-सेंकद
किग्रॅ. कॅलरी	१ किग्रॅ.	१० से.	”     ”	किग्रॅ. कॅलरी	मीटर-किलोग्रॅम-सेंकद
ब्रिटिश थर्मल एकक	१ पौंड	१० फॅ.	६३० ते ६४० फॅ.	बी. टीएच. यू.	फूट-पौंड-सेकंद
थर्म	१०५ पौंड	१० फॅ.	–	थर्म	फूट-पौंड-सेकंद
थर्मल एकक	१ पौंड	१० से.	–	सी. टीएच. यू.	मिश्र
सरासरी कॅलरी : पाण्याच्या १ ग्रॅम वस्तुमानास ०० से. पासून १००० से. पर्यंत तापविण्यास लागणाऱ्या उष्णतेचा १/१०० भाग.

दोन धातूंच्या मिश्रणाने एक मिश्रधातू बनविली तर त्या मिश्रधातूचा वितळबिंदू दोन घटक धातूंच्या वितळबिंदूपेक्षा नेहमी पुष्कळच कमी असतो. इतकेच नव्हे, तर तो वितळबिंदू घटक धातूच्या मिश्रण प्रमाणाला नियमितपणे बदललेला आढळतो. उदा., १० टक्के तांबे (वितळबिंदू १०८३^० से.) व ९० टक्के चांदी (वितळबिंदू ९६०^०से.) या प्रमाणात घटक धातू घेऊन, ती मिश्रधातू वितळवून थंड करीत गेल्यास ८८०^० से. च्या तापमानास तिचे घनीकरण होऊ लागते. आणि चांदीचे स्फटिक वेगळे होत जाऊन राहिलेल्या द्रवात तांब्याचे प्रमाण जास्त होते त्या द्रवाचा गोठणबिंदू कमी होतो व तापमान उतरत जाते. ३० टक्के तांबे व ७० टक्के चांदी घेऊन या मिश्रधातूचा रस करून तो थंड करीत गेल्यास ७७०^० से. ला घनीकरण सुरू होते व चांदीचे स्फटिक ७४०^० से. तापमानापर्यंत बाहेर पडत राहतात व मिश्रधातू या तापमानास गोठते. तेव्हा यात ४० टक्के तांबे व ६० टक्के चांदी असते. या मिश्रधातूस ‘द्रवणक्रांतिक मिश्रधातू’ म्हणतात. आणि ७४०^० से. या गोठणबिंदूस ‘द्रवणक्रांतिकबिंदू’ म्हणतात. याच कमीत कमी तापमानास ही मिश्रधातू वितळते. जास्त घटक असलेल्या धातूंच्या जटिल मिश्रधातूस एकाहून जास्त द्रवणक्रांतिकबिंदू असतात.

घनीकरण होत असताना अनेक पदार्थांचे आकुंचन होते या उलट पाणी, बिस्मिथ-शिसे मिश्रधातू वगैरेंचे घनीकरण होत असताना प्रसरण होते.

उष्णता संचय : एखाद्या पदार्थास उष्णता देत राहिले म्हणजे त्याचे तापमान वाढत जाते व पदार्थाच्या अवस्थेत बदल न झाल्यास, उष्णता व त्यामुळे झालेला तापमानातील बदल सम प्रमाणात होत राहतात. तसेच जास्त वस्तुमानाचा तोच पदार्थ घेतल्यास व काही ठराविक तापमानातून तापवावयाचा झाल्यास, वस्तुमानाच्या प्रमाणात उष्णता द्यावी लागते. पुन्हा एकाच वस्तुमानाचे दोन भिन्न पदार्थ, एकाच तापमानापर्यंत तापवून, एकाच धातूच्या दोन भांड्यांतील सारखे तापमान व वस्तुमान असलेल्या पाण्यात ते टाकले असता त्या दोन भांड्यांतील पाण्याचे तापमान भिन्नभिन्न येते. या सर्व निरीक्षणांवरून प्रत्येक पदार्थाची उष्णता धारिता (विशिष्ट उष्णता) निरनिराळी असावी असा निष्कर्ष अठराव्या शतकाच्या अखेरीस शास्त्रज्ञांनी काढला होता. ज्याप्रमाणे पाण्याच्या गोठणबिंदूस व उकळबिंदूस अनुक्रमे ०^० से. व १००^० से. अशी तापमानाची स्वेच्छ मूल्ये दिली गेली, त्याचप्रमाणे उष्णता संचयाचे एककही स्वेच्छच आहे. तथापि कोणत्याही पदार्थातील उष्णता संचय त्याच्या वस्तुमानाच्या, विशिष्ट उष्णतेच्या व तापमानातील फरकाच्या सम प्रमाणात असतो हे माहीत असल्याने ही स्वेच्छ निवड करणे सोपे होते. भिन्नभिन्न मापन पद्धतींत वापरण्यात येणारी उष्णता संचयाची एकके कोष्टक क्र. २ मध्ये दिली आहेत. सामान्यतः एकक उष्णता संचय म्हणजे ‘एकक वस्तुमानाचे तापमान’ वापरात असलेल्या तापमापकाच्या १ अंशामधून वाढविण्यासाठी द्यावी लागणारी उष्णता होय.

वरील एकके निश्चित करण्यासाठी पाण्याचाच उपयोग केला आहे. तथापि दिलेल्या वस्तुमानाच्या पाण्यात १^० सें तापमान फरक ठेवण्यास लागणारी उष्णता निरनिराळ्या तापमानांत सारखी नसल्यामुळे प्रमाणित एककाची व्याख्या करताना १ ग्रॅ. पाण्याला १४·५^०सें. ते १५·५^० से. म्हणजेच १^० से. इतके तापमान वाढविण्यास लागणारी उष्णता असे धरणे योग्य वाटले. सर्वसाधारण उष्णतामापनात १ ग्रॅ. पाण्याला १^० सें. मधून तापविण्यासाठी लागणारी उष्णता म्हणजे १ कॅलरी धरतात. कोष्टकावरून त्यातील काही एककांचा परस्परांशी असलेला संबंध खालीलप्रमाणे आहे हे दिसून येईल.

१ किग्रॅ. कॅलरी = १,००० कॅलरी

१ थर्म = १०^५ बी. टीएच. यू.

१ बी. टीएच. यू = २५२ कॅलरी किंवा ५/९ सी.टीएच.यू उष्णता ही एक प्रकारची ऊर्जाच आहे म्हणून हल्ली उष्णतेचे मापन ऊर्जेच्या एककातही करतात. [→ एकके व परिमाणे ].

उष्णतेचे स्वरूप : दोन लाकडे एकमेकांवर घासून अग्नी तयार करता येतो, हे मानवांस प्राचीन कालापासून माहीत होते. उष्णतेचे निरनिराळे उपयोगही त्यांना माहीत होते. पण उष्णता म्हणजे काय, तिचे स्वरूप काय यांसंबंधीचे ज्ञान जवळजवळ सोळाव्या शतकापर्यंत कोणासच ठाऊक नव्हते. तथापि त्या शतकात फ्रान्सिस बेकन यांनी उष्णतेच्या उपलब्ध असलेल्या अनेक उपयोगांचा व आविष्कारांचा पद्धतशीर अभ्यास करून एक तात्विक विचारसरणी मांडल्याचा उल्लेख आहे. त्यांच्या मते उष्णता व गती यांचा निकटवर्ती संबंध आहे. अठराव्या शतकाच्या सुरुवातीस न्यूटन यांनी उष्णता म्हणजे अणूंची गती होय, असे म्हटल्याचा उल्लेख आहे. अठराव्या शतकात जोसेफ ब्लॅक या शास्त्रज्ञांनी उष्णता संचय, दोन्ही प्रकारच्या सुप्त उष्णता, विशिष्ट उष्णता वगैरे कल्पना सुस्पष्ट केल्या. या अभ्यासातून निष्कर्षित झालेल्या उष्णतेच्या उपपत्तीस कॅलरिक (उष्मद्रव) उपपत्ती म्हणतात. उष्णता हा वजनरहित ,पूर्ण स्थितिस्थापक, स्वप्रतिसारक व अविनाशी असा एक द्रव पदार्थ आहे. अशी या उपपत्तीची बैठक होती. उष्णतेच्या काही गुणधर्मांचे समाधानकारक स्पष्टीकरण या उपपत्तीने होत होते. उदा. तप्त पदार्थ उष्णता फेकतात (किंवा उत्सर्जित करतात) याचे कारण ऊष्मद्रवाचे कण त्यातील प्रतिसारण गुणधर्मामुळे जोराने एकमेकांस दूर लोटतात, निरनिराळ्या पदार्थाच्या निरनिराळ्या विशिष्ट उष्णता असण्याचे कारण, त्या त्या पदार्थाचे या ऊष्मद्रवाविषयी असलेले निरनिराळे आकर्षण होय. तापविल्यावर पदार्थाचे प्रसरण होते. ते या ऊष्माद्रवातील प्रतिसारणामुळेच, तसेच सुप्त उष्णता पदार्थात मिसळल्यामुळे त्यांचे अवस्थांतर होते. उदा. पाणी = बर्फ + सुप्त उष्णता.

या उपपत्तीमुळे वर उल्लेख केलेल्या गोष्टींचा समाधानकारक खुलासा होत असला, तरी त्यावेळेसही माहीत असलेल्या उष्णतेच्या इतर आविष्कारांचा खुलासा मात्र ओढून ताणून केलेला व असमाधानकारक वाटत होता. उदा. मोठ्या हातोड्याने शिशाच्या ठोकळ्यावर जोराने प्रहार केल्यावर ठोकळ्याचे तापमान वाढलेले आढळते. या नेहेमीच्या अनुभवाचे स्पष्टीकरण असे केले जात असे की, पाण्याने भरलेल्या स्पंजातून तो दाबला असता जसे पाणी बाहेर पडते, तव्दत हातोड्याच्या प्रहारामुळे ठोकळ्यातील ऊष्मद्रव बाहेर पडतो व म्हणून ठोकळा गरम होतो. दोन पदार्थ एकमेकांवर घासल्यामुळे त्यांचे तापमान वाढते. याचे कारण घासल्यामुळे पदार्थाचे जे बारीक कण बाहेर पडतात त्यांची ऊष्मद्रव धारण करण्याची क्षमता कमी असते व त्यामुळे तो ऊष्मद्रव बाहेर पडतो. या उपपत्तीनुसार पूड केलेल्या पदार्थाची विशिष्ट उष्णता त्याच्या घन अवस्थेतल्या विशिष्ट उष्णतेपेक्षा कमी असावी पण या गोष्टीची सत्यता पडताळून पाहण्याचा कोणीही प्रयत्न केला नाही. शिवाय घन अवस्थेतील पदार्थ एकमेकांवर घासल्यामुळे बारीक कण बाहेर पडतात. हे जरी खरे मानले, तरी पाणी ढवळत ठेवल्यामुळे त्याचे तापमान वाढते, याचे स्पष्टीकरण या उपपत्तीप्रमाणे करणे शक्य होत नाही.

काउंट रम्फर्ड या शास्त्रज्ञांनी अठराव्या शतकाच्या अखेरीस, तोफांना बिनधारेच्या वेधकाने (भोके पाडण्याच्या साधनाने) भोक पाडीत असताना उत्पन्न होणाऱ्या उष्णतेसंबंधी अनेक प्रयोग केले भोके पडत असताना धातूचा चुरा फारच थोड्या प्रमाणात पडत असला तरी प्रचंड प्रमाणात उष्णता निर्माण होते ती इतकी की ०^० सें. तापमान असलेले १२ किग्रॅ. पाणी एका प्रयोगात उकळत असलेले त्यांना आढळले. धातूच्या चुऱ्याची विशिष्ट उष्णता (वि.उ) आणि तोफेच्या घन अवस्थेतील धातूची वि.उ. यांत त्यांना विशेष फरक आढळला नाही. तेव्हा ऊष्माद्रव उपपत्ती त्यांना त्याज्य वाटू लागली. पुन्हा अशा तर्‍हेने निर्माण होणारी उष्णता अमऱ्याद प्रमाणात मिळते, असेही त्यांना आढळले. त्यामुळे एका पदार्थात इतकी अमऱ्याद उष्णता असणे शक्य नाही , हेही त्यांना पटू लागले. ह्या निर्माण होणाऱ्या उष्णतेचा आणि गतीचा निकट संबंध असला पाहिजे ह्या निष्कर्षाप्रत ते आले. तरी सुध्दा ऊष्मद्रवावर ठाम विश्वास ठेवणाऱ्या शास्त्रज्ञांस त्यांचे म्हणणे उपेक्षीयच वाटत राहिले. त्याच सुमारास डेव्ही या शास्त्रज्ञांनी एक बंद पेटीत बर्फाचे दोन तुकडे घड्याळातील स्प्रिंगच्या साहाय्याने एकमेकांस घाशीत ठेवून त्यापासून पाणी तयार करून दाखवले तेव्हा मात्र ऊष्मद्रवावर विश्वास ठेवणाऱ्याना, बर्फाचे पाणी होण्यास लागणारी उष्णता आली कोठून ही समस्या सुटेना. कारण ह्या उपपत्तीनुसार पाणी = बर्फ + सुप्त उष्णता हे समीकरण असल्यामुळे व ती मिळण्याचे दुसरे कोणतेच मार्ग उपलब्ध नसल्यामुळे त्या बर्फातील तुकड्यांना घाशीत ठेवण्यासाठी लागणारी यांत्रिक ऊर्जाच उष्णता निर्माण करण्यास कारणीभूत होते, वि.उ. कमी झाल्यामुळे नव्हे, हे मान्य करण्याखेरीज दुसरा पऱ्याय उरला नाही.

तथापि कोणतीही वस्तू गतीत ठेवण्यासाठी ऊर्जेचा पुरवठा करावा लागतो व ऊर्जेपासून उष्णता मिळते असे एकोणिसाव्या शतकाच्या प्रारंभापासून काही शास्त्रज्ञांना पटू लागले होते आणि म्हणून ऊर्जा व उष्णता यांमधील निश्चित संबंध काय आहेत व ते कसे प्रस्थापित करणे शक्य आहे इकडे त्यांचे लक्ष लागले.

यांत्रिक ऊर्जा व उष्णता यांचे संबंध जेम्स प्रेस्कट जूल (१८१८–८९) यांनी प्रायोगिकरीत्या निश्चित केले. त्यांच्या प्रयोगावरून असे सिद्ध झाले की, उष्णता ही ऊर्जेचेच एक रूप आहे व विशिष्ट यांत्रिक वा विद्युत ऊर्जेपासून किती उष्णता मिळेल याचे निश्चित गणितीय संबंध त्यांनी प्रस्थापित केले. ऊष्मद्रवाची उपपत्ती आता पूर्णपणे त्याज्य ठरली आहे.

उष्णता ही एक प्रकारची ऊर्जा या तत्त्वाला उष्णतेचा गत्यात्मक सिध्दांत किंवा उष्णतेचा यांत्रिक सिध्दांत म्हणतात. ऊर्जा व उष्णता यांमधील संबंध दर्शविणारे प्रयोग जूल यांनी सिद्ध केले [→ उष्णतेचा यांत्रिक तुल्यांक].

यानंतर अनेक प्रयोगान्ती उष्णता व यांत्रिक कार्य यांतील संबंध W/H = J या समीकरणाने दर्शविला गेला. येथे W = कार्य. H = उष्णता संचय व J = एक स्थिरांक असून याचे यांत्रिक सममूल्य ४·१८५५ + ०·०००४ निरपेक्ष जूल असे आहे. साधारणपणे ४·१९*१०^७ अर्ग ऊर्जा १ कॅलरी उष्णता निर्माण करते व १०^७ अर्ग = १ जूल जे.आर. भायर यांनी उष्णता ही ऊर्जेचेच एक रूप आहे असे गृहीत धरून वायूच्या दोन प्रकारच्या (स्थिर दाब व स्थिर आयतन) वि.उ.तील फरकावरून तात्त्विकदृष्ट्या हे सममूल्य काढले व ते प्रायोगिक मूल्याशी मिळते जुळते आल्यामुळे, उष्णता ही सुरुवातीस लिहिल्याप्रमाणे ऊष्मद्रव नसून ऊर्जाच आहे, हे पूर्णपणे प्रस्थापित झाले.

विशिष्ट उष्णता : प्रत्येक पदार्थाची उष्णता धारिता मोजण्याचे एकक निश्चित करणे आवश्यक आहे. १ ग्रॅम पदार्थास १^० सें. मधून तापविण्यासाठी द्याव्या लागणाऱ्या उष्णतेस विशिष्ट उष्णता म्हणतात. १ कॅलरी म्हणजे १ ग्रॅम पाण्याचे १^० से. मधून तापमान वाढविण्यास लागणारी उष्णता होय वि. उ.च्या वरील व्याख्येवरून पाण्याची वि.उ. १ कॅलरी आहे हे दिसून येईल. निरनिराळ्या पदार्थाच्या वि.उ. पाण्याच्या वि.उ.च्या संदर्भातच देतात. वि.उ.चे एकक कॅलरी/(ग्रॅ) (से.) किंवा बी.टीएच.यू./(पौ) फॅ.) यांमध्ये दिलेले असते. एखाद्या पदार्थाचे तापमान १^० से.मधून वाढविण्यास द्याव्या लागणाऱ्या उष्णतेस त्याची उष्णता धारिता म्हणतात. उदा. M ग्रॅम वस्तूमान आणि s वि.उ. असलेल्या पदार्थाची उष्णता धारिता H = Ms कॅलरी इतकी असते. काही घन व द्रव पदार्थाच्या वि.उ. कोष्टक क्र. ३ मध्ये दिल्या आहेत.

कोष्टक क्र. ३. काही पदार्थाच्या विशिष्ट उष्णता.
पदार्थ	०से. तापमान	वि.उ.	पदार्थ	०से. तापमान	वि.उ.
पितळ	०	०·०९	पारा	०	०·०३३
तांबे	०	०·०९	पाणी	१५	१·००
चांदी	०	०·५६	ग्लिसरीन	१८·२	०·५८

दोन्ही प्रकारच्या सुप्त उष्णता व वि.उ. यांच्या मापनासंबंधी उष्णतामापन ही नोंद पहावी.

विशिष्ट उष्णतेतील बदल : साधारणपणे पदार्थाच्या अवस्थेत फरक झाला म्हणजे वि. उ.तही बदल होतो. सामान्यपणे पदार्थाची वि.उ. तो पदार्थ द्रव अवस्थेत असताना जास्त असते. वितळल्यामुळे किंवा गोठल्यामुळे धातूंच्या वि. उ.तील फरक फारच थोडा असतो, पण वितळण्यामुळे ज्या धातूच्या आयतनात पुष्कळ फरक पडतो, त्या धातूच्या वि.उ मध्ये अतिशय फरक पडतो.

काही मूलद्रव्ये स्फटिकरूपात तशीच अस्फटिकरूपात मिळतात. उदा. कार्बन-हिरा (स्फटिकी), ग्रॅफाइट (अस्फटिकी); आर्सेनिक-स्फटिकी तसेच अस्फटिकी व फॉस्फरस – पिवळा (स्फटिकी), तांबडा (अस्फटिकी). अशा दोन रूपात मिळणाऱ्या मूलद्रव्यांच्या वि.उ.मध्ये रूपानुसार फरक पडतो.

अशुद्धतेमुळेही पदार्थाच्या वि.उ.मध्ये फरक पडतो. हा प्रकार दोन द्रवांचे मिश्रण केल्याने तर जास्तच प्रमाणात झाल्याचे दाखले आहेत. तापमानात बदल केल्यानेही पदार्थाची वि.उ. तापमानाच्या प्रमाणात बदलते. हिऱ्याच्या बाबतीत हा फरक प्रकर्षाने दिसतो, तो असा :

तापमान ० से.	०	८ ते ९८ च्या दरम्यान	१००	९८५
विशिष्ट उष्णता	०·०९५	०·१४६९	०·१९०	०·४५९

अनेक पदार्थांत उदा., सिलिकॉन, अल्कोहॉल, पाणी यांत तापमानानुसार वि.उ.मध्ये बदल होतो.

आणवीय उष्णतेसंबंधी डुलाँग व पेटिट यांचा नियम : जी जी मूलद्रव्ये घन अवस्थेत मिळतात त्यांच्या आणवीय भारांचा व वि.उ. यांचा गुणाकार हा एक स्थिरांक असतो, असा शोध डुलाँग व पेटिट या शास्त्रज्ञद्वयांनी १८१९ मध्ये लावला. या गुणाकारास आणवीय उष्णता (आ.उ.) म्हणतात. हा स्थिरांक ६·४ च्या जवळपास असतो. अगदी शुध्दावस्थेतील अनेक मूलद्रव्यांवर प्रयोग केल्यावर असे आढळून आले की, वरील नियम अशा मूलद्रव्यांस अगदी काटेकोरपणे लागू पडत नसला, तरी पुष्कळ मूलद्रव्यांस सामान्य तापमानात तो लागू पडतो.

डुलाँग व पेटिट यांच्या नियमाप्रमाणे स्थिर दाब असताना आ.उ. ६ ते ६·२ व स्थिर आयतन असताना ५·९६ यावी व वि.उ. तापमानानुसार बदलू नये, असे दिसून येते. पण प्रत्यक्षात वि.उ. तापमाननुसार बदलते हे सत्य आहे.

जरी कित्येक मूलद्रव्यांची वि.उ. तापमानानुसार बदलत असली तरी तो बदल फार नसल्यामुळे, डुलाँग व पेटिट यांचा नियम अशा मूलद्रव्यांना लागू पडतो, असे म्हणता येते कार्बन (हिरा), बोरॉन व सिलिकॉन या पदार्थांची वि.उ. तापमानानुसार फारच बदलत असली, तरीही या पदार्थांना ५००^० सें. किंवा त्याहून अधिक तापमानास तापविल्यास, त्यांची आ.उ. डुलाँग व पेटिट नियमाप्रमाणे जवळजवळ येते असे दिसून आले आहे.

थोडक्यात म्हणजे डुलाँग व पेटिट यांच्या नियमात बराच सत्यांश आहे पण त्यात पदार्थाची वि.उ. तापमानानुसार बदलते हे हिशेबात धरले नसल्यामुळे तो नियम परिपूर्ण नाही. परिपूर्ण असलेल्या नियमात वि.उ. तापमानानुसार का व कशी बदलते या विचारांचा समावेश असणे जरूरीचे आहे.

या दृष्टीने विसाव्या शतकाच्या पूर्वार्धात आइन्स्टाइन, डेबाय, नेर्न्स्ट व लिंडेमन, बोर्न, कार्मान वगैरे शास्त्रज्ञांनी नियमबद्धरीतीने स्फटिकीभवन होणाऱ्या मूलद्रव्यांच्या वि. उ.संबंधी संशोधन केले. त्यांच्या संशोधनाचा स्थूल गोषवारा खाली दिला आहे.

(१) सामान्य तसेच उच्च तापमानात स्थिर आयतन असताना आ.उ. डुलाँग व पेटिट यांच्या नियमाप्रमाणे ५·९६ (जवळजवळ सहा) या मूल्याप्रत येते.

(२) नीच तापमानात आ.उ. चे मूल्य डुलाँग व पेटिट नियमाने येणाऱ्या मूल्यापेक्षा कमी येते व जसजसे निरपेक्ष शून्य तापमानाकडे [–२७३^० से. कडे, → केल्व्हिन निरपेक्ष तापक्रम] जावे, तसतसे ते मूल्य शून्याप्रत जात रहाते.

(३) निरपेक्ष शून्य तापमानापासून काही विशिष्ट तापमानापर्यंत, स्थिर आयतन असताना, आ.उ. तंतोतंतपणे तापमानाच्या त्रिघाताच्या प्रमाणात बदलते. हा तापमान त्रिघात नियम स्फटिकी पदार्थांसकट सर्व पदार्थांना लागू पडतो.

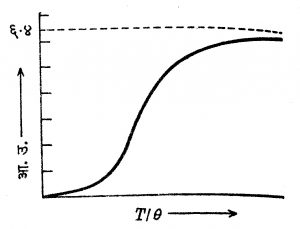
(४) अनेक पदार्थांचे स्थिर आयतन आ.उ. व निरपेक्ष तापमान यांचे संबंधदर्शक आलेख काढले, तर त्या सर्व आलेखांत फारच सादृश्य असलेले दिसते म्हणून अशा आलेखांतील केवळ तापमान अक्षांच्या मापन प्रमाणात सोईस्कर बदल केल्यास, सर्व आलेख एकरूप करता येतात. हेच गणितीय भाषेत पुढीलप्रमाणे मांडता येते : आ.उ. = F (T/θ) येथे F हे फलन (गणितीय संबंध) असून ते सर्व पदार्थांना एकच असते. θ हा प्रत्येक पदार्थाचा तापमान-विशेषक-स्थिरांक असून T निरपेक्ष तापमान आहे. हा आलेख आ. ३ मध्ये दाखविल्याप्रमाणे असतो.

आइन्स्टाइन यांची वि.उ.संबंधीची उपपत्ती : आइन्स्टाइन यांनी प्लांक यांच्या पुंज सिध्दांचा [→ पुंज क्षेत्र सिध्दांत] उपयोग करून तापमानानुसार होणाऱ्या वि. उ. मधील बदलाचे स्पष्टीकरण दिले. प्लांक यांच्या विचारसरणीप्रमाणे प्रत्येक अणू दोलकासारखा वर्तन करीत असतो. ‘मॅक्सवेल-बोल्टस्‌मान सांख्यिकी’ चा [→ सांख्यिकीय भौतिकी] उपयोग करून अशा दोलकांच्या सरासरी ऊर्जेचा (Ē) निरपेक्ष तापमानाशी (T) खालीलप्रमाणे संबंध जोडता येतो. Ē = hv (e^hv/^kT -1) येथे E = अणूची सरासरी ऊर्जा, L = बोल्टसमान स्थिरांक, h = प्लांक स्थिरांक, e = स्वाभाविक लॉगरिथमाचा आधारांक आणि v = कंप्रता (दर सेकंदास होणारी कंपन संख्या).

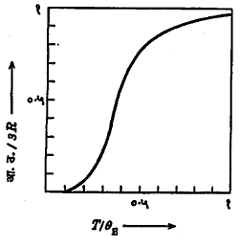
घन पदार्थातील प्रत्येक अणू एका ठराविक कंप्रतेनेच म्हणजे ^vE ने आंदोलन करतो, असे आइन्स्टाइन यांनी मानले. या कंप्रतेला ‘आइन्स्टाइन कंप्रता’ म्हणतात. स्फटिकाच्या शोषण वर्णपटाच्या परीक्षणांत अवरक्त पट्ट्यात (वर्णपटातील तांबड्या रंगाच्या अलीकडील अदृश्य पट्ट्यात) ही कंप्रता आढळते. [→ वर्णपटविज्ञान]. प्रत्येक अणू त्रिमित अवकाशात आंदोलन करीत असल्यामुळे एक ग्रॅम-अणूतील (ग्रॅममध्ये मांडलेल्या व संख्यात्मक दृष्ट्या अणुभाराइतक्याच असलेल्या मूलद्रव्याच्या वस्तुमानातील) अणूंची सरासरी ऊर्जा E = 3 N Ē म्हणजेच 3Nev_E/(ehv/kT-1) एवढी येते. येथे N ही ग्रॅम-अणूतील अणूंच्या संख्या (अँव्होगाड्रो संख्या) आहे. आता पदार्थातील उष्णता ऊर्जा ही आंदोलन ऊर्जाच E आहे, असे धरून व्याख्येनुसार dE/dT = स्थिर आयतन आ.उ. = 3Ry²-e^y /(e^y-1)2 असे येते. येथे y = h_vE /KT =θ_E /T आणि Nk = R आहे. θE चिन्हाला ‘आइन्स्टाइन तापमान-विशेषक’ असे म्हणतात. मॅक्सवेल-बोल्टस्‌मान सांख्यिकीत ज्या प्रमाणे kT ही एका अणूची सरासरी ऊर्जा असते त्याचप्रमाणे hv_E ही एका अणुरूपी दोलकाची आंदोलन ऊर्जा असते असे मानून θE हे तापमान–विशेषक धरले आहे. आता आ.उ./3R आणि T/θ_E हा आलेख काढला, तर तो आ. ४ मध्ये दाखविल्याप्रमाणे येतो. आलेखावरून T = θ_E या तापमानात बहुतेक सर्व पदार्थांच्या बाबतीत वि. उ. =3R असे मूल्य येते, म्हणजे या तापमानास डुलाँग-पेटिट नियमाप्रमाणे आ.उ. मिळते. T > θ_E असल्यास आ.उ. सहाच्या जवळपास येते व T < θ_E असल्यास आ.उ. हळूहळू कमी होत जाऊन T < 0.1θ_E मध्ये जवळजवळ शून्य होते. प्लांक यांच्या सिध्दांतावर आधारलेल्या आइन्स्टइन यांच्या या स्पष्टीकरणावरून आ.उ. तापमानावर अवलंबून असते, हे सिद्ध झाले. हिऱ्याची३३१^० निरपेक्ष तापमानास (५८^० से.) येणारी आ.उ. मिळतीजुळती आहे, असे दिसून आले. पण T < 0.1θ_E असताना आ.उ. शून्य होण्याची शक्यता आहे हे जे भाकीत वरील समीकरणावरून (किंवा आलेखावरून) निघते त्याचा पडताळा पहाण्यासाठी नेर्न्स्ट यांनी अनेक पदार्थांवर प्रयोग केल्यानंतर T < 0.1θ_E असूनसुध्दा (म्हणजे १६^० निरपेक्ष तापमानात) आ.उ. झालेली आढळली नाही. त्यांच्या प्रयोगातील निरीक्षणावरून मात्र ०^० निरपेक्ष तापमानात आ.उ. शून्य होते, असे दिसून आले. सारांश, अतिनीच तापमानात आइन्स्टाइन यांचे वरील स्पष्टीकरण अयशस्वी ठरते.

आइन्स्टाइन यांनी प्लांक यांच्या विचारसरणीचा उपयोग करून अणूमध्ये एकाच कंप्रतेचे आंदोलन होते असे जे मानले ते खरे नसावे, असे कित्येक शास्त्रज्ञांस वाटू लागले. ही आइन्स्टाइनप्रणीत स्फटिकाच्या अवरक्त शोषण वर्णपटातील कंप्रता एकच नसून अनेक आहेत. म्हणून कंप्रता समूहच विचारात घेऊन आ.उ. विषयीचे पुन्हा संशोधन करण्याची कल्पना पुढे आली. नेर्न्स्ट आणि लिंडेमन यांनी सर्व अणू एकाच कंप्रतेने आंदोलन करीत नसून, निम्मे v व राहिलेले निम्मे v/2 अशा दोन कंप्रतांनी आंदोलन करतात, असे गृहीत धरून एक आनुभविक सूत्र मांडले. या सूत्राप्रमाणे वि.उ. मध्ये तापमानानुसार होणारा बदल, आइन्स्टाइन याच्या सूत्रापेक्षा विस्तृत तापमान पट्ट्यात अधिक बरोबर येऊ लागला. तथापि या सूत्रास सैध्दांतिक पाया नाही, हा याचा दोष आहे.

प्लांक यांच्या विचारसरणीनुसार आइन्स्टाइन यांनी या संशोधनास जे नवीन वळन दिले त्याचाच व्यापक विचार नंतरच्या डेबाय, बोर्न व कार्मान यांनी आपल्या संशोधनात केला.

डेबाय यांचे आ.उ. चे सूत्र : v आणि v + dv ह्या कंप्रतापट्ट्यात g (v) dv एवढ्या कंप्रता असतात आणि त्यातील प्रत्येक कंप्रतेस प्लांग दोलकास असते तशी ऊर्जा असते म्हणजे सर्व कंप्रतात

असणारी ऊर्जा E =	∞	g(v)dv.hv	समी. (१) न दर्शविली जाते, असे डेबाय यांनी गृहीत धरले. बोर्न आणि कार्मान यांच्या संशोधनात g(v) चे मूल्य काढण्याची पद्धत वेगळी आहे.
	∫0	(ehv/kt-1)          …        (१)

हाच त्यांच्या संशोधनातील मुख्य फरक आहे. डेबाय यांनी g(v) चे मूल्य काढताना दोन गृहीते घेतली : (१) घन पदार्थ (म्हणजे स्फटिक) हा अखंड माध्यम असतो यामुळे कृष्ण-पदार्थ-प्रारण सिध्दांतात [→ उष्णता प्रारण] ज्या पद्धतीने g (v) काढतात त्याच पद्धतीने त्याचे मूल्य

g (v) = 4πV	(1 + 2)	v2     …     …	(२)
	(v1 + vt)

इतके येते. V = पदार्थाचे आयतन v_l, v_t स्थितिस्थापक संहतीमधील (विकृती घडवून आणणाऱ्या बाह्य प्रेरणेला विरोध करणाऱ्या व प्रेरणा काढून घेतल्यावर मूळ अवस्थेत येणाऱ्या समुच्चयामधील) अनुक्रमे अनुतरंग (ह्या तरंगांत माध्यमातील कण किंवा बिंदू तरंगवेगाच्या दिशेत कंप पावतात) व अवतंरग (ह्या तरंगांत माध्यमातील कण किंवा बिंदू तरंगवेगाच्या दिशेशी काटकोनात कंप पावतात) वेग. समीकरण (२) ने दर्शविलेल्या सर्व तरंगांची संख्या 3N असते यात N ही पदार्थातील अणूसंख्या आहे. पहिल्या गृहीताप्रमाणे, पदार्थ अखंड माध्यम मानला आहे तो वस्तुत दुसऱ्या गृहीताप्रेमाणे तसा तो नसल्यामुळे दोन अणूमध्ये जेवढे अंतर असेल तेवढ्याच लहानात लहान तरंगलांबी असू शकतील, अशी मर्यादा घालून सर्व तरंगाची संख्या 3N धरली गेली. डेबाय यांनी रूढ व पुंज भौतिकी यांची सांगड घातली, असे म्हणता येईल. म्हणजेच

VD	g(v) dv = 3N     …     …     (३)
∫0

असे समीकरण रूपात मांडता येते, ही ती मर्यादा होय. या समीकरणावरून v_D ह्या कंप्रतेची व्याख्या मिळते हिला ‘डेबाय कंप्रता’ म्हणतात. या कंप्रतेचे महत्तम मूल्य v_D असल्यामुळे, ह्याहून मोठ्या कंप्रता घेतल्यास g(v) चे मूल्य शून्य येते व म्हणून समी (३) शून्य येते. यामुळेच पहिल्या समीकरणात ∞ च्या ऐवजी v_D हे सीमांत मूल्य घ्यावे लागते. आइन्स्टाइन यांच्या तापमान-विशेषकाप्रमाणेच डेबाय तापमान-विशेषकाची तशीच व्याख्या करून म्हणजे hvD/kT = θ/T असे धरून, समी. (१) ,(२) ,व (३) च्या साहाय्याने पूर्ण ऊर्जा :

hvD	=	Ѳ	असे धरून, समी. (१), (२) व (३) च्या साहाय्याने पूर्ण ऊर्जा :
kT		T

E =	9RT4	Ѳ/T	z3dz	…     …     (४)
	Ѳ3	∫0	ez-1

मिळते. येथे z = hv/kT आहे व आ. उ. dE/dT असल्यामुळे (४) वरून अखेर खालील अनंत श्रेणी मिळते :

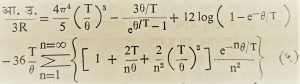
T चे मूल्य मोठे असताना डुलाँग व पेटिट नियमाप्रमाणे आ.उ. मिळते, कारण z = hv/kT असल्यामुळे T जसजसे मोठे होत जाईल तसतसे z शून्याकडे झुकते म्हणून (४) मधील हे z2 /e^z – 1 होते आणि अखेर समाकलन मूल्य E = 3RT होते व dE/dT = आ.उ. = 3R होते या उलट T शून्य निरपेक्ष तापमानाजवळ जाईल तेव्हा आ.उ. = 12r⁴R/5(T/θ)³ होते, म्हणजे आ. उ. निरपेक्ष तापमानाच्या त्रिघाताच्या प्रमाणात बदलते. यास ‘डेबाय त्रिघात नियम’ म्हणतात. पूर्वीसारखाच आ.उ/३R आणि T/θ यांचा आलेख काढला, तर दोन आलेखातील (आ.४ व आ.५) फरक चटकन लक्षात येईल. तो आलेख आ. ५ मध्ये दिला आहे. या दोन आलेखांची तुलना केल्यास,त्यांतील दोन्ही वक्रांची ठेवण T &gt 0.2θ तो पर्यंत सारखीच असते. आइन्स्टाइन यांच्या व डेबाय यांच्या आलेखातील खरी चाचणी T&lt 0.1θ या तापमानात होते. या तापमानाच्या टप्प्यात डेबाय नियमाप्रमाणे आ.उ. तापमानाच्या त्रिघाताच्या समप्रमाणात बदलते, तर आइन्स्टाइन यांच्या आलेखावरून ती शून्य येते.अनेक पदार्थात हा तापमान-त्रिघात नियम लागू पडत असल्याचा मागे उल्लेख केलाच आहे. परंतु डेबाय यांचा नियम अतिनीच तापमानात धातूंना तितकासा लागू पडत नाही. अर्थात आइन्स्टाइन यांच्या सूत्रापेक्षा डेबाय यांच्या सूत्रात पुष्कळच सुधारणा आहे.

अतिनीच तापमानत धातूंच्या बाबतीत लागू पडेल असे विशिष्ट उष्णतेसंबंधीचे फेर्मी यांच्या उपपत्तीवर आधारलेले समीकरण झोमरफेल्ट यांनी मांडले, ते असे :

यात उजव्या बाजूकडील पद डेबाय त्रिघात नियमच आहे व दुसरे पद इलेक्ट्रॉनामुळे होणारे विशिष्ट उष्णतेतील अंशदान (काही भाग दिलेला) आहे γ’ हा इलेक्ट्रॉनीय स्थिरांक आहे व त्याचा γ (=Cp/Cv) या स्थिरांकाशी (Cp म्हणजे दाब स्थिर असताना असणारी वायूची वि. उ. आणि Cv म्हणजे आयतन स्थिर असताना असणारी वायूची वि. उ.) काहीही संबंध नाही. तांबे, चांदी व सोने यांच्या बाबतीत नीच तापमानात Cv/T² यांचा आलेख काढल्यास तो सरळ रेषा दर्शवितो असे प्रयोगावरून दृष्टोत्पत्तीस आले आहे व यावरून धातूंच्या संबंधात डेबाय-झोमरफेल्ट उपपत्तीची सत्यता कळून येते.

घन, द्रव व वायू यांचे औष्णिक प्रसरण : सामान्यतः कोणत्याही अवस्थेतील – घन, द्रव व वायू – पदार्थाचे तापमान वाढविल्यावर प्रसरण होते. पण घन पदार्थ निरनिराळ्या म्हणजे लांब व बारीक सळईवजा, पातळ पत्र्यावजा व ठोकळेवजा मिळत असल्यामुळे त्याचे प्रसरण अनुक्रमे सळईच्या अक्ष दिशेने, परस्परांस लंब असलेल्या दोन दिशांनी तसेच परस्परांस लंब असलेल्या तीन दिशांनी सारख्याच प्रमाणात होते. यालाच अनुक्रमे ‘रैखिक’ ‘पृष्ठीय’ व ‘आयतन’ प्रसरण म्हणतात. द्रव व वायूंच्या बाबतीत केवळ आयतन प्रसरणच असते. पुन्हा काही असमदिक् (ज्यात दिलेल्या कोणत्याही गुणधर्माचे मूल्य दिशेवर अवलंबून असते अशा) घन पदार्थात – स्फटिक पदार्थांत – परस्परांशी लंबरूपात असलेल्या तीन अक्षांच्या दिशांतील प्रसरण भिन्नभिन्न असते. प्रामुख्याने सळईवजा लांबीच असलेल्या समदिक् घन पदार्थाचा रैखिक प्रसरण गुणांक म्हणजे प्रति-सेल्सिअसला व प्रतिसेंटिमीटरमध्ये होणारा लांबीतील फरक होय. याचा पृष्ठीय प्रसरण गुणांक रैखिक गुणांकाच्या दुप्पट व आयतन प्रसरण गुणांक रैखिक गुणांकाच्या तिप्पट असतो.

द्रव पदार्थ कोठल्यातरी भांड्यातच तापवावा लागत असल्यामुळे व द्रवाच्या प्रसरणाबरोबर भांड्याचेही प्रसरण होत असल्यामुळे ,द्रवाचा खरा आयतन प्रसरण गुणांक काढताना, भांड्याचा ज्ञात आयतन गुणांक व द्रवाचा भासमान आयतन गुणांक यांची बेरीज घ्यावी लागते. वायूंच्या बाबतीतही तशीच परिस्थिती असली तरी सर्व वायूंचे प्रसरण फार मोठे असल्यामुळे भांड्याचे प्रसरण उपेक्षणीय ठरते. आयतन प्रसरण गुणांक म्हणजे प्रति-सेल्सिअस प्रति-घन-सेंटिमीटरमध्ये होणारा आयतनातील फरक असतो. पदार्थाच्या तिन्ही अवस्थांतील असे गुणांक प्रायोगिकरीत्या मोजण्याच्या अनेक व अचून अशा पद्धती आहेत [→ ऊष्मीय प्रसरण] .

घन पदार्थातील रेणूंची (किंवा अणूंची) प्रत्यक्ष हालचाल न होता एका रेणूकडून (किंवा अणूकडून) दुसऱ्या रेणूला (किंवा अणूला) उष्णता दिली जाते व अशा प्रकारे पदार्थाच्या एका भागाकडून दुसऱ्या भागाकडे उष्णता वाहून नेली जाते. उष्णता वाहून नेण्याच्या या प्रकाराला संवहन म्हणतात. काच, लाकूड,वगैरे पदार्थातील संवहन धातूंच्या मानाने कमी असते. द्रायूंच्या (वायूंच्या वा द्रवांच्या ) बाबतीत उष्ण भागातील प्रत्यक्ष द्रायूच थंड भागातील द्रायूकडे वाहून उष्णता वाहून नेली जाते. या प्रकाराला उष्णतेने संनयन म्हणतात [→ उष्णता संनयन ,उष्णता संवहन] .

वायूचे औष्णिक गुणधर्म : सतराव्या शतकात तापमापक विश्वासार्ह नव्हते. त्यामुळे वायूचे तापमान वाढविल्यावर होणारे प्रसरण व तापमानबदल यांसंबंधीचे निश्चित नियम निघू शकले नाहीत. तथापि तापमान स्थिर ठेवले असता केवळ दाब बदलून, दिलेल्या वायूच्या (हवेच्या) बदलाचा नियम रॉबर्ट बॉइल यांनी तसेच मॅरिअट यांनी शोधून काढला. दिलेल्या (म्हणजे एका निश्चित वस्तुमानाच्या ) वायूचा दाब व आयतन यांचा गुणाकार ,तापमान न बदलल्यास, स्थिर राहतो. म्हणजे. PV = K          …           …           …                  (६)

हा तो नियम होय. येथे P = दाब, V = आयतन व K = स्थिरांक आहे. पुढील शतकातील संशोधनात कोणताच वायू हा नियम काटेकोरपणे पाळीत नाही, असे आढळून आले. पण नेहमीच्या सामान्य तापमानात हायड्रोजन, ऑक्सिजन, नायट्रोजन, हीलियम वगैरेसारख्या नित्य (सामान्य तापमानात वायू अवस्थेत रहाणाऱ्या) वायूंत हा नियम जवळजवळ पूर्ण लागू पडलेला आढळतो. कार्बन डायऑक्साइड, सल्फर डाय-ऑक्साइड यांसारखे वायू अशा सामान्य तापमानातसुध्दा या नियमानुसार वर्तन करीत नाहीत. सर्वसाधारणपणे वायूचे तापमान जितके उच्च असेल तितक्या प्रमाणात हा नियम लागू पडतो. हा नियम ज्या वायूंना बरोबर लागू पडतो त्यांना ‘परिपूर्ण वायू’ किंवा ‘आदर्श वायू’ म्हणण्याचा प्रघात आहे. सामान्य तापमानात आणि थोड्याफार प्रमाणात वातावरणीय दाबात कोरडी हवा, नायट्रोजन, हायड्रोजन, ऑक्सिजन वगैरे वायूंना हा नियम लागू पडतो.

उष्णतेमुळे वायूंचे होणारे प्रसरण दोन प्रकारांनी मोजणे जरूर असते. एका प्रकारात दाब स्थिर ठेवून आयतन-प्रसरण मोजतात, तर दुसऱ्या प्रकारात आयतन स्थिर ठेवून दाब-प्रसरण मोजतात. दोन्ही प्रकारांनी फार काळजीपूर्वक प्रसरण मोजल्यावर खालील गोष्टी आढळून आल्या. (१) सर्व वायूंच्या बाबतीत पहिल्या प्रकाराने मोजलेले आयतन-प्रसरण गुणांक एकाच मूल्याचे असतात. (२) दुसऱ्या प्रकाराने आलेले दाब-प्रसरण गुणांक (१) एवढ्याच मूल्याचे असतात. (३) दोन्ही प्रकारच्या गुणांकाचे मूल्य १/२७३ = ०·००३६६५ असते. यावरून ०^० सें. तापमान असलेल्या १ मिली .वायू घेतल्यास व दाब स्थिर ठेवून –१^० सें. तापमानातून तो थंड केल्यास त्याचे आयतन १/२७३ ने कमी होईल वायू अशाच तर्‍हेने –२७३^० सें. पर्यंत तार्किकदृष्ट्या थंड करीत गेल्यास २७३/२७३ ने कमी, म्हणजे घेतलेल्या वायूचे आयतनच नष्ट होईल किंवा तो वायू जागाच व्यापणार नाही असे म्हणता येईल. तोच प्रकार आयतन स्थिर ठेवून तापमान –२७३^० सें. पर्यंत कमी केल्यास दाब नष्ट होईल, व्यावहारिक बुध्दीस न पटणारी ही गोष्ट असली, तरी –२७३^० सें. अशांस वायू हा वायुस्वरूपात रहात नाही, हे लक्षात ठेवावयास हवे . –२७३^० सें. या तापमानास निरपेक्ष शून्य तापमान म्हणतात. म्हणेज t⁰ से. व T⁰ निरपेक्ष तापमान यांचा संबंध t⁰ + 273 = T⁰ असा येतो. वरील दोन प्रकारच्या प्रसरणांच्या अभ्यासात,तापमान निरपेक्ष शून्यापासून मोजण्यात आले आहे असे समजल्यास (१) V αT (२) P α T असे सिद्ध करता येते. तापमानाच्या बदलामुळे वायूत आढळणाऱ्या वरील प्रकारच्या प्रसरणाच्या नियमांना ‘चार्लस–गे-ल्युसॅक नियम’ म्हणतात. बॉइल यांच्या नियमाची चार्लस –गे-ल्युसॅक यांच्या नियमाशी सांगड घातल्यास आदर्श वायूचे ‘स्थितिदर्शक समीकरण’ मांडता येते, ते खाली दिले आहे.:

PV = RT     …            …              (७)

येथे R वायु-स्थिरांक आहे. २७३^० निरपेक्ष तापमान असताना (म्हणजे ०^० से. तापमान असताना) एका वातावरणीय दाबात २२·४ लिटर आयतन असताना R या स्थिरांकाचे मूल्य R = २२४०० × ७६ × १३.६ × ९८१/२७३ = ८·३२२ × १०^७ अर्ग एवढे येते. येथे P = दाब, V = आयतन, T = निरपेक्ष तापमान, तसेच ७६,१३·६ व ९८१ हे आकडे अनुक्रमे एका वातावरणीय दाबातील पाऱ्याची उंची (सेंमी.मध्ये), त्याची घनता व गुरुत्वीय प्रवेग यांची मूल्ये आहेत.

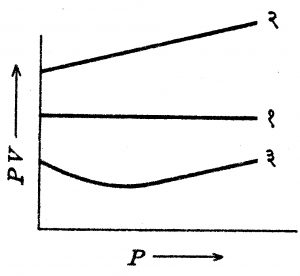
एका वातावरणीय दाबात व ०^० सें. तापमानात सर्वसाधारणपणे कोणत्याही वायूच्या रेणुमूल्याचे आयतन असते. बॉइल यांचा नियम काही नित्य वायूंस चांगला लागू पडत असला, तरी इतर अनेक वायूंना तो लागू पडत नाही. अनेक संशोधकांनी ठराविक वस्तुमान असलेल्या वायूंवर प्रयोग केल्यावर, दाब व आयतन यांचा गुणाकार स्थिर तापमानात स्थिर रहात नाही हे दाखवले. प्रत्येक वायूस एक ठराविक तापमान असे असते की ते तापमान स्थिर ठेवल्यास बॉइल नियम पूर्णपणे पाळला जातो. या तापमानास ‘बॉइल तापमान’ म्हणतात. PV आणि Pचा आलेख आ. ६ मध्ये दाखविल्याप्रमाणे येतो. सर्व वायूंच्या बाबतीत येणाऱ्या अशा आलेखाचे स्वरूप आकृतीत दाखविल्याप्रमाणे असते. बॉइल तापमानाच्यापेक्षा जास्त तापमानात PV गुणाकार P जसा वाढवावा तसा वाढत जातो. याउलट बॉइल तापमानाच्या खालील तापमानात, हा गुणाकार सुरूवातीस P वाढला असता कमी होतो व नंतरच्या वाढीत कमीत कमी होऊन नंतर P जसा वाढेल तसा वाढत जातो.

वायूंच्या गत्यात्मक सिध्दांतानुसार [→ द्रव्याचा गत्यात्मक सिध्दांत] बॉइल नियम सिद्ध करता येत असला, तरी वायूच्या गत्यात्मक सिध्दांतातील पुढील गृहीतेच बरोबर नसावीत या शंकेस वरील फरकामुळे पृष्टी मिळते. ती गृहीते अशी : (१) वायूंचे अणू अथवा रेणू अत्यंत लहान म्हणजे बिंदूरूप असतात व त्यांचे प्रत्यक्ष आयतन उपेक्षणीय असते. (२) त्यांच्यात परस्पर आकर्षण नसते. परंतु प्रत्यक्षात वायूंच्या सर्व रेणूंचे मिळून येणारे आयतन उपेक्षणीय नसते. तसेच त्यांच्यात परस्पर आकर्षणही असते, असे वरील फरकामुळे मानणे आवश्यक आहे, हे व्हॅन डर व्हाल्स या शास्त्रज्ञांनी प्रथम लक्षात आणून, PV = RT ह्या आदर्श वायूच्या समीकरणात फेरबदल सुचविला ,तो असा:

यास ‘व्हॅन डर व्हाल्स समीकरण’ म्हणतात. यात a व b हे स्थिरांक असून १ग्रॅंम वस्तुमानाच्या निरनिराळ्या वायूंत ते निरनिराळे असतात, पण त्याच वायूसाठी स्थिर असतात असे गृहीत धरले होते. [→ स्थिति समीकरण] .

वायूच्या विशिष्ट उष्णता : घन व द्रव पदार्थाना वि. उ. असतात तशाच वायूंनाही असतात पण त्यात एक प्रमुख फरक आहे. एकाच वायूची वि. उ.स्थिर आयतनाखाली व स्थिर दाबाखाली काढल्यास, त्या वेगवेगळ्या असतात. स्थिर दाबाखाली काढलेल्या वि.उ.स c_p व स्थिर आयतनाखाली काढलेल्या वि. उ. सc_v अशी चिन्हे वापरण्यात येतात. C हे अक्षर मोठे (कॅपिटल) दाखवून त्याच्या पायथ्याशी P किंवा V ही अक्षरे मांडली तर त्या त्या प्रकारची ग्रॅम रेणवीय वि. उ. दर्शविण्याचा प्रघात आहे. Mc_p= C_p व Mc_V = C_v येथे M= ग्रॅम रेणू (मोल,ग्रॅममध्ये मोजलेला रेणूभार), स्थिर दाबाखालील वि. उ. ही, कोणताही वायू घेतला तरी, त्या वायूच्या स्थिर आयतनाखाली काढलेल्या वि.उ. पेक्षा नेहमीच जास्त असते. कारण स्थिर दाबाखाली दिलेली उष्णता वायूचे तापमान वाढविण्यासाठी,तसेच प्रसरण झाल्यामुळे होणाऱ्या बहि: काऱ्यासाठी खर्च होते. तर स्थिर आयतनाखाली दिलेली उष्णता फक्त तापमान वाढविण्यासच खर्च होते.

एकोणिसाव्या शतकाच्या पूर्वार्धातच, तात्त्विकदृष्ट्या, उष्णता ही ऊर्जा स्वरूपाची असून तिचे रूपांतरण यांत्रिक ऊर्जेत किंवा यांत्रिक ऊर्जेचे उष्णता ऊर्जेत होऊ शकते, या आधारावर मायर यांनी दोन वि. उ.तील फरकाचा संबंध वायूच्या स्थिरांकाशी व उष्णतेच्या यांत्रिक सममूल्याशी जोडून दाखविला असल्याचा उल्लेख मागे आलाच आहे. तो संबंध असा : C_p – C_v = R/J, येथे R अर्ग/ग्रॅ.रेणू^० से. किंवा C_p – C_v = R, येथे R कॅलरीच्या एककात मांडलेला असतो.

वर दिलेल्या वि. उ. च्या फरकाच्या समीकरणावरूनही कोणती तरी एक प्रकारची वि. उ. मोजल्यास दुसरी काढता येणे शक्य आहे, हे दिसून येईल. प्रयोगाने C_p काढणे सोपे असते.

कोष्टक क्र. ४ मध्ये काही वायूंच्या दोन्ही प्रकारच्या रेणवीय वि. उ. व त्यांची गुणोत्तरे दिली आहेत. वि.उ.चे गुणोत्तर y या अक्षराने दर्शविलो जाते.

कोष्टक क्र. ४. काही वायूंच्या रेणवीय विशिष्ट उष्णता व त्यांची गुणोत्तरे
वायू	Cp कॅलरी / (ग्रॅ.रे.) (से.)	Cv कॅलरी/ (ग्रॅ.रे.) (से.)	Cp/Cv = γ रे. वि. उ. गुणोत्तर
हीलियम	४·९७	२·९८	१·६६
हायड्रोजन	६·८६	४·८८	१·४१
ऑक्सिजन	७·०३	५·०४	१·४०
नायट्रोजन	६·९५	४·९६	१·४०
हवा	६·९५	४·९५	१·४०
कार्बन डाय-ऑक्साइड	८·८३	६·८०	१·३०

अनेक प्रयोगांवरून असे दिसून आले की, या दोन वि. उ.चे गुणोत्तर वायूचे रेणवीय गुणधर्मावर अवलंबून असते. वायूचा रेणू एक-अणू द्वि-अणू किंवा बहु-अणू मिळून झालेला आहे की कसे, याचा अंदाज ह्या गुणोत्तरावरून करता येतो. साधारणतः एक-अणू वायूचे हे गुणोत्तर १·६७ तर द्वि-अणूसाठी १·४० आणि बहु-अणूसाठी १·३० ते १ असे येते.

वायूच्या वि. उ.च्या गुणोत्तराचा प्रायोगिक पडताळा : खालील प्रयोगांनी y चे मूल्य काढता येते : (१) एकदाच अक्रमी (उष्णतेचा लाभ किंवा व्यय न होता) प्रसरण किंवा आकुंचन केल्याने (२) ध्वनी तरंगाच्या वेगाच्या मापनाने, ध्वनी तरंगाचा कोणत्याही वायूत प्रसार होत असताना अक्रमी बदल होत असतात.

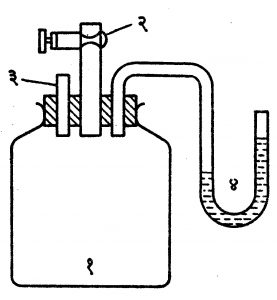
क्लेमां-डिसॉर्म पद्धती : (आ. ७). १० ते १२ लिटर आयतन असलेल्या (१) ह्या काचेच्या मोठ्या बरणीच्या तोंडात रबराचे बुच घट्ट बसवलेले असते. बुचाच्या मध्य भागातून काचेची मोठी नळी जात असून, तिच्या वरच्या भागाला (२) ही तोटी आहे. तिच्या साहाय्याने (१) मधील वायू बाहेर टाकता येतो किंवा आत बंदिस्त करता येतो. (३) ही सायकलची व्हाल्व्ह‌ ट्यूब असून, तिच्यातून पंपाने हवा आत भरून तिचा दाब (४) या दाबमापकाने मोजता येतो. दाबमापकाच्या द्रवातील पातळीत १५–२० सेंमी. फरक पडेल इतकी हवा सुरुवातीस पंपाने बरणीत भरतात. द्रवाच्या पातळ्या पूर्ण स्थिर झाल्यानंतर त्यांतील फरकाची (h₁) नोंद घेतात. (२) ही तोटी अर्धा पाऊण सेकंद उघडी ठेवून लगेच बंद करतात. दाब मापकाची उंची कमी झालेली आढळली, तरी ती हळूहळू स्थिर होते. हवा एकदम काढल्यामुळे झालेला बदल अक्रमी असतो. त्यावेळच्या उंचीची (h₂ची) नोंद घेतात. दाबमापकात वापरलेल्या द्रवाची १ सेंमी. उंची दाबाचे एकक धरल्यास, वातावरणीय दाबाच्या मानाने h₁ व h₂ फारच कमी आहेत असे मानून y = h₁ /h₁ -h₂ हे सूत्र मिळते.

ध्वनि-वेग पद्धती : वायूतील ध्वनि-वेगाशी y चा संबंध खालील समीकरणाने जोडलेला असतो. γ = du² /P    …     …     …        …         (९)

यात d = वायूची घनता P = दाब , v = वायूतील ध्वनि-वेग. वायूचा ध्वनि –वेग काढण्यासाठी कुंट या शास्त्रज्ञांनी शोधून काढलेल्या विशिष्ट नळीचा उपयोग करतात [→ ध्वनि].

वरील प्रयोगाने v चे मूल्य कळते. d व p ची मूल्ये माहीत असल्यामुळे समी. (९) वरून y चे मूल्य काढता येते.

पहा : उष्णता मापन; उष्णता संक्रमण; उष्णतेचा यांत्रिक तुल्यांक; ऊष्मीय प्रसरण; तापमापन; द्रव्याचा गत्यात्मक सिध्दांत.

संदर्भ : 1. Ghosh, S. N.; Deb, S, Heat, Calcutta, 1963,

2 . Saha, M. N.; Srivastava, B. N. A Treatise on Heat, Allahabad & Calcutta, 1965.

3. Zemansky, M. W. Heat and Thermodynamics, New York, 1957.

टोळे, मा. ग.