स्थितिस्थापकता : काही घनरूप द्रव्यावर किंवा वस्तूवर एक वा अधिक प्रेरणा कार्य करीत असताना त्या द्रव्याचा किंवा वस्तूचा आकार किंवा आकारमान ( घनफळ ) अथवा दोन्ही बदलतात आणि या प्रेरणा काढून घेतल्यावर द्रव्याला वा वस्तूला मूळ आकार व आकारमान प्राप्त होतात. घनरूप द्रव्याच्या या गुणधर्माला स्थितिस्थापकता म्हणतात. लावलेल्या प्रेरणा मर्यादित असल्यास त्या काढून घेतल्यावर पूर्वपरिस्थिती प्राप्त करून घेणे हा गुणधर्म जवळजवळ सर्वच द्रव्यांमध्ये असतो. मात्र क्रिया करणार्या या प्रेरणा पुष्कळ जास्त असल्यास त्या काढून घेतल्यावरही वस्तू मूळ रूप धारण करू शकत नाही व तिचे कायमचे विरूपण होते. अशा रीतीने द्रव्याचे एका कमाल प्रेरणेपर्यंत कायमचे विरूपण होत नाही या मर्यादेला स्थितिस्थापक मर्यादा म्हणतात. म्हणजे स्थितिस्थापक मर्यादा ओलांडल्यावर कायमचे विरूपण होते. अशा प्रकारे स्थितिस्थापक द्रव्य स्थितिस्थापकीय रीतीने वर्तन करते किंवा प्रतिसाद देते. कायमच्या विरूपणाची सुरुवात होण्याआधी घनरूप द्रव्यातील दर एकक क्षेत्रफळावरील कमाल प्रेरणा म्हणजे प्रतिबल ही स्थितिस्थापक मर्यादा असते. या मर्यादेपलीकडील प्रतिबलांमुळे द्रव्य आकार्य होते, वाहू लागते किंवा शरण येते (भंग पावते). स्थितिस्थापक मर्यादेने स्थितिस्थापक वर्तनाचा शेवट दर्शविला जातो व नंतर द्रव्याचे आकार्य वर्तन सुरू होते. बहुतेक ठिसूळ द्रव्यांच्या बाबतीत स्थितिस्थापक मर्यादेपलीकडील प्रेरणांमुळे त्यांचे वर्तन आकार्य न होता त्यांचा भंग होतो.
स्थितिस्थापक मर्यादा द्रव्याच्या प्रकारावर अवलंबून असते. उदा., पोलादी दंड, गज वा तार स्थितिस्थापक दृष्ट्या तिच्या मूळ लांबीच्या एक टक्का ताणली जाऊ शकते तर रबरासारख्या विशिष्ट द्रव्यांच्या पट्टीची लांबी अशा रीतीने १,००० टक्क्यांपर्यंत वाढू शकते. पोलाद रबरापेक्षा पुष्कळच अधिक प्रबल असते. तथापि रबरामध्ये कमाल स्थितिस्थापक वाढ होण्यासाठी लागणारी ताण प्रेरणा पोलादासाठी लागणार्या प्रेरणेपेक्षा सु. ०.०१ एवढी कमी असते. ताणाखालील अनेक घनरूप द्रव्यांचे स्थितिस्थापक गुणधर्म या दोन टोकांच्या गुणधर्मांदरम्यानचे असतात. रबर व पोलाद यांचे भिन्न स्थूलमानीय स्थितिस्थापक गुणधर्म हे त्यांच्या अगदी भिन्न अशा सूक्ष्ममानीय संरचनांमुळे निर्माण झालेले असतात. पोलाद व धातू यांची स्थितिस्थापकता लघुपल्ल्याच्या आंतर-आणवीय प्रेरणांमुळे आलेली असते आणि द्रव्य प्रतिबलाखाली नसताना या प्रेरणा अणूंना नियमित आकृतिबंधात टिकवून ठेवतात. प्रतिबलाखाली अणूंमधील बंधने अगदी लहान विरूपणाला भंग पावू शकते. याउलट रबरासारखी द्रव्ये व इतर बहुवारिके यांमध्ये सूक्ष्ममानीय पातळीवर दीर्घ शृंखलायुक्त रेणू असून द्रव्य जसे दीर्घ ( लांब ) होते, तसे हे रेणू उलगडतात व मूळ रूप पुन:प्राप्त होताना ते गुंडाळले जातात. अशा प्रकारे स्थितिस्थापकतेचा गणितीय सिद्धांत ( उपपत्ती ) व अभियांत्रिकीय यामिकीतील अनुप्रयुक्ती ( उपयोग ) यांचा संबंध स्थूलमानीय प्रतिसादाशी असतो प्रतिसादाला कारणीभूत असलेल्या यंत्रणेशी नसतो.
स्थितिस्थापकता हा गणितीय भौतिकीतील विषय असून त्यात घनरूप द्रव्याला लावलेल्या प्रेरणा व त्यांच्यामुळे होणारी विरूपणे यांच्यामधील परस्परसंबंधांचा अभ्यास करतात. अतिशय वैविध्यपूर्ण गुणवैशिष्ट्ये असलेल्या या विषयात गोल, दंडगोल, तार, पातळ पट्ट्या, वक्र कवचे यांसारख्या स्थितिस्थापक वस्तूंचा यामिकी व स्थितिकी या दृष्टींनी अभ्यास करतात. संरचना, बांधकामे, यंत्रभाग, अनेक प्रकारची द्रव्ये इत्यादींच्या स्थैर्य, कंपने, तरंग प्रसारण यांच्या संदर्भातील प्रश्नांचा विचारही यात करतात.
स्थितिस्थापकतेच्या सिद्धांतामध्ये द्रव्यावर किंवा वस्तूवर कार्य करणार्या प्रेरणा व त्यांच्यामुळे होणारे बदल यांच्यामधील परस्परसंबंधांचा विचार करतात. संरचना, बांधकाम व यंत्रभाग यांचा अभिकल्प ( आराखडा ) तयार करणे, कंपनांचा सिद्धांत व ध्वनी, स्फटिकजालकाच्या अणूंमधील प्रेरणा यांसारखे अनेक विज्ञान व तंत्रविद्या यांतील विषय यांमध्ये स्थितिस्थापकतेचा सिद्धांत महत्त्वाचा आहे.
प्रतिबल : दंडगोलाकार दंडाच्या ( शलाकेच्या ) दोन्ही टोकांच्या आडव्या छेदांवर एकसम रीतीने प्रेरणा कार्य करीत असल्यास शलाकेत ताणयुक्त स्थिती निर्माण होते. हे स्थितिस्थापकतेतील सर्वांत साधे उदाहरण आहे. त्याने स्थितिस्थापकतेची मूलभूत संकल्पना स्पष्ट होते. दंडाच्या प्रत्येक टोकावर एकूण F एवढी प्रेरणा पडली आहे. तिच्या काटच्छेदाचे क्षेत्रफळ A असल्यास संपूर्ण शलाकेवर निष्पन्न होणारे प्रतिबल (S) हे F/A एवढे असते. याचा अर्थ प्रतिबल म्हणजे दर एकक क्षेत्रफळावरील प्रेरणा होय [ S = F/A ] अशा ताण प्रतिबलाने शलाका ताणली जाऊन ती लांब व बारीक होते. पोलाद, तसेच बांधकाम व यंत्रभाग यांत वापरली जाणारी द्रव्ये यांच्या बाबतीत लांबीतील अशी वाढ खूप कमी असते. मेट्रिक पद्धतीत प्रतिबलाचे मापन पास्काल या एककात करतात.
प्रतिविकृती : वर उल्लेख केलेल्या दंडाचे दर एकक लांबीवरील लंबन वा दीर्घीकरण म्हणजे प्रतिविकृती (e) होय. प्रतिविकृती प्रतिबलाच्या प्रमाणात असते. या समानुपातित्वाला ( प्रमाणात्मकतेला ) हुक नियम असे म्हणतात व तो S = E.e या समीकरणाने दर्शवितात. यातील E स्थिरांकाला स्थितिस्थापकतेचा ‘ यंग मापांक ( गुणांक ) ’ म्हणतात. स्थितिस्थापकतेविषयीचा हा पहिला नियम इंग्रज भौतिकीविज्ञ ⇨ रॉबर्ट हुक यांनी १६७८ मध्ये सुचविला. स्थितिस्थापक मर्यादा या कमाल बिंदूपर्यंत प्रतिबल कमी असेपर्यंत हुक नियम यथार्थ ठरतो. यंग मापांकाचे एक मूल्य द्रव्याच्या स्थितिस्थापक गुणधर्मांच्या बाबतीत वैशिष्ट्यपूर्ण असते. दंड त्याच्या अक्षीय दिशेत अधिक लांब झाल्याने अक्षाला लंब असलेल्या दिशेत त्याचे आकुंचन होते. त्रिज्येच्या दिशेतील अरीय प्रतिविकृती (er) व लांबीच्या दिशेतील अनुदैर्घ्य प्रतिविकृती (e1) यांच्यातील परस्परसंबंध er = s. e1 या समीकरणाने दर्शवितात. यातील s — er / e1 या अपूर्णांकाला प्वासाँ गुणोत्तर म्हणतात आणि अनेक द्रव्यांच्या बाबतीत हे गुणोत्तर १: ४ एवढे असते. फ्रेंच गणिती ⇨ सिमेआँ देनिस प्वासाँ यांनी ही संकल्पना १८२८ मध्ये सूत्रबद्ध केल्याने या गुणोत्तराला त्यांचे नाव दिले गेले आहे.
केवळ अक्षीय म्हणजे रैखिक प्रतिविकृतीवर आधारलेल्या या साध्या कल्पनेचे त्रिमितीय प्रतिबल व त्रिमितीय प्रतिविकृती यांमध्ये व्यापकीकरण करणे शक्य आहे. ⇨ यामिकी च्या मूलभूत तत्त्वांच्या साहाय्याने या कल्पनेला गणितीय सूत्ररूप देता येते. स्थितिस्थापक वस्तू्ंवर कोणताही भार दिला असता त्यांच्यामध्ये निर्माण होणारी प्रतिबले व प्रतिविकृती शोधण्यासाठी या गणितीय सूत्राचा उपयोग होऊ शकतो. एकोणिसाव्या शतकातील फ्रेंच गणिती ⇨ ऑग्युस्तीन ल्वी कोशी यांनी १८२० मध्ये मुख्यतः स्थितिस्थापकतेचा सर्वसाधारण सिद्धांत सूत्रबद्ध केला.
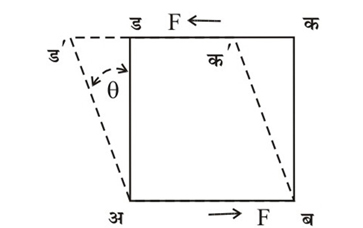
स्थितिस्थापक स्थिरांक : वस्तूंवर क्रिया करणार्या प्रेरणा प्रतिबलांनी व्यक्त करतात व दर एकक क्षेत्रफळावरील प्रेरणेच्या रूपात त्या मोजतात. आ. १ मध्ये चौरस काटच्छेदाचा दंड ( अबकड ) एका टोकाशी पक्का केला असून दुसर्या टोकावर एकसम रीतीने प्रेरणा (F) लावली आहे. यावरून प्रतिबल F/ (डक)2 मिळते. या प्रतिबलाने दंड अधिक लांब व म्हणून अधिक बारीक (अ’ब’क’ड’) होतो. दंडाच्या लांबीतील वाढ भागिले मूळ लांबी म्हणजे
| e = | DL | = | (ब’क’ – बक) |
| L | बक |
या गुणोत्तराने प्रतिविकृती मोजतात. हुक नियमानुसार प्रतिबल हे प्रति- विकृतीच्या प्रमाणात असते. परिणामी प्रतिबलाचे प्रतिविकृतीशी असलेले गुणोत्तर एक स्थिरांक असते. याबाबतीत यंग मापांक E ने दर्शवितात.
| म्हणून E | = | F | ÷ | (ब’क’– बक) | = | F.( बक) |
| (डक)2 | बक | (डक)2 . (ब’क’ – बक) |
प्वासाँ गुणोत्तराची (s) व्याख्या पार्श्व वा रैखिक प्रतिविकृतीचे अनुदैर्घ्य प्रतिविकृतीशी असलेले गुणोत्तर असे करतात, म्हणून
| s | = | (डक – ड’ क’) | ÷ | (ब’क’ – बक) | = | ( बक) . (डक – ड’ क’) |
| डक | बक | (डक) . (ब’क’ – बक) |

आ. १ मध्ये दंड ताणाखाली असून प्रतिबल तन्य आहे. ऋ प्रेरणेची दिशा उलट केल्यास प्रतिबल संकोचक होईल. या प्रकारच्या प्रतिबलांना थेट वा उदग्र परिबले म्हणतात. स्पर्शरेषीय वा कर्तन परिबल आ.२ मध्ये स्पष्ट केले आहे. याबाबतीत अबकड समाकार अबक’ड’ असा होतो आणि यावरील कर्तन प्रेरणा (F) अब आणि कड दिशांमध्ये कार्य करतात. कर्तन प्रति-विकृती q कोनाने मोजतात. वस्तू मुळात घनाकार असल्यास कर्तन प्रतिबल F / ( डक )२ असते. प्रतिबलाचे प्रति- विकृतीशी असलेले गुणोत्तर [ F / ( डक )२ . q ] हे कर्तन किंवा दृढता मापांक (G) आहे. या मापांकाने आकारमानात बदल न होता होणार्या आकारातील बदलाला द्रव्याकडून होणारा विरोध मोजला जातो.
व्याप मापांक (ज्ञ) हा आणखी एक स्थितिस्थापक स्थिरांक असून त्याद्वारे आकारात बदल न होता आकारमानात झालेल्या बदलाला द्रव्याकडून होणारा विरोध मोजतात. आ. ३ मध्ये मूळ समाकार अब वर्तुळाने दर्शविला आहे आणि एकसम म्हणजे जलस्थितिक दाबाखाली (P) अब वर्तुळाचे अ’ब’ वर्तुळ होते. नंतर व्याप मापांक ज्ञ =Pn / D n असा दर्शविता येतो. D n / n ही आयतनी वा मापी विकृती आहे. माप व्यापांकाचा व्यस्तांक म्हणजे संकोच्यता होय.
स्थितिस्थापक स्थिरांकांची मूल्ये ठरविणे : स्थितिस्थापक स्थिरांकाचे मूल्य त्याच्या व्याख्येत सुचविल्याप्रमाणे सरळ ठरविता येते. उदा., ज्ञात तन्य प्रतिबलाला लावलेल्या दंडाचे वा तारेचे सापेक्ष दीर्घीकरण मोजून यंग मापांक ठरविता येतो. कमी थेट असलेल्या पद्धती बहुधा अधिक सोयीस्कर व अचूक असतात. यांमध्ये गतिक पद्धती प्रमुख असून त्यांमध्ये कंपनांची कंप्रता ( दर सेकंदास होणार्या कंपनांची संख्या ) व ध्वनिप्रसारणाचा वेग विचारात घेतात. स्थितिस्थापक स्थिरांक नियमित आकाराच्या नमुन्यांच्या किंवा नमुन्यांतील वेगाच्या भाषेत मिती व घनता यांच्यासह व्यक्त करतात. नंतर या राशी मोजून स्थितिस्थापक स्थिरांकाचे मूल्य मिळू शकते.
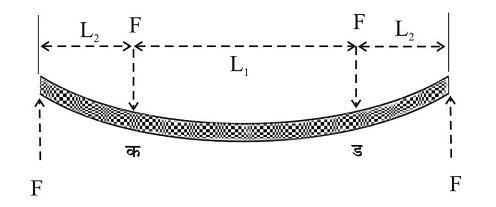
गज किंवा दंड यांचे नमन ( वाकणे ) व परिपीडन ( पिळवटणे ) यांवरूनही स्थितिस्थापक स्थिरांक ठरविता येतात. आ. ४ मधील दंडाची रुंदी ब आणि खोली वा जाडी ज असून तो टोकांशी ऋ प्रेरणांनी टांगला आहे. या प्रेरणांमुळे क आणि ड या बिंदूपाशी गजावर सममित रीतीने भार पडला आहे. कड भागावर एकसम नमन परिबल M = F.L2 आहे. कड हा भाग वर्तुळाच्या चापाच्या रूपात वाकतो आणि नमन सिद्धांतावरून त्याला R =EI/M हे समीकरण लागू पडते ( येथे R = वक्रतेची त्रिज्या, E = यंग मापांक व ख हे त्याच्या आडव्या छेदाचे निरूढी परिबल असून ते आयताकृती छेदाच्या बाबतीत बज३/१२ एवढे असते ). दंडाच्या खालच्या पृष्ठकावर तन्य अनुदैर्घ्य प्रतिबल आहे, तर वरच्या पृष्ठ-कावर संपीडक ( दाबणारे ) परिबल आहे. दंडाच्या मधल्या प्रतलावर प्रति-प्रतिबल नाही आणि हे प्रतल त्याचा तटस्थ अक्ष आहे. T =Ex2 /R = Mx2 /I या समीकरणात तटस्थ अक्षापासून x2 अंतरावरील प्रतिबल दाखविले आहे. अशा प्रकारे पहिल्या समीकरणावरून E चे मूल्य निश्चित करता येते व त्यासाठी I, R व M मोजतात. E माहीत असल्यास दुसर्या समीकरणावरून प्रतिबल ठरविता येते.
प्रत्यक्षातील मर्यादा : प्रत्यक्षात प्रतिबल फक्त प्रतिविकृतीच्या प्रमाणात असते. तसेच विशिष्ट स्थितिस्थापक मर्यादांमध्येच प्रतिविकृती पुन:प्राप्य ( परत मिळविता येण्याजोगी ) असते. प्रतिबलाच्या ज्या मूल्यापेक्षा कमी मूल्याला प्रतिविकृती पुनःप्राप्य असते, त्याला कधीकधी परिपूर्ण स्थितिस्थापकतेची मर्यादा म्हणतात. जोपर्यंत हुक नियम लागू पडतो तोपर्यंत प्रतिबलाच्या मूल्याला कधीकधी प्रमाणशीर मर्यादा किंवा रेषीय स्थितिस्थापकतेची मर्यादा म्हणतात. या मर्यादांच्या मूल्यांपेक्षा जास्त मूल्ये असतानाच्या परिस्थितीमध्ये द्रव्यावर कालाप्रमाणे अवलंबून असणारे परिणाम होतात. प्रतिबल आणखी वाढविल्यास ते द्रव्याच्या अंतिम प्रेरणेइतके वाढू शकते.
स्थितिस्थापकता सिद्धांत : स्थितिस्थापकतेच्या अभिजात सिद्धांतामध्ये प्रतिविकृती नेहमीच कमी मूल्य असलेली गृहीत धरीत. म्हणून तेथे हुक नियम लागू पडतो. प्रतिविकृती पुनःप्राप्य व अध्यारोपणक्षम असते. त्यामुळे दोन वा अधिक प्रतिबलांच्या एकत्रित क्रियेने निर्माण होणारी प्रतिविकृती ही त्या प्रत्येकामुळे निर्माण होणार्या प्रतिविकृतींची बेरीज असते.
स्थितिस्थापकतेच्या गणितीय सिद्धांतात आंशिक ⇨ अवकल समीकरणांची प्रणाली असते. तिच्या जोडीने कमी क्लिष्ट स्वरूपाची समीकरणे असतात. या समीकरणांत प्रतिबलांचा प्रतिविकृतींशी संबंध प्रस्थापित करतात. तसेच दिलेल्या प्रकारच्या द्रव्याच्या स्थितिस्थापक गुणधर्मांचे वैशिष्ट्य ठरविण्यास या समीकरणांची मदत होते. सर्वांत सामान्य किंवा व्यापक बाबतीत पंधरा राशी निश्चित करावयाच्या असतात. या राशी वस्तूमधील स्थान व काल यांच्या ⇨ फलनांच्या रूपात असतात. या राशींची सहा प्रतिबल घटक, सहा प्रतिविकृती घटक व विरूपित वस्तूचे स्थान निश्चित करणारे तीन सहनिर्देशक अशी विभागणी करता येते. स्थितिस्थापकतेविषयीच्या प्रश्नांचे स्थितिक व गतिक या दोन मुख्य वर्गांत विभागणी करता येते.
स्थितिक प्रश्न : कालानुसार न बदलणार्या प्रेरणा स्थितिस्थापक वस्तूंवर लावल्यास त्या वस्तूंच्या समतोलाविषयीचे स्थितिक ( स्थिर ) प्रश्न निर्माण होतात. वस्तू तिच्यावर पडणार्या प्रेरणांखाली टिकून राहण्याइतपत किंवा त्यांना विरोध करण्याइतपत पुरेशी प्रबल आहे की नाही, हे ठरविणे हा मूळ प्रश्न आहे. वस्तूमध्ये निर्माण होणारी प्रतिबले व प्रति-विकृती उचित मूल्यापेक्षा कमी राहतील तोपर्यंत वस्तू पुष्कळ प्रमाणात विरूपित होणार नाही, असे मानणे वाजवी ठरेल. वस्तू ज्या द्रव्यांची बनलेली असते त्या द्रव्यांच्या स्वरूपावर ही मूल्ये अवलंबून असतात. उदा., साध्या कार्बन पोलादाच्या वस्तू , यंत्रभाग इत्यादींचे अभिकल्प तयार करताना पुष्कळदा दर चौ.सेंमी.ला सु. १,४०० किग्रॅ. पेक्षा कमी असलेली प्रतिबले सहन होण्याजोगी असतात, असे गृहीत धरतात. अशा रीतीने ताणाखाली असलेला दंड कार्बन पोलादाचा असल्यास त्याचा अभिकल्प तयार करताना पुढील दक्षता घेतात : म्हणजे त्याच्या आडव्या छेदाचे क्षेत्रफळ (A) पुरेसे जास्त असेल व त्यामुळे त्यावर लावलेल्या प्रेरणेने (F) निर्माण होणारे परिबल (S) हे (S = F/A) दर चौ. सेंमी.ला सु.१,४०० किग्रॅ. पेक्षा कमी असेल.
लांब व बारीक गज दाब दिलेल्या संपीडक अवस्थेत असताना परिस्थिती यापेक्षा पुष्कळच वेगळी असते. कारण गजाची टोके एक-मेकांकडे दाबली जातात, तेव्हा तो वाकण्यासाठी वा वेडावाकडा होण्यासाठी सापेक्षतः थोड्याच दाबाची आवश्यकता असते. अशा गजातील संपीडक परिबल अगदी कमी असले, तरी गज अस्थिर होईल व स्थितिस्थापक अस्थैर्यामुळे मोठ्या प्रमाणात वाकेल.
गतिक प्रश्न : स्थितिस्थापक वस्तू व अभियांत्रिकीय संरचना यांच्याशी निगडित असलेले विविध गतिक प्रश्न आहेत. त्यांचा मुख्यतः कंपनांशी संबंध येतो. कालानुसार बदलणार्या प्रेरणा वस्तूवर लावल्यास कंपने निर्माण होतात. उदा., वार्यामुळे किंवा वाहतुकीमुळे पुलामध्ये निर्माण होणारी कंपने. अशी कंपने कधीकधी धोकादायक ठरू शकतात. पुलासारख्या बांधकामात वा संरचनेत विशिष्ट कंप्रतेच्या आवर्ती प्रेरणांनी कंपने निर्माण झाल्यास त्यांच्यामुळे संरचना भंग पावू शकते. या कंप्रतेला त्या संरचनेची तथाकथित अनुस्पंदन कंप्रता म्हणतात. यामुळे सैन्याचे पथक पुलावरून जाताना शिस्तबद्ध रीतीने पावले टाकत जात नाहीत. तथापि, याच प्रेरणा स्थितिकीय परिस्थितीत लावल्यास त्यांचे धोकादायक परिणाम होत नाहीत. गतिक प्रश्न हे स्थितिक प्रश्नांहून अधिक गुंता-गुंतीचे असतात आणि गतिक प्रश्न सोडविण्यासाठी उपाय योजताना सर्वसाधारणपणे अवकल समीकरणांचा संबंध येतो.
तरंग प्रसारण : स्थितिस्थापक घनरूप द्रव्यांमध्ये कंपनांशिवाय तरंग प्रसारणविषयक प्रश्नही असतात. पृथ्वीतील भूकंपीय तरंग हे याचे चांगले व परिचित उदाहरण आहे. भूकंपीय तरंग हे भूकवचातील तसेच पृथ्वीच्या खोलवरच्या अंतरंगातील स्थितिस्थापक तरंग असतात. भूकंपीय विक्षोभाचे विश्लेषण करताना स्थितिस्थापकता सिद्धांत वापरतात.ज्वालामुखी क्रियेमुळे अथवा खडकांमधील विभंगांना अनुसरून भूकवच सरकण्यामुळे भूकंपीय तरंग निर्माण होतात. भूकंपीय तरंगांच्या, विशेषतः ज्यांची प्रसारणाची गती पृथ्वीच्या संघटनाशी निगडित असते अशा तरंगां-विषयीच्या गणितीय सिद्धांतातून पृथ्वीच्या संरचनेविषयीची लक्षवेधक माहिती मिळाली आहे. ध्वनितरंग हे स्थितिस्थापक तरंगांचे दुसरे महत्त्वाचे उदाहरण आहे. सर आयझॅक न्यूटन यांनी प्रथम ध्वनितरंगांचा अभ्यास केला होता.
वायू व द्रव यांनाही स्थितिस्थापक गुणधर्म असतात. कारण दाबामुळे त्यांचे आकारमान ( घनफळ ) बदलते. घनफळातील लहान बदलांसाठी वायूच्या, द्रवाच्या किंवा घनद्रव्याच्या व्याप मापांकाची (ज्ञ) व्याख्या P = – ज्ञ (V-V0)/ V0 या समीकरणाद्वारे करतात. येथे P दाबाने द्रव्याच्या निश्चित द्रव्यमानाचे V0 घनफळ V एवढे कमी होते. सर्वसाधारणपणे द्रवरूप वा घनरूप द्रव्यापेक्षा वायू अधिक सहजपणे संपीडित होऊ शकत असल्याने द्रव व घन यांसाठी असलेल्या व्याप मापांकाचे मूल्य वायूसाठी पुष्कळच कमी असते. घनरूप द्रव्याच्या उलट द्रव किंवा वायू ही द्रव्ये कर्तन प्रतिबले तोलून धरू शकत नाहीत आणि द्रवांचा व वायूंचा यंग मापांक शून्य असतो.
पहा : आकार्यता; धातूंचे यांत्रिक गुणधर्म.
संदर्भ : 1. Amenzade, Y. W. The Theory of Elasticity, 1979.
2. Boresi, A. P. et al. Advanced Mechanics of Materials, 1993.
3. Borg, S. F. Fundamentals of Engineering : Elasticity, 1990.
4. Goodier, J. N. Theory of Elasticity, 1970.
5. Marsden, J. E. Hughes, T. J. Mathematical Foundations of Elasticity, 1983.
6. Saada, Abel S. Elasticity Theory and Applications, 1974.
ठाकूर, अ. ना.