घन अवस्था भौतिकी

घन अवस्था भौतिकी : या विषयामध्ये कोणताही पदार्थ घन अवस्थेत असताना तो दर्शवीत असलेल्या गुणधर्मांचा विचार केला जातो. साधारणतः पदार्थाच्या घन, द्रव व वायू अशा तीन ठोकळ आणि चौथी आयनद्रायूची (इलेक्ट्रॉन, विद्युत् भारित अणू वा रेणू म्हणजे आयन आणि निर्विद्युत् अणू व रेणू यांच्या आणि ज्यातील इलेक्ट्रॉन व धन विद्युत् भारित आयन यांची संख्या जवळजवळ सारखी असल्यामुळे परिणामतः जो निर्विद्युत् आहे अशा समूहाची) अशा एकूण चार अवस्था मानल्या जातात. वायू अवस्थेमध्ये इतर दोन्ही अवस्थांच्या मानाने शेजारशेजारच्या दोन रेणूंमधील अगर अणूंमधील अंतर बरेच असते. द्रवाच्या दोन रेणूंमधील अंतर कमी असल्याने त्यांचे सापेक्ष स्वातंत्र्य कमी असते. घन अवस्थेतील पदार्थांत मात्र हे अंतर सर्वांत कमी असते [⟶ द्रव्याच्या अवस्था आयनद्रायु भौतिकी], त्यामुळे रेणूंना इतरत्र फिरण्याचे स्वातंत्र्य नसतेच पण केवळ त्यांच्या एकमेकांजवळच्या सान्निध्यामुळे घनाच्या गुणधर्मांवर परिणाम होणे अपरिहार्य ठरते. त्यामुळेच घन पदार्थांच्या गुणधर्मांचा अभ्यास करणे अत्यंत बोधप्रद ठरले आहे. घन अवस्था भौतिकीचा मुख्य उद्देश घन पदार्थांचे विविध गुणधर्म आणवीय आणि अणुकेंद्रीय सिद्धांताच्या रूपात मांडणे आणि त्याचा व्यावहारिक वा तांत्रिक (उदा., ट्रँझिस्टर प्रयुक्ती) उपयोगाच्या दृष्टीने अभ्यास करणे हा आहे. 

साधारणतः सोळाव्या शतकापासून स्फटिक द्रव्यांच्या, मुख्यत्वेकरून खनिज द्रव्यांच्या, अभ्यासामुळे या शास्राच्या इतर अंगांमध्ये जास्त रस घेतला जाऊ लागला. सर्व स्फटिक द्रव्यांचे यांत्रिक व प्रकाशीय गुणधर्म तत्कालीन पद्धतीनुसार निरीक्षिले गेले. या निरीक्षणांनुसार काही स्फटिक द्रव्ये असमदिक् (भिन्न दिशांत भिन्न गुण असणारी) आढळली. निरनिराळ्या गुणधर्मांच्या निरीक्षणांच्या पद्धतींत यानंतर आमूलाग्र बदल होत जाऊन ही प्रगती आजतागायत चालूच आहे.

जालक सिद्धांत : अठराव्या शतकाच्या अखेरीस व एकोणिसाव्या शतकाच्या सुरुवातीस स्फटिकांच्या सममितीय (पदार्थांचे दोन वा अनेक भाग केले असता ते भाग रचनेत, आकारात पूर्णपणे एकमेकांसारखे असल्यामुळे होणाऱ्या) गुणधर्मांचा जास्त अभ्यास झाला. आणवीय सिद्धांताप्रमाणे हे सर्व गुणधर्म अणूंच्या पद्धतशीर रचनेमुळे असले पाहिजेत हे सिद्ध झाले. ब्राव्हे या शास्त्रज्ञांनी त्यांच्या पूर्व निरीक्षणावरून असे सुचविले की, स्फटिकांमधील एकमेकांस लंब अशा तीन दिशांत अणूंची अगर रेणूंची व्यवस्थित रचना झालेली असते. अशा तऱ्हेने सर्व स्फटिकांच्या गुणधर्मांवरून व त्यांमधील सममितीवरून त्यांचे मुख्य प्रकार पाडण्यात आले. त्यात पुन्हा एखादा अणू एकक घटकामध्ये जास्त झाला, तर तो ज्या पद्धतीने सामावला जाऊ शकेल अशा तीन पद्धती विचारात घेऊन स्फटिकाचे १४ प्रकार पाडण्यात आले. त्यांना ब्राव्हे जालक म्हणतात. त्यातून पुन्हा स्फटिकात आढळून येणारे ‘विशेष’ विचारात घेतले जाऊन स्फटिकांचे ३२ बिंदू समूहांत व २३० अवकाश समूहांत वर्गीकरण केले गेले [⟶ स्फटिकविज्ञान].

निर्दोष स्फटिकांचे इलेक्ट्रॉनीय गुणधर्म : धातूंच्या अणूंमधील बाह्यतम परिभ्रमण कक्षांतील इलेक्ट्रॉन हे मोकळे असल्याने ते मुक्त वायूप्रमाणे वागतात असे गृहीत धरून ड्रुडे व लोरेन्ट्स यांनी प्रथमतः मुक्त इलेक्ट्रॉन सिद्धांत पुढे मांडला. नंतर बोर्न, माडेलुंग या शास्त्रज्ञांनीही अशाच प्रकारचे प्रयत्न केले. तथापि यांपैकी कोणताही सिद्धांत प्रायोगिक निष्कर्षांशी न जुळल्याने ते स्वीकारले गेले नाहीत. या संबंधात १९२५ पासून पुढे तरंग-यामिकी (द्रव्य तरंगांस लागू पडणारे प्रेरणाविज्ञान) व ⇨ पुंजयामिकी  यांचा उपयोग करण्यास सुरुवात झाली.

घन पदार्थातील इलेक्ट्रॉनांच्या वर्तणुकीचा अभ्यास पुढे विग्नर, साइट्स, स्लेटर, मॉट वगैरे शास्त्रज्ञांनी केला आणि प्रकाशीय, विद्युत व औष्णिक गुणधर्मांचे स्पष्टीकरण झाले.

अपूर्णतेवर अवलंबून असणारे गुणधर्म : निर्दोष स्फटिकांच्या गुणधर्मांचे वर्गीकरण करण्याचे कार्य सुरू असतानाच स्फटिकातील निरनिराळ्या दोषांवर अवलंबून असणाऱ्या गुणधर्मांचा अभ्यास हा एक स्वतंत्र विषय झाला. या विषयाची प्रगती १९४० पर्यंत सावकाश, पण नंतर मात्र झपाट्याने झाली. पहिल्या महायुद्धापूर्वी या विषयाचा अभ्यास फ्रेंकेल बेअडेकर, टेलर वगैरेंनी केला. तथापि दुसऱ्या महायुद्धापर्यंत हा विषय अपूर्णावस्थेतच होता.

पृष्ठ गुणधर्म : घन पदार्थांच्या पृष्ठांच्या गुणधर्मांचा अभ्यास अलीकडे महत्त्वाचा ठरला आहे. या विषयाला १९४७ नंतर फार मोठी चालना मिळाली. जे. बारडीन यांनी असे सुचविले की, धातूंचे आणि अर्धसंवाहकांचे (ज्यांची विद्युत् संवाहकता धातू व विद्युत् निरोधक यांच्या दरम्यान आहे अशा पदार्थांचे) स्पर्श गुणधर्म (निरनिराळे घन पदार्थ एकमेकांस चिकटवून ठेवल्यास दिसणारे गुणधर्म) हे पृष्ठाभागातील इलेक्ट्रॉनांवर अवलंबून असतात. यानंतर नवनवीन प्रायोगिक उपकरणांच्या मदतीने याविषयाच्या अभ्यासावर जास्त भर दिला गेला.

घन पदार्थांचे प्रकार : घन पदार्थांचे मुख्यत्वे स्फटिकी आणि अस्फटिकी असे दोन प्रकार पाडण्यात येतात. पैकी स्फटिकी पदार्थांचा सखोल अभ्यास झाला आहे. हे पदार्थ लहान लहान स्फटिकांचे बनले असल्याने त्यांतील अणूंची संरचना सुसंबद्ध असते. साधारणतः सर्व धातू आणि खनिजे या प्रकारात मोडतात. याउलट निरनिराळ्या काचा प्लॅस्टिक इ. पदार्थ अस्फटिकी असून त्यांमधील अणूंची संरचना पद्धतशीर वा सुसंबद्ध नसते. प्रस्तुत नोंदीत मुख्यतः स्फटिकी पदार्थांचा विचार केला आहे. स्फटिकी पदार्थांचे पाच प्रकार मानण्यात येतात.

(१) धातू व मिश्रधातू : विद्यूत् व औष्णिक संवाहकता आणि चकाकी ही धातू व मिश्रधातूंची वैशिष्ट्ये होत. यांची विद्युत् संवाहकता जास्त असून ती इलेक्ट्रॉनांच्या संचलनामुळे निर्माण होत.

(२) लवण : यात सोडियम क्लोराइड, लिथियम क्लोराइड इ. पदार्थ मोडतात. यांची विद्युत् संवाहकता आयनीय (आयनाच्यामुळे) असून साधारणतः तापमानाबरोबर वाढत जाते. लवणे अवरक्त (वर्णपटातील तांबड्या रंगाच्या अलीकडील मोठ्या तरंगलांबीच्या) किरणांचे भरपूर शोषण करतात.

(३) संयुजी स्फटिक : अशा प्रकारचे स्फटिक (उदा., हिरा, सिलिकॉन इ.) कठीण किंवा ठिसूळ असे असतात. सर्वांत साध्या एकाणू प्रकाराचा (उदा., हिरा) वैशिष्ट्यपूर्ण गुणधर्म असा की, त्यातील कोणताही अणू त्याच्या संयुजेएवढ्या (एका अणूच्या दुसऱ्या अणूंशी संयोग पावण्याच्या क्षमतेएवढ्या हिरा चतुःसंयुजी आहे) अणूंनी वेढलेला असतो. हे विद्युत् निरोधक असतात. 

घन पदार्थातील अणू, आयन अगर रेणू एकमेकांना अत्यंत घट्ट चिकटून बसलेले असतात. त्यांना एकमेकांपासून दूर करण्याकरिता जी ऊर्जा लागते तिला त्यांची बंधन-ऊर्जा म्हणतात. ही बंधन-ऊर्जा आयनीय व सहसंयुजी स्फटिकांत साधारणतः जास्त असते.

(४) रेणवीय स्फटिक : या प्रकारात अनेक कार्बनी संयुगांचे स्फटिक येतात. या पदार्थांचा बाष्पदाब साधारण तापमानासही भरपूर असतो. वर उल्लेखिलेली बंधन-ऊर्जा रेणवीय स्फटिकात सर्वांत कमी असते.

(५) हा प्रकार म्हणजे हायड्रोजनबंधित स्फटिक होय (उदा., बर्फ, हायड्रोजन क्लोराइड). अनेक रेणूंचे समूह बनविण्याची प्रवृत्ती या प्रकारच्या स्फटिकांत आढळते.

स्फटिकी घनातील अणूंची अंतर्गत रचना : स्फटिकांतील अणूंची रचना आवर्ती (पुनःपुन्हा तशीच आढळणारी) व सुरचित असते. स्फटिकातील अणूंमधील अंतर साधारणतः १०^-८ सेंमी. इतके असते. क्ष-किरणांची तरंगलांबीदेखील इतकीच असल्याने स्फटिकांचा, क्ष-किरणांच्या विवर्तनासाठी (पार्य किंवा अपार्य पदार्थांच्या कडेवरून जाताना किरणांचा दिशाबदल करण्यासाठी) उपयोग होणे शक्य आहे. या कल्पक विचाराने फोन लौए यांनी प्रथमतः यशस्वी प्रयोग केले. फ्रीड्रिख व निपिंग यांच्या सहकार्याने लौए यांनी झिंक सल्फाइड या स्फटिकाचा अभ्यास केला. त्यांना असे दिसून आले की, स्फटिकामधून क्ष-किरण पाठविल्यानंतर मिळणाऱ्या आकृति-विशेषातील बिंदू (लौए बिंदू) हे स्फटिकांच्या प्रकारावर अवलंबून असतात. या पद्धतीने त्यांनी निरनिराळ्या प्रकारच्या स्फटिकांचे आकृति-विशेष मिळविले. या सर्व अभ्यासावरून स्फटिकातील अणू त्रिमित जालकात सुरचित असतात ही गोष्ट सिद्ध झाली [⟶ क्ष-किरण].

---

विवर्तन : पदार्थाची अंतर्गत रचना समजावून घेण्यासाठी साधारणतः क्ष-किरण विवर्तन, ⇨इलेक्ट्रॉन विवर्तन  व न्यूट्रॉन विवर्तन ही तंत्रे अवलंबिली जातात.  

स्फटिकी पदार्थावर कमी वेगाचे न्यूट्रॉन पाठवून विवर्तनाचे निरीक्षण करून त्यावरून चुंबकीय आणि इतर गुणधर्म अभ्यासता येतात. अणुभट्टीतून मिळण्याऱ्या निरनिराळ्या वेगांच्या अगर तरंगलांबीच्या न्यूट्रॉनांद्वारा, क्ष-किरणांतील लौए पद्धतीप्रमाणे, स्फटिकांच्या अंतर्गत रचनेचा अभ्यास करण्यात आला. त्याचप्रमाणे एकाच तरंगलांबीच्या न्यूट्रॉनांचा उपयोग क्ष-किरणातील डेबाय, शेरर आणि हल यांच्या तंत्राने करण्यात आला. न्यूट्रॉन विवर्तनाच्या अभ्यासासाठी बोरॉन ट्रायफ्ल्यूओराइड हा वायू असणारे गायगर–म्यूलर गणित्र (ज्यामध्ये प्रवेश करणाऱ्या विद्युत् भारित कणांची संख्या मोजण्यासाठी त्या कणांमुळे होणाऱ्या आयनीभवनाचा उपयोग करण्यात येतो असे गायगर व म्यूलर यांनी शोधून काढलेले साधन) वापरण्यात आले. अशा रीतीने न्यूट्रॉन विवर्तनाद्वारे लिथियम-पोटॅशियम व सोडियम हायड्राइड, बर्फ वगैरे पदार्थांची संरचना सुस्पष्ट होऊ शकली.

इलेक्ट्रॉन विवर्तनासाठी लागणाऱ्या परीक्ष्य वस्तूची जाडी १०^-४ सेंमी. इतकी, क्ष-किरणांसाठी काही मिमी., तर न्यूट्रॉन विवर्तनासाठी काही सेंमी. इतकी असते.

अणूंच्या रचनेतील दोष : स्फटिकांच्या निरनिराळ्या गुणधर्माच्या स्पष्टीकरणार्थ मांडले जाणारे सिद्धांत हे साधारणतः दोषरहित स्फटिकांना लागू पडतात. तथापि धातूंत अगर अर्धसंवाहकांत प्रत्यक्षात असणाऱ्या दोषांचा अभ्यास करणे हेही महत्त्वाचे आहे. कारण अगदी आदर्श वा दोषरहित स्फटिक व्यवहारात मिळविणे हे जवळजवळ अशक्यच असते. पण संशोधन आणि उपयुक्तता या दृष्टीने निरनिराळे दोष वा अपूर्णत्व असणारे स्फटिक महत्त्वाचे आहेत. उदा., स्फटिकांतील अशुद्धीमुळेच त्यांना विशेष उपयुक्त गुणधर्म प्राप्त होतात. या प्रकारच्या अशुद्धीचे वर्गीकरण खालीलप्रमाणे करता येईल [⟶ अर्धसंवाहक].

इलेक्ट्रॉन किंवा पोकळी : सध्याच्या दृष्टीकोनानुसार स्फटिकातून स्वैर संचार करणारा इलेक्ट्रॉन हा त्या स्फटिकातील एक दोष मानला जातो. हा इलेक्ट्रॉन जर अशुद्धी अणूपासून आलेला असेल, तर तो इलेक्ट्रॉन व उरणारा आयन हे दोघेही दोष अथवा अपूर्णता म्हणून वागतात. अर्थात हा इलेक्ट्रॉन परत अशुद्धी आयनाशी जोडला जाऊ शकतो.

एक्साइटॉन : मुक्त इलेक्ट्रॉन व पोकळी तयार करण्याच्याऐवजी एखादा फोनॉन (ऊष्मीय ऊर्जाकण) वा फोटॉन (प्रकाश ऊर्जाकण) इलेक्ट्रॉन-पोकळी जोडी निर्माण करू शकतो. या प्रकारास एक्साइटॉन म्हणतात. अशुद्धी केंद्राची ऊर्जा-पातळी स्थानिक स्वरूपाची असते, तर एक्साइटॉन ही संपूर्ण जालकाचीच क्षोभित अवस्था असते.

एक्साइटॉन कल्पनेचा उपयोग स्फटिकांच्या सिद्धांतात खालील गुणधर्मांच्या स्पष्टीकरणासाठी करून घेण्यात आला आहे.

(अ) बऱ्याच विद्युत् निरोधकांचे (विद्युत् प्रवाहास तीव्र विरोध करणाऱ्या पदार्थांचे) व काही अर्धसंवाहकांचे शोषण वर्णपट [⟶ वर्णपटविज्ञान].

(आ) ‘फॉस्फर’ मधील (विशिष्ट तरंगलांबीचे प्रारण म्हणजे तरंगरूपी ऊर्जा शोषून घेऊन ते दृश्य प्रकाशाच्या रूपाने बाहेर टाकणाऱ्या पदार्थातील) काही दृश्य प्रकार.

(इ) दुय्यम उत्सर्जनाच्या बाबतीत (एखाद्या पृष्ठभागावर दुसऱ्या एखाद्या उद्‌गमापासून निघणाऱ्या इलेक्ट्रॉनांचा भडिमार केल्याने त्या पृष्ठभागापासून इलेक्ट्रॉन उत्सर्जित होण्याच्या बाबतीत).

फोटॉन : अर्धसंवाहकातील परस्पर क्रियांचे मध्यस्थ म्हणून फोटॉनाचे महत्त्व जास्त आहे. स्फटिकामध्ये फोटॉनाचे साधारणतः फोनॉनामध्ये वा इलेक्ट्रॉन-पोकळी जोडीमध्ये रूपांतर होत असते. बोस-आइन्स्टाइन सांख्यिकीनुसार [⟶ सांख्यिकीय भौतिकी] फोनॉन आणि फोटॉन यांच्या समुदायांच्या गुणधर्मांसंबंधी निष्कर्ष काढता येतात. उदा., प्लांक यांचा प्रारण नियम (विद्युत् चुंबकीय ऊर्जेच्या निरनिराळ्या तापमानांत होणाऱ्या वितरणासंबंधीचा नियम) हा त्यांपैकी एक होय.

फोनॉन : फोनॉन हे फोटॉनाप्रमाणेच (जालक कंपनांचे) तरंगरूप होत. फोनॉन हे ध्वनीचे पुंज (सर्वांत लहान अविभाज्य राशी, क्वांटम) असतात. स्फटिकाचा फोनॉन वर्णपट स्पष्ट करण्यासाठी डेबाय तापमान महत्त्वाचे असते. हे तापमान खालील समीकरणाने दिले जाते :

kT_D = hν_m           

  

येथे k बोल्टस्‌मान विश्वस्थिरांक, T_D डेबाय तापमान, h प्लांक विश्वस्थिरांक, V_m महत्तम कंप्रता (दर सेकंदास होणारी कंपन संख्या) आहे. जालक कंपनांचा विचार केल्यास स्फटिकी घनांच्या बाबतीत स्थिर आकारमानातील आणवीय विशिष्ट उष्णता C_v साठी पुढील समीकरण मिळते.

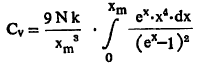
यात  T = निरपेक्ष तापमान , N = अणूंची घनता आहे [⟶ उष्णता] .

औष्णिक समतोलाच्या बाबतीत फोनॉनाचे कार्य मध्यस्थाप्रमाणे असते, म्हणजे इलेक्ट्रॉन, अशुद्धी कण आणि फोनॉन यांमधील परस्पर क्रियेमुळेच मुक्त इलेक्ट्रॉनांची घनता स्थिर राहते. तसेच तापमानावर अवलंबून असणाऱ्या इतरही अनेक विक्रिया केवल फोनॉनामुळे सुरू होतात.

जालकांकडून इलेक्ट्रॉन वा पोकळी यांचे होणारे प्रकीर्णन (विखुरले जाणे) हे फोनॉनाद्वारेच होत असते.

केवळ इलेक्ट्रॉन अथवा पोकळी यांचा विचार करून स्फटिकांची औष्णिक निरोधकता स्पष्ट करता येत नाही. त्यासाठी फोनॉन विचारात घ्यावेच लागतात. ⇨ अतिसंवाहकतेचे कारणही फोनॉनाच्यामुळे असावे असे मानतात.

अशुद्धी अणू : अर्धसंवाहकाच्या बाबतीत आढळणाऱ्या स्फटिकातील सर्व अपूर्णतांमध्ये परका अणू ही सर्वांत महत्त्वाची अशुद्धी होय. अर्धसंवाहकाचा उपयोग केल्या जाणाऱ्या सर्व उपकरणांमध्ये अशा प्रकारच्या दोषांचा विचार करावाच लागतो. अशुद्धीमुळे निर्माण होणाऱ्या काही परिणामांपैकी काही महत्त्वाचे परिणाम पुढे दिले आहेत.

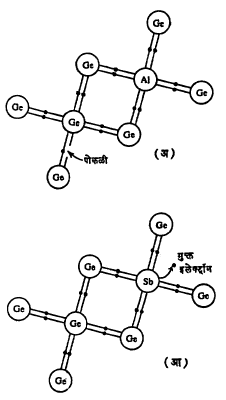
अशुद्धीमुळे स्फटिकाच्या वर्णपटात नवीन इलेक्ट्रॉनीय ऊर्जा पातळीची भर पडते. अशुद्धी दोन प्रकारच्या असून काही इलेक्ट्रॉन देतात तर काही घेतात. त्यांना अनुक्रमे दाता आणि ग्राहक असे म्हणतात. उदा., जर्मेनियमामध्ये अशुद्धी म्हणून असलेल्या  ⇨ आवर्त सारणीच्या (मूलद्रव्यांच्या इलेक्ट्रॉन रचनेनुसार केलेल्या कोष्टकरूप मांडणीच्या) पाचव्या स्तंभातील मूलद्रव्यांची इलेक्ट्रॉन देण्याकडे प्रवृत्ती असते, तर तिसऱ्या स्तंभातील मूलद्रव्ये इलेक्ट्रॉन घेऊ पाहतात. जर्मेनियमामध्ये ॲल्युमिनियम अशुद्धी मिसळल्यास ॲल्युमिनियमाच्या अणूच्या बाह्य कक्षेत तीनच इलेक्ट्रॉन असल्याने जर्मेनियमामधील एक इलेक्ट्रॉन ॲल्युमिनियमाकडे येतो आणि अशा तऱ्हेने इलेक्ट्रॉनाच्या जागी एक पोकळी निर्माण होते (आ. १ अ).

याउलट जर्मेनियमामध्ये अँटिमनी अशुद्धी मिसळल्यास असे दिसून येते की, अँटिमनीजवळ बाह्य कक्षेत पाच इलेक्ट्रॉन असल्याने पाचवा इलेक्ट्रॉन देण्याकडे तिचा कल जातो व तोच इलेक्ट्रॉन जर्मेनियमाच्या वहन पट्ट्यात जातो (आ. १ आ).

स्फटिकात अशुद्धी असणे म्हणजेच स्फटिकाचे पूर्णत्वापासून झुकणे होय. या अशुद्धीमुळे (विद्युत् भारित, अभारित वा त्यांच्या समूहामुळे) प्रकीर्णन होत असते.

त्याचप्रमाणे अशुद्धी कणांचे इतरही अनेक रासायनिक, चुंबकीय व प्रकाशीय गुणधर्मांवर परिणाम झालेले दिसून येतात.

जालक दोष : स्फटिक जालकात अनेक प्रकारचे दोष असू शकतात. त्यांपैकी शोट्‌की आणि फ्रेंकेल दोष हे महत्त्वाचे आहेत. जालकात एखादी जागा रिकामी राहणे याला शोट्‌की दोष म्हणतात व एखादा अणू जालकातील स्वतःची जागा सोडून जेव्हा आंतरकोशीय (स्फटिक कोशांत अणूंच्या किंवा आयनांच्या नेहमीच्या स्थानाव्यक्तिरिक्त) भागात जातो तेव्हा फ्रेंकेल दोष निर्माण होतो. स्फटिक जर निरपेक्ष शून्य तापमानास वाढविला गेला नसेल, तर अशा दोषांची संख्या (n) पुढील समीकरणाने दिली जाते.

येथे n_o=स्फटिकातील एकंदर अणू, W=दोष निर्माण करण्यासाठी लागणारी ऊर्जा. स्फटिक तापविल्यास

अशा दोषांची संख्या कमी होते. फ्रेंकेल दोष निर्मितीस लागणारी ऊर्जा ही नेहमी शोट्‌की दोषासाठी लागणाऱ्या ऊर्जेपेक्षा कमी असते. या दोषांचे स्वरूप आ. २ वरून स्पष्ट होईल.

जालक दोष हे प्रायोगिक दृष्ट्या महत्त्वाचे असे इतर अनेक गुणधर्म दर्शवितात. (१) हे दोष इलेक्ट्रॉन व पोकळीप्रमाणे प्रकीर्णन केंद्रे म्हणून वागू शकतात. (२) काही स्फटिकांच्या प्रकाशीय गुणधर्मांवर जालक दोषांचा बराच परिणाम झालेला असतो.

त्याचप्रमाणे या दोषांमुळे यांत्रिक व चुंबकीय गुणधर्मही बदलू शकतात.

स्थानभ्रंश : स्थानभ्रंश या दोषाचा अभ्यास मुख्यत्वे टेलर आणि ओरोवान यांच्यामुळे सुरू झाला. निर्दोश स्फटिकाच्या मानाने सदोष स्फटिकात आढळणारा कमकुवतपणा हा त्यातील स्थानभ्रंशामुळे असतो असे त्यांनी सुचविले. या दोषाचे दोन प्रकार आहेत.

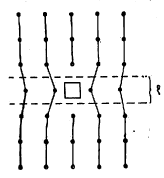
पहिल्या प्रकारास ‘कड स्थानभ्रंश’ म्हणतात. स्फटिकात एखादा स्तर मध्येच जादा झाला आहे असे समजल्यास या दोषाची कल्पना येते.             

आ. ३ मध्ये दर्शविलेल्या अर्ध्या स्तराच्या शेवटी त्यास अथवा या कागदाच्या पृष्ठास ९० अंशाचा कोन करून हा दोष असतो. आपण त्याच्या अखेरीच्या टोकापासून जसजसे दूर जाऊ, त्यांप्रमाणे हा फरक कमी होत जाऊन शेवटी जालक पूर्ववत पूर्णावस्थेस जातो. या दोषाला स्फटिकांची ऊर्जी वगैरे संदर्भांत फार महत्त्व आहे.

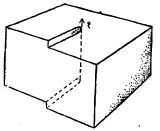
स्थानभ्रंशाचा दुसरा प्रकार म्हणजे ‘मळसूत्री स्थानभ्रंश’ हा होय. जालकातील काही भागाची हालचाल होऊन तो भाग एका अणुस्तरातून वर सरकला आहे असे समजल्यास या दोषाची कल्पना येते (आ. ४). या दोषाचा आधार घेऊन स्फटिकाच्या वाढीबद्दल माहिती मिळते.

या सर्व दोषांप्रमाणेच जर एखादा कण स्फटिकातून फिरत असेल, तर तोही दोषच समजला जातो. कारण अशा कणामुळे स्फटिकात तापमान वाढ, आयनीभवन (आयन निर्माण होणे) इ. गोष्टी उद्‌भवतात .

यांत्रिक गुणधर्म : घन पदार्थ त्याच्या आकारमानात बदल करू पाहणाऱ्या प्रेरणेस विरोध करतात म्हणजे एका विशिष्ट मर्यादेपर्यंत ही प्रेरणा असल्यास प्रेरणा दूर होताच पदार्थ मूळ आकार धारण करतात या गुणधर्मास स्थितिस्थापकता असे म्हणतात [⟶ स्थितिस्थापकता].

असमदिकता : काही स्फटिक त्यांच्यातील निरनिराळ्या दिशांमध्ये निरनिराळे गुणधर्म दर्शवितात या गुणधर्मास असमदिकता असे म्हणतात. ही असमदिकता खालील उदाहरणावरून स्पष्ट होईल.

जस्तामधील ऊष्मीय प्रसरण गुणांक (एकक तापमानात व एकक लांबीत होणारी वाढ) हा एका दिशेत ६·३९ x १०^-५ (से.)^-१ तार तिच्याशी ९० अंशाचा कोन करणाऱ्या दिशेत १·४१ x १०^-५ (से.)^-१ इतका असतो. याच दोन दिशांत रोधकता (एकक लांबी आणि एकक क्षेत्रफळाच्या संवाहकाचा विद्युत् रोध) अनुक्रमे ६·०६ x १०^-६ ओहम-सेंमी. व ५·८३ x १०^-६ ओहम-सेंमी. अशी असते. या गुणधर्माप्रमाणे विशिष्ट उष्णतादेखील बदलत असते. ही असमदिकता असण्याचे कारण म्हणजे निरनिराळ्या दिशांत अणूंची निरनिराळ्या पद्धतीने झालेली रचना होय.

स्फटिकाची वाढ : स्फटिक तयार होण्याचे साधारणतः तीन प्रकार आहेत. तयार केलेल्या संपृक्त (विरघळलेल्या पदार्थाचे प्रमाण दिलेल्या परिस्थितीत जास्तीत जास्त असलेल्या) विद्रावापासून, वितळून तयार झालेल्या द्रवापासून अगर बाष्परूपातून घन पदार्थांचे स्फटिकीभवन होऊ शकते. स्फटिकांची वाढ ही स्फटिकांची अंतर्गत रचना, द्रव व इतर बाह्य कारणांवर अवलंबून असते. स्फटिक वाढीची उपपत्ती स्पष्ट करण्याचे अनेक प्रयत्न झाले आहेत. हे प्रयत्न गिब्ज, वुल्फ वगैरे शास्त्रज्ञांनी केले. 

ज्याप्रमाणे भिंत बांधतात त्याप्रमाणे निसर्गात स्फटिक तयार होत असतात. या कल्पेनेनुसार आ. ५ मध्ये स्फटिक वाढीचे चित्र दाखविले आहे. या रचनेतील अणू अगर रेणू त्यांच्या गतिजन्य शक्तीमुळे कायम हालचाल करीत असतात. त्यामुळे एखाद्या ठिकाणी ते एकाएकी जाऊन बसू शकतात किंवा एखाद्या ठिकाणाहून ते तडकाफडकी बाहेर पडू शकतात. तथापि अशा रीतीने होणारी वाढ व्यवस्थित नसते, हे ताबडतोब दिसून येते.

---

१९४९ साली फ्रांक यांनी असे सुचविले की, निरनिराळे स्तर हे बरोबर एकावर एक असे न राहता मळसूत्राप्रमाणे जर त्यांची रचना होत गेली, तर स्फटिकांची वाढ कशी होते हे सहज स्पष्ट करता येईल. स्फटिकामधील जवळजवळचे दोन भाग एकमेकांपासून घसरले आहेत असे समजल्यास मळसूत्री स्थानभ्रंशाची कल्पना येते. आ. ६ मध्ये दर्शविलेली प्रतिकृती उजव्या हाताच्या मळसूत्राची आहे, कारण या ठिकाणी स्फटिक वाढीचा मार्ग खालून उजवीकडे जातो. फ्रांक यांच्या सिद्धांताचा प्रायोगिक पुरावा ग्रिफिन यांनी दिला.

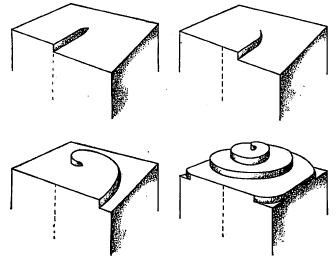
स्फटिकाच्या वाढीचे प्रायोगिक रीत्या निरीक्षण करण्यासाठी निरनिराळी तंत्रे अवलंबिण्यात आली आहेत. अशा तऱ्हेने निरीक्षिलेले काही प्रकार आ. ७ मध्ये दाखविले आहेत.

 

औष्णिक गुणधर्माचा जालक सिद्धांत : जालकात अणूंची स्वतःचा स्थानाजवळ आंदोलने होतात. औष्णिक गुणधर्म या जालक आंदोलन कल्पनेने व संबंधित फोनॉन कल्पनेने स्पष्ट होतात. पदार्थाचे स्थितिस्थापकीय गुणांक हे दोन अणूंमधील प्रेरणेवर अवलंबून असतात. यांचे गुणांक ठरविण्यासाठी प्रथमतः जोन्स, झेनर इत्यादींनी काही अंशी यशस्वी प्रयोग केले. बॅरेट यांनी काढलेले निष्कर्ष झेनर यांनी सुधारलेल्या भाकितानुसार आहेत (उदा., सोडियम व लिथियमामधील स्थानांतरे वगैरे).

विद्युत् निरोधक व प्रकाशीय गुणधर्म : विद्युत् निरोधक म्हणजे तौलनिक दृष्ट्या कमी संवहन करणारा वा पूर्णपणे संवहन न करणारा पदार्थ होय. प्रत्यावर्ती (उलट सुलट) दिशेने वाहणाऱ्यां प्रवाहाच्या क्षेत्रामध्ये काही पदार्थांची विद्युत् निरोधक वैशिष्ट्ये ही त्यांच्या कंपनसंख्येनुसार बदलत असतात.

चुंबकीय गुणधर्मांप्रमाणेच ज्या प्रकाशीय गुणधर्मांचा नीट उलगडा होत नव्हता ते गुणधर्म पुंजसिद्धांतामुळे स्पष्ट केले गेले. विशेषतः ही प्रगती धातूंच्या बाबतीत उल्लेखनीय झाली. उदा., सोने, तांबे अगर    पितळेसारख्या मिश्रधातू यांच्या रंगाचे आणि क्षार धातू (लिथियम, सोडियम, पोटॅशियम इ.) वर्णपटाच्या जंबुपार (दृश्य वर्णपटातील जांभळ्या रंगाच्या पलीकडील लहान तरंगलांबीच्या) भागात पारदर्शक का होतात याचे उत्कृष्ट स्पष्टीकरण मुक्त इलेक्ट्रॉन सिद्धांताने मिळते.

लोहविद्युत् : ही संज्ञा लोहचुंबकत्वाप्रमाणे विजेच्या बाबतीत होणाऱ्या पदार्थाच्या वर्तणुकीस लावली गेली. दोन्ही प्रकारांसाठी सहकारी रेणवीय परिणाम हा मूलभूत आहे. हा परिणाम म्हणजे चुंबकत्वामध्ये काही धातू मूलद्रव्यांमधील इलेक्ट्रॉन परिवलनरूपाने (स्वतःभोवती फिरण्यामुळे चुंबकत्वाच्या उगमाने) तर विद्युत् निरोधनाच्या बाबतीत कायमच्या अथवा स्थानिक प्रत्यावर्ती क्षेत्रातून निर्माण झालेले द्वि-ध्रुव (सारख्या मूल्यांच्या व परस्परांशी विरुद्ध असलेल्या दोन विद्युत् भारांचे सान्निध्य) या रूपाने दिसून येतो.

स्वयंस्फूर्त विद्युत् ध्रुवण (निरोधकाच्या एकक घनफळात असणारी द्वि-ध्रुव परिबलांची संख्या निरोधकाच्या कणातील धन व ऋण विद्युत् बाह्य विद्युत् प्रेरणेने अलग होऊन द्वि-ध्रुव निर्माण होतात ध्रुवांतील अंतर व त्यांपैकी एका ध्रुवावरील विद्युत् भार यांचा गुणाकार म्हणजे द्वि-ध्रुव परिबल होय) असणारे भाग अथवा क्षेत्रनिर्मिती हे अशा पदार्थांचे वैशिष्ट्य होय. विद्युत् क्षेत्र लावले असता या क्षेत्राची दिक्‌स्थिती बदलणे शक्य आहे. लोहविद्युत् स्फटिकाच्या विशिष्ट दिशेला दाब दिला असता दुसऱ्या एका विशिष्ट दिशेला विद्युत् भार निर्माण होतो. या गुणधर्मास दाबविद्युत् असे म्हणतात. असे स्फटिक असममित असतात [⟶ दाबविद्युत् लोहविद्युत्].

चुंबकीय गुणधर्म : चुंबकत्व हा एकट्या लोखंडाचाच गुणधर्म नसून इतरही पदार्थ हा गुणधर्म कमी अधिक प्रमाणात दर्शवितात आणि त्यांच्या चुंबकीय क्षेत्रातील वर्तणुकीनुसार त्यांचे समचुंबकीय (चुंबकीय पार्यता निर्वाताच्या पार्यतेपेक्षा जास्त असणारे) व प्रतिचुंबकीय (चुंबकीय पार्यता निर्वातापेक्षा कमी असलेले) असे दोन प्रकार पाडणे शक्य आहे. समचुंबकीय पदार्थ चुंबकाकडून आकर्षिले जातात व चुंबकीय क्षेत्रात टांगले असता क्षेत्राच्या दिशेनेच त्यांची दिक्‌स्थिती होते. पण प्रतिचुंबकीय पदार्थ हे चुंबकाद्वारे दूर सारले जाऊन चुंबकीय क्षेत्रात टांगले असता क्षेत्राच्या विरुद्ध दिशेने त्यांची स्थिती राहते [⟶ चुंबकत्व].

लोहचुंबकत्व : लोहचुंबकीय पदार्थ हे इतर पदार्थांपासून साधारणतः खालील गुणधर्मांनी वेगळे म्हणून ओळखले जातात. (१) असे पदार्थ कमी सामर्थ्याच्या चुंबकीय क्षेत्रात तुलनेने जास्त चुंबकीकरण स्थापन करतात. (२) त्यांच्या प्रवणतेत चुंबकीकरणाची तीव्रता व चुंबकीय प्रेरणा यांच्या गुणोत्तरात व चुंबकीय क्षेत्रात सरळ प्रमाण नसते. मात्र त्यांचे चुंबकत्व हे केवळ तत्कालीन क्षेत्रावरच असते असे नाही, तर तत्पूर्वी लावलेल्या चुंबकीय क्षेत्रावरही अवलंबून असते.

लोहचुंबकीय पदार्थाबाबतचा मुख्य शोध म्हणजे ते पदार्थ एका विशिष्ट तापमानापर्यंतच (क्यूरी तापमान) त्यांची सर्व वैशिष्ट्ये दर्शवितात आणि त्यानंतर मात्र ते पदार्थ समचुंबकीय बनतात. म्हणून लोहचुंबकत्व हा समचुंबकत्वाचा एक निराळा प्रकार असावा असे समजले जाते.

चुंबकीय आकारांतर : चुंबकीकरणामुळे चुंबकीय द्रव्याच्या (उदा., लोह किंवा पोलाद) आकारमानात होणारा बदल हा परिणाम महत्त्वाचा आहे. या परिणामासंबंधीचा सुरुवातीच्या प्रयोगांचा फारसा उपयोग होऊ शकला नाही पण १९२५ मध्ये वेब्‌स्टर यांनी लोहस्फटिकांवर आणि होंडा व काया यांनी १९२६ साली निकेलावर केलेल्या संशोधनामुळे बरीच माहिती उपलब्ध झाली.

---

वेब्‌स्टर यांनी लोहस्फटिकाच्या (100), (110) आणि (111) या प्रतलांपासून मिळविलेले निष्कर्ष आ. ८ मध्ये दर्शविले आहेत. या आकृतीवरून हे स्पष्ट दिसून येते की, (100) या दिशेने चुंबकीकरण करणे सोपे आहे. कारण क्षेत्र जसजसे वाढवावे तसतसे प्रसरण वाढत जाते. इतर दोन दिशांत असे दिसून येत नाही.

निरनिराळ्या लोहचुंबकीय पदार्थांत निरीक्षण केलेल्या विविध परिणामांवरून हेच दिसून येते की, चुंबकीय आकारांतर हे केवळ चुंबकीकरणामुळे निर्माण झालेल्या प्रेरणांमुळे उत्पन्न होते असे समजता येत नाही. फौलर व काप्यिट्स यांनी लोहचुंबकत्वाचे हायझेनबेर्क पुंजतत्त्वानुसार स्पष्टीकरण दिले आहे [⟶ चुंबकीय आकारांतर].

मुक्त इलेक्ट्रॉन प्रतिकृती : जास्त विद्युत् संवाहकता व कमी विशिष्ट उष्णता ही धातूंची प्रमुख वैशिष्ट्ये होत. इलेक्ट्रॉनाच्या शोधानंतर ड्रूडे आणि लोरेंट्स यांनी प्रत्येक धातूत काही मुक्त इलेक्ट्रॉन असतात या गृहीताच्या आधारे, या वैशिष्ट्यांचे स्पष्टीकरण देण्याचा प्रयत्न केला. पण यामुळे सर्व गुणधर्म स्पष्ट होऊ न शकल्याने पुढे सुधारित मुक्त इलेक्ट्रॉन प्रतिकृती मांडण्यात आली. कोणत्याही धातूमधील अगर घन पदार्थातील इलेक्ट्रॉन हा इतर इलेक्ट्रॉन व अणु केंद्रांच्या सान्निध्यात असतो. त्यामुळे त्याची स्थितिजन्य ऊर्जा जालकाप्रमाणेच आवर्ती (पुनःपुन्हा तशीच) असते. झोमरफेल्ट यांच्या कल्पनेनुसार मुक्त म्हणजेच विद्युत् संवहन करणारा इलेक्ट्रॉन धातूमध्ये प्रत्येक ठिकाणी कायम असणाऱ्या स्थितिवर्चसात वावरत असतो. कमी किंवा निरपेक्ष शून्य तापमानावर इलेक्ट्रॉनाची स्थितिजन्य ऊर्जा पुरेशी नसल्याने अशा तापमानास आपणास तापायनिक उत्सर्जन (उष्णतेद्वारे संवाहकांच्या पृष्ठभागापासून इलेक्ट्रॉन बाहेर पडणे) दिसत नाही. हे सर्व इलेक्ट्रॉन E_s उंचीच्या स्थितिजन्य ऊर्जा पेटीत ठेवले आहेत, असे समजल्यास असे दिसून येते की, तळातील इलेक्ट्रॉनाला धातूच्या बाहेर ओढण्यासाठी किमान एवढी तरी ऊर्जा पुरवावी लागेल. तथापि या इलेक्ट्रॉनाला मूळची E_f इतकी ऊर्जा असल्याने प्रत्यक्षात E_s– E_f = ø इतकीच ऊर्जा पुरवावी लागते. अशा तऱ्हेने धातुचे स्वरूप आकृतीद्वारे दर्शविता येते (आ. ९).

झोमरफेल्ट यांच्या कल्पनेनुसार हे मुक्त इलेक्ट्रॉन म्हणजे संयुजी (अणूंच्या संयोगात एका अणूतून दुसऱ्या अणूत संक्रमित होणारे वा दोन अणूंत समाइक राहणारे) इलेक्ट्रॉन होत. प्रत्येक घ.सेंमी. मध्ये १०^१२ इतकी घनता असणारा इलेक्ट्रॉन वायूमधील इलेक्ट्रॉन कसे विखुरलेले असतात हे पाहणे महत्त्वाचे आहे. 

फेर्मी-डिरॅक सांख्यिकीनुसार [⟶ सांख्यिकीय भौतिकी] E व E+ dE या ऊर्जापट्ट्यात असणारे इलेक्ट्रॉन N(E) dE खालील समीकरणाने दिले जातात.

येथे V = घनफळ, m = इलेक्ट्रॉनाचे वस्तुमान, h = प्लांक स्थिरांक, E_f ही फेर्मी ऊर्जा असून तिचे वैशिष्ट्य असे आहे की, या ऊर्जेच्या पातळीपर्यंतच्या सर्व जागा इलेक्ट्रॉनांनी व्यापलेल्या असतात आणि त्यावरील सर्व जागा मोकळ्या असतात. ही ऊर्जा खालील सूत्राने दिली जाते.

येथे n ही मुक्त इलेक्ट्रॉन घनता आहे.

निरपेक्ष शून्य तापमानास इलेक्ट्रॉन घनता ऊर्जेनुसार कशी बदलत जाते हे आ. १० वरून स्पष्ट होईल. जास्त तापमानास फेर्मी आणि बोल्टस्‌मान या दोन्ही सांख्यिकींनुसार वरील आलेख एकच येतो. फेर्मी ऊर्जा ही काही इलेक्ट्रॉन-व्होल्ट (१ इलेक्ट्रॉन-व्होल्ट म्हणजे १ व्होल्ट विद्युत् वर्चोभेदातून जाताना इलेक्ट्रॉनाला प्राप्त होणारी ऊर्जा, १·६ × १०^-१२ अर्ग) इतकी असते. या प्रतिकृतीमुळे स्फटिकांच्या काही गुणधर्मांची उपपत्ती सिद्ध करता आली पण इतर काही गुणधर्मांच्या बाबतीत तसे जमले नाही.

मुक्त इलेक्टॉन या प्रतिकृतीनुसार येणारी विशिष्ट उष्णता ही प्रत्यक्ष निरीक्षण केलेल्या विशिष्ट उष्णतेच्या मानाने कमी आहे [⟶ सांख्यिकीय भौतिकी] .

मुक्त इलेक्ट्रॉनाचे समचुंबकत्व : जेव्हा काही विद्युत् भार एखाद्या अक्षाभोवती फिरत असतो, तेव्हा चुंबकीय द्वि-ध्रुव परिबल निर्माण होत असते. डेबाय सिद्धांतानुसार ज्याप्रमाणे विद्युत् द्वि-ध्रुवाची दिक्‌स्थिती काढली जाते, त्याप्रमाणे रूढ सांख्यिकीचा उपयोग करून हे चुंबकीय परिबल काढल्यास ते खालील सूत्राने दिले जाते.

जेव्हा  μH&lt &lt kT तेव्हाच  M = XH = (nμ_B² /kT. H .

येथे μ= चुंबकीय पार्यता, H = क्षेत्र तीव्रता, n =मुक्त इलेक्ट्रॉन घनता, μ_B = १ बोर मॅग्नेटॉन (चुंबकीय परिबलाचे एकक) = ०·९१७ × १०^-१२ अर्ग /ओर्स्टेड, X = समचुंबकीय प्रवणता, M = चुंबकीय परिबल. हे समीकरण खरे असले तर n = १०^२२/(सेंमी.)^३ हे मूल्य घालून X ही राशी १०^-४/(सेंमी.)^३ इतकी यावयास हवी व त्याप्रमाणे ती तापमानाच्या व्यस्त प्रमाणात बदलावयास हवी. परंतु प्रत्यक्षात मात्र ही प्रवणता १०^-६/(सेंमी.)^३ इतकी येते व ती तापमानावर बिलकूल अवलंबून राहत नाही. अर्थात प्रायोगिक व सैद्धांतिक मूल्यांमधील हा फरक पाउली यांनी दर्शविल्याप्रमाणे फेर्मी-डिरॅक सांख्यिकीचा उपयोग केल्यास फक्त क्षार धातूसाठीच कमी होतो. वर निर्देशिलेल्या काही गुणधर्मांप्रमाणेच धातूंचे तापायनिक उत्सर्जन, प्रकाश विद्युत् परिमाण (निरोधित संवाहकावर प्रकाश टाकल्यामुळे त्याच्या ऋण भारात घट होणे किंवा त्याला धन भार प्राप्त होणे) वगरे गुणधर्मांच्या उपपत्तीची माहिती मिळाली.

---

धातूमधील हॉल परिणाम : एखाद्या धातूच्या ठोकळ्यावर आ. ११ मध्ये दर्शविल्याप्रमाणे X अक्षाच्या दिशेने विद्युत् क्षेत्र E_x व त्याला ९० अंशाचा कोन करून Z अक्षाच्या दिशेने H_z चुंबकीय क्षेत्र लावले, तर वरील दोन्ही दिशांना लंब म्हणजे Y अक्षाच्या दिशेने विद्युत् वर्चस् (विद्युत् दाब) निर्माण होते. या परिणामास हॉल परिणाम म्हणतात. लावलेल्या विद्युत् क्षेत्रामुळे इलेक्ट्रॉन प्रवाह वाहून नेतात व चुंबकीय क्षेत्रामुळे या इलेक्ट्रॉनांवर लोरेंट्स प्रेरणेने कार्य होऊन शेवटी स्थिर स्थितीत ठोकळ्याचा वरचा भाग धन व खालचा भाग ऋण बनतो. थोडक्यात हॉल वर्चस् हे आपणास विद्युत् भार वाहकाविषयी माहिती पुरविते. त्याचप्रमाणे वाहकांची घनता, माध्य मुक्त पथ (इतर इलेक्ट्रॉनांशी टक्कर होताना दोन लागोपाठच्या टकरींतील इलेक्ट्रॉनांच्या मार्गाचे सरासरी अंतर), गतिशीलता (एकक विद्युत् क्षेत्रामुळे इलेक्ट्रॉनाला मिळणारा वेग) वगैरे काढता येतात. त्यामुळे धातूमधील इलेक्ट्रॉनांच्या वागणुकींवर बराच प्रकाश पडतो.

चुंबकीय व विद्युत् क्षेत्रांमुळे इलेक्ट्रॉनावर खालील प्रेरणा कार्यान्वित होते.

येथे e = इलेक्ट्रॉन विद्युत् भार, v = इलेक्ट्रॉनाचा वेग, H = चुंबकीय क्षेत्र, E = विद्युत् क्षेत्र, अक्षरांवरील बाण राशी सदिश असल्याचे दर्शवितो. स्थिर स्थितीत F_y = ० व H_x = ० आहेच, म्हणून

E_y = V_x·H_z

= J_x·H_z /ne

येथे v_x = X दिशेतील इलेक्ट्रॉनाचा सरासरी वेग = J_x/ne, J_x = X दिशेतील विद्युत् प्रवाह घनता.

हॉल गुणांक R_H याची व्याख्या : R_H = E_y/J_x·H_z अशी केली जाते. म्हणून R_H = ¹/_ne, (n = इलेक्ट्रॉन घनता).

अशा तऱ्हेने ह्या परिणामाचे निरीक्षण केल्याने धातूतील वाहक कोणत्या प्रकारे वागतात हे समजून येते. या परिणामाचा हॉल जनित्रे व इतर अनेक उपकरणे तयार करण्यासाठी उपयोग केला जातो. तसेच अर्धसंवाहकाचा प्रकार ठरविण्यासाठी देखील या परिणामाचा उपयोग केला जातो.

घन पदार्थांची पट्टा उपपत्ती : निरनिराळे गुणधर्म वापरणाऱ्या निरनिराळ्या पद्धतींपैकी घन पदार्थांसाठी एक इलेक्ट्रॉन फलन पद्धती सर्वत्र जास्त वापरली गेली आहे. या पद्धतीनुसार एखाद्या इलेक्ट्रॉन समूहाचे तरंग फलन हे एकेका इलेक्ट्रॉनाच्या, शर्ती असणाऱ्या, अनेक तरंग फलनांचे एकत्रीकरण करून दिले जाते. अर्थात यातही रेणू व घन पदार्थांच्या रचनेसाठी दोन पद्धती आहेत. त्यांपैकी हाइटलर-लंडन पद्धत ही जेव्हा अणू एकमेकांपासून दूर असतात, तेव्हा उपयोगी पडते तर दुसरी म्हणजे ब्लॉक पद्धत ती रेणूंना लागू करण्यात आली आहे.

क्रॉनिग-पेनी प्रतिकृती : आवर्ती विद्युत् वर्चसामधील इलेक्ट्रॉनांची वैशिष्ट्ये आपणास क्रॉनिग व पेनी यांनी सुचविलेल्या सोप्या पद्धतीने दर्शविता येतात. हे वर्चस् आ. १२ मध्ये दर्शविल्याप्रमाणे असते असे गृहीत धरले जाते. विद्युत् वर्चस् 0 &lt X &lt a या भागासाठी शून्य, तर – b &lt X &lt a या भागासाठी V₀ इतके असते. या

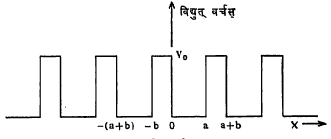
दोनही भागांसाठी श्रोडिंजर समीकरण मांडून ती सोडविल्यास खालील समीकरण मिळते.

येथे , m = इलेक्ट्रॉन वस्तुमान, E = ऊर्जा, V₀ विद्युत् वर्चस्, P चे मूल्ये स्फटिकातील आवर्ती वर्चसावर क्लिष्ट प्रकारे अवलंबून असते,

या समीकरणाची डावी बाजू आ. १३ मधील आलेखात Y सहनिर्देशकाने दर्शविली आहे व X सहनिर्देशकाने α a दर्शविला आहे.

परंतु उजव्या बाजूचे ± १ या दरम्यानच बदलत असते.

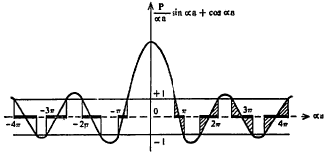
+१ पेक्षा ते जास्त होऊ शकत नाही वा -१ पेक्षा ते कमी होऊ शकत नाही. म्हणून ± १ अंतरावर X अक्षास समांतर अशा दोन रेषा काढून वरील समीकरणावरून हे स्पष्ट होईल की डाव्या बाजूचे मूल्य +१ व -१ या दरम्यानच असले पाहिजे.

आ. १३ वरून खालील महत्त्वाची वैशिंष्ट्ये स्पष्ट होतात.

(१) इलेक्ट्रॉनाच्या वर्णपटात निरनिराळे अनुमत (जेथे इलेक्ट्रॉन वावरू शकतो असे) पट्ट असतात म्हणजे वर्णपट अखंड नसतो. कोणत्याही दोन पट्ट्यांमधील ऊर्जेत इलेक्ट्रॉन वावरू शकत नाही. यांस निषिद्ध पट्ट असे म्हणतात.

(२) इलेक्ट्रॉन ज्यात वावरू शकतो अशा ऊर्जा पट्ट्यांची रुंदी ऊर्जेबरोबर वाढत जाते.

(३) कोणत्याही एका विशिष्ट पट्ट्याची रुंदी P बंधन-ऊर्जेबरोबर वाढत जाते हे आ. १४ वरून स्पष्ट होईल.

(४) ऊर्जा विरुद्ध k म्हणजे तरंगांक (तरंगलांबीचा व्यस्तांक) हा आलेख काढल्यास (आ. १५) k = ^{n π} /_a n = 1, 2, 3….. असताना आलेखात खंड पडतो आणि निरनिराळे विभाग तयार होतात.

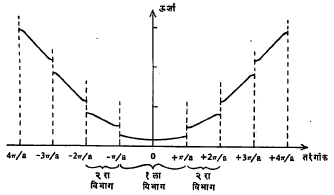
त्यांना ब्रीय्वँ या शास्त्रज्ञांच्या नावावरून ब्रीय्वँ विभाग असे म्हणतात. पहिला विभाग k = ^-π /_a पासून k = ^+π/_a पर्यंत पसरलेला असतो. दुसरा विभाग हा दोन उपविभागांत विभागलेला असतो. त्यापैकी पहिला उपविभाग –^{2 π} /_a पासून – ^π /_a पर्यंत, तर दुसरा उपविभाग + ^π /_a पासून     + ^{2 π} /_a पर्यंत पसरलेला असतो. तेथून पुढील सर्वच विभाग दोन उपविभागांत विभागलेले असतात. त्याचप्रमाणे ऊर्जा वाटप अन्वस्त [पॅराबोलिक →   अन्वस्त] प्रकारचे असते.

धातू, अर्धसंवाहक व निरोधक यांतील फरक : वरील पट्टा सिद्धांत धातू, अर्धसंवाहक आणि निरोधक यांतील फरक दर्शविण्यात यशस्वी झाला आहे. या सिद्धांतानुसार या तिन्ही प्रकारांच्या रचना आ. १६ मध्ये दर्शविल्याप्रमाणे मांडता येतील.

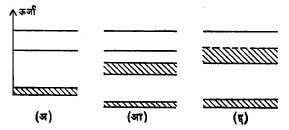
आकृतीत दर्शविलेली रचना शून्य तापमानास अस्तित्वात असते म्हणजे कोणत्याही घन पदार्थात इलेक्ट्रॉनांनी अर्धवट भरलेला असा कमाल ऊर्जेचा पट्टा असेल, तर तो पदार्थ धातूप्रमाणे वागतो. हा पट्टा अगदीच रिकामा असेल तर तो पदार्थ निरोधक बनतो. या स्थितीत संवहन पट्टा व संयुजी पट्टा या दोन पट्ट्यांत बरेच अंतर असते. हे अंतर अर्धसंवाहकात तुलनेने कमी असते. त्यामुळे एका पट्ट्यातील इलेक्ट्रॉन औष्णिक क्षोभाने दुसऱ्या पट्ट्यात जाऊन विद्युत् संवहन करू शकतात.

सर्व धातू, मिश्रधातू, अर्धसंवाहक, ट्रँझिस्टर वगैरे पदार्थ व्यावहारिक उपयुक्ततेच्या दृष्टीने महत्त्वाचे असल्याने त्यांचे गुणधर्म, रचना वगैरेंचा बराच अभ्यास झालेला आहे.          

      

संदीप्ती : जेव्हा एखादा पदार्थ कोणत्याही रूपामध्ये काही ऊर्जा शोषून घेतो तेव्हा त्यापैकी ऊर्जा दृश्य अगर त्या नजिकच्या भागातील तरंगांच्या रूपाने बाहेर सोडली जाते, या आविष्काराला संदीप्ती म्हणतात आणि अशा पदार्थांना फॉस्फर (संदीपक) म्हणतात. संदीप्ती दोन टप्प्यांतून होते. ते म्हणजे–इलेक्ट्रॉन उत्तेजित करणे व फोटॉन उत्सर्जित करणे हे होत. इलेक्ट्रॉन क्षोभित करण्याचे कार्य फोटॉन, इलेक्ट्रॉन अगर इतर कणांच्या मार्फत करता येते. दशलक्षात काही भाग किंवा शेकड्यात काही भाग या प्रमाणात मूळ पदार्थांत अशुद्धीरूपाने असलेले पदार्थ (उदा., मँगॅनीज, तांबे, रुपे वगैरे) उत्तेजक म्हणून चांगले काम देतात. या शोधामुळे पुष्कळ अकार्बनी फॉस्फर तयार करता आले. विशेष महत्त्वाचे मूळ पदार्थ म्हणजे सिलिकेट, फॉस्फेट, कॅल्शियम वा मॅग्नेशियम ऑक्साइड वगैरे होत.

 

संदीप्ती देणारे स्फटिक घनांचे काही महत्त्वाचे प्रकार पुढीलप्रमाणे आहेत. (१) शुद्धावस्थेत संदीप्त होणारी संयुगे. उदा., समॅरियम व गॅडोलिनियम सल्फेटे व मॉलिब्डेटे. (२) थॅलियम किंवा इतर जड धातूंनी उत्तेजित केलेली क्षार हॅलाइडे (क्षार धातूंची फ्ल्युओराइडे, ब्रोमाइडे इ.). (३) झिंक सल्फाइड (ZnS) कॅडमियम सल्फाइड (CdS) यांनी उत्तेजित असे तांबे, चांदी, सोने, मँगॅनीज इ. धातू. (४) मँगॅनिजाकडून उत्तेजित होणारे सिलिकेट फॉस्फर (Zn₂ SiO₄ ). (५) कार्बनी स्फटिक-अँथ्रॅसीन वगैरे. (६) ऑक्साइड फॉस्फर (ZnO, Al₂O₃).

संदीप्तिनिर्मित्ती स्पष्ट करण्यासाठी काही सैद्धांतिक प्रतिकृती तयार करण्यात आलेल्या असून त्यांवरून काही महत्त्वाचे निष्कर्ष काढण्यात आले. त्याचप्रमाणे तापमानानुसार संदीप्तीत होणारे बदल संदीप्ती दर्शविणाऱ्या पदार्थांचे शोषण व उत्सर्जन वर्णपट, संदीप्तीक्षमतेमध्ये उत्तेजक पदार्थांच्या तीव्रतेनुसार होणारा बदल वगैरे गोष्टींचाही अभ्यास झाला आहे [→ संदीप्ति].

वर्णकेंद्रे : शुद्ध क्षार हॅलाइड स्फटिक संपूर्ण दृश्य वर्णपटात पारदर्शक असतात. जास्त तापमानात देखील हे स्फटिक पारदर्शक राहू शकतात. स्फटिकात रंग आणणे हे निरनिराळ्या प्रकारे शक्य होते (उदा., निरनिराळ्या प्रकारच्या अशुद्धी वापरून). ज्यांची लवणे रंगीत आहेत असे आयनिक (आयनांच्या जालकांनी तयार झालेले) स्फटिक स्फटिकांत रंग आणू शकतात. त्याचप्रमाणे ऋणायन (विद्रावातून विद्युत् प्रवाह वाहू दिल्यास ऋण विद्युत् अग्राकडे जाणारे आयन) ठराविक प्रमाणात जास्त घालून, क्षारवाफेत स्फटिक तापवून नंतर लगेच थंड करून, स्फटिक रंगीत बनविणे शक्य आहे हे जवळजवळ एकोणिसाव्या शतकाच्या मध्यापासून ज्ञात आहे. जेव्हा सोडियमवाफेत सोडियम क्लोराइडाचा स्फटिक तापविला जातो तो पिवळा बनतो. क्ष-किरण, गॅमा किरण, न्यूट्रॉन, इलेक्ट्रॉन वगैरेंचा उपयोग करून देखील स्फटिकात रंग आणणे किंवा मुळातच असणारा रंग गडद करणे शक्य असते.

जेव्हा स्फटिक रंगीत बनतो, तेव्हाच त्यात वर्णकेंद्रे आहेत असे आपण समजतो. वर्णकेंद्र हा प्रकाश शोषण करून घेणारा जालक दोष आहे. वर्णकेंद्राच्या प्रकारांपैकी ‘फ’ (F) हा प्रकार सर्वांत साधा प्रकार होय. हे नाव रंगासाठी असणाऱ्या फार्ब या जर्मन शब्दापासून आले आहे. साधारणतः क्षारवाफेत तापवून अगर क्ष-किरणांमुळे अशी वर्णकेंद्रे निर्माण केली जातात. या प्रकाराखेरीज वर्णकेंद्रांच्या इतरही प्रकारांचा शोध लागला असून त्यांचे स्वरूप व रचना देखील काही अंशी निश्चित करण्यात आल्या आहेत.

---

‘फ’ प्रकारचे वर्णकेंद्र निर्माण होत असताना जास्त क्षार-अणू क्षार हॅलाइड स्फटिकात ऋणायनांच्या जागी बसतात, असे सामान्यतः समजले जाते म्हणजे तितक्याच ऋणायनांच्या मोकळ्या जागा निर्माण होत असल्या पाहिजेत. ऋणायनांची मोकळी जागा आवर्ती जालकामध्ये धन भाराप्रमाणेच वागते. थोडक्यात ऋणायनांच्या 

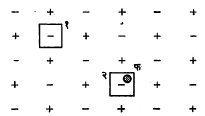मोकळ्या जागेभोवती फिरणारा इलेक्ट्रॉन हे चित्र हायड्रोजन अणूप्रमाणे दिसते. अशा ऋणायनांच्या मोकळ्या जागेला चिकटून राहिलेल्या इलेक्ट्रॉनालाच ‘फ’ वर्णकेंद्र म्हणतात (आ. १७). ही कल्पना बोर यांनी मांडली.

‘व’ (V) केंद्रे : जास्त प्रमाणात क्षार धातू तापवून फ-वर्णकेंद्रे निर्माण करता येतात तर स्फटिक हॅलोजन वाफेत तापवून उलट प्रकारची केंद्रे निर्माण करणे शक्य व्हावे, पण अशा केंद्रात इलेक्ट्रॉनांऐवजी विवरे (पोकळ्या) असावीत. या कल्पनेनुसार पोटॅशियम ब्रोमाइड व आयोडाइड यांमध्ये जास्त हॅलोजन भरून अशी केंद्रे निर्माण करणे शक्य आहे. अशा प्रकारे जंबुपार भागात अनेक प्रकारच्या शोषण पट्ट्यांची मालिकाच तयार होते. या पट्ट्यांना ‘व-पट्ट’ म्हणतात.

आ. १८ मध्ये पोटॅशियम क्लोराइड स्फटिकातील ‘व’ आणि ‘फ’ पट्ट दर्शविले असून त्यांच्या  स्पष्टीकरणासाठी निरनिराळ्या प्रतिकृती बनविण्यात आल्या आहेत. सध्या ‘व’ वर्णकेंद्रांचा शोषण पट्ट्याशी संबंध जोडणे शंकास्पद मानले जात आहे. त्याला कोन्झिग वगैरेंची इलेक्ट्रॉन परिवलन अनुस्पंदनाची मोजमापे कारणीभूत आहेत [→ अनुस्पंदन].

लेसर व मेसर : लेसर -LASER- हा मूळ इंग्रजी शब्द Light Amplification by Stimulated Emission of Radiation यातील आद्याक्षरे घेऊन तयार करण्यात आला आहे. तसेच मेसर-MASER- हा शब्द Microwave Amplification by Stimulated Emission of Radiation यातील आद्याक्षरे घेऊन तयार करण्यात आला आहे. लेसर शलाकांतून समकला किरण (ज्यांचे अवस्थाकोन बदलत नाहीत एकसारख्या अवस्थेतील) मिळतात म्हणजेच त्यांच्यापासून जवळजवळ एकवर्णी प्रकाशीय कंप्रतेचे किरण मिळतात व त्यामुळे एखाद्या इष्ट दिशेने त्यांची शलाका अचूकपणे पाठविता येते किंवा अतिशय बारीक स्थानी त्यांचे केंद्रीकरण करता येते. या शलाकांच्या निर्मितीची शक्यता प्रथम शॉलो व टाउन्स यांनी १९५८ मध्ये सूचित केली. अत्याधुनिक लेसरमध्ये गॅलियम आर्सेनाइडासारख्या निरनिराळ्या अर्धसंवाहक पदार्थांचा उपयोग केला जातो. लेसर व मेसर यांचे मूलभूत तत्त्व एकच असते. फरक इतकाच की लेसर शलाकांचे कार्य प्रकाशीय तरंगांवर चालते तर मेसर शलाकांचे सूक्ष्मतरंगांवर (१ मिमी. ते ३० सेंमी. तरंगलांबी असणाऱ्या तरंगांवर) चालते. घन अवस्थेतील मेसरचा उपयोग अत्यंत संवेदनशील सूक्ष्मतरंग ग्रहणीसाठी लागणाऱ्या निरनिराळ्या विवर्धकांच्या दृष्टीने महत्त्वाचा आहे [⟶   मेसर लेसर सूक्ष्मतरंग].

अतिसंवाहकता : निरपेक्ष शून्याच्या (ज्या तापमानास कायम घनफळ असलेल्या आदर्श वायूंचा दाब शून्य होतो त्या तापमानाच्या) वर काही अंश तापमानात ठेवलेल्या शुद्ध धातूमध्ये अथवा मिश्रधातूमध्ये हे आविष्कार दिसून येतात. विद्युत् रोध अजिबात नसणे हे अशा पदार्थाचे वैशिष्ट्य होय, या आविष्काराचा शोध कामर्लिंग-ऑनेस या शास्त्रज्ञांनी १९११ साली लावला. तथापि अशा पदार्थांच्या संपूर्ण प्रतिचुंबकत्वाचा शोध १९३३ साली लागला. अतिसंवाहक स्थिती विशद करणारे सिद्धांत बारडीन, कूपर व स्क्रीफर यांनी मांडून त्याचे स्पष्टीकरण त्यांनी दिले आहे [⟶ अतिसंवाहकता].

मॉसबावर परिणाम : यात गॅमा किरणांचे प्रत्यागति-विरहित (मागच्या बाजूने जाणारा धक्का न बसता) अनुस्पंदनी (एकमेकांची कंप्रता सारखी असल्यामुळे) शोषण होते. हा परिणाम अभ्यासण्याच्या प्रयोगात चल उगमापासून निघालेले गॅमा किरणांचे अचल आपाती स्फटिकातील सर्व अणूंकडून झालेले शोषण मोजतात. या परिणामाचा उपयोग अतिशय अचूक कंप्रताप्रमाण म्हणून करता येतो. तसेच अणुकेंद्रातील अतिसूक्ष्मरचना, स्फटिकरचना रसायनशास्त्र, धातुविज्ञान इ. अभ्यासात करतात. ह्या परिणामाचा शोध मॉसबावर या शास्त्रज्ञांनी १९५७ साली लावला [→  किरणोत्सर्ग].

घन पदार्थांच्या सर्वांगीण अभ्यासासाठी क्ष-किरण, इलेक्ट्रॉन विवर्तन वगैरेंप्रमाणेच अणुकेंद्रीय चुंबकीय अनुस्पंदन, इलेक्ट्रॉन परिवलनीय अनुस्पंदन यांसारखी तंत्रे वापरण्यात येतात [→ अनुस्पंदन].

अणुकेंद्रीय चुंबकीय अनुस्पंदन : या पद्धतीत अणुकेंद्राचे चुंबकीय गुणधर्म तो स्थिर चुंबकीय क्षेत्रात ठेवून आणि त्या क्षेत्राच्या लंब दिशेत जास्त कंप्रतेचे व आवर्ती चुंबकीय क्षेत्र लावून होणाऱ्या अनुस्पंदनी शोषणावरून तपासले जातात. राबी वगैरेंनी आणवीय व रेणवीय शलाकांद्वारे अणुकेंद्रीय चुंबकीय परिबल व परिवलन मोजण्यासाठी या पद्धतीचा अवलंब केला [→ अणुकेंद्रीय व आणवीय परिबले]. तसेच पर्सेल वगैरेंनीही या विषयात खूप संशोधन केले आहे. या पद्धतीने अणुकेंद्रीय परिबलामुळे निर्माण झालेले समचुंबकत्व तसेच घन व द्रव पदार्थांच्या काही गुणधर्मांचा अभ्यास करता येतो. तसेच इलेक्ट्रॉन पट्टरचना, प्रतिचुंबकत्व, लोहविद्युत् वगैरे बाबींचाही अभ्यास करता येतो.

इलेक्ट्रॉन परिवलनीय अनुस्पंदन : अणुकेंद्रीय चुंबकीय अनुस्पंदनाप्रमाणेच काही पदार्थांत हा परिणाम आढळतो. यात अनुस्पंदन अणुकेंद्राबाहेरील इलेक्ट्रॉनांकडून होत असल्यामुळे ते अणूतील इलेक्ट्रॉनांच्या मांडणीवर अवलंबून असते. ज्या पदार्थात इलेक्ट्रॉन कवच इलेक्ट्रॉनांनी संपूर्ण भरलेले असेल किंवा इलेक्ट्रॉन जोडीने असल्यास जर त्यांचे परिणामी परिवलन शून्य असेल तर अशा पदार्थात परिवलनीय अनुस्पंदनी शोषण मिळत नाही. पदार्थ समचुंबकीय असल्यास या परिणामाला इलेक्ट्रॉन समचुंबकीय अनुस्पंदन असे म्हणतात.

या अनुस्पंदनाचे निरीक्षण सामान्यतः निर्वातावस्थेत केले जाते. अनेक समचुंबकीय पदार्थांच्या भौतिक आणि रासायनिक गुणधर्मांच्या संशोधनाच्या दृष्टीने हे एक महत्त्वाचे साधन आहे. उपयोगाची काही क्षेत्रे अशी : स्फटिकातील आयनांची इलेक्ट्रॉन संरचना कशी आहे ते पाहणे निरनिराळ्या रासायनिक विक्रियांमधील समचुंबकीय पदार्थाचे अस्तित्व दर्शविणे क्ष-किरण, गॅमा किरण, इलेक्ट्रॉन, न्यूट्रॉन यांच्या पदार्थांबरोबर होणाऱ्या परस्पर क्रियांमुळे निर्माण झालेल्या पदार्थांचा अभ्यास करणे समचुंबकीय पदार्थातील अणुकेंद्राचे गुणधर्म तपासणे तद्वत अर्धसंवाहकाचे गुणधर्म तपासणे इत्यादी.

समचुंबकीय पदार्थांमध्ये एकूण कोनी संवेग (निरूढी परिबल व कोनीय वेग यांचा गुणकार निरूढी परिबल म्हणजे कोनीय प्रवेगास होणारा विरोध) नष्ट न होणारे अणू व रेणू असतात. त्यांच्यामुळे चुंबकीय क्षेत्र निर्माण होऊन ते लहान चुंबकाप्रमाणे स्थिर चुंबकीय क्षेत्राशी समांतर असते. रूढ भौतिकीच्या नियमाप्रमाणे जर या चुंबकांची समतोल अवस्था बदलविली, तर ते परत पहिल्याप्रमाणे चुंबकीय क्षेत्राशी समांतर अशी रचना करण्याचा प्रयत्न करतात व त्यामुळे त्यांची गती दोलायमान होऊन तिची कंप्रता वाढत्या चुंबकीय क्षेत्राच्या ऊर्जेबरोबर वाढत जाते. ही गती म्हणजेच परांचन (ज्या अक्षाभोवती परिभ्रमण होते त्या अक्षाचे परिभ्रमण) होय. चुंबकाची समतोल अवस्था वाढविण्यास जर प्रत्यावर्ती चुंबकीय क्षेत्राचा किंवा विद्युत् चुंबकीय तरंगांचा उपयोग केला, तर हे तरंग स्वतःच्या कंप्रतेनेच चुंबक हलविण्याचा प्रयत्न करतात. जेव्हा या तरंगाची कंप्रता दोलायमान गतीच्या कंप्रतेबरोबर असते, तेव्हा तरंगामध्ये व समचुंबकीय पदार्थामध्ये मोठ्या प्रमाणावर परस्पर क्रिया होऊन बरीच ऊर्जा शोषली जाऊ शकते.

पुंजसिद्धांतानुसार या प्रकाराकडे एक वर्णपटीय आविष्कार म्हणून पाहिले जाते. परंतु दोन्ही दृष्टिकोनातून हेच दिसून येते की, स्थिर चुंबकीय क्षेत्र व कंप्रता यांच्या काही विशिष्ट गुणोत्तरासच हे अनुस्पंदन घडू शकते.

V   या कंप्रतेला ऊर्जापुंज hV  इतका असतो. अनुस्पंदन होण्याची अट पुढे दिल्याप्रमाणे आहे. hV = g μ_B H, येथे μ_B = बोर मॅग्नेटॉन,   H = चुंबकीय क्षेत्र आणि g हा प्रमाण स्थिरांक असून त्याचे मूल्य साधारणतः २ असते. २०० गौस चुंबकीय क्षेत्र समजून h वगैरेंची मूल्ये या सूत्रात घातल्यास मिळणारी कंप्रता ही सूक्ष्मतरंगांच्या कंप्रतेइतकी येते म्हणून सूक्ष्मतरंगांचा उपयोग समचुंबकीय पदार्थांच्या या अनुस्पंदनाद्वारे होणाऱ्या अभ्यासासाठीही करतात.

पहा : अर्धसंवाहक ट्रँझिस्टर तंत्रविद्या.

संदर्भ : 1 . Kittel, C. Introduction to Solid State Physics, New York, 1956 .  

           2. Seitz, F. Turnbull, D. Solid State Physics, New York, 1955.

           3. Wanuier, G. H. Elements of Solid State Theory, Cambridge, 1960.

           4. Wert, C. Thomson, R. Physics of Solids, New York, 1964.                                                  

केसकर, कृ. शं.

“