गोलीय हरात्मके : गोलीय हरात्मके ही गणितशास्त्रातील एका विशिष्ट प्रकारची फलने (गणितीय संबंध) होत. ट्रिटाइज ऑन नॅचरल फिलॉसॉफी या १८७९ मध्ये प्रसिद्ध केलेल्या ग्रंथात टॉमसन आणि टेट यांनी गोलीय हरात्मकांची पुढीलप्रमाणे व्याख्या दिली. लाप्लास यांच्या
![]()
या समीकरणाचा क्ष, य, झ मधील प घाताचा समघाती असा जो निर्वाह (समीकरण सोडवून मिळणारे उत्तर) असेल त्यास प घाताचा घन गोलीय हरात्मक म्हणतात. उदा.,
![]()
ही फलने समघाती असून लाप्लास समीकरणाची पूर्तता करतात. म्हणून ती अनुक्रमे १,-१, ० आणि प घातांची घन गोलीय हरात्मके आहेत.
घन गोलीय हरात्मकांच्या संदर्भात लॉर्ड केल्व्हिन यांचे महत्त्वाचे प्रमेय आहे, ते असे : जर वप हे प घाताचे घन गोलीय हरात्मक असेल (आणि र२= क्ष२+ य२+झ२ असेल), तर र–२प-१ ·वप हे (-प-१) घाताचे घन गोलीय हरात्मक असते.
आदिबिंदू (०, ०, ०) हा ध्रुवबिंदू मानून (क्ष, य, झ) बिंदूचे ध्रुवीय सहनिर्देशक [→ भूमिति] जर (र, थ, भ) असतील, तर
क्ष = र·ज्या थ·कोज्या भ
य = र·ज्या थ·ज्या भ
झ = र·कोज्या थ
अशी रूपांतर समीकरणे मिळतात. यावरून ध्रुवीय सहनिर्देशकांमध्ये लाप्लास समीकरण
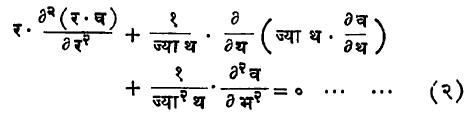
असे मिळते. याचा निर्वाह वप हे (र, थ, भ) यांचे फलन असले पाहिजे. आता वप = रप·सप हे प घाताचे गोलीय हरात्मक असे आहे. असे समजू की, सप हे फक्त थ आणि भ यांचेच फलन असेल. वप चे हे मूल्य समीकरण (२) मध्ये घातले, रप हा समाईक अवयव काढून टाकला आणि कोज्या थ = म लिहिले, तर
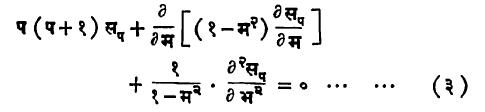
असे समीकरण मिळते. यामधील सप या फलनास प घाताचे पृष्ठ गोलीय हरात्मक म्हणतात. र = १ धरल्यास, सप = वप होईल. यावरून सप म्हणजे वप चे (आदिबिंदू मध्य आणि त्रिज्या र = १ असणाऱ्या) एकक गोलाच्या पृष्ठभागावरील मूल्य होय असे दिसून येते.
लझांद्र फलन : वर उल्लेखिलेले सप हे पृष्ठ गोलीय हरात्मक, जर फक्त थ चेच फलन असेल तर त्यास प घाताचे लझांद्र फलन म्हणतात आणि ते लप (म) असे लिहितात. समीकरण (३) वरून, लप (म) साठी
![]()
हे लझांद्र समीकरण मिळते. जर प हा धन पूर्णांक असेल तर लप (म) ही प घाताची म मधील बहुपदी मिळते व या बहुपदीस लझांद्र बहुपदी असे म्हणतात.
लझांद्र संबद्ध समीकरण : समजा, फ हे फक्त थ चे आणि ह हे फक्त भ चे अशी फलने आहेत की, सप = फ x ह असेल. सप चे हे मूल्य समीकरण (३) मध्ये घातले आणि फ x ह ने भागले, तर
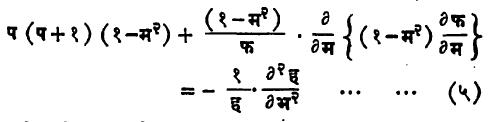
असे समीकरण मिळते. या समीकरणाच्या उजव्या बाजूवर थ चे मूल्य बदलले तरी परिणाम होणार नाही. याचाच अर्थ थ चे मूल्य बदलले तरीही डाव्या बाजूवर काहीही परिणाम होणार नाही. म्हणजेच उजवी बाजू (आणि म्हणून डावी बाजू) स्थिरांक असली पाहिजे. हा स्थिरांक त२ आहे असे समजल्यास
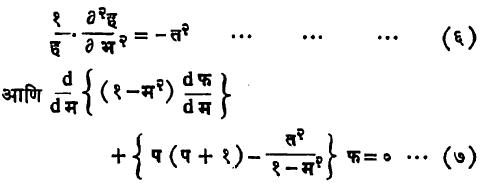
अशी समीकरणे लिहिता येतील. यांतील समीकरण (६) चा निर्वाह
ह = अ·कोज्या (त भ) + ब·ज्या (त भ), (अ, ब स्थिरांक) असा मिळतो. समीकरण (७) ला, प घाताचे, त क्रमाचे लझांद्र संबद्ध समीकरण म्हणतात आणि ते लतप (म) असे लिहितात. लतप (म) आणि लप (म) यांचा परस्पर संबंध
![]()
असा दाखविता येतो. यावरून ल०प (म) = लप (म) हे सहज लक्षात येईल.
वरील विवेचनावरून, जर फ हे प घाताचे त क्रमाचे लझांद्र संबद्ध फलन असेल, तर
(अ कोज्या त भ + ब ज्या त भ) फ
हे प घाताचे पृष्ठ गोलीय हरात्मक असून,
रप(अ कोज्या त भ + ब ज्या त भ) फ, आणि
र-प-१ (अ कोज्या त भ + ब ज्या त भ) फ,
ही अनुक्रमे प आणि (-प-१) घातांची घन गोलीय हरात्मके असली पाहिजेत, असे दिसून येईल.
गोलीय हरात्मकांचे गुणधर्म : (१) दिलेल्या कोणत्याही म घाताची, परस्परांशी एकघाती संबंध नसलेली, अशी (२ म+१) पृष्ठ गोलीय हरात्मके अस्तित्वात असतात. यांच्यापासून तयार केलेली कोणतीही एकघाती पदावली म घाताचे पृष्ठ गोलीय हरात्मक असते. त्या उलट कोणचेही म घाताचे पृष्ठ गोलीय हरात्मक हे या (२ म + १) पैकी हरात्मकांपासून एकघाती पदावलीने तयार होते.

गोलीय हरात्मक असते.
एकक गोलावर जर असा वक्र असेल की ज्याच्या प्रत्येक बिंदूशी दिलेल्या गोलीय हरात्मकाचे मूल्य शून्य होईल, तर त्या वक्रास त्या हरात्मकाची पातरेषा असे म्हणतात. वर दिलेल्या हरात्मकाच्या प दिशा जर एकरूप असतील तर त्या हरात्मकाच्या पातरेषा म्हणजे एकक गोलावरील परस्परांस समांतर अशी प अक्षांश वर्तुळे असतात व ती गोलाच्या पृष्ठभागांचे पट्टिकांमध्ये विभाजन करतात. अशा वेळी पट्टिका गोलीय हरात्मक मिळते. जर या प दिशा एकाच प्रतलात (पातळीत) दोन लगतच्या दिशांमध्ये π / प इतका कोन करून असतील तर पातरेषा, गोलाच्या एकाच व्यासातून जाणारी प (रेखांश) वर्तुळे असतात व ती गोलाचे खंडभागांत विभाजन करतात. अशा वेळी खंड गोलीय हरात्मके मिळतात. जर (प-त) दिशा एकरूप असून, उरलेल्या त दिशा अक्षास लंब असणाऱ्या प्रतलात π / त कोन साधून असतील तर (प-त) अक्षांश वर्तुळे आणि त रेखांश वर्तुळे अशा पातरेषा असून, गोलपृष्ठाचे गोलीय आयताकार भागांत विभाजन होते. अशा वेळी कटिबंधीय हरात्मके मिळतात.
(३) गोलीय हरात्मके समाकल रूपातही [→ अवकलन व समाकलन] लिहिता येतात.
![]()
हे समाकल लाप्लास समीकरणाची पूर्तता करते म्हणजेच ते गोलीय हरात्मक आहे, असे दाखविता येते. याचाच एक विशिष्ट प्रकार म्हणजे, जर फ (त) हे [-π, π ] मध्ये समाकलनीय असेल, तर
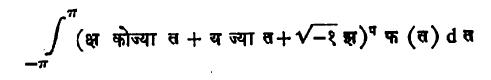
हे समाकल प घाताचे गोलीय हरात्मक असते.
लझांद्र फलनासाठीही पुढीलप्रमाणे समाकल आहेत.
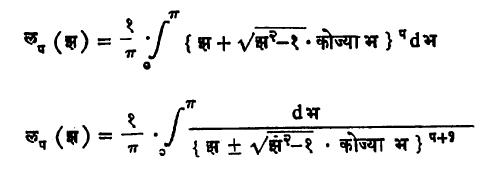
यांना अनुक्रमे लाप्लास यांचे प्रथम व द्वितीय समाकल असे म्हणतात.
(४) लझांद्र समीकरणाचा लप (म) व्यतिरिक्त दुसराही निर्वाह असतो. त्यास शप (म) म्हटल्यास
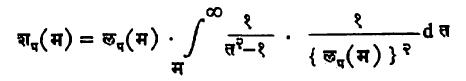
असे सूत्र मिळते. अ आणि ब कोणतेही स्थिरांक असले तर
अ लप (म) + ब शप (म) हा लझांद्र समीकरणाचा व्यापक निर्वाह [→ अवकल समीकरणे] होय.
(५) लझांद्र बहुपदीसाठी पुढे दिल्याप्रमाणे आवर्ती सूत्रे मिळतात.
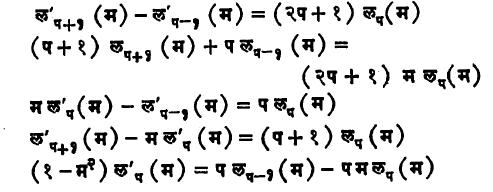
(६) रॉडरिग यांचे सूत्र
![]()
(७) ब आणि प हे धन पूर्णांक असतील, तर
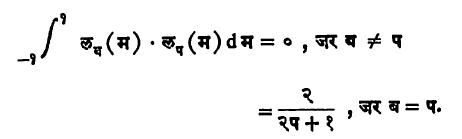
वरील सूत्रांच्या साहाय्याने फ (क्ष) हे फलन [-१, १] अंतरालात डीरिक्ले यांच्या अटींचे [→ फूर्ये श्रेढी] पालन करीत असेल, तर लझांद्र फलनांच्या साहाय्याने फ (क्ष) चा विस्तार पुढीलप्रमाणे मांडता येतो.
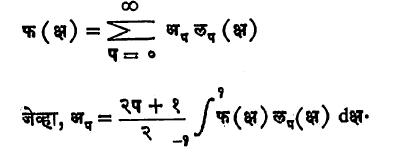
अनुप्रयोग : लाप्लास यांनी १७८५ मध्ये खालील कल्पना मांडली. क१, क२, क३,….. वस्तुमानाचे कण अ१, अ२, अ३, ……या बिंदूंच्या ठिकाणी असतील (आणि या कणांव्यतिरिक्त अवकाशात इतर काहीही नसेल), तर त्यांच्यामुळे ब या दिलेल्या बिंदूपाशी जी गुरुत्वाकर्षण प्रेरणा निर्माण होईल त्या प्रेरणेच्या दिशेत असलेला घटक,
![]()
या फलनाचे त्या दिशेने अवकलन केल्याने मिळतो. याच व फलनाला पुढे ग्रीन या गणितज्ञांनी वर्चस् फलन असे नाव दिले आणि तेच सर्वत्र रूढ झाले आहे. वर्चस् फलनातील सर्व पदे एकाच साच्याची असल्याने, लझांद्र यांनी त्यातील एक पद घेऊन त्याचा अनंत श्रेढीत विस्तार मांडता येतो हे दाखविले. समजा, आ हा आदिबिंदू असेल, आब = र, आअ = ह आणि कोज्या ∠ बआअ = म असे लिहिले, तर
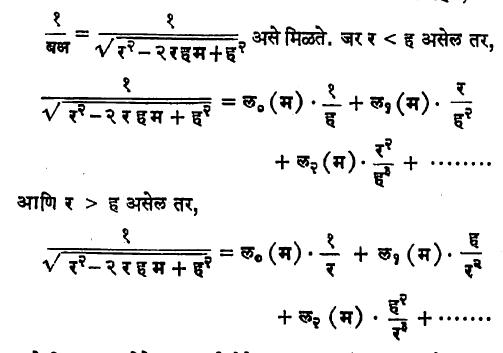
असे सिद्ध करता येते. अशा रीतीने लझांद्र बहुपदी आणि वर्चस् फलन यांचा संबंध स्पष्ट होतो.
वर गुरुत्वाकर्षणासाठी जे वर्चस् फलन दिले आहे त्याच प्रकारचे वर्चस् फलन विद्युत्, चुंबकीय इ. क्षेत्रांसाठी असते. या सर्व वर्चस् फलनांचा समान गुणधर्म म्हणजे ती लाप्लास समीकरणाची पूर्तता करतात. गोलीय हरात्मके ही लाप्लास समीकरणांचे निर्वाह असल्याने वर्चस् फलनांचा संबंध येतो. अशा अभ्यासात हरात्मकांचा उपयोग महत्त्वाचा ठरतो. इतकेच नव्हे, तर प्वासाँ समीकरण

यामिकीमधील श्रोडिंजर समीकरण इत्यादींच्या अभ्यासातही गोलीय हरात्मकांचा खूप उपयोग होतो.
ध्रुवीय गोलीय सहनिर्देशकांमध्येच नुसती ही हरात्मके येतात असे नाही. विवृत्तीय ध्रुवीय सहनिर्देशक वापरल्यास विवृत्तीय हरात्मके मिळतात. तसेच चितीय ध्रुवीय सहनिर्देशक वापरल्यास चितीय हरात्मके मिळतात. यामध्ये बेसेल फलनाचा समावेश होतो. भौतिकीशास्त्रातील बऱ्याच समस्यांच्या अभ्यासात यांचा उपयोग होतो.
या लेखात फक्त त्रिमितीय अवकाशातील हरात्मकांचा विचार केला आहे. परंतु तीनहून जास्त मितींच्या अवकाशासाठीही याच प्रकारची हरात्मके असतात.
संदर्भ : 1. Ganesh Prasad, A Treatise on Spherical Harmonics and the Function of Bessel and Lame, 2 Vols., 1930-32.
2. Mac-Robert, T.M. Spherical Harmonics, Oxford, 1967,
3. Whittaker, E. T. Watson, G. N. A Course of Modern Analysis, Cambridge, 1962.
गुर्जर, ल. वा.
“