चुंबकत्व

चुंबकत्व : काही खनिजांत लोखंड किंवा पोलादाच्या लहान तुकड्यांना आकर्षित करण्याचे सामर्थ्य असते. अशा खनिजांना अयस्कांत (लोडस्टोन) म्हणतात. अयस्कांताचा हा गुणधर्म ग्रीक लोकांना निदान ख्रि. पू. आठव्या शतकापासून माहीत होता, असा पुरावा मिळतो. हे खनिज मॅग्नेशिया प्रांतात विपुल प्रमाणात सापडत असल्यामुळे त्याला मॅग्नस हे नाव पडले. पुढे त्या शब्दाचा अपभ्रंश होऊन त्याला आंग्ल भाषेत मॅग्नेट म्हणू लागले. अयस्कांताला नैसर्गिक चुंबक अशी संज्ञा आहे. लोखंड, निकेल, कोबाल्ट आणि काही मिश्रधातूंमध्ये कृत्रिम रीतीने चुंबकत्व आणता येते. अयस्कांताचा तुकडा लोखंडाच्या किसात बुडवून काढल्यास कीस त्याच्या काही भागाला पुंजक्याप्रमाणे चिकटतो. सामान्यतः दोन्ही टोकांजवळ कीस जास्त चिकटतो व मध्ये फारसा चिकटत नाही.

पंधराव्या शतकापर्यंत चुंबकाच्या लोहाकर्षणाव्यतिरिक्त अन्य दोन गुणधर्मांचा शोध लागला होता. चुंबक एखाद्या पीळ नसलेल्या दोरीने आडवा टांगल्यास तो नेहमी एका दिशेत – अंदाजे दक्षिणोत्तर दिशेत – स्थिर राहतो. तेथून तो फिरविला असता परत त्याच दिशेत येतो. चिनी लोकांना हा गुणधर्म दुसऱ्या शतकात निश्चित माहीत होता, असा पुरावा आहे. चुंबकाच्या या दिक्‌शोधक गुणधर्मांवरच होकायंत्राचे कार्य चालते. चुंबकाचा दुसरा गुणधर्म म्हणजे चुंबकीय प्रवर्तन (चुंबकाच्या केवळ सान्निध्याने काही पदार्थांस चुंबकत्व प्राप्त होण्याची क्रिया) हा होय. हा गुणधर्म ग्रीक आणि रोमन लोकांना पहिल्या शतकातच माहीत असल्याचे नमूद आहे. एखादा साध्या लोखंडाचा तुकडा चुंबकाला लागून किंवा त्याला स्पर्श न करता त्याच्या सान्निध्यात ठेवल्यास त्या तुकड्यात प्रवर्तनाने लोहाकर्षणाचा गुणधर्म येतो. तो तुकडा मृदू लोखंडाचा असल्यास चुंबकापासून दूर नेल्यावर त्यातील चुंबकत्व नाहीसे होते परंतु तो तुकडा पोलादाचा असल्यास चुंबकापासून दूर नेल्यावरही त्यात थोडासा चुंबकत्वाचा गुणधर्म शिल्लक राहतो. पोलादात चुंबकीय निस्सारकता (अवशिष्ट चुंबकत्व नाहीसे करण्यासाठी लागणारी चुंबकीय प्रेरणा) जास्त असल्याने कृत्रिम टिकाऊ चुंबक तयार करताना पोलाद वा त्यासारखे इतर धातू वापरतात. एकोणिसाव्या शतकाच्या सुरुवातीपर्यंत कृत्रिम चुंबक ‘स्पर्श पद्धतीने’ तयार करीत असत. या पद्धतीत अयस्कांताचे किंवा एखाद्या कांड चुंबकाचे एक टोक पोलादाच्या एका तुकड्याच्या एका टोकाकडून दुसऱ्या टोकाकडे चिकटवून ओढत नेतात. नंतर ते वर उचलून पहिल्याच प्रमाणे ओढतात. असे बऱ्याच वेळा ओढल्याने त्या पोलादाच्या तुकड्यात कायमचे चुंबकत्व येते.

चुंबकत्वाच्या शास्त्रशुद्ध अभ्यासाचा पाया विल्यम गिल्बर्ट (१५४० – १६०३) यांनी सोळाव्या शतकाच्या शेवटी घातला. पृथ्वीला चुंबकीय क्षेत्र असते, हाही त्यांचाच शोध आहे. गिल्बर्ट यांच्या नंतर बराच काळ चुंबकत्वशास्त्रात फारशी प्रगती झाली नाही. कुलंब (१७३६ – १८०६) यांनी दोन चुंबकीय ध्रुवांतील आकर्षक किंवा प्रतिसारक प्रेरणेसंबंधी नियम शोधून काढले. त्यानंतर गौस (१७७७ – १८५५), केल्व्हिन (१८२४ –१९०७) आदी शास्त्रज्ञांनी त्यात भर घालून महत्त्वाचे सिद्धांत मांडले. त्यानंतरचा महत्त्वाचा टप्पा १८१९ साली ओर्स्टेड यांच्या शोधांनी गाठला. एखाद्या तारेतून विद्युत् प्रवाह सोडला असता तिच्याभोवती चुंबकीय क्षेत्र तयार होते, हे त्यांनी दाखविले. १८२० साली अँपिअर यांनी विद्युत् प्रवाह वापरून कृत्रिम चुंबक बनविता येतो, हे सिद्ध केले. ॲरागो यांनी त्याच वर्षी पहिला विद्युत् चुंबक तयार केला. या चुंबकत्वाचा उगम विद्युत् प्रवाहामुळेच होते, हे आता सिद्ध झाले आहे. विद्युत् प्रवाहाच्या साहाय्याने अतिशय सामर्थ्यवान चुंबक तयार करता येतात.

चुंबकत्वापासून विद्युत् प्रवाह कसा मिळविता येईल, याविषयी फॅराडे (१७९१ – १८६७) यांनी अनेक वर्षे प्रयोग केले. त्यांची परिणती विद्युत् चुंबकीय प्रवर्तन (संवाहकाशी निगडित असलेले चुंबकीय क्षेत्र बदलत असताना त्यात विद्युत् दाब निर्माण होणे) व त्याचे नियम या शोधात झाली. या विद्युत् चुंबकीय प्रवर्तनावरच विद्युत् जनित्र (यांत्रिक शक्तीचे विद्युत् शक्तीत रूपांतर करणारे यंत्र), दूरध्वनी वगैरे अनेक उपकरणे आधारलेली आहेत.

चुंबकत्वासंबंधीच्या काही मूलभूत कल्पना : पीळरहित धाग्याने टांगलेल्या चुंबकाच्या उत्तर दिशेकडे राहणाऱ्या टोकाला ‘उत्तर दिशादर्शक ध्रुव’ व दक्षिण दिशेकडे राहणाऱ्या टोकाला ‘दक्षिण दिशादर्शक ध्रुव’ असे म्हणतात. चुंबकाचे दोन तुकडे केल्यास दोन्ही तुकड्यांत एक एक नवा ध्रुव निर्माण होऊन पुन्हा दोन स्वतंत्र परंतु पूर्ण चुंबक बनतात म्हणजे प्रत्येकाला एक उत्तर व एक दक्षिण ध्रुव असतोच. मुक्त किंवा सुटा एक ध्रुव मिळूच शकत नाही, असा अनुभव येतो.

सैद्धांतिक पार्श्वभूमीवर मुक्त चुंबकीय ध्रुव अस्तित्वात असले पाहिजेत, अशी कल्पना १९३१ मध्ये डिरॅक यांनी मांडली. त्याचप्रमाणे असे मुक्त ध्रुव असलेच तर त्यांचे गुणधर्म काय असतील, याबद्दल काही कल्पना सुचविण्यात आल्या. त्यांच्या अनुरोधाने मुक्त ध्रुव मिळविण्यासाठी अनेक तऱ्हेचे प्रयोग करण्यात आले. परंतु ते सर्व निष्फळ ठरले.

१९७५ मध्ये प्राइस, शर्क, ऑस्बर्न व पिन्स्की या शास्त्रज्ञांनी आपल्याला उच्च ऊर्जा विश्वकिरणांत (बाह्य अवकाशातून येणाऱ्या अतिशय भेदक किरणांत) मुक्त चुंबकीय ध्रुव मिळाल्याचा दावा केला आहे. सकृत्‌दर्शनी त्यांचा शोध ग्राह्य वाटतो, परंतु अद्याप त्याला सर्वमान्यता मिळालेली नाही. अशी मान्यता मिळून मुक्त ध्रुवांचे अस्तित्व प्रस्थापित झाले, तर भौतिकीत फार मोठी क्रांती होईल. प्रस्तुत नोंद मुक्त ध्रुव अस्तित्वात नाहीत, असे गृहीत धरून लिहिली आहे.

चुंबकीय प्रवर्तन :  चुंबकत्वातील ही मूलभूत राशी मानण्यात येते व तिच्या संदर्भात इतर चुंबकीय राशींच्या व्याख्या दिल्या जातात. चुंबकत्वविषयक विविध राशींच्या व्याख्या देताना पूर्वी एकाकी उत्तर ध्रुवाचे अस्तित्व मानून त्याच्या संदर्भात त्या देत असत. परंतु एक ध्रुव मिळूच शकत नाही व चुंबक हा नेहमी दोन परस्परविरूद्ध (उत्तर व दक्षिण) ध्रुवांच्या जोडीतच मिळतो, असा निष्कर्ष अनेक प्रयोगान्ती आला आहे. दोन परस्परविरूद्ध परंतु सममूल्य चुंबकीय ध्रुवांनी बनलेल्या चुंबकाला शास्त्रीय परिभाषेत चुंबकीय द्विध्रुव असे म्हणतात.

एक ध्रुवाचे अस्तित्वच नसल्याने त्याच्यावर आधारलेल्या व्याख्याही गैरलागूच ठरतात. म्हणून हल्लीच्या पद्धतीत चुंबकीय राशींच्या व्याख्या निराळ्या तऱ्हेने देतात. तीच पद्धत येथे अवलंबिली आहे.

या पद्धतीनुसार चुंबकत्वासंबंधीची मूलभूत राशी म्हणजे चुंबकीय प्रवर्तन B ही सदिश राशी होय. केव्हा केव्हा B लाच चुंबकीय स्त्रोत घनता असेही म्हणतात. पुढील तीन व्याख्यांनी B ह्या राशीचे संपूर्ण वर्णन मिळते.

(१) B चे अस्तित्व : विशिष्ट प्रदेशात एखादा गतिमान विद्युत् भार सोडला असता जर विद्युत् भारावर त्याच्या मार्गाला नेहमी लंबदिशेनेच असणारी प्रेरणा लागू होत असेल, तर मग त्या प्रदेशात चुंबकीय प्रवर्तन क्षेत्र आहे असे म्हटले जाते.

(२) B ची दिशा : वरील प्रयोगावरून विद्युत् भाराच्या गतीची दिशा हळूहळू बदलत गेल्यास शेवटी अशी दिशा येते की, तेव्हा त्या विद्युत् भारावरील प्रेरणा शून्य होते. चुंबकीय प्रवर्तन क्षेत्रात ज्या दिशेने विद्युत् भार सोडला असता त्याच्यावरील प्रेरणा शून्य होईल, ती त्या प्रवर्तन क्षेत्राची दिशा होय.

(३) प्रवर्तनाचे मूल्य : विद्युत् भारावरील सदर प्रेरणेचे मूल्य F = q v B sin θ या समीकरणाने मिळते. या समीकरणात q हा विद्युत् भार असून v हा त्याचा वेग आहे. θ हा प्रवर्तनाची दिशा व वेगाची दिशा यांतील कोन आहे. या समीकरणावरून चुंबकीय प्रवर्तनाच्या (B) एककाची व्याख्या खालीलप्रमाणे करतात. एक कुलंब विद्युत् भार १ मी./से. इतक्या वेगाने प्रवर्तनाच्या लंब दिशेने जात असता त्यावर १ न्यूटन इतकी प्रेरणा निर्माण होत असल्यास त्या ठिकाणी चुंबकीय प्रवर्तनाचे मूल्य १ टेस्ला किंवा १ वेबर/मी.^२ इतके असते.

---

विद्युत् प्रवाहजन्य चुंबकीय क्षेत्र : एकादा विद्युत् वाहक तारेतून विद्युत् प्रवाह सोडला असता तिच्या भोवती निर्माण झालेल्या चुंबकीय प्रवर्तनाचे मूल्य ब्यो व साव्हार यांच्या नियमाने मिळतो. dI इतक्या अत्यल्प लांबीच्या तारेतून i अँपिअर विद्युत् प्रवाह जात असता तारेपासून r इतक्या अंतरावर असलेल्या बिंदूवर चुंबकीय प्रवर्तक B हे

B =	μ0 i dl sin θ	इतके असते. यात μo हा स्थिरांक असून त्यास
	4 π r2

मुक्त अवकाशाची पार्यता (एखाद्या पदार्थातून चुंबकीय प्रेरणा रेषा जाण्याची सहजता चुंबकीय प्रवर्तन व चुंबकीय प्रेरणा यांचे गुणोत्तर) असे म्हणतात. त्याचे मूल्य ४π × १०^-७ हेन्‍री / मी. असते. तसेच θ हा विद्युत् प्रवाहाची दिशा आणि तार व इष्ट बिंदू यांना जोडणारी रेषा यांतील कोन आहे. या प्रवर्तनाची दिशा अँपिअर यांच्या उजव्या हाताच्या नियमानुसार मिळते. उजव्या हाताचा अंगठा सरळ ठेवून बाकीची बोटे मिटल्यावर जर विद्युत् प्रवाह अंगठ्याच्या दिशेने जात असेल, तर बोटे प्रवर्तनाची दिशा दर्शवितात. तारेजवळील कोणत्याही

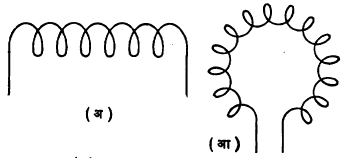
बिंदूच्या ठिकाणी प्रवर्तनाची दिशा काढण्यासाठी तारेवर मध्य घेऊन या बिंदूतून जाणारे वर्तुळ काढावे व या वर्तुळावर त्या बिंदूतून जाणारी स्पर्शिका काढल्यास तेथील प्रवर्तन या स्पर्शिकेच्या दिशेने असते निरनिराळ्या आकाराच्या वेटोळ्यांतील विद्युत् प्रवाहामुळे निर्माण होणारे चुंबकीय प्रवर्तन काढण्यासाठी संबंध वेटोळ्याचे असंख्य लहान तुकडे केले आहेत, अशी कल्पना करतात. मग वरील नियम प्रत्येक लहान तुकड्याला लावून निर्माण होणाऱ्या प्रवर्तनाची सदिश बेरीज काढतात.

आ. १ मध्ये दाखविलेल्या दोन्ही प्रकारच्या परिनलिकांच्या अक्षावर प्रवर्तन μ₀ n i इतके असते. यात n हे परिनलिकेच्या एकक लांबीत असलेले वेढे आहेत. r त्रिज्या असलेल्या व n वेढे असलेल्या वर्तुळाकार वेटोळ्यात i अँपिअर इतका प्रवाह वाहत असल्यास त्याच्या केंद्राशी  

μ0 n i

2r

इतके प्रवर्तक असते. 

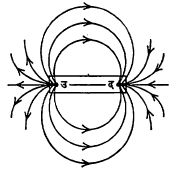
चुंबकीय प्रेरणा रेषा : चुंबकाच्या उत्तर ध्रुवापासून निघून बाहेरून चुंबकीय प्रेरणा रेषा आ. २ मध्ये दर्शविल्याप्रमाणे दक्षिण ध्रुवाला जाऊन मिळतात, अशी कल्पना आहे. कोणत्याही बिंदूवरील चुंबकीय प्रवर्तन हे त्या बिंदूमधून जाणाऱ्या प्रेरणा रेषेला तेथे काढलेल्या स्पर्शिकेच्या दिशेत असते. चुंबकाप्रमाणेच विद्युत् प्रवाह वाहत असलेल्या तारेच्या वेटोळ्यामुळेही  प्रेरणा रेषा नि्र्माण होतात. एका पुठ्ठ्यावर चुंबक ठेऊन त्याच्याभोवती लोखंडाच्या किसाचा एक पातळ थर पसरून हळूहळू टिचक्या मारल्या असता प्रेरणा रेषांची कल्पना लोखंडाच्या किसाच्या थरात तयार झालेल्या आकृतीवरून येते. चुंबकीय क्षेत्र एकविध (सर्वत्र सारखे) असल्यास प्रेरणा रेषा एकमेकींस समांतर असतात. नैकविध (सर्वत्र सारखे नसणाऱ्या) क्षेत्रात त्या वक्र असतात. प्रेरणा रेषा एकमेकींस छेदीत नाहीत व क्षेत्राच्या तीव्रतेच्या समप्रमाणात त्यांची घनता कमी जास्त असते.

इ. स. १९३१ च्या सुमारास हामोस व थैसन यांनी आणि एफ्. बिटर यांनी स्वतंत्रपणे Fe₂O₃ च्या चूर्णाचे १०^-४ सेंमी. इतके सूक्ष्म कण द्रवामध्ये निलंबित करून सूक्ष्मदर्शकाच्या साहाय्याने छायाचित्रे घेऊन प्रेरणा रेषांचे चित्रीकरण केले. या पद्धतीचा उपयोग चुंबकित अथवा अचुंबकित स्फटिकांचे संशोधन करण्यासाठी होतो.

वेगवेगळ्या स्फटिकांच्या प्रकाशीय अक्षाभोवतीचे वरील प्रकारच्या चूर्णाने बनलेल्या प्रेरणा रेषांच्या प्रतिरूपाचे अवलोकन केल्यास पदार्थाच्या चुंबकीय गुणधर्माचे संशोधन करता येते. या रेषांची कल्पना फॅराडे यांनी

मांडली. या रेषा खरोखरीच अस्तित्वात असून सर्व चुंबकीय आविष्कार त्यांच्या मुळेच होतात, असे फॅराडे यांचे मत होते. ही कल्पना आता सोडून देण्यात आलेली असून प्रेरणा रेषा ही चुंबकीय क्षेत्राचे चित्रण करण्याचा एक मार्ग होय, असे मानतात. म्हणून त्यांना हल्ली क्षेत्ररेषा हे नाव देण्यात आले आहे.

चुंबकीय परिबल : एकविध प्रवर्तनात एखादा कांड चुंबक ठेवल्यास त्यावर प्रेरणायुग्म (दोन समांतर, सममूल्य व परस्परांस विरूद्ध असणाऱ्या प्रेरणा) कार्य करते. या प्रेरणायुग्माचे परिबल Τ = M B sinθ या समीकरणाने मिळते या समीकरणात M हे त्या चुंबकाचे चुंबकीय परिबल असून θ हा चुंबक आणि प्रवर्तक-सदिश यांतील कोन आहे. असेच प्रेरणायुग्म विद्यत् प्रवाह असलेल्या तारेच्या वेटोळ्यावरही कार्य करते. तारेच्या वेटोळ्याचे समतुल्य चुंबकीय परिबल M= μ_० n i A इतके असते. यात i विद्युत् प्रवाह, n वेटोळ्यातील वेढे व A हे वेटोळ्याचे क्षेत्रफळ होय.

---

चुंबकीय स्त्रोत : प्रवर्तनाशी लंबदिशेने A इतक्या क्षेत्रफळातून जाणारा चुंबकीय स्त्रोत Φ = BA वेबर इतका असतो.

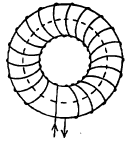
चुंबकीकरण : आ. ३ मध्ये दाखविलेल्या आकाराचे वेटोळे घेऊन त्याच्या अंतर्भागात कोणतेही द्रव्य नाही असे मानल्यास आकृतीतील तुटक रेषेने दर्शविलेल्या रेषेवर कोठेही निर्माण झालेले चुंबकीय प्रवर्तन

B₀ = μ_० n i_r या समीकरणावरून मिळते येथे n म्हणजे परिनलिकेच्या एकक लांबीतील तारेच्या वेढ्यांची संख्या असून i_r हा तारेतून जाणारा (खरा) विद्युत् प्रवाह आहे. परिनलिकेच्या अंतर्भागात कोणतेही द्रव्य भरल्यास वेटोळ्यातला विद्युत् प्रवाह न बदलला, तरी ही अंतर्भागातील प्रवर्तन बदलून ते B इतके होते. B = B₀ +B_m असे लिहिल्यास B_m हे प्रवर्तन परिनलिकेतील द्रव्यावर B₀ च्या झालेल्या परिणामामुळे उत्पन्न झाले असले पाहिजे. परिनलिकेचा अंतर्भाग द्रव्य रहित ठेवून तिच्या आतील प्रवर्तन B_m ने वाढविण्यासाठी वेटोळ्यातील विद्युत् प्रवाह (समजा) i_m ने वाढवावा लागतो. मग

B_m = μ_o ni_m  .^_.. B = μ_० n i_r + μ₀ n i_m = μ₀ ( n i_r + n i_m)

तेव्हा द्रव्यातील प्रवर्तनाचे (B चे) आपणाला दोन भाग मानता येतील. एक भाग B_o = μ_o n i_r हा केवळ वेटोळ्यातून जाणाऱ्या i_r या खऱ्या विद्युत् प्रवाहामुळे निर्माण झालेला आहे. दुसरा भाग B_m = μ_o n i_m हा परिनलिकेतील द्रव्याच्या अणूंमधील इलेक्ट्रॉनांच्या गतीवर B_o च्या परिणामामुळे उत्पन्न झाला आहे. i_m या काल्पनिक प्रवाहाशी तो समतुल्य आहे. B च्या वरील समीकरणापैकी n i_r हा भाग फक्त खऱ्या विद्युत् प्रवाहावरच अवलंबून राहतो. परिनलिकेत द्रव्य असो वा नसो हा भाग आहे तसाच राहतो. म्हणून या भागाला चुंबकीय क्षेत्र किंवा चुंबकीकरण प्रेरणा H (= n i_r ) हे नाव दिले आहे. H ही सदिश राशी आहे (एकक-अँपिअर प्रतिमीटर). त्याचप्रमाणे द्रव्यामुळे उत्पन्न होणारे प्रवर्तन n i_m या राशीला सम प्रमाणात असते. μ_o n i_m या राशीला चुंबकीकरण तीव्रता I (= μ_o n i_m ) असे म्हणतात. I ही सुद्धा सदिश राशी असून ती त्या द्रव्याच्या प्रतिएकक घनफळात निर्माण झालेले चुंबकीय परिबल दर्शविते.

तेव्हा वरील समीकरण	→	=	μ0	→	+	→
	B			H		I

असे लिहिता येईल (येथे μ_o = ४π × १०^-७ हेन्‍री प्रतिमीटर, ही मुक्त अवकाशाची पार्यता होय). असे दिसून येते

की, अनेक माध्यमांत	I	= Xm हा स्थिरांक असतो.
	H

त्याला त्या माध्यमाची चुंबकीय प्रवणता असे म्हणतात (एकक- हेन्‍री प्रतिमीटर). मात्र लोहचुंबकीय माध्यमात X_m चे मूल्य H वर अवलंबून असते, हे लक्षात ठेवणे जरूर आहे.

Xm	=
μ0

या राशीला द्रव्याची सापेक्ष चुंबकीय प्रवणता असे  म्हणतात. ही राशी परिमाणरहित आहे.

I	=  Xm	... I = Xm· H = μ0 X.H
H

.^.. B = μ₀ ( 1 + X) H

(1+ X) = μ_r या राशीला माध्यमाची सापेक्ष पार्यता असे म्हणतात व μ = μ₀ (1+X) या राशीला द्रव्याची (निरपेक्ष) पार्यता असे म्हणतात. हे उघड आहे की, लोहचुंबकीय माध्यमाच्या बाबतीत μ व μ_r स्थिरांक असणार नाहीत, परंतु इतर माध्यमांच्या बाबतीत ते स्थिरांक असतात. X व μ_r यांच्या मूल्यांच्या अनुरोधाने पदार्थाच्या चुंबकीय गुणधर्मांची वैशिष्ट्ये लक्षात येतात व त्यानुसार पदार्थाचे कोष्टकात दिल्याप्रमाणे वर्गीकरण करता येते.

काही द्रव्यांच्या सापेक्ष चुंबकीय प्रवणतेची (X) मूल्ये

द्रव्य
तांबे	}	प्रतिचुंबक	– १·० × १० -५
सोने			– ३·६ × १०-५
पारा			– ३·२ × १०-५
पाणी			– ०·९ × १०-५
हायड्रोजन	}	समचुंबक	– ०·२ × १०-८
ॲल्युमिनियम			+ २·२ × १०-५
मॅंगॅनीज			+ ९८ × १०-५
प्लॅटिनम			+ ३६ × १०-५
हवा			+ ३६ × १०-८
लोह	}	लोहचुंबक	+ ८·८ × १०४ (कमाल मूल्य सु.)
लोह (स्फटिक)			+ १·४ × १०६ (कमाल मूल्य सु.)
सिलिकॉन-लोह(स्फटिक)			+ ३·८ × १०६ (कमाल मूल्य सु.)
Fe3 O4	}	लोहीचुंबक	+ १०० (कमाल मूल्य सु.) + ५,००० (कमाल मूल्य सु.)
फेराइट

ज्या पदार्थांच्या बाबतीत Xचे मूल्य ऋण (सु. १०^-५ व १०^-८) असेल, ते पदार्थ चुंबकीय क्षेत्रात ठेवले असता त्यांचे आतील प्रवर्तन (B) बाहेरच्या प्रवर्तनापेक्षा (B₀ पेक्षा) कमी होईल. त्याची μ_r एकापेक्षा (किंचित) कमी असेल. अशा पदार्थांना प्रतिचुंबकीय पदार्थ असे म्हणतात. बिस्मथ, तांबे, चांदी, पाणी वगैरे पदार्थ प्रतिचुंबकीय आहेत. प्रत्येक पदार्थ मूलतः प्रतिचुंबकीय असतो, परंतु हा गुण पुष्कळदा इतर परिणामांमुळे झाकला जातो, हे प्रयोगाने व सैद्धांतिक रीत्या सिद्ध झालेले आहे. शक्तिमान चुंबकाकडून प्रतिचुंबकीय पदार्थांचे प्रतिसारण होते (त्यावरून त्यांना हे नाव मिळाले आहे), मात्र हे प्रतिसारण अत्यंत दुर्बल असते.

ऑक्सिजन, ॲल्युमिनियम, प्लॅटिनम यांसारख्या पदार्थांच्या बाबतीत X धन परंतु तिचे मूल्य अल्प (१०^-८ व १०^-५) असते. त्यामुळे त्याची μ_r एकापेक्षा किंचित जास्त असते म्हणून चुंबकीय क्षेत्रात ठेवले असता त्यांच्या आतील प्रवर्तन (B) बाहेरच्या प्रवर्तनापेक्षा (B₀ पेक्षा) किंचित जास्त होते. अशा पदार्थांना सामर्थ्यवान चुंबकाकडून दुर्बलपणे आकर्षण होते. अशा पदार्थांना समचुंबकीय पदार्थ असे म्हणतात.

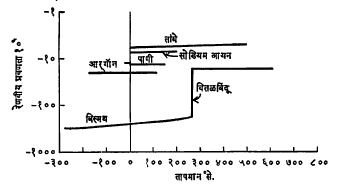
समचुंबकीय पदार्थांची X तापमान वाढवले, तर कमी होत जाते व शेवटी एका विशिष्ट तापमानाला (समचुंबकीय क्यूरी बिंदू) ती शून्य होते. या मर्यादेपलीकडे तापमान वाढविल्यास तो पदार्थ प्रतिचुंबकीय झाल्याचे आढळते म्हणजे त्यांची X ऋण होते.

लोखंड, निकेल आणि त्यांच्या कित्येक मिश्रधातू यांच्या बाबतीत X चे मूल्य खूपच जास्त (१०^३ किंवा त्याहून अधिक) असते, तसेच μ_r चेही मूल्य एकापेक्षा खूप जास्त असते. चुंबकीय क्षेत्रात ठेवले असता यांच्या अंतर्भागातील B बाहेरच्या B₀ पेक्षा खूपच जास्त असते. असे पदार्थ लोहचुंबकाकडून जोरदारपणे आकर्षित केले जातात. या प्रकारच्या पदार्थांना   लोहचुंबकीय पदार्थ असे म्हणतात.

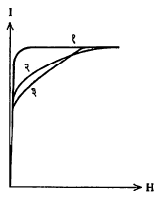
लोखंडासारख्या लोहचुंबकीय पदार्थांचा I हा H च्या सम प्रमाणात नसतो म्हणजेच X स्थिरांक नसतो. त्यामुळे अशा पदार्थावरील बाह्य क्षेत्र H वाढवत जाऊन त्यानुसार मिळणारी I ची मूल्ये मोजली आणि H व I यांचा आलेख काढला, तर तो सरळ रेषा न येता आ. ४ प्रमाणे वक्र येतो. इतकेच नव्हे तर उच्च H पासून प्रारंभ करून त्याचे मूल्य हळूहळू कमी करत गेल्यास हाच आलेख उलट दिशेने मिळत नाही. म्हणून लोह चुंबकीय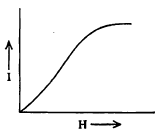

पदार्थांचे चुंबकीकरण ही व्युत्क्रमी क्रिया नाही असे म्हणतात.

या शिवाय चुंबकीय पदार्थांचे आणखी वर्ग आहेत. चुंबकत्वाच्या या विविध प्रकारांची उपपत्ती पुढे दिली आहे.

---

चुंबकीय वर्चस् : चुंबकीय प्रवर्तन क्षेत्रात P व Q हे दोन बिंदू घेतले, तर त्या दोन बिंदूंतील चुंबकीय वर्चोभेद (दोन बिंदूंमधील चुंबकीय ऊर्जा स्थितीतील फरक)

		Q	→	→
VP Q	=	P ∫	H .	dl	या समाकलाने  [→ अवकलन व समकालन]

मिळतो. अनंत अंतरावर वर्चस् शून्य कल्पिल्यास Pया बिंदूस चुंबकीय

	P	→	→		1	P	→  →
वर्चोभेद	– ∫	H .	dl	किंवा  –		∫	B. dl
					μ0
	∞					∞

इतका असतो. चुंबकीय वर्चसाच्या वृद्धिफलनावरून कोणत्याही बिंदूपाशी चुंबकीय क्षेत्र काढता येते. हे वर्चस् V अदिश असून त्याशिवाय चुंबकीय सदिश वर्चस्  A अशीही एक राशी वापरण्यात येते.

चुंबकीय चालक प्रेरणा : चुंबकीय प्रवर्तन रेषा चुंबकाच्या एका टोकातून चुंबकाबाहेरून निघून त्या दुसऱ्या टोकापाशी आल्यावर चुंबकातून पुन्हा मूळ ठिकाणी येतात. अशा रीतीने प्रवर्तन रेषांचे मंडल पूर्ण होते. अशा मंडलास ⇨चुंबकीय मंडल असे म्हणतात. चुंबकीय स्रोत हा एक प्रकारचा प्रवाह आहे अशी कल्पना केल्यास या मंडलाची विद्युत् मंडलाशी तुलना करून विद्युत् प्रवाहाबद्दलच्या ओहम नियमानुरूप

चुंबकीय स्तोत्र =	चुंबकीय चालक प्रेरणा	असे समीकरण मांडता येते.
	चुंबकीय प्रतिरोध

याला हॉप्‌किन्सन यांचे समीकरण असे म्हणतात. अशा प्रकारच्या समीकरणाचा उपयोग दोन चुंबकाग्रांमधील क्षेत्रातील प्रवर्तनाची तीव्रता काढण्याकरिता व विशेष प्रकारचे चुंबक बनविण्यासाठी होतो.

वरील सर्व चुंबकीय राशींची भिन्नभिन्न मापन पद्धतींतील एकके व त्यांची नावे यांसाठी ‘एकके व परिमाणे’ ही नोंद पहावी.

चुंबकीय राशीमापन : वेगवेगळ्या पद्धतीने चुंबकीय क्षेत्र निर्माण करून त्याच्या साहाय्याने एखाद्या वस्तूचे चुंबकीकरण करता येते. निरनिराळ्या चुंबकीय राशींचे आलेख काढून त्यावरून वस्तूची चुंबकीय पार्यता आणि चुंबकीय प्रवणता यांचा अभ्यास करता येतो व त्या अभ्यासावरून निरनिराळी शास्त्रीय व यांत्रिक उपकरणे बनविताना सुयोग्य धातूंची निवड करता येते. चुंबकीय क्षेत्र निर्माण करून चुंबकीय राशीमापन करण्याच्या अनेक पद्धती आहेत.

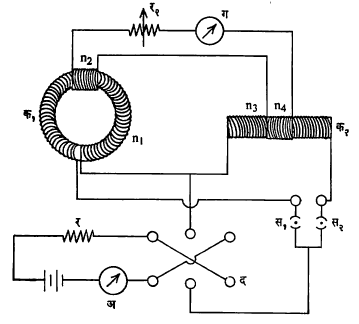प्रक्षेपी गॅल्व्हानोमीटरची पद्धती : प्रक्षेपी (ज्यामध्ये मापकाच्या वेटोळ्याने घेतलेला झोका मोजून त्यावरून मापकातून गेलेला विद्यत् भार काढता येतो अशा) ⇨ गॅल्व्हानोमीटराच्या साहाय्याने पार्यता काढण्याची पद्धत रोलंड या शास्त्रज्ञांनी १८७३ साली शोधून काढली. या पद्धतीतील परीक्ष्य कड्याच्या आकाराचे घेऊन त्याच्याभोवती प्रत्येक मीटर लांबीत n₁ वेढे असलेली चक्राकृती परिनलिका गुंडाळतात. यावर n₂ वेढ्यांचे एक दुय्यम वेटोळे गुंडाळतात ते प्रक्षेपी गॅल्व्हानोमीटरची ग ला जोडतात. स_१ ही चावी जोडली असता प्राथमिक वेटोळ्यातून द या दिक्‌रिपवर्तकामार्फत (विद्युत् प्रवाहाची दिशा बदलणाऱ्या साधनामार्फत) अ या विद्युत् प्रवाहमापकातून i इतका प्रवाह गेल्यास त्यामुळे उत्पन्न झालेले चुंबकीय क्षेत्र H = n₁ i इतके असेल व त्यामुळे कड्याचे चुंबकीकरण होऊन त्या चुंबकीय क्षेत्रामुळे दुय्यम वेटोळ्यातून चुंबकीय स्रोत जाईल. प्रवर्तन B इतके होत असल्यास आणि क_१ वेटोळ्याच्या अनुप्रस्थ (अक्षास काटकोन करणाऱ्या) छेदाचे क्षेत्रफळ A असल्यास दुय्यम मंडलातून व प्रक्षेपी गॅल्व्हानोमीटरातून जाणारे विद्युत् भार मूल्य इतके असेल व त्यामुळे गॅल्व्हानोमीटरात θ इतका प्रक्षेप (झोक्याची लांबी) झाल्यास  (येथे R हा प्रेक्षपी गॅल्व्हानोमीटर व त्याच्या मंडलातील सर्व घटकांचा मिळून विद्युत् रोध आहे.)

k चे मूल्य काढण्यासाठी प्रमाणित वेटोळे असल्यास क_२ चा उपयोग करतात. यात प्रती मी. लांबीत n₃ वेढे असल्यास स_२ चावी दाबताच क_२ वेटोळ्यात i₁ विद्युत् प्रवाहामुळे n₃ i₁ इतके चुंबकीय चुंबकीय क्षेत्र निर्माण होऊन त्यामुळे दुय्यम वेटोळ्यातून μ₀ n₃ i चुंबकीय स्त्रोत जाईल आणि त्यामुळे प्रक्षेपी गॅल्व्हानोमीटर θ₁ इतका प्रक्षेप झाल्यास  असे समीकरण होईल. येथे A₁ हे क_२ वेटोळ्याचे अनुप्रस्थ क्षेत्रफळ असून n₄ त्यावरील दुय्यम वेटोळ्यातील वेढे आहेत.

वरील दोन समीकरणांवरून

B = μ0	n3 n4 A1 i1	.	θ	आणि H=n1i
	An2		θ1

अशी दोन समीकरणे मिळतात. प्रथम दिक्‌‌परिवर्तकाच्या साहाय्याने बऱ्याच वेळा उलटसुलट प्रवाह पाठवून

परीक्ष्याचे पूर्णपणे निकर्षण (चुंबकत्व नाहीसे करणे) करतात आणि नंतर +i पासून -i पर्यंत एकदम प्रवाह बदलून निर्माण होणाऱ्या प्रक्षेपाची नोंद करतात. याच पद्धतीने निरनिराळ्या मूल्यांच्या i साठी प्रक्षेपांच्या नोंदी करतात. या पद्धतीचे दोन मुख्य फायदे आहेत. (१) कड्याला अग्रे नसल्याने अग्रांचा परिणाम होत नाही. (२) बाहेरील चुंबकीय क्षेत्राचा प्रयोगावर फारसा परिणाम होत नाही. आ. ६ मध्ये प्रातिनिधिक लोहचुंबकीय पदार्थाच्या नमुन्याचा B – H आलेख दाखविला आहे.

---

प्रत्यावर्ती विद्युत‌् प्रवाह पद्धत : प्रत्यावर्ती (उलटसुलट दिशेने वाहाणारा) विद्युत्‌ प्रवाह चाचणीचा प्रमुख उपयोग चुंबकीय पार्यता काढण्यासाठी तसेच रोहित्र विद्युत् दाब बदलणारे साधन) वगैरेंच्या अंतरकातील (गाभ्यातील) पातळ पत्र्यामध्ये होणारा ऊर्जाक्षय जाणून घेण्यासाठी होतो. अशा वेळी प्रवर्तन सेतू वापरतात. आ. ७ मध्ये दाखविलेल्या प्रवर्तन सेतूमध्ये आपणास हव्या तेवढ्या स कंप्रतेचा (दर सेकंदास होणाऱ्या कंपन संख्येचा ) विद्युत‌् प्रवाह आंदोलकाच्या (आंदोलने निर्माण करणाऱ्या इलेक्ट्रॅानीय उपकरणाच्या) साहाय्याने अ या विद्युत प्रवाहमापकातून पाठविता येईल व तो मोजला जाईल. सेतूच्या दोन संलग्न भुजांमध्ये प्रत्येकी र_१ इतका रोध ठेवतात. इतर दोन भुजांपैकी एकीमध्ये इष्ट माध्यमाच्या कड्यावर तारेच्या वेढ्यांनी गुंडाळलेले वेटोळे व आणि चौथ्यामध्ये र ही रोध पेटी आणि मूल्य बदलू शकणारा प्रवर्तक (केवळ प्रत्यावर्ती विद्युत प्रवाहास वा त्याच्या बदलास विरोध करणारे साधन) ल असतो. त्याचे मूल्य जुळवून वि या विवर्धकाशी (विद्युत‌् शक्तीचे वर्धन करणाऱ्या साधनाशी) जोडलेल्या उ या उपकरणाच्या साहाय्याने सेतू संतुलित करता येते. उ हा दूरध्वनी ग्राही (संदेश ग्रहण करणारे साधन) असल्यास संतुलन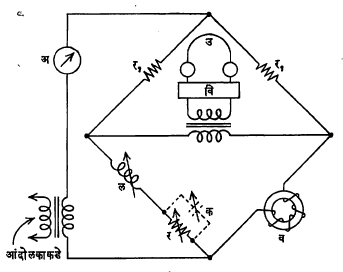

झाल्याची खूण म्हणजे त्यांतून काहीही आवाज ऐकू येईनासा होतो. अशा वेळी वेटोळ्याचा प्रत्यावर्ती प्रवाहाला होणारा विद्युत‌् रोध तसेच ल आणि र यांवरून चुंबकीय पार्यता काढता येते. सुधारलेल्या मॅक्सवेल सेतूमध्ये ल ऐवजी र रोधपेटीस मूल्य बदलू शकणारे धारित्र (विद्युत‌् भार साठविणारे साधन) क समांतर जोडतात.

असमान चुंबकीय क्षेत्र पद्धत : चुंबकीय पदार्थातील अत्यल्प पार्यता आणि प्रवणता मोजण्यासाठी ही पद्धत वापरतात. सामर्थ्यवान विद्युत् चुंबकाच्या दोन ध्रुवांच्या मध्यभागी समचुंबकीय पदार्थ ठेवल्यास तो

क्षेत्राच्या तीव्रतर भागाकडे खेचला जातो आणि प्रतिचुंबकीय पदार्थ दूर ढकलला जातो. कारण ध्रुवांमधील अंतरात प्रती मी. मध्ये होणारा क्षेत्रबदल एकसारखा नसतो. फॅराडे यांनी ही खेचणारी अथवा दूर ढकलणारी प्रेरणा ताणकाट्याच्या साहाय्याने मोजली. तसेच पदार्थांचे चुंबकीय दृष्ट्या वर्गीकरण केले आणि त्यांची चुंबकीय प्रवणताही मोजली. फॅराडे यांच्या ताणकाट्यात पी. क्यूरी यांनी सुधारणा करून समचुंबकीय अथवा प्रतिचुंबकीय पदार्थावर तापमानाचा काय परिणाम होतो, याचे संशोधन केले.

नैकविध चुंबकीय क्षेत्रामध्ये चुंबकीय पदार्थ ठेवल्यास त्याच्यावर चुंबकीय प्रेरणा लागू होते. या तत्त्वावर आधारलेली दोन-तीन साधने तयार करण्यात आली व त्यांच्या साहाय्याने निरनिराळ्या अवस्थांतील पदार्थांच्या प्रवणता अचूक व अल्प काळात मोजता येऊ लागल्या.

तीव्र चुंबकीय क्षेत्रमापन : विसाव्या शतकाच्या सुरुवातीस विद्युत् चुंबकाच्या विशिष्ट रचनेने ५ टेस्ला इतके तीव्र चुंबकीय प्रवर्तन निर्माण करण्यात आले होते. त्यानंतर काप्यिट्स या शास्त्रज्ञांनी विशिष्ट पद्धती वापरून ८,००० अँपि. एवढा प्रचंड विद्युत् प्रवाह अल्प काळ पाठवून अतितीव्र पण क्षणिक (०·०००३ सेकंद) असे ५० टेस्ला इतके प्रवर्तन निर्माण केले. अशी तीव्र क्षेत्रे खालील पद्धतीने मोजता येतात.

(१) क्षेत्रफळ माहित असलेले एक तारेचे लहान वेटोळे या मापनात वापरतात. हे वेटोळे चुंबकीय क्षेत्रातून एकदम काढून घेतल्यास किंवा वेटोळे १८०^० तून फिरविल्यास त्यामुळे उत्पन्न झालेला विद्युत् भार प्रक्षेपी गॅल्व्हानोमीटराने मोजून त्यावरून क्षेत्रमूल्य काढता येते.

(२) चुंबकीय क्षेत्रामुळे होणाऱ्या इतर विविध परिणामांचा उपयोग करून चुंबकीय क्षेत्राची तौलनिक मापने करता येतात. (आणखी काही क्षेत्रमापकांची माहिती ‘चुंबकीय क्षेत्रमापन’ या नोंदीत पहावी).

भूचुंबकीय मापने : भुचुंबकीय क्षेत्राच्या संदर्भात नतिकोन, दिक्‌पात कोन व क्षेत्राचा क्षैतिज (क्षितिज समांतर) घटक या राशी महत्त्वाच्या आहेत [→ भूचुंबकत्व चुंबकीय क्षेत्रमापक].

मंदायन वक्र : लोखंडासारखे द्रव्य विद्युत् प्रवाहाद्वारे निर्माण केलेल्या चुंबकीय क्षेत्रात ठेवून त्या क्षेत्राचे मूल्य क्रमशः वाढवीत गेल्यास, चुंबकीकरणाची तीव्रता अ (आ. ८) या बिंदूपर्यंत वाढत जाऊन त्यास संपृक्तता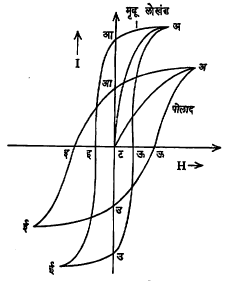

येते म्हणजे काहीही केले तरी या मर्यादेपुढे चुंबकीकरणाची तीव्रता वाढू शकत नाही (आ. ८ मध्ये पोलाद आणि मृदू लोखंड यांच्याकरिता चुंबकीकरणाची तीव्रता I व चुंबकीय क्षेत्र H यांचे आलेख दिले आहेत). यानंतर क्षेत्र क्रमशः शून्यापर्यंत कमी करीत गेल्यास चुंबकीकरणाची तीव्रता आ पर्यंतच कमी होते. म्हणजे चुंबकीय क्षेत्र शून्य झाले असता सुद्धा वस्तूतील चुंबकीकरणाची तीव्रता शून्य होत नाही. या गुणधर्मास चुंबकीय अवशेषता असे म्हणतात. यामुळे त्या वस्तूमध्ये काही चुंबकत्व शिल्लक राहते.

विरूद्ध दिशेत चुंबकीय क्षेत्र वाढवीत गेले असता निकर्षण कसे होते हे वक्राच्या आइ भागाने दर्शविले आहे, इ बिंदूपाशी I चे मूल्य शून्य करण्याकरिता विरुद्ध दिशेने टइ इतके चुंबकीय क्षेत्र लावावे लागते, यास निस्सारक प्रेरणा म्हणतात. या विशिष्ट लोखंडी सळईतील चुंबकत्व नष्ट करण्यास इतक्या विरोधी- चुंबकीय प्रेरणा आवश्यकता असते. निस्सारक प्रेरणेच्यापुढे विरूद्ध दिशेने चुंबकीय क्षेत्र वाढवीत गेल्यास वक्राचा इई हा भाग मिळून ई येथे त्या वस्तूला विरुद्ध दिशेने संपृक्तता येते. विरुद्ध दिशेने चुंबकीय क्षेत्र क्रमाक्रमाने कमी करीत गेल्यास H शून्य होईल तेव्हा वक्र उ या बिंदूप्रत येतो व तेथून H परत वाढवीत गेल्यास उऊअ हा वक्र मिळतो. अआइईउऊअ या आकृतीला मंदायन वक्र असे म्हणतात. अशा तऱ्हेने चुंबकीय क्षेत्रात वरीलप्रमाणे चक्रीय परिवर्तन होत असताना, चुंबकीकरणाच्या तीव्रतेतसुद्धा चक्रीय परिवर्तन होते. या संबंध चक्राला मंदायन वक्र असे म्हणतात.

---

वरील वक्राकृतीच्या अभ्यासावरून असे दिसून येईल की, चुंबकीय क्षेत्राची तीव्रता क्रमशः कमी केली जात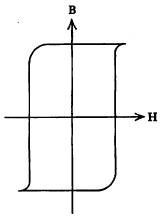

असताना चुंबकीकरणाची तीव्रता मागे रेंगाळल्यासारखी दिसते. या घटनेस चुंबकीय मंदायन म्हणतात. पोलाद व मृदू लोखंड यांच्या मंदायन वक्रांची तुलना केल्यास असे दिसून येईल की, पोलादाची चुंबकीय अवशेषता लोखंडापेक्षा कमी असली तरी चुंबकीकरणाच्या तीव्रतेच्या परिवर्तनाला पोलादात जास्त विरोध होतो (पोलादाची निस्सारक प्रेरणा लोखंडापेक्षा जास्त असते). यामुळे कायम चुंबकांसाठी पोलाद वापरतात, तर जेथे फक्त तात्कालिक चुंबकीकरणाच्या आवश्यकता असते अशा ठिकाणी (उदा., विद्युत् घंटा, तारायंत्र) मृदू लोखंड वापरतात. निरनिराळ्या माध्यमांच्या मंदायन वक्रांचा अभ्यास करून विशिष्ट प्रयुक्तीसाठी सुयोग्य माध्यमाची निवड करता येते. उदा., चांगला कायम चुंबक बनविण्यासाठी निस्सारक प्रेरणा जास्त असलेले माध्यम (उदा., पोलाद) निवडतात. एका मंदायन वक्रास माध्यमामध्ये काही ऊर्जेचा क्षय होऊन तिचे उष्णतेत रूपांतर होते. हा ऊर्जाक्षय मंदायन वक्राने वेढलेल्या आकृतीच्या क्षेत्रफळाच्या सम प्रमाणात असतो. म्हणून रोहित्रासारख्या साधनाच्या अंतरकासाठी हे क्षेत्रफळ किमान आहे असे माध्यम (उदा., मृदू लोखंड) निवडतात.

विशिष्ट प्रयुक्तींसाठी आता खास मिश्रधातू तयार करण्यात आल्या आहेत. म्यू-मेटल, हायपरनिक, परमिनव्हार, प्रम-ॲलॉय इ. व्यापारी नावांनी त्या ओळखल्या जातात. फेराइटे ही लोहाची ऑक्साइडे व इतर पदार्थ यांपासून बनवितात. यांच्या एका प्रकारचा उपयोग कमी मंदायन आणि जास्त रोध असल्यामुळे ट्रँझिस्टरयुक्त रेडिओ ग्राहीच्या आकाशकात (एरियलमध्ये) करतात. यामुळे ग्राहीची संवेदनक्षमता पुष्कळच वाढते. दुसऱ्या प्रकारच्या फेराइटाचा मंदायन वक्र आ. ९ मध्ये दाखविल्याप्रमाणे जवळजवळ आयताकार असतो. याचा उपयोग संगणकामध्ये (गणितकृत्ये करणाऱ्या यंत्रामध्ये) माहिती साठविण्यासाठी स्मरण मंडल म्हणून करण्यात येतो [→ संगणक].

बार्कहाउझेन परिणाम : १९१९ साली बार्कहाउझेन यांनी लोखंडाच्या चुंबकीकरणाची तीव्रता अखंडपणे वाढत जात नसून ती टप्प्याटप्प्यांनी वाढते असे प्रयोगाद्वारे दाखविले. चुंबकीकरणासाठी लोखंडाचा तुकडा आ. १० (अ) मध्ये दाखविल्याप्रमाणे क या तारेच्या वेटोळ्यात ठेवला आणि या मंडलातून विद्युत् प्रवाह सुरू केल्यास शेजरीच ठेवलेल्या ख वेटोळ्यास विवर्धकाद्वारे जोडलेल्या शिरःश्रवणीत कानांवर बसवून ध्वनिसंकेत ऐकण्याच्या साधनात) टक्‌टक् आवाज ऐकू येतो. आ. १० (आ) मध्ये चुंबकीकरण वक्राचा या प

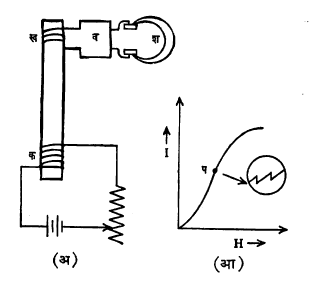ठिकाणचा अगदी छोटा भाग विस्तारित करून वर्तुळात दाखविला आहे. या प्रत्येक टप्प्याच्या वेळी ख वेटोळ्यात क्षणिक सूक्ष्म विद्युत् चालक प्रेरणा निर्माण होऊन त्यामुळे टक् असा आवाज होतो. या प्रयोगावरून चुंबकीकरणाच्या तीव्रतेमधील वाढ टप्प्याटप्प्याने होत जाते हे सिद्ध होते.

चुंबकत्वाचे विविध प्रकार व त्यांची सैद्धांतिक उपपत्ती : चुंबकत्वाच्या सर्व आविष्कारांचा उगम पदार्थांच्या अणुरचनेत आहे. प्रत्येक अणूमध्ये केंद्रस्थानी धन विद्युत् भारित अणुकेंद्र असून त्याच्या भोवती ऋण भारयुक्त इलेक्ट्रॉन विशिष्ट परिभ्रमण करीत असतात. त्याचबरोबर अणुकेंद्रही आपल्या अक्षाभोवती परिवलन करीत असतो व प्रत्येक इलेक्ट्रॉन आपल्या अक्षाभोवती परिवलन करीत असतो. यांपैकी प्रत्येक गतीमुळे अणूला व त्या अणूंपासून बनलेल्या पदार्थाला चुंबकीय गुणधर्म प्राप्त होतात. [→ अणु व आणवीय संरचना अणुकेंद्रीय व आणवीय परिबले]. अणुकेंद्राच्या परिवलनाचा परिणाम इतका सूक्ष्म असतो की, त्यामुळे प्राप्त होणारे चुंबकत्व दुर्लक्षणीय असते. म्हणून फक्त इलेक्ट्रॉनांच्या परिभ्रमण आणि परिवलन गतींमध्ये निष्पन्न होणारे चुंबकत्व विचारात घेतले जाते.

प्रतिचुंबकत्वाचा गुण हा इलेक्ट्रॉनांच्या कक्षीय परिभ्रमणाशी निगडित आहे तर समचुंबकत्व, लोहचुंबकत्व आणि चुंबकत्वाचे इतर प्रकार हे बव्हंशाने इलेक्ट्रॉन-परिवलनावर अवलंबून आहेत, असे प्रयोगावरून सिद्ध करता येते. इलेक्ट्रॉनांच्या कक्षीय किंवा  परिवलन गतींमध्ये विद्युत् प्रवाह निर्माण झाल्यासारखीच परिस्थिती निर्माण होते आणि त्यामुळे त्या इलेक्ट्रॉन व इलेक्ट्रॉनयुक्त अणू, रेणू किंवा आयन (विद्युत् भारित अणू, रेणू वा अणुगट) यांना चुंबकीय परिबल प्राप्त होते. परंतु पाउली यांच्या विवर्जन तत्त्वानुसार [→  अणु व आणवीय संरचना] विशिष्ट कक्षांत भ्रमण करणाऱ्या इलेक्ट्रॉनांच्या कक्षीय व परिवलन गती परस्परांविरूद्ध असतात. त्यामुळे सर्वसामान्यतः विशिष्ट अणू, रेणू किंवा आयनातील विविध इलेक्ट्रॉनांच्या गतींमुळे निर्माण होणारी चुंबकीय परिबले परस्परांचे निराकरण करतात आणि सामान्यतः अणू, रेणू किंवा आयन यांचे निष्पन्न चुंबकीय परिबल शून्य होण्याची प्रवृत्ती असते. O₂ रेणूसारखे काही अपवाद वगळता सम संख्येच्या इलेक्ट्रॉनयुक्त अणू-रेणू-आयनांचे निष्पन्न चुंबकीय परिबल शून्य होते, तर इतर अणूंच्या बाबतीत परिबलांचे अंशतः निराकरण होऊन एकूण अणू-रेणूस काही अवशिष्ट चुंबकीय परिबल प्राप्त होते.

प्रतिचुंबकत्व : चुंबकीय परिणामांच्या दृष्टीने पाहता कक्षेत फिरणारा इलेक्ट्रॉन हा त्याच आकाराच्या विद्युत् प्रवाहयुक्त वेटोळ्याशी समतुल्य असतो. अशा इलेक्ट्रॉनकक्षेशी बाह्य चुंबकीय क्षेत्र निगडित केल्यास लेंट्स यांच्या नियमानुसार समतुल्य वेटोळ्यात विद्युत् चुंबकीय प्रवर्तनामुळे विरुद्ध दिशेने जाणारा विद्युत् प्रवाह निर्माण होईल आणि त्यामुळे त्या वेटोळ्यातून जाणारा चुंबकीय स्रोत कमी होईल. म्हणजेच, अशा पदार्थातील चुंबकीय प्रवर्तन क्षेत्राचे मूल्य त्या बाहेरील मूल्यापेक्षा कमी असेल. अशा तऱ्हेने आणवीय संरचनेच्या दृष्टिकोनातून प्रतिचुंबकत्वाची कारणमीमांसा देता येते.

या विवेचनावरून असे दिसून येईल की, सर्वच द्रव्यांत अंगभूत प्रतिचुंबकत्व असेलच पाहिजे. ज्या द्रव्याच्या अणु-रेणुला निष्पन्न चुंबकीय परिबल असते त्यांच्यातही प्रतिचुंबकत्व असतेच, पण सामान्यतः समचुंबकत्वाच्या तुलनेने प्रतिचुंबकत्वाचा आविष्कार दुर्बल असल्याने तो समचुंबकत्वात झाकला जाऊन पदार्थ समचुंबक आहे असे वाटते. परंतु ज्या द्रव्याच्या अणु-रेणुचे निष्पन्न चुंबकीय परिबल शून्य असेल तेथे फक्त प्रतिचुंबकत्वाच प्रकट होते आणि अशी द्रव्ये प्रतिचुंबकीय गुणधर्म दाखवितात.

---

लांझव्हँ यांची उपपत्ती : लांझव्हँ यांनी प्रतिचुंबकत्वाची पुढीलप्रमाणे दिलेली उपपत्ती सर्वसामान्य झाली आहे. H चुंबकीय क्षेत्र लागू झाले असता अणूमधील इलेक्ट्रॉनाची कक्षा H च्या दिशेभोवती

ωL = H	μ0 e	या लार्‌मॉर कंप्रतेने परांचन करू  लागते
	2m

(कक्षेचा अक्ष H च्या दिशेभोवती फिरू लागतो) व त्यामुळे इलेक्ट्रॉनाच्या कक्षीय वेगातील बदल

∆V = -H	μ0er	इतका होतो
	2m

येथे ( e = इलेक्ट्रॉनीय विद्युत्‌ भार, m = इलेक्ट्रॉनाचे वस्तुमान, r = इलेक्ट्रॉनकक्षेची त्रिज्या). या वेगबदलांमुळे इलेक्ट्रॉनाच्या कक्षीय गतिजन्य, चुंबकीय परिबलात होणारा फरक

∆M = -H	μ02 e2 r2	इतका होतो.  Z अणुक्रमांक असणाऱ्या अणूमध्ये
	4 m

Z इलेक्ट्रॉन असतात व एक मोल (ग्रॅम रेणू) वस्तुमानात असे N अणू असल्याने त्यातील एकूण इलेक्ट्रॉनांची संख्या Z N होईल आणि एक मोलमध्ये होणारा M मधील फरक

– ZN	μ02 e2	.	2	r-2	.	H होतो (येथे r-2 ही r2 ची संख्याशास्त्रीय सरासरी होय)
	4 m		3

यावरून Xm =	∆M	= -ZN	μ02e2r-2
	H		6 M

हे रेणवीय प्रतिचुंबकीय प्रवणतेचे समीकरण मिळते (लांझव्हँ समीकरण). हे समीकरण रूढ भौतिकीनुसार काढले असले, तरी  ⇨पुंजयामिकीनुसार त्याचे स्वरूप हेच येते. या समीकरणावरून प्रतिचुंबकीय प्रवणतेचे मूल्य ऋण असते हे दिसून येते. त्याचप्रमाणे समीकरणांच्या उजव्या बाजूला येणाऱ्या राशी, द्रव्याचे तापमान किंवा रासायनिक संयोग स्थिती यावर अवलंबून नाहीत. म्हणजेच विशिष्ट अणूंची प्रतिचुंबकीय प्रवणता वेगवेगळ्या संयुगांत किंवा तापमानांत स्थिरमूल्यी राहते. या सूत्रानुसार काढलेली X_m ची मूल्ये प्रयोगाशी चांगली जुळतात (आ. ११) व म्हणून ही उपपत्ती सर्वसामान्य झाली आहे.

समचुंबकत्व : समचुंबकत्व म्हणजे काय याबद्दल थोडे विवेचन ‘चुंबकीकरण’ या उपशीर्षकाखाली पूर्वी आलेच आहे. क्यूरी यांच्या प्रयोगावरून असे दिसून आले की, कित्येक पदार्थांची समचुंबकीय प्रवणता त्या पदार्थांच्या निरपेक्ष तापमानाच्या व्यस्त प्रमाणात असते. म्हणजेच Xm = Cm/T (येथे Cm त्या पदार्थाचा क्यूरी स्थिरांक आणि T पदार्थाचे निरपेक्ष तापमान). परंतु वाइस यांनी असे दाखवून दिले की, पदार्थातील अणू वा रेणूंमधील परस्पर क्रिया दुर्लक्षणीय नसेल तर

क्यूरी समीकरण Xm =	Cm	या स्वरूपात लिहावे लागेल. याला क्यूरी-वाइस नियम म्हणतात.
	T -θ

यातील θ हा त्या पदार्थासाठी स्थिरांक असून त्याला पदार्थाचे समचुंबकीय क्यूरी तापमान असे म्हणतात.

गुणात्मत विवेचन : पदार्थाच्या अणू किंवा रेणूमधील इलेक्ट्रॉनांच्या परिवलनजन्य चुंबकीय परिबलाचे पूर्णपणे निराकरण होत नसल्यास तो पदार्थ समचुंबक बनतो. परंतु अणूमधील पूर्ण भरलेल्या कवचांतील [→ अणु व आणवीय संरचना] इलेक्ट्रॉनांमुळे निर्माण होणाऱ्या चुंबकीय परिबलाचे पूर्णपणे निराकरण झालेले असते. म्हणून अपुऱ्या भरलेल्या कवचातील इलेक्ट्रॉनांच्या परिवलनामुळे त्या अणूला किंवा रेणूला चुंबकीय परिबल प्राप्त होते. अशा अणू किंवा रेणूंना परिवलन चुंबक असे म्हणू.

अशा प्रकारच्या अणूंनी बनलेल्या पदार्थास बाह्य चुंबकीय क्षेत्र H लावल्यास ते पदार्थातील परिवलन चुंबकांना स्वतःला समांतर दिशेने संरेखित (सरळ रेषेत मांडणी करण्याची क्रिया) करू पाहते. त्याच बरोबर ऊष्मीय गती हे संरेखन विस्कटून टाकण्याचा प्रयत्न करते. या दोन परस्परविरोधी क्रियांमधून निष्पन्न होईल तेवढ्याच मानाचे संरेखन प्रत्यक्षात येते आणि त्याच प्रमाणात पदार्थाला H च्या दिशेने चुंबकत्व प्राप्त होते.

नेहमीच्या तापमानाला अणूंची ऊष्मीय गतिजन्य ऊर्जा सामर्थ्यवान चुंबकीय क्षेत्रात ठेवलेल्या परिवलन चुंबकाच्या चुंबकीय ऊर्जेपेक्षा सु. १०० ते १,००० पट जास्त असते. म्हणून अशा तापमानाला पदार्थ अतिदुर्बलपणेच चुंबकित होऊ शकतो. म्हणजेच त्याच्या समचुंबकीय प्रवणतेचे मूल्य अल्प असते. तापमान कमी केल्यास उष्मीय ऊर्जा कमी होते म्हणून संरेखनाचे प्रमाण वाढून चुंबकीकरण जास्त जोरदार होते म्हणजेच समचुंबकीय प्रवणता वाढते. अशा रीतीने क्यूरी नियमाचे स्पष्टीकरण करता येते.

लांझव्हँ (रूढ भौतिकीय) उपपत्ती : समजा की विशिष्ट द्रव्यातील परिवलन चुंबकांचे प्रत्येकी चुंबकीय परिबल M₁ = n μ_B (μ_B = बोर मॅग्नेटॉन, हे इलेक्ट्रॉनांचे चुंबकीय परिबल मोजण्याचे एकक आहे) असून द्रव्याच्या एकक घनफळात असे N परिवलन चुंबक आहेत व हे चुंबक बाह्य चुंबकीय क्षेत्र H शी θ हा कोन करतात (θ = ०^० ते १८०^० यामधील काहीही असू शकेल). मग अशा एका परिवलन चुंबकाची चुंबकीय ऊर्जा -M₁ H cos θ  इतकी येईल आणि त्याच्यामुळे द्रव्याला H च्या दिशेने प्राप्त होणाऱ्या चुंबकीय परिबलाचे

M₁ cosθ होईल. म्हणून द्रव्याच्या एकक घनफळाचे H च्या दिशेने होणारे एकूण चुंबकीय परिबल यासारख्या सर्व राशींच्या बेरजेने मिळेल व ही बेरीज समाकलनाने काढावी लागेल. हे गणितकृत्य करता,

I = NM1	(    coth α –	1	)
		α

असे समीकरण मिळते (येथे α =	M1 H	असून k बोल्टस्‌मान स्थिरांक व T निरपेक्ष तापमान आहे).
	K T

α हा एकापेक्षा अतिशय लहान असल्यास आसन्नीकरण करून (अंदाजी मूल्य मांडून) I =	N M12	H
	3 k T

... Xm =	I	=	N M12	=	(N M12/3k)
	H		3 k T		T

हे समीकरण क्यूरी समीकरणाशी जुळले आहे. या उपपत्तीस θ हा कोन कोणतेही मूल्य धारण करू शकतो, असे मानले असून ते पुंजयामिकीप्रमाणे योग्य नाही. त्याचप्रमाणे परिवलन चुंबक परस्परांवर काहीही प्रेरणा लागू करत नाहीत, हेही गृहीत धरले आहे. परिवलन चुंबकांच्या परस्परक्रिया लक्षात घेतल्यास वरील समीकरणावरून क्यूरी-वाइस नियम मिळू शकतो.

---

पुंजवादानुसार सुधारणा : व्हॅन व्ह्‌‌लेक यांनी समचुंबकत्वाची पुंजवादानुसार मीमांसा दिली. या मीमांसेत अणू किंवा रेणूचे चुंबकीय परिबल J वर [अणूतील सर्व इलेक्ट्रॉनांच्या एकत्रित कोनीय संवेगांकावर, → अणुकेंद्रीय व आणवीय परिबले] अवलंबून असते आणि असा अणू बाह्य चुंबकीय क्षेत्रात ठेवल्यास तो (2J + 1) ऊर्जास्थिती धारण करू शकतो. अशा अनेक अणूंचे विविध ऊर्जास्थितींतील वंटन (वितरण) बोल्टस्‌मान सांख्यकीप्रमाणे [→ सांख्यकीय भौतिकी] होईल, असे मानून त्या पदार्थाच्या चुंबकीय प्रवणतेसाठी आसन्नीकरण करून पुढील समीकरण मिळते.

X =	N J (J + 1) g2 μB2
	3 k T

[येथे g लांडे गुणक आणि μ_B बोर मॅग्नेटॉन, → अणुकेंद्रीय व आणवीय परिबले]. अणूचा कक्षीय परिभ्रमणांक L शून्य असल्यास वरील समीकरण रूढ भौतिकीनुसार येणाऱ्या समीकरणासारखेच होते.

विरल मृत्तिकांच्या आयनांचे समचुंबकत्व : या गटातील मूलद्रव्यांच्या (अणुक्रमांक ५७ ते ७१ असलेल्या मूलद्रव्यांच्या) अणूमधील 4f या आतल्या कवचात इलेक्ट्रॉन पूर्ण भरलेले नसतात. या गटातील मूलद्रव्यांच्या स्फटिकांच्या समचुंबकीय प्रवणतेची प्रायोगिक मूल्ये वरील सूत्राशी उत्तमपणे जुळतात, हे आ. १२ मधील आलेखावरून दिसून येईल. या मूलद्रव्यांची चुंबकीय प्रवमता मूल्ये सामान्यतः जास्त असतात. ही चुंबकीय प्रवणता अंतर्भागातील कवचामधल्या इलेक्ट्रॉनांमुळे उत्पन्न होत असल्यामुळे स्फटिकातील विद्युत् क्षेत्रांचा तीवर विशेष परिणाम होत नाही व इलेक्ट्रॉनांच्या कक्षीय गतीचाही ह्यांच्यावर विशेष परिणाम होत असलेला दिसत नाही.

समचुंबकत्वाचे दोन प्रकार : स्थूलमानाने बोल्टस्‌मान सांख्यिकीचा वापर करून ज्याची उपपत्ती देता येते, त्या समचुंबकत्वाला व्हॅन व्ह्‌लेक ⇨समचुंबकत्व  असे म्हणतात. या प्रकारची समचुंबकीय प्रवणता तापमान वाढले असता कमी होते.

संवहन इलेक्ट्रॉनांच्यामुळे उत्पन्न होणारी धांतूमधील समचुंबकीय प्रवणता, तापमान वाढले असले तरी स्थिरमूल्यी राहते. या आविष्काराचे स्पष्टीकरण फेर्मी-डिरॅक सांख्यिकीचा [→ सांख्यकीय भौतिकी] वापर करता येते, हे पाउली यांनी दाखविले. या प्रकाराला पाउली समचुंबकत्व असे म्हणतात.

लोह गटातील आयनांचे समचुंबकत्व : या गटातील अनेक धांतूच्या लवणांचे स्फटिक समचुंबक असतात. यांच्या समचुंबकीय प्रवणतेचे प्रयोगावरून मापन करून तिच्यावरून व व्हॅन व्ह्‌‌‌‌‌‌लेक समीकरण वापरून त्या

आयनासाठी J चे मूल्य काढता येते. ही मूल्ये काढली असता असे दिसून येते की, या गटातील आयनांच्या बाबतीत चुंबकत्वाची उत्पत्ती फक्त इलेक्ट्रॉनांच्या परिवलनामुळेच होत असते. स्फटिकातील विद्युत् क्षेत्रामुळे इलेक्ट्रॉनांच्या कक्षा जणू काही अडकून बसतात व त्यामुळे बाह्य चुंबकीय क्षेत्रात त्यांचे परिवलन होऊ शकत नाही.

लोहचुंबकत्व :लोहचुंबकत्वाची वैशिष्ट्ये : वरील दोन्ही प्रकारांपेक्षा लोहचुंबकत्वाचा आविष्कार अनेक दृष्टींनी वेगळा व प्रयुक्तींच्या दृष्टीने महत्त्वाचा आहे. लोहचुंबकत्व हे एक प्रकारचे समचुंबकत्वच आहे तरी लोहचुंबकीय प्रवणतेचे मूल्य समचुंबकीय प्रवणतेपेक्षा काही हजारपट मोठे असू शकते म्हणेजच अगदी दुर्बल चुंबकीय क्षेत्रात ठेवूनही लोहचुंबकीय पदार्थांचे चुंबकत्व खूप जोरदार असते. यामुळे सर्वसामान्य चुंबकही त्यांना जोरदारपणे आकर्षित करतो म्हणून हे चुंबकत्व फार पूर्वीपासून माहीत झाले होते. लोहचुंबकीय प्रवणतेचे मूल्य स्थिर नसून ते बाह्य क्षेत्राच्या (H च्या) मूल्यानुसार बदलते. त्याचप्रमाणे ते पदार्थाच्या पूर्वेतिहासावर अवलंबून असते. समचुंबकीय पदार्थाचे संपृक्तावस्थेपर्यंत चुंबकीकरण करण्यास ज्या मूल्याचे बाह्य क्षेत्र लागते त्याच्या केवळ १०^-६ पटीच्या बाह्यक्षेत्राने लोहचुंबकीय पदार्थ संपृक्त होऊ शकतो. तापमान वाढवीत गेले असता लोहचुंबकीय प्रवणता कमी होत जाते व विशिष्ट तापमानाच्या वर तो पदार्थ समचुंबक बनतो. ह्या तापमानाला लोहचुंबकीय क्यूरी तापमान असे म्हणतात. लोहचुंबक पदार्थाचे चुंबकीकरण व्युत्क्रमी नसते, हे मागे दाखविले आहेच. सर्वांत महत्त्वाचा विशेष म्हणजे अशा पदार्थांवरील बाह्य चुंबकीय क्षेत्र काढून घेतले, तरी त्यांमध्ये काही चुंबकत्व शिल्लक राहते. त्यामुळे त्याच्यापासून कायम चुंबक बनविता येतात. लोहचुंबक पदार्थांची तौलनिक पार्यता (μ_r) फार जास्त असल्याने रोहित्रासारख्या अनेक प्रयुक्तींमध्ये त्याचा उपयोग होतो. मागे उल्लेख केलेले मंदायन वक्र हाही लोहचुंबकत्वाचा एक महत्त्वाचा विशेष आहे.

लोहचुंबकत्वाची उपपत्ती : सर्वसामान्य तापमानाला लोह, कोबाल्ट व निकेल ही मूलद्रव्ये व त्यांच्या मिश्रधातू व लवणे घन स्वरूपात असताना लोहचुंबकत्वाचा आविष्कार दाखवितात. या तीनही मूलद्रव्यांच्या    अणूतील 3d हे अंतर्गत कवच इलेक्ट्रॉनांनी पूर्णपणे भरलेले नसते. या अपूर्ण कवचातील व इलेक्ट्रॉनांच्या परिवलन परिबलाचे पूर्णपणे निराकरण झालेले नसते व त्यामुळे त्यांच्या अणू किंवा आयनांना परिवलन चुंबकीय परिबल प्राप्त होते आणि तेच लोहचुंबकत्वाचे मूळ आहे.

वाइस यांची उपपत्ती : या द्रव्यात चुंबकत्वाचा गुण विशेष प्रभावी होण्याला काय कारण असावे, याची कारणपरंपरा प्रथम वाइस यांनी आपल्या रेणवीय क्षेत्रसिद्धांताने दिली. त्यांच्या मताप्रमाणे लोहचुंबकीय पदार्थाच्या स्फटिकांत एक तीव्र अंतर्गत चुंबकीय क्षेत्र असते. याला त्यांनी रेणवीय क्षेत्र हे नाव दिले. रेणवीय क्षेत्रामुळे लगतच्या अणूमधील इलेक्ट्रॉन परिवलन परिबले परस्परांना समांतर होतात त्यामुळे संबंध पदार्थाला मोठे चुंबकीय परिबल प्राप्त होते म्हणजेच चुंबकीकरण तीव्रता खूप होते आणि म्हणून चुंबकीय प्रणवता

Xm	(	=	I	)
			H

ही मोठी असते. या रेणवीय क्षेत्राची तीव्रता H_w ही पदार्थाच्या चुंबकीकरण तीव्रतेच्या सम प्रमाणात असते असे वाइस यांनी गृहीत धरले.

या परिकल्पनेत एक अडचण आली ती म्हणजे रेणवीय क्षेत्रामुळे कोणत्याही लोहचुंबकीय पदार्थातील सर्व अणु-चुंबक परस्परांना समांतर होऊन तो पदार्थ आपोआपच संपृक्तावस्थेइतका चुंबकित व्हावयास पाहिजे, पण असे प्रत्यक्षात घडत नाही.

---

लघुक्षेत्र सिद्धांत : या अडचणीचे निराकरण करण्यासाठी लघुक्षेत्र सिद्धांताची कल्पना वाइस यांनी पुढे मांडली. या कल्पनेनुसार लोहचुंबकातील कोट्यावधी अणूंचे मिळून (सरासरीने १०^१२ ते १०^१५) एक एक गट बनतात. प्रत्येक गट म्हणजे एक लघुक्षेत्र होय. त्याचे सरासरी आकारमान १०^-१४ घ. मी. असते. प्रत्येक क्षेत्रातील सर्व अणु-चुंबकांची चुंबकीय परिबले परस्परांना समांतर स्थितीत संरेखित झालेली असल्याने तो एक सूक्ष्म चुंबकच झालेला असतो. परंतु या सर्व सूक्ष्म चुंबकांच्या चुंबकीकरणाच्या दिशा इतस्ततः असल्याने सर्वांचा मिळून बाह्य चुंबकीय परिणाम शून्य येतो आणि तो पदार्थ अचुंबकित आहे, असे वाटते. लगतच्या लघुक्षेत्रांच्या दरम्यान त्यांना अलग करणारे क्षेत्र तट असतात.

लघुक्षेत्राचे दर्शन : लघुक्षेत्राचे अस्तित्व अनेक प्रयोगांनी सिद्ध झाले आहे. बिटर यांनी लोखंडाच्या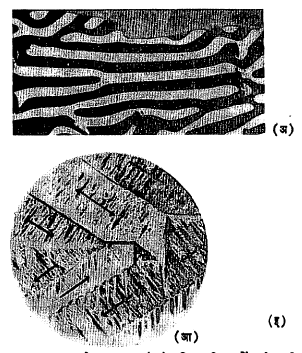

ऑक्साइडाच्या अतिसूक्ष्म कणांचे निलंबन लोहचुंबकीय पदार्थांच्या गुळगुळीत पृष्ठावर लावले. मग हे कण पृष्ठावरील लघुक्षेत्राच्या आकारानुसार संरेखित झाले. त्यांची सूक्ष्मदर्शकातून छायाचित्रे घेऊन त्यांवरून लघुक्षेत्र रचनेचे चित्रण मिळविले. या चित्रांना बिटर चित्रणे असे म्हणतात. लघुक्षेत्र रचनेची चित्रणे ⇨कर परिणामाचा उपयोग करून व इलेक्ट्रॉनांच्या शलाकांच्या साहाय्याने मिळविता येतात (आ. १३).

या पद्धती वापरून पदार्थातील लघुक्षेत्र रचना तर समजतेच, पण त्याशिवाय त्या पदार्थाचे चुंबकीकरण हळूहळू वाढवत गेले असता लघुक्षेत्र रचना कशी बदलत जाते, तेही समजून घेता येते (आ. १४).

चुंबकीय असमदिकता : लोहाचे स्फटिक घनाकार असतात. असा एक स्फटिक घेऊन त्याचे चुंबकीकरण करताना असे दिसून येते की, या स्फटिकाचे चुंबकीकरण त्याच्या बाजूच्या समांतर दिशेने करू गेल्यास चुंबकीकरण फार सुलभतेने होते. म्हणजेच दुर्बल बाह्य क्षेत्रानेही त्याला जास्त चुंबकीकरण तीव्रता येते. म्हणून या दिशेला लोहाचा चुंबकीकरणाचा सुलभ अक्ष असे म्हणतात. याउलट संपूर्ण घनाच्या कर्णाच्या दिशेने चुंबकीकरण करणे अवघड जाते म्हणून या दिशेला चुंबकीकरणाचा दुष्कर अक्ष असे म्हणतात. सर्वच लोहचुंबकीय द्रव्यांत असे सुलभ व दुष्कर अक्ष असतात, असे दिसून येते. या आविष्काराला चुंबकीय असमदिकता असे म्हणतात. आ. १५ मधील चुंबकीकरणाच्या आलेखावरून ही गोष्ट स्पष्ट होईल. अचुंबकित लोहचुंबकीय द्रव्यातील लघुक्षेत्राचे चुंबकीकरण सुलभ अक्षाच्या दिशेने झालेले असते. कारण त्यामुळे त्या पदार्थाची ऊर्जा किमान होते. इतर कोठल्याही दिशेने त्या पदार्थाचे चुंबकीकरण केल्यास त्याची ऊर्जा वाढते. लोहाप्रमाणेच इतर लोहचुंबकीय द्रव्यातही सुलभ आणि दुष्कर अक्ष असतात.

चुंबकीय आकारांतर : चुंबकीकरण केले असता लोहचुंबकीय पदार्थाची मोजमापे बदलतात. याला ⇨ चुंबकीय आकारांतर  असे म्हणतात. या आकारांतरामुळे पदार्थात अंतर्गत परिबले उत्पन्न होऊन पदार्थाला आकारांतीय ऊर्जा प्राप्त होते. याउलट पदार्थाला बाह्य प्रेरणा लावून किंवा इतर पद्धतीने त्याचे आकारांतर केल्यास त्याचे चुंबकत्व बदलते. तापविणे, ठोकणे वगैरे क्रिया करून जेव्हा एखादा ठोकळा तयार केला जातो तेव्हा त्यात काही अंतर्गत विकृती उत्पन्न होतात. त्यांचाही त्या ठोकळ्याच्या चुंबकीय गुणधर्मावर परिणाम होतो.

चुंबकीय स्थैतिक ऊर्जा : एखादा पदार्थ चुंबकित केला असता त्याच्या दोन्ही टोकांवर मुक्त चुंबकीय ध्रुव निष्पन्न होतात. हे ध्रुव पदार्थाच्या अंतर्भागात जे चुंबकीय क्षेत्र निर्माण करतात त्यामुळे पदार्थातील सर्व मूळ चुंबकांना जी ऊर्जा प्राप्त होते, तिला त्या पदार्थाची चुंबकीय स्थैतिक ऊर्जा असे म्हणतात.

---

लघुक्षेत्र रचनेचे कारण : निसर्गात कोणत्याही प्रणालीची ऊर्जा किमान होईल अशी रचना अस्तित्वात 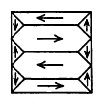  येते.  एखादा दांडा सबंध एकच लघुक्षेत्र झाला, तर त्याची चुंबकीय स्थैतिक ऊर्जा जास्त होते. वेगवेगळ्या दिशांनी चुंबकित झालेली अशी त्याची अनेक लघुक्षेत्रे पडली असता त्याच्याशी संबंधित चुंबकीय स्थैतिक ऊर्जा कमी होते ( हे गाणिताने सिद्ध करता येते किंवा लहान लहान चुंबकांचे प्रतिरूप करून त्यावरून सिद्ध करता येते). यामुळे पदार्थात अनेक लघुक्षेत्रे निर्माण होतात. लघुक्षेत्रे विशिष्ट मर्यादेपेक्षा लहान झाले, तर पुन्हा तत्संलग्न ऊर्जा वाढते म्हणून विशिष्ट मर्यादेपेक्षा लहान लघुक्षेत्र निर्माण होत नाहीत. शेवटी एक गोष्ट लक्षात ठेवावयाची ती ही की, अंतिम स्थितीत चुंबकीय स्थैतिक ऊर्जा, आकारांतर ऊर्जा, असमदिकता ऊर्जा व लघुक्षेत्र तटांशी संलग्न ऊर्जा यांची बेरीज किमान झाली पाहिजे. या दृष्टीने लोहाच्या घनातील अगदी सोपी संभाव्य लघुक्षेत्र रचना आ. १६ मध्ये दाखविली आहे.

रेणवीय क्षेत्रोत्पत्तीचे कारण : वाइस यांनी सुचविलेल्या रेणवीय क्षेत्राच्या उपपत्तीचे कारण हायझेनबेर्क यांनी पुंजयामिकीच्या साहाय्याने दिले. यांच्या मतानुसार दोन नजिकच्या अणूंमधील इलेक्ट्रॉनांच्या परिवलनांमध्ये एक पुंजयामिकीय प्रेरणा अमलात येते. या प्रेरणेला विनिमय परस्परक्रिया असे नाव देण्यात आले. या प्रेरणेचे मूल्य धन चिन्हांकित असल्यास त्या दोन इलेक्ट्रॉनांची परिवलन परिबले परस्परांना समांतर होतात आणि ऋण चिन्हांकित असल्यास ती परस्परांना प्रतिसमांतर (विरूद्ध दिशा असलेली) होतात. या प्रेरणेचे चिन्ह ^R/_r या गुणोत्तरावर अवलंबून असते (R =  अणूची त्रिज्या, r = 3d कवचाची त्रिज्या).

2·2 &gt ^R / _r &gt 1·5  असल्यास प्रेरणा धन चिन्हयुक्त होऊन परिवलन परिबले परस्परांना समांतर होतात व पदार्थ लोहचुंबकीय गुणधर्म प्रकट करतो. ^R / _r &lt 1·5 असल्यास परिवलन परिबले परस्परांना प्रतिसमांतर होऊन पदार्थ प्रतिलोहचुंबकीय होतो.

हॉइस्लर यांनी तांबे, ॲल्युमिनियम व मँगॅनीज यांच्यापासून एक मिश्रधातू तयार केली (Cu₂AIMn) यांपैकी कोणतीही धातू लोहचुंबकीय नसूनही ही मिश्रधातू लोहचुंबकीय होते. या गोष्टीचे स्पष्टीकरण वरील उपपत्तीच्या आधारे समाधानकारकपणे देता येते.

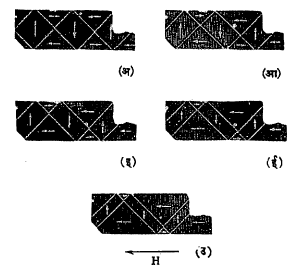
लघुक्षेत्र रचना व चुंबकीकरण : चुंबकीकरणामुळे लघुक्षेत्र रचनेत होणारे फेरफार आ. १७ मध्ये दर्शविले आहेत. अ मध्ये अचुंबकित पदार्थातील दोन शेजारची लघुक्षेत्रे क आणि ख दाखविली आहेत. पदार्थाचे ‘सुलभ अक्ष’ सु चौकोनाच्या बाजूला समांतर आहेत. या पदार्थाला H हे अल्प बाह्य क्षेत्र लावले असता होणारी स्थिती आ मध्ये दाखविली आहे. क क्षेत्राची चुंबकीकरण दिशा H च्या दिशेशी जास्त मिळतीजुळती आहे. तेव्हा क या लघुक्षेत्राचे आकारमान वाढून ख चे कमी होते व त्या दोहोंमधील क्षेत्र-तट गघ हा ख च्या बाजूला सरकतो. बाह्य क्षेत्र काढून घेतल्यास परत पूर्वीची स्थिती येऊ शकते म्हणून हा बदल व्युत्क्रमी आहे.

त्याहून जास्त जोरदार H लावल्यास क क्षेत्र सबंध पदार्थ व्यापून टाकते व जणू काही गघ हा क्षेत्र-तट पदार्थाच्या बाहेर घालविला जातो (आ. १७ इ). हा बदल व्युत्क्रमी नसतो. शेवटी H जास्त तीव्र केल्यास सबंध क हे क्षेत्रच फिरून H ला समांतर होते. हा बदल व्युत्क्रमी असतो. क्षेत्रांच्या मधील तटांचे सरकणे व क्षेत्राचे फिरणे या गतीवर पदार्थातील अशुद्ध द्रव्ये, अंतर्गत ताण, पदार्थाची स्फटिक रचना वगैरेंचा फारच परिणाम होतो. त्यामुळे पदार्थाच्या लोहचुंबकीय गुणधर्मात मोठे फेरफार होऊ शकतात. या गोष्टींच्या अभ्यासावरून विशिष्ट उपयोगीसाठी खास प्रकारच्या उपयुक्त लोहचुंबकीय धातू निर्माण करणे शक्य झाले आहे.

 

प्रतिलोहचुंबकत्व : हा आविष्कार मँगॅनीज, क्रोमियम, तांबे, लोह इ. धातूंच्या लवणांमध्ये आढळून येतो. या प्रकारच्या पदार्थाची चुंबकीय प्रवणता X_m धन चिन्हयुक्त असून तापमान वाढवीत गेले असता ती प्रथम वाढत जाते व एका विशिष्ट तापमानापलीकडे (नील तापमान) गेल्यानंतर समचुंबकीय पदार्थाप्रमाणे पुन्हा कमी होत जाते (आ. १८).

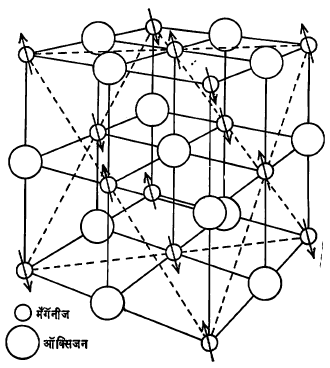
अशा प्रकारच्या पदार्थांपैकी मँगॅनीज ऑक्साइडाच्या (MnO) स्फटिकाची रचना आ. १९ मध्ये दाखविली आहे. त्यावरून असे दिसेल की, लगतच्या Mn आयनांची परिवलन परिबले परस्परांना प्रतिसमांतर असतात. ही रचना न्यूट्रॉन विवर्तनाच्या (अडथळ्याच्या कडेवरून जाताना होणाऱ्या दिशाबदलाच्या) प्रयोगांवरून निश्चित करण्यात आली आहे. प्रतिसमांतर परिवलन असलेल्या रेणूंचे चुंबकीय परिबल परस्परांचे निराकरण करते, त्यामुळे एकूण पदार्थाची चुंबकीय प्रवणता अल्प होते.

लोहीचुंबकत्व : काही लोहचुंबकीय पदार्थांत लगतच्या चुंबकीय आयनांची चुंबकीय परिबले परस्परांना प्रतिसमांतर असतात. अशा तऱ्हेने पदार्थांत मूलभूत आणवीय चुंबकाचे दोन गट असतात व हे दोन प्रकारचे आणवीय चुंबक एकाआड एक असे संरेखित झालेले असतात, परंतु या दोन गटांतील आयनांची चुंबकीय परिबले समान मूल्याची नसतात. त्यामुळे अशा पदार्थाला या दोन गटांच्या एकूण चुंबकीय परिबलांच्या वजाबाकी इतके निष्पन्न चुंबकीय परिबल प्राप्त होते. या पदार्थांचे चुंबकीय गुणधर्म सामान्यतः लोहचुंबकीय पदार्थांसारखेच असतात. आ. २० वरून लोहचुंबक, प्रतिलोहचुंबक आणि लोहीचुंबक प्रकारच्या पदार्थांतील आणवीय रचनेतील फरक लक्षात येईल.

---

Fe₃O₄ हे लोहीचुंबक संयुग उदाहरणार्थ घेऊ. त्याची स्फटिकरचना Fe³⁺ (↑) Fe²⁺ (↑) Fe³⁺ (↓) O₄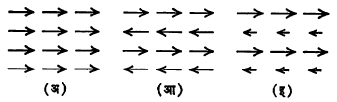

अशी व्यक्त करता येते (प्रत्येक Fe पुढील बाण त्याच्या चुंबकीय परिबलाची दिशा दाखवितात). ही रचना न्यूट्रॉन विवर्तनावरून निश्चित झाली आहे. पहिला Fe³⁺ आयन + ५ बोर मॅग्नेटॉन, Fe²⁺ आयन +४ बोर मॅग्नेटॉन व दुसरा Fe³⁺ आयन – ५ बोर मॅग्नेटॉन इतके चुंबकीय परिबल एकूण रेणूला देतो. म्हणून सबंध रेणूचे निष्पन्न चुंबकीय परिबल (५ + ४ – ५ = ) + ४ बोर मॅग्नेटॉन येते. नील यांनी या पदार्थांच्या चुंबकत्वाची उपपत्ती दिलेली असून ती लोहचुंबकत्वाच्या उपपत्ती सारखीच आहे.

फेराइटे : लोहीचुंबक ऑक्साइडांना सामान्यतः फेराइट ही संज्ञा देतात. यांचे स्फटिक वेगवेगळ्या प्रकारचे असतात. त्यांतील स्पिनेल वर्गातील [घनीय समूहातील, → स्फटिकविज्ञान] फेराइटे औद्योगिक उपयोगाच्या दृष्टीने जास्त महत्त्वाची आहेत आणि त्यांचेच वर्णन येथे दिले आहे.

या वर्गातील फेराइटांचे रासायनिक सूत्र सर्वसामान्यपणे XFe₂O₄ असे लिहिता येते. सामान्यतः X हे Mg, Mn, Fe, Co, Ni, Cu, Zn किंवा Cd यांपैकी एकाचे आयन असतात. कित्येकदा त्यांची मिश्रणेही वापरतात.

अनेक इलेक्ट्रॉनीय उपकरणांत फेराइटांचा मोठ्या प्रमाणावर वापर होत आहे. या संबंधात त्यांचे प्रमुख उपयुक्त गुणधर्म म्हणजे उच्च पार्यता व उच्च विद्युत् रोध (यांची रोधकता धातूच्यापेक्षा सु. १०^११ पटीने जास्त असते) हे होत. हे गुणधर्म त्या फेराइटाचे घटक, त्यांची सूक्ष्मरचना, त्यांच्या कणांचे आकारमान व त्यांत अंतर्भूत झालेली इतर अशुद्धी द्रव्ये यांच्यावर अवलंबून असतात. या बाबींमध्ये जरूरीनुसार फेरबदल करून विशिष्ट प्रकारच्या उपयोगासाठी खास फेराइटे बनविण्यात आली आहेत. फेराइटांची रोधकता फार असल्याने मंदायन चक्रात त्यामध्ये होणारा ऊर्जाक्षय लोखंड वा पोलादाच्या अंतरकापेक्षा खूप कमी होतो. म्हणून उच्च रेडिओ कंप्रतेसाठी वापरल्या जाणाऱ्या रोहित्र, प्रवर्तक वगैरे साधनांत फेराइटांचे अंतरक वापरतात. त्यांच्या चुंबकीय आकारांतराचा उपयोग तापमानाचे नियंत्रण करण्यासाठी करता येतो. त्याचप्रमाणे एकाच आकाशकातून सूक्ष्मतरंग संदेशांचे प्रेषण आणि ग्रहण करण्यासाठी उपयुक्त अशा घूर्णकारी (जायरेटर) या साधनांत फेराइटाचा उपयोग होतो.

चुंबकीय क्षेत्राचे प्रकाशावर होणारे परिणाम : (१) झीमान परिणाम : प्रकाश उगम तीव्र चुंबकीय क्षेत्रात ठेवला असता त्याच्या वर्णपटातील वर्णरेषांचे दोन किंवा अधिक रेषांत विभाजन होते. याला झीमान परिणाम असे म्हणतात [→ अणुकेंद्रीय व आणवीय परिबले].

(२) फॅराडे परिणाम : काचेसारखे काही पदार्थ चुंबकीय क्षेत्रात ठेवून त्यांमधून रेखीय ध्रुवित (एकाच विशिष्ट प्रतलात कंप पावणारा) प्रकाश जाऊ दिल्यास त्या प्रकाशाच्या कंपन प्रतलाचे विशिष्ट कोनातून घूर्णन होते. याला फॅराडे परिणाम असे म्हणतात.

(३) चुंबकीय कर परिणाम : चुंबकित केलेल्या लोहचुंबकीय पदार्थाच्या पृष्ठभागापासून परावर्तित झालेल्या प्रकाशाचे अंशतः विवृत्ताकार ध्रुवण [→ प्रकाशकी] होते. याला कर परिणाम असे म्हणतात.

एखाद्या द्रवातून प्रकाश जात असताना प्रकाशाच्या मार्गाला अनुप्रस्थ दिशेने चुंबकीय क्षेत्र लावल्यास प्रकाशाचे द्विप्रणमन (दोन निरनिराळ्या दिशांनी जाणाऱ्या किरणांत विभाजन होणे) होते. याला कॉटाँ मूटाँ परिणाम असे म्हणतात. त्याचप्रमाणे चुंबकीय क्षेत्रात ठेवलेल्या नैकजिनसी पदार्थातून प्रकाश जाऊ दिल्यास त्याचे द्विप्रणमन होते. याला फोख्ट परिणाम असे म्हणतात.

ऊष्माचुंबकीय परिणाम : समचुंबकीय किंवा लोहचुंबकीय पदार्थाची चुंबकीकरण तीव्रता बदल्यास त्याच्या तापमानात होणाऱ्या व्युत्क्रमी बदलाला ऊष्माचुंबकीय परिणाम असे म्हणतात. यामुळे चुंबकित केलेल्या समचुंबकीय पदार्थाच्या भोवतालचे चुंबकीय क्षेत्र एकदम कमी केल्यास त्या पदार्थाच्या तापमानात घट होते. या गोष्टीचा उपयोग अतिनीच तापमान उत्पन्न करण्यासाठी केला जातो [→ नीच तापमान भौतिकी].

चुंबकीय रोध : विद्युत् संवाहक किंवा अर्धसंवाहक पदार्थ चुंबकीय क्षेत्रात (H) ठेवल्यास त्या पदार्थांचा विद्युत् रोध बदलतो. H फार तीव्र नसल्यास रोधामधील बदल H² च्या सम प्रमाणात असतो. शुद्ध धातूमधील रोधबदल सामान्यतः धन असतो व मिश्रधातूच्या बाबतीत तो ऋण असतो.

हॉल परिणाम : एखाद्या संवाहक किंवा अर्धसंवाहक पदार्थाच्या पट्टीमधून क्ष अक्षाच्या दिशेने विद्युत् प्रवाह जात असता त्याला झ अक्षाच्या दिशेने चुंबकीय क्षेत्र लावल्यास य अक्षाच्या दिशेने त्या पट्टीत विद्युत् वर्चोभेद निर्माण होतो. याला हॉल परिणाम म्हणतात. या परिणामावरून पदार्थातून विद्युत् प्रवाहाचे संवहन करणारे मूलकण कोणते असावेत, याबद्दल माहिती मिळते. या वर्चोभेदाचे मापन करून त्यावरून H चे मूल्य काढता येते [→ अर्धसंवाहक].

घूर्णचुंबकीय परिणाम : एखाद्या चुंबकाच्या चुंबकीकरणाची दिशा एकदम बदलल्यास तो चुंबक घूर्णन (स्वतःभोवती फिरणे) करू लागतो. याला आइन्स्टाइन-डी हास परिणाम असे म्हणतात. याउलट एखाद्या चुंबकीय पदार्थाचा कोनीय संवेग (निरूढी परिबल व कोनीय वेग यांचा गुणाकार, निरूढी परिबल म्हणजे वस्तूने कोनीय प्रवेगास केलेल्या विरोधाचे माप) एकदम बदलल्यास त्याला चुंबकत्व प्राप्त होते. याला बार्नेट परिणाम असे म्हणतात.

एखाद्या आणवीय संचाचा कोनीय संवेग P_j व चुंबकीय परिबल μ_j असेल, तर या दोघांच्या गुणोत्तराला (P_j / μ_j ) घूर्णचुंबकीय गुणोत्तर असे म्हणतात व μ_j / P_j या गुणोत्तराला चुंबकीय यांत्रिक गुणोत्तर असे म्हणतात. आणवीय रचनेवरून [→ अणुकेंद्रीय व आणवीय परिबले]

μj	= g	μ0 e	(g = लांडे गुणक)
Pj		2 m

अशा आणवीय संचांनीयुक्त विशिष्ट चुंबकीय पदार्थाची चुंबकीकरण तीव्रता ∆ I ने बदलली व त्यामुळे त्याचा कोनीय संवेग ∆ P ने बदलला, तर

∆ I	= g	μ0 e	असे येते.
∆ P		2 m

∆ I व ∆ P ची मूल्ये प्रयोगावरून मोजून या समीकरणावरून g चे प्रायोगिक मूल्य काढता येते.

त्या पदार्थाचे चुंबकत्व पूर्णपणे इलेक्ट्रॉनाच्या परिवलनामुळे असेल तर g चे मूल्य २ यावयास पाहिजे. लोहगटातील मूलद्रव्यांची प्रायोगिक मूल्ये लोह १·९४ ते २·००, कोबाल्ट १·८४ ते १·९४ व निकेल १·९१ ते २·०० अशी आहेत. यावरून लोहचुंबकीय मूलद्रव्यांचे चुंबकत्व बहुतांशी इलेक्ट्रॉन परिवलनजन्यच आहे, हे सिद्ध होते.

---

चुंबकत्वाचे विविध उपयोग : व्यवहारात चुंबकत्वाचे अनेक ठिकाणी उपयोग होतात. विद्युत् जनित्र, ध्वनिग्राहक, ध्वनिनिक्षेपक, शीतकपाटाची दारे, लोहचुंबकीय चक्र इ. साधनांत लोहचुंबकाचा उपयोग होतो. अवजड लोखंडी वस्तू उचलण्यासाठी कित्येक टन वजन उचलू शकणारे विद्युत् चुंबक वापरतात. ⇨इलेक्ट्रॉन सूक्ष्मदर्शकात चुंबकीय भिंगे वापरतात. फीत मुद्रकाच्या (टेपरेकॉर्डरच्या) साहाय्याने ध्वनिमुद्रण किंवा चित्रमुद्रण व त्याचे पुनरुत्पादन करता येते. त्याचे कार्यही चुंबकत्वावर आधारलेले आहे [→ ध्वनिमुद्रण व पुनरुत्पादन]. लोहचुंबकीय अंतरकावर गुंडाळलेल्या प्रवर्तकाच्या प्रत्यावर्ती विद्युत् प्रवाहाला होणारा रोध, अंतरकांच्या चुंबकीकरणाची तीव्रता कमी जास्त करून वाढविता किंवा कमी करता येतो. अशा तऱ्हेने मोठे विद्युत् प्रवाह नियंत्रित करता येतात. चुंबकीय विवर्धक या साधनामध्ये या तत्त्वांचा उपयोग करतात.

विशिष्ट साधनासाठी विशिष्ट प्रकारचे चुंबकीय गुणधर्म असणारी लोहचुंबकीय द्रव्ये आणि मिश्रधातू तयार करण्यात आली आहेत. चुंबकत्वाची उपपत्ती समजून आल्यामुळेच हे करणे शक्य झाले आहे.

संगणकात माहिती साठविण्याचे काम सध्या फेराइट द्रव्ये आणि ट्रँझिस्टरयुक्त मंडले यांच्या साहाय्याने करण्यात येते. हे काम ‘चुंबकीय बुडबुडे’ या नवीन कल्पनेच्या साहाय्याने कमी आकारमानात आणि कमी खर्चात करता येईल तसेच संगणकाचा वेगही वाढविता येईल, असा विचार काही शास्त्रज्ञांनी मांडला आहे. हे बुडबुडे दंडगोलाकार लघुक्षेत्राच्या स्वरूपात काही चुंबकीय पदार्थांत असून एका चौ. सेंमी. मध्ये काही लक्ष इतके असू शकतात. बाह्य चुंबकीय क्षेत्राने हे बुडबुडे निर्माण करता येतात व पदार्थात हवे तसे फिरवता येतात आणि असे ते फिरवले जात असताना ज्या मार्गावरून ते जातात त्या मार्गावरील चुंबकीय परिबलांची दिशा बदलून स्मृतिसंचय करता येतो. जास्त चुंबकीय क्षेत्र लावून हे बुडबुडे नष्ट करता येतात व नवीन बुडबुडे निर्माण करून पुन्हा स्मृतिसंचय करता येतो.

संदर्भ : 1. Brailsford, F. Physical Principles of Magnetism, New York, 1966.

2. Carey, R. Isaac, E. D. Magnetic Domains and Techniques for their Observation London, 1966.

3. Chikazumi, S. Physics of Magnetism, New York, 1964.

4. Rado, G. T. H. Magnetism, 4. Vols., New York, 1963-65.

गलगली, दुं. गि.; जोशी, वि. भि.; घन, प. द.; पुरोहित, वा. ल.