खेळ सिद्धांत

खेळ सिद्धांत : व्यवहारातील संघर्षात्मक प्रसंगांच्या सैद्धांतिक अमूर्त प्रतिकृतींमधील डावपेचांचा अभ्यास करण्यासाठी गणितीय विश्लेषणाचा उपयोग करणे हा खेळ सिद्धांताचा उद्देश आहे. अशा प्रतिकृतींचे स्वरूप ब्रिज, बुद्धिबळे इ. प्रत्यक्षातील खेळांच्या स्वरूपासारखेच असते म्हणून त्यांना ‘खेळ ’ असे संबोधिले जाते. डावपेचांच्या खेळांच्या सिद्धांतासंबंधी एमील बॉरेल यांनी १९२१ मध्ये प्रथम उल्लेख केला. १९२८ साली जॉन फोन नॉयमान या हंगेरियन गणितज्ञांनी खेळ सिद्धांत प्रस्थापित केला व पुढे मॉर्गेनश्टेर्न यांच्या सहकार्याने त्यांनी अर्थशास्त्रातील काही प्रश्नांकरिता या सिद्धांताचा अधिक विकास केला. खेळ सिद्धांतातील ‘किमान-कमाल प्रमेय ’ या महत्त्वाच्या प्रमेयाचा बॉरेल यांनी प्रथम निर्देश केला होता. परंतु पुढे नॉयमान यांनीच त्याचे सर्वसाधारण अटींसाठी व्यापकीकरण केले. अब्राहम वॉल्ड व नॅश यांनीही या विषयात महत्त्वाची कामगिरी केलेली आहे. प्रत्यक्षातील बहुतेक खेळांचे पूर्ण विश्लेषण करणे अतिशय अवघड आहे तर काही खेळांच्या बाबतीत ते अशक्य ठरते, कारण असे विश्लेषण करण्यासाठी फार क्लिष्ट वर्गवारीनुसार नोंदी करणे व प्रचंड प्रमाणावर आकडेमोड करणे आवश्यक असते. तथापि सुलभ स्वरूपातील वा लहान प्रमाणावरील बऱ्याचशा खेळांचे विश्लेषण करता येते. सांख्यिकीय निर्णय [→निर्णय पद्धति], क्रियात्मक अन्वेषण (एखाद्या क्रियेचा हेतू व परिणामकारकता ठरविण्यासाठी आणि महत्तम कार्यक्षमता मिळविण्यासाठी त्या क्रियेते करण्यात येणारे विश्लेषण) इ. विषयांत खेळ सिद्धांताचा उपयोग करण्यात येतो तसेच अर्थशास्त्र, समाजशास्त्र, राज्यशास्त्र, युद्धशास्त्र, व्यवस्थापनशास्त्र इ. विषयांतील प्रतिकृतींचे खेळ सिद्धांताच्या साहाय्याने विश्लेषण करण्यात आलेले आहे.

संभाव्यता सिद्धांतात खेळांचा (उदा., फाशांचे खेळ) शुद्ध संभवाचाच विचार करण्यात येतो, तर खेळ सिद्धांतात खेळाडूच्या नियंत्रणाखालील बाबींना म्हणजे खेळाच्या ठराविक नियमांनुसार त्याला उपलब्ध असलेल्या डावपेचांना महत्त्व असते. खेळ सिद्धांतातील संज्ञांच्या व्याख्या उदाहरणांद्वारे खाली स्पष्ट केल्या आहेत. अवतरणातील शब्द म्हणजे संज्ञा होत.

(१) खेळणारी प्रत्येक व्यक्ती म्हणजे‘खेळाडू ’ होय. ब्रिजसारख्या खेळात दोन-दोन व्यक्ती सहकार्याने खेळतात व त्यादृष्टीने दोन व्यक्तींचा एक संघ म्हणजे एकच खेळाडू मानणे आवश्यक ठरते.

(२) बुद्धिबळाचा‘खेळ ’ सापशिडीपेक्षा अवघड आहे.

(३) अ आणि क बुद्धिबळाचे दोन‘डाव’खेळतात.

(४) बुद्धिबळाच्या एका‘खेळी ’त अ ने राजा पुढे सरकविला.

(५) अ ने दहाव्या खेळीत वझिराची सुरेख‘निवड ’ किंवा ‘पसंती ’ करून क वर मात केली. डावाच्या एखाद्या स्थितीत खेळाडूला शक्य असलेल्या पर्यायी योजनांपैकी त्याने स्वीकारलेली एक ‘योजना ’ म्हणजे ‘निवड ’ किंवा ‘पसंती ’ म्हणता येईल. 

(६)‘डावपेच ’ म्हणजे सर्व परिणामांचा (फायदा वा नुकसान) योग्य विचार करून तयार केलेली परिपूर्ण योजना होय. अर्थात ही योजना नेहमी विजयच संपादून देईल असे नाही. प्रतिस्पर्धी खेळाडूचा डावपेच, नैसर्गिक परिस्थिती वगैरे गोष्टींमुळे परिपूर्ण योजनासुद्धा अयशस्वी ठरणे शक्य असते. प्रत्येक खेळाडूचे रास्त ध्येय असे असते की, प्रतिस्पर्ध्याच्या उत्तम डावपेचात सुद्धा त्याला जास्तीत जास्त फायदा व्हावा, असे खेळ सिद्धांत सुचवितो. 

(७) नफा-तोटा आव्यूह : समजा, अ आणि क यांचा एक खेळ चालू असून अ ला अ_१ व अ_२ आणि क ला क_१, क_२ व क_३ असे पेच खेळणे शक्य आहे आणि खेळांच्या ठरलेल्या नियमांनुसार प्रत्येकाचे मूल्यमापन केलेले आहे. कोष्टक क्र. १ मध्ये दाखविलेल्या प्रमाणे अ चे डावपेच रांगेत व क चे डावपेच स्तंभात आणि विशिष्ट डावपेच वापरल्यास अ ला होणारा नफा-तोटा दर्शविल्यास तयार होणारऱ्या कोष्टकास अ चा नफा-तोटा आव्यूह म्हणतात. अर्थात प्रत्येक खेळातील नफा-तोटा पैशाच्या स्वरूपातच असेल असे नाही. कोष्टकात दर्शविल्याप्रमाणे (अ_१,क_१) असा खेळ झाल्यास अ ला ३ रु. नफा होतो म्हणजे क ला ३ रु. तोटा होतो. (अ_२,क_१) खेळ झाल्यास अ ला (-२) रु. नफा म्हणजे क ला २ रु. नफा होतो. हा आव्यूह २×३ अशा परिमाणांचा आहे. अर्थात उपलब्ध डावपेचांच्या संख्यांवर आव्यूहाची परिमाणे अवलंबून राहतात. अशा खेळांना ‘चौकोनी खेळ’ म्हणतात.

(८) एखाद्या खेळामध्ये उद्‌भवणाऱ्या प्रत्येक प्रसंगी एका आगाऊ तयार केलेल्या सूचनांच्या परिपूर्ण जंत्रीनुसार खेळाडूने एका निश्चित डावपेचाची निवड केल्यास त्या डावपेचाला‘विशुद्ध डावपेच ’ म्हणतात. अशा सूचनांची जंत्री म्हणजे खेळामधील प्रत्येक प्रसंगी कोणत्या डावपेचाची निवड करावी याचा संपूर्ण आराखडाच असतो आणि ही जंत्री तयार करण्यामध्ये इतर खेळाडूंच्या सर्व संभाव्य किंवा निवडी केवळ संभवावर अवलंबून असलेल्या सर्व घटना घेतलेल्या असतात. ब्रिज, बुद्धिबळे यांसारख्या खेळांमध्येसुद्धा विशुद्ध डावपेचांची संख्या अतिशय प्रचंड असते व या सर्व डावपेचांचे वर्गीकरण करणे अतिशय क्लिष्ट असल्यामुळे अशा खेळांचे खेळ सिद्धांताच्या साहाय्याने परिपूर्ण विश्लेषण करणे शक्य होत नाही.

खेळांचे वर्गीकरण :खेळाडूंच्या संख्येनुसार, खेळातील नफ्या-तोट्यानुसार आणि खेळास लागणाऱ्या वेळेनुसार अथवा खेळींच्या संख्येनुसार खेळांचे वर्गीकरण करण्यात येते.

(१) खेळाडूंच्या आवश्यक संख्येनुसार खेळांचे पुढीलप्रमाणे वर्ग पडतात : (अ) एकपात्री खेळ.उदा., पत्त्यांतील पेशन्सचा खेळ. (आ) द्विपात्री खेळ. उदा., बुद्धिबळ, ब्रिज (दोन खेळाडूंचा संघ म्हणजे एकच खेळाडू मानल्यास), दोन सेनानींचे युद्ध वगैरे. (इ) बहुपात्री खेळ :यात आवश्यक खेळाडूंची संख्या क्ष ही दोनपेक्षा जास्त असली तरी प्रत्येक डावात खेळाडूंची संख्या क्ष इतकी असलीच पाहिजे असे मात्र नव्हे. उदा., पत्त्यांतील रमीचा खेळ. 

(२) खेळात होणाऱ्या नफ्या-तोट्यानुसार पुढील वर्ग होतात :(अ) शून्य-बेरीज खेळ :जिंकणाऱ्या खेळाडूंचा नफा अधिक हरणाऱ्या खेळाडूंचा तोटा यांची बेरीज शून्य होत असेल, तर त्या खेळास शून्य-बेरीज खेळ असे म्हणतात किंवा हरलेले सर्व पैसे जर पूर्णपणे विजेत्यांतवाटण्यात आले तर त्यासही शून्य-बेरीज खेळ म्हणतात. (आ) अशून्य-बेरीज खेळ :एखाद्या खेळात विजेत्यांच्या फायद्यातून खाद्यपेये, खेळण्याच्या जागेचे भाडे इत्यादींसारख्या गोष्टींचा खर्च वजा होणार असेल, तर त्याला अशून्य-बेरीज खेळ म्हणतात. 

(३) विशाल व सरलीकृत खेळ :कोणत्याही खेळाच्या नियमांवरून त्याची दोन अमूर्त स्वरूपे तयार करता येतात. प्रत्यक्ष खेळ खेळण्याची सर्व वैशिष्ट्ये विचारात न घेता त्या खेळातील नियमांचे तांत्रिक संज्ञांच्या प्रणालीमध्ये रूपांतर करून खेळाचे वर्णन करण्यासाठी त्या प्रणालीचा उपयोग केल्यास त्या खेळास‘विशाल खेळ ’ म्हणतात. सरलीकृत खेळातही खेळातील वैशिष्ट्ये लक्षात घेत नाहीत तथापि त्यात सर्वसाधारण डावपेचांची निवड करण्याची मुभा असेत. विशाल खेळात खेळींची संख्या मोठी असणे शक्य असून प्रत्येक खेळीच्या वेळी खेळाडूला निवड करणे भागच असते, तर सरलीकृत खेळात प्रत्येक खेळाडूला फक्त एकच खेळी करता येते व ही खेळी म्हणजे त्याच्या विशुद्ध डावपेचांच्या संचातील एकाच डावपेचाची निवड असते. विशाल खेळ हे चौकोनी स्वरूपाचे खेळ नसतात. परंतु काही गणितीय तत्त्वांच्या साहाय्याने त्यांचे चौकोनी खेळात रूपांतर करता येते. अशा प्रकारे मुळांत विशाल असलेल्या खेळांचे चौकोनी खेळांत रूपांतर केल्यास हे खेळ सरलीकृत स्वरूपाचे होतात. 

(४) खेळास लागणाऱ्या वेळेनुसार किंवा खेळींच्या संख्येनुसार खेळांचे दोन वर्ग पडतात. (अ) समर्याद खेळ :यात खेळींची संख्या मर्यादित असते. बहुतेक खेळांत विशुद्ध डावपेचांची संख्या मर्यादित असल्यामुळे आणि प्रत्येक खेळीच्या वेळी मर्यादित पर्याय उपलब्ध असल्यामुळे मर्यादित खेळींनंतर खेळ संपतो. (आ) अमर्यादित अथवा अनंत खेळ :यात खेळींच्या संख्येवर बंधन नसते. अशा स्वरूपाचे खेळ त्यांच्या मूळच्या स्वरूपात अतिशय क्लिष्ट असतात व त्यांचे आदर्श स्वरूपात रूपांतर केल्यास अनंत डावपेचांचे खेळ तयार करता येतात. अशा प्रकारच्या रूपांतरामुळे अनेक प्रकारच्या खेळांचे सरलीकृत द्विपात्री खेळात रूपांतर करता येते. या खेळात प्रत्येक खेळाडूचा विशुद्ध डावपेच शून्य आणि एक यांमधील सत् संख्यांनी [→संख्या ] निर्देशीत करण्यात येतो. अशा खेळांना चौरस खेळ म्हणतात. 

द्विपात्री शून्य-बेरीज खेळ : (१)आव्यूह खेळ :कोणताही द्विपात्री शून्य-बेरीज खेळ सरलीकृत खेळाच्या स्वरूपात आव्यूह खेळ म्हणून मांडता येतो. याउलट संख्यात्मक घटक असलेला कोणताही आव्यूह द्विपात्री खेळ म्हणून मानता येतो. 

समजा, अ आणि क या सेनानींचे युद्ध चालू आहे. दोघांचे डावपेच खाली दर्शविले आहेत. 

युद्धप्रदेश, हवामान, युद्धसाहित्य इ. गोष्टी विचारात घेऊन अ सेनानीने ठरविलेला नफा-तोटा आव्यूह कोष्टक क्र. २ मध्ये दर्शविला आहे. कोष्टकातील संज्ञांचे स्पष्टीकरण पुढीलप्रमाणे आहे : विजय – ठाणे जिंकले, बरोबरी – ठाणे जिंकले नाही पण मनुष्यहानी कमी, पराजय – ठाणे हरले व जबर मनुष्यहानी.

द्विपात्री (अथवा इतर कोणत्याही बहुपात्री) खेळांत सहसा विरुद्ध पक्षांना एकमेक कोणत्या प्रसंगी कोणते डावपेच वापरणार आहेत हे माहीत नसते, ते या डावपेचांचे फक्त परिणाम जाणू शकतात. कोष्टक क्र.२ मधील अ सेनानीने अ_१ हा पेच वापरणे योग्य नाही, कारण ज्याप्रमाणे त्याच्या विजयाची शक्यता आहे त्याचप्रमाणे क सेनानीने क_२ चा वापर केल्यास अ चा हमखास पराभव होईल. याच कारणासाठी अ_२ हा पेचही उपयुक्त ठरत नाही. अशा प्रसंगी खेळ सिद्धांत उपयुक्त ठरतो. अ ने अ_३ वापरल्यास कमीत कमी बरोबरी निश्चित आहे आणि क सेनानी कच्चा असेल, तर विजयाची पण शक्यता आहे. क नेही जर क_२ हा डावपेच वापरला, तर त्यालाही बरोबरीची खात्री व कदाचित विजयाची शक्यता म्हणजेत क हा ठाणे हरणार नाही हे निश्चित. अशा प्रकारे खेळ सिद्धांत अ ला अ_३ आणि क ला क_२ हे डावपेच सुचवितो.

(२) किमान-कमाल प्रमेय व पल्याण बिंदू : दोन खेळाडूंच्या परस्पर ध्येयांचा समान बिंदू म्हणजे पल्याण बिंदू होय. यासाठी कोष्टक क्र. २ मधील नफा-तोट्याचा आव्यूह गृहीत धरू आणि विजय, बरोबरी व पराजय यांना अनुक्रमे १०,५ व ० गुण मानू. यातील पल्याण बिंदू शोधण्यासाठी पुढील पद्धती वापरतात : (प) नफा-तोटा आव्यूहातील रांगांच्या शेवटी रांगांतील किमान संख्या लिहितात व ह्या किमान संख्यातील कमाल संख्येस कंस करतात. (फ) प आणि फ मधील कंस केलेल्या संख्या एकच असतील, तर तो स्तंभ व ती रांग जेथे छेदतील त्याला पल्याण बिंदू म्हणतात आणि त्या चौकोनातील संख्येस खेळाचे मूल्य म्हणतात. पल्याणावर (म्हणजे खोगिरावर) अशा प्रकारचा एक बिंदू असतो.

थोडक्यात, कमाल-किमान अ = किमान-कमाल क असेल, तर त्या आव्यूहात पल्याण बिंदू असतो. समजा, त्याचे मूल्य ज आहे, अ हा ज इतके मूल्य खात्रीने जिंकू शकेल पण क त्याला ज पेक्षा जास्त मूल्य कधीच जिंकू देणार नाही. उदा., (अ_३,क_२) डाव झाल्यास अ ची बरोबरी निश्चित आहे. पण क च्या खेळाने अ चा जास्तीत जास्त नफाही बरोबरी हाच होऊ शकतो. यावरून किमान-कमाल प्रमेय पुढीलप्रमाणे मांडता येते.  कुठल्याही स्पर्धात्मक खेळात अ आणि क हे दोन्हीही खेळाडू विशुद्ध डावपेच वापरणार असतील, तर अ खेळाडूसाठी असा एक कमाल-किमान डावपेच अस्तित्वात असतो की, ज्यामुळे त्याचा ज नफा निश्चित असतो आणि क खेळाडूसाठी किमान-कमाल डावपेच असा असतो की, ज्यामुळे अ चा नफा ज पेक्षा जास्त होऊ शकत नाही.

(प) आणि (फ) मधील कंसांतील संख्या समान नसतील त्या आव्यूहात पल्याण बिंदू नसतो पण खेळाचे मूल्य त्या दोन संख्यांच्या दरम्यान असते.

(३) संमिश्र डावपेच :एखादा खेळ पुन्हा पुन्हा खेळला गेल्यास संमिश्र डावपेचांचा उपयोग करता येतो. म्हणजेच पुन्हा पुन्हा खेळता येईल अशा खेळात निरनिराळे डावपेच वापरण्याची सापेक्ष वारंवारताठरविता येते. उदाहरणादाखल कोष्टक क्र. ३ मध्ये दर्शविलेला २×२ परिमाणाचा आव्यूह विचारात घेऊ. या आव्यूहात पल्याण बिंदू नाही. त्यामुळे अ किंवा क ला एकच विशुद्ध डावपेच वापरून चालणार नाही. अ ने कायम अ_१ हा डावपेच वापरला, तर त्याला ७ नफ्याबरोबरच ३ तोटाही होण्याची तेवढीच शक्यता आहे. त्यामुळे येथे संमिश्र डावपेच उपयोगी पडतील. समजा, अ ने अ_१ अर्ध्या वेळा आणि अ_२ अर्ध्या वेळा खेळण्याचे ठरविले, तर अ चा नफा क च्या निर्णयानुसार पुढीलप्रमाणेबदलेल :

क_१ कायम, १/२ (-३)+ १/२ (६)= १·५० रुपये. 

क२ कायम, १/२ (७)+ १/२ (१)= ४·०० रुपये. 

याचबरोबर क ने सुद्धा क_१ अर्ध्यावेळा व क_२ अर्ध्यावेळा खेळावयाचे ठरविले तर अ चा नफा १/२[१/२ (-३)+ १/२ (६)] + १/२[१/२ (७)+ १/२ (१)]= २·७५ रुपयेइतका होईल.यामुळे सर्वांत उत्तम डावपेच कोणता असा अ आणि क यांना प्रश्न पडेल. याकरिता असे गृहीत धरू की, अ_१ हा डावपेच क्ष प्रमाणात आणि अ_२ हा (१-क्ष) प्रमाणात अ वापरतो. यावरून क_१ कायम असताना, 

ज (अ,क_१) = क्ष (-३) + (१-क्ष) (६) = ६– ९ क्ष ….(i) 

क_२ कायम असताना, 

ज (अ,क_२) = क्ष (७) + (१-क्ष) (१) =१ +६क्ष … (ii)

(i) आणि (ii) जेव्हा समान असतील तेव्हा सर्वोत्तम डावपेच मिळतो. यावरून६– ९ क्ष=१ +६क्ष असे मांडून क्ष = १/३ असे मिळते. म्हणजे अ ने अ_१ आणि अ_२हे डावपेच१: २ या प्रमाणात खेळावेत. यावरून  ज (अ) = १/३ (-३)+२/३ (६) = ३ …. …. ….(iii) 

म्हणजेच क ने कोणताही डावपेच वापरला आणि अ ने अ_१ आणि अ_२ हे १: २ या प्रमाणात वापरले तर अ चा किमान ३ रू. नफा निश्चित आहे. याचप्रमाणे क चाहीसर्वोत्तम संमिश्र डावपेच काढता येईल. क ने क_१ आणि क_२ हेय:(१–य)या प्रमाणात वापरले असे मानल्यास 

ज (क, अ_१)= य (-३) +(१-य) (७) 

= (६) +(१-य) (१) = ज (क, अ_२) 

म्हणून य = २/५ आणि ज (क) = ३ …………(iv) 

यावरून जर क ने क_१ आणि क_२ हे डावपेच २ : ३ या संमिश्र प्रमाणात वापरले, तर तो सर्वोत्तम संमिश्र डावपेच होईल. (iii) व (iv) वरून ज (अ) = (क) आणि हेच समीकरण शून्य-बेरीज खेळात लागू असते. वरील पद्धतींखेरीज आलेखावरून व ⇨आव्यूह सिद्धांताच्या साहाय्यानेही सर्वोत्तम संमिश्र डावपेच काढता येतो.

(४) सममित खेळ : एखाद्या खेळाच्या नफा-तोटा आव्यूहातील जर कुठल्याही रांगा आणि स्तंभ यांच्या अदलाबदलीने तोच आव्यूह मिळत असेल, तर त्या खेळास सममित खेळ म्हणतात.

(५) चौरस खेळ : चौरस खेळांची दोन उदाहरणे खाली दिली आहेत. (अ) टिंब-फुलीचा खेळ :या खेळात एक ३×३ चा चौरस असून दोन खेळाडू आवश्यक असतात. समजा अ हा खेळाडू (O) आणि क हा (X) अशा चिन्हांनी निर्देशित केले आहेत. नऊ चौकोनांपैकी एका चौकोनात एक खेळाडू त्याचे एकच चिन्ह काढतो. मग दुसरा खेळाडू त्याचे चिन्ह उरलेल्या आठपैकी एका चौकोनात काढतो. याप्रमाणे एका पाठोपाठ एक असे खेळतात. प्रत्येक खेळाडूचे उद्दिष्ट असे असते की त्याने त्याची तीन चिन्हे एका सरळ रेषेत आणावयाची व त्याचवेळी विरुद्ध पक्षाची एका रेषेत येऊ द्यावयाची नाहीत. ज्याची चिन्ह प्रथम एका रेषेत येतील तो विजेता व कोणाचीच न आल्यास बरोबरी होते. पहिली खेळी साधारणपणे आलटून पालटून दोघेही करतात.

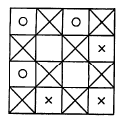
(आ) या खेळाची सुरुवात आ. १ मध्ये दर्शविलेल्या स्थितीपासून होते. दोन खेळाडू (O) व (X) असे निर्देशित केले जातात. आळीपाळीने प्रत्येकजण एक खेळी करतो. प्रत्येक खेळाडू एका खेळीस त्याच्या तीन चिन्हांपैकी एक चिन्ह जवळच्या रिकाम्या चौकोनात हलवितो. ज्यावेळी एखाद्या खेळाडूला खेळी असूनसुद्धा त्याचे चिन्ह कुठेच हलविता येत नाही त्या वेळी त्याचा पराजय होतो.

विशाल खेळ:या प्रकारच्या खेळांच्या संदर्भात येणाऱ्या संज्ञांचे उदाहरणांद्वारे खाली स्पष्टीकरण केले आहे. 

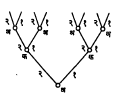
(अ) एका खेळात अ हा प्रथम [१,२] यांपैकी एक संख्या क्ष निवडतो. अ ची निवड माहीत झाल्यावर क हा [१,२] या संख्यांपैकी एक संख्या य निवडतो व क चा खेळ माहीत झाल्यावर अ हा पुन्हा [१,२] पैकी एक संख्या झ निवडतो आणि डाव सुरु करण्यापूर्वी ठरल्याप्रमाणे डावाचे मूल्य ज (क्ष,य,झ) होते. समजा, डाव ज (१,१,१) झाला तर अ चा फायदा २ आहेस, वगैरे. हा डाव आठ प्रकारे खेळता येईल व खेळाच्या मूल्यावर अ किंवा क स्वतःचा डावपेच ठरवील. हा विशाल खेळसुद्धा सरल करून सोडविता येतो व त्यातील सर्वोत्तम डावपेच तसेच पल्याण बिंदू (एक किंवा अधिक ) काढता येतात.

वरील डावाचा आलेख वा वृक्ष आ. २ मध्ये दर्शविल्याप्रमाणे काढता येईल. हा खेळ एकूण आठ भिन्न प्रकारे खेळता येतो असे या आलेखावरून दिसून येईल. प्रत्येक बिंदू खालच्या पातळीतील एकाच बिंदूस जोडला आहे. शेवटी एकच बिंदू शिल्लक राहतो आणि तीच खेळाची सुरुवात आहे. प्रत्येक फांदीच्या टोकाला त्या खेळाचे मूल्य लिहिल्यास हा आलेख परिपूर्ण होईल.

(आ) ज्या खेळात प्रत्येक खेळाडूस त्याने केलेल्या डावपेचांच्या निवडीचे त्यांच्या मीमांसेसहित पूर्ण स्मरण आहे त्याला ‘परिपूर्ण स्मरण खेळ ’ म्हणतात. पत्त्यांतील रमी हा परिपूर्ण स्मरण खेळ आहे कारण त्यात एकच खेळाडू स्वतःचा डाव पूर्ण खेळतो. याउलट ब्रिजमध्ये दोन खेळाडूंचा मिळून एक संघ होत असल्यामुळे तो परिपूर्ण स्मरण खेळ नाही.

(इ) विशाल खेळात डावपेचांचे गुणदोष विचारात न घेता जर एखाद्या संभवात्मक वा दैवी योजनेने (उदा., नाण्याची वा फाशाची फेक) डावपेचांची निवड केली, तर त्या डावपेचांना ‘संभवात्मक किंवा दैवी डावपेच ’ म्हणतात.

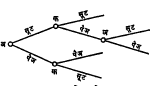
(ई) सुलभ पोकर : पत्त्यांतील राजा, राणी व गुलाम या तीन नीट पिसलेल्या पानांपैकी प्रत्येकी एकच पान दोन खेळाडू (अ आणि क) काढतात. या काढलेल्या पानांपैकी कोणाचे पान भारी आहे या अंदाजावर खेळाडू पैज मारतात किंवा सूट देतात. लागोपाठ ‘दोन पैजा ’ किंवा ‘दोन सूट ’ दिल्यास डाव थांबतो व भारी पान ज्याचे असेल तो खेळाडू पैसे वा डाव जिंकतो. त्याचप्रमाणे एकाच्या पैजेनंतर दुसऱ्या खेळाडूने सूट दिली तर दुसरा खेळाडू डाव हरतो. किती व काय हरायचे हे दोघा खेळाडूंनी आपसात अगोदरच ठरवावयाचे असते. आ. ३ मध्ये या खेळाचा वृक्ष दाखविला असून त्यावरून या डावात पत्त्यांचे वाटप एकूण सहा प्रकारांनी होऊ शकते व प्रत्येक प्रकार पाच तऱ्हांनी खेळला जाईल असे दिसून येते.याशिवाय प्रत्येक खेळाडूस खालील चार डावपेचांपैकी फक्त एकच वापरता येतो.

अ१ – कोणत्याही पत्त्याला सूट देणे.

अ२ – राणीला सूट देणे व राजाला पैज लावणे.

अ३ – राजाला सूट देणे व राणीला पैज लावणे.

अ४ – नेहमीच पैज लावणे.

क१ – अ ची पैज असल्यास सूट देणे.

क२ – अ ची सूट असल्यास सूट देणे व अ ची पैज असल्यास पैज लावणे.

क३ – क२ च्या उलट म्हणजे अ ची सूट असल्यास पैज लावणे व अ ची पैज असल्यास सूट देणे.

क४ – कायम सूट लावणे.

सूट व पैज यांत अनुक्रमे लहान आणि मोठी पैज असा बदल करता येईल. असा डावात अ आणि क यांनी आपला डावपेच अगोदरच जाहीर केला, तर एखादा निःपक्ष पंचसुद्धा त्यांच्यासाठी डाव खेळू शकेल. थोडक्यात म्हणजे नफा-तोटा माहीत झाल्यास हा खेळ विशुद्द डावपेचांचा सरलीकृत खेळ तयार होतो आणि मग त्याचा नफा-तोटा आव्यूह मांडता येतो.

बहुपात्री खेळ : या खेळांचे मुख्यतः दोन प्रकार आहेत.(१) सहकारी खेळ : या प्रकारात एकमेकांचा खेळ व डावपेच यांसंबंधी आपसात वाटाघाटी करणे, गट करणे इत्यादींना परवानगी असते. पत्त्यांतील रमी, झब्बू वगैरे खेळ सहकाराने खेळतां येतात.

(२) असहकारी खेळ : या प्रकारात सहकार्य, वाटाघाटी वगैरेंना परवानगी नसते.

प्रत्यक्ष व्यवहारात मुख्यतः असहकारी खेळच प्रत्ययास येतात. यामुळे खेळ सिद्धांतात असहकारी खेळांवरच विशेष भर देतात. एखाद्या ‘सहकारी ’ खेळातील वाटाघाटी, बोलणी, वायदे इ. खेळाचे एक अंग समजून त्याचे ‘असहकारी ’ खेळात रूपांतर करतात व मग त्याचे विश्लेषण करतात. शून्य-बेरीज द्विपात्री खेळात जसा पल्याण बिंदू असतो, तसा बहुपात्री शून्य-बेरीज खेळात असलेल्या बिंदूंना समतोल बिंदू म्हणतात. कोणत्याही एका खेळाडूने समतोल बिंदू डावपेच वापरावयाचा असे ठरविले, तर इतर खेळाडूंनाही योग्य फायद्यासाठी त्याचाच वापर करावा लागेल असा या समतोल बिंदूचा व्यावहारिक दृष्ट्या अर्थ आहे. विशुद्ध डाव पेचांनी बिंदू समतोल मिळेलच असे नाही, पण संमिश्र डावपेचांनी मात्र तो मिळू शकतो.

बहुपात्री अशून्य-बेरीज खेळांना सिद्धांत अद्याप स्पष्ट झालेला नाही. सहकारी खेळाचा असहकारी खेळसुद्धा सहजपणे करता येत नाही व खेळात थोडासा जरी सहकार आढळला, तरी खेळ सिद्धांत योग्य निर्णय देऊ शकत नाही.

संदर्भ : 1. Dresher, M. Games of Strategy : Theory and Applications, Engelwood Cliffs, N. J., 1961.

    2. Luce, R. D., Raiffa, H. Games and Decisions, New York, 1957.

    3. McKinsey, J. C.C. Introduction to the theory of Games, New York, 1952.

    4. Von Neumann, J., Morgenstern, O. Theory of Games and Economic Behaviour, Princeton, 1955. Behaviour, Princeton,                  1955.

ओक, अ. द.

“