पुंज सिद्धांत

पुंज सिद्धांत : अणु-रेणू यांच्या एवढ्या (≈ १०^-८ सेंमी.) किंवा त्यापेक्षा जास्त सूक्ष्म आकारमानाच्या पदार्थकणांच्या वर्तणुकीचे (प्रेरणेच्या प्रभावाखालील होणाऱ्या गतीचे) किंवा कणाच्या प्रारणाबरोबर (तरंगरूपी ऊर्जेबरोबर; उदा., दृश्य प्रकाश, जो विद्युत्‌ चुंबकीय स्वरूपाचा असतो) होणाऱ्या परस्परक्रियेचे वर्णन करण्याकरिता पुंज सिद्धांताचा वापर करावा लागतो. सूक्ष्म पदार्थकणांच्या  क्षेत्रात न्युटन यांच्या नियमांवर आधारलेल्या रूढ कण यामिकीच्या (प्रेरणेखाली असणाऱ्या कणाचा किंवा गतिमान कणाचा गतिमार्ग गणितीय रित्या काढावयाच्या शास्त्राचा) आणि प्रारणाकरिता रूढ तरंग सिद्धांताचा उपयोग केल्यास त्यापासुन जे निष्कर्ष, निघतात ते प्रयोगाने सापडलेल्या निष्कर्षांशी जुळत नाही. सूक्ष्म कणांचा बाबतीत काही विशिष्ट राशींचे (उदा., अणूनधील इलेक्ट्रॉनाची ऊर्जा, कोनीय संवेग–म्हणजे कणाचे द्रव्यमान, त्याच्या परिभ्रमण अक्षापासूनच्या अंतराचा वर्ग व कोनीय वेग यांचा गुणाकार करून मिळणारी राशी) चलन अखंडपणे न होता त्यांच्यांत होणारा बदल ठराविक टप्पांच्या स्वरूपात होतो, हे मानणे यालाच पुंज सिद्धांत म्हणतात. ज्या राशीत असा खंडित बदल होतो त्या राशीचे पुंजीकरण केले आहे असे म्हटले जाते. पुंज सिद्धांत प्रस्थापित होण्याच्या आधी सूक्ष्म वस्तूच्या काही राशींचे चलन खंडित स्वरूपाचे असते हे माहीत होते. सर्व पदार्थ अणू किंवा रेणू या पृथक कणांपासून बनले आहेत असे मानले, तर (m = अणूंचे द्रव्यमान असेल तर) एखाद्या सूक्ष्म पदार्थकणाचे द्रव्यमान = nm या सूत्राने दर्शविता येते. येथे n हा पुर्णांक असून त्याची मुल्ये १, २, ३… ही असतात. यावरून असे दिसेल की, सूक्ष्म पदार्थकणांवर द्रव्यमान नेहमी m याच्या पूर्ण पटीतच बदल पावते. याचप्रमाणे सूक्ष्म पदार्थकणावर असणारा विद्युत्‌ भारही e या इलेक्ट्रॉनीय विद्युत्‌ भाराच्या पूर्णांक पटीतच सापडतो. या दोन्ही राशींचे पुंजीकरण झाले आहे हे यावरून लक्षात येईल. सूक्ष्म पदार्थकण व (प्रकाशासारखी) प्रारण ऊर्जा यांमध्ये जेव्हा परस्परक्रिया घडते तेव्हा त्या वेळी होणारी ऊर्जेची देवघेव हीसुद्धा एका ठराविक पुंजमापातच होते, ही संकल्पना माक्स प्लांक (१८५८–१९४७) यांनी १९०० साली प्रथम पुढे मांडली. त्यांच्या सिद्धांताप्रमाणे प्रारण कंप्रता (दर सेंकदास होणाऱ्या कंपनांची संख्या) जर y असेल, तर तिच्या ऊर्जेच्या पुंजकण hν एवढ्या मूल्याचा असतो. येथे h हा वैश्विक (सर्व परिस्थितींत सर्वत्र स्थिर राहणारा) प्लांक स्थिरांक असून त्याचे मूल्य h = ६.६२५६ × १०^-३४ जूल-सेंकद किंवा ६.६२५५ × १०^-२७ अर्ग-सेकंद एवढे असते. पदार्थकण hy या मापातच प्रारण ऊर्जेचे शोषण किंवा उत्सर्जन करतात असा याचा अर्थ होतो. निराळ्या भाषेत सांगावयाचे म्हणजे पदार्थकणाजवळची कोणत्याही क्षणी असलेली प्रारण ऊर्जा nhy (n= 0, 1, 2, 3, …..) या सूत्राने दर्शविता येते. पदार्थकण व प्रारण ऊर्जा यांमधील संबंधाचे पुढील भागात आधिक विवेचन  केले आहे.

ऊर्जा उत्सर्जन : कृष्ण पदार्थ प्रारण : सर्व पदार्थ हे अणू-रेणुकणांपासून बनले आहेत, याचा उल्लेख मागे आला आहेच. दोन पदार्थकण एकमेकांशी परस्परक्रिया करू शकतात किंवा एकमेकांवर प्रेरणा लावू शकतात. उदा., सूर्य पृथ्वीवर गुरुत्कर्षणी आकर्षी प्रेरणा लावीत असल्यामुळे पृथ्वी त्याभोवती एका ठराविक भ्रमणकक्षेत फिरते. दोन पदार्थकणांवर जर विद्युत्‌ भार असेल तर, त्या भाराच्या चिन्हानुसार त्यांमध्ये आकर्षी किंवा प्रतिकर्षी (प्रतिसारक) प्रेरणा मिळते. दोन विद्युत्‌ भारित पदार्थकणांमध्ये जरी निर्वात असला (म्हणजे त्यामध्ये द्रव्यमाध्यम नसले ), तरी ही प्रेरणा मिळते. याचे विवरण करण्याकरिता विद्युत्‌ क्षेत्र ही संकल्पना पुढे आली. या विवरणाप्रमाणे एक विद्युत्‌ भारित पदार्थकण आपल्या सभोवती (स्वतःच्या स्थानापासून अनंतापर्यंत) एक क्षेत्र निर्माण करतो. हे क्षेत्र जेथे असते त्या जागी असलेल्या दुसऱ्या विद्युत्‌ भारित कणांवर कार्य करून त्यावर प्रेरणा निर्माण करते. पदार्थकणाजवळ निरनिरळ्या प्रकारची ऊर्जा असू शकते. तो गतिमान असेल, तर त्याच्या जवळ गतिज ऊर्जा असते. विद्युतीय प्रेरणेमुळे त्याजवळ विद्युतीय ऊर्जा सापडते. याशिवाय रासायनिक ऊर्जा इ. प्रकारच्या ऊर्जा पदार्थजवळ असू शकतात पण या सर्व ऊर्जा कणाजवळच स्थानांकित असतात, असे दिसते. उदा., गतिमान कणाची गतिज ऊर्जा त्या कणामध्येच स्थानांकित असते त्यामुळे ती कणाबरोबर त्याच गतीने जाते. याउलट विद्युत्‌ भारित पदार्थकणाभोवती जे क्षेत्र निर्माण होते त्याची ऊर्जा सर्व आसमंतात पसरलेली असते, असे दाखविता येते. निर्वात अवकाशात जर क्षेत्र असेल, तर त्यात सुद्धा ऊर्जा असते असा निष्कर्ष काढता येतो. पदार्थकणाजवळ जर ऊर्जा असेल, तर काही परिस्थितींत त्यापैकी काही भाग प्रारणाच्या स्वरूपात उत्सर्जित करू शकतो. उदा., कंपित कंपकाटा (आपटल्यावर ज्याची दोलन कंप्रता स्थिर असते असा चिमट्यासारखा काटा) सभोवतालच्या परिसरात ध्वनितरंगांच्या स्वरूपात प्रारण ऊर्जा उत्सर्जित करतो आणि तो जसजसी ऊर्जा उत्सर्जित करतो तसतशी त्याच्या जवळची ऊर्जा कमी होत जाते.

दोलायमान इलेक्ट्रॉनमुळे  होणारे विद्युत्‌ चुबंकिय प्रारणाचे (प्रारण म्हणजे गतिशील विद्युत्‌ चुंबकिय क्षेत्र) उत्सर्जन ही या प्रकारच्या ऊर्जा उत्सर्जन क्रियेचे सर्वांत सोपे उदाहरण आहे. इलेक्ट्रॉन आपल्या स्थानापाशी कंपने करू लागला म्हणजे त्यापासून विद्युत्‌ चुंबकिय ऊर्जा निर्माण होते. रेडिओ तरंगनिर्मितीकरिता सर्वसामान्यपणे उपयोगात असलेल्या हॅर्टझ् द्विध्रवाच्या (जवळजवळ असलेल्या विरुद्ध चिन्हाच्या व बदलत्या विद्युत्‌ भारांच्या जोडीच्या) कार्यामागे हीच मूलभूत क्रिया असते. निरनिरळ्या कंप्रतेच्या विद्युत्‌ चुंबकिय तरंगांना माध्यमाची आवश्यकता असत नाही व त्यांचा निर्वातामध्ये एकच C=३ X १०^१० सेंमी. प्रती से. एवढा वेग असतो असे आढळते. वायुअणूंमध्ये (किंवा वायुरेणूंमध्ये) इलेक्ट्रॉन आहेत व ते काही परिस्थितींत विद्युत्‌ चुंबकीय प्रारण उत्सर्जित करते. वायुअणूंमधील अंतर जास्त असल्यामुळे प्रत्येक अणू स्वतंत्रपणे उत्सर्जन करतो. या कारणाकरिता अणुंपासून मिळणारे उत्सर्जन पृथक प्रकाश-तरंग रेषेच्या स्वरूपात असते. याउलट घन पदार्थामध्ये अणू एकमेकांच्या इतके जवळ असतात की, त्यांपासून होणारे उत्सर्जन नजीक असलेल्या अणूंच्या उपस्थितीमुळे प्रभावित होते. त्यामुळे घन पदार्थ तापवून त्यास ऊर्जा दिली असता त्यापासून मिळणारा उत्सर्जन वर्णपट अखंडित स्वरूपाचा असतो. निरनिराळे घन पदार्थ त्याच तापमानापर्यंत तापवले असता जवळजवळ एकाच प्रकारचा वर्णपट प्रदर्शित करतात. सर्व तप्त घन पदार्थांचा वर्णपट ज्या मूलभूत वर्णपटाशी आसन्नपणे (जवळजवळ) जुळतो त्यास कृष्ण पदार्थ वर्णपट असे म्हणतात. ⇨ कृष्ण पदार्थ म्हणजे काळा पदार्थ. त्यावर पडणाऱ्या सर्व प्रकाश-तरंगाचे तो जवळजवळ संपुर्णपणे शोधण करीत असल्यामुळे त्यावरून परावर्तित होणऱ्या प्रकाशाचे प्रमाण नगण्य असते व या परिस्थितीमुळेच तो डोळ्यांना काळा दिसतो. जे पदार्थ नीच तापमानाकरिता चांगले शोषक असतात, त्यांचे तापमान ठेवले असता ते चांगला उत्सर्जक होतात. या न्यायाने कृष्ण पदार्थ तापवला असता तो उत्तम प्रारण उत्सर्जक म्हणुन कार्. करतो. त्यामुळे प्रदीप्त अवस्थेत कृष्ण पदार्थ  इतर कोणत्याही पदार्थापेक्षा जास्त तेजस्वी दिसतो. आदर्श कृष्ण पदार्थ उत्सर्जकाची व्यवहारी प्रतिकृती तयार करण्याची रित एल्. बोल्टसमान (१८४४-१९०६) यांनी शोधून काढली. कोणत्याही घन पदार्थात एक पोकळबंदिस्त विवर (उदा., दंडगोल आकाराचे) तयार करून त्यास फक्त एका बाजुने एक बारिक छिद्रे ठेवले, तर ते उपकरण प्रदिप्त केले असता छिद्रातुन येणारे प्रारण, कृष्ण पदार्थ प्रारणाबरोबर एकरुप असते, असे त्यांनी सिद्ध केले. तप्त घन पदार्थापासून मिळणाऱ्या अंखडित प्रारणाचे विवेचन करण्याकरिता त्यामध्ये निरनिरळ्या कंप्रतांचे सूक्ष्म हरात्मक आंदोलन (ज्यांच्या समतोलाचा भंग झाला असता स्थांनातराशी समप्रमाणात असण्याऱ्या एका पुनःस्थापक प्रेरणेमुळे ज्यांना आंदोलक गती प्राप्त होते अशा भौतिक प्रणाली) आहेत असे गृहीत धरले जाते. कल्पना निश्चित करण्याकरिता या आंदोलकांमध्ये इलेक्ट्रॉन किंवा जालकातील अणू दोलायमान होतात असे मानता येईल. प्रारणात सर्व कंप्रता सल्यामुळे या आंदोलकांच्या कंप्रता सुद्धा ०ते ०० या मर्यादेत आहेत असे समजले जाते. विवराच्या पोकळ भागात काय होते याचा विचार करता, तप्त भिंतीमधील आंदोलकाच्या प्रारण आतील अवकाशात उत्सर्जित होते आणि ते विवरच्या विरुद्ध  बाजूच्या भिंतीवर पडून त्याचे अशतः शोषण व अंशत: परावर्तन होते. सर्व बाजूनी शोषण किंवा उत्सर्जन करण्याऱ्या ठराविक तापमानाच्या भिंती व अवकाशातील प्रारण यामध्ये काळानंतर स्थिर अथवा समतोल अवस्था प्रस्थापित होते. विवर बंदिस्त असल्यामुळे  आतील तरंगाकरिता काही मर्यादा अटी पडतात. रूढ तरंग सिद्धांताचा उपयोग करून लॉर्ड रॅली (१८४२–१९१९) व जे. एच जीन्स, (१८७७–१९४६) यांनी असे दाखविले की,  आणि  या तरंगलांबी मर्यादेत असणाऱ्या आंदोलकांची संख्या या सूत्राने मिळते. (A एक स्थिरांक). याचा अर्थ  असा होतो की, आसन्नपणे तरंगलांबी उत्सर्जित करणाऱ्या आंदोलकांची संख्या वरील सूत्राने दर्शविली जाते. T या  तापमानाच्या प्रत्येक आंदोलकाजवळ सरासरी ऊर्जा kT असते. (येथे k  हा बोल्टसमान स्थिरांक आहे) असे रूढ सिद्धांतानुसार मानले, तर या तरंगलांबीच्या प्रारणात असणारी ऊर्जा या सूत्राने मिळते. वरील सूत्रावरुन असा निष्कर्ष निघतो की, प्रारणाची (किंवा आंदोलकाची) तरंगलांबी कमी होते तशा त्याची ऊर्जा त्वरेने वाढत जाते.एवढेच नव्हे तर, संपुर्ण बंदिस्त प्रारण ऊर्जा अनंत होते हा असंभाव्य असा निष्कर्ष पण मिळतो. प्रत्यक्ष प्रयोगाने प्रारणामधील तरंगलांबीनुसार ऊर्जा वितरण मोजले, तर एका ठराविक तरंगलांबी करिता ऊर्जा महत्तम होते व त्यापेक्षा कमी व जास्त तरंगलांबीकरिता त्यामधील ऊर्जा त्वरेने कमी होत जाते असे आळते. आ. मध्ये रॅली-जीन्स सूत्रानुसार मिळणारे व प्रयोगाने आढळणारे ऊर्जा वितरण वक्र दाखविले आहेत, प्रयोगाने मिळलेल्या ऊर्जा वितरणाशी जुळणारे वितरण मिळविण्याकरिता प्लांक यांनी असे गृडात धरले की,  कंप्रतेच्या आंदोलकांची ऊर्जा (शोषण आणि उत्सर्जन क्रिया ध्यानात घेता)  या सूत्राने मिळते (n=0,1,2,3,…पुर्णांक) ही अट लक्षात घेता आंदोलकाची सरासरी ऊर्जा रूढ भौतिकीप्रमाणे असणाऱ्या kT या मुल्याची न राहता तिचे मूल्य. या सूत्राने मिळते. (येथे हा स्वाभाविक लॉगारिथमाचा आधारांक आहे, → लॉगरिथ) सरासरी ऊर्जा नव्या सिद्धांताप्रमाणे आंदोलकांच्या कंप्रतेवर अवलंबुन राहते हे लक्षात घेण्याजोगे आहे. अधिक अचुक गणित केल्यास आंदोलकाची ऊर्जाएवढी नसून ती  एवढी असते.

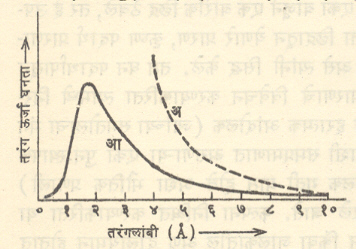
असे आढळुन येते. आधुनिक ⇨पुंजयामिकीप्रमाणे सुद्धा हेच सूत्र मिळते. आंदोलकाचे तापमान कमी करित गेल्यास त्याची ऊर्जा कमी होत जावी व निरपेक्ष शुन्य व्हावे. अशी कोणाचीही अपेक्षा असणार. तथापि पुंज सिद्धांतानुसार हे बरोबर नसून आंदोलकाची ऊर्जा पेक्षा कधीच कमी होत शकत नाही असे कळते. या किमान  ऊर्जेला शून्य बिंदु ऊर्जा म्हणतात व तिचे अस्तित्व प्रयोगाने सिद्ध झाले आहे.

प्लांक यांच्या सिद्धांताप्रमाणे या तरंगलांबी मर्यादेत असणाऱ्या प्रारणाची ऊर्जा असल्यास

यावरून ही ऊर्जा या तरंगलांबीकरिता महत्तम मूल्य धारण करते असे आढळते.

हे सूत्र डब्लू. वीन (१८६४-१९२८) यांच्या नियमाशी जुळते. कृष्णपदार्थापासून एकंदर उत्सर्जित उर्जेचे (प्रती सेंकद) मुल्य हेही सहज काढता येते

हे सूत्र जे. श्टेफान (१८३५-९३) यांनी सुचविलेल्या अनुभवजन्य सूत्राशी जूळते [→ उष्णता प्रारण)

ऊर्जा प्रसारण : फोटॉन : पदार्थकण व प्रारण यांच्यामध्ये ऊर्जेची देवघेव फक्त या पुंज मापाच्या स्वरूपात होते असे नसून तिचे अवकाशात प्रसरणही पुंजकणाच्या स्वरूपात होते ही कल्पना अल्बर्ट आइनस्टाइन (१८७९–१९५५) यांनी प्रकाशविद्युत्‌ परिणामाचे [→ प्रकाशविद्युत्‌ )विवेचम करण्याकरिता मांडली. या कल्पनेप्रमाणे प्रारण ऊर्जा तरंगाच्या स्वरूपात आसंमतात पसरत न जाता ती (काही परिस्थितीत) पुंजाच्या केद्रींत अवस्थेत प्रगत पावते. या प्रारणपुंजाला ⇨ फोटॉन ही संज्ञा दिली आहे. धातुपटालावर योग्य कंप्रतेचे प्रकाश प्रारण टाकले असता त्यापासुन इलेक्टॉनांचे उत्सर्जन होते आणि उत्सर्जित इलेक्ट्रॉनांची गतिज ऊर्जा प्रारण कंप्रतेवर अवलंबून असते. आइनस्टाइन यांनी या परिणामाकरिता दिलेले सूत्र सार्थ आहे,असे प्रयोगाने दाखविले गेले आहे.

विद्युत्‌ चुबंकीय ऊर्जा फोटॉन या कणाच्या स्वरूपात प्रसारित होते. याला ⇨ कॉम्पटन परिणामापासूनसुध्दा पुष्टी मिळते. या परिणामात ऊर्जा असणाऱ्या क्ष-किरणपुंजाची पदार्थातील (जवळजवळ) मुक्त अशा इलेक्ट्रॉनाबरोबर टक्कर होऊन त्यापैकी काही ऊर्जा इलेक्ट्रॉनाला मिळते. टकरीमुळे क्ष-किरणांची ऊर्जा कमी होते व किरणाच्या गतिमार्गात विचलन होते. क्ष-किरणाचा विचलन कोन व त्याच्या ऊर्जेत झालेली घट या राशींचे (क्ष-किरण ऊर्जा फोटॉनामध्ये केंद्रीत आहे असे गृहीत धरून) गणन करता येते. अशा रीतीने मिळालेली मूल्ये प्रयोगात निरीक्षिलेल्या मूल्यांशी जुळतात, असे दिसून आले आहे.

आणवीय विशिष्ट उष्णता : घन पदार्थांच्या विशिष्ट उष्णतेचे विवेचम करण्याकरिता आइनस्टाइन यांनी असे मानले आहे की, घन पदार्थातील अणू त्यामध्ये एका ठराविक आकृतीबंधनानुसार निरनिरळ्या ठिकाणी स्थानबंधित अवस्थेत असतात. ते आपल्या स्थिर स्थानाभोवती या एकाच कंप्रतेने आंदोलने करू शकतात. या गृहितीनुसार घन पदार्थामधील हरात्मक आंदोलकास एकच कंप्रता आहे असे होते.पदार्थाचे तापमान वाढविले, तर त्यांची कंपन ऊर्जा वाढते. अणूच्या या कंपनक्रियेचे पुंजीकरण केले ( म्हणजे त्याची ऊर्जा आहे असे मानले), तर घन पदार्थाच्या विशिष्ट उष्णता करिता खालील सूत्र मिळते.

या सूत्रामुळे प्रयोगाद्वारे मिळालेल्या अनेक गोंष्टीचा खुलासा मिळतो. ही कल्पना पी.जे. डब्ल्यू. डेबाय (१८८४–१९६६) यांनी पुढे विस्तारित केली. घन पदार्थामधील सर्व अणूंना कंपन कंप्रता एकच नसून त्यांना एका ठराविक मर्यादेतील भिन्न कंप्रता असू शकतात, असे गृहीत धरून त्यांनी अतिनीच तापमानाकरिता विशिष्ट उष्णता प्रमाणे चलन का दाखविते याचा खुलासा केला. [→ उष्णता)

आणवीय संरचना : नील्स बोर (१८८५–१९६२) यांनी आणवीय संरचना (विशेषतः होयड्रोजन अणूची) आणि त्यापासून मिळणाऱ्या उत्सर्जन वर्णपट रेषांचे केलेले पुंज सिद्धांतीय विश्लेषण हा एक फार महत्त्वाचा टप्पा ठरतो. बोर सिद्धांतामध्ये एक मध्यवर्ती धन विद्युत्‌ भारित अणुकेंद्राभोवती इलेक्ट्रॉन वर्तुळकार मार्गकक्षेत फिरतो असे मानले आहे, पण त्याच्या गतीवर काही स्वेच्छ अटी घालव्यात लागतात. या अटी पुढीलप्रमाणे आहेत : (१) अणूमधील इलेक्ट्रॉंनांना काही ठराविक कक्षाच अनुज्ञात असतात. या कक्षांकरिता इलेक्ट्रॉनाच्या कोनीय संवेगाचे (G) पुंजीकरण खालील सूत्रानुसार करवे लागते.

या कक्षांमध्येच इलेक्ट्रॉन फिरत असला, तर तो विद्युत्‌ चुबंकीय प्रारण उत्सर्जित करित नाही. रूढ सिद्धांताप्रमाणे इलेक्ट्रॉनाला प्रवेगी गती मिळाली की, त्याच्यापासून ऊर्जा उत्सर्जित व्हावयास पाहिजे. या कारणाकरिता या कक्षांना स्थिर असे म्हटले जाते. या अटीमुळे इलेक्ट्रॉनला या ठराविक ऊर्जा पातळ्याच उपलब्ध होतात. या पातळ्यांची ऊर्जा.

या सूत्राने मिळते. येथे इलेक्ट्रॉनावरील विद्युत्‌ भार इलेक्ट्रॉनाचे द्रव्यमान आहे. (२) सामान्यापणे इलेक्ट्रॉन सगळ्यात कमी ऊर्जा पातळीत असतो. त्याला जर बाहेरून ऊर्जा दिली, तर तो ती ठराविक पुंजातच स्वीकारू शकतो, उदा., इत्यादी. ही अट प्लांक यांच्या अटीच्या सद्दश आहे. समजा जर त्याला एवढी ऊर्जा पुरविली, तर तो तिचे शोषण करून, या मूळकक्षेतून उडी मारून या जास्त ऊर्जेच्या कक्षेत जातो. कोणतीही प्रणाली नेहमी किमान ऊर्जा स्थितीत जाण्याचा प्रयत्न करते. या सिद्धातानुसार  मधील इलेक्ट्रॉन उस्फूर्तपणे (या कालखंडात)  कडे परत उडी मारतो. या दोन कक्षांतील ऊर्जा फरक प्रारण पुंजाच्या स्वरूपात उत्सर्जित केला जातो.

यावरून असे दिसते की, इलेक्ट्रॉनाची कक्षेतील भ्रमण कंप्रता व उत्सर्जित प्रकाश कंप्रता या एकमेकीपासुन भिन्न आहेत. प्लांक यांच्या मूळ सिद्धांतात इलेक्ट्रॉनाची आंदोलन कंप्रता एव ते उत्सर्जित करत असलेल्या प्रारणाची कंप्रता एक मानल्या होत्या.

जे. जे. बाल्मर यांच्या हायड्रोजनाच्या वर्णपट रेषा श्रेणीच्या कंप्रता खालील अनुभवजन्य सूत्राने मिळतात हे माहीत होते.

R = रिडबर्ग स्थिरांक (जे. आर‌्. रिडबर्ग यांच्या नावाने ओळखण्यात येणारा). बोर सिद्धांताप्रमाणे वरील सूत्राचा खुलासा मिळाला. त्याचबरोबर

अशा रीतीने गणन केलेले R चे मूल्य मूळ रिडबर्ग  स्थिरांकाशी अचूक रीतीने जूळते असे आढळले.

डब्ल्यू. विल्सन व आर्नोल्ट झोमरफेल्ड यांनी असे दाखविले की, बोर यांनी वापरलेली पुंजीकरणाची अट ही जास्त सर्वव्यापी सिद्धांताचे एक विवक्षित उदाहरण आहे. त्यांच्या कल्पनेप्रमाणे एखाद्या प्रणालीत आदी स्थाननिर्देशिक असून त्यांस आवर्ती चलन असेल व त्यांच्या तदनुरुप संवेग निर्देशिक असे असतील, तर सर्वसामान्य पुंजीकरण नियम

असा असतो. यामध्ये h= प्लांक स्थिरांक आणि या स्थाननिर्देशकाने दर्शविलेल्या गतीने नियमन करणारा पुंजांक. या कल्पनेनुसार इलेक्ट्रॉनाच्या कक्षा वर्तुळाकारच असल्या पाहीजेत असे नसून त्या विवृत्ताकार (लंबगोलाकार) असू शकतात. या प्रकारच्या कक्षांकरिता इलेक्ट्रॉनाच्या दोन स्थाननिर्देशकांनुसार त्याच्या गतीकरिता दोन पुंजीकरण अटी व दोन पुंजांक लावतात. इलेक्ट्रॉन कक्षेची अवकाशातील दिक‌्स्थिती निश्चित करण्याकरिता आणखी एक पुंजांक लागतो. जर अणूवर बाहेरून विद्युत्‌ क्षेत्र किंवा चुंबकीय क्षेत्र लावले, तर त्याची आवश्यकता असते. असे क्षेत्र नसेल, तर हे पुंजीकरण करावे लागत नाही.

बोर यांच्या मूळ सिद्धांताप्रमाणे शक्य असलेल्या अनेक वर्णपट रेषा प्रत्यक्षात आढळत नाहीत. याचे विवेचन करण्याकरिता काही निवड नियम  गृहीत धरावे लागतात. इलेक्ट्रॉन संक्रमणामुळे मिळणाऱ्या  निरनिरळ्या वर्णपट रेषांची तीव्रता किती असेल याविषयीचीही काही माहिती या सिद्धातापासून मिळत नाही. उदा., हायड्रोजनच्या बाल्मर श्रेणीमधील पहिली रेषा (तरंगलांबी ६५६३ ). हिची तीव्रता सर्वांत जास्त असते व त्यानंतर अनुक्रमे येणाऱ्या रेषांची तीव्रता अखंडीतपणे कमी होत जाते. याचा खुलासा बोर सिद्धांपासून मिळत नाही. ही न्यूनता काढून टाकण्याकरिता बोर यांनी अनुरूपता (संगतता) तत्त्व पुढे मांडले. अणुकेंद्रापासून बऱ्याच दूर असलेल्या ऊर्जा पातळ्यामधील संक्रमणाकरिता पुंज व रूढ सिद्धांतानुसार मिळणाऱ्या वर्णपट रेषांच्या कंप्रता जवळजवळ सारख्या असतात. या गोष्टीचा उपयोग करून बोर यांनी असे मानले की, या कंप्रतांच्या सापेक्ष तीव्रतेची जी मूल्ये रूढ सिद्धांतानुसार मिळतात तीच मूल्ये पुंज सिद्धांताकरिता यथार्थ मानता येतात. या अनुरूपतेच्या कल्पनेचा विस्तार करून ही यथार्थता सर्वच ऊर्जा पातळ्यांकरीता लागू पडते असे अनुरूपता तत्त्वात गृहीत धरले जाते. या तत्त्वाचा उपयोग करून निवड नियमांचे समर्थन करणे किंवा वर्णपट रेषांच्या तीव्रतेविषयी थोडे फार समाधानकारक रीत्या ज्ञान मिळविणे शक्य होते.

पुंज सिद्धांतामधील कल्पनांचा उपयोग करून व परिभ्रमण गती असणाऱ्या द्वी-आणवीय उत्सर्जन वर्णपटाचे [→ वर्णपटविज्ञान ) बऱ्याच प्रमाणात विवेचन करता आले. या रेणूच्या कंपन क्रियेकरिता प्लांक हरात्मक आंदोलन, तर परिभ्रमण गतीकरिता घूर्णक प्रतिकृती म्हणून गृहीत धरल्या जातात [→ पुंजयामिकी]. त्यांच्या ऊर्जा पातळ्या काढण्याकरिता योग्य अशा पुंजीकरण अटींचा उपयोग करण्यात येतो.

वर निर्देश केलेल्या गतिच्या व्यतिरिक्त इलेक्ट्रॉनांना परिवलन गती (स्वतःभोवती फिरण्याची गती) असते, असी सूचना जी. ई. ऊलेनबेक व एस‌्. ए. गाउडश्मिट यांनी केली. त्यामुळे परिवलन कोनीय संवेगनाचे पुंजीकरण करणे आवश्यक ठरते. त्यानुसार या संवेगाला फक्त   एवढेच मूल्ये असू शकते असे दिसते. हे मूल्य कोणत्याही परिस्थितीत बदल पावत नाही. त्यांचे सैद्धांतिक समर्थन डब्ल्यू. पाउली यांनी पुंजयामिकीचा उपयोग करून नंतर दिले. पुंजीकरण नियमाप्रमाणे परिवलन गतीचा कोनीय संवेग सदिश एका निश्चित दिशेला समांतर किंवा प्रतिसमांतर (समांतर पण विरुद्ध दिशेत) या दोनच अवस्थांत राहू शकतो अथवा या पुंजांकाला   ही दोनच मूल्ये असू शकतात. त्यामुळे अणूमधील इलेक्ट्रॉनांकरिता एकंदर चार पुंजांक लागतात हे स्पष्ट होते. येथे हे मात्र लक्षात ठेवले पाहिजे की, इलेक्ट्रॉनाला परिवलन गतीमुळे कोनीय संवेग असे जरी मानावे लागले, तरी त्याचा कोनीय वेग किती आहे या प्रश्नाला उत्तर नाही. इलेक्ट्रॉनीय परिवलन लक्षात घेता नियमविरुद्ध झीमान परिणाम [→ अणूकेंद्रीय व आणवीय परिबले] काही मुलद्रव्यांच्या विशेषतः, क्षार-अल्कली-मूलद्रव्याच्या (उदा., सोडियम, पोटॅशियम इ.) उत्सर्जनक वर्णपट श्रेणीतील रेषांमधील द्विक (वर्णपट रेषांची संगत जोडी) अथवा सूक्ष्म संरचना (वर्णपट रेषांचे विभाजन होऊन दोन अगर अधिक अगदी जवळजवळ असणारे घटक मिळणे) याबद्दलचा सैद्धांतिक खुलासा मिळतो.

मूलद्रव्यांच्या ⇨ आवर्त सारणीमध्ये (इलेक्ट्रॉनीय संरचनेनुसार केलेल्या मुलद्रव्यांच्या कोष्टकरूप मांडणामध्ये) हायड्रोजनानंतर क्रमांकाने येणाऱ्या अणूंमध्ये इलेक्ट्रॉनांची संख्या सारखीच वाढत असते. हायड्रोजनामध्ये एक इलेक्ट्रॉन, तर हीलियमामध्ये २, लिथियमध्ये ३, बेरिलियमामध्ये ४ इलेक्ट्रॉन याप्रमाणे वाढ होत जाते. अणूच्या भौतिकीय व रासायनिक गुणधर्मांचे विवरण करण्याकरिता हे इलेक्ट्रॉन एकाच कक्षेत नसून ते निरनिरळ्या कवचांत अणूकेद्रांभोवती वितरित झालेले असतात, असे समजले जाते. अणूकेंद्रापासूनच्या सगळ्यांत जवळच्या  म्हणजे पहिल्या कवचात २ इलेक्ट्रॉन, तर त्यानंतरच्या दुसऱ्या कवचात ८ इलेक्ट्रॉन, त्यानंतरच्या तिसऱ्या व चौथ्या कवचांत अनुक्रमे ८ व १८ इलेक्ट्रॉन असतात आणि पाचव्या कवचातही इलेक्ट्रॉनांची संख्या १८ असते, असे गृहीत धरावे लागते.या विशिष्ट तऱ्हेने कवचभरण का होते याचे उत्तर बोर सिद्धातापासून मिळत नव्हते. इलेक्ट्रॉनीय परिवलन पुंजयामिकीयांचा उपयोग करून पाउली यांनी याचे विवरण केले. त्यांनी असे दाखविले की, अणूमध्ये कोणत्याही दोन इलेक्ट्रॉनांना एकरूप असे चार पुंजांक असू शकत नाहीत, या तत्त्वाला पाउली विवर्जन तत्त्व असे म्हणतात. याचे समर्थन पुंजयामिकीनुसारच करता येते. [→ अणू व आणवीय संरचना].

फोटॉन सिद्धांत : वरील विवेचनात पुंज सिद्धांताप्रमाणे प्रकाशीय प्रारणाचे फोटॉन या कणाच्या स्वरूपात उत्सर्जन, शोषण व प्रसारण होते असा उल्लेख आला आहे. यावरून अशी शंका येण्याचा संभव आहे की, प्रकाश म्हणजे विद्युत्‌ चुंबकीय तरंग आहेत. या पूर्वी रूढ असलेल्या कल्पनेचा त्याग केला आहे की काय? याचा खुलासा करण्याकरिता फोटॉन सिद्धांतात काय नक्की गृहीत धरले आहे याचा गोषवारा पुढे दिलेला आहे : (१) प्रकाश म्हणजे विद्युत्‌ चुंबकीय तरंगपुंज आहेत, यांना फोटॉन म्हणतात. (२) प्रकाशाचे उत्सर्जन अथवा शोषण फोटॉनच्या पूर्णांक पटीतच होते. त्याची निर्मिती अथवा नाश पूर्णांक पटीतच होतो. (३) फोटॉनाची ऊर्जा

तर संवेग असतो. फोटॉन कणाच्या गतिराशी E व p आणि त्याच्या तरंगराशी v व यांमधील संबंध वरील समीकरणांनी स्पष्ट केला जातो. (४) फोटॉन अवकाशात प्रसारण पावतात तेव्हा ते v कंप्रता असलेल्या विद्युत्‌ चुंबकीय तरंगाप्रमाणे व्यतिकरण, विवर्तन व ध्रुवीकरण [→ प्रकाशकी] हे आविष्कार दाखवितात.

याचा अर्थ असा होतो की, फोटॉन सिद्धांत हा प्रकाश तरंग सिद्धांताला पर्यायी नसून तो त्याला पुरवणीदाखल आहे, असे समजले पाहिजे. इलेक्ट्रॉनासारख्या कणाच्या बाबतीतसुद्धा या दोन्ही कल्पनांचा उपयोग करावा लागतो, असे नंतरच्या प्रयोगाने सूचित केले. सी. जे. डेव्हिसन, एल्‌. एच. गर्मर यांनी १९२७ साली इलेक्ट्रॉनचे धातुस्फटिकाद्वारे तरंगाप्रमाणे विवर्तन होते असे दाखविले.

या दोन्ही कल्पनांचा समन्वय पुंजयामिकी अथवा तरंगयामिकी सिद्धांतात केला आहे. एकाच मूलभूत श्रोडिंजर तरंग समीकरणांचा उपयोग करून कणाच्या बाबतीत आढळणाऱ्या या दोन प्रकारच्या आविष्कारांचे संयुक्तिक व सुसंगत असे विवेचन करता येते. त्यापासूनच पुंजीकरण अटी, निवड नियम, वर्णपट रेषांच्या तीव्रता इ. सर्व राशींबद्दल काही निराळी गृहीते न धरता खुलासा मिळतो. वर वर्णन केलेल्या पुंज सिद्धांतानुसार किरणोत्सर्गी (भेदक कण वा किरण बाहेर टाकणाऱ्या) अणुकेंद्रातून आल्फा कणाचे उत्सर्जन प्रोटॉन, न्युट्रॉन, इलेक्ट्रॉन आदि गतिमान कणांचे अणुकेंद्राद्वारे प्रकीर्णन (आघात वा परस्परक्रिया होऊन कणाची दिशा बदलणे) यांसारख्या ज्या आविष्काराचे विवेचन करणे शक्य नव्हते त्यांचे विवेचन नव्या सिद्धांतानुसार करता येते.

पहा : पुंजयामिकी

संदर्भ : 1. Born, M. Atomic Physics, London, 1963.

2. Borowitz, S. Beiser, A. Essetials of Physiscs, Reading, Mass., 1966.

3. Feynmann, R. P. Leightn, R. B. Sands, M. The Feynmann, Leactures on Physics, 3 Vols., Bombay, 1966.

4. Mathews, P. T. Introduction to Quantum Mechanics, New York, 1961.

5. Pauling L. Wilson, E. B. Introduction to Quantum Mechanics, New York, 1935.

6. Sproull, R. l. Modern Physics, New York, 1956.

7. Thewlis, J., Ed, Encyclopaedic Dictionary of Physics, Vol. V, Oxford, 1962.

चिपळोणकर, व. त्रि.

“