पुंजयामिकी : द्रव्य (विशेषत: सूक्ष्मकण) व विद्युत् चुंबकीय प्रारण (तरंगरूपी ऊर्जा) यांचे गुणधर्म, त्यांचे वर्तन व त्यांच्यामधील परस्परक्रियेची मीमांसा पुंजयामिकीत केली जाते. रूढ यामिकी [प्रेरणांची वस्तूंवर होणारी क्रिया व त्यामुळे निर्माण होणारी गती यांसंबंधी रूढ शास्त्र; → यामिकी] व जे. सी. मॅक्सवेल (१८३१–७९) यांच्या विद्युत् चुंबकीय तत्त्वप्रणालीची [→ विद्युत् चुंबकीय प्रारण] जागा पुंजयामिकीने घेतली आहे. आणवीय व त्यापेक्षा सूक्ष्म स्तरावर घडणारे आविष्कार यांचे विशदीकरण करण्याकरिता पुंजयामिकी विशेष यशस्वी ठरली आहे. पुंज सिद्धांत व त्याला कारणीभूत झालेल्या आविष्कारांचा येथे संक्षेपाने उल्लेख केला आहे. याचे सविस्तर विवेचन ‘पुंज सिद्धांत’ या नोंदीत केले आहे.
भौतिकीमध्ये कण व प्रारण यांमधील परस्परक्रियेला विशेष महत्त्व आहे. कोणत्याही एका कणाच्या गतिकीय स्थितीचे वर्णन त्याचे द्रव्यमान, वेग व स्थान या राशींचा उपयोग करून केले जाते. रूढ भौतिकीप्रमाणे कणाची वर्तमान व भविष्यकालातील गती न्यूटन यांच्या नियमांचा वापर करून मिळवता येते. प्रारण (उदा., प्रकाश) हे तरंगाच्या स्वरूपात प्रसारित होते. तरंगलांबी (λ), कंप्रता (एका सेकंदात होणाऱ्या कंपनांची संख्या, ν) व प्रसारणवेग (c) या राशींच्या साहाय्याने प्रारणाचे वर्णन केले जाते. प्रकाशासारख्या विद्युत् चुंबकीय प्रारणाचे (अथवा तरंगांचे) विवेचन मॅक्सवेल यांनी प्रथम सूत्रबद्ध केलेल्या आठ अवकल समीकरणांच्या साहाय्याने करता येते. एच्. ए. लोरेन्ट्स (१८५३–१९२८) यांनी दाखविल्याप्रमाणे इलेक्ट्रॉनासारख्या विद्युत् भार असलेल्या कणाच्या आंदोलनामुळे विद्युत् चुंबकीय तरंग अथवा प्रारण उत्सर्जित केले जाते. याउलट प्रारण पदार्थावर पडले असता त्यापैकी काही ऊर्जेचे शोषण होते. इलेक्ट्रॉनासारख्या द्रव्यकणावर विद्युत् अथवा चुंबकीय क्षेत्रे लावली असता त्याच्या गतीत होणाऱ्या बदलाचे न्यूटन यांच्या रूढ गतिनियमानुसार स्पष्टीकरण करता येते. आधुनिक काळात प्रारण व कण यांच्या परस्परक्रियेविषयी असे काही आविष्कार सापडले की, ज्यांचे विशदीकरण न्यूटन व मॅक्सवेल-लोरेन्ट्स यांच्या रूढ मीमांसेप्रमाणे करणे शक्य होत नव्हते. ⇨ कृष्ण पदार्थात हरात्मक आंदोलक (ज्यांच्या समतोलाचा भंग झाला असता स्थानांतराशी सम प्रमाणात असणाऱ्या एका पुन:स्थापक प्रेरणेमुळे ज्यांना आंदोलक गती प्राप्त होते अशा भौतिक प्रणाली) असतात आणि ते अवकाशात प्रारण उत्सर्जित करतात व त्यांवर पडणाऱ्या सर्व प्रारणाचे शोषण करतात. आंदोलकाची ऊर्जा nhν एवढीच असू शकते (n = पूर्णांक, h = प्लांक स्थिरांक, ν = कंप्रता) व हा आंदोलक ऊर्जेचे उत्सर्जन hν या पुंजाच्या (क्वांटमच्या) पटीतच करू शकतो असे माक्स प्लांक (१८५८–१९४७) यांनी दाखविले. प्रकाशविद्युत् परिणामात [→ प्रकाशविद्युत्] धातूमधील इलेक्ट्रॉनाबरोबर जेव्हा प्रकाश परस्परक्रिया करतो तेव्हा अल्बर्ट आइन्स्टाइन (१८७९–१९५५) यांच्या मीमांसेनुसार तो इलेक्ट्रॉनास hν एवढी ऊर्जा एकाच क्षणी पुरवू शकतो. यावरून साधारण तरंगाप्रमाणे प्रकाशामधील ऊर्जा अवकाशात पसरत जात नसून ती एकत्रित स्वरूपातच राहते, असे सिद्ध होते. ⇨ कॉम्पटन परिणामामध्ये प्रकाश व इलेक्ट्रॉन यांमध्ये परस्पर आघात होतो त्या वेळी प्रकाश hν ऊर्जा व hν / c संवेग (म्हणजे द्रव्यमान × वेग ही राशी) असणाऱ्या कणाप्रमाणे वागतो असे आढळते. नील्स बोर (१८८५–१९६२) यांच्या मीमांसेप्रमाणे हायड्रोजन अणूमधील इलेक्ट्रॉन काही ठराविक ऊर्जेचाच स्वीकार करू शकतो. अशा प्रकारे ऊर्जा स्वीकारून उत्तेजित झालेला (E1 ऊर्जेचा) इलेक्ट्रॉन परत आपल्या नीच ऊर्जा पातळीवर (E2) येतो तेव्हा तो मिळालेली ऊर्जा प्रारणाच्या स्वरूपात उत्सर्जित करतो. E1–E2= hν या समीकरणाने या प्रारणाची कंप्रता मिळते. बोर यांनी प्लांक-आइन्स्टाइन अटीचा उपयोग केला व त्याशिवाय इलेक्ट्रॉनाच्या कोनीय संवेगाचे (द्रव्यमान, परिभ्रमण अक्षापासूनच्या अंतराचा वर्ग व कोनीय वेग यांच्या गुणाकाराने मिळणाऱ्या राशीचे) पुंजीकरण केले (म्हणजे त्याला पृथक् मूल्येच असू शकतात असे गृहीत धरले). या सर्व अटी अथवा निर्बंध रूढ गणितीय रीतीवर लादले गेले होते. रूढीय गणन आणि या अटी यांमधील सैद्धांतिक संबंध स्पष्ट होत नव्हता आणि हे निर्बंध का येतात याचेही स्पष्टीकरण मिळत नव्हते. बोर यांच्या मीमांसेमुळे सैद्धांतिक विवेचनात आश्चर्यकारक प्रगती झाली याबद्दल शंका नसली, तरी तीमध्ये काही उणीवा होत्या हे तितकेच स्पष्ट होते. उदा., या मीमांसेप्रमाणे वर्णपट रेषांची तीव्रता, त्यांची सूक्ष्मरचना व द्विआणवीय (ज्यात दोन अणू आहेत अशा) रेणूचा परिभ्रमणीय वर्णपट [→ वर्णपटविज्ञान (रेणवीय वर्णपट)] यांचे विशदीकरण समाधानकारकपणे करता येत नव्हते. ज्या प्रणालीमध्ये अनेक कण आहेत (उदा., हीलियम अणू) त्यांच्या रचनेचे सैजद्धांतिक विश्लेषण करण्याकरिता बोर पद्धती उपयोगी पडत नाही असे आढळते.
यानंतर थोड्याच काळात ल्वी व्हीक्तॉर द ब्रॉग्ली (१८९२ – ) यांनी असे दाखविले की, प्रत्येक गतिमान इलेक्ट्रॉन अथवा द्रव्यकणाबरोबर λ तरंगलांबीचे तरंग (λ = h/p, h = प्लांक स्थिरांक, p = कण संवेग) निगडित असतात. या तरंगामुळे इलेक्ट्रॉन व अणूसारख्या द्रव्यकणांचे प्रकाश-तरंगाप्रमाणे विवर्तन (अडथळ्याच्या कडेवरून जाताना दिशेत बदल होणे) हा आविष्कार मिळू शकतो. सी. जे. डेव्हिसन (१८८१–१९५८) व एल्. एच्. गर्मर (१८९६ – ) यांनी १९२७ मध्ये हा आविष्कार प्रयोगशाळेत इलेक्ट्रॉनाकरिता सिद्ध केला. असेच प्रयोग न्यूट्रॉन, हायड्रोजन अणू यांबाबतीत करण्यात आले आहेत. यावरून एकाच वेळी कण व तरंग ही दोन्ही स्वरूपे या कणांना आहेत असा जर कोणी निष्कर्ष काढला, तर तो चुकीचा ठरेल. वरील प्रयोगांवरून एवढेच दिसते की, कणाचा संवेग व त्याचे अवकाश सहनिर्देशक (एखाद्या संदर्भव्यूहाच्या सापेक्ष अवकाशातील स्थान दर्शविणाऱ्या संख्या) यांमध्ये एक मूलभूत आवर्ती संबंध आहे. असाच आवर्ती संबंध त्याची ऊर्जा व काल यांमध्ये मिळतो. या संबंधाचे स्पष्टीकरण व्हेर्नर हायझेनबेर्क (१९०१–७६) यांच्या ⇨ अनिश्चिततेच्या तत्त्वानुसार करता येते. रूढ भौतिकीप्रमाणे कोणत्याही एका कणाच्या गतिज स्थितीविषयी पूर्ण ज्ञान होण्याकरिता लागणाऱ्या राशी या सर्व एकाच वेळी अचूकतेने मोजता येणे शक्य आहे, असे समजले जात होते. उदा., कणाचे स्थान व त्याचा संवेग या राशी एकाच वेळी मोजण्यात काही अडचण नाही असे मानले होते. या दोन राशींच्या कोणत्याही एका क्षणी मिळालेल्या मूल्यावरून कणाची काही काळानंतर काय स्थिती होईल, हे न्यूटन यांचे नियम वापरून निश्चितपणे वर्तविणे शक्य आहे असा समज होता. हायझेनबेर्क यांच्या तत्त्वाप्रमाणे कोणत्याही एका राशीचे मापन करण्याच्या क्रियेमुळे त्याच्या दुसऱ्या राशीच्या मापनाच्या अचूकतेवर परिणाम होतो. या तत्त्वाप्रमाणे जर एखाद्या कणाचे स्थान निश्चित करण्यामध्ये स्थान सहनिर्देशक q यामध्ये Δq एवढी त्रुटी असेल व त्याच्या संवेगमापनात येणारी त्रुटी Δp असेल, तर यांमध्ये खालील संबंध असतो.
| Δ q . Δ p ≥ h / 2π (h = प्लांक स्थिरांक) | … | … | (१) |
| Δ E . Δ t ≥ h/2π | … | … | … | (२) |
या सूत्राने मिळतो. अशाच प्रकारचा परस्परसंबंध कणाच्या इतर निरीक्ष्यांत राहतो असे दाखविता येते. वरील तत्त्वाचे असे स्पष्टीकरण करता येते की, कोणत्याही कणाचे अथवा प्रणालीचे निरीक्षण करावयाचे असल्यास त्याच्या गतिज स्थितीत विक्षोभ निर्माण करावा लागतोच आणि यामुळे प्रत्येक निरीक्षण क्रियेमुळे त्याच्या मूळ स्थितीत निश्चितपणे बदल होतो. निरीक्ष्या कण जर सूक्ष्म असेल, तर अशा रीतीने होणाऱ्या बदलाचे प्रमाण अर्थातच जास्त होते. यामुळे द ब्रॉग्ली तरंगामुळे मिळणारे परिणाम अणू व इलेक्ट्रॉन यांसारख्या सूक्ष्मकणांच्या बाबतीतच महत्त्वाचे ठरतात. हेच विवेचन निराळया शब्दांत करावयाचे असल्यास असे म्हणता येईल की, रूढ भौतिकीप्रमाणे अनेक कणांचे एकाच वेळी निरीक्षण करून मिळणारी माहिती ज्याप्रमाणे सांख्यिकीय स्वरूपाची असते त्याप्रमाणेच आधुनिक पुंजयामिकीनुसार एका कणाच्या बद्दलची माहितीसुद्धा निश्चित स्वरूपाची नसून ती सांख्यिकीय स्वरूपाचीच असते. आणवीय आकारमानाचे सर्व कण सतत इतस्तत: अशी हालचाल करतात असे समजण्यास जागा आहे. यामुळे कोणत्याही एका सांत कालखंडात असा कण कोणत्या स्थानी असेल असे निश्चितपणे सांगता येत नाही. कणाच्या या पुंजीय हालचालीविषयी कोणत्याही प्रकारचे अनुमान करता येत नाही. पुंजयामिकीचा उपयोग करून पुरेसा मोठा कालखंड घेतला असता कणाचे सरासरी स्थान काय असू शकेल, याविषयी मात्र अंदाज बांधता येतो. गणितीय रीत्या मिळालेल्या माहितीची प्रत्यक्षात तुलना करावयाची असेल, तर अनेक कणांचे एकाच वेळी निरीक्षण करून किंवा एका कणाचे निरनिराळ्या वेळी निरीक्षण करून प्रयोगाद्वारे माहिती मिळवावी लागेल.
 उदाहरणादाखल असे समजू की, एका प्रणालीत १० कण असून ते एका उद्गम बिंदूपासून निरनिराळ्या अंतरावर पसरले आहेत. निरीक्षण करून पाहिले असता समजा आपणास असे आढळते की, १० पैकी ५ कण बिंदूपासून ३ सेंमी. अंतरावर आहेत, २ कण ४ सेंमी., तर ३ कण ५ सेंमी. अंतरावर आहेत. आता प्रणालीत एकच कण आहे असे समजले, तर उद्गम बिंदूपासून ३ सेंमी. अंतरावर असण्याची त्याची संभाव्यता ५/१० एवढी राहील. ही माहिती सांख्यिकीय स्वरूपाची आहे असे म्हटले जाते. कारण तीत आपणास निश्चित उत्तर न मिळता संभाव्यतेचे मूल्य फक्त मिळते. अनेक कणांचे निरीक्षण करून मिळालेली माहिती अशा प्रकारे सांख्यिकीय स्वरूपाची असते हे लक्षात येते.
उदाहरणादाखल असे समजू की, एका प्रणालीत १० कण असून ते एका उद्गम बिंदूपासून निरनिराळ्या अंतरावर पसरले आहेत. निरीक्षण करून पाहिले असता समजा आपणास असे आढळते की, १० पैकी ५ कण बिंदूपासून ३ सेंमी. अंतरावर आहेत, २ कण ४ सेंमी., तर ३ कण ५ सेंमी. अंतरावर आहेत. आता प्रणालीत एकच कण आहे असे समजले, तर उद्गम बिंदूपासून ३ सेंमी. अंतरावर असण्याची त्याची संभाव्यता ५/१० एवढी राहील. ही माहिती सांख्यिकीय स्वरूपाची आहे असे म्हटले जाते. कारण तीत आपणास निश्चित उत्तर न मिळता संभाव्यतेचे मूल्य फक्त मिळते. अनेक कणांचे निरीक्षण करून मिळालेली माहिती अशा प्रकारे सांख्यिकीय स्वरूपाची असते हे लक्षात येते.
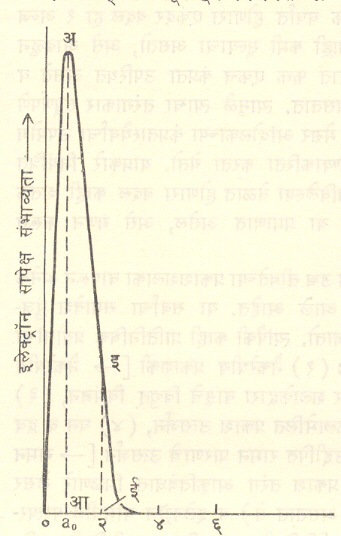
याचे स्पष्टीकरण आ. १ वरून मिळते. आकृतीमध्ये हायड्रोजन अणूमधील इलेक्ट्रॉन अणुकेंद्रापासून निरनिराळ्या अरीय अंतरावर असण्याची पुंजयामिकीप्रमाणे मिळणारी सापेक्ष संभाव्यता दाखविली आहे. येथे बोर यांच्या पहिल्या कक्षेतील इलेक्ट्रॉन ao अंतरावर असतो, असे गृहीत धरले आहे. या ठिकाणी इलेक्ट्रॉन सापडण्याची संभाव्यता (अआ) महत्तम आहे. केंद्रापासून २Ǻ अंतरावर (Ǻ = १०-८ सेमी.) असण्याची संभाव्यता कमी असून ती इई एवढी आहे, ही माहिती सांख्यिकीय स्वरूपाची आहे. याचे विशदीकरण असे करता येते. एकरूप अशा अनेक हायड्रोजन अणूंचे निरीक्षण करून त्यांतील इलेक्ट्रॉनांचे केंद्रापासूनचे अंतर मोजले, तर या सर्व प्रदत्तावरून (गोळा केलेल्या माहितीवरून) संभाव्यता मिळते. पुंजयामिकीच्या साहाय्याने या संभाव्यतेचेच सैद्धांतिक रीत्या मूल्यमापन करता येते. यामुळे एका ठराविक क्षणी व स्थानी नक्की काय होईल, हे पुंजयामिकीचा उपयोग करून वर्तविता येत नाही. ज्या निरनिराळ्या घटना घडणे शक्य असते त्यांच्या सापेक्ष संभाव्यता काय राहतील याचे मूल्यमापन या यामिकीप्रमाणे करता येते. द ब्रॉग्ली यांची परिकल्पना याच परिस्थितीचा परिपोष आहे. वर उल्लेख केलेल्या सर्व गोष्टींवरून असा निष्कर्ष निघतो की, इलेक्ट्रॉन, अणू इत्यादींसारख्या सूक्ष्म द्रव्यकणांकरिता व त्यांच्या प्रारणाबरोबर होणाऱ्या परस्परक्रियेचे वर्णन करण्याकरिता रूढ भौतिकीशास्त्र अपुरे पडते.
या सर्व गोष्टींचे एकत्रीकरण पुंजयामिकीमध्ये अथवा तरंगयामिकीमध्ये सुसंबद्धरीत्या करण्यात आले आहे. हायझेनबेर्क , ई. श्रोडिंजर (१८८७–१९६१) व पी. ए.एम्. डिरॅक (१९०२ – ) या शास्त्रज्ञांनी पुंजयामिकीस तिचे सध्याचे निश्चित व सुविकसित स्वरूप दिले आहे. या यामिकीच्या साहाय्याने अणूरेणूंची वर्तणूक, वर्णपट रेषांची सूक्ष्म रचना, आल्फा व बीटा कणांचे अणूकेंद्रातून उत्सर्जन [→ किरणोत्सर्ग], इलेक्ट्रॉन-पॉझिट्रॉन यांची निर्मिती यांसारख्या आविष्कारांचे यशस्वीरित्या स्पष्टीकरण होऊ शकते. त्याचप्रमाणे ⇨ घन अवस्था भौतिकी, रासायनिक बंध [→ रासायनिक संरचना संयुजा पुंज रसायनशास्त्र] वगैरे विषयांतील अनेक बाबींचा पुंजयामिकीमुळे उलगडा होतो.
पुंजयामिकीचे तीन ढोबळ विभाग मानता येतात (१) श्रोडिंजर-हायझेनबेर्क यांची असापेक्षीय [जिच्यात सापेक्षता सिद्धांताचा उपयोग केला जात नाही अशी→ सापेक्षता सिद्धांत] मीमांसा. हीमध्ये कणाची निर्मिती अथवा विनाश होत नाही व यामध्ये विचारात घेतलेल्या कणाचा वेग प्रकाशवेगापेशा बराच कमी आहे, असे गृहीत धरलेले असते. कणाची परिवलन गती व तीमुळे मिळणारे चुंबकीय परिणाम यांचा विचार या प्रणालीत समाधानकारकपणे करता येत नाही. (२) डिरॅक यांनी सूत्रबद्ध केलेली सापेक्षीय मीमांसा . हीमध्ये कणाचा वेग प्रकाशवेगाशी समतुल्य असतो, असे मानलेले असते. या मीमांसेप्रमाणे कणाची (इलेक्ट्रॉनाची) परिवलन गती व तीमुळे उद्भवणारे चुंबकीय परिणाम यांचे विवेचन करणे सुलभ होते. इलेक्ट्रॉन-पॉझिट्रॉन जोडीच्या निर्मितीचेही विवेचन या तत्त्वप्रणालीनुसार करता येते. (३) पुंज क्षेत्र प्रणाली . अणूकेंद्र व त्यामधील आणि इतर मूलभूत कणांकरिता [→ मूलकण] ही मीमांसा उपयुक्त ठरते. हीमध्ये परस्परक्रिया करणाऱ्या कणांतील अंतर अतिशय कमी असते. कणाची निर्मिती व नाश या क्रियेचे वर्णन या प्रणालीद्वारे समाधानकारक रीत्या करता येते. ही प्रणाली ज्याचे शून्यगति -द्रव्यमान शून्य आहे (उदा., न्यूट्रिनो, फोटॉन) अथवा अशून्य आहे (उदा., प्रोटॉन , न्यूट्रॉन) अशा दोन्ही प्रकारच्या कणांकरिता वापरता येते [→ पुंज क्षेत्र सिद्धांत ].
श्रोडिंजर-हायझेनबेर्क असापेक्षीय पुंजयामिकी : या पद्धतीत दोन गणितीय रीती उपलब्ध आहेत : (१) श्रोडिंजर यांची अवकल तरंग समीकरणावर [→ अवकल समीकरणे] आधारलेली मीमांसा व (२) हायझेनबेर्क यांनी आव्यूहाचा [→ आव्यूह सिद्धांत] उपयोग करून मांडलेली मीमांसा. विशिष्ट प्रश्नाचा निर्वाह (उत्तर) मिळविण्याकरिता काही वेळा पहिली रीत सोपी ठरते, तर काही कार्याकरिता दुसरी रीत सुलभ होते. या दोन्ही रीती सैद्धांतिक दृष्ट्या समतुल्य आहे असे दाखविले गेले असल्यामुळे त्यांपैकी कोणत्याही रीतीचा उपयोग करून मिळणारे निर्वाह एकरूप असणार हे उघड आहे. सामान्यपणे अवकल पद्धती समजण्यास जास्त सोपी असल्यामुळे , पुढील बहुतेक सर्व विवेचन याच पद्धतीच्या अनुषंगाने करण्यात आले आहे. या ठिकाणी एक सर्वसामान्य स्पष्टीकरण करणे इष्ट आहे. कोणत्याही भौतिकीय आविष्काराचे विशदीकरण करण्याकरिता एक विशिष्ट प्रतिमान (मॉडेल) गृहीत धरले जाते., त्यामुळे त्यापासून मिळणाऱ्या स्पष्टीकरणास निरपेक्ष सार्थकता असत नाही. म्हणजे हे स्पष्टीकरण अंतिम सत्य दर्शविते असे मानण्याचे कारण नाही. विवेचनाकरिता प्रतिमान गृहीत धरल्यामुळे त्यावर काही मर्यादा पडणे स्वाभाविकच असते. कारण प्रत्यक्ष प्रणाली व तीकरिता गृहीत धरलेले प्रतिमान यांमध्ये संपूर्ण साधर्म्य कधीच मिळणार नाही, हे स्पष्ट आहे. पुंजयामिकी अणू-रेणू यांसारख्या सूक्ष्मकणांचे गुणधर्म आणि हे कण व प्रारण यांमधील परस्परक्रियेचे वर्णन करण्याकरिता आवश्यक ठरते. कणाचे आकारमान वाढवीत गेल्यास आणि अशा मोठ्या आकारमानाच्या कणाच्या गतीचे वर्णन करण्याकरिता पुंजयामिकीची व्याप्ती वाढवून उपयोग केला, तर त्यापासून मिळणारे निष्कर्ष रूढ यामिकीचा उपयोग केला असता मिळणाऱ्या निष्कर्षाशी सुसंगत असले पाहिजेत, हेही स्पष्ट आहे. कारण सर्वसामान्य द्रव्यकणांकरीता रूढ भौतिकीशास्त्राची यथार्थता असंख्य प्रयोगांद्वारे अगोदरच प्रस्थापित झालेली आहे.
पुंजयामिकीची मूलभूत गृहीते : श्रोडिंजर समीकरण : विवेचनाच्या सोईकरिता येथे X हा एकच स्थल सहनिर्देशक व t हा काल सहर्निर्देशक असलेल्या प्रणालीचा विचार केला आहे.
(१) द्रव्यमान m असलेल्या प्रत्येक कणाकरिता एक Χ तरंग फलन (तरंगाशी संबंधित असलेल्या चल राशींमधील गणितीय संबंध) असते. हे गृहीत द ब्रॉग्ली यांच्या परिकल्पनेबरोबर समतुल्य आहे.
(२) दुसऱ्या गृहीतावरून Χ हे तरंग फलन पूर्तता करीत असलेल्या अवकल समीकरणाविषयी माहिती मिळते. ज्या कणाकरिता रूढ भौतिकीप्रमाणे स्थितिज ऊर्जा V(x) एवढी असून संपर्ण ऊर्जा E आहे, त्याकरिता
| – | h2 | . | d2 Χ | + V(x) Χ = E Χ | … | … | (३) | |
| 8 π2m | dx2 |
असे काल-निरवलंबी श्रोडिंजर समीकरण मिळते. हे समीकरण मिळते. हे समीकरण सूक्ष्म कणाकरिता न्यूटन यांच्या F=m.a (F=प्रेरणा, m=द्रव्यमान व a=प्रवेग) या सूत्राचे स्थान घेते.
श्रोडिंजर समीकरण मिळविण्याकरिता एक पर्यायी पद्धत आहे. यामध्ये न्यूटन यामिकीनुसार मिळणारे हॅमिल्टोनीयन समीकरण (डब्ल्यू. आर्. हॅमिल्टन या गणितज्ञांच्या नावाने ओळखण्यात येणारे समीकरण) प्रथम मांडले जाते. यामध्ये
| H(px, X) =K (pX)+V(x) =E | … | … | (४) |
येथे H = हॅमिल्टोनीयन (फलन), Px = कणाचा संवेग, K = कणाची गतिज ऊर्जा, E = कणाची संपूर्ण ऊर्जा आणि V(x) = कणाची स्थितिज ऊर्जा. वरील समीकरणात
| Px= | h | . | ∂ | (येथे i = | √ | ) | |||
| 2 πi | ∂ x | 1 |
| म्हणजे | K=- | h2 | . | ∂2 | आणि | H=- | H | ∂ | |||
| 4π2 | ∂ x2 | 2 πi | ∂ t |
पुंजयामिकीमध्ये ‘h’ या स्थिरांकाऐवजी h=h/2π हा डिरॅक स्थिरांक वापरणे लिहिण्याच्या दृष्टीने सोयीचे पडते.h वापरला असता वरील समीकरणे
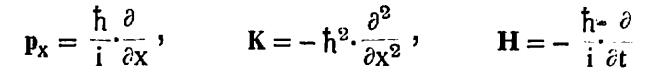
ही रूपे धारण करतात. हे कारक वापरून त्यांची वर क्रिया केली जाते. ही पद्धत वापरली असता त्यापासून श्रोंडिजर समीकरण अचूकपणे मिळते, हीच गोष्ट या पद्धतीच्या समर्थनार्थ देता येते. वरील कारकांचा उपयोग केला असता प्रत्यक्षात समी. (३) पेक्षा जास्त व्याप्ती असलेले समीकरण मिळते. अनेक भौतिकीय प्रश्नांमध्ये V या स्थितिज ऊर्जेचे मूल्य फक्त स्थान सहनिर्देशकावरच अवलंबून असते ते कालाप्रमाणे बदलत नाही. यामुळे श्रोडिंजर फलन
| Χ(x, t) = ψ X (X). ψ t (t) |
या स्वरूपात मांडणे शक्य होते. यामध्ये ψX फक्त x बरोबर, तर ψ t फक्त t चलन दाखविते. यावर कारकांची क्रिया केली असता पुढील दोन स्वतंत्र समीकरणे मिळतात.

यांपैकी पहीले समीकरण बंदीस्त कणाकरीता तर दुसरे मुक्त कणाकरिता लागू पडते, असे दाखविता त्यामुळे समी. (५) अणूमधील स्थायी ऊर्जा पातळ्या काढण्याकरिता उपयोगी पडते, पुंजयामिकीचे विशदीकरण मुख्यतः अशाच प्रकारच्या उदाहरणाच्या साहाय्याने केले असल्यामुळे या पुढील भागात समीस (५) याचाच उपयोग केला आहे. लेखनाच्या सुलभतेकरिता या भागात ψ X बद्दल ψ t हे चिन्ह सर्रास वापरले आहे.
ज्याप्रमाणे न्यूटन यांचे गतिनियम दुसऱ्या अधिक मूलभूत अशा नियमांपासून किंवा गृहीतांपासून मिळवता येत नाहीत त्याप्रमाणेच श्रोंडिंजर यांच्या समीकरणाला उपपत्ती देता येत नाही. याउलट सी. ए. कुलंब यांचा नियम प्रयोगाने मिळालेल्या निष्कर्षांवर आधारित आहे. त्याप्रमाणे श्रोंडिंजर समीकरण कोणत्याही प्रयोगान्ती मिळालेल्या निष्कर्षावर आधारित नाही. या समीकरणाचा उपयोग करून मिळणारे निष्कर्ष हे प्रयोगाने यथार्थ आहेत असे दाखविता येते व याच रीतीने या तत्त्वप्रणालीची यथार्थता सिद्ध होते, असे म्हणता येते. वरील समीकरणावरून हे लक्षात येईल की, या मीमांसेमध्ये संवेग व ऊर्जा यांची अक्षय्यता गृहीत धरण्यात आली आहे. फलनाच्या सममिती गुणधर्मावरून या गृहीताचे समर्थन कसे करता येते हे पुढे दाखविले आहे. वरील समीकरण भौतिकीतील इतर विषयांत वापरण्यात येणाऱ्या तरंग समीकरणाशी बरेचसे मिळतेजुळेते आहे, हे मात्र दाखविता येते. जिची दोन्ही टोके बंदीस्त आहेत अशी तार छेडली असता तिच्यावर तरंग निर्माण होतात आणि ते अप्रगामी अथवा स्थिर स्वरूपाचे असतात. आ. २ मध्ये अशा तरंगाचा एक प्रकार दाखविला आहे. या प्रकारामध्ये ‘२’ याने दाखविलेल्या सर्व स्थानी तारेची काहीच हालचाल होत नाही व ही निस्पंद स्थाने होत. याउलट ‘१’ याने दाखनिलेल्या सर्व ठिकाणी तारेची सगळ्यात जास्त हालचाल होते व ही प्रस्पंद स्थाने होत.
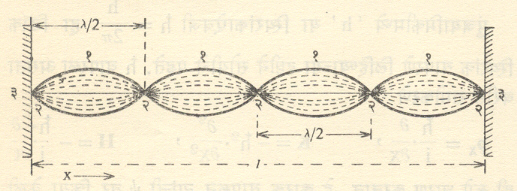
तारेची हालचाल या राशीने दर्शविली तर तारेच्या एका टोकापासून x अंतरावर असलेल्या बिंदूचे विचलन
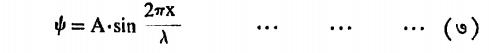
या समीकरणाने मिळते. यामध्ये तरंगलांबी. या उदाहरणात एक महत्त्वाची गोष्ट लक्षात घेण्यासारखी आहे दोन्ही टोकांना तार बांधली गेली असल्यामुळे तेथे कोणत्याही तरंगप्रकारात निस्पंदच मिळाले पाहीजेत हे स्पष्ट आहे. या सीमानिर्बंधामुळे( l=तारेची लांबी) अशी पृथक् तरंगलांबी मूल्येच शक्य होतात. यामुळे तरंगलांबीचे पुंजीकरण होते असे म्हणता येईल.
श्रोडिंजर यांच्या मीमांसेमध्ये भौतिकीय राशीचे पुंजीकरण वर येणाऱ्या अशा प्रकारच्या निर्बंधामुळेच करावे लागते. तारेवरील तरंग प्रकार आणि एका कनाकरिता वापरण्यात येणारी श्रोडिंजर मीमांसा यांमधील साधर्म्य व फरक खालील कोष्टकावरून स्पष्ट होईल.

बंदीस्त कणाकरीता त्याची ऊर्जा पृथक् मूल्येच का धारण करू शकते याची उपपत्ती वरील उदाहरणावरून मिळते.
दोलायमान तारेकरिता ψ ही राशी तारेवरील कोणत्याही एका बिंदूचे विचलन दाखवीत असल्यामुळे तिची कल्पना करणे सोपे जाते. श्रोडिंजर समीकरमआतील ψ या राशीला असा सरळ भौतिकीय अर्थ देता येणे शक्य होत नाही. माक्स बोर्न (१८८२–१९७०) यांच्या मते Iψ Idx किंवाψψ* (x, t) याचे मूल्य, तरंग-फलनाने निर्देशिलेला कण t या क्षणी x व x+dx यामध्ये सापडण्याची संभाव्यता दाखवितो याचा अर्थ होतो की ही कणांची संभाव्यता घनता दर्शविते. पुंजयामिकीमध्ये मिळणाऱ्या माहितीचे स्वरूप सांख्यिकीय असते आणि त्यामुळे त्यापासुन मिळणारी उत्तरे संभाव्यतेच्या स्वरूपात का असतात यांचे विविचन मागे अलेच आहे. या राशीला काही सरळ भौतिकीय सार्थकता नाही पण या मुळे या तत्त्वप्रणालीमध्ये काही कमतरता आहे असे मानण्याचे कारण नाही रुढ विद्युत् चुंबकीय मिमांसेमध्ये उपयोगात आणलेल्या विद्युत् क्षेत्र किंवा चुंबकीय क्षेत्र या दोन राशींचे सरळ मापन करता येत नाही. त्यामुळे मिळणाऱ्या प्रारणाची तिव्रता वर अवलंबून असते व ही राशी मात्र मोजता येते कींवा निरीक्ष्य आहे. असाच काहीसा प्रकार येथे घडतो असे समजता येईल.ψ निरिक्ष्य नाही पण | ψ |2 निरीक्ष्य आहे.
| ψ |2 ही संभाव्यता घनता असल्यामुळे कोणत्याही एका क्षणी, कण कोठे तरी अवकाशात असलाच पाहीजे हे क्रमप्राप्त असल्यामुळे
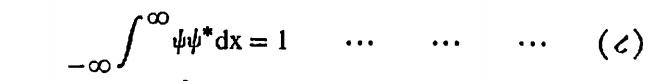
या समीकरणाची पूर्तता झाली पाहीजे, हे स्पष्ट आहे. वरील समीकरणास प्रसामान्यीकरण म्हणतात.
| ψ |2 याला दिलेल्या अर्थानुसार ψ आणि त्याचे अवकलांक [ → अवकलन व समाकलन] हे सर्व सहनिर्देशांकांच्या मूल्यांकरिता सांत, एकमूल्यी संतत राहिले पाहीजेत असे निर्बंध घालता येतात. अनंततेकरिता ψ → 0 ही अटसुद्धा त्याबरोबर पाळली पाहीजो असा निर्बंध घालता येतो. बंदिस्त कणाकरिता वरील निष्कर्ष अर्थातच यथार्थ ठरतात. याकरिता यथार्थ असणारे समी. (५)
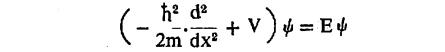
हे खालील कारक किंवा आयगेन मूल्य (उचित मूल्य याचे स्पष्टीकरण खाली दिले आहे) समीकरणाच्या स्वरूपात मांडता येते.
| A ψ =∝ψ | … | … | … | … | (९) |
वरील समीकरणात A हा कराक ψ वर क्रिया करतो तेव्हा त्यामुळे परत ψ हे फलन या सहगुणकासह मिळते. A या कारकास तद्रूप अशा भौतिकीय राशीचे हे निरीक्ष्य मूल्य असते असे आढळते. कारण ψ करिता घातलेल्या अटींची फक्त काही ठराविक Eया राशीच्या मूल्यांकरिता पूर्तता होते, से सामान्यपणे आढळते, समी. (९) व वरील अटींची पूर्तता करणारा कोणताही ψ याला आयगेन फलन म्हणतात. E याच्या ज्या पृथक् मुल्यांकरिता वरील अटी पाळल्या जातात, त्यांना त्यांची आयगेन मूल्ये म्हणतात. वरील अटींमुळे ψ वर निर्बंध घातले जातात व त्यामुळे या राशीचे पुंजीकरण होते. यावरुन पुंजीकरण हे पूर्वीच्या मीमांसेप्रमाणे गृहीत कृत्य नसून वर घातलेल्या निर्बंधांमुळे ते अनिवार्य हेते असे कळते.
भौतिकीत कणाची ऊर्जा, स्थान, संवेग इ. राशी निरीक्षण करून मोजता येतात. कणाकरिता आयगेन फलन माहीत असेल, तर त्यावरून या राशीची मूल्ये गणितीय रीत्या काढता येतातत. मागे वर्णन केल्याप्रमाणे अशा रीतीने मिळणारी माहिती सांख्यिकीय स्वरूपाची असते. याचा अर्थ असा करता येतो की, इष्ट राशीचे मापन करण्याकरिता अनेक एकरूप पुंज प्रणालींवर एकरूप प्रयोग करण्यात आले, तर त्यापासून मिळणाऱ्या प्रदत्तावरून त्या राशीकरिता एक सरासरी असे उत्तर मिळते. या मूल्यास राशीचे अपेक्षित मूल्य असे म्हणता येईल. पुंजयामिकी पद्धतीप्रमाणे राशीचे सर्वसाधारणपणे अपेक्षित मूल्यच मिळू शकते. काही विशिष्ट परिस्थितीत काही राशिंचे निश्चित मूल्यसुद्धा मिळू शकते.(उदा., ऊर्जा पातळ्यांची ऊर्जामूल्ये) या प्रत्येक राशीला जर निरीक्ष्य म्हटले तर तदनुरुप एक कारक असतो. हा कारक अवकल स्वरूपाचा असू शकतो.(उदा.,P या संवेगाचा कारक) किंवा तो एका संख्येच्या स्वरूपाचा सुद्धा असू शकेल.(उदा., x याचा कारक). या कारकांना पुढील गुणधर्म असतात : (१) त्यांचे स्वरूप रेषीय (एकघाती) असते. (२) ते घातांकाचा नियम पाळतात, म्हणजे Fm.Fn=Fm+n (३) क्रमनिरपेक्षता नियम ते पाळतातच असे नाही. या कारकाची क्रिया ज्ञात ψ फलनावर केली असता त्यापासून तदनुरूप राशीचे अपेक्षित मूल्य मिळते. कारकाच्या द्वारे करावयाच्या क्रियेबद्दल सूचना दिली जाते. कारक जर असेल, तर याचा अर्थ असा होतो की त्या मागून येणाऱ्या फलनाचा xया सहनिर्देशकाच्या सापेक्ष अवकलांक काढावयाचा. कणाच्या स्थानाचे अपेक्षित मूल्य खालील समीकरणाने मिळते.
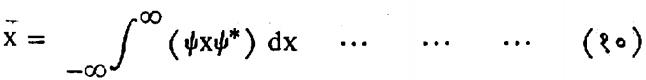
वरील समीकरणात x हा ψ आणि ψ * आणि यांच्यामध्ये लिहीण्याचा प्रघात समितीकरिता पडला आहे.

सर्वसाधारणपण कारक असलेल्या निरीक्ष्याचे अपेक्षित मूल्य Pλ हे Pψ या समीकरणाने मिळते म्हणून
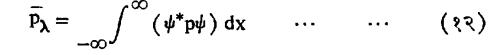
वर वर्णन केल्याप्रमाणे सूक्ष्मकणांविषयीचे प्रश्न सोडविण्याकरिता एक नवीन पद्धत उपलब्ध होते. या रीतीमध्ये प्रश्नांप्रमाणे श्रोडिंजर समीकरणाचे योग्य ते रूप घेऊन त्यामध्ये करिता घातलेल्या अटी पूर्ण करणारा निर्वाह शोधला जातो. या पद्धतीचा उपयोग प्रत्यक्षात कसा करतात हे दाखविण्याकरिता काही उदाहरणे पुढे दिली आहेत.
रेषीय हरात्मक आंदोलक : या आंदोलकामध्ये F=-kx या प्रकारची पुुनःस्थापक प्रेरणा कार्य करते. आंदोलन करणाऱ्या कणाचे द्रव्यमान m व आंदोलन कंप्रता ν k = 4π2mν2 हे दाखविता येते. यावरून कणाची स्थितिज ऊर्जा V= 1/2 kx2 एवढी असते असे कळते. श्रोडिंजर समिकरणात याचा उपयोग केल्यास
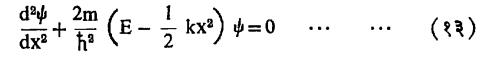
याचा निर्वाह ψ = Au e–∝2/2 या प्रकारचा मिळतो. येथे u हे x चे एक फलन आहे म्हणजे u=f(x) तर A= स्थिरांक व

आधारांक आहेत. ψ वर नेहमीच्या अटी घातल्यावर

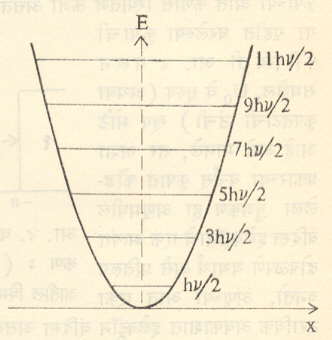
ही पूजीकरण अट मिळते (येथे n=0, 1, 2, 3………….) वरील समीकरण प्लांक यांच्या मुळ E= nhν या समीकरणाशी सदृष्य आहे. फरक एवढाच की N=0 म्हणजे या आंदोलकाची नीचतम ऊर्जा शून्य नसून एवढी आहे. याला शून्यबिंदू ऊर्जा म्हणतात.आंदोलकाने ऊर्जा ऊत्सर्जन केल्यास nचे मूल्य एकाने कमी होते. आंदोलकाने ऊर्जेचे शोषण केल्यास n चे मूल्य एकाने वाढते. आ. ३. मध्ये आंदोलकाच्या ऊर्जा पातळ्या दाखविल्या आहेत. या खालील देन पातळ्यांकरिता मिळणारी आयगेन फलने अनुक्रमेपुढे दिली आहेत.

दृढ घूर्णक : या प्रणालीमध्ये एका दांड्याच्या टोकाशी दोन गोलक डंबेलप्रमाणे जोडले आहेत असे गृहीत धरले आहे. दांडा दृढ असल्यामुळे या प्रणालीला स्थितिज ऊर्जा असत नाही त्यामुळे x च्या ऐवजी कोन आणि द्रव्यमान m च्या ऐवजी निरूढी परिबल हे एका कणाचे द्रव्यमान व r हे त्याचे भ्रमणअक्षापासूनचे अंतर असून त्यांची बेरीज वस्तूतील सर्व कणांकरिता घ्यावयाची असते) वापरून खालील श्रोडिंजर समीकरण मांडता येते.
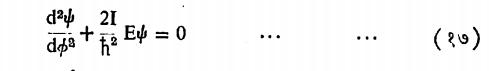
यामध्ये घूर्णकाचे घूर्णन एका प्रतलामध्ये होत आहे असे मानले आहे. वरील समीकरणाकरिता
हा निर्वाह मिळतो. येधे Aआणि Eहे स्थिरांक असतात. याकरिताऊर्जा
या स्वरूपात मिळते. घूर्णकाचे घूर्णन फक्त एका प्रतलातच होते हा निर्बंध काढल्यास ही मूल्य धारण करते असे दाखविता येते.
चौकोनी वर्चस् कूपात कोंडलेला पुंजकण : पुंजयामिकीच्या नियमांची पूर्तता करणाऱ्या कणास पुंजकरण असे येथे म्हटले आहे. चौकोनी वर्चस् कूपाच्या भिंती सरळ सतात. कण जेव्हा कूपाच्या बाहेर असतो तेव्हा त्याची स्थितिज ऊर्जा स्थिर असून तिचे मूल्य एवढे असते, तर कूपाच्या आत कणास स्थितिज ऊर्जा असत नाही असे मानले आहे. या गृहीत धरलेल्या कूपाची परिस्थिती आ.४ वरून समजेल. चे मूल्य (अथवा कूपतटाची उंची) खूप मोठे आहे असे मानले, तर अशा प्रकारच्या वर्चस् कूपात कोंडलेला पुंजकण हा अणूमधील बंदिस्त इलेक्ट्रॉनाचे एक अत्यंत ढोबळपणे यथार्थ असे प्रतिरूप बनतो.
आ. 4 वर्चस् कूपात कोंडलेला पुंजकण : (1) बाह्य विभाग, (2) आतील विभाग
अणूच्या आत एका ठराविक अवकाशात इलेक्ट्रॉन बंदिस्त असतो आणि तो त्याच्या बाहेर येऊ शकत नाही. ही जी त्याबद्दलची महत्त्वाची गोष्ट आहे तिचा अंतर्भाव वरील उदाहरणात होतो.
आकृतीतील (२) या आतील विभागाकरिता आणि स्थितिज ऊर्जा शून्य असल्यामूळे तदनुरूप
या श्रोडिंजर फलनाकरिता खालील समीकरण मिळते.
आकृतीतील(१) या बाह्य विभागाकरिता आणि कणाची स्थितिज ऊर्जा स्थिर व एवढी आहे. यावरून याकरिता खालिल श्रोडिंजर समीकरण मिळते.
हे निर्वाह मिळतात. येथे दोन्ही ठिकाणी जर सर्व xमूल्यांकरिता सांत रहावयास पाहीजे असेल, तर c=0=G असे कळते.
हा सर्व xकरिता संतत राहिला पाहीजे. याचा अर्थ
या अटीवरून खालील समीकरणे मिळतात.
या अटींची पूर्तता करण्याकरिता A,B,D,E,F या स्थिरांकांची मूल्ये उचित अशी घ्यावी लागतात.
या स्थिरांकांची प्रत्यक्ष मूल्ये गणिताने काढण्याकरिता लागणारी रीत किचकिट असल्यामुळे ती येथे दिली नाही. त्याऐवजी खालील विशिष्ट उदाहरणाचा विचार केला आहे.
(१) चे मूल्य जर खूप जास्त असेल, तर व x=+a करिता ही अट पूर्ण होते. या परिस्थितीत समी. (२७) व (२८)
ही स्वरूपे धारण करतात. यावरून आणि
असे दिसते. [पहा आ. ५ (इ) ]. वर घातलेल्या निर्बंधामुळे बंदिस्त पुंजकणाच्या ऊर्जेला फक्त पृथक् मूल्येच धारण करता येतात किंवा त्यांचे पुंजीकरण होते हे स्पष्ट कळते.
चे मूल्य या क्षेत्रातच सांत असते व त्याबाहेरील क्षेत्रात शून्य असते याचा अर्थ पुंजकण
आ ५. वर्चस्व कूपात कोंडलेल्या पुंजकरणाच्या आयगेन फलनामध्ये अटींनुसार होणारे बदल : (अ) सांत उंचीच्या वर्चस् कूपात कोंडलेला पुंजकण : पुंज अटी घालण्यापूर्वी मिळणारे आयगेन फलन (आ) पुंज अटींची पूर्तता करणारे तेच आयगेन फलन (इ) अनंत उंचीच्या वर्चस कूपात कोंडलेल्या पुंजकणाकरिता आयगेन फलन (ई)अनंत उचिच्या वर्चस् कूपाकरिता (१) स्थितिज ऊर्जा,
आयगेन फलन, n=1,e=eआयगेन फलन, (उ) अरुंद भिंती असलेल्या वर्चस् कूपात कोंडलेला पुंजकण.(अ) ते (उ) सर्वत्र (१)वर्चस् कूपाच्या बाहेरील विभाग,(२) वर्चस् कूपाच्या आतील विभाग.
वर्चस् कूपाबाहेर येण्याची संभाव्यता शून्य आहे असे दिसते. हा निष्कर्ष रूढ भौतिकीचा उपयोग केला असता मिळणाऱ्या निष्कर्षांशी सुसंगत आहे.
(२) U० चे मूल्य कमी असेल,तर वर लिहील्याप्रमाणे समीकरणावर करावयाचे आवश्यक गणितकृत्य किचकट होते. या परिस्थितीत मिळणारी आयगेन फलने वक्ररूपाने आ. ५ (अ) व (आ) मध्ये दाखविली आहे. फलनाच्या अटी घालण्यापूर्वीची परिस्थिती, (अ) मध्ये तर अटींची पुर्तता केल्यानंतर मिळणारे फलन (आ) मध्ये दिले आहे. आ. ५ (इ) मध्ये वर्चस् कूपाच्या भिंती अनंत उंचीच्या असल्यास काय होते हे दाखविले आहेत.
आ ५ (आ) वरून हे स्पष्ट होते की, असताना सुद्धा चे मूल्य बाह्य विभागाकरिता एकदम शून्य न होता ते अंतराप्रमाणे हळूहळू कमी होत जाते. याचा अर्थ असा होतो की, या परिस्थितीत वर्चस् कूपात असलेला कण कूपाच्या बाहेर असण्याची संभाव्यता शून्य असत नाही. हा परिणाम रूढ यामिकीपासून मिळणाऱ्या निष्कर्षापेक्षा अगदी निराळा आहे. असताना या यामिकीप्रमाणे कणाचे कूपाच्या भिंतीपासून परावर्तन होईल व तो भिंतीचे अंतर्भेदन करू शकणार नाही. या विभागात कणाची गतिज ऊर्जा ऋण स्वरूपाची होईल हे उघड आहे. कणाने भिंतित केलेल्या अंतर्गमनाचे प्रमाण या फरकावर अवलंबून राहते. जेवढे (Uo-E)चे मूल्य कमी तेवढे अंतर्गमनाचे प्रमाण जास्त असते हे आ. ५ (ई) वरून स्पष्ट होईल.
वर्चस् कूपाभोवती असलेल्या वर्चस् भिंतिची रुंदी कमी असेल, तर या परिणामाचे प्रमाण वाढते व त्याचे प्रत्यक्ष निरिक्षण करणे शक्य होते. अशा परिस्थितीस आ. ५ (उ) वर्चस् तट योजना म्हणतात. वर्चस् तटाचे अंतर्गमन यास सुरंग परिणाम म्हणतात. या परिणामामुळे वर्चस् कूपाच्या आत संपूर्ण ऊर्जा E असलेला कण जवळजवळ तीच ऊर्जा घेऊन कूपाच्या बाहेर येऊ शकतो. रूढ भौतिकीप्रमाणे कणाची ऊर्जा असल्याशिवाय कण वर्चस् तट ओलांडून बाहेर येऊ शकत नाही. बाहेर येण्याकरिता त्याची ऊर्जा (E) UO पेक्षा जास्त पाहीजे व तो तट ओलांडून बाहेर आल्यानंतर त्याची गतिज (अथवा संपूर्ण) ऊर्जा एवढीच राहते. या गोष्टी लक्षात घेता पुंजयामिकीचा निष्कर्ष किती निराळा हे हे कळू शकते. या प्रक्रियेचा उपयोग करून इलेक्ट्रॉनाचे क्षेत्र उत्सर्जन व जड किरणोत्सर्गी अणू केंद्रातून होणारे आल्फा कणाचे उत्सर्जन [→कीरणोत्सर्ग) या क्रीयेचे विशदीकरण करण्यात आले आहे.
आल्फा कणाच्या उत्सर्जनाचे विशदीकरण : तरंगयामिकीच्या सुरंग परिणामानुसार हे विशदीकरण १९२८ साली जॉर्ज गॅमो व आर्. डब्ल्यू. गर्नी आणि ई. यू. कॉँडन यांनी स्वतंत्रपणे दिले. किरणोत्सर्गी जड अणूकेंद्राच्या सभोवती सर्व बाजूंनी एक विद्यूत् स्थितिक (स्थिर विद्यूत् भारांमुळे निर्माण झालेला) वर्चस् तट आहे हे आल्फा कणाच्या प्रकीर्णनासंबंधीच्या (इतर कणांशी आघात वा परस्पक्रिया होऊन कणाची दिशा बदलण्यासंबंधीच्या) प्रयोगावरून सिद्ध होते. अणूकेंद्रातील आल्फा कणाची संपूर्ण ऊर्जा E त्याच्या सभोवती असलेल्या वर्चस् तटाच्या उंचीपेक्षा (uपेक्षा) कमी असली पाहीजे हे उघ़ड आहे नाहीतर तो कण अणूकेद्रामध्ये राहणारच नाही गॅमो याच्या विशदिकरणाकरिता आ. ६ मध्ये दाखविलेला वर्चस् तट गृहीत धरला जातो. सेंमी. ते सेंमी.या अंतरापर्यंत आल्फा कण व अणूकेंद्र यांमध्ये प्रतिसारण होते असे गृहीत धरल्यामुळे या अंतरापर्यंत वर्चस् तटाचा आकार या पदावलीने दर्शविला जातो (z = अणूक्रमांक, eo = इलेक्ट्रॉनवरील विद्यूत् भार, अणूकेंद्रापासून अंतर. प्राथमिक गतिज ऊर्जा eअसलेला जर एक
आ. ६ जड अणुकेंद्राभोवती आल्फा कणाकरिता असणारा वर्चस् तट (गॅमो) व आतमधील कणाच्या ऊर्जा पातळ्या (अणूकेंद्रापासूनची अंतरे१०-१२ सेंमी. एककात आहेत)
वेगवान आल्फा कण अणूकेंद्राच्या रोखाने सोडला तर या प्रतिसारण प्रेरणेमुळे त्यांची गतिज ऊर्जा सरखी कमी होत जाऊन तिचे स्थितिज स्वरूपाची होते (e=ν)त्या बिंदूपलीकडे अणूकेंद्राजवळ कण जाऊ शकणार नाही हे उघड आहे. अंतराकरिता आल्फा कणावर अणुकेंद्रीय आकर्षण प्रेरणा कार्य करीत असून कणाची स्थितिज ऊर्जा स्थिर राहते असे मानले आहे. वर्चस् तटाची त्रिज्या ही अणूकेंद्र त्रिज्या rO बरोबर धरली जाते. अणुकेंद्रामधील बंदिस्त आल्फा कणाकरिता निरनिराळ्या ऊर्जा पातळ्या असतात असे दाखविता येते. आकृतीत दाखविलेल्या पातळ्यांपैकी अआ या पातळीवर असलेल्या कणाचा विचार केल्यास तरंगयामिकीनुसार आतमध्ये असलेल्या ऊर्जेसहीत आल्फा कण बाहे येण्याची संभाव्यता वर अवलंबून राहते, असे दाखनिता येते. येथे w=वर्चस् तटाची स्थानिक रुंदी (उदा., अइ) आणि या राशीचे त्या रुंदीवरील सरासरी मूल्य pयाने दर्शविले आहे. या विशदीकरणावरून आल्फा कणाची बाहेर येण्याची संभाव्यता त्याच्या वाढत्या ऊर्जेनुसार वाढत जाते, या गायगर-नटॉल नियमापासून [→कीरणोत्सर्ग]मिळणाऱ्या निष्कर्षाचे स्पष्टीकरण मिळते.
श्रोडिंजर समीकरणाचे व्यापकीकरण : आतापर्यंत श्रोडिंजर समीकरणाचे विवेचन फक्त एका सहनिर्देशकाच्या अनुषंगाने केले आहे. सर्वसामान्य प्रश्नांकरिता त्याच्या खालील त्रिमितीय स्वरूपाचा उपयोग करावा लागतो.
तदनुरुप प्रसामान्यीकरण अट अशी होते. पूर्वीप्रमाणे हे सर्व x,y,z करिता सांत संतत, एकमूल्यी राहून त्याचे मूल्य अनंततेकरत शून्य झाले पाहिजे या अटींची पूर्तता करणारे निर्वाह शोधले जातात.
हायड्रोजन अणू : हायड्रोजन अणूमध्ये एक इलेक्ट्रॉन व एक प्रोटॉन असून त्यांमध्ये कूलंब आकर्षण प्रेरणा (विरुद्ध विद्युत् भार असलेल्या कणांमधील आकर्षण प्रेरणा) आहे. त्यामुळे अणूची स्थितिज ऊर्जा असते व त्याकरिता काल-निरवलंबी श्रोडिंजर समीकरण
विवेचनात m हे चिन्ह पुंजांकाकरिता वापरण्यात आले असल्यामुळे या व याच्या पुढील विवेचनाकरिता इलेक्ट्रॉनाचे द्रव्यमान (m) या चिन्हाने दर्शविले आहे. X, y, z ऐवजी हे ध्रुवीय सहनिर्देशक वापरले, तर त्यातील चलांचे विलगीकरण होऊन खालील तीन समीकरणे मिळतात.
यामध्ये a,mहे विलगीकरण प्रचल आहेत आणि
पूंजयामिकीच्या नेहमीच्या अटींची पूर्तत करण्याकरिता यावरून अणूच्या ऊर्जा पातळ्या मिळतात व त्या बोर मीमांसेप्रमाणे येणाऱ्या मूल्यांशी जूळतात. समी. (३६) मधील सांत व एकमूल्यी असावयास पाहीजे असेल, तर आणि असे दाखविता येते. (l,m,nयांला पुंजांक म्हणतात).
समी (३७)मधील क करित वरिल अटी लावल्यास त्याचा निर्वाह असा मिळतो. येथे mहा पुर्णांक असून त्याचे मूल्य m याने मिळते. जर l=0असेल तर अणूला गोलीय सममिती असल्यामुळे अणुकेंद्रापासुन इलेक्ट्रॉन कोणत्याही दिशेत एका ठराविक अतरावर सापडण्याची संभाव्यता सारखीच असते हे समजण्यासारखे आहे.
वरील विवेचनात l,व m यांचा विलगीकरण प्रचल म्हणून जरी अंतर्भाव करण्यात आला असला, तर त्यांना एक निश्चित भौतिकीय अर्थ आहे हे दाखविता येते . पुढील उपउपशीर्शकाखाली वर्णन केलेल्या कोनीय संवेगाकरिता योग्य असे कारक वापरून त्यांची वर क्रिया केली, तर संपूर्ण कोनीय संवेगाचे मूल्य या सूत्राने दिले जाते असे दिसते. कोनीय संवेगाच्या कोणत्याही एका विशिष्ट दिशेत (सामन्यपणे z-दिशा गृहीत धरली जाते) असणाऱ्या घटकाचे सुद्धा पुंजीकरण होते व त्याचे मूल्य या सूत्राने मिळते असे दाखविता येते. याचा अर्थ असा होतो की, संपूर्ण कोनीय संवेगास फक्त काही पृथक् अशीच मूल्ये धारण करता येतात एवढेच नव्हे, तर त्याच्या एका विशिष्ट दिशेतील घटकावर सुद्धा पृथक् अशीच मूल्ये धारण करण्याचे बंधन असते. या दुसऱ्या अटीमुळे कोनीय संवेगाचे अवकाशपूंजीकरण होते अस म्हटले जाते येथे एक प्रश्न उद्भवतो की, अणूला z-दिशा कोणती हे कसे कळते ? या परिणामाचे निरीक्षण करण्याकरिता अणूवर का विशिष्ट दिशेत एक चुंबकीय क्षेत्र लावणे आवश्यक ठरते. चुंबकीय क्षेत्र दिशेस Z-दिशा मानण्याचा प्रघात आहे. चुंबकीय क्षेत्रामुळे संवेगाचे अवकाश पुजीकरण होते, ते ताबडतोब प्रस्थापित होते व ही क्रिया चुंबकीय क्षेत्राच्या बलावर अवलंबून असत नाही. त्यामुळे लावलेले क्षेत्र कमीकमी करीत ते शून्य मूल्यापर्यंत नेले, तरी अवकाश पुंजीकरण तसेच टिकून राहील असे मानता येईल. पुंजयामिकीप्रमाणे कोनीय संवेगाचा घटक ज्या दिशेत फक्त ठराविक पृथक मूल्ये धारण करतो त्या दिशेची निवड अशा प्रकारे स्वेच्छेनुसार करत येईल. कोनीय संवेग lआणि कोन हे हायझेनबेर्क यांच्या अनिश्चितता तत्त्वानुसार एकमेकांशी निगडित असल्यामुळे कोनीय संवेगाचे मूल्य जर अचूकपणे माहीत असेल, तर त्याची दिशा बरोबर माहीत होणार नाही हे उघड आहे. अवकाश-पुंजीकरण अटीमुळे संवेगाचा z-दिशेतील घटक आचूकपणे माहीत करून घेणे शक्य होणार नाही. या सर्व अटी पाळल्या जावयाच्या असतील, तर असा निष्कर्ष निघतो की, संपूर्ण कोनीय संवेगाचे मूल्य व त्याच कोणत्याही एका दिशेतील घटकाचे मूल्य या दोनच गोष्टी फक्त अचूकपणे जाणून घेणे शक्य होते.
बोर मीमांसेप्रमाणे पहील्या इलेक्ट्रॉन कक्षेची त्रिज्या या सूत्राने मिळते. याचे मूल्य एवढे असते. आ. ७ मध्ये अणूच्या निरनिराळ्या अवस्थांकरिता इलेक्ट्रॉन अणूकेंद्रापासून निरनिराळ्या अंतरावर मिळण्याच्या सापेक्ष संभाव्यता दाखविल्या आहेत.
आकृतीवरून असे दिसते की, n=1,l=oसाठी या अंतराकरिता इलेक्ट्रॉन मिळण्याची सापेक्ष संभाव्यता महत्तम मूल्य धारण करते. बोर प्रतिमानामध्ये अणूतील इलेकट्रॉन केंद्राभोवती एका
आ. 7. अणूकेंद्रापासून निरनिराळ्या अरीय अंतरावर इलेक्ट्रॉन मिळण्याच्या सापेक्ष संभाव्यता.
ठराविक आकारमानाच्या कक्षेत फिरतो व त्यास त्यामुळे कक्षीय कोनीय संवेग असतो. पुंजयामिकीप्रमाणे या अवस्थेमधील l=0 इलेक्ट्रॉनाकरिता कक्षीय कोनीय संवेगाचे अपेक्षित मूल्य शून्य असते असे दाखविता येते. पुन्हा या केंद्रापासून इलेक्ट्रॉन ठराविक स्थानावर नसून त्याची संभाव्यता या बिंदूपासून सारखी कमी होत जाते. (l=0) इलेक्ट्रॉनाच्या पुंजयामिकीप्रमाणे मिळणाऱ्या S अवस्था बोर याच्या वर्तूळाकार कक्षेच्या अनुरूप असतात. फक्त बोर यांच्या मीमांसेनुसार त्यांना कोनीय संवेग असतो, तर पुंजयामिकीनुसार त्यांना कोनीय संवेग शून्य असतो. इलेक्ट्रॉनच्या कोनीय संवेगाचे अपेक्षित मूल्य ज्याकरित शून्य असत नाही अशा आयगेन अवस्था हायड्रोजन अणूकरिता असू शकतात. अशा अवस्थांकरिता कोनीय संवेगाचे मूल्य या सूत्राने मिळते. n याच्या सापेक्ष याला यांपैकी कोणतेही मूल्य असू शकते. M या पुंजांकामुळे कोनीय संवेगाच्या z-अक्षावरील घटकाचे मूल्य निश्चित होते. याला m=-1,-(l=1),…,
l-1,l वरील विवेचनावरून असे दिसते की, पुंजयामिकीनुसार कोनीय संवेगाचे हे एक नैसर्गिक एकक आहे. त्याचप्रमाणे m = 1 याचा अर्थ कोनीय संवेगाचा z- अक्षावरील h एवढा आहे असा होतो. वरील विश्लेषणाचे असेही विशदीकरण कराता येईल की, जोपर्यंत बाहेरून चुंबकीय क्षेत्र लावलेले नसते तेव्हा अणूला सामान्य पणे गोलाकार सममिती असल्यामिळे त्याच्या कोनीय संवेगाची दिशा माहीत नसते, पण त्याचे मूल्य व z-अक्षावरील घटकाचे मूल्य या दोन्ही राशी मात्र अचूकपणे ज्ञात असतात. पुंजयामिकीनुसार अणूमधील इलेकट्रॉन केंद्राभोवती एका वर्तुळाकार कक्षेत फिरतो असे मानावयास काही आधार नाही, तरी त्यास एक ठराविक मूल्याचा कोनीय संवेग असतो हे मात्र निश्चितपणे समजते. आतापर्यंतच्या प्रतिमानामध्ये इलेक्ट्रॉन परिवलन गती लक्षात घेतली गेलेली नाही. याचा विचार नोंदिच्या पुढील भागात केला आहे.
मागे विवेचन केल्याप्रमाणे n, l, mया तीन पुंजांंकांमुळे आयगेन निश्चित होते. त्यामुळे या आयगेन अशी संज्ञा देता येते. कोणत्याही अणू अवस्थेची ऊर्जा n या पुंजांकानेच ठरत असल्यामुळे अणूच्या एका ऊर्जा पातळीकरिता एकापेक्षा अधिक आयगेन उपलब्ध होतात. एकच ऊर्जामूल्य पण अनेक आयगेन असलेल्या अवस्थांना अपभ्रष्ट अवस्था असे म्हणतात. हायड्रोजन अणूमध्ये सर्वांत प्रबल प्रेरणा ही इलेक्ट्रॉन व अणूकेंद्र यांमधील कुलंब आकर्षण प्रेरणा होय. अणूवर बाह्य चुंबकीय क्षेत्र लावले, तर त्यामुळे अणूच्या ऊर्जेत महत्त्वाचे परिणाम घडून येतात. पण यामुळे अणूत उत्पन्न होणारी जादा ऊर्जा इतकी कमी मूल्याची असते की , ती हीशोबात घेउन श्रोडिंजर समीकरण सोडविण्यापेक्षा बाह्य क्षेत्राविरहित श्रोडिंजर समीकरण सोडवून आलेल्या निर्वाहामध्ये होणारी दूरुस्ती विक्षोभाच्या स्वरूपात घेणे सोपे ठरते. बाह्य चुंबकीय क्षेत्रामुळे ऊर्जेमध्ये होणारी वाढ या सूत्राने मिळते. याचा एक परिणाम असा होतो की, आयगेन अवस्थेमधील अपभ्रष्टता नाहीशी होते.
कोनीय संवेगः श्रोडिंजर मीमांसेप्रमाणे हायड्रोजन अणूकरिता मिळणाऱ्या निष्कर्षाचे विवेचन करताना कोनीय संवेगाचा उल्लेख करण्यात आलेला आहे. त्याचे मूल्य काढण्याकरिता वापरण्यात येणाऱ्या पद्धतीचे खाली वर्णन केले आहे. जर प्रणालीचे वर्णन x, y, zया संहनिर्देशकांच्या सापेक्ष करण्यात येत असेल, तर कोनीय संवेगाचे या अक्षांभोवतालचे घटक खालील कारकांच्या साहाय्याने मिळविता येतात.
एखाद्या इलेक्ट्रॉन अवस्थेकरिता हे कोनीय घटक आहेत की नाहीत हे ठराविण्याकरिता त्याच्या आयगेन वर या कारकांची क्रिया करावयाची म्हणजे कारकासूत्राप्रमाणे चे अंशतः अवकलन करावयाचे. या क्रीयेपासून दोन परिणाम मिळू शकतात. जर कारकांची क्रिया केल्यानंतर परत मूळ मिळाले म्हणजे या स्वरूपाचा निर्वाह मिळाला, तर याचा अर्थ असा होतो की, x या अक्षाभोवती इलेक्ट्रॉनला या मूल्याचा कोनीय संवेग आहे. याउलट या क्रीयमुळे जर च्या स्वरूपातच फरक पडतो असे दिसले तर त्यावरून असा निष्कर्ष निघतो की, गृहीत इलेक्ट्रॉन अवस्थेकरिता या अक्षाभोवती ठराविक कोनीय संवेग निगडित नाही व त्याकरिता हे उचित फलनही नाही. हायड्रोजन अणूसाठी x,y,z भोवती कोनीय संवेगाकरिता ठराविक मूल्ये मिळत नाहीत. मात्र ध्रूवीय सहनिर्देशांक वापरल्यास या करकापासून z-अक्षाभोवती असलेल्या कोनीय संवेगाकरिता हे आयगेन मूल्य मिळते याचा उल्लेख मागे करण्यात आला आहे.
हायझेनबेर्क यांची आव्यूह यामिकी : अणूच्या इलेक्ट्रॉनाला ऊर्जा पुरवली असता तो उत्तेजित होतो. या उत्तेजित अवस्थेत अणू सरासरी आयुःकालापर्यंत राहतो यानंतर तो उत्स्फूर्तपणे मूळ अवस्थेत जातो. हे संक्रमण होण्याकरिता लागणारा काल तदनुरूप संक्रमण संभाव्यतेच्या व्यस्त प्रमाणात राहतो. जर संक्रमण संभाव्यता जास्त असेल, तर संक्रमण करण्याकरिता लागणारा काल कमी असतो. या क्रियेमध्ये उत्सर्जित होणाऱ्या प्रारणाची कंप्रता व संक्रमण संभाव्यता या (व अशा इतर काही महत्त्वाच्या ) राशींचे गणन करण्याकरिता हायझेनबेर्क यांच्या आव्यूह यामिकीचा जास्त उपयोग होतो, म्हणून या यामिकीचा खाली संक्षेपाने विचार केला आहे.
हायझेनबेर्क यांच्या मते आणवीय रचनेसंबंधी किंवा यामिकीसंबंधी मीमांसा करताना ज्या राशींचे प्रत्यक्ष निरीक्षण होऊ शकते अशा राशींचा फक्त त्यात समावेश करावा उदा., अणूकडून उत्सर्जित झालेल्या प्रारणाची कंप्रता, तीव्रता, त्याची ध्रुवीकरण (कंपने एखाद्या विशिष्ट प्रतलातच होण्याची ) अवस्था इत्यादींसारख्या राशींचाच मीमांसेकरिता अंतर्भाव करण्यात यावा. हायझेनबेर्क बोर्न आणि पी, योर्डान यांनी या राशींकरिता प्रत्येकी एक आव्यूह वापरून सर्व आणवीय आविष्कारांचे स्पष्टीकरण दिले.
अणूच्या या दोन अवस्थांमध्ये होणाऱ्या संक्रमणामुळे उत्सर्जन होणाऱ्या प्रारणाची कंप्रता
या समीकरणाने मिळते. यापासून सुरूवात आणवीय वर्णपटातील रेषेच्या कंप्रतेकरिता खालील तऱ्हेच्या आव्यूह रचता येतो.
या आव्यूहामधील पंक्ती व स्तंभ अनंततेपर्यंत जातात असे मानले आहे. या आव्यूहातील चौथ्या पंक्तीतील दुसऱ्या स्तंभाची संख्या अणूच्या चौथ्या ऊर्जापातळीपासून दुसऱ्या ऊर्जापातळी पर्यंत संक्रमण झाले असता मिळणारी कंप्रता दर्शविते असे समजले जाते. याच प्रथेचा उपयोग करून तदनरूप परमप्रसराकरिता (कंपनाच्या एका आवर्तनात होणारे महत्तम स्थानांतरण ज्यावरून उत्सर्जित प्रारणाची तीव्रता मिळते) असाच एक आब्यूह मांडता येतो.
हायझेनबेर्क मीमांसेमध्ये येणाऱ्या आव्यूहात अनंत स्तंभ व पंक्ती असतात. यामधील प्रत्येक संख्या (किंवा दोन) स्थिर आणवीय अवस्थेशी निगडित असल्यामुळे याचा अर्थ असा होतो की, या सर्व अवस्था पृथक् आहेत आणि त्यांची संख्या अनंत आहे. काही परिस्थितीत पुंजयामिकीनुसार अनुज्ञात (ग्राह्य असलेल्या) अवस्थांचा जेव्हा अखंड समुच्चय मिळतो. अशा वेळी आव्यूहातील संख्या घटकांकरिता निराळे स्वरूप गृहीत धरावे लागते व त्यावर गणितीय कृत्य करण्याकरिता वेगळी पद्धत वापरावी लागते.
पुंजयामिकीमध्ये येणाऱ्या प्रत्येक निरीक्ष्याबद्दल एक आव्यूह मांडता येतो. या आव्यूहांपासून बरोबर निष्कर्ष मिळविण्याकरिता त्यांना काही विशिष्ट गुणधर्म (उदा., दोन आव्यूहांची बेरीज,गुणाकार) आव्यूह मीमांसेपासूनच मिळतात. ( आब्युह सिद्धांत). आब्यूहांपासून बेरीज वा गुणाकार केले असता त्यापासून परिणामी आव्यूहच मिळतात. आव्यूहाच्या गुणाकाराला क्रमनिरपेक्षता गुणधर्म नाही म्हणजे या स्थल सहनिर्देशकांचे व या संवेग सहनिर्देशकांचे f हे फलन असेल, तर पुजंयामिकीकरिता त्याचे अवकलांक खालील सूत्रांनी मिळतात असे गृहीत धरले जाते.
असे निष्कर्ष मिळतात. येथे p आणिq हे निरीक्ष्य सुद्धा आव्यूहांच्या स्वरूपात आहेत हे उघड आहे.
या यामिकीचा उपयोग करून हरात्मक आंदोलक, हायड्रोजन अणू इ. आविष्कारांचे विश्लेषण देता येते. यापासून मिळणारे सर्व निष्कर्ष श्रोडिंजर मिमांसा वापरुन मिळालेल्या निष्कर्षाशी एकरूप असतात. कोणत्याही q, pयाच्या f फलनाच्या आव्यूह निदर्शनामधील घटक त्याचे श्रोडिंजर फलन माहीत असल्यास खालील सूत्राचा उपयोग करून मिळविता येतो.
आणवीय वर्णपट रेषांकरिता संक्रमण संभाव्यता : रूढीय मीमांसेप्रमाणे पुंजयामिकीत प्रारणांचे प्रेषण अणूच्या द्वीध्रुवी विद्यूत् परिबलावर [→ अणूकेंद्रीय व आणवीय परिबले ] अवलंबून असते. N या अवस्थेकरिता या परिबलाचे घटक खालील सूत्राने मिळतात असे दाखविता येते.
येथे n या अवस्थेकरिता असलेले आयगेन फलन आहे. Dt= घनफळ = dx dy dz अणूकरिता परिबल pअसतो व त्याचे घटक वरील सूत्रानुसार मिळतात. ज्या कक्षेकरिता ऊर्जेला आयगेन मूल्ये असतात अशा स्थायी कक्षांकरिता चे मूल्य शून्य असते असे दाखविता येते. स्थाय़ी कक्षांमध्ये इलेक्ट्रॉन प्रारणाचे उत्सर्जन का करत नाही याचा उलगडा पुंजयामिकीमुळे होतो. बोर मीमांसेमध्ये ही गोष्ट गृहीत धरण्यात आली होती.
डिरॅक यांनी असे दाखविले आहे की, जेव्हा अणू अवस्थेमधून अवस्थेत संक्रमण करतो तेव्हा तो जे प्रारण उत्सर्जित करतो ते त्याचा संक्रमण परिबलावर अवलंबून असते. हे संक्रमण परिबल काढण्याकरिता वापरून रूढ यामिकीच्या सदृश असे गणन करून संक्रमण संभाव्यता व प्रारण तीव्रता यांचे मूल्यमापन केले जाते. संक्रमण क्रियेमध्ये मूळ अवस्थेत विक्षोभ होत असल्यामुळे याकरिता श्रोडिंजर कालसापेक्ष समीकरण वापरणे योग्य ठरते.
याचा निर्वाह या स्वरूपाचा असतो. संक्रमण परिबलाच्या घटकाकरिता
यामध्ये कालावर अवलंबून राहणारा घटक मिळतो यावरून या संक्रमणाने मिळणाऱ्या प्रारणाची कंप्रता
या बोर सूत्राने मिळते हे कळते.
असे मांडता येईल. जेथे हा सदीश आहे ज्याचे घटक
या सारख्या सूत्रांनी मिळता.
वर्णपट रेषेची तीव्रता-प्रतिसेकंद संक्रमणे
येथे ही राशी आव्यूहाच्या स्वरूपात देणे सोईस्कर ठरते.
याच मीमांसेप्रमाणे मिळालेल्या प्रारणाची ध्रुवीकरण अवस्था, निवड नियम (कोणत्या निरनिराळ्या ऊर्जा पातळ्यांमध्ये इलेक्ट्रॉनांचे वा अणूकेंद्रीय कणांचे संक्रमण होऊ शकते हे सांगणारे नियम)इत्यादी विषयी संपूर्ण माहीती मिळते. यावरून असे दाखविता येते की, संपूर्ण पुंजस्थिरांक n यामध्ये घडणाऱ्या बदलावर काहीही निर्बंध नाहीत, पण असे निवड नियम मिळतात. यावरून या पुंजांकामध्ये होणारा बदल फक्त एकच असू शकतो, तर यामध्ये हा बदल शून्य कींवा एक असा असू शकतो असे दिसते.
हायड्रोजनसम अणूकरिता विश्लेषण : आतापर्यंतचे विवेचन ज्यामध्ये फक्त दोनच घटक कण आहेत अशा हायड्रोजन प्रणालीबद्दल करण्यात आले आहे. ही मीमांसा इतर अणूंच्या (उदा., हायड्रोजन अणूसारख्य़ा प्रणालीकरिता वापरता येते. यामध्ये अणुकेंद्रावरील विद्युत् भार असल्यासमुळे श्रोडिंजर समीकरण
हे स्वरूप धारण करते. यानंतरचे विश्लेषण मागे दाखविल्याप्रमाणेच करता येते.
इलेक्ट्रॉन परिवलन : आतापर्यंत विवेचन केलेल्या मीमांसेद्वारे वर्णपटातील रेषांची सूक्ष्मरचना व नियमविरूद्ध झीमान परिणाम [→ अणुकेंद्रीय व आणवीय परिबले]यांचे स्पष्टीकरण मिळत नाही. जी. ई. ऊलेनबेक व एस्. ए. गाउडश्मिट यांनी इलेक्ट्रॉन स्वतः भोवती भोवऱ्यासारखा फिरतो अथवा त्याला परिवलन गती आहे ही कल्पना १९२५ साली माडली. याचा परिणाम लक्षात घेण्याकरिता डब्ल्यु. पाउली यांनी एक नवीन कोनीय संवेग सदीशाची कल्पना केली.
ही तीन घटक असलेली सदिश चल राशी व तिचे घटक खालील आव्यूह स्वरूपात देता येतात.
z-अक्षाभोवती परिवलन गतीमुळे येणारा कोनीय संवेग एवढा असतो असे निरीक्षणावरून संमजते. या गोष्टीशी सुसंगत अशी ही गृहिते आहेत. यामुळे परिवलन गतीमुळे इलेक्ट्रॉनाच्या मुक्तता मात्रांत (गती निर्धारित करणाऱ्या चलांच्या संख्येत) एकाने भर पडते.
परिवलन गती विचारात घेता हायड्रोजनसम अणूमध्ये आता इलेक्ट्रॉन अवस्था निश्चित करण्याकरिता असे चार पुंजांक आवश्यक होतात. यापैकी (या पूर्वीच्या विवेचनातील m)यांचे स्पष्टीकरण आधी आलेच आहे. हा पुंजांक परिवलन गतीमुळे येणाऱ्या कोनीय संवेगाचे अवकाश पुंजीकरण निश्चित करतो. इतर अणूंच्या बाबतीत सुद्धा हेच विधान करता येते. याकरिता अणूच्या भोवताली असलेल्या इलेक्ट्रॉनांपैकी शेवटला इलेक्ट्रॉन हा अणूकेंद्र व इतर इलेक्ट्रॉन यांमुळे निर्मान झालेल्या मध्यवर्ती क्षेत्रात असतो असे मानले म्हणजे झाले. याला फक्त ही दोनच मूल्ये असू शकतात. असे या परिस्थितीतही गृहीत धरता येते. पाउली यांच्या विवर्जन तत्त्वाचा [→ अणू व आणवीय संरचना] उपयोग केला असाता मूलद्रव्यांच्या ⇨ आवर्त सारणीमध्ये येणाऱ्या अणूंच्या क्रमाची उपपत्ती लावता येते. परिवलन गतिमुळे वर्णपट रेषांची सूक्ष्मरचना (उदा., सोडियम d-द्विकाची रचना म्हणजे सोडियममुळे मिळणाऱ्या ५, ८९६· ३५७ A व ५, ८९०·१८६ A या तरंगलांबीच्या रेषांची रचना) कळून येते. काही अणूंमध्ये आढळणाऱ्या लोहचुंबकत्व [→चुंबकत्व] या आविष्काराचे स्पष्टीकरण मिळते. या संदर्भात दोन महत्त्वाच्या गोष्टी आढळतात. लोहचुंगकत्व इलेक्ट्रॉन परिवलन गतीमुळे निर्माण होते आणि इलेक्ट्रॉनाच्या कक्षीय कोनीय संवेगाचा यामध्ये काहीही भाग नसतो. चुंबकीय यांत्रिक गुणोत्तर =चुंबकीय परिबल / कोनीय संवेग चंबुकत्व याचे मूल्य परिवलन गतिकरिता (येथे इलेक्ट्रॉनाचा विद्युत् भार, m=त्याचे द्रव्यमान व c= प्रवेशवेग) एवढे धरावे लागते, तर कक्षीय कोनीय गतीकरिता त्याचे मूल्य इतकेच असते. या दोन गतीकरिता चुंबकीय यांत्रिक गुणोत्तरामध्ये वरीलप्रमाणे फरक आहे हे नियमविरुद्ध झीमान परिणाम आणि आइन्स्टाइन व डब्ल्यू. द हास यांनी केलेला प्रयोग यांवरून समजते. बहुकण प्रणालीकरिता पुंजयामिकी : पुंजयामिकीचे स्पष्टीकरण करण्याकरिता आतापर्यंत दिलेल्या उदाहरणात फक्त दोन घटक कण असणाऱ्या प्रणालीचा (उदा., हायड्रोजन अणू ज्यामध्ये प्रोटॉन व इलेक्ट्रॉन एवढेच दोन घटक आहेत) विचार करण्यात आला आहे. अशा प्रणालीकरिता गणितीय रीत्या सम्यक् निर्वाह मिळविणे शक्य असते. अणूकेद्र व दोन इलेक्ट्रॉन असे तीन घटक असणाऱ्या हीलीयम अणू (व त्याहून अधिक घटक असणारे आवर्त सारणीमध्ये त्यानंतर येणारे अणू) याकरिता पुंजयामिकी सिद्धांताचा उपयोग करून निर्वाह मिळविण्यात अडचण पडते. हीलियम अणूकरिता (अ) अणूकेंद्र व इलेक्ट्रॉन (१) (आ) अणूकेंद्र व इलेक्ट्रॉन (२) (इ) इलेक्ट्रॉन (१)व (२) यामधील परस्परक्रियांचा विचार करणे आवश्यक ठरते. या सर्व परिणामांचा संकलितरित्या विचार करून सम्यक् निर्वाह मिळविणे शक्य होत नाही. या कार्याकरिता आसन्न गणितीय रीतीचा वापर करावा लागतो. या मीमांसेकरिता ज्या आसन्न गणितीय रीती उपलब्ध आहेत त्यांमध्ये डी. आर्. हारट्री व व्ही. फॉक यांनी संशोधिलेली स्वयंसुसंगत क्षेत्र प्रतिरूप पद्धत सर्वांत समाधानकारक मानली जाते. या पद्धतीमध्ये अणूकेंद्राभोवती असणाऱ्या व इलेक्ट्रॉनमधील प्रतिसारण परस्परक्रिया, गोलीय सममिती असणाऱ्या एका समतुल्य विद्युत् क्षेत्राच्या स्वरूपात दाखविली जाते. हे अतिरिक्त क्षेत्र इलेक्ट्रॉनांच्या सरासरी परिणामामुळे निर्माण होते व त्यामुळे अणूकेंद्रामुळे निर्माण झालेल्या मूळ क्षेत्रामध्ये परिवर्तन घडून येते. कोणत्याही एका इलेक्ट्रॉनावर कार्य करीत आसलेल्या परिणामी वर्चसास गोलीय समिती असल्यामुळे, हायड्रोजन किंवा हायड्रोजनसम अणूकरिता फलनाच्या गोलीय विभागाचे जे स्वरूप असते त्यात फारसा बदल होत नाही, फलनाच्या अरीय विभागात मात्र बराच फरक घडून येतो असे आढळते. हायड्रोजन अणूच्या निरनिराळ्या अवस्थेतील इलेक्ट्रॉनाचे निर्देशन (व ऊर्जा निश्चिती) करणाकरिता वापरलेली पद्धत हीलियम इ. अणूंच्या व्यापक मीमांसेकरिता देखील यथार्थ ठरते. अनेक इलेक्ट्रॉन असणाऱ्या अणूच्या कोणत्याही एका इलेक्ट्रॉनाची अवस्था खाली दिलेल्या पुर्वीच्याच पुंजांकाच्या द्वारे दर्शविता येते. एकरुपता सिद्धांतानुसार या पुंजांकांना जुन्या बोर पुंज सिद्धांताप्रमाणे देण्यात आलेला अर्थच देता येतो.
(१) कक्षीय परिभ्रमण पुंजांक / : यामुळे इलेक्ट्रॉनाच्या कक्षीय कोनीय संवेगाचे मूल्य निश्चित होते.
(२) परिवलन पुंजांक (परिवलनांक) S : या पुंजाकामुळे इलेक्ट्रॉनाच्या परिवलन गतीमुळे मिळणाऱ्या कोनीय संवेगाचे मूल्य ठरते.
(३) आंतरिक पुंजांक j : इलेक्ट्रॉनाच्या संपूर्ण कोनीय संवेगमूल्याची निश्चिती करणारा पुंजांक
(४) चुंबकीय पुजांक m : एका ठराविक दिशेत मिळणाऱ्या इलेक्ट्रॉनाच्या कोणत्याही प्रकारच्या कोनीय
संवेगाच्या घटकाचे मूल्य निश्चित करणारा पुंजांक
आधुनिक पुंजयामिकीप्रमाणे हे पुंजांक पूर्णांक वा अर्धपुर्णांक यांपैकी कोणत्याही स्वरूपात असू शकतात. इलेक्ट्रॉनाची ऊर्जा प्रमुख पुंजांकावरून (n) ठरते, तर अणूकेंद्रापासून ठराविक ठिकाणी इलेक्ट्रॉन सापडण्याच्या संभाव्यतेचे मूल्यमापन करण्याकरिता सर्वच पुंजांकांची मूल्ये माहीत असावी लागतात. अणूच्या निरनिराळ्या इलेक्ट्रॉनांमध्ये परस्परक्रीया होत असल्यामुळे त्यांमध्ये एक प्रकारचे युग्मन (संयोग) होते. रसेल साँडर्स युग्मनामध्ये प्रत्येक इलेक्ट्रॉनाचा कक्षीय संवेग या सदिशाचा मिळून सर्व इलेक्ट्रॉनांकरिता एक परिणमी कक्षीय संवेग सदिश होतो, तर त्यांच्या परिवलन संवेगांचे सदिश रीत्या एकीकरण [→सदिश]होऊन त्यायोगे परिणामी परिवलन संवेग S हा बनतो. यानंतर या प्रकारे एकत्र येऊन अणूमधील इलेक्ट्रॉनांकरिता संपूर्ण कोनीय संवेग मिळतो. या प्रकारच्या युग्मनाला L–S यूग्मन असे सुद्धा म्हणतात. दुसऱ्या प्रकारच्या युग्मनामध्ये प्रत्येक इलेक्ट्रॉनाकरिता मिळणारे असे परिणामी कोनीय संवेग एकत्र येऊन अणूच्या सर्व इलेक्ट्रॉनांकरिता देतात. या प्रकारास j-jयुग्मन म्हणतात. या युग्मन प्रकाराबद्दलच्या जास्त माहितीकरिता अणूकेंद्रीय व आणविय परिबले, अणू व आणवीय संरचना आणि वर्णपटविज्ञान या नोंदी पहाव्यात.
सापेक्षीय पुंजयामिकी : श्रोडिंजर सिद्धांताप्रमाणे इलेक्ट्रॉनाच्या वर्तणुकीचे वर्णन दुसऱ्या कोटीच्या एका अवकल समीकरणाच्या साहाय्याने करता येते. यामध्ये फक्त एकच तरंग फलन याचा समावेश केलेला असतो. इलेक्ट्रॉनाची परिवलन गती लक्षात घेण्याकरिता पाउली यांनी मागे वर्णन केल्याप्रमाणे दोन तरंग फलने व यांचा उपयोग केला. ही फलने दोन युगपत् दुसऱ्या कोटीच्या अवकल समीकरणांची पूर्तता करतात. या प्रकारे काही आविष्कारांचे समाधानकारक विशदीकरण मिळाले, तरी परिवलन गतीकरिता 1/2 पुंजांक का वापरावे लागतात व चुंबकीय यांत्रिक गुणोत्तराचे मूल्य या गतीकरिता नेहमीपेक्षा दुप्पट का धरावे लागते याचे स्पष्टीकरण त्यापासून मिळते नव्हते. या सर्व गोष्टींचा खुलासा सापेक्षता सिद्धांताचा उपयोग करून मिळतो. श्रोडिंजर समीकरण ह सापेक्षीय नाही. लोरेन्ट्स रुपांतरण [→अवकाश काल]केले असता हे समीकरण निश्चल राहत नाही. ओ. क्लाईन व डब्ल्यू. गॉर्डन यांनी हॅमिल्टोनीयन
(p= संवेग, c=प्रकाशवेग ,m= शून्यगति-द्रव्यमान)
असे मांडून सापेक्षीय रीत्या निश्चिल राहील असे एक तरंग फलन प्रथम शोधून काढले. क्लाईन-गॉर्डन समीकरणाचा उपयोग इलेक्ट्रॉनाकरिता करण्यामध्ये येणाऱ्या विविध अडचणी डिरॅक यानी दाखविल्या आणि त्यांनी एक पर्यायी रीतही सुचविली. डिरॅक सिद्धांतात इलेक्ट्रॉनाची स्थिती दर्शविण्याकरिता चार तरंग फलन घटक वापरले आहेत. हे चार फलन घटक पहील्या कोटीच्या चार यूगपत् अवकल समीकरणांची पूर्तता करतात. इलेक्ट्रॉनावर जर अदिश वर्चस् V व वर्चस् एवढे असेल, तर डिरॅक यांची युगपत् समीकरणे खालील स्वरूपात मिळतात. (येथे Mगतिमाम इलेक्ट्रॉनाचे सापेक्षीय द्रव्यमान आहे.)
फलनाचे खालीलप्रमाणे प्रसामान्यीकरण केल्यास
आणि
या पदावल्या अनुक्रमे इलेक्ट्रॉन dxdydz या अत्यल्प घनफळामध्ये असून त्याच्या परिवलन दिशा पुंजीकरण दिशेला समांतर व प्रतिसमांतर (समांतर परंतु दिशा पुंजीकरण दिशेला विरुद्ध) असण्याची संभाव्यता दाखवितात. वरील डिरॅक फलने लोरेन्टस रूपांतरण केल्यास निश्चल राहतात.
डिरॅक सिद्धांताने इलेक्ट्रॉन परिवलन गतीच्या विविध गुणधर्मांचे स्पष्टीकरण मिळते [→ इलेक्ट्रॉन]. या गतीकरिता पुंजांक १/२ का असतात व त्याकरिता चुंबकीय यांत्रिक गुणोत्तर नेहमीपेक्षा दुप्पट का असते याची उपपत्ती मिळते. या सिद्धांताचा उपयोग केल्यास हायड्रोजन अणूच्या ऊर्जा पातळ्यांच्या सूक्ष्मरचनेविषयीचा खुलासा मिळतो. सापेक्षीय कारणामुळे मिळणारी पातळ्यांची सूक्ष्मरचना बोर आणि आर्नोल्ट झोमरफेल्ट यांनी मिळविलेल्या रचनेशी मिळतीजुळती आहे असे आढळते. डिरॅक सिद्धांताप्रमाणे याशिवाय इलेक्ट्रॉनाच्या कक्षीय गती व परिवलनीय गती यांमध्ये परस्परक्रिया होऊन त्याच्या ऊर्जेत सूक्ष्म फरक पडतो. या सर्व गोष्टींचा परिणाम असा होतो की, बोर व श्रोडिंजर यांच्या सिद्धांतानुसार मिळणाऱ्या ऊर्जा पातळ्यांच्या संख्येत बरीच भर पडते. हायड्रोजन अणूच्या निम्नतम ऊर्जा पातळ्यांमध्ये सापेक्षता सिद्धांतामुळे होणारा फरक आकृती ८ मध्ये (अ) व (आ) या स्तंभांमध्ये दाखविला आहे. आधुनिक पुंज विद्युत् गतिकीचा उपयोग करून मिळणारा फरक स्तंभ (इ) मध्ये दाखविला आहे. याविषयीचा खुलासा पुंज विद्युत् गतिकी यापुढे येणाऱ्या उपशीर्षकाखाली केला आहे. डिरॅक यांच्या सिद्धांतापासून मिळणारा दुसरा फार महत्त्वाचा निष्कर्ष म्हणजे इलेक्ट्रॉन व त्याचा प्रतिकण (तितकेच द्रव्यमान पण विरुद्ध चिन्हाचा विद्युत् भार असलेला कण) पॉझिट्रॉन [→ पॉझिट्रॉन] याच्या उत्पत्ती व नष्टीकरण क्रियांवषयीचा खुलासा हा होय.
आ. ८. हायड्रोजन अणूच्या निम्नतम ऊर्जा पातळ्या : (अ) बोर-श्रोडींजर सिद्धांताप्रमाणे (आ) डिरॅक सापेक्षीय सिद्धांताप्रमाणे (इ) आधुनिक पुंज विद्युत् गतिकी सिद्धांताप्रमाणे. (आ) व (इ) यांमधील पातळ्यांचे विभाजन पटीने विवर्धित करून दाखविलेले आहे.
इलेक्ट्रॉन-पॉझिट्रॉन युग्माची उत्पत्ती नष्टीकरण : सापेक्षीय सिद्धांताप्रमाणे हॅमिल्टोनीयन
या स्वरूपात असल्यामुळे या समीकरणावरून इलेक्ट्रॉन धन आणि ऋण ऊर्जा अशा दोन्ही प्रकारच्या अवस्थांमध्ये मिळणार हे दिसून येते. वरील विवेचनात इलेक्ट्रॉनाच्या संपूर्ण ऊर्जेत त्याच्या शून्यगति-द्रव्यमानामुळे असणाऱ्या ऊर्जेचा समावेश केलेला असतो. डिरॅक समीकरणावरून धन ऊर्जा अवस्था पासून अनंतापर्यंत पसरलेल्या असतात, तर ऋण ऊर्जा अवस्था च्या खाली परत ऋण अनंतापर्यंत असतात असे कळते. निम्नतम धन अवस्था व उच्चतम ऋण अवस्था यांमधील अंतर एवढे असून याचे मूल्य १·०२ एवढे होते.
ऋण ऊर्जा अवस्थेमधील इलेक्ट्रॉनांचे निरीक्षण करता येत नाही याचे कारण डिरॅक यांनी खालीलप्रमाणे दिले आहे. त्यांच्या मते विश्वातील सर्व ऋण ऊर्जा अवस्था इलेक्ट्रॉनांनी संपूर्णपणे भरल्या आहेत. ऋण ऊर्जा अवस्था पृथक् असल्या तरी त्याची संख्या अनंत आहे व पाउली यांच्या विवर्जन तत्त्वानुसार त्या सर्व भरल्या गेल्या आहेत. ऋण ऊर्जा अवस्थामंधील इलेक्ट्रॉनांचे एका अवस्थेपासून दुसऱ्या अवस्थेत संक्रमण होणे शक्य नसल्यामुळे हे इलेक्ट्रॉन अनिरीक्ष्य होतात. आता या अवस्थांची संख्या अनंत असल्यामुळे त्या भरण्याकरिता अनंत इलेक्ट्रॉन लागणार व त्यामुळे खरे पाहिले असता अनंत अशी विद्युत् भार घनता निर्माण व्हावयास पाहीजे. डिरॅक यांच्या मते हे इलेक्ट्रॉन अनिरीक्ष्य असल्यामुळे ते या विद्युत्भार घनतेचे परिणाम दाखवू शकत नाहीत. त्यामुळे सैद्धांतिक विश्लेषणात ही विद्युत् भार घनता लक्षात घेण्याचे कारण नाही. आ. ९ वरून वरील विवेचन जास्त स्पष्ट होईल. (१) घन ऊर्जा अवस्था विभाग व (३) ऋण ऊर्जा अवस्था विभाग यांमध्ये (२) असाध्य विभाग आहे. ऋण ऊर्जा अवस्थेत असलेल्या इलेक्ट्रॉनाला पुरेशी ऊर्जा पुरवली तर तो अ या अवस्थेपासून आ या अवस्थेत येऊ शकतो.
आ अवस्थेतील इलेक्ट्रॉन नेहमीचा निरीक्ष्य इलेक्ट्रॉन होतो. अ येथे जी पोकळी निर्माण होते ती धन विद्युत् भार + e0 असलेल्या धन इलेक्ट्रॉना प्रमाणे वर्तणूक दाखविते. इलेक्ट्रॉनाच्या एवढेच द्रव्यमान पण तेवढाच धन विद्युत् भार असलेल्या पॉझिट्रॉन अशा इलेक्ट्रॉन पोकळीरूपी कणाचा शोध सी. डी. अँडरसन यांनी १९३२ च्या सुमारास लावला. १·०२ MeV पेक्षा जास्त ऊर्जेचा गॅमा किरण पदार्थातून गेला असता त्याचे इलेक्ट्रॉन पॉझिट्रॉन या युग्मात रूपांतर होते.
आ.9 डिरॅक सिद्धांताप्रमाणे इलेक्ट्रॉनाच्या ऊर्जा अवस्था : (1) धन ऊर्जा अवस्था, (2) असाध्य विभाग, (3) ऋण ऊर्जा पृथक् अवस्था (इलेक्ट्रॉनांनी पूर्ण भरलेल्या)
हा आविष्कार सुद्धा त्यानंतर थोड्याच काळात आढळला. पॉझिट्रॉन म्हणजे इलेक्ट्रॉन पोकळी असे वर्णन करता येईल. या क्रियेचे स्पष्टीकरण आ.९ मघील अ व आ या ठिकाणी केले आहे. अ येथील ऋण ऊर्जा इलेक्ट्रॉनाला अधिक ऊर्जा पुरवली गेल्यामुळे एकाच वेळी आ येथे एक नेहेमीचा इलेक्ट्रॉन तर अ येथे एक पोकळी म्हमजे पॉझिट्रॉन कसा निर्माण होतो हे लक्षात येते. याउलट तयार झालेल्या पोकळीला स्थैर्य नसते. इ या धन ऊर्जा अवस्थेतील एखादा इलेक्ट्रॉन ई या पोकळीत पडून तो ती परत भरू शकतो. अशा वेळी १·०२ MeV एवढीच ऊर्जा गॅमा किरणाच्या स्वरूपात उत्सर्जित केली जाते. डिरॅक सिद्धांताप्रमाणे प्रारणाचे कणात रूपांतर व कणाचे परत प्रारणात रूपांतर अशा दोन फार महत्त्वाच्या क्रियांचे प्राक्कथन व विशदीकरण करण्यात आले आहे. या दोन्ही क्रिया प्रत्यक्षात वरीलप्रमाणे घडतात हे प्रयोगाने सिद्ध झाले आहे. डिरॅक सिद्धांतामुळे भौतिकीत पॉझिट्रॉन हा पहिला प्रतिकण सापडला हे लक्षात घेण्याजोगे आहे.
पुंज विद्युत् गतिकी : रुढ भौतिकीप्रमाणए इलेक्ट्रॉनाला
या प्रमाणाची त्रिज्या असावी (येथे निर्वाताची विद्युत् पार्यता) इलेक्ट्रॉनाचे परिमित आकारमान लक्षात घेऊन तदनुरूप विद्युत् गतिकी सिद्धांताची मांडणी करण्याचा लोरेन्टस यांनी प्रयत्न केला इलेक्ट्रॉनाच्या स्वनिर्मित विद्युत् चुंबकीय क्षेत्राशी होणाऱ्या तीव्र परस्परक्रिमुळे या प्रयत्नाला यश मिळाले नाही. डिरॅक सिद्धांतामध्ये इलेक्ट्रॉनाच्या कक्षीय व परिवलनीय गतींमध्ये परस्परक्रिया होऊन इलेक्ट्रॉनाच्या ऊर्जा पातळ्यांत सूक्ष्म फरक पडतो. (हा फरक हायड्रोजन अणूकरिता सु. एवढा असतो.) हायड्रोजन अणूमधील इलेक्ट्रॉन व प्रोटॉन यांमध्ये चुंबकीय परस्परक्रिया होऊन त्यामुळे अणूच्या निम्नतम अवस्थांचे विभाजन होते. (या परस्परक्रियेमुळे ऊर्जेत पडनारा फरक या प्रमाणाचा असतो) १९४७ साली डब्ल्यू. ई. लँब व आर्. सी. रेदरफोर्ड यांनी असे दाखविले की, हायड्रोजन अणूंच्या या अवस्था (ज्या डिरॅक सिद्धांतानुसार अपभ्रष्ट आहेत म्हणजे त्यांची ऊर्जा एकच आहे) अपभ्रष्ट नसून त्यांमध्ये १,०६० मेगॅहर्ट्झशी अनुरूप एवढा (आ ८. मध्ये दाखविल्याप्रमाणे) ऊर्जा फरक आहे. याबरोबरच या अवस्थेची ऊर्जा डिरॅक यांनी दिलेल्या मूल्यापेक्षा ८, १३० मेगॅहर्ट्झशी अनुरूप ऊर्जेने अधिक आहे. ऊर्जा पातळ्यांमध्ये होणाऱ्या स्थानभ्रष्टतेला लँब स्थानच्युती असे म्हणतात. एका ऊर्जा पातळीपासून दुसऱ्या पातळीमध्ये इलेक्ट्रॉनाचे संक्रमण झाल्यामुळे प्रारणाचे उत्सर्जन होते. या क्रियेमध्ये प्रारणाच्या विद्युत् चुंबकीय क्षेत्राची इलेक्ट्रॉनावर जी प्रतिक्रिया होते त्यामुळे हा परिणाम मिळतो असे मानले जाते. सामान्यपणे सर्व सैद्धांतिक विवेचनात (याच्यात पुंजमिकीचाही समावेश होतो) इलेक्ट्रॉनाचा विद्युत् भार बिंदूच्या स्वरूपात असून त्याला आकारमान नसते असे मानलेले असते. हा विद्युत् भार बिंदू बाहेरून लावलेल्या विद्युत् चुंबकीय क्षेत्राशी किंवा स्वतःच्याच क्षेत्राशी परस्परक्रीया करु शकतो. दुर्दैवाने या दूसऱ्या प्रकारच्या परस्परक्रियेमुळे त्याची स्वयंऊर्जा अनंत होईल असा निष्कर्ष मिळतो. एस् टॉमॉनागा आणि जे एस् श्विंगर यांनी सुचविलेल्या पद्धतीने परस्परक्रियेमुळे मिळणाऱ्या ऊर्जासूत्रातून अशी अनंत ऊर्जा दर्शविणारी पदे गाळता येतात. या पद्धतीमध्ये परत प्रसामान्यीकरण केले जाते. हे कृत्य केले असता परस्पर क्रिया ऊर्जा पदावलीमध्ये काही कमी मूल्याची पदे राहतात. यामुळे होणारा उर्जेतील फरक कणाच्या (म्हणजे इलेक्ट्रॉनाच्या) शून्य बिंदू गतीमुळे निर्माण होतो असे दाखविता येते. अशा तऱ्हेने लँब स्थानच्युतीचे समाधानकारक स्पष्टीकरण देता येते. या नवीन पुंज विद्युत् गतिकीचा उपयोग केल्यास इलेक्ट्रॉनाला परिवलन गतीमुळे डिरॅक यांनी दाखविल्याप्रमाणे १ बोर मॅग्नेटॉन एवढे चुंबकीय परिबल नसून त्याचे मूल्य थोडे जास्त असते असे दाखविता येते. हा निष्कर्ष सुद्धा बरोबर आहे असे प्रयोगाने सिद्ध झाले आहे. रूढ विद्युत् गतिकीसंबंधीचे विवेचन ‘विद्युत् गतिकी’ या नोंदीत केले आहे.
भौतिकीय राशींकरिता अक्षय्यता नियम : रूढ भौतिकीत अनेक राशींकरिता अक्षय्यता नियम उपलब्ध आहेत. या राशींमध्ये ऊर्जा, रेषीय व कोनीय संवेग, द्रव्यमान, विद्युत् भार यांचा मुख्यतः समावेश होतो. [→ द्रव्य आणि ऊर्जा यांची अक्षय्यता , संवेगाची अक्षय्यता]. या राशी विक्रियेमुळे अक्षय राहतात असे रूढ भौतिकीत गृहीत धरावे लागते. पुंजयामिकीमध्ये या राशींच्या अक्षय्यतेचा संबंध प्रणालीची भौतिकीय अवस्था दाखविणाऱ्या (हॅमिल्टोनीयन) तरंग फलनाच्या विवक्षित प्रकारच्या सममितीशी जोडता येतो. निरनिराळ्या प्रकारचे रुपांतरण अथवा बदल केले असता तरंग फलनात जे तदनुरूप बदल मिळतात त्यांवरून फलनाची सममिती निश्चित केली जाते. X,y,z,या सहनिर्देशक समूहामध्ये एका भौतिकीय प्रणालीची (उदा., हायड्रोजन अणू)अवस्था या तरंग फलनाने दर्शविली आहे असे समजू. आपण जर याच प्रणालिचे x, y, z या सहनिर्देशक समूहाच्या सापेक्ष निरीक्षण केले (येथे x=-x,y=-y,z=-z), तर आपण तरंग फलनावर पर्यसन (ब्युत्क्रम अथवा उलट) रूपांतरण कृत्य केले असे होते. तरंग फलनाला सममिती असेल, तर या कृत्यामुळे दोन प्रकारचे परिणाम शक्य होतात. (१) आपणास परत हीच अवस्था मिळेल. (२)तरंग फलन – या स्वरूपात मिळेल, म्हणजे तरंग फलन तेच राहील पण त्याच्या चिन्हात बदल होईल. जर पहिल्या प्रकारचा बदल मिळाला, तर पुंज अवस्थेला सम समता आहे असे म्हणतात. चे चिन्ह बदलले, तर त्या अवस्थेची समता विषम आहे असे म्हणतात [→समता] जर तरंग फलन पर्यसन रूपांतरणाकरिता सममित असेल, तर त्याच्या आयगेन फलनाची समता कालानुसार बदलत नाही म्हणजेच त्याकरिता समता अक्षय राहते असे म्हणता येते. पुंजयामिकीमध्ये अशा अवस्था सुद्धा सापडतात की, ज्यांचे तरंग फलन पर्यसन रूपांतरणाकरिता सममित असत नाही. याचा अर्थ असा होतो की, या अवस्थाकरिता समतेला निश्चित मूल्य नाही म्हणजे याकरिता समता अक्षय राहत नाही. बीटा व म्यू-मेसॉन या कणांचा ऱ्हास ज्या दुर्बल परस्परक्रियांमुळे घडून येतो अशा क्रियांच्या तरंग फलनाला सममिती असत नाही अशा विक्रियेकरिता समता अक्षय राहत नाही असा निष्कर्ष टी. डी. ली आणि सी. एन्. यांग यांनी १९५७ मध्ये प्रथम सुचविला व तो प्रत्यक्ष प्रयोगाने सिद्ध झाला आहे. त्याबरोबरच सामर्थ्यवान परस्परक्रिया (उदा., न्यूक्लिऑनमधील)किंवा विद्युत् चुंबकीय परस्परक्रिया यांमध्ये समता अक्षय राहत नाही असा पुरावा मात्र उपलब्ध नाही.
X, y, z, सहनिर्देशक समूहाच्या सापेक्ष एका अणूपासून बनलेली भौतिकीय प्रणाली निर्वात अवकाशात आहे असे समजू. यावर कोणत्याही प्रकारचे क्षेत्र कार्य करीत नाही असे मानू. जर आपण या अणूला z-अक्षाभोवती या कोनातून फिरविले, तर त्याच्या अवस्थेत काही फरक पडणार नाही हे उघड आहे. पुंजयामिकीमध्ये हा गुणधर्म असणाऱ्या काही अवस्था आढळतात. या प्रणालीचे z-अक्षाभोवती या कोनामधून परिभ्रमण केल्यास मिळणारे तरंग फलन हे (मूळ तरंग फलन Xपरिभ्रमण गुणक) या स्वरूपात मिळते. परिभ्रमण गुणक हा या कोनाच्या समप्रमानात बदलतो. प्रणालीचे z- अक्षाभोवती परिभ्रमण करण्याकरिता वापरलेला कारक असा मानला, तर अशा अवस्थांकरिता
या समीकरनाने ही क्रिया दाखविता येते. येथे m=सत् संख्या व परिभ्रमण गुणक आहेत.
वरील समीकरणाची पूर्तता करणारी तरंग फलने z-अक्षाभोवतालच्या परिभ्रमणाकरिता सममिती दर्शवितात असे म्हटले जाते. अशा अवस्थांकरिता प्रणालीला अक्षाभोवती एवढा निश्चित कोनीय संवेग असून तो सतत अक्षय राहतो. याच प्रकारे इतर अक्षांभोवतीचे परिभ्रमण विचारात घेऊन तदनुरूप अक्षाभोवती असलेला कोनीय संवेग अक्षय राहतो असे दाखविता येते. या प्रत्येक अक्षाकरिता समी. (६७) सारख्या अटीची पूर्तता झाली पाहीजे हे उघड आहे.
रेषीय संवेगाच्या अक्षय्यतेकरिता वरच्या प्रमाणेच विवेचन करून त्याकरिता आवश्यक अशी अट मिळविता येते. समजा x,y,z,समूहाच्या सापेक्ष एका प्रणालीची अवस्था ने दर्शविली आहे. यावर Dx (a)हा कारक वापरला, तर प्रणाली X-अक्षाच्या दिशेने अंतरामधून स्थलांतरित केली जाते. या स्थलांतरामुळे चे नवे स्वरूप
या समीकरणाने जर मिळत असेल, तर तरंग फलनाला X-अक्ष दिशेत स्थलांतराकरिता सममिती आहे असे म्हणता येते. येथे हा स्थलांतरण गुणक आहे. याचा अर्थ असा होतो की, प्रणालीला x-अक्ष दिशेत kh एवढा रेषीय संवेग घटक असून तो कालानुसार अक्षय राहतो.
अशाच तऱ्हेची मीमांसा वापरुन ऊर्जेची अक्षय्यता सिद्ध करता येते. ज्या अवस्थेकरिता कालविलंबामुळे मूळ तरंग फलनामध्ये फक्त कला फरक (एखाद्या संदर्भाच्या सापेक्ष असणाऱ्या स्थितीत फरक) पडतो पण त्याकरिता ऊर्जा अक्षय राहते.
येथे DT (T) हा कालविलंब घडवून आणणारा कारक आहे, त्यामुळे मूळ फलनाला या कलागुणकाने गुणले जाते. या पदावलीमध्ये ऋण चिन्ह वापरण्याची प्रथा आहे.
वरील सर्व विवेचनाचा सारांश पुढीलप्रमाणे देता येईल. (१) कालामधील स्थलांतराकरिता जर तरंग फलन सममित असेल, तर त्याकरिता ऊर्जा अक्षय राहते. (२)x,y,z,या अक्षांवरील स्थलांतराकरिता जर तरंग फलन सममित असेल, तर त्याकरिता रेषीय संवेग अक्षय राहतो. X,y,z, या अक्षांभोवतील परिभ्रमणाकरिता जर तरंग फलन सममित असेल, तर त्याकरिता कोनीय संवेग अक्षय राहतो (४) पर्यसन रुपांतरणाकरिता जर तरंग फलन सममित असेल, तर समता अक्षय राहते.
पुंज सांख्यिकी : एका समूहातील कणामध्ये समतोल अवस्थेत ऊर्जा वितरण कसे असते याचा विचार रूढ यामिकीप्रमाणे मॅक्सवेल व एल्. बोल्टसमाल यांनी केला. त्यांच्या विश्लेषणात (१) कणामध्ये परस्परक्रिया नाही,(२) त्यांच्यात परस्पर आघात होऊन गतिज ऊर्जेची देवघेव होते, (३) कण एकमेकांपासून ओळखता येतात आणि (४) वरील परिस्थितीत त्यामध्ये अतिसंभाव्य ऊर्जा वितरण प्रस्थापित होते, या गोष्टी गृहीत धरल्या होत्या. विवेचनामध्ये प्रत्येक कणाची अवस्था त्याचे तीन स्थानीय सहनिर्देशक x,y,z,व तीन संवेगी सहनिर्देशक यांनी निश्चित केली जाते असे मानले असते. जवळजवळ एकाच जागी असलेले व जवळजवळ तेच संवेग घटक असलेले कण (x,x+dx), (y,y+dy) (z,z+dz), (px,px+dpx) (Py, py+dpy), (pz, pz+dpz) या विभागात असणार. हे कण षट्मितीय कला अवकाशाच्या dx dy dz dpx dpy dpzया अत्यल्प घनफळामध्ये असले पाहीजेत हे स्पष्ट आहे. या अत्यल्प घनफळामध्ये असणाऱ्या कणांची संख्या (nj)ही विश्लेषण करून
एवढी आहे असे दाखविता येते. यामध्ये ही कणाची ऊर्जा दाखविते तर k= बोल्टस्मान स्थिरांक, T= तापमान .Bयाचे मूल्य काढण्याकरिता या अटीचा उपयोग केला जातो. N =समूहातील एकंदर कणसंख्या तर Eसमूहाची एकंदर ऊर्जा
समूहातील कण जर रूढ भौतिकीप्रमाणे न वागता ते पुंजयामिकीच्या नियमांचे पालन करीत असतील, तर त्याकरिता प्रथम तीन महत्त्वाच्या गोष्टी लक्षात घ्याव्या लागतात. (१) अनिश्चितता तत्त्वाप्रमाणे असल्यामुळे कला अवकाशाच्या अत्यल्प घनफळाचे मूल्य यापेक्षा कमी असू शकत नाही. (२) पुंजयामिकीप्रमाणे बऱ्याच वेळी समूहामधील कणांकरिता फक्त काही विशिष्ट पृथक् ऊर्जामूल्ये अनुज्ञात असतात. (३) कणाच्या परिवलन गतीनुसार कोणत्याही एका अवस्थेत असू शकणाऱ्या कणांची संख्या निश्चित होते जर कणाकरिता परिवलन पुंजांक हा पूर्णांकाच्या स्वरूपात असेल त्याकरिता मिळणारे तरंग फलन सममित असते. अशा परिस्थितीत एका अवस्थेत असणाऱ्या कणसंख्येवर कोणतीच मर्यादा नसते. या प्रकारच्या कणांकरिता सत्येंद्रनाथ बोस व आइन्स्टाइन यांची सांख्यिकी योग्य ठरते. फोटॉन, मेसॉन यांसारखे मूलभूत कण व हीलीयम (He4)सारखे अणू यांकरिता ही सांख्यिती अनुरूप ठरते. याउलट जर कणाकरिता परिवलन पुंजांक १/२ असेल किंवा तो अर्धपूर्णांकाच्या स्वरूपात असेल तर त्याकरिता ई. फेर्मी व डिरॅक यांची सांख्यिकी वापरावी लागते. धातूमधील इलेक्ट्रॉन समूहाकरिता ही सांख्यिकी सुयोग्य ठरते.
बोस आइन्स्टाइन सांख्यिकी : या सांख्यिकीमध्ये समूहातील कण एकरूप असल्यामुळे एक कण दुसऱ्या कणापासून वेगळा ओळखता येत नाही असे मानले असते. समतोल अवस्थेत जर अतिसंभाव्य ऊर्जा वितरणाचा शोध घेतला तर
असे सूत्र मिळते. यामध्ये Ei ऊर्जा असलेल्या कणांची संख्या Nj याने दाखविली आहे. रूढ सांख्यिकीशी तुलना करता येते Ei ऊर्जेला विशिष्ट रुंदी असते. त्यामुले Ei,Ej+dej यांमध्ये पुंजयामिकीनुसार अनुज्ञात असलेल्या सर्व पृथक् ऊर्जा पातळ्यांचा समावेश केला जातो. gi=अपभ्रष्ट नसलेल्या वरील पातळ्यांची संख्या. वरील सूत्रात (k= बोल्टस्मान स्थिरांक व T= तापमान) दाखविता येते. सामान्यपणे aया स्थिरांकाचे मूल्य काढण्याकरिता
या पूर्वी निर्देशित केलेल्या अटीचाच उपयोग केला जातो. येथे n= समूहकणांची एकंदर संख्या व Ie=समूहाची एकंदर ऊर्जा. बोस यांनी आपल्या विवेचनामध्ये या अटीचा उपयोग केला नाही, कारण त्यांच्या मते फोटॉनाचे शोषण होण्याची शक्यता असल्यामुळे त्यांची संख्या स्थिर राहते हे मानणे योग्य नाही. बोस यांचे मूळ विश्लेषण फोटॉन कणांच्या समूहाकरिता केले होते. आइन्स्टाइन यांनी त्याचा उपयोग योग्य वायुकणांकरिता केला. वायुकणांकरिता ही अट अर्थातच यथार्त ठरते. वायुकणांकरिता
या सूत्राने मिळतो असे दाखविता येते असेल, तर बोसआइन्स्टाइन सांख्यिकी व रूढ सांख्यिकी यांपासून मिळणाऱ्या निष्कर्षात फारसा फरक नसतो असे आढळते. सूत्रात m = कणांचे द्रव्यमान व N=एकक आयतनामध्ये असणाऱ्या कणांची संख्या आहे. तापमान कमी केले असता चे मूल्य कमी होईल असे कळते. आइन्स्टाइन यांनी द्रवरूप हीलियमाकरिता (ज्याकरिता परिवलन स्थिरांक पूर्णांक आहे) ही सांख्यिकी वापरून त्याची काही आश्चर्यकारक गुणधर्मांचे विशदीकरण केले आहे. ही सांख्यिकी फोटॉन कणांच्या समूहाकरिता वापरून त्यापासून प्लांक प्रारण नियम [→उष्णता प्रारण] मिळविता येतो. ज्या कणाकरिता बोस आइन्स्टाइन सांख्यिकी वापरणे आवश्यक असते अशा कणांस बोसॉन अशी संज्ञा दिली जाते. यामध्ये फोटॉन व इतर परिवलनरहीत कणांचा (उदा.., निम्नतम अवस्थेतील आल्फा कण यांचा ) समावेश होतो.
फेमी डिरॅक सांख्यिकी : ज्या कणाकरिता परिवलन पुंजांक १/२ किंवा अर्धपूर्णांकाच्या स्वरूपात असतो त्याकरिता संपूर्न तरंग फलन प्रतिसममित असते. या समूहामध्ये ऊर्जा असणाऱ्या कणांची संख्या niअसेल तर या सांख्यिकीप्रमाणे
वरील सूत्रात Iei ला विशिष्ट रुंदी असून त्यामध्ये (म्हणजे ei,ei=deiया विभागात) पुंजयामिकीनुसार अनुज्ञात असलेल्या (अपभ्रष्ट नसलेल्या) या पृथक् ऊर्जा पातळ्यांचा समावेश केलेला आढळतो. असे दाखविता येते. याच मूल्याचा असतो. इलेक्ट्रॉनाकरिता द्रव्यमान mकमी मूल्याचे असल्यास त्याकरिता धातूमधील मूक्त इलेक्ट्रॉनांकरिता फेर्मी डिरॅक सांख्यिकीपासून मिळणारे निष्कर्ष रूढ सांख्यिकीपासून मिळणाऱ्या निष्कर्षांपेक्षा फारच वेगळे असतात. ज्या अणूंकरिता परिवलन पुंजांक अर्धपूर्णांकाच्या स्वरूपात असतात त्याकरिता हीच सांख्यिकी वापरणे योग्य ठरते. ज्या कणांकरिता ही सांख्यिकी योग्य ठरते अशा कणांना फेर्मिऑन असे म्हणतात. यामध्ये इलेक्ट्रॉन, प्रोटॉन व न्यूट्रॉन यांचा समावेश होतो. या सर्वांकरिता कोनीय संवेग इतका असतो. बोसॉन नसलेला आणि फेर्मिऑनही नसलेला असा एकही कण आढळलेला नाही. [→ साख्यिकीय भौतिकी ]
संदर्भ : 1. Bohm, D. Quantum Theory, Bombay, 1960.
2. Born, m Atomic physics, London, 1962.
3. Brackenridge, j n Rosen berg R. M. Principles of Physics and Chemistry Physics, New York, 1970.
4. Cook, C. S. Modern Atomic and Nuclear Physics, New York, 1961.
5. Feynman R. P. Leighton R. B sandas, M The Feynman Lectures on Physics Vol, Bombay, 1966.
6. Gurney R. W. Elentery Quantum mechanics Lincoln, 1963.
7. Harris L. Loeb A. L. Introduction to Waνe Mechanics, New York, 19 1963.
8. Herzberg G. Atomic spectra and atomic Structure, New York, 1944.
9. LiνeseY D. L Atomic And Nuclear Physicl Waltham mass 1966.
10. Osgood T. H. Ruark A. E. Hutchisson E Atoms Radiation & Nuclei, New York, 1955.
11. Park, D. Introduction to Quantum Theory New York 1964.
12. Pauling L. Wilson E. B. Introduction to Quantum Mechanics, New York, 1935.
13. Powell J. L. crascan B Quantum Mechanics Reading Mass, 1961.
14. Sandorfy C. Electronic Spectra And Quantum Chemistry Englewood Coiffl N. J., 1964.
15. Trigg G. Quantum Mechanics, Princeton 1964.
भावे श्री द. चिपळोणकर व त्रि.
“