पाय् (π) : प्रतलावर काढलेल्या कोणत्याही वर्तुळाचा परिघ (लांबी) आणि त्याचा व्यास (लांबी) यांचे गुणोत्तर एकच (कायम) असते, हे गुणोत्तर दर्शविण्याकरिता π (पाय्) हे ग्रीक अक्षर वापरतात [मात्र ही परिस्थिती यूक्लिडीय भूमितीमध्येच सत्य असते. अयूक्लिडीय भूमितीमध्ये हे गुणोत्तर वर्तुळाच्या आकारमानानुसार बदलत जाते. उदा., गोलीय भूमितीत गोलावरील वर्तुळाच्या बाबतीत व्यास जसजसा वाढत जाईल तसतसे हे गुणोत्तर कमी होत जाते आणि भास गोलावर ते वाढत जाते →भूमिति]. हे गुणोत्तर तीनापेक्षा अधिक आहे हे ध्यानात आले होते परंतु त्याचे नेमके मूल्य परिमेय संख्या [→संख्या] म्हणून व्यक्त करण्याचे सर्व प्रयत्न फसत होते. π चे मूल्य ३(१/७) आणि ३(१०/७१) यांच्या दरम्यान असल्याचे आर्किमिडीज यांनी प्रथम दाखविले. पुरातन काळातील ज्यू लोकांच्या ग्रंथामध्ये (बुक ऑफ किंग्जमध्ये) π चे मूल्य ३ मानले आहे ते प्रत्यक्ष मूल्यापेक्षा ५ % ने कमी आहे. ईजिप्तमधील लोकांनी यापेक्षा जास्त आसन्न (जवळजवळ असणारे) मूल्य मिळविले. ऱ्हिंंड पपायरस (इ.स.पू. १७००) मध्ये π चे मूल्य ३(१३/८१) किंवा (१६/९)२ असे दिले आहे.ते प्रत्यक्षापेक्षा जवळजवळ १ % ने जास्त आहे. बौधायनादि भारतीय गणितज्ञांनी शुल्बसूत्रात π चे मूल्य ३.०८८ असे दिले आहे. हे मूल्य π च्या नेमक्या मूल्यापेक्षा ५ % ने कमी आहे. त्यापेक्षा अधिक नजीकचे मूल्य चिनी गणितज्ञ आँग हाँग (इ.स. ७८-१३९) यांनी √१० असे दिले आहे. त्यानंतर भारतीय गणितज्ञ आर्यभट (इ.स. ४७६ ?) यांनी हे मूल्य ६२,८३२/२०,००० असे दिले. हे दशांश अपूर्णांकात ३.१४१६ येते. चार दशांश स्थळापर्यंत ते बरोबर आहे. आजकाल ३.१४१६ हेच मूल्य स्थूलमानाने योग्य म्हणून वापरले जाते. तसेच सर्वसाधारण व्यवहारात २२/७ हे मूल्य वापरण्यात येत असून ते फक्त तीन दशांश स्थळापर्यंत बरोबर आहे. १८५३ च्या सुमारास विल्यम शँक्स यांनी गणितीय श्रेढीचा [→श्रेढी] उपयोग करून ७०७ दशांश स्थळापर्यंत π चे मूल्य काढले होते. जादवपूर विद्यापीठातील (प. बंगाल) एस्. के.मुकर्जी यांनी असे अपूर्णांकी मूल्य शोधून काढले असून ते π च्या १४ दशांश स्थळापर्यंत बरोबर येते,असे दाखविले आहे.
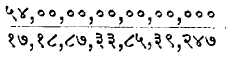
πचे सोळा दशांश स्थळांपर्यंतमूल्य ३.१४१५९२६५१५८९७९३२ असे आहे. इलेक्ट्रॉनीय संगणकाच्या (गणकयंत्राच्या) साहाय्याने π चे मूल्य १९६२ मध्ये १,००,००० दशांश स्थळापर्यंत काढण्यात आले पण π चे अचूक मूल्य काढणे शक्य नाही कारण π ही संज्ञा परिमेय नाही. π ही संख्या अपरिमेय असल्याचे फ्रेंच गणितज्ञ ए. एम्. लझांद्र यांनी १७९४ मध्ये दाखविले.
गणिताच्या इतिहासात काही प्रश्न यक्षप्रश्न म्हणून ओळखले जातात [→गणितातील अनिर्वाहित प्रश्न]. त्यांपैकी एक म्हणजे वर्तुळाचे ‘चौरसीकरण’ म्हणजेच केवळ कंपास व सरळपट्टी या दोन उपकरणांच्या साहाय्याने दिलेल्या वर्तुळाशी समक्षेत्र चौरस काढणे. हा प्रश्न प्राचीन ग्रीक गणितज्ञांनी मांडला. या प्रश्नाची उकल करण्याचे प्रयत्न भारतीय व पाश्चात्त्य गणितज्ञांनी कित्येक वर्षे केला. शेवट फ्रेंच गणितज्ञ एव्हारीस्त गाल्वा (१८११-३२) यांच्या बीजगणितातील संशोधनानंतर कोणत्या रचना कंपास व सरळपट्टी या उपकरणांनी शक्य आहेत व कोणत्या नाहीत याचा निर्णय लागला आणि जर्मन गणितज्ञ सी. एल्. एफ्. लिंडेमान (१८५२-१९३९) यांनी π ही संख्या बीजातीत (परिमेय संख्या सहगुणक असलेल्या कोणत्याही समीकरणाचे बीज नसलेली) असल्याचे दाखविल्यानंतर ‘वर्तुळाचे चौरसीकरण’ अशक्य असल्याचे प्रस्थापित झाले.
π चे आसन्न मूल्य काढण्याच्या पुष्कळ पद्धती उपलब्ध आहेत. कित्येक निरनिराळ्या ⇨ फुर्ये श्रेढींच्या साहाय्याने हे मूल्य काढता येते परंतु त्याकरिता श्रेढीतील पुष्कळ पदे घ्यावी लागतात. जेम्स ग्रेगरी (१६३८-७५) या स्कॉटिश गणितज्ञांनी स्प–१(क्ष) करिता
स्प–१क्ष = क्ष –क्ष३/३+क्ष५/५-क्ष७/७+….. अशी श्रेढी दिली.
यात क्ष=१ घालून मिळणार्या श्रेढीला जी. डब्ल्यू. लायप्निट्स यांनी ती सिद्ध केली म्हणून लायप्निट्स श्रेढी म्हणतात.
π/४= १-१/३ + १/५ – १/७
पण या श्रेढीची अभिसारिता [→श्रेढी] फारच मंद असल्याने π चे मूल्य काढण्याकरिता हिचा उपयोग होत नाही. त्याकरिता

या सूत्राचा उपयोग करून अभिसारितेचा वेग वाढविणे योग्य होईल.
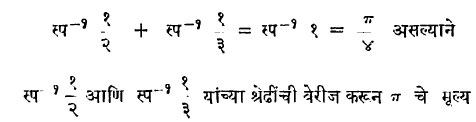
मिळविण्याकरिता कमी पदे पुरतील.

व्हेगा (१७५६-१८०२)या गणितज्ञांनी π चे मूल्य १४० दशांश स्थळापर्यंत काढले होते. अर्थात यापेक्षाही अधिक वेगवान अभिसारिता असलेल्या श्रेढी मिळविणे शक्य आहे. उदा.,

लक्षात येईल. वर मांडलेली लायप्निट्स श्रेढी ही नीलकंठ नावाच्या भारतीय गणितज्ञांनी १६२५ साली मांडली होती. तसेच
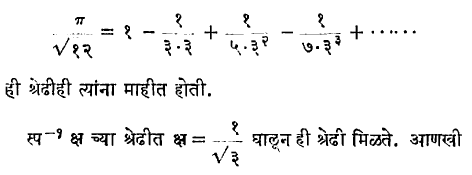
एक उपयुक्त श्रेढी पुढीलप्रमाणे,

π चे मूल्य परंपरित अपूर्णाकांच्या भाषेतही मांडता येते, ते पुढीलप्रमाणे,

अनंत गुणाकाराच्या भाषेमध्ये π चे मूल्य पुढीलप्रमाणे मांडता येते.

संदर्भ : Smith, D. E. History of Mathematics, New York, 1953.
गुर्जर, ल. वा.; राईलकर, म. रा.