पर्याप्तीकरण

पर्याप्तीकरण : एखादा निर्णय, अभिकल्प (आराखडा) किंवा प्रणाली जास्तीत जास्त आदर्श, कार्यतत्पर किंवा कार्यनिष्ठ करण्याच्या तंत्राला पर्याप्तीकरण म्हणता येईल. विशिष्ट गणिती सिद्धांत, पद्धती व तंत्र यांचा विचार पर्याप्तीकरणात येतो. निर्णय सिद्धांताप्रमाणे निश्चित माहितीच्या आधारे घेण्यात येणाऱ्‍या निर्णयात पर्याप्तीकरणाचा विशेष उपयोग होतो [⟶ निर्णय पद्धती]. पर्याप्तीकरणाची विविध तंत्रे आहेत. तंत्रविद्येच्या विकासाबरोबर पर्याप्तीकरणाला विशेष महत्त्व आले आहे. त्यामुळे त्यामागील गणिती सिद्धांतांचे संशोधन झाले आहे. किंबहुना ⇨ नियंत्रण प्रणाली व पर्याप्तीकरणाच्या पद्धती यांचा यापुढील विकास गणिती संशोधनावर अवलंबून आहे, असे म्हटल्यास वावगे होणार नाही. तसेच संगणकाच्या (गणितकृत्ये करणाऱ्‍या यंत्राच्या) विकासामुळे पर्याप्तीरकरणाच्या तंत्राचा व्यवहारात उपयोग करणे शक्य झाले आहे.

जे. बी. जे. फूर्ये या फ्रेंच गणितज्ञांनी १८२३ मध्ये रेखीय (किंवा रेषीय कार्यक्रमण या गणिती प्रतिकृतींचा दैनंदिन व्यवहारातील निर्णय घेण्यास उपयोग होईल असे दाखवून दिले होते. १९३९ साली रशियन गणितज्ञ एल्. व्ही. कांटोरोव्ह्यिच यांनी उत्पादन, नियोजन व व्यवस्थापन यांमध्ये रेखीय कार्यक्रमणाचा उपयोग या विषयावर प्रबंधिका प्रसिद्ध केली होती. १९२८ मध्ये जॉन फोन नॉयमान यांनी ⇨खेळ सिद्धांत मांडून या विषयाचा गणिती पाया घातला, तरी १९४७ पर्यंत गणिती प्रतिकृतींचा उपयोग केला गेला नाही परंतु त्यानंतर अमेरिकेच्या संरक्षण खात्याने ⇨ संक्रियात्मक अन्वेषणाचे तंत्र वापरावयास सुरुवात केली व या विषयात गणिती प्रतिकृतींचा वापर सुरू झाला. १९४७ मध्ये फोन नॉयमान यांनी रेखीय कार्यक्रमण व आव्ह्यू खेळ यांची तुल्यता दाखवून दिली तसेच ⇨ द्वित्व तत्त्वाची संकल्पना मांडली. त्यानंतर सिंप्लेक्स पद्धतीकरिता (हिचे वर्णन पुढे दिले आहे) १९५१ साली संगणक कार्यक्रमण [⟶ संगणक] तयार केले गेले. हल्ली हजारो चल पदे (बदलणाऱ्‍या राशी) असलेले समीकरणे संगणकाच्या साहाय्याने सोडविता येतात.

गणिती प्रतिकृती : एखाद्या उत्पादन केंद्रात विविध वस्तूंचे उत्पादन करताना पुष्कळच गोष्टींचा विचार करावा लागतो. उदा., स्पर्धेमुळे वस्तूंच्या किंमतींत होणारे बदल, कच्चा मालाची उपलब्धता, विविध यंत्रांची कार्यक्षमता, यंत्रे नादुरुस्त होण्याची शक्यता, बाजार पेठेतील विविध कालखंडात बदलणारी मागणी इ. बाबींचा एकमेकींवर होणारा परिणाम लक्षात घेऊन उत्पादन राशी ठरवावी लागते. अशा परिस्थितीत गणिती प्रतिकृती तयार करून विविध बाबींचे होणारे परिणाम व पर्याप्त उत्पादन काढता येते. गणिती प्रतिकृतीत एकच पर्याय उपलब्ध होत नाही, तर अनेक पर्याय उपलब्ध होतात. त्यामुळे व्यवस्थापकाला निर्णय घेण्यास सोपे जाते. कोणत्याही प्रणालीच्या गणिती प्रतिकृतीमध्ये त्या प्रणालीच्या क्षमतेचा निकष उद्दिष्ट फलनाने दर्शविला जातो. क्षमतेच्या निकषामध्ये भांडवलावरील नफा, उत्पादन खर्च, संरक्षण खात्याची संरक्षणक्षमता इ. येऊ शकतील. यंत्राची कार्यक्षमता, कच्च्या मालाचा पुरवठा, मालाच्या किंमती, वस्तूचा साठा इ. बाबींमुळे समीकरणाच्या चलांवर निर्बंध येतात. बऱ्‍याचशा गणिती प्रतिकृतींमध्ये समीकरणे रेखीय (एकघाती) असतात. त्यामुळे येथे रेखीय कार्यक्रमणाचा प्रथम विचार केला आहे.

रेखीय कार्यक्रमण प्रतिकृती : एका कारखान्यामध्ये दोन वस्तूंचे (समजा x व y) उत्पादन करावयाचे आहे. कारखान्याचे तीन विभाग आहेत. प्रत्येक विभागातील यंत्रांची व मनुष्यबळाची संख्या लक्षात घेता b₁, b₂ व b₃ हे स्थिरांक कार्यक्षमता दर्शवितात. प्रत्येक वस्तूला प्रत्येक विभागात लागणारा वेळ (a₁₁, a₁₂, a₂₁, a₂₂, a₃₁ व a₃₂ हे स्थिरांक) माहीत आहे. प्रत्येक वस्तूच्या उत्पादनामुळे होणारा नफा (x मुळे C व y मुळे D; C व D स्थिरांक) माहीत आहे. वस्तूचे उत्पादन अर्थात ऋण (–) असणार नाही. या प्रश्नाची रेखीय प्रतिकृती खालीलप्रमाणे होईल.

max. (Cx + Dy)                           …         …         …         (१)

(Cx + Dy) हे उद्दिष्ट फलन असून त्याचे मूल्य जास्तीत जास्त करणे (max.) हा हेतू आहे.

निर्बंध :

a₁₁ x + a₁₂ y ≤ b₁                          …         …         …         (२)

a₂₁ x + a₂₂ y ≤ b₂                         …         …         …         (३)

a₃₁ x + a₃₂ y ≤ b₃                         …         …         …         (४)

x ≥ 0 ; y≥0                                    …         …         …         (५)

वस्तू x वस्तू y किती संख्येने उत्पादित कराव्यात म्हणजे जास्तीत जास्त नफा होईल व प्रत्येक विभागाच्या कार्यक्षमतेच्या मर्यादा ओलांडल्या जाणार नाहीत, ही येथे समस्या आहे.

आ. १ मध्ये (२), (३) व (४) या असमांचे मूल्य शून्य धरून आलेख काढलेले दाखविले आहेत. हे तिन्ही निर्बंध पाळावयाचे असल्यास उद्दिष्ट फलन (१) चा निर्वाह (उत्तर) पअआइ या बहुभुजातील किंवा बहुभुजाच्या बाजूंवरील बिंदू असावयास पाहिजे. वरील बहुभुज हा निर्वाह संच म्हणता येईल. ईउ ही रेषा θ या ढाळाने (उताराने) काढली आहे [tan θ = D/C]. ईउ या रेषेवरील कोणत्याही बिंदूचे सहनिर्देशक घेऊन उद्दिष्ट फलनाचे मूल्य काढल्यास एकच येईल म्हणून या रेषेस सम-नफा रेषा म्हणता येईल. ईउ या रेषेस ऊए आणि कख या समांतर रेषा काढल्या आहेत. या दोन्ही रेषांवरील बिंदूंचे सहनिर्देशक घेऊन उद्दिष्ट फलनाचे मूल्य काढल्यास पूर्वीपेक्षा जास्त येईल. कख या रेषेच्या पलीकडे समांतर रेषा काढल्यास त्यावरील बिंदू बहुभुजाच्या बाहेर जातील म्हणजे निर्वाह संचात असणार नाहीत. म्हणून दिलेले निर्बंध पाळण्यात न आल्यामुळे काढलेला निर्वाह इष्ट निर्वाह होणार नाही. उद्दिष्ट फलनाचे जास्तीत जास्त मूल्य आ या बिंदूचे सहनिर्देशक घेऊन काढता येते. वरील अनेकवर्णी (अनेक चल असलेल्या) समीकरणाचे अनेक निर्वाह येतात.

वरील उदाहरणात दोनच चल आहेत. परंतु प्रत्यक्ष व्यवहारात चलांची संख्या मोठी असते. चलांची संख्या n आहे असे समजल्यास निर्वाह संच n–मितीय अवकाशातील एका अतिप्रतलातील बिंदूंचा संच होईल. येथे रेखीय प्रतिकृती व्यापक स्वरूपात पुढीलप्रमाणे मांडता येईल.

उद्दिष्ट फलन

max. हे पर्याप्तीकरण दर्शविण्याकरिता वापरले आहे. त्याचा अर्थ फलनाचे मूल्य जास्तीत जास्त करणे असा आहे. min. हे संक्षिप्त रूप हेच मूल्य कमीत कमी करावाचे असल्यास वापरण्यात येते.

उद्दिष्ट फलनाचे निर्बंध खालीलप्रमाणे

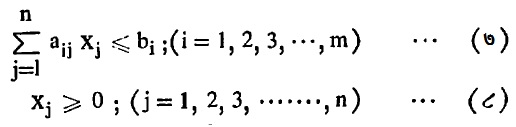
कोणत्याही असमेचे रूपांतर समीकरणात करता येते. उदा., x > 5 ही असमा x – x₁ = 5 अशी व x < 5 ही असमा x + x₂ =5 अशा समीकरण रूपाने मांडता येतात. x₁ व x₂ हे चल असून त्यांना शिथिल चल म्हणतात. त्यातील x₁ ≥ 0 ; x₂ ≥ 0.

उद्दिष्ट फलनाचे मूल्य x₀ असे समजून व शिथिल चलाचा उपयोग करून उद्दिष्ट फलन व असमा (७) खालीलप्रमाणे विस्तारित स्वरूपात मांडता येतात :

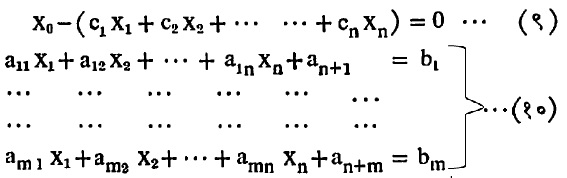
समीकरण (१०) मध्ये a_n+1, ………, a_n+m हे शिथिल चल आहेत.

सदिशांच्या साहाय्याने [⟶ सदिश] (६), (७) व (८) मध्ये दिलेला प्रश्न खालीलप्रमाणे मांडता येतो.

max. px                          …         …         …         (११)

निर्बंध :

Ax ≤ b                            …         …         …         (१२)

x ≥ 0                              …         …         …         (१३)

येथे A = [a_ij], m × n आव्यूह, (i = 1, 2, …….., m), (j = 1, 2,…………,m);

x = (x₁, x₂, …, x_n)^T, T हे अक्षर पक्षांतरित सदिश दर्शविते;

p = (p₁, p₂,……., p_n) ; b = (b₁, b₂, …….,b_m)^T.

चलांच्या संख्येपेक्षा समीकरणांची संख्या कमी असल्यास (९) व (१०) समीकरणांना अनेक निर्वाह असतात. जर इष्ट निर्वाह अस्तित्वात असेल, तर (n-m) इतक्या चलांचे मूल्य शून्य घेऊन एक तरी इष्ट निर्वाह मिळू शकतो. हा इष्ट निर्वाह पर्याप्त असेलच असे नाही. जर उद्दिष्ट फलनाला निम्न बंध [अधोबंध; ⟶ फलन] असेल, तर (n–m) चलांचे मूल्य  शून्य ठेवून उद्दिष्ट फलनाचे लघुतम मूल्य अस्तित्वात असते. अनेकवर्णी समीकरणे सोडविण्याच्या निरनिराळ्या पद्धती आहेत तसेच पर्याप्तीकरणाच्याही विविध पद्धती आहेत. त्यांपैकी सिंप्लेक्स पद्धत व तिचे नियम एका लहान उदाहरणाद्वारे खाली दिले आहेत.

सिंप्लेक्स पद्धत : एका औद्योगिक प्रश्नाची गणिती प्रतिकृती खालीलप्रमाणे आहे.

निर्बंध :

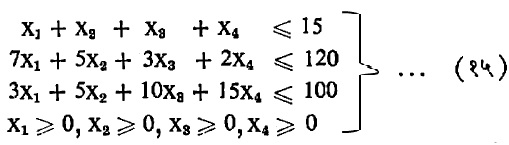
उपसादन पहिले : (पर्याप्त मूल्याच्या जास्तीत जास्त जवळचे मूल्य काढण्याच्या प्रक्रियेतील म्हणजे उपसादन प्रक्रियेतील पहिली पायरी). उद्दिष्ट फलनाचे (x₀) हे मूल मूल्य आहे असे समजून व x₅, x₆, x₇ हे शिथिल चल वापरून (१४) व (१५) वर मांडले आहेत.

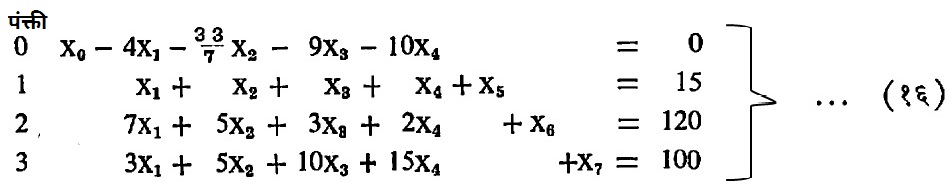
वर दिलेल्या नियमाप्रमाणे (n – m = ७ – ३ = ४) ४ चलांची मूल्ये शून्य घेता येतील. x₁, x₂, x₃ व x₄ या चलांची मूल्ये शून्य घेऊन x₀, x₅, x₆ व x₇ यांची मूल्ये अनुक्रमे ०, १५, १२० व १०० येतात. यावरून उद्दिष्ट फलनाचे प्राथमिक मूल्य शून्य येते. समीकरण संच (१६) वरून असे दिसून येते की, x₁ ते x₄ या चलांची मूल्ये १ धरल्यास उद्दिष्ट फलनाचे मूल्य वाढेल. तसेच या वर्तमान निर्वाहात x₁ ते x₄ या चलांचे मूल्य शून्य आहे. ह्या चलांना वर्तमान निर्वाहातील मूलेतर चल म्हणतात. तसेच x₀, x₅, x₆ व x₇ यांना मूल चल असे म्हणतात. समीकरण संच (१६) मधील पंक्ती क्र. ० मधील मूलेतर चलांचे गुणक (ऋण असल्यास) हे मूलेतर चलांच्या मूल्यात एकक वाढ केल्यास उद्दिष्ट फलनाच्या मूल्यात होणारी वाढ दर्शवितात आणि मूलेतर चलांचे गुणक धन असल्यास उद्दिष्ट फलनाचा

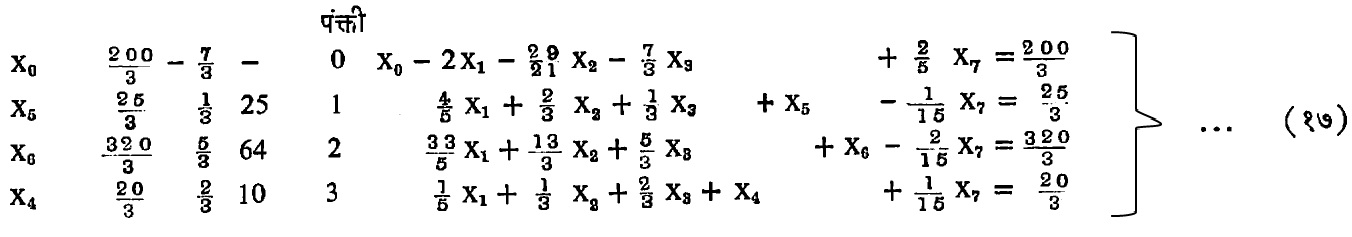 ऱ्‍हास दर्शवितात. उदा., x₄ चे मूल्य शून्य आहे ते एक केल्यास उद्दिष्ट फलनाचे मूल्य १० ने वाढेल. उद्दिष्ट फलनाचे पर्याप्तीकरण करावयाचे असल्यामुळे पहिल्या उपसादनापेक्षा जास्त मूल्याला निर्वाह काढला पाहिजे. दुसरे उपसादन काढताना वर्तमान निर्वाहातील मूल चलांपैकी एका चलाच्या

ऐवजी मूलेतर चल मूल चल घेऊन निर्वाह काढला पाहिजे. उद्दिष्ट फलनात जास्तीत जास्त वाढ x₄ हा चल मूल चल घेतल्यास होते. तसेच x₄ चे मूल्य जास्त केल्यास उद्दिष्ट फलनाच्या मूल्यात वाढ होईल. परंतु x₄ मध्ये वाढ केल्यास इतर चलांची मूल्ये कमी करावी लागतील. समीकरण संच (१६)  मधील पंक्ती क्र. १, २, ३ वरून असे दिसून येईल की, x₄ चे मूल्य १५/१ पेक्षा जास्त केल्यास x₅; १२०/२ पेक्षा जास्त केल्यास x₆; व १००/१५ पेक्षा जास्त केल्यास x₇ ह्या चलांचे मूल्य ऋण होते. परंतु दिलेल्या निर्बंधाप्रमाणे ते ० किंवा धन असावयास पाहिजे. वरील x₄ च्या मूल्यांपैकी सर्वांत कमी म्हणजे १००/१५ = ६·६७ इतक्यापर्यंत वाढविल्यास उद्दिष्ट फलनात  जास्तीत जास्त वाढ होईल. यापेक्षा जास्त घेतल्यास इष्ट निर्वाह होणार नाही. म्हणून (१६) पैकी तिसऱ्‍या पंक्तीतील मूल चल X₇ च्या ऐवजी x₄ हा मूल चल म्हणून दुसऱ्‍या उपसादनात घेतला जाईल. नवीन निर्वाहाकरिता मूल चलांची निवड करताना खालील नियम मांडता येतील.

नियम (१) : वर्तमान निर्वाहातील जास्तीत जास्त ऋण गुणक असलेला उद्दिष्ट फलनातील [(१६) मधील पंक्ती ०] मूलेतर चलांची नव्या उपसादनाकरिता मूल चल म्हणून निवड करा. सर्वच मूलेतर चलांचे गुणक धन वा शून्य असतील, तर पर्याप्त निर्वाह मिळाला असे समजावे.

नियम (२) : वर्तमान निर्वाहातील प्रत्येक पंक्तीतील उजव्या बाजूचे स्थिरांक व त्याच पंक्तीतील नियम १ मध्ये निवड केलेल्या चलाचे गुणक यांची गुणोत्तरे काढा. सर्वांत कमी गुणोत्तर येणाऱ्‍या पंक्तीतील वर्तमान मूल चलाच्या ऐवजी नियम १ मधील चल मूल चल म्हणून घ्या. गुणोत्तराचे मूल्य शून्य किंवा ऋण असल्यास ती गुणोत्तरे विचारात घ्यावयाची नाहीत.

उपसादन दुसरे : x₀, x₄, x₅, x₆ हे मूल चल व x₁, x₂, x₃, x₇ हे मूलेतर चल होतील. मूलेतर चलांचे मूल्य शून्य धरले आहे. समीकरण संच (१६) मधील पंक्ती ३ मधील x₄ चा गुणक एक करून व पंक्ती ०, १ व २ यांतून x₄चे निराकरण केल्यास खालील समीकरण संच (१७) मिळतो.

उपसादन तिसरे : नियम (१) व (२) प्रमाणे तिसऱ्‍या उपसादनात x₄ या मूल चलाच्या ऐवजी x₃ हा मूल चल म्हणून येईल. संच (१७) मधील पंक्ती ३ मध्ये x₃ चा गुणक एक करून व बाकीच्या पंक्तींतून x₃ चे निराकरण करून संच (१८) मिळतो. x₀, x₃, x₅, x₆ हे मूल चल व x₀, x₁, x₂, x₄ यांचे मूल्य शून्य आहे.

उपसादन चवथे : नियम (१) व (२) प्रमाणे x₅ च्या ऐवजी x₁ हा मूल चेल होतो. वरीलप्रमाणेच बदल करून संच (१९) मिळतो.

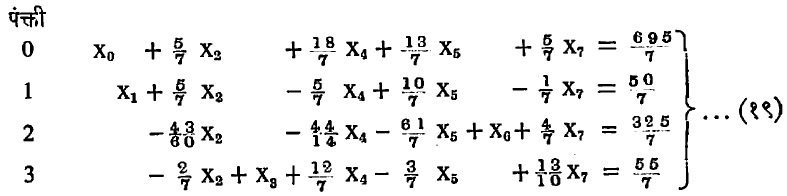
उद्दिष्ट फलनातील (१९) मधील पंक्ती ० मधील चलांचे गुणक धन असल्यामुळे पर्याप्त निर्वाह मिळाला आहे. पर्याप्त मूल्ये :

x₀ = 695/7,  x₁ = 50/7,  x₆ = 325/7, x₃ = 55/7,  x₂ = x₄ = x₅ = x₇ = 0

उद्दिष्ट फलनाचे लघुतम मूल्य काढावयाचे असल्यास नियम (१) मध्ये थोडा फरक करावा लागतो. तो नियम पुढीलप्रमाणे होईल. नियम (१) : वर्तमान निर्वाहातील जास्तीत जास्त धन (+) गुणक असलेला उद्दिष्ट फलनातील मूलेतर चल नव्या उपसादनाकरिता मूल चल म्हणून निवड करा. उपसादनाकरिता मूल चल म्हणून निवड करा. सर्वच्या सर्व मूलेतर चलांचे गुणक ऋण किंवा शून्य असतील, तर पर्याप्त निर्वाह मिळाला असे समजावे. नियम (२) तसाच रहातो. तसेच

असे मांडता येते. म्हणून उद्दिष्ट फलनाचे चिन्ह बदलून लघुतम मूल्य काढण्याच्या प्रश्नाचे महत्तम मूल्य काढण्याच्या प्रश्नात रूपांतर करता येईल.

समीकरण संच (१६) मधील उद्दिष्ट फलनातील चलांचे गुणक बदलल्यास किंवा निर्बंधांतील स्थिरांक बदलल्यास होणारे फरक समीकरण संच (१९) च्या साहाय्याने तपासता येतात. चल किंवा स्थिरांक यांच्यात बदल करताना काही विशिष्ट मर्यादेनंतर उपसादन (४) मधील पर्याप्त रहात नाही. अशा बदलाच्या परिसीमा ठरविता येतात. उदा., समीकरण संच (१६) व (१९) यांतील पंक्ती क्र. ० अनुक्रमे खाली दिली आहेत.

समी. (२०) मधील x₂ गुणक δ ने वाढविला, तर समी. (२१) मधील x₂ चा गुणक (5/7 – δ) असे होईल. δ चे मूल्य 5/7 पेक्षा जास्त असल्यास x₂ चा गुणक ऋण होईल व उपसादन चारमधील निर्वाह पर्याप्त होणार नाही. अशा तऱ्‍हेने उद्दिष्ट फलनाची संवेदनक्षमता अभ्यासता येते व विविध पर्याय उपलब्ध होतात. संगणकावर (गणकयंत्रावर) अशा तऱ्‍हेचे अन्वेषण करणे सोपे जाते.

द्वित्व तत्त्व : द्वित्व तत्त्वाचा आधार घेऊनही अन्वेषण करणे सुलभ जाते. प्रथमतः द्वित्व तत्त्वाचा उपयोग करून व्यापक स्वरूपात एक प्रश्न खाली मांडला आहे.

आदिम व द्वैती या नावांची अदलाबदल होऊ शकते. (२५), (२६) व (२७) मध्ये दिलेला प्रश्न आदिम समजल्यास (२२), (२३) व (२४) मधील प्रश्न त्याचा द्वैती होईल. आदिम व द्वैती प्रश्नांत खाली दिल्याप्रमाणे संबंध असतात.

(१) आदिम प्रश्नातील गुणकांचा j स्तंभ व द्वैती प्रश्नातील गुणकांची j पंक्ती हे सारखे असतात.

(२) आदिम प्रश्नातील उद्दिष्ट फलनातील गुणकांची पंक्ती व द्वैती प्रश्नातील उद्दिष्ट फलनातील गुणकांची पंक्ती व आदिम प्रश्नातील निर्बंधांतील स्थिरांकांचा स्तंभ हे सारखे असतात.

(३) आदिम व द्वैती प्रश्नातील असमांची आणि पर्याप्तीकरणाचील दिशा विरुद्ध असतात.

(४) (अ) आदिम प्रश्नाचा इष्ट निर्वाह x_j* (j = 1, 2, …, n) व द्वैती प्रश्नाचा इष्ट निर्वाह y_i* (i = 1, 2, …, m) असेल, तर खालील समीकरण (अ) त्यांमधील संबंध दर्शविते.

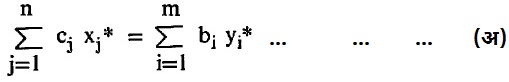
(आ) आदिम किंवा द्वैती प्रश्नांपैकी एकाच पर्याप्त निर्वाह अस्तित्वात दुसऱ्‍याचा पर्याप्त निर्वाह अस्तित्वात असतो. आदिम प्रश्नाच्या उद्दिष्ट फलनाचे मूल्य द्वैती प्रश्नाच्या उद्दिष्ट फलनाच्या मूल्यापेक्षा जास्त असत नाही. दोन्ही प्रश्नांचे पर्याप्त मूल्य एकच असते.

(इ) जर *x_j (j = 1, 2, …, n) हा आदिम प्रश्नाचा एक इष्ट निर्वाह असेल, *y_i (i = 1, 2, …, m) हा द्वैती प्रश्नाचा संवादी इष्ट निर्वाह असेल,  तर खालील समीकरणांची पूर्ती झाल्यासच *x_j व *y_i हे अनुक्रमे आदिम व द्वैती प्रश्नाचे पर्याप्त निर्वाह असतात.

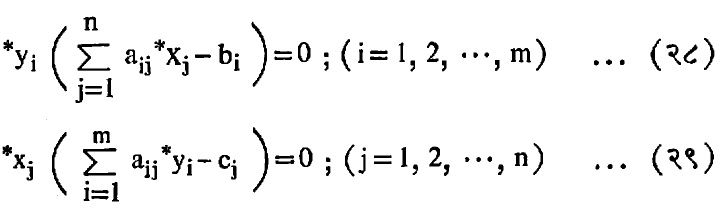
समीकरणे (२८) व (२९) यांच्याद्वारे मिळणाऱ्‍या तत्त्वाला पूरक शिथिलता प्रमेय म्हणतात.  

(१४) हे उद्दिष्ट फलन व (१५) हे निर्बंध असलेला प्रश्न आदिम प्रश्न समजल्यास त्याचा द्वैती प्रश्न खाली दिल्याप्रमाणे होईल.

(१९) या समीकरण संचातील पंक्ती क्र. ० मधील शिथिल चल x₅, x₆, x₇ यांचे गुणांक हे अनुक्रमे y₁, y₂ व y₃ यांची पर्याप्त मूल्ये येतात. म्हणजे y₁=13/7, y₂=0, y₃=5/7 ही मूल्ये (३१) मधील असमांमध्ये घातल्यास खालीलप्रमाणे असमा मिळतात व (३१) मधील सर्व निर्बंध पाळले जातात.

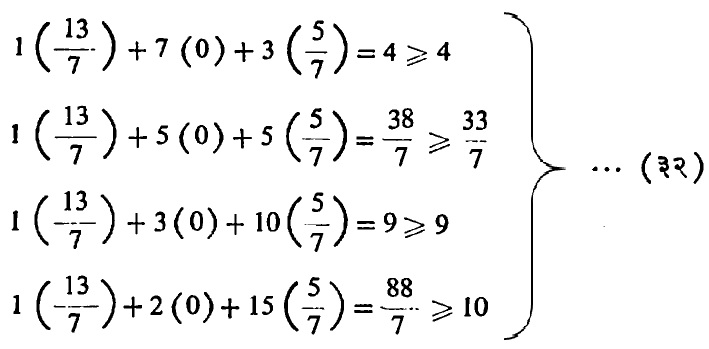
तसेच (३२) मधील असमांतील उजव्या व डाव्या बाजूंतील फरक घेतल्यास अनुक्रमे ०, ५/७, ० व १८/७ असे मिळतात. (१९) या संचातील पंक्ती क्र. ० मधील x₁, x₂, x₃ व x₄ चे गुणक पाहिल्यास अनुक्रमे ०, ५/७, ० व १८/७ येतात. आदिम प्रश्नाचा पर्याप्त निर्वाह काढल्यावर वरीलप्रमाणे द्वैती प्रश्नाने दुजोरा मिळाल्यास पर्याप्त निर्वाह मिळाला असे समजावे. सिंप्लेक्स पद्धती वापरताना नियम (२) प्रमाणे एखाद्या उपसादनात दोन चलांचे गुणोत्तर सारखे येण्याचा संभव असतो. त्यामुळे त्यापुढील उपसादनात चलांची निवड करताना अडचण येते. त्याकरिता विविध नियम मांडण्यात आलेले आहेत. एखाद्या उपसादनात चलांचे मूल्य ऋण येत असल्यास तो निर्वाह इष्ट निर्वाह होऊ शकत नाही. अशा परिस्थितीत द्वैती प्रश्नाचा उपयोग होतो. तसेच द्वैती प्रश्नाच्या सिद्धांतावरही वेगळी द्वैती सिंप्लेक्स पद्धत उपलब्ध आहे.

परिवहन जाल प्रतिकृती : व्यापार व उद्योगधंद्यात एखाद्या व्यवस्थापनाच्या अखत्यारीखाली बरीच उत्पादन केंद्रे असतात, तसेच उत्पादित वस्तूचे वितरण करणे सुलभ जावे म्हणून निरनिराळ्या ठीकाणी साठा ठेवावा लागतो. कोणत्या उत्पादन केंद्रातून कोणत्या साठा केंद्राला पुरवठा करावा म्हणजे परिवहनाचा खर्च कमीत कमी होईल असा प्रश्न व्यवस्थापनापुढे असतो. अशा तऱ्‍हेच्या समस्या परिवहन जाल गणिती प्रतिकृती मांडून सोडविता येतात. अशा जाल प्रतिकृतीच्या विशिष्ट गुणधर्मामुळे पर्याप्तीकरणाची समस्या सोडविण्यास सोपे जाते. मोठ्या उद्योगाच्या वितरण व्यवस्थेत देशाच्या निरनिराळ्या भागांत साठा केंद्रे ठेवतात व तेथून माल किरकोळ विक्री करणाऱ्‍या दुकानांना पुरविला जातो. अशा परिस्थितीत साठा केंद्रांची स्थलनिश्चिती आणि उत्पादन केंद्रापासून साठा केंद्रापर्यंतचे मार्ग निश्चित करण्याकरिता परिवहन जाल प्रतिकृती उपयोगी पडते. प्रत्येक  समस्येची गणिती प्रतिकृती मांडताना योग्य ते फेरफार करावे लागतात. एखाद्या व्यापारी व्यवस्थापनाजवळ मर्यादित भांडवल आहे व भांडवलाची गुंतवणूक करण्याचे विविध पर्याय उपलब्ध आहेत वा एखाद्या व्यवस्थापनाला निरनिराळ्या विक्रेत्यांकडून वस्तू घ्यावयाच्या आहेत. विक्रेत्यांमध्ये कशा तऱ्‍हेने वाटप करावे म्हणजे कमीत कमी किंमत पडेल. अशा तऱ्‍हेच्या वाटपाच्या समस्याही परिवहन जाल प्रतिकृतीने सोडविता येतात. व्यवस्थापनाच्या एखाद्या प्रतिनिधीला मुख्यालयाहून निघून निरनिराळ्या गावी जाऊन परत मुख्यालयाला यावयाचे असेल, तर कमीत कमी मार्ग कोणता घ्यावा ? एखाद्या प्रकल्पात निरनिराळी कामे करावयाची असतात. प्रत्येक काम करण्यास विशिष्ट वेळ लागतो. काही कामे अशी असतात की, दुसरी काही कामे केल्याशिवाय त्यांची सुरुवात करता येत नाही (उदा., पाया घातल्याशिवाय वरच्या इमारतीचे काम करता येत नाही). म्हणून संपूर्ण प्रकल्प पूर्ण करण्यास लागणारा कालखंड किती ? यामध्ये मोठ्यात मोठा मार्ग कोणता होतो? यालाच अभियांत्रिकीमध्ये क्रांतिक मार्ग पध्दती म्हणतात. यंत्राची देखभाल व त्यांची पुनःस्थापना यांची योजना आखण्याची समस्या कमीत कमी खर्चात कशी सोडवावी ? अशा तऱ्‍हेच्या बऱ्‍याच समस्या परिवहन जाल प्रतिकृतीने सोडविणे शक्य होते.

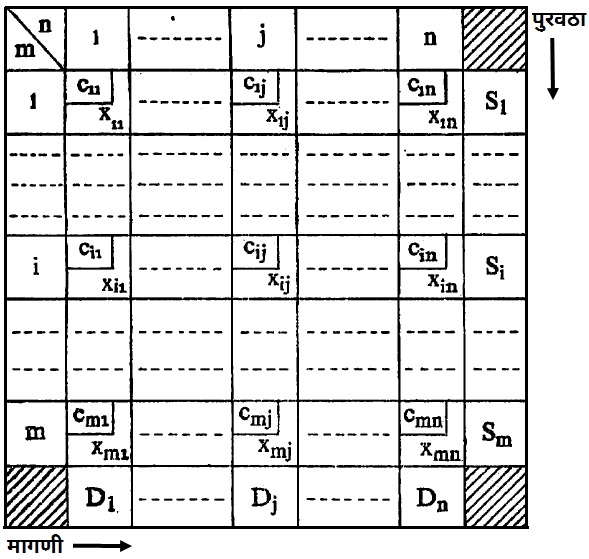
परिवहन जाल प्रतिकृतीमध्ये समजा m पुरवठा केंद्राची संख्या, n मागणी केंद्राची संख्या, दोन केंद्रे i व j यांना जोडणाऱ्‍या मार्गावरून एकक वस्तूच्या परिवहनाचा खर्च x_ij आहे असे धरले आहे. तसेच संपूर्ण उपलब्ध पुरवठा हा संपूर्ण मागणीइतका धरला तरी प्रतिकृतीची व्यापकता कमी होत नाही. याशिवाय परिवहन जाल प्रतिकृतिचा विशेष गुणधर्म म्हणजे पर्याप्त निर्वाहात एका तरी निर्वाहातील मूल्ये पूर्णांक असतात म्हणून x_ij चे मूल्य पूर्णांक धरल्यास प्रतिकृतीची व्यापकता कमी होत नाही. तसेच मार्गावरून  पाठविलेल्या वस्तूत वाढ किंवा घट होत नाही असे गृहीत धरले आहे. वाढ वा घट होत असल्यास योग्य तो बदल करून ही प्रतिकृती वापरता येते. परिवहन जाल प्रतिकृती खालीलप्रमाणे मांडतात.

समी. (३३) ते (३७) मधील प्रतिकृतीत विशिष्ट कालखंड अध्याहृत आहे. ही प्रतिकृती कोष्टक क्र. १ मध्ये दाखविली आहे.

समी. (३३) ते (३७) मधील प्रतिकृती आदिम प्रश्न समजल्यास त्याचा द्वैती प्रश्न खाली दिल्याप्रमाणे होईल.

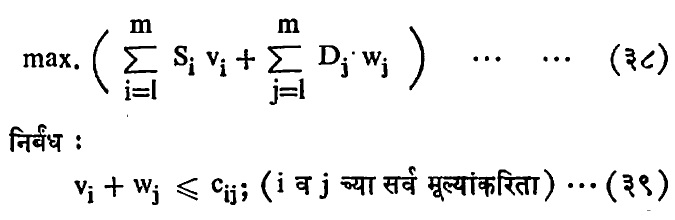
जर x_ij* (सर्व i, j च्या मूल्यांकरिता) आदिम प्रश्नातील निर्बंध (३४, ३५ व ३६) पूर्ण करत असेल आणि v_i* व w_j* द्वैती प्रश्नातील निर्बंध (३९) पूर्ण करत असतील, तर पूरक शिथिलता प्रमेय खाली दिल्याप्रमाणे मांडता येते.

x_ij* (v_i* + w_j* – c_ij) = 0 (सर्व i व j च्या मूल्यांकरिता)    …   …   …   (४०)

_xij* हा पर्याप्त निर्वाह होतो.

परिवहन जाल प्रतिकृतिच्या पर्याप्तीकरणाच्या विविध पद्धती असल्या, तरी प्रत्येक उपसादनात x_ij, v_i व w_j यांची घेतलेली चाचणी मूल्ये खालील तीन अटींपैकी दोन अटी पूर्ण करतात. प्रत्येक उपसादनात या दोन अटी निराळ्या असू शकतील. अटी : (१) आदिम प्रश्नातील निर्बंध (३४, ३५, ३६); (२) द्वैती प्रश्नातील निर्बंध (३९) आणि (३) पूरक शिथिलता प्रमेय (४०). या तिन्ही अटी पूर्ण होत असल्यास पर्याप्त निर्वाह मिळाला असे समजावे.

परिवहन जाल प्रतिकृतीमध्ये बेरीज व वजाबाकी करावी लागत असल्यामुळे ती सोपी असते.

गतिकीय कार्यक्रमण प्रतिकृती : उत्पादन क्षेत्रात नियोजन करताना नियोजन पल्ल्यातील कालखंड विचारात घ्यावे लागतात. एखाद्या कालखंडातील उत्पादन मागणीपेक्षा जास्त असल्यास त्या कालखंडाच्या शेवटी उत्पादित माल शिल्लक राहील. उत्पादित माल साठविण्याला खर्च येतो व त्यामुळे उत्पादनाचा खर्च वाढतो. तसेच उत्पादन एका विशिष्ट राशीत करावे लागते. गणिती प्रतिकृतीवरून असे दिसून आले आहे की, कालखंड हा एक महत्त्वाचा चल आहे. एका कालखंडात घेतलेल्या निर्णयाचे पुढील कालखंडातील निर्णयावर होणारे परिणाम समजून घ्यावे लागतात. अशा परिस्थितीत गतिकीय कार्यक्रमण प्रतिकृतीचा उपयोग होतो. प्रतिकृती सोडविताना नियोजन पल्ल्यातील शेवटच्या कालखंडापासून सुरुवात करून पहिल्या कालखंडातील मागे यावे लागते. अशा पद्धतीस आवर्ती (किंवा परिवर्ती) पद्धत म्हणतात.

गतिकीय कार्यक्रमण प्रतिकृती सुलभ होण्याच्या दृष्टीने पुढील गोष्टी गृहीत धरल्या आहेत. (१) मागणी (D_t) व उत्पादन (x_t) निश्चितपणे माहीत आहेत. (२) प्रत्येक कालखंडातील मागणी त्याच कालखंडात पूर्ण केली जाते. (३) नियोजन पल्ल्याच्या सुरुवातीस व शेवटी साठा (i_t) शून्य आहे. (४) उत्पादन शून्य असल्यास उत्पादन खर्च शून्य असतो. उत्पादन खर्च [C_t (x, i)] हा उत्पादन राशी व साठा यांचे रेखीय फलन आहे. (५) उत्पादन, साठा व मागणी यांची मूल्ये पूर्णांकी आहेत.

गतिकीय कार्यक्रमण प्रतिकृती समी. (४१) मध्ये दिली आहे.

या प्रतिकृतीत कालखंड (महिना, वर्ष …) नियोजन पल्ल्याच्या शेवटपासून मोजणे सोयीचे असते. म्हणून कोणत्याही कालखंडाचा विचार करताना नियोजन पल्ल्याच्या अंतापर्यंत शिल्लक असणाऱ्‍या कालखंडांची संख्या n ने दर्शवितात. उदा., नियोजन पल्ला सहा महिन्यांचा असेल व पहिला महिना जानेवारी असेल, तर शेवटला महिना जून होईल. जूनचा उल्लेख १ ने, मे चा २ ने व जानेवारीचा ६ ने होईल. उत्पादन खर्चाचे दोन भाग असतात. एक प्रत्यक्ष उत्पादन राशीवर व दुसरा साठा ठेवण्याकरिता लागणारा खर्च. कोणत्याही कालखंडातील उत्पादन ठरविताना सुरुवातीचा साठा माहीत असणे जरूर आहे. या ठिकाणी साठा (i) हा अवस्था चल होतो. वर्तमान कालखंडातील उत्पादन ठरविताना त्यामागील नजीकच्या कालखंडाच्या शेवटी राहणारा साठा (वर्तमान कालखंडाच्या सुरुवातीचा साठा) ०, १, २, ३,…. असा असू शकेल. तसेच उत्पादन राशीचे मूल्य ०, १, २, ३, ४,…. असे असू शकेल. अशा परिस्थितीत सुरुवातीच्या साठ्याचे (i) प्रत्येक मूल्य विचारात घेऊन उत्पादनाच्या उपलब्ध पातळीचा (राशीचा) पर्यायी खर्च काढावा लागतो. प्रत्येक i च्या मूल्याकरिता कमीत कमी खर्चाची उत्पादन पातळी ठरविता येते. पर्यायी उत्पादन खर्च खाली कोष्टक क्र. २ प्रमाणे काढणे सोयीचे असते.

n=1, 2, 3, ………, N

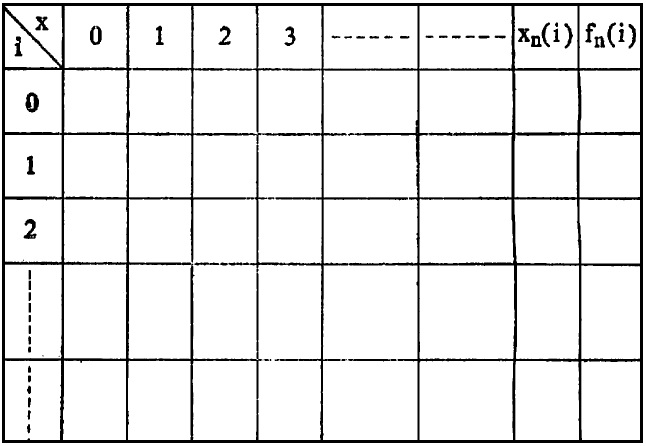
प्रत्येक कालखंडाकरिता एक कोष्टक तयार करावे लागते. कोष्टकाला कालखंडाचा क्रमांक दिलेला असतो. (n=1, 2, ………). x_n(i) ज्या उत्पादन राशीमुळे किंवा धोरणामुळे कमीत कमी खर्च मिळतो. आणि (i) सुरुवातीच्या साठा असतो. f_n(i) पर्याप्त खर्च (कमीत कमी) व (i) हा सुरुवातीच्या साठा असतो. f_n (i) मध्ये वर्तमान कालखंडांच्या पुढील नियोजन पल्ल्याच्या अंतापर्यंतच्या कालखंडातील संवादी खर्च असतात. उदा., i चे मूल्य १ असेल व x चे मूल्य ३ असेल आणि कालखंडातील मागणी २ असेल तर ती वजा जाता वर्तमान कालखंडाच्या शेवटी साठा २ असताना जो पर्याप्त (लघुतम) खर्च असेल तो विचारात घेतला जाईल. अशा तऱ्‍हेने कोष्टकातील प्रत्येक खर्चाच्या मूल्यात पुढील सर्व कालखंडातील खर्चाचा समावेश होतो. सहा महिन्यांचा नियोजन पल्ला घेतल्यास सहा कोष्टके उपलब्ध होतील. n चे मूल्य सहा असताना जानेवारीतील (नियोजन पल्ल्याच्या सुरुवातीस) पर्याप्त उत्पादन धोरण [सुरुवातीचा साठा शून्य सेमी. (४२) पहा] ठरविले जाते. त्या धोरणानुसार फेब्रुवारीच्या सुरुवातीचा साठा लक्षात घेऊन (n=5) या कोष्टकावरून फेब्रुवारीचे उत्पादन धोरण ठरविले जाते. तसेच पुढील चार महिन्यांचे ठरविले जाईल. सहा महिन्यांच्या नियोजन पल्ल्यातील प्रत्येक महिन्याचे उत्पादन धोरण अशा प्रकारे ठरविले जाते. व्यापक स्वरूपात वरील पद्धत समी. (४४) मध्ये मांडली आहे.

गतिकीय कार्यक्रमण प्रतिकृतीमध्ये खालील गुणधर्मांचा समावेश असतो. 

(१) निर्णायक चल व संबंधित निर्बंध यांचे कालखंडाप्रमाणे समूह बनविले जातात व कालखंड अनुक्रमाने विचारात घेतले जातात. (२) वर्तमान कालखंडातील पर्याप्त धोरण ठरविताना त्यापूर्वीच्या नजीकच्या कालखंडाचा परिणाम अवस्था चलाच्या मूल्याने ठरविला जातो. याला ए. ए. मार्कोव्ह या रशियन गणितज्ञांच्या नावावरून मार्कोव्ह गुणधर्म म्हणतात. (३) प्रणालीची वर्तमान अवस्था माहीत असल्यास वर्तमान धोरणाचा पुढील कालखंडावर होणारा परिणाम निश्चित असतो. (४) वर्तमान कालखंडातील पर्याप्त निर्णय हा वर्तमान व त्यापुढील सर्व कालखंडांवर होणाऱ्‍या आर्थिक परिणामांच्या निकषावर तपासले जातात.

समीकरण (४४) या गतिकीय कार्यक्रमण आवर्तनाचे आणखी व्यापक स्वरूप खाली दिले आहे. D_n (S) अवकाशातील S  च्या प्रत्येक मूल्याकरिता

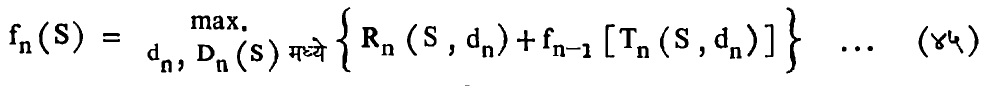
समी. (४५) मध्ये S प्रणालीची अवस्था (Sn या अवकाशातील बिंदूंचा संच), n कालखंड, D_n(S) प्रणालीची अवस्था S असताना d_n या निर्णयाची सर्व इष्ट मूल्ये, R_n(S , d_n) प्रणालीच्या S अवस्थेतील d_n ह्या निर्णयाचे वर्तमान आर्थिक परिणाम आणि T_n(S , d_n) म्हणजे (n–1) या कालखंडात प्रणालीची स्थानांतरित अवस्था.

वरील प्रतिकृतीमध्ये उत्पादनाची पातळी प्रत्येक कालखंडात बदलणे शक्य आहे. अशा तऱ्‍हेने बदलती पातळी प्रत्यक्ष व्यवहारात जास्त खर्चाची होऊ शकते. कारण उत्पादनाकरिता यंत्रांची विशिष्ट योजना करावी लागते व उत्पादित वस्तूंचा गट विशिष्ट राशीचा असावा लागतो. तसेच बाजारातून विकत घेताना वस्तूंची संख्या जशी वाढत जाते तशी किंमतीत घट होते किंवा वटाव मिळतो. अशा वेळी खर्चाचेफलन रेखीय रहात नाही. फलन अंतर्वक्र किंवा बहिर्वक्र असल्यास पर्याप्त मूल्य काढण्याच्या पद्धती उपलब्ध आहेत.

गतिकीय कार्यक्रमण प्रतिकृतीमध्ये नियोजन क्षितीजातील कालखंड वाढविल्यास किंवा कमी केल्यास प्रत्येक महिन्यातील उत्पादन धोरण बदलावे लागते, असे दिसून येईल. N च्या मूल्यात बदल करून पर्याप्त उत्पादन धोरणात होणारे बदल तपासता येतात. सरकत्या योजनेचा विचार या प्रतिकृतीमध्ये करता येतो. मागे दिलेल्या उदाहरणात जानेवारीचे उत्पादन झाल्यावर फेब्रुवारीचे उत्पादन धोरण ठरविताना पल्ल्याच्या अंतापर्यंत पाच कालखंड उपलब्ध आहेत असे न धरता सहा कालखंड उपलब्ध आहेत असे समजून धोरण ठरविले जाते. त्यापुढील महिन्यांचे उत्पादन  धोरण प्रत्येक वेळी सहा कालखंड आहेत असे धरून केले जाते.

व्यवहारात आधीच्या कालखंडातील निर्णयांचा परिणाम वर्तमान कालखंडातील निर्णयावर होतो, तसेच वर्तमान कालातील निर्णयाचा परिणाम त्यापुढील कालखंडावर होतो व ही प्रक्रिया अनंत कालखंडापर्यंत चालू असते. म्हणून गतिकीय कार्यक्रमण प्रतिकृतीमध्ये सांत कालखंडांचा पल्ला न घेता अनंत कालखंड घेणे जरूर असते. उत्पादन केंद्रात उत्पादन खंडित न होऊ देता कच्चा मालाचा साठा किती असावा व साठा किती असल्यास नवीन माल मागविला पाहिजे असा प्रश्न असतो. त्याकरिता तयार केलेली नियमावली  वारंवार बदलून चालत नाही, तर विशिष्ट कालखंडावर स्थिर ठेवावी लागते. तसेच मोठ्या किंमतीच्या यंत्राची पुनःस्थापना करावी का त्याच्या देखभालीवर खर्च करावा अशी समस्या असते. ह्या ठिकाणी भविष्यातील बऱ्‍याच कालखंडांचा विचार करणे जरूर असते. पुनःस्थापनाचा कालखंड मोठा असल्यामुळे स्थिर धोरण अवलंबिता येते. यासारख्या समस्यांकरिता अनंत कालखंडाची गतिकीय कार्यक्रमण प्रतिकृती वापरतात. त्यात स्थिर धोरण गृहीत धरून धोरण अवकाशात व मूल्य अवकाशात अनुक्रमिक आसन्नीकरणाचे (पायरी पायरीने इष्ट मूल्याच्या जास्तीत जास्त जवळचे मूल्य मिळविण्याचे) तंत्र वापरून पर्याप्त निर्वाह काढतात. विविध धोरणांची तुलना करण्याकरिता तीन प्रकारचे निकष लागतात. (१) प्रत्येक कालखंडातील सरासरी लाभांश : हा वर्तमान कालखंडाच्या आधीच्या कालखंडांतील लाभांशांच्या बेरजेला कालखंडांच्या संख्येने भागून काढतात. उदा.,

प्रत्येक धोरणाकरिता लाभांशांची एक अनंत श्रेणी मिळेल. त्यावरून विविध धोरणांची इष्टता ठरविता येईल. (२) वटवलेला लाभांश : पुढील कालखंडांत मिळणाऱ्‍या लाभांशांचे वर्तमान कालखंडातील मूल्य काढतात. भांडवलावर अपेक्षित व्याजाचा दर r असेल, तर

  

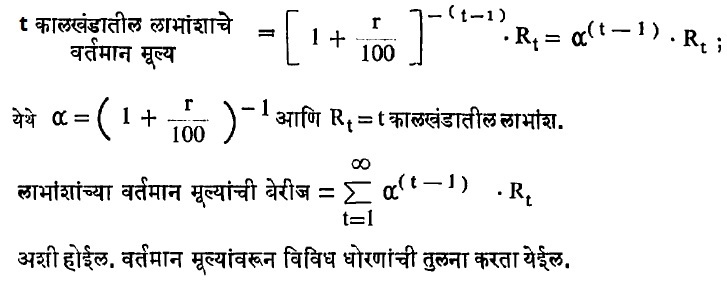
(३) तुल्य सरासरी लाभांश : या निकषात वटलेले मूल्य व सरासरी मूल्य या दोन्हींची सांगड घातली जाते. यामध्ये मूल लाभांशाच्या श्रेणीच्या वटवलेल्या मूल्याइतके वटवलेले मूल्य असलेली अनंत श्रेणी बनविली जाते. प्रत्येक कालखंडात वटविण्यापूर्वीचा लाभांश सारखाच असतो व त्यास तुल्य सरासरी लाभांश म्हणतात. उदा., p(α) हे वर्तमान मूल्य (वटवलेले मूल्य) एका विशिष्ट धोरणाने मिळत असल्यास n च्या सर्व मूल्यांकरिता R_n = (1 – α) p(α)   …    …    (४६) ही लाभांशांची नवीन अनंत श्रेणी मिळेल. लाभांशांच्या वर्तमान मूल्यांची बेरीज खालीलप्रमाणे होईल.

नैकरेखीय कार्यक्रमण प्रतिकृती : रेखीय कार्यक्रमण प्रतिकृतीचा विचार करताना प्रत्यक्ष व्यवहारात घडणाऱ्‍या काही गोष्टींचा समावेश केला जात नाही. मोठ्या प्रणालीची अकार्यक्षमता किंवा कार्यक्षमता, रासायनिक द्रव्याचे मिश्रण करताना दोन्ही द्रव्यांच्या आकारमानाच्या बेरजेपेक्षा आकारमानात होणारी वाढ किंवा घट, मालाची विक्री ज्या प्रमाणात होते त्या प्रमाणात होणारे उत्पन्न अशा बाबींचा समावेश असणारे समीकरण रेखीय असणारे असत नाही. कोणतीही गणिती प्रतिकृती ही प्रत्यक्ष परिस्थितीशी जास्तीत जास्त जुळेल अशी करण्याचा प्रयत्न असतो. म्हणून बऱ्‍याच वेळा नैकरेखीय प्रतिकृतीच्या ऐवजी परिसीमा निर्बंधित करून रेखीय प्रतिकृती वापरल्यास व्यवहारोपयोगी माहिती मिळते, परंतु परिसीमा विस्तृत असल्यास रेखीय फलन समजून काढलेली माहिती चूक ठरते. एखाद्या नवीन कारखान्याला नवीन उत्पादन सुरू करावयाचे आहे व नियोजनाच्या सुरुवातीच्या पुढील दहा–पंधरा वर्षातील फायदा-तोट्याचा आढावा घ्यावयाचा आहे. अशा वेळी बाजारातील मागणीचा उपलब्ध माहितीनुसार अंदाज करावा लागतो. तसेच उत्पादन खर्चाचा (कच्च्या मालाच्या किंमती व मजुरी यांच्या अशाश्वतीमुळे) अचूक अंदाज करणे शक्य होत नाही. अशा वेळी नैकरेखीय प्रतिकृती वापरणे योग्य ठरते. परंतु एकदा उत्पादन सुरू झाल्यावर प्रचलांच्या (विशिष्ट परिस्थितीत अचल राहणाऱ्‍या राशींच्या) परिसीमा निश्चितपणे माहीत झाल्यावर रेखीय प्रतिकृती वापरणे शक्य होते. त्याचप्रमाणे एकाच वेळी एखाद्या कारखान्यात बऱ्‍याच वस्तूंचे उत्पादन करावयाचे आहे व प्रत्येक वस्तूच्या पर्याप्त उत्पादनाचा कार्यक्रम गतीकीय कार्यक्रमण पद्धतीने ठरविल्यास ज्या वेळी सर्व वस्तूंचे उत्पादन एकाच वेळी करण्यास सुरुवात होईल त्या वेळी प्रत्येक वस्तूचे पर्याप्त उत्पादन धोरण अमलात आणता येणार नाही. अशा वेळी नैकरेखीय कार्यक्रमण प्रतिकृती उपयोगी पडते.

नैकरेखीय कार्यक्रमण प्रतिकृतीचे उदाहरण खाली दिले आहे उद्दिष्ट फलन : max. C (x₁, x₂, ……, x_n)   …   …   …   (४८)

निर्बंध :

a_i (x₁, ……, x_n) ≤ 0 ; (i =1,  2,…,m)                 …                …                 …                    …                 …             (४९)

यामध्ये C (x_j) व a_j (x_j) ही नैकरेखीय फलने आहेत [j = 1, 2,…, n]. x_j ची मूल्ये सत् [⟶ संख्या] आहेत. द्विघाती नैकरेखीय प्रतिकृती समी. (५०) व (५१) मध्ये दिली आहे.

C(x) हे फलन विचाराधीन परिसीमांमध्ये पुढील अटी पूर्ण करते असे मानले आहे. (१) विचाराधीन परिसीमांमध्ये C(x) ह्या फलनाचे अखंडितपणे अवकलन [⟶अवलकन व समाकलन] करता आले पाहिजे. (२) C(x) > C(x’) ही अट पूर्ण करून x च्या मूल्यांचा जो संच होईल तो संच संवृत व परिबद्ध [⟶संच सिद्धांत] असला पाहिजे. या अटींची पूर्तता होणे शक्य असल्यास व C(x) या फलनाच्या आंशिक अवकलजांची [∂C(X)/ ∂x_j]  ; (j=1,2, …, n) मूल्ये शून्य असतील, तर X या बिंदूच्या सहनिर्देशकाने C(x) फलनाचे महत्तम मूल्य मिळाले असे समजावे.

∂C(x) / ∂x_j = 0 ही आंशिक अवकल समीकरणे [⟶अवकल समीकरण] नैकरेखीय असतात, त्यांमुळे त्यांचा निर्वाह काढणे हे C(x_j) या फलनाचे पर्याप्त मूल्य काढण्याइतकेच अवघड असते. परंतु फलन द्विघाती असल्यास आंशिक अवकल समीकरणे रेखीय असतात व पूर्वी दिलेल्या पद्धतीने त्यांचे पर्याप्तीकरण करता येते. विविध पर्याप्तीकरणाच्या पद्धतींमध्ये आनुक्रमिक आसन्नीकरण कसे केले जाते हे खाली दिले आहे.

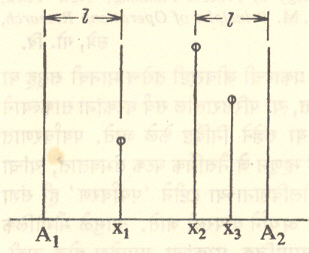
अंतराल छेद पद्धतीत n चलांपैकी एका वेळी एक चल घेऊन बाकीचे चल स्थिर आहेत असे समजतात म्हणून एका चलाचाच विचार पुढे केला आहे. प्रचलांच्या विषयी उपलब्ध असलेल्या माहितीप्रमाणे किंवा प्राथमिक चाचणीने C(x) फलनाचे पर्याप्त मूल्य असलेले अंतराल ठरविले जाते. या अंतरालात C(x) हे फलन एकबहुलकी (फलनाचे मूल्य महत्तम आहे असे x चे एकक मूल्य दिलेल्या अंतरालात असणे) आहे असे गृहीत धरल्यास ही परिस्थिती व्यवहारातील परिस्थितीस मिळतीजुळती असते. आ.२ मध्ये A₁ A₂ हे अशा तऱ्‍हेचे अंतराल विचारात घेतले आहे.

A₁ A₂ या अंतरालात x₁ व x₂ ही मूल्ये घेऊन C(x₁) व C (x₂) ही फलनाची मूल्ये काढतात. जर x₁ < x₂ आणि C(x₂) ≥ C(x₁), तर फलन एकबहुलकी असल्यामुळे C(x) चे पर्याप्त मूल्य A₁ x₁ या अंतरालात असणार नाही. म्हणून दुसऱ्‍या उपसादनात x₁A₂ या अंतरालाचाच विचार केला जाईल. x₃ हे मूल्य घेऊन C (x) फलनाचे मूल्य काढतात. जर C(x₃) < C(x₂), तर C(X) पर्याप्त मूल्य x₃A₂ या अंतरालात असणार नाही. म्हणजे ते x₁x₃ या अंतरालाच आहे. अशा तऱ्‍हेने प्रत्येक उपसादनात अंतराल कमी कमी होत जाते व अंतरालाची परिसीमा इष्ट इतकी कमी झाल्यावर पर्याप्त मूल्य मिळते. रेखीय प्रतिकृतीसारखे या पद्धतीत एकच पर्याप्त मूल्य मिळत नाही. परंतु पर्याय मूल्य असलेल्या अंतरालाची रुंदी कमी करता येते. छेद घेण्याच्या सुद्धा विविध पद्धती आहेत. एका पद्धतीत प्रत्येक वेळी अंतराल निम्म्याने कमी केले जाते. दुसऱ्‍या पद्धतीत पहिल्या उपसादनात x₁ व x₂ यांची मूल्ये अशा तऱ्‍हेने घेतात की, A₁ व A₂ पासून अनुक्रमे x₁ व x₂ चे l अंतर सारखे असते. ते जर 0·618H (H = A₁,A₂ अंतर) असेल, तर त्या पद्धतीला सुवर्ण छेद पद्धत किंवा इटालियन गणितज्ञ लेओनार्दो फीबोनात्ची यांच्या नावावरून फीबोनात्ची पद्धत म्हणतात [⟶सुवर्ण छेद]. त्यानंतर वर दिलेल्या पद्धतीने अंतरालाची कक्षा कमी कमी करतात. दुसऱ्‍या उपसादनात x चे एक मूल्य कायम ठेवून x₃ चे मूल्य अशा तऱ्‍हेने घेतात की x₁ पासूनचे अंतर 0·618 H₁ (H₁ = x₁ – A₂ अंतर) ही क्रिया अंतराल इष्ट इतक्या रुंदीचे कमी होईपर्यंत करतात.

दुसऱ्‍या प्रकारच्या पद्धतीत C(x_j) या फलनाचे एका बिंदूचे सहनिर्देशक घेऊन मूल्य काढतात. X_j या चलाची मूल्ये पायरी पायरीने वाढवून सुरुवातीच्या प्राथमिक मूल्यापासून C(x₁) ह्या फलनाचे मूल्य वाढवून पर्याप्त मूल्य काढतात. पायरीचे मूल्य ठरविताना निरनिराळ्या पद्धती वापरतात. जास्तीत जास्त चढ असलेल्या दिशेने चलांची मूल्ये वाढविण्याची पद्धत अवलंबतात. विभाग मर्यादित रेखीयकरण म्हणजे नैकरेखीय फलन छोट्या छोट्या अंतरालांत रेखीय फलन आहे असे समजून अंती पर्याप्त मूल्य काढणे होय [⟶ नैकरेषीय आविष्कार]. जर नैकरेखीय प्रतिकृतीचे उद्दिष्ट फलन n नैकरेखीय फलनांची बेरीज असेल, तर प्रत्येक फलनाचे पर्याप्त मूल्य काढून उद्दिष्ट फलनाचे पर्याप्त मूल्य काढतात.

यदृच्छ प्रक्रिया व प्रतीक्षावली प्रक्रिया यांचे पर्याप्तीकरण करण्याच्या पद्धती स्वतंत्र आहेत. खेळ सिद्धांतामुळे सुद्धा पर्यायी धोरणे उपलब्ध होतात व त्यांतून पर्याप्त धोरण निवडता येते.

पहा : खेळ सिद्धांत; प्रतीक्षावली सिद्धांत; यदृच्छ प्रक्रिया.

संदर्भ : 1. Gale, D. Linear Programming: Methods and Applications, New York.

2. Handley, G. F. Linear Programming, Reading, Mass, 1962.

3. Handley, G. F.  Non-linear and Dynamic programming, Reading, Mass.,1964.

4. Hillier, F. S.; Lieberman, G. J. Introduction to Operations Research, San Francisco, 1974.

5. Loomba, N. P. Linear Programming: An Introductory Analysis, New York, 1964.

6. Rudd, D. F.; Watson, C. C. Strategy of Process Planning, New York, 1968.

7. Wagner, H. M. Principles of Operations Research, New Delhi, 1974.

सप्रे, गो. वि.