परासमापक

परासमापक : परास म्हणजे एखाद्या इष्ट वस्तूचे निरीक्षकापासूनचे अंतर होय. त्याचे मापन करण्यासाठी वापरल्या जाणाऱ्या साधनाला परासमापक (किंवा अंतरदर्शक) असे म्हणतात. ध्वनितरंग, प्रकाशकिरण, उच्च ऊर्जेचे विद्युत् चुंबकीय तरंग किंवा स्पंद किंवा लेसर किरण [→ लेसर] अशा विविध आविष्कारांवर आधारलेले परासमापक तयार करण्यात आलेले आहेत. मापनाची अचूकता, वापरातील अवघडपणा अथवा सोपेपणा, किंमत या गोष्टी भिन्न परासमापकांच्या बाबतीत वेगवेगळ्या असतात. त्याचप्रमाणे विशिष्ट परिस्थितीत एखादा विशिष्ट प्रकारचा परासमापकच सुयोग्य ठरतो. उदा. पाणबुडी, खडक यासारखे पाण्यात बुडालेले लक्ष्य शोधण्यासाठी किंवा त्यांचा परास मोजण्यासाठी ध्वनितरंगावर आधारलेले सोनार [→ सोनार व सोफार] हेच साधन वापरावे लागते.

भूसर्वेक्षण करणे शत्रूची जहाजे, तोफा, विमाने इत्यादींवर अचूक मारा करणे कॅमेऱ्याच्या भिंगाचे इष्ट वस्तूवर बिनचूक केंद्रीकरण करणे अशा कार्यांसाठी परासमापकाचा उपयोग होतो. दुसऱ्या महायुद्धापर्यंत प्रकाशकिरणावर आधारलेल्या परासमापकांचाच मुख्यत: उपयोग केला जाई. विद्युत् चुंबकीय तरंग किंवा स्पंदांचा उपयोग करून परासमापन करणारी साधने [→ रडार] मुख्यत: दुसऱ्या महायुद्धाच्या काळात प्रगत झाली. लेसर पद्धतीचा परासमापक प्रथम १९६१ मध्ये तयार झाला.

प्रकाशकीय परासमापक : या प्रकारचे मापक वापरण्यास सोपे असून तुलनेने स्वस्त असतात. लक्ष्याचे अंतर फार नसल्यास (सु. १,००० मी. पर्यंत) परासमापनातील त्रुटी खूपच कमी असते परंतु रात्री किंवा धूळ, धुके वगैरेंमुळे दूरच्या वस्तू स्पष्ट दिसू शकत नसतील, तर यांचा उपयोग करता येत नाही. त्याचप्रमाणे फार दूरच्या लक्ष्यांचा परासही याच्या साहाय्याने मापता येत नाही.

समानुपाती परासमापक व त्रिमितिदर्शक परासमापक असे प्रकाशीय परासमापकाचे दोन मुख्य प्रकार आहेत. पहिल्या प्रकारचा परासमापक प्रथम ए. बार व डब्ल्यू. स्ट्राउड यांनी १८८८ मध्ये तयार केला, तर दुसऱ्या प्रकारचा परासमापक प्रथम सी. झाइस यांनी १८९३ मध्ये बनविला. या उपकरणांच्या रचनेचे मूळ स्वरूप कायमच राहिलेले असून त्यात वेळीवेळी सुधारणा केल्या गेल्या आहेत.

समानुपाती प्रकाशीय परासमापकाचे तत्त्व व परास त्रिकोण : या प्रकारच्या परासमापकात लक्ष्य हा शिरोबिंदू कल्पून व विशिष्ट अंतरावरील दोन बिंदूंना जोडणारी रेषा ही पाया कल्पून एक काटकोन त्रिकोण (परास त्रिकोण) बनविला जातो. मापकाच्या साहाय्याने प्रत्यक्ष किंवा अप्रत्यक्षपणे लक्ष्याजवळ पायाने अंतरित केलेला कोन (परास कोन, θ) मापला जातो. मग पाया रेषेची लांबी (हिलाच आधार अंतर म्हणतात) व परास कोन यांच्यावरून पुढील सूत्राने परास काढता येतो.

परास = आधार अंतर X कोस्प θ [कोस्प म्हणजे कोस्पर्शक गुणोत्तर → त्रिकोणमिति]. आ. १ मध्ये परास त्रिकोण दाखविला असून त्यावरून वरील सूत्राची सिद्धता सहज करता येईल.

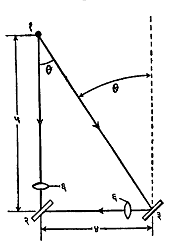(२) या बिंदूच्या ठिकाणी एक अर्धपारदर्शक आरसा ठेवलेला असून त्यातून सरळ लक्ष्य दिसू शकते. (३) येथे एक आरसा बसविलेला असून तो (आकृतीला लंब असलेल्या अक्षाभोवती) फिरविता येतो. त्याच्यावरून परावर्तन होऊन दुसरी काहीशी अंधुक प्रतिमा तयार होते. या दोन्ही प्रतिमा बरोबर एकीवर एक पडतील म्हणजेच समानुपाती होतील अशा प्रकारे हा आरसा फिरवावा लागतो. आरसा फिरविण्यासाठी बसविलेल्या गुंडीला  एकदम वस्तूच्या अंतराच्या रूपातच अंशांकित केलेली मोजपट्टी जोडलेली असल्याने काहीही गणित न करता एकदम परासमूल्यच मिळू शकते.

परासमापनातील त्रुटी : या उपकरणाच्या साहाय्याने काढलेल्या परासमूल्यात येणारी त्रुटी ही परासाच्या वर्गाच्या समप्रमाणात असते व आधार अंतराच्या व्यस्त प्रमाणात असते. त्याचप्रमाणे परास कोनाच्या मापनात होणाऱ्या त्रुटीच्या ती समप्रमाणात असते. तेव्हा जास्त अचूक मापनासाठी आधार अंतर शक्य तितके जास्त  ठेवणे जरूर असते. त्याचप्रमाणे परास कोनाच्या मानातील त्रुटी कमीत कमी करणे आवश्यक ठरते. आधार अंतर वाढविले की, उपकरण अवजड होते. जेथे उपकरणाची वाहतूक करण्याची आवश्यकता नसेल तेथे आधार अंतर शक्य तितके जास्त ठेवतात. उदा., भूसर्वेक्षण करताना वरील आकृतीतील (२) व (३) हे बिंदू जमिनीवरील दोन स्थळे घेऊन त्यांमधील अंतर कित्येक शेकडो मीटर ठेवतात परासमापकातून दिसणाऱ्या प्रतिमांचे वर्धन केल्यास वर्धनाच्या व्यस्त प्रमाणात त्रुटी कमी होते. उदा., १ मी. व ३ मी. आधार अंतर असलेल्या व प्रतिमेचे १५ पट वर्धन करणाऱ्या परासमापकामध्ये १ किंमी. अंतराच्या मापनात अनुक्रमे ८·६ मी. व ३·२ मी. इतकी त्रुटी येते. ८ किमी. अंतराकरिता याच मापकाच्या त्रुटी अनुक्रमे ५६४ मी. व २०४ मी. येतात.

भग्न प्रतिमा परासमापक : ‘भग्न प्रतिमा’ पद्धतीच्या परासमापकाचे एकूण कार्य वरील प्रकारानेच होते. फक्त एवढाच फरक असतो की, (१)–(२) या मार्गाने येणाऱ्या किरणांनी प्रतिमेचा फक्त खालचा भाग व (१)–(३)–(२) या मार्गाने येणाऱ्या किरणांनी प्रतिमेचा फक्त वरचाच भाग तयार होतो. हे दोन्ही भाग बरोबर एकावर एक येऊन एक सलग प्रतिमा मिळेल असे समायोजन करावे लागते.

कॅमेऱ्यातील परासमापक : छायाचित्र घेताना वस्तूच्या कॅमेऱ्यापासूनच्या अंतरानुसार त्याचे केंद्रीकरण करणे आवश्यक असते. यासाठी अनेक कॅमेऱ्यांमधून समानुपाती पद्धतीचा परासमापक बसविलेला असून तो कॅमेऱ्याच्या भिंगाच्या मागेपुढे होण्याच्या गतीशी संलग्न केलेला असतो. याच्या संपूर्ण माहितीसाठी 

 ‘कॅमेरा’ या नोंदीतील 

 ‘अंतरदर्शक’ हा परिच्छेद पहावा.

लष्करी उपयोगासाठी समानुपाती परासमापक : शत्रूचे ठाणे किंवा जहाज, रणगाडा यांसारख्या लक्ष्यावर अचूक मारा करता येण्यासाठी त्याचा परास काढणे आवश्यक असते. यासाठी जास्त अचूक परासमापन करणाऱ्या समानुपाती परासमापकाची रचना आ. २ मध्ये दाखविली आहे.

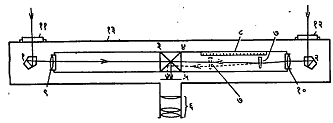
या परासमापकात आरशांऐवजी लोलक वापरलेले असतात. कारण त्यांतून होणाऱ्या अंतर्गत परावर्तनाने मिळणाऱ्या प्रतिमा जास्त तेजस्वी असतात. (१) व (२) या दोन पंचकोनी लोलकांवर लक्ष्यापासून येणारे किरण पडतात व अंतर्गत परावर्तनाने ते बरोबर एका काटकोनातून वळतात. नंतर ते (९) व (१०) या वस्तुभिंगांतून जाऊन (३) व (४) या काटकोनी लोलकांत त्यांचे पुन्हा अंतर्गत परावर्तन होते व (५) या पातळीत लक्ष्याच्या दोन प्रतिमा तयार होतात. त्या (६) या नेत्रिकेतून पाहिल्या जातात. (७) हा विचलक लोलक डावी-उजवीकडे सरकवून उजवीकडून येणाऱ्या किरणांमुळे तयार होणाऱ्या प्रतिमेचे विस्थापन करता येते. प्रारंभी लक्ष्य अनंत अंतरावर असताना त्याच्या दोन्ही प्रतिमा समानुपाती दिसतील अशी स्थिती साधण्यात येते. मग उपकरण इष्ट लक्ष्यावर रोखून विचलक लोलक अशा तऱ्हेने सरकवितात की, त्या स्थितीत इष्ट लक्ष्याच्या दोन्ही प्रतिमा समानुपाती होतील. या परिस्थितीत विचलक लोलकाचे स्थान (८) या मोजपट्टीवर नोंदले जाते. या पट्टीवर प्रत्यक्ष लक्ष्याचे अंतरच अंशांकित केलेले असते. ज्ञात अंतरावरील लक्ष्यावर उपकरण वापरून हे अंशांकन केलेले असते.

ही सर्व प्रणाली एका धातूच्या नळीत बंदिस्त केलेली असून त्या नळीला (१) व (२) या लोलकांच्या समोर दोन भोके (किंवा ‘खिडक्या’) ठेवलेल्या असतात. या भोकांतून प्रकाशकिरण लोलकांत प्रवेश करतात. या भोकांमधील अंतर हेच या उपकरणाचे आधार अंतर होय.

त्रिमितिदर्शक परासमापक : समानुपाती परासमापकापेक्षा त्रिमितिदर्शक परासमापक वापरण्याला जास्त अवघड आहे परंतु त्याच्या साहाय्याने जास्त अचूक मापन करता येते, हा त्याचा विशेष गुण आहे. हा परासमापक म्हणजे एक प्रचंड द्विनेत्री दूरदर्शकच (दुर्बिणच) आहे. याची रचना आ. ३ मध्ये दाखविली आहे.

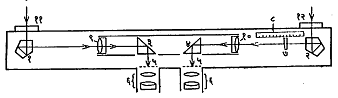
(९) हे वस्तुभिंग व (६) हे डावीकडचे नेत्रिका भिंग मिळून डाव्या डोळ्यासाठी एक दूरदर्शक बनतो. त्याचप्रमाणे (१०) हे वस्तुभिंग व (६) हे उजवीकडचे नेत्रिका भिंग मिळून उजव्या डोळ्यासाठी दुसरा दूरदर्शक बनतो. या दोन दूरदर्शकांतून दोन डोळ्यांनी एकाच वेळी लक्ष्याकडे पाहिले जाते. नेत्रिकांसमोर (५) हे जाळी पडदे असे ठेवलेले असतात की, त्यांची दोन नेत्रिकांमधून दिसणारी (संयुक्त) प्रतिमा अनंत अंतरावर असल्यासारखी दिसेल. त्याच वेळी उपकरण लक्ष्यावर केंद्रित केले असता त्याची संयुक्त प्रतिमा जाळी पडद्याच्या अलीकडे ‘तरंगत’ असल्यासारखी दिसते. (७) हा विचलक हळूहळू डावीकडे सरकवत गेल्यास लक्ष्याची प्रतिमा निरीक्षकापासून जास्त जास्त दूर गेल्यासारखी दिसते. शेवटी जेव्हा जाळी पडदा व लक्ष्य या दोघांच्याही प्रतिमा एकाच ठिकाणी असल्यासारख्या दिसतील तेव्हाचे (८) या मोजपट्टीवरील वाचन लक्ष्यांचा परास देते. पुष्कळ सराव केल्याशिवाय या उपकरणाचा नीट वापर करता येत नाही.

लेसर परासमापक : हे उपकरण आकारमानाने लहान असून वजनाने हलके असल्याने सहज इकडे तिकडे नेता येते. ते दिवसा किंवा रात्री वापरता येते. लक्ष्याचे अंतर कितीही असले, तरी त्याची अचूकता कमी होत नाही. सामान्यत: त्याच्यावरून मिळणाऱ्या परासात सु. ५ मी. इतकी अल्प त्रुटी येते. सुमारे १२ किमी. किंवा त्याहून जास्त परास मोजण्यास हे उत्तम उपकरण आहे. प्रथम या उपकरणातील दूरदर्शक लक्ष्यावर केंद्रित करतात. त्यामुळे उपकरणातील (आ. ४) लेसर उद्गम बरोबर लक्ष्यावर रोखला जातो. मग एक गुंडी दाबली की लेसर किरणांचा एक अत्यंत शक्तिशाली व निरुंद असा स्पंद लक्ष्यावर प्रक्षेपित केला जातो. त्याचबरोबर एक उच्च कंप्रतेचा (३० मेगॅहट्रेझ किंवा त्याहून अधिक कंप्रतेचा कंप्रता म्हणजे म्हणजे दर सेकंदाला होणारी आंदोलन संख्या) इलेक्ट्रॉनीय आंदोलक [⟶ आंदोलक, इलेक्ट्रॉनीय] आंदोलने सुरू करतो व ही आंदोलने एका इलेक्ट्रॉनीय प्रयुक्तीकडून मोजण्याचे कार्यही त्याबरोबरच सुरू होते. लेसर स्पंद लक्ष्यावर आदळतो व त्याच्या ऊर्जेपैकी अल्प अंश उपकरणाच्या दिशेने परावर्तित होतो. परावर्तित भाग उपकरणावर येऊन पडला की, एका अत्यंत संवेदनशील घटकाकडून [प्रकाशविद्युत् नलिकेकडून ⟶ इलेक्ट्रॉनीय प्रयुक्ति] नोंदला जातो व त्याबरोबर आंदोलकाची आंदोलने थांबतात. अशा 

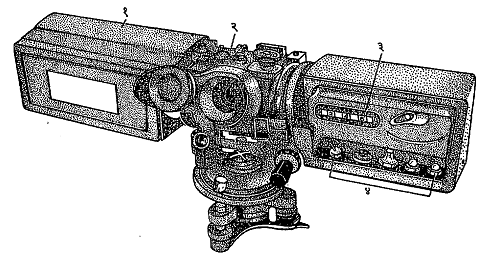
तऱ्हेने लेसर स्पंद उपकरणापासून निघून लक्ष्यापर्यंत जाऊन परत येण्यासाठी लागणाऱ्या कालखंडात (का) आंदोलकाची पूर्ण होणारी आंदोलन संख्या (न) मोजली जाते. आंदोलकाची कंप्रता (क) ज्ञात असल्याने त्यावरून एका आंदोलनाला लागणारा काल (१/क) माहीत होतो. लेसर किरण प्रकाशवेगाने (३ × १०८ मी./ से.) जातात. यावरून

का= न × १/क

परास = १/२ × ३ × १०८ × न / क

⇨ रडार  परासमापकाच्या साहाय्याने खूप दूरच्या स्थिर किंवा गतिमान लक्ष्यांचा परास काढता येतो व ⇨ डॉप्लर परिणामाचा उपयोग करून लक्ष्याचा वेगही काढता येतो.

संदर्भ : 1. Jacobs, D. H. Fundamentals of Optical Engineering, New York, 1943.

2. Malov, V. S. Telemechanics, New York, 1964.

3. Smith, W. J. Modern Optical Engineering, New York, 1966.

4. Stehling, K. R. Lasers and their Applications, New York, 1966.

कोगेकर, ना. वा. पुरोहित, वा. ल.

“