तरंग मार्गदर्शक

तरंग मार्गदर्शक : विद्युत् चुंबकीय तरंगांना बंदिस्त प्रेषण मार्ग उपलब्ध करून देणाऱ्या पोकळ संवाहकांना तरंग मार्गदर्शक म्हणतात. व्यापक अर्थाने समांतर प्रेषण तारांची जोडी [→प्रेषण मार्ग] व ⇨ समाक्ष केबल  ह्या प्रयुक्ती तरंग मार्गदर्शकच होत पण व्यवहारामध्ये विद्युत् चुंबकीय तरंग परिसीमित करून ते लांबीच्या दिशेत प्रेषित करणाऱ्या धातूच्या पोकळ नळीलाच मर्यादित अर्थाने तरंग मार्गदर्शक असे म्हटले जाते. अत्यंत उच्च कंप्रतांना (सूक्ष्मतरंग कंप्रतांना कंप्रता म्हणजे दर सेकंदास होणाऱ्या कंपनांची संख्या) नित्याच्या प्रेषण पद्धती ऐवजी तरंग मार्गदर्शक हाच एक चांगला पर्याय आहे. प्रेषण कार्यक्षमतेच्या दृष्टीने तरंग मार्गदर्शक समाक्ष केबलीपेक्षा अधिक श्रेष्ठ आहेत.

सूक्ष्मतरंग प्रेषणासाठी सामान्यपणे पोकळ तरंग मार्गदर्शक आणि समाक्ष केबल या प्रयुक्ती वापरात असल्या, तरी काही विशिष्ट कामांसाठी निराळ्या प्रकारचे तरंग मार्गदर्शकही वापरतात. काही प्रसंगी एकेरी संवाहकाचा (जी-स्ट्रिंग) तंरग मार्गदर्शक म्हणून उपयोग होतो. दुसऱ्या महायुद्धात सूक्ष्मतरंग पट्टीचा शोध लागला. यात संवाहकाची पातळ, लहान पट्टी एका विद्युत् अपारकाच्या (ज्यातून एकदिश विद्युत् प्रवाह जाऊ शकत नाही अशा पदार्थाच्या) ठोकळ्यावर बसविलेली असून अपारकाच्या खाली एक धातूची चकती वापरलेली असते. अशा प्रकारच्या सूक्ष्मतरंग पट्ट्यांचा⇨ मुद्रित मंडलांमध्ये अधिकाधिक उपयोग होऊ लागला आहे. विद्युत् अपारक दंड हे वेगळ्या प्रकारच्या तरंग मार्गदर्शकाचे आणखी एक उदाहरण आहे.

तरंग मार्गदर्शकामध्ये अस्तित्वात असलेल्या तरंगांच्या क्षेत्र घटकांनी मॅक्सवेल समीकरणांची [विद्युत् चुंबकीय तरंगांबाबत विद्युत् चुंबकीय क्षेत्र घटकांतील संबंध दर्शविणाऱ्या जेम्स क्लार्क मॅक्सवेल यांनी शोधून काढलेल्या चार समीकरणांची →विद्युत् चुंबकीय तरंग] पूर्ती करणे आवश्यक आहे. त्याचप्रमाणे या घटकांनी विशिष्ट सीमाअटीही पुऱ्या केल्या पाहिजेत. पोकळ तरंग मार्गदर्शकाच्या भिंती तांबे, पितळ किंवा ॲल्युमिनियम यांसारख्या उत्तम संवाहकाच्या बनविलेल्या असतात. या पदार्थांची विद्युत् संवाहकता परिमित असली, तरी या प्रश्नापुरती ती अपरिमित आहे, असे मानता येईल. परिपूर्ण संवाहकाच्या अंतर्भागात विद्युत् क्षेत्र नसते. यावरून व मॅक्सवेल समीकरणांचा उपयोग करून सीमा अटी पुढीलप्रमाणे मिळतात. परिपूर्ण संवाहक आणि विद्युत् अपारक (सामान्यपणे हवा) यांच्या अंतरपृष्ठभागवर चा (विद्युत् क्षेत्राचा) स्पर्शीय घटक आणि चा (चुंबकीय क्षेत्राचा) अभिलंब घटक हे शून्य असतात.

प्रेषण प्रकार : एकजिनसी विद्युत् अपारक भरलेल्या एकविध तरंग मार्गदर्शकात ऊर्जा प्रेषण होण्याचे जे प्रकार आहेत, ते दोन वर्गात विभागता येतात. या प्रत्येक वर्गात अंतर्भूत असलेल्या प्रकारांची संख्या अगणित आहे.

(अ)अनुप्रस्थ विद्युत् क्षेत्र (TE) प्रकार : या प्रकारामध्ये विद्युत् क्षेत्र सर्व ठिकाणी ऊर्जा प्रसारण दिशेस लंब असते. ऊर्जेचे (या ठिकाणी विद्युत् चुंबकीय) परिणामी प्रसारण मार्गदर्शकाच्या अक्षाच्या दिशेत होत असते. चुंबकीय क्षेत्राचाही अक्षाच्या दिशेस अभिलंब असलेला घटक असतो पण त्याबरोबर अक्षाला समांतर असा दुसराही घटक असतो. या प्रकाराला H–तरंग असेही म्हणतात.

(आ) अनुप्रस्थ चुंबकीय क्षेत्र (TM) प्रकार : या प्रकारामध्ये चुंबकीय क्षेत्र सर्व ठिकाणी ऊर्जा प्रसारण दिशेस लंब असते पण विद्युत् क्षेत्राचे अनुप्रस्थ व अक्षास समांतर असे दोन्ही घटक असतात. या प्रकारांना E – तरंग असेही म्हणतात.

आयताकार तरंग मार्गदर्शक गणितीय रीत्या सर्वांत समजण्यास सोपा आहे. तो व्यवहारात अधिक वेळा वापरला जातो. तरंग मार्गदर्शकाचे गुणधर्म व वैशिष्ट्ये या तरंग मार्गदर्शकाच्या अनुषंगाने चांगले विशद करता येतात.

आयताकार तरंग मार्गदर्शक : या मार्गदर्शकातील भिन्नभिन्न प्रेषण प्रकार त्याचा प्रमुख प्रकार (TE किंवा TM) देऊन त्यापुढे दोन पादांक लिहून दर्शवितात. उदा., आयताकार मार्गदर्शकातील प्रभावी प्रकार TE_1,0 हा आहे. यातील क्षेत्रांची रचना आ. १ मध्ये दाखविली आहे. १ हा पादांक तरंग मार्गदर्शकाच्या लांब बाजूच्या दिशेतील (X – अक्ष) क्षेत्र वितरणामध्ये क्षेत्र तीव्रतेच्या बदलाचे अर्धआवर्तन पुरे होते असे दर्शवितो, तर ० हा पादांक आखूड बाजूच्या दिशेतील (Y – अक्ष) चुंबकीय व विद्युत् क्षेत्र तीव्रतेत काहीच बदल होत नाही हे दर्शवितो.

मज्जाव (याचे स्पष्टीकरण पुढे दिले आहे) कंप्रतेपेक्षा अधिक कंप्रता असलेल्या TE_1,0प्रकारच्या तरंग प्रकारामधील विद्युत् आणि चुंबकीय क्षेत्रांची मूल्ये समीकरण (१) वरून मिळतात.

मार्गदर्शकाद्वारे नियमित केलेले विद्युत् तरंग वर उदाहरणादाखल घेतलेल्या प्रकारापेक्षा अनेक विविध तऱ्हांनी मार्गदर्शकातून प्रेषित होऊ शकतात. मात्र या सर्व प्रकारांमध्ये या तरंगांना काही त्याच सीमा अटी पाळाव्या लागतात.

तरंग मार्गदर्शकाचा सगळ्यात महत्त्वाचा गुणधर्म हा आहे की, आदान विद्युत् चुंबकीय तरंगाची तरंगलांबी जर एका λ_cया क्रांतिक मूल्यापेक्षा कमी असेल, तर आदान तरंगात नगण्य क्षीणन होऊन तो मार्गदर्शकातून प्रेषित होतो. या तरंगलांबीच्या क्रांतिक मूल्यास मज्जाव तरंगलांबी म्हणतात. λ_c चे मूल्य तरंग मार्गदर्शकाचे परिमाण, त्याचा आकार व विद्युत् चुंबकीय क्षेत्र वितरण प्रकार यांनी ठरते. जर आदान तरंगाची मुक्त अवकाशातील तरंगलांबी λ_cपेक्षा जास्त असेल, तर अशा तंरगाचे मार्गदर्शकात इतक्या जलद गतीने क्षीणन होते की, तो मार्गदर्शकाच्या बाहेर येऊ शकत नाही. हा परिणाम मार्गदर्शकाच्या भिंतीच्या विद्युत् संवाहकतेवर अवलंबून नसतो. जरी काही कारणामुळे भिंतीची संवाहकता खरोखरीच अनंत करता आली असती, तरी मार्गदर्शकाच्या वर्तनात फरक पडला नसता. आयताकार तरंग मार्गदर्शकामधीत प्रभावी प्रेषण प्रकारासाठी (TE_1,0) मज्जाव तरंगलांबी मार्गदर्शकाच्या छेदाच्या मोठ्या बाजूच्या लांबीशी (a) पुढीन सूत्राने संबद्ध असते.

 λ_c= 2a    …    …    …    …    …    …    (२)

तरंग मार्गदर्शकामध्ये तरंगाची प्रेषित होण्याची परिणामी गती व परिणामी तरंगलांबी या दोन्ही परिमाणांची मूल्ये त्यांच्या मुक्त अवकाशातील मूल्यांपेक्षा भिन्न असतात. अक्षीय दिशेत मोजलेल्या ज्या अंतरात तरंगक्षेत्र बदलाचे एक आवर्तन पुरे होते, त्यास मार्गदर्शकातील तरंगलांबी म्हणतात. हे अंतर चालून गेल्यास तरंगाच्या कलेमध्ये (एखाद्या संदर्भापासून कोनामध्ये मोजलेल्या तरंगाच्या गतिविषयक स्थितीमध्ये) २π अरीयमान [→कोन] एवढा फरक पडतो.

मार्गदर्शकामधील तरंगलांबी, गट वेग आणि कला वेग : मार्गदर्शकामधून तरंगाचे प्रेषण होत असते तेव्हा मार्गदर्शकामधील तरंगलांबी λ_g, मुक्त अवकाशातील तरंगलांबी λआणि मज्जाव तरंगलांबी λ_c यांतील संबंध समीकरण (३) ने दर्शविला जातो. 

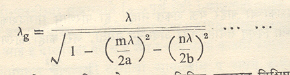 (६)

या सूत्रांमध्ये m आणि n हे त्या त्या विशिष्ट प्रकारात विशिष्ट मूल्य (०,१,२,३… इ.) असलेले पूर्णांक आहेत.

मार्गदर्शकातील क्षेत्रे निर्माण करणारे तरंग घटक प्रकाशाच्या c या वेगाने (३ x १०^१० सेंमी./ सेकंद) मार्गक्रमण करीत असतात पंरतु तरंग मार्गदर्शकातील तरंगलांबी λ_g हा घटक तरंगांच्या तरंगलांबीपेक्षा जास्त असतो. यामुळे तरंग मार्गदर्शकामधील क्षेत्रे अक्षाच्या दिशेने ज्या वेगाने सरकत असतात, त्याला कला वेग v_p म्हणतात. हा वेग प्रकाशवेगापेक्षा जास्त असतो, मार्गदर्शकामधील कला वेग आणि प्रकाशवेग यांतील संबंध खालील सूत्राने दर्शविला जातो.

असे समीकरण मिळते हे सहज ध्यानात येईल. यावरून हे लक्षात येईल की v_g जितक्या प्रमाणात c पेक्षा कमी असतो त्याच प्रमाणात कला वेग v_p हा c पेक्षा जास्त असतो.

समीकरण (५) मध्ये m= o व n= o अशी मूल्य वापरल्यास λ_c चे मूल्य अनंत येते. अशा तरंग प्रकारास TE_0,0म्हणता आले असते परंतु असा तरंग प्रकार धातूच्या पोकळ तरंग मार्गदर्शकात असू शकत नाही, हे क्षेत्र समीकरणांच्या निर्वाहावरून (समीकरणे सोडवून मिळणाऱ्या उत्तरावरून) लक्षात येईल. त्याचप्रमाणे m आणि n या पादांकांना दुसरी कोणतीही मूल्ये असल्यास येणारी मज्जाव तरंगलांबी TE_1,0प्रकारामधील मज्जाव तरंगलांबीपेक्षा कमी असते, हेही समीकरण (५) वरून तपासता येईल. म्हणजे TE_1,0तरंग प्रकारापेक्षा दुसऱ्या तरंग प्रकारांची मज्जाव कंप्रता जास्त असते आणि म्हणून TE_1,0हा प्रेषणाचा प्रभावी प्रकार समजला जातो.

E तरंगांचे (किंवा TM प्रकारांचे) विवेचन जवळजवळ TE प्रकाराप्रमाणेच करता येते. या तरंगांच्या बाबतीत क्षेत्रांची रचना TE प्रकारापेक्षा वेगळी असली, तरी समीकरणे (५) व (६) यांची येथेही पूर्ती हाते परंतु m किंवा n या दोन पादांकांपैकी कोणत्याच पादांकाचे मूल्य शून्य असू शकत नाही. म्हणजे आयताकार तरंग मार्गदर्शकामध्ये TM_1,0 अथवा TM_0,1 हे प्रकार संभवत नाहीत. आतापर्यंतच्या विवेचनावरून हे स्पष्ट होते की, मार्गदर्शकाचे परिमाण अंदाजे विद्युत् चुंबकीय तरंगलांबीच्या आकारमानाचेच असावे लागते. त्यामुळे तरंग मार्गदर्शक अति-उच्च कंप्रतेकरिताच का वापरण्यात येतात, हे लक्षात यते. सूक्ष्मतरंगांकरिता ही प्रयुक्ती विशेष उपयुकत आहे. विविध कंप्रतापट्ट्यांकरिता उपयुक्त अशा आयताकार मार्गदर्शकाची परिणामे (TE_{1, 0}  प्रकाराकरिता) सोबतच्या कोष्टकात दिली आहेत. त्यावरून त्याच्या प्रत्यक्ष आकारमानाविषयी कल्पना येऊ शकते. 

वर्तुळाकार तरंग मार्गदर्शक : हे मार्गदर्शक वृत्तचितीच्या आकाराचे असून त्यांचा काटछेद वर्तुळाकार असतो म्हणून त्यांना वर्तुळाकार मार्गदर्शक असे म्हटले आहे. यांतील क्षेत्रांची रचना वरील तरंग मार्गदर्शकांपेक्षा भिन्न असली, तरी दोन्ही प्रकारच्या तरंग मार्गदर्शकांच्या बाबतीत मॅक्सवेल समीकरणे हीच आधारभूत आहेत, हे उघड आहे.

वर्तुळाकार तरंग मार्गदर्शकातील भिन्न भिन्न प्रेषण प्रकार दर्शविण्यासाठी वरीलप्रमाणेच दुहेरी पादांक पद्धत वापरतात. कोणत्याही प्रेषण प्रकाराच्या बाबतीत मार्गदर्शकातील अनुप्रस्थ क्षेत्राचे स्पर्शीय आणि अरीय अशा दोन घटकांमध्ये वियोजन (विभागणी) करता येते. या दोन्ही घटकांच्या तीव्रतेत तरंग मार्गदर्शकाच्या भिंतीशी समकेंद्री अशा वर्तुळाकार मार्गावर आवर्ती बदल होत असतो. कोणत्याही क्षेत्र घटकाच्या तीव्रतेची तरंग मार्गदर्शकाच्या भिंतीशी समकेंद्री अशा वर्तुळाकार मार्गावरीलपूर्ण आवर्तने m ने दर्शविली जातात तर n चे मूल्य अरीय मार्गावरकोणत्याही क्षेत्र घटकाच्या होणाऱ्या दिशाबदलांच्या संख्येपेक्षा एकाने अधिक असते.

वर्तुळाकार तरंग मार्गदर्शकामध्ये TE_1,1हा प्रभावी प्रेषण प्रकार आहे. दुसरा महत्त्वाचा प्रकार म्हणजे TM_0,1किंवा वर्तुळाकार चुंबकीय प्रकार होय. आ.२ मध्ये वर्तुळाकार मार्गदर्शकामधील काही प्रेषण प्रकार दाखविले आहेत.

तरंग मार्गदर्शकाची शक्ती वाहून नेण्याची क्षमता (P) मार्गदर्शकामध्ये विद्युत् भंग न होता विद्युत् क्षेत्राचे (E) जेवढे जास्तीत जास्त मूल्य असू शकेल, त्यावर अवलंबून असते. समुद्रसपाटीला असणाऱ्या प्रमाणित तापमान, दाब आणि आर्द्रता या स्थितीमध्ये सूक्ष्मतरंग कंप्रतेच्या कमाल विद्युत् क्षेत्राचे मूल्य मार्गदर्शकामध्ये ३०,००० व्होल्ट प्रती सेंमी. पर्यंत असू शकते.

आयातकार तरंग मार्गदर्शकाची TE_1,0  या प्रकारासाठी कमाल शक्तिक्षमता P आणि कमाल विद्युत् क्षेत्र तीव्रता E_max  यांच्यामध्ये पुढील संबंध आहे.

P वॉटमध्ये, व्यक्त करण्यासाठी  E_max व्होल्ट/सेंमी. मध्ये आणि a व b ही मार्गदर्शकाची आंतर परिमाणे सेंमी. मध्ये असली पाहिजेत. मार्गदर्शकाची शक्तिक्षमता समुद्रसपाटीपासून उंची वाढत जाईल तसतशी कमी होत जाते.

तरंग मार्गदर्शकातील क्षीणन : तरंग मार्गदर्शकामधून तरंग (z अक्षाच्या दिशेत) मार्गक्रमण करीत असला म्हणजे त्याची शक्ती

P_z = p₀e^–αz  …    …      …     …      (११)

या घातीय नियमानुसार कमी होऊ लागते. P₀ ही  z = o  ह्या अंतरावरील शक्ती असून P_z ही z अंतरावरील शक्ती आहे. α ला क्षीणन स्थिरांक म्हणतात व त्याने तरंग मार्गदर्शकाच्या व्ययी गुणधर्माचे मापन केले जाते. तरंग मार्गदर्शकाच्या आतील भिंतीवर निर्माण होणाऱ्या विद्युत् प्रवाहामुळे व विद्युत् अपारक-व्ययामुळे उर्जेचे शोषण होते.  क्षीणन स्थिरांकाचे मूल्य तरंग मार्गदर्शकाच्या भिंतीची संवाहकता, मार्गदर्शकाची भूमितीय परिमाणे, प्रेषण प्रकार आणि कंप्रता या गोष्टींवर अवलंबून असते. इतर सर्व राशी त्याच राहिल्यास वाढत्या संवाहकतेबरोवर किंवा (घनफळ/पृष्ठफळ) या गुणोत्तराचे मूल्य जास्त असल्यास α चे मूल्य कमी होते म्हणून सामान्यपणे पोकळ तरंग मार्गदर्शक तांबे किंवा पितळ या धातूंचे बनविलेले असतात. क्वचित अतिशय उच्च कंप्रतेसाठी वापरावयाचे मार्गदर्शक चांदीचे बनविलेले असतात किंवा त्यांना आतून चांदीचा मुलामा दिलेला असतो.

आयातकार तरंग मार्गदर्शकामधील क्षीणन मज्जाव कंप्रतेच्यावर कंप्रता वाढवीत गेल्यास प्रथम कमी होत जाऊन त्यानंतर लहानशा कंप्रतापट्ट्यामध्ये काहीसे स्थिर राहते आणि पुन्हा उच्च कंप्रतांना वाढू लागते. हा बदल पुढील दोन घटनांमुळे होतो. ऊर्जा-व्यय कमी राहण्यासाठी अनुकूल ठरेल असा मार्गदर्शकातील क्षेत्रांच्या रचनेत बदल होतो म्हणून सुरुवातीस क्षीणन कमी होते. परंतु उच्च कंप्रतांना त्वक् परिणामही (संवाहकातील विद्युत् प्रवाह अंतर्भागापेक्षा पृष्ठभागाजवळ केंद्रित होणे यामुळे संवाहकांचा परिणामी रोध वाढतो) वाढू लागतो. यामुळे व्यय वाढतो आणि म्हणून क्षीणनही वाढू लागते. कंप्रता वाढवीत गेल्यास सर्व आयताकार तरंग मार्गदर्शकामध्ये सर्वच प्रेषण प्रकारांच्या बाबतीत क्षीणनामध्ये वर वर्णिलेला बदल होत गेलेला आढळतो. आ. ३ मध्ये हवाभरित तांब्याच्या आयताकार तरंग मार्गदर्शकातील क्षीणनामध्ये कंप्रतेबरोबर होणारा बदल दाखविला आहे.

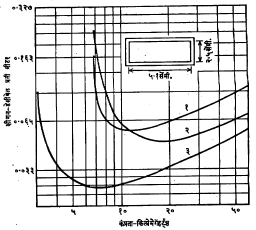
तांब्याच्या आयताकार तरंग मार्गदर्शकाच्या बाबतीत TE_1,0 प्रेषण प्रकारासाठी x – पट्टामध्ये होणारे क्षीणन ०·१ डेसिबेल/ मी. एवढे अल्प आहे. मार्गदर्शकाची लांबी बेताची असेल तेव्हा हे क्षीणन अल्प असले, तरी लांबी बरीच जास्त असली म्हणजे क्षीणनही खूप वाढते. म्हणून दूर अंतरापर्यंतच्या सूक्ष्मतरंग प्रेषणासाठी आयताकार मार्गदर्शक उपयुक्त ठरत नाहीत. याउलट TE_0,1 प्रेषण प्रकारामध्ये कार्यान्वित केलेल्या वर्तुळाकार मार्गदर्शकाच्या बाबतीत क्षीणन वाढत्या कंप्रतेबरोबर सतत कमी होत जाते, असे दिसून येते. मार्गदर्शकाचे आकारमान लहान राहून क्षीणन पुष्कळ कमी राहील अशी उच्च कंप्रता निवडता येते. उदा., ६ मिमी. मुक्त अवकाश तरंगलांबीचे सूक्ष्मतरंग निवडल्यास वर्तुळाकार मार्गदर्शकाच्या बाबतीत TE_0,1 प्रेषण प्रकारामध्ये आयताकार मार्गदर्शकापेक्षा क्षीणन शंभर पटींहूनही कमी असते. परंतु वर्तुळाकार मार्गदर्शकाच्या बाबतीत TE_0.1 प्रेषण प्रकाराचे TM_1,1 प्रकारात रूपांतर होण्याची शक्यता असल्यामुळे दूर पल्ल्याच्या प्रेषणासाठी हे रूपांतर अन्य उपाययोजना करून राखणे आवश्यक असते.

जोड, बाक आणि सांधे : काही विशिष्ठ परिणाम घडवून आणण्यासाठी तरंग मार्गदर्शक एकत्र जोडतात. त्यांना बाक किंवा पीळ देतात किंवा त्यांची जालांमध्ये मांडणी करतात. यांपैकी शेवटच्या प्रकारास सांधे असे नाव आहे.

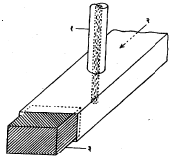
जोड : तरंग मार्गदर्शकांचा विस्तार करण्यासाठी किंवा त्यांत मंडल घटक समाविष्ट करण्यासाठी समरूप तरंग मार्गदर्शकांची टोके एकत्र जोडतात. यासाठी दोन मार्गदर्शकांची टोके घासून जोड नीट व्हावा म्हणून या घासलेल्या टोकांना जोडकडी बसवितात. ही जोडकडी एकमेकांवर घट्ट दाबून सीमा-जोड तयार करतात. या जोडाजवळ दोन्ही मार्गदर्शकांचा चांगला स्पर्श व्हावा लागतो. ही अडचण उत्पन्न होऊ नये म्हणून काही वेळा संकोचक जोड वापरतात. या जोड विभागाची योग्य अशी रचना करून त्यांच्या प्रत्यक्ष जोडजागी विद्युत् प्रवाहाचे मूल्य लघुत्तम राहील, अशी व्यवस्था केलेली असते. अशा परिस्थितीत या दोन विभागांच्या प्रत्यक्ष संपर्काला तेवढे महत्त्व राहत नाही.

समाक्ष केबलीमधून वाहणाऱ्या ऊर्जेचे तरंग मार्गदर्शकामध्ये संक्रमण करण्यासाठी निराळ्या प्रकारचा जोड वापरतात. यासाठी केबलीच्या मार्गदर्शकात बसवावयाच्या टोकाचे आकाशकात (अँटेनात) रूपांतर करतात. समाक्ष केबलीमधील तरंगाचे आयताकार तरंग मार्गदर्शकात TE_1,0 प्रकाराने क्षेपण करण्यासाठी समाक्ष केबलीचा अक्ष मार्गदर्शकाच्या छेदाच्या अधिक लांब बाजूला लंब ठेवतात (आ. ४) समाक्ष केबलीच्या बाहेरचा संवाहक तरंग मार्गदर्शकाच्या भिंतीजवळच थांबतो, परंतु आतील संवाहक  मार्गदर्शकात नेलेला असतो. हा संवाहक विद्युत् प्रेरणा रेषांना समांतर असून तो एषणी आकाशक म्हणून कार्य करतो.

तरंग मार्गदर्शकाच्या दोन्ही बाजूंच्या अग्रांत विशेषक संरोध (सर्व प्रकारचा एकूण विद्युत् रोध) जोडलेला असल्यास समाक्ष केबलीकडून येणारी आदान शक्ती दोन्ही दिशांना सारखी विभागली जाते. ती एकाच दिशेने जावी म्हणून मार्गदर्शकाच्या एका बाजूला धातूची पट्टिका वापरून मंडल संक्षेपित करतात.

बाक आणि पीळ : तरंग मार्गदर्शकाला बाक देऊन प्रेषणाच्या दिशेत बदल करता येतो. सरळ मार्गदर्शकापेक्षा वाकविलेल्या भागाची अभिलक्षणे किंचीत वेगळी असतात आणि म्हणून त्या जागी संरोधामध्ये थोडा बदल होतो. बाकाजवळ अनेक तरंग प्रकार निर्माण होतात आणि कंप्रता मज्जाव कंप्रतेपेक्षा जास्त असल्यास या वेगवेगळ्या तरंग प्रकारांद्वारे बरीचशी शक्ती वाहून नेली जाते.

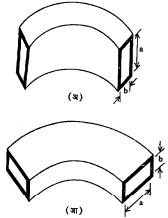मार्गदर्शक प्रभावी प्रकारात कार्यान्वित असल्यास आणि बाकामुळे कार्यान्वित होणाऱ्या इतर सर्व तरंग प्रकारांची मज्जाव कंप्रता उपयोजित कंप्रतेपेक्षा जास्त असल्यास प्रेषण दिशा बदलण्यासाठी बाक हा अतिशय सोईस्कर उपाय आहे. आयताकार मार्गदर्शकाच्या बाबतीत दोन प्रकारचे बाक वापरतात. त्यांना E–प्रतल आणि H–प्रतल बाक असे म्हणतात. (आ. ५).

प्रेषण दिशा तीच ठेवून विद्युत् चुंबकीय तरंगाचे ध्रुवण-प्रतल (ज्या विशिष्ठ प्रतलात तरंगाचा विद्युत् क्षेत्र घटक कंप पावतो ते प्रतल) इच्छित कोनातून फिरविण्यासाठी पीळ वापरतात. आयताकार तरंग मार्गदर्शकाला त्याच्या अक्षाभोवती पीळ देऊन आ. ६ मधील ९०^° चा पीळ तयार झाला आहे.

सांधे : काही विशिष्ट गुणधर्माचे तरंग मार्गदर्शक जाल म्हणजे सांधा होय. याची सामान्य उदाहरणे म्हणजे टी (tee)–सांधा, जादूचा टी–सांधा आणि दिशिक युग्मक ही होत.

टी-सांध्याचे H–प्रतल किंवा शाखांतर टी आणि  E–प्रतल किंवा एकसरी टी असे दोन प्रकार आहेत.

H —प्रतल टी : या सांध्यामध्ये शाखा मार्गदर्शक मुख्य मार्गदर्शकाच्या अरुंद बाजूवर चुंबकीय क्षेत्राच्या प्रतलात बसविलेला असतो. शाखा मार्गदर्शकात संकेतभरण केले म्हणजे हा संकेत सांध्याजवळ दुभागतो आणि  मुख्य मार्गदर्शकातील दोन भुजांमध्ये सांध्यापासून समान अंतरावर तो समकलेत (सारख्या कलेत) असतो (आ. ७).

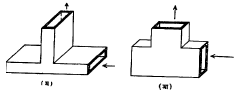E- प्रतल टी : या सांध्यामध्ये शाखा मार्गदर्शक मुख्य मार्गदर्शकाच्या रुंद बाजूवर विद्युत् क्षेत्राच्या प्रतलात बसविलेला असतो. शाखा मार्गदर्शकात संकेतभरण केले म्हणजे संकेत सांध्याजवळ दुभागतो आणि मुख्य मार्गदर्शकातील दोन भुजांमध्ये सांध्यापासून समान अंतरावर तो प्रतिकलेत (निरनिराळ्या कलेत) असतो (आ. ७).

जादूचा टी : एका एकरेषीय मार्गदर्शकाला एकाच बिंदूपाशी एक H–प्रतल टी व दूसरे E–प्रतल टी असे दोन शाखा मार्गदर्शक जोडून ही सेतु–रचना तयार होते. शाखा मार्गदर्शक क्र. ४ मध्ये (आ. ८) संकेतभरण केले असता आणि क्र. १ व क्र. २ या एकरेषीय शाखांचा शेवट त्यांच्या विशेषक संरोधात केलेला असल्यास या सेतुरचनेत सममिती असल्यामुळे आदान शक्ती दोन शाखांमध्ये सारखी विभागली जाईल. तसेच वरील सममितीमुळेच क्र. ३ च्या शाखेस संकेत दिला जाणार नाही. H–प्रतल टी शाखेच्या आदान संरोधाचा मार्गदर्शकाच्या विशेषक संरोधाशी सामान्यपणे सुजोड असणार नाही म्हणजे आदान शाखेत स्थिर तरंग निर्माण होतील.

त्या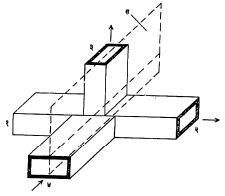चप्रमाणे E–प्रतल शाखेत शक्तिभरण केल्यास वरच्या सारखीच स्थिती उद्‌भवते. एकरेषीय क्र. २ व क्र. १ या शाखांचा शेवट त्यांच्या विशेषक संरोधाने केला असता आदान शक्ती या दोन शाखांत समान विभागली जाईल व क्र. ४ शाखेस शक्ती दिली जाणार नाही. आदान शाखेत स्थिर तरंग मात्र निर्माण होतील.

एकरेषीय शाखांवरील दोन सुजोड भारांच्या जागी दोन समान मूल्यांचे व सारखा कला कोन असणारे संरोध आणले, तरी या रचनेची सममिती बिघडत नाही. अशा परिस्थितीत क्र. ३ व क्र. ४ या शाखांमध्ये युग्मन होत नाही. थोडक्यात या रचनेच्या एका शाखेत संकेतभरण करून दुसऱ्या शाखेचा शून्यस्थिती अभिज्ञातक (ओळखण्याचे साधन) म्हणून उपयोग करणाऱ्या सेतु–मंडलाशी असणारे साम्य स्पष्ट होते.

या सेतु–रचनेचा सूक्ष्मतरंग मंडलामध्ये अनेक प्रकारे उपयोग करतातः उदा., आपाती आणि परावर्तित तीव्रतेचे मापन.

दिशिक युग्मक :   तरंग मार्गदर्शकाबरोबर वापरावयाची एक मापन प्रयुक्ती म्हणजे दिशिक युग्मक होय. यात दोन प्रेषण मार्ग एका छेदन बिंदूत किंवा छेदन प्रदेशात युग्मित केलेले असतात. हे युग्मन असे असते की, एका मार्गदर्शकातून एका दिशेत जाणारा विद्युत् चुंबकीय तरंग दुसऱ्या मार्गदर्शकात पहिल्या मार्गदर्शकातील तरंगाच्या विरुद्ध दिशेत जाणारा तरंग प्रवर्तित करतो. मात्र अशा प्रकारचा एकच तरंग केवळ आदर्श युग्मकामध्ये प्रवर्तित होतो. प्रत्यक्षात मात्र विरुद्ध दिशांनी मार्गक्रमण करणारे दोन तरंग प्रवर्तित होत असतात. यांपैकी एका तरंगाची शक्ती दुसऱ्यापेक्षा पुष्कळच कमी असते आणि म्हणूनच या युग्मकाला दिशिक गुणधर्म प्राप्त होतो.

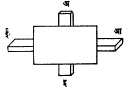आ. ९ मध्ये चार मार्गदर्शक अग्रांचे तरंग मार्गदर्शक जाल दाखविले आहे. यात अग्रे अ व इ आणि आ व ई एकमेकांपासून विलग केलेले असतात.

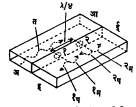
दिशिक युग्मकाचा एक सामान्य प्रकार तरंग व्यतिकरण (तरंगमालिका एकमेकींवर अध्यारोपित होण्याच्या) गुणधर्मावर आधारलेला आहे. आ. १० मध्ये दाखविल्याप्रमाणे दोन आयताकार तरंग मार्गदर्शक त्यांच्या अरुंद बाजूंनी जोडलेले असतात. त्यांच्या समाईक अरुंद बाजूमध्ये λ/४ एवढ्या अंतरावर दोन सारख्या आकारमानाची व व्याप्तीची भोके ठेवलेली असतात. या जालात अ या अग्रातून तरंगाचे प्रसारण होत आहे असे मानल्यास बहुतेक संपूर्ण तरंग आ अग्रापर्यंत पोहोचतो. पहिल्या किंवा दुसऱ्या भोकामधून या तरंगाचा काही भाग दुसऱ्या मार्गदर्शकात शिरतो व तेथे त्याचे दोन विरुद्ध दिशांत जाणाऱ्या तरंग घटकांत विभाजन होते. (आकृतीत हे घटक १_प  व २_प आणि १_म व २_म या चिन्हांनी दाखविले आहेत). १_प आणि २_प हे घटक ई अग्राकडे जाऊ लागले म्हणजे ते समकलेत एकत्र होतात परंतु इ अग्राच्या दिशेत २_म हा घटक  १_म च्या प्रतिकलेत असतो आणि म्हणून हे घटक एकमेकांचा निरास करतात व इ अग्राकडे तरंग पोहोचत नाही. म्हणून अग्रे अ आणि इ यांच्यामध्ये पूर्णतः विलगीकरण असते व याच कारणामुळे आ आणि ई या अग्रांमध्येही असेच विलगीकरण असते.

दिशिक युग्मक अग्रदिशिक (आपाती) तरंगाचे किंवा पश्चदिशिक (परावर्तित) तरंगांचे विवेचक रीत्या मापन करण्यासाठी अतिशय उपयुक्त आहे.

पहा : सूक्ष्मतरंग

संदर्भ : 1. Henney, K. Radio Engineering Handbook, New York, 1959.

            2. Redwood, M. Mechanical Waveguides, New York, 1960.

            3. Terman, F. E. Electronic and Radio Engineering, Tokyo, 1955.

शिरोडकर सु. स.