नियमालेखन : (नोमोग्राफी). एखाद्या समीकरणाने दोन वा अधिक चलांसंबंधी (बदलत्या राशींसंबंधी) जो गणितीय नियम व्यक्त होतो त्याचे, विशिष्ट प्रकारे काढलेल्या आलेखाच्या वा संरेखनपटाच्या साहाय्याने, समजण्यास व वापरण्यास सोपे आणि व्यवहारोपयोगी असे चित्ररूप दर्शन घडविणे हा नियमालेखन शास्त्राचा मुख्य उद्देश होय. स्थापत्य, युद्धशास्त्र आणि उद्योगधंदे यांमध्ये तंत्रज्ञांना नियमालेखनाचा हरघडी उपयोग होतो.
गणनकार्यासाठी आलेखाचा उपयोग फार पूर्वीपासून केला जात असे. उदा., हिपार्कस यांनी इ. स. पू. १५० मध्ये गोलीय त्रिकोणासंबंधी प्रश्न सोडविण्यासाठी आलेखाचा उपयोग केल्याचे आढळते. एकोणिसाव्या शतकात फ्रान्समध्ये लोहमार्ग तयार करावयाचे काम चालू असताना नियमालेखनाविषयीच्या विचारास चालना मिळाली. त्या शतकात तत्संबंधी जी प्रगती झाली तीतील मोठा वाटा स्थापत्यविशारदांकडे जातो. मॉरीस द ओकॅग्ने यांनी या विषयावर बरेच लेख व पुस्तके लिहून त्याच्या विकीसास विशेष गती दिली. त्यांना आधुनिक नियमालेखनशास्त्राचे जनक म्हटल्यास ते योग्य ठरेल.
मापप्रमाण : एक (वक्र किंवा सरळ) रेषा (अक्ष) घेऊन तीवर एक आदिबिंदू आ घ्या. जर क्ष ही संख्या या रेषेवर दर्शविणारा बिंदू आ पासून फ (क्ष) इतक्या अंतरावर असेल, तर ते फलन (चलांमधील गणितीय संबंध) फ – निदर्शक मापप्रमाण होय. जर फ (क्ष) = क्ष असेल, तर ते सम मापप्रमाण आहे असे म्हणतात. उदाहरणे : (१) सम मापप्रमाण असेल, तर १, २, ३,… या संख्यांचे निदर्शक बिंदू आ पासून अनुक्रमे १, २, .३,… इतक्या अंतरावर असतील, हे उघड आहे. नेहमी वापरात असणाऱ्या आलेखात असे सम मापप्रमाण घेतले जाते [→ आलेख]. (२) फ (क्ष) = क्ष२ असेल, तर १, २, ३,… या संख्या दर्शविणारे बिंदू आ पासून अनुक्रमे १, ४, ९,… इतक्या अंतरावर असतील.
प्रथम आपण क्ष, य या दोन चलांमधील फ (क्ष, य) = ० या समीकरणाने व्यक्त केलेल्या गणितीय नियमाच्या आलेखनाचा विचार करू. सामान्य आलेखपटावर आदिबिंदूत छेदणारे व परस्परांस लंब असे क्ष, य अक्ष असतात व त्यांवर सम मापप्रमाण घेतलेले असते. ज्या बिंदूंचे (क्ष, य) हे सहनिर्देशक, फ (क्ष, य) = ० या समीकरणाची पूर्तता करतात, अशा सर्व बिंदूंपासून मिळालेला वक्र तो या नियमाचा निदर्शक वक्र होय. या वक्राचा आकार फ या फलनावर अवलंबून असतो आणि तो काढावयास सोपा असेलच असे नाही. समजा, क्ष′= ग (क्ष), य′= ह (य) हे असे रूपांतरण शक्य आहे की, त्यामुळे फ (क्ष, य)= ० चे रूपांतरण क क्ष′+ घ य′+ ख = ० या क्ष′, य’ मधील एकघाती समीकरणाचा होते. आता क्ष′, य′ अक्ष घेऊन [म्हणजेच क्ष आणि व अक्षांवर अनुक्रमे ग (क्ष) आणि ह (य) फलनांनुसार मापप्रमाणे योजून] जर या एकघाती समीकरणाचा आलेख काढला, तर ती एक सरळ रेषा मिळेल. याचाच अर्थ असा की, दिलेल्या समीकरणाचा [फ (क्ष, य)= ०] जो वक्र त्याचे नवीन मापप्रमाण युक्त अक्षांच्या आलेखात एका सरळ रेषेवर प्रक्षेपण झाले. सरळ रेषा ही काढावयास अधिक सोपी आणि त्यावरून निष्कर्ष काढणेही अधिक सुलभ असते. उलट रूपांतरणाने दिलेल्या समीकरणाचे गुणधर्म अभ्यासता येतात. असे करण्यात विशिष्ट मापप्रमाणात अक्ष तयार करणे त्रासाचे पडते हे खरे पण एकदा आलेखपट तयार झाला की, त्याच प्रकारच्या अनेक समीकरणांचा एकदम अभ्यास सुलभतेने करता येतो, हा मोठाच फायदा मिळतो.
एखाद्या दिलेल्या वक्राचे सरळ रेषेवर प्रक्षेपण करून त्या वक्राचा अभ्यास करण्याची ही नियमालेखन शास्त्राची पायाभूत कल्पना लीऑ ललन यांनी प्रथम मांडली आणि जे. मसाऊ आणि शार्ल ललमांद यांनी ती प्रगत अवस्थेस नेली. ज्या वेळी काटेकोरपणापेक्षा लवकर निर्वाह (उत्तर) मिळविणे श्रेयस्कर असेल, त्या वेळी ही पद्धत उपयोगी पडते. पुढे दिलेल्या उदाहरणावरून ही पद्धत स्पष्ट होण्यास मदत होईल.
(१) समजा, क्ष२ + ४य२ = ४ हे समीकरण दिले आहे. त्याचा वक्र म्हणजे एक विवृत्त (लंबवर्तुळ) आहे. आता क्ष′= क्ष२ आणि य′= य२ या रूपांतराने क्ष′+य′= ४ हे एकघाती समीकरण मिळते. क्ष, य अक्षांवर क्ष२, य२ ही मापप्रमाणे घेतली, तर ही एक सरळ रेषा होते.

(२) चक्रवाढ व्याजाचा दरसाल दर शेकडा दरवअसेल,तरअमुद्दलाची क्ष वर्षानी होणारी रास य हीय = अ (१ + व / १००)क्ष या नियमाने मिळते. हाच नियम लॉगरिथम वापरून लॉग य = क्ष लॉग (१ + व / १००) + लॉग अ असा लिहिता येईल आताय′= लॉग य आणि क्ष′= क्ष असे रूपांतर वापरले आणि लॉग (१ + व /१००), लॉग अ या स्थिरांकाऐवजी क, ख लिहिले, तर य′= क क्ष′+ख असे समीकरण मिळते. ही सरळ रेषा आहे. क्ष, य अक्षांवर अनुक्रमे सम व लॉग य अशी मापप्रमाणे आहेत. क्ष′(म्हणजेच क्ष)च्या कोणत्याही मूल्यासाठी य′(पर्यायाने य) आलेखावरून वाचता येईल (आ. १). अशा प्रकारच्या आलेखपटास अर्ध-लॉगपट आणि ज्याच्या दोन्ही अक्षांसाठी लॉग मापप्रमाण आहे त्यास लॉगपट म्हणतात.
त्रिमिती सहनिर्देशक भूमितीच्या [⟶ भूमिति] साहाय्याने तीन चलांमधील फ(क्ष, य, झ) = ० या नियमाचा निर्देशक असे पृष्ठ मिळते. या नियमाचे द्विमिती आलेखपटावर पुढे दिल्याप्रमाणे निदर्शन करता येते. झ = झ० हा स्थिरांक समजून जे समीकरण (क्ष, य मधील) मिळेल त्याचा निदर्शक वक्र काढा. त्यालगत झ चे मूल्य झ० लिहा. अशातऱ्हेने झ च्या झ१झ२,… या वेगवेगळ्या मूल्यांसाठी, प्रत्येकी एक असे निरनिराळे वक्र काढा. एकंदर आकृती भूगोलातील समोच्च रेषायुक्त आकृतीप्रमाणे दिसेल. यावरून दिलेल्या नियमाविषयी माहिती वाचता येईल. ज्या वेळी दिलेला नियम अ (झ) X फ (क्ष) + ब (झ) X ग (य) +क (झ) = ० असेल त्या वेळी क्ष′= फ (क्ष), य′= ग (य) वापरून, झ = झ०, झ१, … इत्यादी मूल्यांसाठी अ (झ०) क्ष′+ब (झ०)य′+क (झ०) = ० अशा क्ष′, य′ यांमधील सरळ रेषा मिळतात.
संरेखन-पट : वेगवेगळी मापप्रमाणे घेतलेले अक्ष विशिष्ट प्रकारे एकमेकांजवळ ठेवून गणितीय नियमांचा अभ्यास सुलभतेने करता येतो, अशा अक्षांना संरेखन-पट म्हणतात. ही कल्पना द ओकॅग्ने यांनी प्रथम मांडून तिचा विस्तार केला. पुढील उदाहरणांवरून ही कल्पना स्पष्ट होईल.
(१) सेल्सिअस आणि फॅरेनहाइट या तापमान मोजण्याच्या दोन पद्धती आहेत. त्यांचा तुलनात्मक अभ्यास करण्याकरिता खालील संरेखन-पट उपयोगी पडतो. क्ष अक्षावर सम मापप्रमाण घेऊन, य अक्षावर फ (य) = ३२ + ९/५ य या फलनानुसार मापप्रमाण घेतले. आता हे दोन्ही अक्ष एकमेकांवर असे ठेवा की, क्ष अक्षावरील ० दाखविणारा बिंदू आणि य अक्षावरील ३२ ही संख्या दर्शविणारा बिंदू एकमेकांवर बसतील. आता क्ष अक्षावरील संख्या म्हणजे सेल्सिअस आणि य अक्षावरील संख्या म्हणजे फॅरेनहाइट असे समजले असता दोन्ही पद्धतींचा तुलनात्मक संरेखन-पट मिळेल.
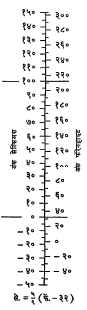
(२) गुणाकार, भागाकार इत्यादींसाठी वापरतात असणारी ⇨ गणकपट्टी हाही संरेखन-पटाचाच एक प्रकार होय. यामध्ये झ = क्ष·य हे समीकरण लॉग झ = लॉग क्ष + लॉग य असे लिहिले पाहिजे. क्ष, य, झ या तीन अक्षांवर लॉग मापप्रमाण घेऊन ते एकमेकांच्या लगत सरकवता येतील अशी रचना असते.
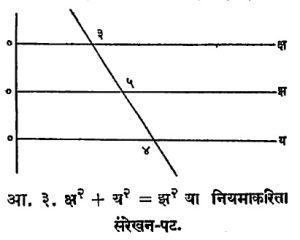
(३) क्ष, य, झ या तीन चलांमध्ये ह (झ) = फ (क्ष) + ग (य) असा नियम असेल, तर त्यासाठी खाली दिल्याप्रमाणे संरेखन-पट फायदेशीर होतो. क्ष, य, झ हे तीन अक्ष एकमेकांस समांतर असून झ अक्ष क्ष आणि य अक्षांच्या मधोमध, दोहोंपासून समान अंतरावर घेतात. क्ष, य अक्षांवर अनुक्रमे फ (क्ष), ग (य) असे आणि झ अक्षावर १/२ ह (झ) अशी मापप्रमाणे घेऊन क्ष, य, झ अक्षांचे आदिबिंदू (अनुक्रमे ट, ठ, ड) अक्षांना लंब अशा रेषेवर असतील अशा प्रकारे घेतात. आता समजा, एक सरळ रेषा क्ष, य, झ अक्षांना अनुक्रमे क, ख, घ या बिंदूंमध्ये छेदते. प्राथमिक भूमितीवरून २ डघ = टक + ठख हे सहज दाखविता येईल पण घेतलेल्या मापप्रमाणावरून क, ख, घ बिंदू जी क्ष, य, झ यांची मूल्ये दर्शवितात ती म्हणजे टक = फ (क्ष), ठख = ग (य) आणि डघ = १/२ ह (क्ष). या दोन्ही समीकरणांवरून ही मूल्ये म्हणजे दिलेल्या समीकरणाचे निर्वाह होत, हे लक्षात येईल. एकदा हा संरेखन-पट तयार झाला की, नुसती पट्टी (सरळ रेषादर्शक) ठेवून क्ष, य, झ ची निर्वाहमूल्ये ताबडतोब काढता येतात. आ. ३ मध्ये क्ष२ + य२ = झ२ याकरिता तयार केलेला संरेखन-पट दाखविला आहे.
संरेखन-पट तयार करताना नेहमी सरळ रेषाच अक्ष म्हणून वापराव्यात असे नाही. काही वेळा वक्र रेषा अक्ष म्हणून घेणे सोयीचे ठरते. कोणताही संरेखन-पट तयार करताना त्रास पडतो हे खरे पण एकदा तो तयार झाला की, नुसत्या पट्टीच्या साहाय्याने आपण पाहिजे असलेली मूल्ये ताबडतोब काढू शकतो. अर्थात यामध्ये काटेकोरपणात थोडी कमतरता येण्याचा संभव असतो.
पाहा : आलेख.
संदर्भ : 1. Adams, D. P. Nomography : Theory and Applications, Hamden, 1964.
2. Allcock, H. J. and others, Nomogram, London, 1963.
3. Otto, E. Nomography, New York, 1964.
आगाशे, क. म.