त्रिकोणमिति

त्रिकोणमिति : गणितशास्त्राच्या या शाखेत कोनांच्या विशिष्ट फलनांचा (गणितीय संबंधांचा) अभ्यास होतो. एखाद्या विशिष्ट प्रश्नातील ज्ञात कोन आणि अंतरे यांवरून अज्ञात कोन आणि अंतरे शोधण्यास त्रिकोणमितीचा उपयोग होतो. प्रत्यक्ष मोजण्यास अवघड अशी डोंगराची किंवा तत्सम गोष्टींची उंची किंवा नदीची रुंदी इत्यादींचे अचूक मोजमाप त्रिकोणमितीच्या साहाय्याने सहजपणे करता येते. स्थापत्यशास्त्रात मोठाले प्रकल्प, इमारती, रस्ते यांचे आराखडे बनविण्यात त्रिकोणमितीची महत्त्वपूर्ण मदत होते. ग्रह आणि तारे यांची स्थाने निश्चित करणे, त्यांच्या भ्रमणमार्गाचे गणित करणे इ. ज्योतिषशास्त्रीय अभ्यासात गोलीय त्रिकोणमिती उपयोगी पडते. नौकानयन, विमानविद्या, भूसर्वेक्षण, प्राक्षेपिकी (प्रक्षेपित पदार्थांसंबंधीचे शास्त्र) या विषयांत त्रिकोणमितीला अनन्यसाधारण महत्त्व प्राप्त झाले आहे. त्रिकोणमितीय फलने आवर्ती (कोनांच्या मूल्यांतील ठराविक अंतरांनंतर पुनःपुन्हा तीच मूल्ये धारण करणारी) असल्याने त्यांचा उपयोग जेथे कंपनांसारख्या आवर्ती घटनांच्या गुणधर्मांचा अभ्यास करणे आवश्यक असते तेथे (उदा., प्रकाश, ध्वनी, विद्युत्‌ प्रवाह, रेडिओ, दूरचित्रवाणी यांमध्ये) होतो.

प्रतलीय त्रिकोणमिती

त्रिकोणमितीय फलने : कोणताही एखादा कोन [⟶ कोन] दिलेला असेल, तर त्याच्या त्रिकोणमितीय फलनांची व्याख्या, सहनिर्देशक भूमितीच्या [⟶ भूमिति] साहाय्याने खाली दिल्याप्रमाणे करतात.

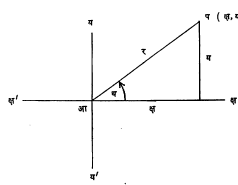
आ. १ मध्ये दाखविल्याप्रमाणे आप ही रेषा क्ष अक्षाशी थ कोन करीत असेल, प चे सहनिर्देशक (क्ष, य) असतील आणि आप = र असेल, तर थ या कोनाच्या त्रिकोणमितीय फलनांच्या व्याख्या पुढे दिल्याप्रमाणे करतात.

कोज्या थ =	क्ष	, ज्या थ =	य	, स्प थ =	य
	र		र		क्ष
छे थ =	र	, कोछे थ =	र	, कोस्प थ =	क्ष
	क्ष		य		य

स्प थ =	ज्या थ	, कोस्प थ =	१	=	कोज्या थ
	कोज्या थ		स्प थ		ज्या थ
छे थ =	१	, कोछे थ =	१
	कोज्या थ		ज्या थ

यातील स्प, छे, कोछे, कोस्प ही अनुक्रमे स्पर्शक, छेदक, कोछेदक आणि कोस्पर्शक यांची लघुरूपे होत. कोज्या याला कोटिज्या, स्पर्शक याला स्पर्शज्या आणि कोस्पर्शक याला कोस्पर्शज्या अशीही नावे देण्यात येतात. वरील व्याख्यांवरून हे परस्परसंबंध सहजच लक्षात येतील.

---

वर दिलेल्या व्याख्या या थ च्या कोणत्याही मूल्यासाठी (म्हणजेच कोणत्याही कोनासाठी) सत्य आहेत. परिभ्रमण करणाऱ्या आप या रेषेची जी अंतिम स्थिती (आणि पर्यायाने तिच्यावरील प बिंदूचे सहनिर्देशक क्ष, य यांची मूल्ये व चिन्हे) असेल ती थ च्या मूल्यावर अवलंबून असेल, हे उघड आहे. मात्र कोणत्याही थ साठी र चे चिन्ह धन (+) घ्यावयाचे असते. यावरून ० &lt थ &lt ९०^° असेल, तर क्ष &gt ० , य &gt ० असून सर्व त्रिकोणमितीय फलने धन चिन्हांकित असतील. परंतु जर ९०^° &lt थ &lt १८०^° असेल, तर क्ष &lt ०, य &gt ० असून कोज्या, स्प, कोस्प, छे ही फलने (क्ष &lt ० असल्याने) ऋण चिन्हांकित असतील, तर ज्या, कोछे धन चिन्हांकित असतील. या उदाहरणांवरून थ हा कोन दिल्यावर त्याची फलने कोणत्या चिन्हांची असतील हे सहज काढता येते. वर दिलेल्या व्याख्यांवरून ०^°, ९०^°, १८०^°, २७०^°, ३६०^° इ कोनांची काही फलने सहज लिहिता येतात. उदा., कोज्या ०^° = १, ज्या ०^° = ०, कोज्या ९०^° = ०, ज्या ९०^° = १, कोज्या १८०^° = –१, ज्या १८०^° = ० वगैरे. मात्र छे ९०^°, कोछे ०^°, स्प ९०^° अशा काही फलनांची मूल्ये अनिर्णित राहतात.

कोणत्याही थ साठी, क्ष ≤ र य ≤ र असेलच पाहिजे हे सहज दाखवता येते. त्यावरून थ कोनासाठी,

 –१ ≤ कोज्या थ ≤१ –१ ≤ ज्या थ ≤ १

असलेच पाहिजे, हे सिद्ध होते. मात्र स्प थ या फलनाला अशा मर्यादा नाहीत.

वर दिलेल्या नेहमीच्या वापरातल्या फलनांव्यतिरिक्त इतर काही फलने जुन्या ग्रंथांत आढळतात ती अशी : शरज्या थ = १ – कोज्या थ, कोशरज्या थ = १ – ज्या थ यांचा उल्लेख सूर्यसिद्धांतात (इ. स. पाचवे शतक) आणि आर्यभटांच्या आर्यभटीय या ग्रंथांत आढळतो.

त्रिकोणमितीय फलनांचे गुणधर्म : कोणत्याही थ साठी, र^२= क्ष^२+ य^२, हे समीकरण (आ. १) सत्य असते. याला र^२ ने भागून (^क्ष/_र)^२+ (^य/_र)^२ = १ म्हणजेच (कोज्या थ)^२ + (ज्या थ)^२ = १ हे नित्यसमीकरण (चलाच्या कोणत्याही मूल्याकरिता सत्य असणारे समीकरण) मिळते. हेच कोज्या^२ थ + ज्या^२ थ = १ असे लिहिण्याचा प्रघात आहे. याला कोज्या^२ थ ने भागून १ + स्प^२ थ = छे^२ थ, हे समीकरण मिळते. तसेच कोस्प^२ थ + १ = कोछे^२ थ हेही समीकरण सिद्ध करता येईल.

वरील विवेचनावरून दिसून येईल की, ही सर्व फलने एकमेकांशी संबंधित असून त्यांपैकी कोणत्याही एकाचे मूल्य माहीत असेल, तर बाकी सर्वांची मूल्ये काढता येतात.

त्रिकोणमितीय फलनांसाठी पुढील सूत्रे सिद्ध करता येतात.(१) ज्या (९०^° ± थ) = कोज्या थ(२) कोज्या (९०^° ± थ)= ∓ ज्या थ

(3) कोज्या (१८०^°± थ)= – कोज्या थ

(४) ज्या (१८०^°± थ)= ∓ ज्या थ.

---

आवर्ती गुणधर्म : कोणत्याही थ च्या मूल्यासाठी, ज्या (३६०^° + थ) = ज्या थ, हे सूत्र सिद्ध करता येते. यावरून असे दिसून येते की, थ या कोनातील प्रत्येक ३६०^° च्या वाढीनंतर ‘ज्या’ फलनाचे तेच मूल्य मिळते. यामुळे ‘ज्या’ फलन आवर्ती असून त्याचा आवर्तनकाल ३६०^° आहे असे म्हणतात. त्याचप्रमाणे कोज्या फलन आणि स्प फलन ही फलनेही आवर्ती असून त्याचे आवर्तनकाल अनुक्रमे ३६०^° आणि १८०^° आहेत, हे दाखविता येईल. तसेच छे, कोछे, कोस्प हीसुद्धा आवर्ती असून त्यांचे आवर्तनांक अनुक्रमे ३६०^°, ३६०^°, व १८०^° असतात हे दाखविता येईल.

त्रिकोणमितीय फलनांच्या आवर्ती गुणधर्माचा आणि या फलनासंबंधीच्या विविध सूत्रांचा उपयोग करून ०^° ते ९०^° या कक्षेतील कोनांकरिता निरनिराळ्या त्रिकोणमितीय फलनांची मूल्ये देणारी कोष्टके तयार करण्यात आलेली आहेत. या कोष्टकांवरून कोणत्याही कोनाच्या त्रिकोणमितीय फलनांची मूल्ये काढता येतात [⟶ गणितीय कोष्टके].

आलेख : क्ष अक्षावर कोनमान (थ) आणि य अक्षावर फलनमूल्ये प्रस्थापित करून आलेख काढल्यास, त्रिकोणमितीय फलनांचे आवर्ती गुणधर्म आणि इतर वैशिष्ट्ये उत्तम प्रकारे प्रदर्शित करता येतात.

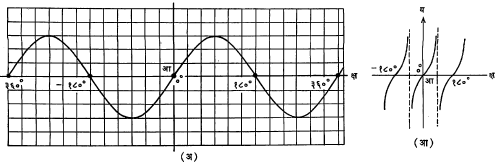
आ. २ मध्ये ‘ज्या’ आणि ‘स्प’ फलनांचे आलेख नमुन्यादाखल दाखविले आहेत.

कोनांच्या बेरजेची फलने : थ आणि द हे कोणतेही दोन कोन असल्यास थ + द आणि थ–द या कोनांची फलने थ आणि द या कोनांच्या त्रिकोणमितीय फलनांद्वारे पुढीलप्रमाणे मांडता येतात.

 (१) ज्या ( थ ±द) = ज्या थ·कोज्या द ±ज्या द·कोज्या थ(२) कोज्या (थ ±द) = कोज्या थ·कोज्या द ±ज्या थ·ज्या द

 वरील सूत्रांत थ = द घातल्यास खालील सूत्रे मिळतात. 

(३) ज्या (२ थ) = २ कोज्या थ·ज्या थ(४) कोज्या (२ थ) = कोज्या^२ थ–ज्या^२ थ

                                      = १-२ ज्या^२ थ = २ कोज्या^२ थ-१

या सूत्रांत २ थ = अ घातल्यास पुढील सूत्रे मिळतील.

(५) ज्या ^अ/_२= ±√^{१–कोज्या अ}/_२(६) कोज्या ^अ/_२ = ±√^{१ + कोज्या अ}/_२

(७) स्प ^अ/_२ = ±√^{१–कोज्या अ}/_{१+कोज्या अ}वर दिलेल्या (१) आणि (२) वरून, दोन त्रिकोणमितीय फलनांची बेरीज फलनांच्या गुणाकार रूपात मांडणारी, गुणाकार–सूत्रे मिळतात ती अशी :

---

(८) ज्या थ ±ज्या द = २ ज्या ^{थ ±द}/_२· कोज्या ^{थ ±द}/_२(९) कोज्या थ ±कोज्या द = २ कोज्या ^{थ + द}/_२· कोज्या ^थ–द/_२(१०) कोज्या थ–कोज्या द = – २ ज्या ^{थ + द}/_२· ज्या ^थ–द/_२

व्यस्त त्रिकोणमितीय फलने : त्रिकोणमितीय फलनांच्या व्याख्येवरून जर थ चे मूल्य दिले असले, तर ज्या थ चे एकमेव मूल्य मिळते. समजा ज्या थ = क आहे. आता, ‘ज्या’ फलनाच्या गुणधर्मावरून असे दिसून येते की, थ, १८०^°– थ, थ+प X ३६०^°, १८०^°– थ+प X ३६०^° (प = ०, ±१, ±२…) हे सर्व कोन असे आहेत की, ज्यांच्या ‘ज्या’ फलनांचे मूल्य ज्या थ इतकेच म्हणजे क असेल. म्हणजेच असा जर प्रश्न विचारला की, ‘ज्या’ फलनमूल्य क असणारा कोन कोणता, तर त्याला अनेक उत्तरे संभवतात. हेच सूत्ररूपाने, व्यस्त फलनाच्या [⟶ फलन] परिभाषेचा उपयोग करून पुढीलप्रमाणे लिहिता येईल. ज्या^-१ (क) = प X १८०^°+ (-१)^प थ, (प = ०, ±१, ±२,…). येथे ज्या ^–१ (क) म्हणजे ‘ज्या’ फलनाचे मूल्य क असणारा कोन. ज्या ^–१ (क) च्या अनेक संभाव्य मूल्यांपैकी –९०^° आणि ९०^° या दरम्यानच्या मूल्याला ज्या ^–१ (क) चे प्रमुख मूल्य म्हणतात.

वरीलप्रमाणेच कोज्या ^–१ (क) ची व्याख्या करता येईल. त्याच्या अनेक संभाव्य मूल्यापैकी ०^° आणि १८०^° यांमधील मूल्यास प्रमुख मूल्य म्हणतात. स्प^–१ (क) च्या अनेक संभाव्य मूल्यांपैकी –९०^° व ९०^° यांमधील मूल्यास प्रमुख मूल्ये म्हणतात. उदा., ज्या ^–१ (^१/_२) = प × १८०^°+ (–१)^प (३०^°) असे समीकरण मिळते. याच्या उजवीकडील राशीस ज्या ^–१ (^१/_२) चे सर्वसामान्य मूल्य म्हणतात. ज्या ^–१ (^१/_२) चे प्रमुख मूल्य ३०^° होय.

त्रिकोणमितीय समीकरणे : ज्या समीकरणांमध्ये त्रिकोणमितीय फलने हीच चलपदे म्हणून वापरलेली असतात त्यांस त्रिकोणमितीय समीकरणे म्हणतात. उदा., ज्या थ –२ कोज्या थ +१ = ०. ही समीकरणे सोडवून अज्ञात थ ची त्रिकोणमितीय फलनांची निर्वाह मूल्ये मिळतात. त्यावरून थ साठी व्यस्त त्रिकोणमितीय फलनांच्या रूपात सर्वसामान्य किंवा प्रमुख मूल्य शोधून काढता येते. उदा.,

  ज्या थ–२ कोज्या थ + १ = ०

 हे समीकरण सोडवून ज्या थ = –१ किंवा ज्या थ =^३/_५ ही निर्वाह मूल्ये मिळतात. यावरून थ = प X १८०^° + (–१)^प. (–९०^°) अथवा थ = प X १८०^°+ (–१)^प ज्या^–१ (^३/_५)

त्रिकोणाचे गुणधर्म : कखग हा कोणताही त्रिकोण असेल, तर त्याचे शिरोकोन क, ख, ग, आणि या कोनांच्या विरुद्धच्या बाजूंची लांबी अनुक्रमे का, खा, आणि गा अशा दाखविण्याचा प्रघात आहे. त्रिकोणाच्या परिवर्तुळाची त्रिज्या त ने दर्शवू. यांच्या परस्परसंबंधांची खालील सूत्रे सिद्ध करता येतात.

(१) ज्या सूत्र :	का	=	खा	=	गा	= २ त
	ज्या क		ज्या ख		ज्या ग
(२) कोज्या सूत्र : कोज्या क =		खा२+गा२–का२
		२ खागा

याचप्रमाणे कोज्या ख आणि कोज्या ग यांसाठी सूत्रे मांडता येतील.

---

 (३) प्रक्षेप सूत्र : का = खा कोज्या ग + गा कोज्या ख

(४) त्रिकोण कखग चे क्षेत्रफळ

= √ अ (अ–का) (अ–खा) (अ–गा)

अ = त्रिकोणाची अर्धपरिमिती = ^१/_२ (का + खा + गा)

या सूत्रांच्या साहाय्याने त्रिकोणाच्या तीन बाजू आणि तीन कोन या सहा गोष्टींपैकी कोणत्याही तीन (यात किमान एक बाजू असावी) माहीत असल्यास उरलेल्या सर्व शोधून काढता येतात. याला त्रिकोणशोधन अथवा त्रिकोण सोडविणे असे म्हणतात. खाली दिलेल्या उदाहरणावरून याचा उपयोग व्यवहारात कसा होतो हे स्पष्ट होईल. उदा., नदीच्या एका तीरावरून दुसऱ्‍या तीरावरील एका झाडाचा उन्नत कोन थ आहे (झाडाचा शेंडा दिसण्यासाठी समपातळीवरून दृष्टी ज्या कोनातून वर न्यावी लागते त्या कोनाला उन्नत कोन म्हणतात). १० मी. अंतर मागे जाऊन पाहिले असता त्याच झाडाचा उन्नत कोन द आहे. यावरून नदीची रूंदी आणि झाडाची उंची खाली दिल्याप्रमाणे काढता येते.

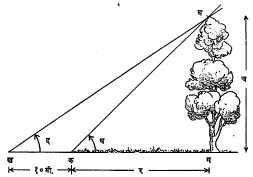
समजा, झाडाची उंची च असून नदीची रुंदी र आहे. आ. ३ वरून

स्प थ = ^च/_र आणि स्प द = ^च/_{र + १०}

 च = र·स्प थ = (र + १०)·स्प द

 र = ^{१० X स्प द}/_{स्प थ—स्प द} आणि च = र·स्प थ = ^{१० X स्प द}/_{स्प थ–स्प द·}स्प थ

थ, द हे कोन प्रत्यक्ष मोजून माहीत असल्याने स्प थ आणि स्प द या दोन्ही गोष्टी माहीत आहेत. म्हणून र आणि च ची मूल्ये काढता येतील.

वैश्लेषिक त्रिकोणमिती : कलनशास्त्रातील व्याख्येनुसार त्रिकोणमितीय फलनांचे अवकलज खाली दिल्याप्रमाणे मिळतात [⟶ अवकलन व समाकलन].

^d/_{d क्ष} (ज्या क्ष) = कोज्या क्ष, ^d/_{d क्ष} (कोज्या क्ष) = – ज्या क्ष,

^d/_{d क्ष} (स्प क्ष) = छे^२ क्ष इत्यादी.

---

 ‘ज्या’ आणि ‘कोज्या’ ही फलने संतत असून ‘स्प’ हे फलन ± प X ९०^°, (प = १, २, ३, …..) या मूल्यांव्यतिरिक्त इतरत्र संतत असते. आलेखावरून हे अधिक स्पष्ट होते.

मॅक्लॉरिन विस्तारसूत्रानुसार [⟶ अवकलन व समाकलन] थ हे कोनाचे अरीयमान [⟶ कोन] असेल, तर ज्या थ आणि कोज्या थ यांची मूल्ये अनंत श्रेढी रूपांत मांडणारी खालील सूत्रे मिळतात. 

ज्या थ = थ –	थ३	+	थ५	–	थ७	+……………..
	३!		५!		७!
ज्या थ = १–	थ२		थ४		थ६	+……………..
	२!		४!		६!

(प! = १ X २ X ३ X…………. X प)

या सूत्रांचा वापर करून कोणत्याही कोनाची ‘ज्या’ व ‘कोज्या’ फलने (आणि त्यांवरून इतर त्रिकोणमितीय फलने) पाहिजे तितक्या काटेकोरपणे काढता येतात. त्रिकोणमितीय फलन–मूल्यांची कोष्टके यावरूनच तयार केली जातात. वर दिलेल्या सूत्रांमध्ये थ कोनाचे अरीयमान असल्याकारणाने ती सत्‌ संख्या [⟶संख्या] असली पाहिजे हे उघड आहे.

व्यापकीकरण : वर दिलेल्या सूत्रांतील उजव्या बाजूच्या राशी थ सदसत्‌ संख्या असली, तरी अभिसारी अनंत श्रेढी आहेत, हे दाखवता येते. म्हणून थ सदसत्‌ असता, या अनंत श्रेढींच्या सीमांना अनुक्रमे ज्या थ आणि कोज्या थ अशी नावे देतात. यामुळे त्रिकोण मितीचे व्यापकीकरण करणे शक्य होते. 

वरील सूत्रानुसार थ = i अ, i = √–१ असेल ,तरकोज्या अ + i ज्या अ = e^iअ असे दाखवता येईल. येथे e हा स्वाभाविक लॉगरिथमाचा आधारांक [⟶ लॉगरिथम] असून जर क ही सदसत्‌

संख्या असेल, तरeक = १ +		क	+	क२	+…. हे सूत्र वापरले आहे
		१!		२!
[⟶ इ]. यावरून पुढील सूत्रे सहज सिद्ध होतात.
कोज्या थ =	eiथ + e–iथ		, ज्या थ =			eiथ–e–iथ
	२					२i

---

न ही कोणतीही परिमेय (जी दोन पूर्णांकाच्या गुणोत्तराच्या स्वरूपात मांडता येते अशी) संख्या असल्यास

(कोज्या थ +i ज्या थ)^न = (e^iथ)^न = e^{iन थ}                                      = कोज्या (न थ) + i ज्या (न थ)

असे समीकरण मिळते. यालाच द म्वाव्हर प्रमेय (आब्राआम द म्वाव्हर या फ्रेंच गणितज्ञांच्या नावावरून) म्हणतात.

साध्या त्रिकोणमितीय फलनांसाठी सिद्ध केलेली सर्व सूत्रे (योग्य त्या फरकाने) व्यापकीकृत त्रिकोणमितीय फलनांसाठीही सिद्ध करता येतात.

त्रिकोणमितीय श्रेढी : त्रिकोणमितीय फलनांनी बनलेल्या श्रेढींना उदा., अ_० + अ_{१ ·} कोज्या क्ष + ब_१ · ज्या क्ष + अ_२ · कोज्या २ क्ष + ब_२ · ज्या २ क्ष +…… प्रगत गणितीय विश्लेषणात महत्त्वाचे स्थान प्राप्त झाले आहे. यामधील अत्यंत महत्त्वाच्या म्हणजे ⇨ फूर्यें श्रेढी होत. यामधील सहगुणक

अ_म = १/_π  -π∫^π फ (ट) · कोज्या (मट) · d_ट

ब_म = ^१/_π -π∫^πफ (ट) · ज्या (मट· d_ट)

या सूत्रांनी मिळतात. यातील फ (ट) हे फलन (–π, π) या अंतरालात समाकलनीय असते. खूपशी आवर्ती फलने फ (क्ष) अशी आहेत की, त्यांसाठी फ (क्ष) सीमा असलेल्या अभिसारी फूर्ये श्रेढी मिळतात.

गोलीय त्रिकोणमिती

गोलाच्या पृष्ठावरील कोन व त्रिकोण यांचा अभ्यास गोलीय त्रिकोणमितीमध्ये होतो. नेहमीच्या परिचयांतील गोलीय पृष्ठ म्हणजे पृथ्वी गोल मानली असता तिचा पृष्ठभाग, आकाशाचा पोकळ गोल इत्यादी. ग्रह आणि तारे आकाशगोलाच्या आंतरवक्रतेवरचे बिंदू होत. गोलीय त्रिकोणाच्या फलनासाठी जी सूत्रे वापरतात त्यांचे प्रतलीय त्रिकोणाशी संबद्ध असलेल्या सूत्रांशी साम्य आहे. गोलीय पृष्ठाची वक्रता कमी होत गेली म्हणजेच गोलाची त्रिज्या अनंतापर्यंत वाढली म्हणजे प्रतल पृष्ठ मिळते.

गोलाच्या मध्यबिंदूतून जाणाऱ्‍या प्रतलाने गोलपृष्ठाचा होणारा छेद वर्तुळाकार असतो व त्याला बृहत्‌ वृत्त म्हणतात. अन्य प्रतलाने होणाऱ्‍या छेदास लघुवृत्त म्हणतात. बृहत्‌ वृत्ताची त्रिज्या गोलाच्या त्रिज्येशी समान असते. पृथ्वीच्या पृष्ठावरील विषुववृत्त किंवा ध्रुवबिंदूंतून जाणारी रेखावृत्ते ही बृहत्‌‌ वृत्ताची उदाहरणे आहेत परंतु विषुववृत्ताला समांतर असणारी अक्षवृत्ते ही लघुवृत्ताची उदाहरणे आहेत.

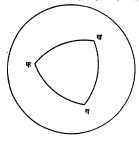
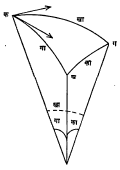
गोलीय त्रिकोण : तीन बृहत्‌ वृत्ते एकमेकांना छेदतात तेव्हा त्यांच्या चापांनी तयार झालेल्या गोलपृष्ठावरील आकृतीला गोलीय त्रिकोण म्हणतात (आ. ४). गोलीय त्रिकोणाचे तीन भाग दिले असता उरलेल्या तीन भागांची माहिती काढणे हाच गोलीय त्रिकोणमितीतील महत्त्वाचा भाग आहे. प्रतलीय त्रिकोणमितीप्रमाणेच त्याच फलनांचा उपयोग करून गोलीय त्रिकोणाचे विवेचन करण्याची पद्धत आहे. गोलीय त्रिकोणाच्या बाजूंचे मापन त्या चापांनी गोलाच्या मध्याशी त्रिज्यांतर्भूत केलेल्या कोनांनी करतात. तसेच कोणताही गोलीय कोन त्याच्याशी संगत असलेल्या द्वितल कोनात [⟶ कोन] मोजला जातो. गोलीय त्रिकोणामध्ये प्रत्येक बाजू अर्धवर्तुळापेक्षा लहान असली व प्रत्येक कोन दोन काटकोनांपेक्षा लहान असला, तर तो त्रिकोण सोडविणे सोईस्कर असते. तसे नसेल तर त्या त्रिकोणाचा संलग्‍न त्रिकोण विचारात घेऊन प्रश्न सोडविता येतो. गोलीय त्रिकोणात तीन कोन व बाजूंनी मध्याशी केलेले त्रिज्यांतर्गत कोन असे एकूण सहा कोन असतात. त्यांची त्रिकोणमितीय फलने संबंधित असतात.

---

आ. ५ मध्ये          Ðका  + Ðखा + Ðगा       &lt    ३६०^°

                             Ðका  +Ðखा + Ðगा    &lt    ५४०^°

                                                                   &gt   ५४०^°

(१) ज्या सूत्र : ^{ज्या क}/_{ज्या का} = ^{ज्या ख}/_{ज्या खा} = ^{ज्या ग}/_{ज्या गा}(२) कोज्या सूत्र : कोज्या का = कोज्या खा·कोज्या गा + ज्या खा·ज्या गा·कोज्या क

हेच सूत्र ध्रुवीय त्रिकोणास (बाजूच्या ध्रुवांनी होणाऱ्या त्रिकोणास) लावल्यास,

कोज्या क = –कोज्या ख·कोज्या ग + ज्या ख·ज्या ग·कोज्या का.

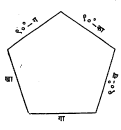नेपिअर नियम : गोलीय त्रिकोणात निदान एकतरी कोन काटकोन असेल, तर त्याला काटकोन त्रिकोण म्हणतात. गोलीय त्रिकोणात तिन्ही कोन काटकोन असू शकतात. काटकोन त्रिकोणासंबंधी दहा नियम मांडता येतात. त्यांनाच नेपिअर (जॉन नेपिअर या इंग्रज गणितज्ञांच्या नावावरून) नियम म्हणतात. ते नियम थोडक्यात मांडण्यासाठी आ. ६ चा उपयोग होतो. या पंचभुज आकृतीतील बाजू दर्शविल्याप्रमाणे लिहिल्यास आणि त्यांच्यातील कोणताही भाग मधला भाग मानून त्याच्या बाजूंचे दोन भाग संलग्‍न व उरलेले दोन भाग विरुद्ध मानल्यास ते दहा नियम दोन सूत्रांमध्ये गोवता येतात. ती दोन सूत्रे अशी :

(१) मधल्या भागाची ज्या = विरुद्ध भागांच्या कोज्यांचा गुणाकार.(२) मधल्या भागाची ज्या = संलग्‍न भागांच्या स्पर्शज्यांचा गुणाकार. वरील नियमांच्या साह्याने गोलीय काटकोन त्रिकोण सोडविणे शक्य होते.

नेपिअर सादृश्य सूत्रे : तिर्यक्‌ गोलीय त्रिकोण सोडविण्यासाठी नेपिअर सादृश्य सूत्रांचा उपयोग होतो. गोलीय त्रिकोणाचे एकूण पाच भाग त्यात गुंफलेले असतात. नेपिअर सादृश्य सूत्रे खाली दिली आहेत.

(१)	ज्या १/२ (क–ख)	=	ज्या १/२ (क–ख)
	स्प १/२ (का+खा)		स्प १/२ गा

(२)	कोज्या१/२ (क–ख)	=	स्प१/२ (का+खा)
	कोज्या१/२ (का+खा)		स्प १/२ गा

---

 ह्याप्रमाणेच आणखी चार सूत्रे लिहिता येतील. तसेच ध्रुवीय त्रिकोणांच्या गुणधर्मांचा उपयोग करून खालील सूत्रे मांडता येतील.

(३)	ज्या१/२ (का–खा)	=	स्प१/२ (क–ख)
	ज्या१/२ (का+खा)		कोस्प १/२ ग

(४)	कोज्या१/२ (का–खा)	=	स्प१/२ (क+ख)
	कोज्या१/२ (का+खा)		कोस्प १/२ ग

व्यवहारात गोलीय त्रिकोणमितीचा उपयोग मुख्यत्वेकरून ज्योतिषशास्त्र आणि नौकानयनशास्त्र यांमध्ये होतो. त्याच्या मदतीने अंतरे काढता येतात दिशा ठरविता येतात विमानांची व जहाजांची स्थाने निश्चित करता येतात तसेच निरीक्षण स्थानांचे अक्षांश–रेखांश निश्चित करता येतात.

इतिहास : त्रिकोणमिती या नावावरूनच दिसून येते की, या शास्त्राचा प्राथमिक हेतू त्रिकोणासंबंधी मोजमाप करणे हा होता. ज्योतिषशास्त्र हे हिंदूंच्या सहा वेदांगांपैकी एक. प्राचीन भारतात ज्योतिषशास्त्रातील गणनक्रिया सुलभ करण्याच्या प्रयत्नातून त्रिकोणमितीच्या प्राथमिक कल्पना उदयास आल्या. त्यामुळे प्रतलीय त्रिकोणमितीपूर्वी गोलीय त्रिकोणमितीचा विकास होत गेला असे आढळते. ग्रीक गणितज्ञ हिपार्कस (इ. स. पू. १३०) यांनी या विषयाचा पाया घातला असे मानतात. त्यांनीच ज्योतिर्विद म्हणून त्रिकोणमितीचा व्यवस्थित उपयोग करून घेतला. त्यांच्यानंतर टॉलेमी (इ. स. सु. ९०–१६९) यांनी दुसऱ्‍या शतकात Almagest हा ग्रंथ लिहिला. हा ग्रंथ ज्योतिषशास्त्रावर लिहिलेला आहे व त्याचे एकूण तेरा भाग आहेत. त्यांपैकी एका भागात पूर्ण जीवांचे कोष्टक दिलेले आहे. ते ३०′ (मिनिटे) एवढ्या लहान अंतरालाने दिलेले आहे. या सारणीमध्ये दिलेली मूल्ये पाच दशांश स्थळांपर्यंत बरोबर आहेत. त्या काळच्या गणितशास्त्राच्या प्रगतीच्या मानाने ही गोष्ट विशेष लक्षणीय आहे. त्याचा सु. एक हजार वर्षांपर्यंत ज्योतिषशास्त्र आणि त्रिकोणमिती या दोहोंवर प्रभाव पडलेला दिसतो. मेनलेअस (इ. स. पहिले शतक) यांना गोलीय त्रिकोणमितीचे अग्रदूत मानतात. हीरो (इ. स. पहिले शतक) यांनी स्थापत्यशास्त्रात आणि सर्वेक्षणशास्त्रात त्रिकोणमितीचा उपयोग करण्याचा प्रयत्न केला. टॉलेमी यांच्यानंतर हे शास्त्र पूर्वेकडे मुख्यत्वे हिंदू आणि अरब गणितज्ञांनी वाढविले. प्रसिद्ध हिंदू गणितज्ञ आर्यभट (इ. स. ४७६ –?), ब्रह्मगुप्त (सातवे शतक) आणि भास्कराचार्य (बारावे शतक) यांनी ‘ज्या–कोष्टके’ तयार केली. ग्रीक गणितज्ञ (पूर्ण) जीवांचा वापर करीत असत. त्याच्या पुढचा टप्पा हिंदू गणितज्ञांनी गाठला आणि अर्धजीवा वापरून कोष्टके बनविली. ही कोष्टके म्हणजे हल्लीची ज्या–कोष्टके होत. ही कोष्टके त्यांनी गोलीय व प्रतलीय काटकोन त्रिकोणांची चर्चा करताना वापरली.

सूर्यसिद्धांत या हिंदू ग्रंथात या अर्धजीवांच्या कोष्टकांचा उल्लेख आढळतो. त्यानंतर मुसलमानांनी आठव्या शतकाच्या अखेरीस, खलिफांच्या कारकीर्दीत हिंदू व ग्रीक संशोधनांची भाषांतरे केली आणि त्यांचा अभ्यास चालू ठेवला. नवव्या शतकामध्ये अल्‌–बटानी या अरब गणितज्ञांनी स्पर्शज्या व कोस्पर्शज्या या फलनांच्या व्याख्या देऊन त्यांची कोष्टके तयार केली. ही कोष्टके १^° च्या अंतरालाने दिलेली आहेत. दहाव्या शतकामध्ये अब्‌–अल वेफा या गणितज्ञांनी छेदक व कोछेदक यांच्या व्याख्या तयार केल्या व त्रिकोणमितीय फलनांच्या परस्परांतील संबंधांचा अभ्यास केला.

पाश्चात्त्य देशांत पंधराव्या शतकात या शास्त्राचे पुनरुज्‍जीवन झाले. मुख्यत्वे रेगिओमोनटानुस (१४३६–७६) यांच्या प्रयत्नाने ज्योतिषशास्त्राहून भिन्न अशा स्वतंत्र शास्त्राचा दर्जा त्रिकोणमितीस प्राप्त झाला. वैश्लेषिक त्रिकोणमिती प्रगत करण्याचे श्रेय योहान बेर्नुली (१६६७–१७४८), द म्वाव्हर (१६६७–१७५४) व लेनर्ड ऑयलर (१७०७–८३) यांनाच दिले पाहिजे. जॉन नेपिअर (१५५०–१६१७) यांच्या नित्यसमीकरणाचा गोलीय त्रिकोणमितीत फार उपयोग होतो. लॉगरिथमाच्या साह्याने त्रिकोणमितीतील गणनक्रिया करावयास त्यांनीच सुरुवात केली.

संदर्भ : 1. Loney, S. L. Plane Trigonometry, London, 1963.

            2. Rider, P. R. Plane and Spherical Trigonometry, New York, 1942.

            3. Todhuniter, I Leathem, J. G. Spherical Trigonometry, London, 1963.

पेण्ढरकर, का. दि.

“