विद्युत् गतिकी

विद्युत् गतिकी : विद्युत्, चुंबकीय व यांत्रिक आविष्कार यांमधील परस्परसंबंधांचा अभ्यास विद्युत् गतिकीमध्ये केला जातो. विद्युत् प्रवाहामुळे निर्माण होणारे चुंबकीय क्षेत्र, बदलणाऱ्या चुंबकीय क्षेत्रांमुळे प्रवर्तित झालेल्या विद्युत् चालक प्रेरणा (विद्युत् प्रवाह वाहण्यास कारणीभूत होणाऱ्या प्रेरणा), चुंबकीय क्षेत्रातील विद्युत् प्रवाहावरील प्रेरणा, विद्युत् चुंबकीय तरंगांचे प्रसारण, विद्युत् आणि चुंबकीय क्षेत्रीतील विद्युत् भारित कणांचे वर्तन या गोष्टींचा विद्युत् गतिकीमध्ये समावेश होतो. ही भौतिकीची एक शाखा असून पुष्कळ विद्युत् यंत्रांचे अभिकल्प (आराखडे) विद्युत् गतिकीय तत्त्वांवर आधारलेले असतात. विद्युत् गतिकीचे निरनिराळे विभाग याप्रमाणे आहेत : (१) रूढ विद्युत् गतिकी या विभागात विद्युत् व चुंबकीय क्षेत्रे आणि विद्युत् भारित कण यांचा ⇨ जेम्स मॅक्सवेल यांनी प्रथम घालून दिलेल्या विचार केला जातो. (२) पुंज विद्युत् गतिकी या विभागात पुंजयामिकीची तत्त्वे विद्युत् आणि चुंबकीय आविष्कारांस लावून अभ्यास केला जातो. (३) विद्युत् भारित कणांची गती प्रकाशाच्या गतीच्या जवळ पोहोचलेली असते, तेव्हा ते विद्युत् भारित कण व क्षेत्रे यांचा केलेला अभ्यास सापेक्षीय विद्युत् गतिकीमध्ये मोडतो. (४) आंतरतारकीय अवकाशातील तारे व अन्य खस्थ पदार्थ यांवरील तसेच वातावरणाच्या बाह्यसीमेपलीकडील अवकाशातील आयनीभूत (विद्युत् भारित अणू, रेणू वा अणुगट यांनी युक्त ) माध्यमांत होणाऱ्या विद्युत् चुंबकीय आविष्कारांचा अभ्यास वैश्विक विद्युत् गतिकी या विभागात केला जातो. येथे मुख्यत्वे रूढ विद्युत् गतिकीचा विचार केलेला आहे आणि इतरांची अगदी थोडक्यात माहिती दिली आहे.

रूढ विद्युत् गतिकी : एकमेकांपासून भिन्न अंतरावर असणाऱ्या विद्युत् भारांमध्ये होणाऱ्या परस्परक्रियेचे व त्यामुळे त्यांच्या गतिअवस्थेमध्ये होणाऱ्या बदलाचे विश्लेषण रूढ विद्युत् गतिकीत केले जाते. +q₁ हा विद्युत् भार त्यापासून r अंतरावर असणाऱ्या +q₂ या दुसऱ्या विद्युत् भारावर प्रेरणा लावतो. ही प्रेरणा या दोहोंमध्ये कोणतेही जड माध्यम नसतानाही कार्यान्वित होताना आढळते.ही क्रिया विशद करण्यासाठी विद्युत् चुंबकीय क्षेत्राची संकल्पना पुढे आली. या कल्पनेप्रमाणे q₁ हा विद्युत् भार असलेल्या स्थानी त्यामुळे E₂ या मूल्याचे विद्युत क्षेत्र मिळते. अंतिम परस्परक्रिया E₂ हे क्षेत्र व q₂ हा विद्युत भार यांमध्ये घडत असते. असेच गुरुत्वाकर्षणी परिणामाचे वर्णन करण्यासाठी गृहीत धरले जाते. इतर क्षेत्रांच्या तुलनेत विद्युत् चुंबकीय क्षेत्राचे एक वैशिष्ट्य असते. कोणताही विद्युत् चुंबकीय बदल हा अवकाशात c या प्रकाशाच्या वेगानेच प्रसारित केला जात असतो. त्यामुळे क्षेत्रजनक विद्युत् भार q₁ मध्ये जर काळानुसार काही बदल झाले, तर त्यायोगे होणारे परिणाम q₂ या क्षेत्रस्थानबिंदूपर्यंत पोहोचण्याकरिता r/c एवढा कालखंड जावा लागतो. ही वस्तुस्थिती विद्युत् चुंबकीय क्षेत्राच्या वर्तनात महत्त्वाचा फरक घडवून आणते.

ऊर्जा व संवेग (कणाचा वेग व द्रव्यमान यांच्या गुणाकाराने मिळणारी राशी) या राशी अक्षय्यता नियम पालन करतात [® द्रव्य आणि ऊर्जा यांची अक्षय्यता; संवेगाची अक्षय्यता]. q₂ या विद्युत् भाराच्या या गतिराशीत जर बदल झाला, तर त्याचा प्रतिसाद q₁ या क्षेत्रजनक विद्युत् भारापर्यंत पोहोचणे त्याच क्षणी शक्य होत नाही. त्यामुळे ऊर्जा व संवेग यांची देवघेव विद्युत् भार q₂ व स्थानिक विद्युत् क्षेत्र यांमध्ये होते, असे मानावे लागते. म्हणजे विद्युत् क्षेत्राला जड पदार्थाचे गुणधर्म आहेत, असा याचा अर्थ होतो.

विद्युत् क्षेत्र शेवटी विद्युत् भारापासूनच निर्माण होत असते, हे जरी खरे असले, तरी ते काही वेळा विद्युत् भाराशिवाय पण मिळत असते, ही गोष्ट लक्षात घ्यावयास हवी. रेडिओ प्रेषक एका विशिष्ट विद्युत् मंडलाद्वारे विद्युत् चुंबकीय क्षेत्रे प्रेषित करत असतो. प्रेषित विद्युत् क्षेत्राचा उगम मंडलाशी संबंध राहत नाही. यावरून विद्युत् क्षेत्राला स्वतंत्र भौतिकीय अस्तित्व आहे, असे म्हणता येते. एके काळी विद्युत् चुंबकीय क्षेत्राला जड माध्यमाचा आधार आवश्यक असतो, असे मानले जात असे. रिक्त अवकाशात जड माध्यम नाही, तरी त्यामध्ये क्षेत्रे प्रेषित होतात, हे विशद करण्यासाठी सबंध अवकाशात ईथर [ईथर-२] नावाचे एक आदर्श माध्यम सर्वत्र मरलेले आहे, असे मानले जात असे. या माध्यमांचा शोध घेण्यासाठी ⇨ आल्बेर्ट आब्राहाम  मायकेलसन व ⇨ एडवर्ड विल्यम्स मॉर्ली यांनी प्रयोग केले; पण ते असफल ठरले. यामुळे आधुनिक भौतिकीमध्ये विद्युत् चुंबकीय क्षेत्रे असणे हा अवकाशाचा एक विशिष्ट गुणधर्म आहे, असे मानले जाते. या प्रयोगाच्या निष्पत्तीचे विशदीकरण करण्याकरिता अॅल्बर्ट आइन्स्टाइन यांनी ⇨सापेक्षता सिद्धांताची मीमांसा दिली.

विद्युत् गतिकीमध्ये वापरण्यात येणारे सर्व सैद्धांतिक नियम विद्युत् चुंबकीय मीमांसेपासूनच मिळतात. या मीमांसेतील ⇨मॅक्सवेल विद्युत् चुंबकीय समीकरणांचा गतिकीकरिता पाया म्हणून उपयोग केला जातो. माहितीसाठी जेम्स क्लार्क मॅक्सवेल यांचे मुख्य नियम व इतर साहाय्यकारी समीकरणे पुढे दिली आहेत.

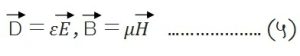या समीकरणांत

	= विद्युत् क्षेत्र प्रवर्तन (वा विद्युत् विस्थापन),
	= चुंबकीय प्रवर्तन,
ρ	= अवकाश भार घनता
	= विद्युत् प्रवाह घनता
ε	= विद्युत् अपार्यता स्थिरांक (वा विद्युत् पार्यता)
μ	= चुंबकीय पार्यता असे आहे. (curd या संज्ञेच्या स्पष्टीकरणासाठी ‘सदिश’ ही नांद पहावी ).

वरील समीकरणे प्रयोगाद्वारे मिळालेल्या निष्पत्तीची व्याप्ती वाढवून मिळविली गेली आहेत. यांपैकी पहिले समीकरण दोन विद्युत् भारात मिळणाऱ्या कुलंब परस्परक्रियेपासून मिळाले आहे. चुंबकीय ध्रुवांमध्ये प्रयोगाने आढळणाऱ्या परस्परक्रियेवर दुसरे समीकरण आधारित आहे. स्थिर चुंबकीय क्षेत्रामध्ये एक विद्युत् प्रवाहवाहक तार ठेवली असता तीवर एक प्रेरणा मिळते. या प्रयोगामध्ये चुंबकीय क्षेत्र व विद्युत् प्रवाह यांमध्ये होत असते. या आविष्काराचे निर्देशन करण्यासाठी ए. एम्. अँपिअर यांनी मंडल सिद्धांत दिला. हा सिद्धांत बायो-साव्हार (जे. बी. बायो व एफ्. साव्हार यांच्या प्रयोगावर आधारलेल्या) नियमाच्या स्वरूपातसुद्धा दिला जातो. यांचे तिसरे समीकरण या सिद्धांतावर आधारलेले आहे. फॅराडे-लेंट्स यांच्या विद्युत् चुंबकीय प्रवर्तन परिणामावर समीकरण (४) आधारलेले आहे. विद्युत् वाहकाला चुंबकीय क्षेत्राच्या सापेक्ष गती दिली, तर त्यामध्ये परस्परक्रिया होते. विद्युत् वाहकामध्ये विद्युत् क्षेत्र निर्माण होते, या भौतिकी तत्त्वाचा उपयोग या समीकरणात केलेला आहे (या समीकरणांच्या व संज्ञांच्या अधिक माहितीसाठी ‘मॅक्सवेल विद्युत् चुंबकीय समीकरणे’ ही नोंद पहावी ).

वरील समीकरणांवरून हे स्पष्ट होते की, (१) विद्युत् भार स्थिर असतील, तर त्यांमुळे फक्त विद्युत् स्थैतिक परिणाम किंवा क्षेत्र निर्माण होते. (२) विद्युत् भारांना जर स्थिर गती असेल, तर त्यामुळे विद्युत् प्रवाह मिळतो. अशा परिस्थितीत त्याच्या परिसरात विद्युत् व चुंबकीय अशी दोन्ही क्षेत्रे किंवा परिणाम प्रत्ययास येतात. वरील समीकरणात मुक्त एकाकी विद्युत् भारित कणाचे गतिवर्णन आढळत नाही.

अशा कणाच्या गतिविशेषाचे वर्णन ⇨हेंड्रिक आंटोन लोरेन्ट्स यांनी प्रथम दिले. q विद्युत् भार असलेला कण जर वेगाने

गतिमान होत असेल, तर त्यामुळे निर्माण होणारे विद्युत् चुंबकीय परिणाम

या समीकरणापासून मिळणाऱ्या

या विद्युत् प्रवाह मूलघटकाप्रमाणे असतात, असे लोरेन्ट्स यांनी दाखविले. येथे

I	= विद्युत् प्रवाह,
	विद्युत् प्रवाह मूलघटकाची लांबी असून अशा मूलघटकामुळे निर्माण होणाऱ्या चुंबकीय क्षेत्राचे मूल्य बायो-साव्हार नियमाद्वारे मिळते.

कोणतीही गती सापेक्ष असते म्हणजे तिचे मूल्य गृहित संदर्भ-व्यूहावर [®संदर्भ-व्यूह ] अवलंबून असते. संदर्भ-व्यूह निरीक्षकाच्या गतिअवस्थेमुळे ठरत असतो. त्यामुळे लोरेन्ट्स यांच्या सिद्धांताप्रमाणे खालील निष्कर्ष मिळतात.

(१) विद्युत् भाराला जर निरीक्षकाच्या सापेक्ष गती असेल, तर निरीक्षकाला चुंबकीय क्षेत्राचा पण प्रत्यय येतो. (२) निरीक्षकाला विद्युत् भाराएवढीच गती असेल, तर त्याला चुंबकीय क्षेत्र आढळणार नाही. अशा अवस्थेत त्याला फक्त विद्युत् क्षेत्राचाच अनुभव मिळेल. (३) चुंबकीय क्षेत्राच्या सापेक्ष जर निरीक्षकाला गती असेल, तर त्याला विद्युत् क्षेत्राचा प्रत्यय मिळतो. (४) q हा विद्युत् भार v वेगाने चुंबकीय व विद्युत् क्षेत्रांतून प्रवास करीत असेल, तर त्यावरील परिणामी प्रेरणा

वरील समीकरण विद्युत भार वेगाच्या चुंबकीय क्षेत्राच्या उदग्र दिशेत असणारा घटकच या प्रेरणेकरिता प्रभावी ठरतो, असे दिसते. विद्युत् क्षेत्रामुळे मिळणारी प्रेरणा विद्युत् क्षेत्र दिशेतच असते, तर चुंबकीय क्षेत्रामुळे निर्माण होणारी प्रेरणा उदग्र गती घटक व चुंबकीय क्षेत्र दिशा या दोहोंच्या उदग्र दिशेत असते, हे कळते.

वरील निष्कर्षावरून हे स्पष्ट होते की, विद्युत् क्षेत्र व चुंबकीय क्षेत्र या दोन राक्षी संपूर्णपणे स्वतंत्र नसून त्या एकाच तत्त्वाची दोन रूपे आहेत, असे म्हणता येते. या कारणासाठी चुंबकीय क्षेत्र हा सापेक्षतेमुळे निर्माण होणारा एक आविष्कार आहे, असे वर्णन केले जाते.

वरील समीकरणांत दोन गोष्टी गृहीत धरण्यात आलेल्या आढळतात. (१) निरीक्षकाला विद्युत् भाराच्या सापेक्ष गती असली, तरी विद्युत् क्षेत्रामुळे निर्माण होणाऱ्या

या प्रेरणामूल्यामध्ये फरक पडत नाही. तसा विचार केला असता कुलंब  नियम स्थिर विद्युत् भाराकरिता  प्रायोगिक दृष्ट्या व

सैद्धांतिक दृष्ट्यासुद्धा निर्देशित केलेला असतो. हा परस्परक्रिया नियम स्थिर विद्युत् भाराप्रमाणे गतिमान विद्युत् भारासाठी तितकाच यथार्थ आहे असे मानले, तर त्यापासून मिळणारे निष्कर्ष हे प्रयोगाने मिळालेल्या निष्पत्तीबरोबर सुसंगत असतात. आइन्स्टाइन यांच्या सापेक्षता सिद्धांताचा उपयोग करून हा निष्कर्ष यथार्थ आहे, हे सिद्ध करता येते.

(२) गतीमुळे विद्युत् भारात फरक पडत नाही, हे वरील विश्लेषणातील दुसरे गृहीत आहे. या संदर्भात पदार्थाच्या द्रव्यमानात (m) त्याच्या वेगानुसार फरक पडताना आढळतो, या निष्पत्तींची आठवण करणे योग्य ठरते. विद्युत् भार q याच्या मूल्यात गतीमुळे फरक पडत नाही, हे प्रयोगाने व सापेक्षता सिद्धांताच्या साहाय्याने सिद्ध झाले आहे. विद्युत् गतिकीमधील गणितीय विश्लेषणाचे उद्दिष्ट असे असते. न्यूटन मीमांसेनुसार मिळणाऱ्या यामिकी समीकरणांना सर्वसामान्य परिवर्तनी स्वरूप देता येते. हे कार्य झोझेफ ल्वी लाग्रांझ  यांनी केले [→ यामिकी]. या पद्धतीमध्ये यामिकीसाठी ‘किमान कार्यतत्त्वा’चा [→चलनकलन] उपयोग करून कोणत्याही प्रणालीची गतिवैशिष्ट्ये मिळविता येतात. विद्युत् यामिकीमध्ये मॅक्सवेल यांच्या समीकरणापासून अशाच प्रकारचे सर्वसामान्य तत्त्व मिळविणे शक्य झाले आहे. विद्युत् गतिकी व सामान्य गतिकी यांच्या गणितीय विश्लेषणामध्ये बरेच साम्य आढळते. विद्युत् चुंबकीय क्षेत्रासाठी त्यामुळे एक सामान्य कार्यपद्धती मिळते; पण येथे हे स्पष्ट केले पाहिजे की, या दोन गणितीय मीमांसांमध्ये बरेच मूलभूत स्वरूपाचे फरक पण आहेत. म्हणून विद्युत् गतिकीचे नियम न्यूटन मीमांसेचा उपयोग करून मिळविता येत नाहीत. [→ यामिकी ].

विद्युत् चुंबकीय वर्चस् फलने :

व

या क्षेत्रांचे वर्णन सदिश वर्चस्

व अदिश वर्चस् Φ या राशींच्या स्वरूपात करणे गणितीय दृष्ट्या

जास्त सुलभ व समाधानकारक ठरते. क्षेत्रमूल्य व वर्चसे यांमधील संबंध खालील समीकरणांनी मिळतो.

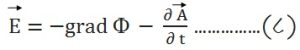यांशिवाय गणितीय विश्लेषणासाठी आणखी काही राशी व सूत्रे उपयुक्त ठरतात. ती प्रथम पुढे दिली आहेत

विद्युत् भार घनता : वा कार्यासाठी प्रथम बिंदू विद्युत् भार कणांऐवजी विद्युत् अवकाश भार घनता या कल्पनेचा उपयोग केला जातो. जर ΔV या अल्पधनफळ घटकात q विद्युत् भार असेल, तर त्यासाठी विद्युत् भार घनता खालील सूत्राने निश्चित होते.

या घनतेचे स्वरूप जरा विचित्र प्रकारचे आहे. कारण ΔV मध्ये विद्युत् भार फक्त एकाच बिंदूस्थानी असतो. त्यामुळे घनफळ-घनता तशी पाहिली असता घनफळात सर्वत्र शून्य विद्युत् भारस्थानी अनंत मूल्याची अशी होते. सरासरीने या घनतेला भौतिकीय अर्थ येतो. विद्युत् भार अक्षय्यता तत्त्वाप्रमाणे

हे समीकरण मिळते. विद्युत् माराला गती मिळाली की, त्यामुळे विद्युत् प्रवाह मिळतो. त्यामुळे संपूर्ण विद्युत् प्रवाह मूल्यासाठी

हे समीकरण मांडता येते. मॅक्सवेल यांच्या समीकरणांचा उपयोग करून

हे समीकरण मांडता येते.

अदिश वर्चस् Φ व ρ यांमधील संबंध असा निर्देशित करता येतो. dV या घनफळ घटकातील विद्युत् भार ρdV यामुळे r अंतरावर निर्माण होणारे वर्चस्

एवढे असेल, म्हणून

हे समीकरण मिळते.

बायो- साव्हार नियमाचा उपयोग करून

असे दाखविता येते.

बायो-साव्हार नियमाचाच उपयोग करून गतिमान विद्युत् भारावर चुंबकीय क्षेत्रामध्ये मिळणाऱ्या प्रेरणेचे मूल्य काढता येते. या नियमाप्रमाणे

	= विद्युत् प्रवाह घटक,
	= चुंबकीय प्रवर्तन असल्यास

n	= विद्युत् वाहक संख्या प्रती एकक घनफळ,
	= त्याचा स्थिर वेग,
q	= त्यावरील विद्युत् भार असल्यास

	= प्रत्येक भिद्युत् बाइकावरील प्रेरणा

विद्युत् क्षेत्र		व चुंबकीय प्रवर्तन		यांमध्ये गतिमान असणाऱ्या बिंदू विद्युत् भारावरील प्रेरणा

यापूर्वी उद्धृत केलेल्या लोरेन्ट्स समीकरणाने मिळते.

अदिश वर्चस् Φ व सदिश वर्चस्		यांमध्ये असणारा संबंध लोरेन्ट्स यांनी खालील विश्लेषणाने स्पष्ट केला.
समीकरण (१२) वरून ρ व		मध्ये संबंध आहे, हे स्पष्ट होते. समीकरणे (१३) व (१४) यांवरून Φ व
मध्ये संबंध असला पाहिजे, हे उघड होते.

 

मध्ये रूपांतरण करण्याकरिता यामध्ये grad f ही स्वेच्छ राशी मिळविली, तर यामुळे समीकरण (७) मध्ये

च्या मूल्यात काही फरक पडत नाही. कारण कोणत्याही राशीकरिता curl grad (    ) = 0 असते. ‍f हे (x, y, z, t) याचे एक फलन आहे. समीकरण (८) नुसार E चे मूल्य अचल ठेवण्याकरिता

Φ मध्ये आवश्यक रूपांतरण समीकरण (१६) ने मिळते. या रूपांतरणाला लोरेन्ट्स गेज रूपांतरण असे म्हणतात.

f  या फलनावर काहीही निर्बंध नसतो; पण त्यावर एक निर्बंध घातला, तर त्यामुळे A व f यांमधील संबंध समीकरणाला गणितीय दृष्ट्या विशेष सोपे असे रूप येते. या गणनामध्ये

या समीकरणांपासून सुरुवात करून समीकरणे (१६) व (१७) यांचा उपयोग केला असता

असे समीकरण मिळते. f हे स्वेच्छ फलन असल्यामुळे

ही असट घातली असता

या समीकरणाला लोरेन्‌ट्स अट असे म्हणतात.

विद्युत् गतिकीमध्ये लोरेन्ट्स रूपांतरण समीकरणे व अट यांचा उपयोग करून वर्चसासाठी मिळणाऱ्या गणितीय समीकरणाचे सुलभीकरण केले जाते. हे स्पष्ट करण्यासाठी पुढील भागात दोन सुलभ दाखल्यांकरिता विश्लेषण दिले आहे.

अदिश व सदिश वर्चसांकरिता तरंग समीकरणे : या विश्लेषणामध्ये

व Φ  यांकरिता समीकरणे (१३) व (१४) यथार्थ आहेत व त्यांवर लोरेन्ट्स अटीचे बंधन

घातले आहे, असे गृहीत धरले जाईल. सांत मूल्याचा विद्युत् भार व विद्युत् प्रवाह घनतेकरिता ही गृहिते यथार्थ असतात.

मॅक्सवेल समीकरण (१) याचा उपयोग येथे केला आहे.

वरील समीकरण विद्युत् भाराच्या जवळच्या विभागात यथार्थ असते. विद्युत् भारापासून पुरेशा दूर अंतरावर

	असेल व

याचा उपयोग केला असता

दोन्हीकडे

ही पदे मिळविली, तर

लोरेन्ट्स अटीचा वापर केला असता

याचप्रमाणे

असे दाखविता येते.

प्रतिप्रवेगी वर्चस् : विद्युत् भार प्रवेगित किंवा प्रतिप्रवेगित झाला असता त्यापासून त्याच्या सभोवताली असणाऱ्या अवकाशात विद्युत् चुंबकीय क्षेत्रे प्रक्षेपित केली जातात. प्रत्यक्षात या कार्याकरिता प्रवेशित विद्युत् भार न वापरता त्यासाठी द्विध्रुवाचा उपयोग करतात. +q व – q हे विद्युत् भार एकमेकांपासून s अंतरावर असतील, तर त्यामुळे

सदिश विद्युत् परिबल असलेला द्विध्रुव तयार होतो. या द्विध्रुवाचे परिबल जर कालानुसार बदलत असेल, तर त्यामुळे विद्युत् चुंबकीय क्षेत्राचे उत्सर्जन होते.

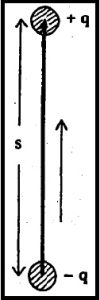
आतापर्यंत वर्णन केलेल्या गणितीय पद्धतीचा वापर करून अशा द्विध्रुवापासून (r, θ, Φ) या क्षेत्रबिंदूपाशी असणारी विद्युत् वर्चस् मूल्ये व त्यांपासून विद्युत् व चुंबकीय क्षेत्र मूल्ये गणन करता (हिशोबाने काढता) येतात. यासाठी लागणारे गणितीय कृत्य किचकट असते. हे गणित कसे केले जाते याचे येथे एका सोप्या दाखल्याच्या संदर्भात विवेचन केले आहे.

एका संदर्भ-व्यूहाच्या आरंभबिंदूपाशी एक काल्परिवर्ती (कालपरत्वे बदलणारा) बिंदु विद्युत् भार q = q₀ e^jωt आहे, अशी कल्पना करू या. हा विद्युत् भार r₀ त्रिज्या असलेला अतिसूक्ष्म विभाग व्यापतो असे गृहीत धरू या. क्षेत्रबिंदू जर पुरेसा दूर असेल, तर तेथे मिळणारे वर्चस् हे r व t यांमुळेच निश्चित होईल, अशी अपेक्षा करता येते. अशा अंतराकरिता व अदिश वर्चसाकरिता

हे समीकरण यथार्थ असेल. यामध्ये Φ =Φ’/r धरून समीकरण सोडविले, तर

हा निर्वाह मिळतो. येथे

exp या संज्ञेपुढील e या अपरिमेय संख्येचा घातांक दर्शवितो. वरील पदावलीमधील पहिले पद बाहेर पसरत जाणाऱ्या तरंगाचे निर्देशन करते, तर दुसरे पद बाहेरून आत येणारा तरंग दाखवितो. भौतिकीनुसार पहिल्या पदालाच अर्थ देता येतो, म्हणून

याचाच विचार केला आहे. यामधील Φ’₁ चे मूल्य काढयाकरिता असा तर्क वापरता येतो की, r च्या लहान मूल्याकरिता

Φ ≈q/4πr ……………………(२२)

असे मानता येते. (२१) व (२२) समीकरणांची तुलना करून

Φ’₁ ≈q₀/4πr ……………………(२३)

हे उत्तर मिळविता येते, त्यामुळे शेवटी

उगम स्थानापासून क्षेत्रबिंदूपर्यंत कोणत्याही विद्युत् चुंबकीय बदलाला (r/u) एवढा वेळ लागतो. त्यामुळे तेथील वर्चस् उगमस्थानापाशी असणाऱ्या अवस्थेच्या क्षणिक मूल्याच्या r/u एवढ्या कालखंडाने किंवा विलंबाने मागे पडते. येथे असणारे विद्युत् वर्चस् t या काली असणाऱ्या विद्युत् भाराचे निर्देशन करीत नाही. ते त्यापूर्वी

कालखंड असणाऱ्या परिस्थितीनुरूप असते. म्हणून कालपरिवर्ती विद्युत् भारामुळे निर्माण होणाऱ्या वर्चसांना विलंबित वर्चसे अशी संज्ञा दिली जाते (आपण कोणत्याही क्षणी जो तारा पाहतो त्याचे त्या क्षणी दर्शन होत नाही. प्रकाशाला तेथून आपल्यापर्यंत येण्यास जेवढा काल लागतो तेवढ्या कालखंडापूर्वी असणाऱ्या त्यांच्या अवस्थेचे दर्शन होत असते). वरील निष्पत्ती आपण बिंदू विद्युत् भारासाठी मिळविली. बिंदू भाराऐवजी जर ρ एवढा अवकाश भार संदर्भ-व्यूहाच्या आरंभबिंदूपाशी असेल, तर त्यामुळे निर्माण होणारे वर्चस् मूल्य

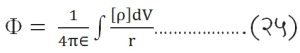येथे क्षेत्रबिंदूच्या अनुसार [ρ] ही कालविलंबित अवकाश-विद्युत् भार घनता दाखविते. असाच गणितीय तर्क वापरून

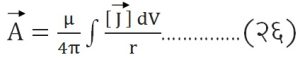हे समीकरण मिळविता येते.

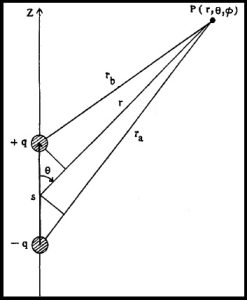
आंदोलनी द्विध्रुवामुळे निर्माण होणारी विद्युत् व चुंबकीय क्षेत्रे :  आ. २ मध्ये संदर्भ-व्यूहाच्या आरंभबिंदूपाशी एक

विद्युत् परिबल असणारा विद्युत् द्विध्रुव ठेवला आहे, अशी कल्पना करा. P (r, θ, Φ) या क्षेत्रबिंदूपाशी Φ व

या वर्चसांची मूल्ये काढावयाची आहेत. द्विध्रुवाचे परिबल

हे कालपरिवर्ती आहे. त्याचे फलन

या प्रमाणे होत आहे. असे समजू या

[j=√-1 =सदिशकारक, ω = 2πf (f = कंप्रता), t = काल]. त्यामुळे मिळणारा विद्युत् प्रवाह

I = dq/dt = jωq₀e^jωt = I₀e^jωt  ………… (२७)

Is = jωp

यामुळे निर्माण होणारे अदिश वर्चस् Φ (r, θ, φ)

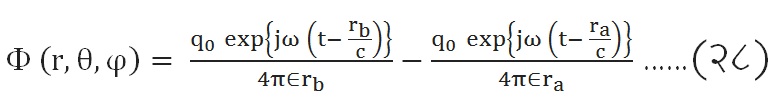r_a = r+(s/2)cos θ आणि r_b = r – (s/2)cos θ

याचा वापर केला असता

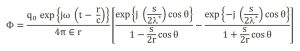हे समीकरणामध्ये λ* = रिक्त अवकाशातील तरंगलांबी, c = प्रकाशवेग असेल, तर

λ/2π = c/ω = λ*

याचे श्रेणीत विस्तारण केल्यास

सदिश वर्चस

काढण्याकरिता आ. ३ चा उपयोग करावयाचा आहे.

व Φ वरून

व

यांची मूल्ये काढता येतात.

द्विध्रुवापासून मोठ्या अंतराजवळ असणाऱ्या क्षेत्रबिंदूसाठी

यावरून चुंबकीय क्षेत्राचा हा घटक प्रेषित क्षेत्राचे निर्देशन करतो, हे उघड होत. अशाच प्रकारे

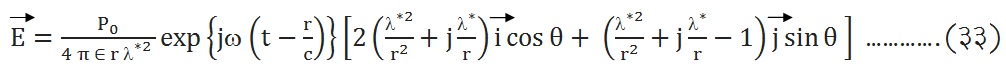द्विध्रुवापासून पुरेशा लांब अंतरावर

यावरून हे प्रेषित विद्युत् क्षेत्र आहे, हे स्पष्ट असते.

तरंग उद्गमापासून बऱ्याच अंतरावर ढोबळमानाने अशी परिस्थिती असते. हे समीकरण (३३) व (३४) वरून समजते. आ. ४ मध्ये याविषयीचा खुलासा मिळेल.

सदिश अरीय (त्रिज्यीय) दिशेच्या प्रतलात असतो, तर

हा याच्या उदग्र दिशेत असतो. ऊर्जेची प्रेषण दिशा पॉयंटिंग सदिश

हा दाखवतो. ही दिशा अरीय दिशाच असते.

व

व यांमधील सापेक्ष दिशा प्रतलीय तरंगात असल्याप्रमाणेच मिळतात, हे लक्षात घेण्याजोगते आहे.

[→विद्युत् चुंबकीय तरंग].

वरील विश्लेषणात गणनाच्या सुलभतेकरिता दोन विरुद्ध प्रकारच्या बिंदू विद्युत् भारांमुळे निर्माण झालेला द्विध्रुव विचारात घेतला होता. ज्या विद्युत् भार वितरणासाठी परिणामी द्विध्रुवी परिबल मिळतो, त्यासाठी वरील यथार्थ राहील, हे उघड आहे. या वितरणापासून विद्युत् चुंबकीय तरंगाचे प्रेषण होण्याकरिता परिणामी परिबलाला

या प्रकारचे कालानुसार परिवर्तन आवश्यक असते. विश्लेषणात

व

या प्रयोगांनी निरीक्ष्य राशी आहेत; तर V,

या राशी गणितीय दृष्ट्या

साहाय्यक राशी आहेत. त्यांचे सरळ निरीक्षण करणे शक्य नसते, हा मुद्दा लक्षात ठेवणे आवश्यक आहे.

लिनार्ड-विखर्ट वर्चस् पद्धत : गतिमान विद्युत् भाराचे विद्युत् चुंबकीय क्षेत्र मूल्याचे गणन करण्याकरिता लिनार्ड-विखर्ट पद्धतीचा उपयोग करतात. पुढे दिलेल्या सोप्या उदाहरणाद्वारे य पद्धतीचा परिचय करून घेता येतो.

Z₁Z₂ = रेषीय विद्युत् भार मुलघटक, ν = रेषीय विद्युत् भार घनता, s = घटक लांबी, q = घटक विद्युत् भार = νs असल्यास अवरोधी वर्चस् मीमांसेप्रमाणे

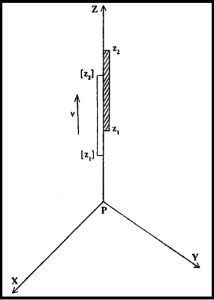
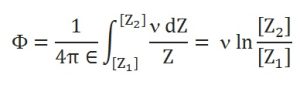आ. ५ मध्ये [Z₁] [Z₂] या अवरोधी अवस्था दाखविल्या आहेत. ( समीकरणामध्ये ln ही संज्ञा स्वाभाविक लॉगरिथम असून तीकरिता आधारांक e ही अपरिमेय संख्या असते).

क्षेत्रबिंदू P संदर्भ-व्यूहाच्या आरंभबिंदूपाशी भाहं. Z₁ – [Z₁] = Z₁/c कालखंडात घटकाच्या Z₁ टोकाने काटलेले अंतर = ν [Z₁] / c

[Z₁] = Z₁/ (1 + ν/c) अशाच प्रकारे  [Z₂] = Z₂/ (1 + ν/c)

विद्युत् मूलघटकाच्या गतीमुळे अदिश वर्चस् मूल्यात काहीही फरक पडत नाही. अशास पद्धतीने

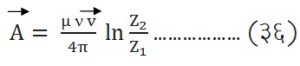हे समीकरण मिळते. यामध्ये पण काही फरक होत नाही. विद्युत् भार घटक लांबी Z₂-Z₁ = s याचे मूल्य शुन्यापर्यंत करीत गेले, तर गतिमान बिंदू विद्युत् भारासाठी

एवढे होते आणि

या समीकरणाचा उपयोग करून P येथे

तर

= 0 असे दाखविता येते.

याच पद्धतीचा उपयोग करून प्रवेगित बिंदू विद्युत् भारामुळे v = अचल नाही) कोणत्याही एका सामान्य क्षेत्रबिंदूपाशी P (r, θ, Φ) मिळणारी विद्युत् आणि चुंबकीय क्षेत्र मूल्ये काढता येतात. यासाठी लागणारे गणित विशेष जटिल बनते. सापेक्षता सिद्धांताचा उपयोग फरून ही मूल्ये शोधून काढणे जास्त सुलभ ठरते [ → सापेक्षता सिद्धांत ].

वरील विश्लेषणाचा उपयोग विद्युत् चुंबकीय प्रारण प्रेषित करणाऱ्या आकाशकाच्या मंडलाचे कार्य विशद करण्यासाठी केला जातो. अशाच प्रकारचे प्रेषण गतिमान विद्युत् भारित कण जड पदार्थामधून गेले असता काही परिस्थितीत मिळते. यास ब्रेम्सस्ट्राहलुंग व चेरेनकॉव्ह प्रारण अशी संज्ञा देतात.

ब्रेम्सस्ट्राहलुंग प्रारण : या आविष्कारामध्ये वेगवान इलेक्ट्रॉन (ऊर्जा >> 10 Mev) हे जड पदार्थामधून गेले असता त्यांवर पदार्थातील अणुकेंद्रीय विद्युत् क्षेत्राचा प्रभाव पडून ते प्रवेगित होतात. विश्वकिरण वर्षावामध्ये आढळणारे गॅमा किरण अशा प्रकारे निर्माण होत असतात. या प्रक्रियेद्वारे प्रेषित होणारे प्रारण अखंडित स्वरूपाचे असते. त्याकरिता आढळणाऱ्या कंप्रता मर्यादा (दर सेकंदास होणाऱ्या कंपनांच्या संख्यांच्या मर्यादा)  ν = 0; ν _max = इलेक्ट्रॉन ऊर्जा/ प्लांक स्थिरांक. या सूत्राने मिळतात. कमी ऊर्जेच्या इलेक्ट्रॉनांसाठी प्रेषण समदिक असते. इलेक्ट्रॉन ऊर्जा जशी वाढत जाते, तसे प्रेपण अग्रगामी दिशेत मर्यादित होऊ लागते. अशा परिस्थितीत θ ही प्रेषणाची कोनीय मर्यादा θ = m_ec²/T (m_e = इलेक्ट्रॉन द्रव्यमान, T = ऊर्जा ) या समीकरणाने मिळते.

इलेक्ट्रॉनाची परिवलन दिशा गतिदिशेला समांतर असेल, तर त्याचे अनुदैर्घ्य ध्रुवीकरण झाले आहे, असे मानतात. कारण त्यामुळे मिळणारे ब्रेम्सस्ट्राहलुंग प्रारण वृत्तध्रुवित झालेले आढळते. किरणोत्सर्गी (भेदक का वा किरण बाहेर टाकणाऱ्या अणूमधून उत्सर्जित होणाऱ्या बीटा (इलेक्ट्रॉन) कणाची परिवर्तन दिशा काढण्यासाठी या निष्पत्तीचा उपयोग करतात.

चेरेनकॉव्ह प्रारण : एखाद्या जड पदार्थ माध्यमातून अतिवेगवान विद्युत् भारित कण जात आहेत. त्याचा वेग या माध्यमातील प्रकाशवेगापेक्षा जास्त आहे, तर त्यायोगे आघात तरंग स्वरूपाच्या विद्युत् चुंबकीय प्रारणाचे उत्सर्जन होताना आढळते. यास चेरेनकॉव्ह प्रारण असे म्हणतात. या आविष्कारामध्ये विद्युत् चुंबकीय विक्षोभ निर्माण करणारा गतिमान कण त्यामुळे निर्माण होणाऱ्या प्रगत तरंगापासून जणू पळ काढतो, असे वर्णन केले जाते. अतिवेगवान कणाचे अभिज्ञान करण्यासाठी (ओळख पटविण्यासाठी) या आविष्काराचा उपयोग केला जातो. [→ अणुकेंद्रीय भौतिकी].

चिपळोणकर, द. त्रिं.

पुंज विद्युत् गतिकी : विद्युत् चुंबकीय प्रारणाचे (तरंगरूपी ऊर्जेचे) गुणधर्म, तसेच विद्युत् भारित द्रव्य (विशेषकरून अणू व इलेक्ट्रॉन) यांच्याशी या प्रारणाची होणारी परस्पर क्रिया यांचा अभ्यास पुंज विद्युत् गतिकीत करतात (या शाखेला प्रकाशाचा किंवा प्रारणाचा पुंज सिद्धांत असेही म्हणतात). या शाखेच्या नियामक समीकरणांचे क्षेत्र व्यापक असून त्यात आणवीय भौतिकी, रसायनशास्त्र, समग्र द्रव्याचे गुणधर्म व रूढ विद्युत् चुंबकीय सिद्धांत ही सर्व येतात; तसेच ज्ञानेंद्रियांमार्फत ज्यांचे सहज आकलन होते ते सर्व आविष्कार अखेरीस पुंज विद्युत् गतिकीच्या नियमांच्या भाषेत समजण्याजोगे असतात, असे मानले जाते. व्यवहारात पुंज विद्युत् गतिकी ही संज्ञा विद्युत् चुंबकीय प्रारणाच्या पुंज स्वरूपाशी निगडित असलेल्या विशिष्ट आविष्कारांना लागू पडते. अणूंकडून होणाऱ्या प्रकाशाच्या उत्सर्जनाचा व शोषणाचा अभ्यास, इलेक्ट्रॉन व इतर मूलकणांबरोबर होणाऱ्या प्रकाशाच्या आधारभूत परस्परक्रिया इ. आविष्कार यांमध्ये येतात.

इ. स. १९२५ साली पुंजयामिकीचा पाया घातला गेल्यानंतर थोड्याच कालावधीत पॉल डिरॅक, व्हेर्नर कार्ल हायझेनबेर्क व व्होल्फगांग पाउली यांनी पुंज विद्युत् गतिकीला सुव्यवस्थित, सूत्रबद्ध रूप दिले. अशा तन्हेने १९३०-४० दरम्यान सूक्ष्ममानीय (आणवीय) आविष्कार स्पष्ट करण्यासाठी ही शाखा पुढे आली व तिने रूढ विद्युत् गतिकीची जागा घेतली. यामुळे प्रकाशाचे कणरूप व तरंगरूप विशद करणे शक्य झाले व त्यात समन्वय साधला. १९६७ साली ⇨स्टीव्हन वाइनयर्ग व ⇨अब्दुस सलाम यांनी पुंज विद्युत् गतिकी व दुर्बल अणुकेंद्रीय परस्परक्रियेचा सिद्धांत यांना एकीकृत रूप दिले. पुंज विद्युत् गतिकीच्या अधिक माहितीसाठी ‘पुंज यामिकी’ ही नोंद पहावी.

सापेक्षीय विद्युत् गतिकी : विद्युत् भारित कणांच्या गती जेव्हा प्रकाशाच्या गतीशी तुल्य एवढ्या असतात, तेव्हा हे कण आणि विद्युत् व चुंबकीय क्षेत्रे यांच्यात होणाऱ्या परस्परक्रियांचा अभ्यास सापेक्षीय विद्युत् गतिकीत करतात. १९०५ साली अॅल्बर्ट आइन्स्टाइन यांनी मर्यादित सापेक्षता सिद्धांत सूत्रबद्ध केल्यावर या शाखेचा झपाट्याने विकास झाला आणि ती भौतिकीतील एक अचूक शाखा बनली. या शाखेत सर्व स्थूलमानीय विद्युत् गतिकीय आविष्कारांचे अगदी बारीकसारीक तपशीलांसहित व पूर्ण अचूकतेने वर्णन व भाकितही केले जाते. अशा रीतीने ही शाखा विद्युत् उद्योगाचा आधार बनली आहे. सूक्ष्ममानीय आणवीय आविष्कारांना हिचे नियम लागू पडत नाहीत, हे लक्षात आल्याने तिच्या मर्यादा स्पष्ट झाल्या. [→ सापेक्षता सिद्धांत ].

वैश्विक विद्युत् गतिकी : आंतरतारकीय अवकाश, तारे व इतर खस्थ पदार्थ, तसेच वातावरणापलीकडील अवकाश येथे आढळणाऱ्या आयनीभूत माध्यमातील विद्युत् चुंबकीय आविष्कारांचा अभ्यास वैश्विक विद्युत् गतिकीत करतात. ही आयनीभूत द्रव्ये उत्कृष्ट विद्युत् संवाहक चुंबकीय क्षेत्ररेषांशी त्यांचा निकटचा संबंध (दुवा) असतो. ही द्रव्ये या रेषांना अनुसरून मुक्तपणे पुढे जाऊ शकतात; मात्र या रेषा छेदून (पार करून) ती पुढे जाऊ शकत नाहीत. सांख्यिकीय (संख्याशास्त्राच्या दृष्टीने पाहता दोन्हीतील या दुव्यामुळे चुंबकीय क्षेत्रामधील आणि आयनीभूत द्रव्याच्या क्षुब्ध गतीमधील ऊर्जा समान होण्याची प्रवृत्ती दिसते. आकाशगंगा व सूर्याचा पृष्ठभाग या दोन्ही ठिकाणच्या विद्युत् भारित कणांचा त्यांना विश्वकिरणाच्या ऊर्जेकडे नेणारा प्रवेग, दीर्घिकामधील आघात, चुंबकीय क्षेत्रांचे दीर्घिकेच्या संरचनेशी असलेले परस्परसंबंध, सौर डाग व तेजःशृंगे [→ सूर्य ] आणि व्हॅन अॅलन प्रारण पट्ट [ → प्रारण पट्ट] या आविष्कारांचा विचार वैश्विक विद्युत् गतिकीत केला जातो.

ठाकूर, अ. ना.

पहा : पुंजयामिकी; मॅक्सवेल विद्युत् चुंबकीय समीकरणे; यामिकी; सापेक्षता सिद्धांत.

संदर्भ : 1. Alfven, H. Cosmic Electrodynamic, New York, 1981.

2. Corson, D.; Lorrain, P. Introduction to Electromagnetic and Waves, San Francisco, 1962.

3. Griffiths, D. J. Introduction to Electrodynamics, New Delhi, 1989.

4. Gupta, S. N. Quantum Electrodynamics, 1977.

5. Jackson, J. D. Classical Electrodynamics, New York, 1975.

6. Konapinski. E. Electromagnetic Fields and Relativistic Particles, New 1981.

7. Piddington, J. H. Cosmic Electrodynamics. New York, 1981.

8. C. Gauge Theories of the Strong, Weak and Electromagnetic Interactions, 1983.