संच सिद्धांत : (संच उपपत्ती). गणितातील व तर्कशास्त्रातील प्रश्नांची मांडणी व सोडवणूक करण्याची एक रीत म्हणून संच सिद्धांत किंवा संचविज्ञान ही प्रणाली पुढे आली.
गणितात संच ही अव्याख्यात संज्ञा आहे, पण सर्वसाधारणतः संच म्हणजे वस्तंचा समूह असे मानले जाते. या वस्तू वास्तव असतील किंवा काल्प-निकही असू शकतील. कुटुंब हा माणसांचा, गुच्छ हा फुलांचा व कळप हा गायींचा संच होय. बुद्धीबळाच्या नियमांची यादी हा कल्पनांचा संच होय. संचातील वस्तूत काही सारखेपणा असलाच पाहिजे, अशी अट नसते. संचा-तील वस्तूत किमान सारखेपणा हाच की, त्या एका संचात आहेत. संचातील वस्तूंना संचाचे घटक किंवा सदस्य असे म्हणतात. इंद्रधनुष्यातील रंगांचा संच घेतल्यास तांबडा रंग हा त्या संचाचा सदस्य होय.
सर्वसाधारणतः रोमन लिपीतील मोठया अक्षरांनी संच दाखविला जातो उदा., A, B, X, Y, U इत्यादी. संचाचे सदस्य रोमन लिपीतील लहान अक्षरांनी दाखविले जातात उदा., a, b, x, y, u इत्यादी. तसेच संचाचे सदस्य महिरपी कंसात मांडले जातात. उदा., रोमन लिपीतील स्वरांचा संच V पुढीलप्रमाणे दाखवितात. V = { a, e, i, o, u }. यातील i हे अक्षर V या संचाचे सदस्य आहे. ही स्थिती ∈ हे चिन्ह वापरून i ∈V अशी दाख-वितात, उलट x हे अक्षर V या संचाचे सदस्य नाही, ही स्थिती x ∉ V अशी दाखविली जाते. सर्वसाधारणतः मोठया अक्षराने दाखविलेल्या संचाचे सदस्य त्याच प्रकारच्या लहान अक्षरांना विविध पादांक देऊन लिहिण्याची प्रथाही आहे. उदा., A = { a1, a2, a3, . . . }.
एखादया संचातील सदस्य दोन पद्धतींनी दाखविता येतात. पहिल्या पद्धतीत त्या सदस्यांची यादी देऊन, उदा., वर V हा रोमन लिपीतील स्वरांचा संच त्या स्वरांची यादी देऊन लिहिला आहे. दुसऱ्या पद्धतीत हाच संच संचातील सदस्यांची निवड ज्या गुणधर्माच्या आधाराने केली तो गुणधर्म देऊनही लिहिता येतो. या पद्धतीने वर दिलेला V हा संच पुढीलप्रमाणे लिहिता येतो.
V = { v | v हा रोमन लिपीतील स्वर आहे }.
दोन्ही पद्धतींनी लिहिलेला संच खाली दाखविला आहे.
A = { २, ४, ६, ८ } A = { x | १ < x < १०, x हासमअंक }.
परिस्थितीनुसार विवक्षित संच यादोन्हीं पैकी कोणत्याही पद्धतीने दाखविला जातो. या पद्धतींना अनुक्रमे ‘ यादी पद्धत ’ व ‘ गुणधर्म पद्धत ’ अशी नावे आहेत.
संचांचेप्रकार : सांत संचातील सदस्यांची संख्या परिमित असते. उदा., ‘वर्गातील विदयार्थी’, ‘या पृष्ठावरील अक्षरे’. या दोन्ही संचांत परिमित सदस्य असल्याने हे संच सांतहोत. सांत संचातील सदस्यांची वेळ पडल्यास यादी देता येते. याउलट – धन पूर्णांकांचा संच ’ यातील सदस्यांच्या गणतीला शेवट नाही . म्हणून अशा संचांना अनंत संच असे म्हणतात. असा संच एक तर गुणधर्म पद्धतीने देता येतो किंवा पहिले काही सदस्य चिन्हांनी दर्शवून त्यांच्यापुढे काही (सर्वसाधारणतः तीन ) टिंबे देऊन संच अनंत असल्याचे दर्शवितात. उदा., P हा धन पूर्णांकांचा संच P = { १, २, ३, ४, . . . } असा दाखवितात. [→ संख्या].
एखादा संच गुणधर्म पद्धतीने दिला असता, असे होणे शक्य असते की, तो गुणधर्म असलेली वस्तू कल्पनेतही शक्य नाही. उदा., ‘२ ने भाग जाणारी विषम संख्या ’. त्यामुळे अशागुणधर्माने दिलेल्या संचात एकही सदस्य असत नाही. संच रिकामाच राहतो. अशा संचाला रिक्त संच म्हणतात. रिक्त संच एकच आहे. तो f या चिन्हाने दाखवितात. ‘एकापेक्षा मोठी वर्गसंख्या की जी मूळ संख्या आहे’, अशी कोणतीच संख्या नसल्याने हा गुणधर्म असलेल्या संख्यांचा संचही रिकामाच राहणार.
ज्या संचात एकच घटक आहे, अशा संचाला एक-सदस्य संच असे म्हणतात. उदा., A = { x | x + २ = ० } या संचात एकच सदस्य आहे. तो म्हणजे -२ ही संख्या. म्हणून A = {-२} हा एक -सदस्य संच आहे.
A व B हे दोन संच असे आहेत की, A चा प्रत्येक घटक B चा सदस्य आहे व B चा प्रत्येक सदस्य A चा घटक आहे. अशा वेळी केवळ सदस्यांकडे पाहिले तर दोन्ही संच एकच आहेत किंवा एकाच संचाला A व B ही दोन नावे दिली आहेत, असा निष्कर्ष निघतो. अशा वेळी A व B हे संच समान असल्याचे A = B असे दाखवितात. उदा., A ={ २, ३, ५ } आणि B= {x ( x -२) (x-३) (x-५) = हे दोन्ही संच एकच आहेत. म्हणून A = B.
A व B या संचांतील घटकांशी एकास – एक जुळणी ( म्हणजेच एकास- एक संगती ) करता येत असेल, तर A व B या संचांना समानांक किंवा समतुल्य संच असे म्हणतात. उदा., A ={ a, c, e }, B = {१, ३, ५} व C = { २, ६, १० } हे तीन संच आहेत. त्यांच्यात a ↔ १ ↔ २, c ↔ ३ ↔ ६, e ↔५↔ १० अशी एकास – एक जुळणी बसविता येते. म्हणून A, B व C हे समानांक संच आहेत. ही स्थिती A ≃ B ≃ C अशी दाखवितात.
समानांकता ही सांत संचामध्ये असते असे नाही. अनंत संचात देखील एकास- एक जुळणीने समानांकता दाखविता येते. उदा., N = { १, २, ३, ४, … } व E = { २, ४, ६, ८, … } या दोन संचांत n ↔२n ही एकास-एक जुळणी मिळते. म्हणून N≃E .
A आणि B हे दोन संच असे आहेत की, A चा प्रत्येक घटक B मध्ये उपस्थित आहे. अशा वेळी A हा B चा उपसंच आहे, असे म्हणतात. ही स्थिती A ⊂ B किंवा B ⊃ A अशी दाखवितात. अशा वेळी B हा A चा ऊर्ध्वसंच आहे असेही म्हणतात. उदा., A = { २, ३, ४ } आणि B = { १, २, ३, ४, ५ } हे संच आहेत, तर A हा B चा उपसंच आहे,आणि B हाA चा ऊर्ध्वसंच आहे. A = B असेल तर A हा B चा उपसंच असतोच पण B हाही A चा उपसंच असतो.
A हा संच B चा उपसंच नाही, असे म्हणता येते. समजा, A = { २, ३, ४, ७ } व B = { २, ३, ४, ८ } अशी स्थिती आहे. येथे ७ हा A चा सदस्य आहे पण तो B चा सदस्य नाही,म्हणून A हा B चा उपसंच नाही. हे A ⊄ B असे दाखवितात.
यावरून असे म्हणता येते की, A चा एकही सदस्य B चा सदस्य नाही, अशी स्थिती नसते, तेव्हा A हा B चा उपसंच होतो. हीच अट रिक्त संच f व कोणताही ( अ – रिक्त ) संच Aयांच्या संदर्भात पाहिली तर असे दिसून येते की, f हा A चा उपसंच आहे. म्हणून रिक्त संच कोणत्याही संचाचा उपसंच असतो. तसेच उपसंचाच्या व्याख्येवरून हे स्पष्ट आहे की प्रत्येक संच हा स्वतःचाच उपसंच असतो. म्हणजे A ⊂A.
A हा B शी समान नाही आणि A हा B चा उपसंच आहे अशी स्थिती जेव्हा असते तेव्हा A ला B चा सार्थ ( किंवा उचित ) उपसंच म्हणतात. ही स्थिती A ⊂ B अशी दाखवितात.साहजिकच रिक्त संच f हा कोणत्याही रिक्त नसलेल्या संचाचा सार्थ उपसंच असतो.
संच सिद्धांतातील काही तार्किक अडचणी टाळण्यासाठी खालील गोष्ट मानावी लागते. एका वेळी विचारात घेतले जाणारे सर्व संच हे कोणत्या तरी एका मोठया संचाचे उपसंचआहेत. या मोठया संचाला विश्र्वसंच किंवा पार्श्र्वसंच असे म्हणतात व निरनिराळ्या संदर्भात तो ‘U’, ‘E’, W ‘X’ अशा निरनिराळ्या अक्षरांनी दाखविण्याची प्रथा आहे.
संचांवरील क्रिया व त्यांच्या आकृत्या : जॉन व्हेन या तर्कशास्त्रज्ञांनी १८९४ साली चौकोन व वर्तुळे किंवा लंबवर्तुळे यांच्या साहाय्याने संचांच्या विविध स्थिती दाखविण्याची पद्धती सुरू केली. या पद्धतीत विश्वसंच चौकोनाने दाखवितात, तर निरनिराळे संच सर्वसाधारणतः वर्तुळांनी किंवा लंबवर्तुळांनी दाखवितात. जरूर असेल तर संच दाखविण्यासाठी वर्तुळे व लंब – वर्तुळे यांच्यापेक्षा निराळ्या आकृत्याही वापरतात. संचाचे घटक बिंदूंनी दर्शविले जातात.
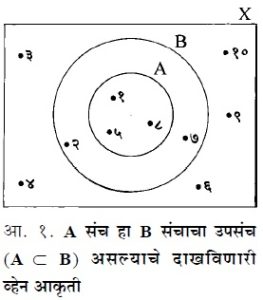
उदाहरणार्थ, X = { १, २, ३, ४, ५, ६, ७, ८, ९, १० } हा विश्वसंच आहे. A = {१, ५, ८ } हा संच असून B = {१, २, ५, ७, ८ } हा दुसरा संच आहे. येथे हे स्पष्ट आहे की, A हा B चा उपसंच आहे. ही स्थिती व्हेन आकृतीच्या साहाय्याने आ. १ प्रमाणे दाखविता येते.
ज्याप्रमाणे अंकगणितात दोन संख्यांवर बेरीज,गुणाकार इत्यादी कृत्ये करता येतात, आणि बीजगणितात दोन राशी दिल्या असता त्यांची बेरीज, वजाबाकी, गुणाकार अशा (व्दिपद) क्रिया करता येतात, त्याच प्रमाणे दोन संचांवर संयोग, छेद यानावांनी ओळखल्या जाणाऱ्या व इतरही काही क्रिया करतात. या क्रियांच्या साहाय्याने संचांचे ‘बीजगणित’च तयार होते. वर सांगितलेल्या व्हेन आकृतींच्या साहाय्याने या क्रिया दाखविता येतात.
संचावर मुख्यतः एकूण पाच क्रिया करतात. त्यांचे विवरण पुढीलप्रमाणे :
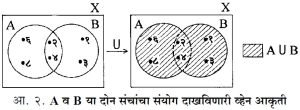
(१) संचांचा संयोग : A व B हे दोन संच आहेत. या दोन संचांतील सर्व घटकांचा समावेश करणारा जो संच असेल त्याला A व B यांचा ‘ संयोग ’ असे म्हणतात व तो A ∪ B असा दाखवितात. व्यापक रीत्या A ∪B = { x| x ∊A आणि/किंवा x ∊ B } उदा., A = { २,४,६,८ } आणि B = { १,२,३,४ } या संचांच्या बाबतीत A B = { १,२,३,४,६,८ }. येथे विश्वसंच X हा सर्व धन पूर्णांकांचा संच आहे असे मानता येते किंवा X = { १,२,३,४,५,६,७,८ } असेही समजता येते. ही क्रिया व्हेन आकृतीच्या साहाय्याने दाखवितात.
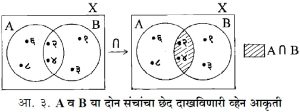
(२)संचांचा छेद :विश्वसंच X हा धन पूर्णांकांचा संच आणि A = { २,४,६,८ } व B = { १,२,३,४ } हे संच घेतले असता, या दोन्ही संचात समाईक असणाऱ्या घटकांचा संच { २,४ } हा होय. या संचाला A व B या संचाचा‘ छेद ’असे म्हणतात व तो संच A ∩B असा दाखवितात. व्यापक रीत्या A ∩ B = { x| x ∊ A आणि x ∊ B }. दोन संचांचा छेद घेण्याची क्रिया व्हेन आकृतीच्या साहाय्याने दाखविता येते. जर दोन संचांत समाईक घटकच नसतील तर त्यांचा छेद रिक्त संच होईल.
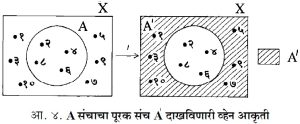
(३) दिलेल्या संचाचा पूरक संच : समजा, X = { १,२,३,४,५, ६,७,८,९,१० } हा विश्वसंच आहे. त्यात A = { २,४,६,८ } हा दिलेला संच आहे. X मधील जे घटक A मध्ये नाहीत अशा घटकांच्या संचाला A चा पूरक संच असे म्हणतात व तो Á किंवा Ā या चिन्हाने दाखवितात. प्रस्तुतच्या उदाहरणात Á = { १,३,५,७,९,१० } हा संच होय.
(४) संचांची वजाबाकी : A व B हे दोन संच आहेत. A मध्ये समाविष्ट असणारे B चे घटक काढून घेतल्यास उरलेला संच A – B असा दाखवितात आणि या कियेला ‘ A मधून B ची वजाबाकी ’ असे म्हणतात. आ. ५ मध्ये A – B ही क्रिया व्हेन आकृतीने दाखविली आहे. व्यापक रीत्या A – B = { x|x ∈A, x ∉B } A = { २,४,६,८ }, B = {१,२,३,४} असल्यास A – B = { ६,८ }.
(५) संचाचा सममित फरक : A व B हे दोन संच आहेत. A व B या दोन्ही संचात समाविष्ट असणारे सर्व घटक घेऊन त्यांच्यातून A ∩ B चे घटक काढून टाकल्यास उरलेल्या घटकांच्या संचाला ‘ A व B या दोन संचांचा सममित फरक ’ असे म्हणतात व तो A DB असा दाखवितात. A = { २,४,६,८ }, B = { १,२,३,४ }∴ A DB = { १,३,६,८ }. आ. ६ मध्ये A DB ही क्रिया व्हेन आकृतीने दाखविली आहे.
गुणधर्म : संच व त्यांच्यावरील वर दिलेल्या क्रिया यांच्या संदर्भात काही महत्त्वाचे गुणधर्म आढळून येतात. खाली हे गुणधर्म मांडून त्या गुण-धर्मांची नावे कंसात लिहिली आहेत. यात A, B, C इ. संच X या विश्वसंचाचे कोणतेही उपसंच आहेत. या सर्व गुणधर्मांचा पडताळा व्हेन आकृत्यांचा उपयोग करून सहज घेता येतो.
कार्तीय गुणाकार : समजा, एखादया संचाचे a व b असे दोन घटक आहेत. त्यांची क्रमित जोडी (a, b) अशी दाखविली जाते. क्रमित जोडी (a, b) हिची तांत्रिक व्याख्या{{a},{a, b} }अशा रीतीने, म्हणजे दोन संचांचा संच अशा पद्धतीने दिली जाते.परंतु अनौपचारिक रीत्या असे म्हणता येते की, ( a, b ) या क्रमित जोडीत a हा पहिला घटक व b हा दुसरा घटक आहे व त्यांच्या क्रमाला महत्व आहे. म्हणूनच क्रमित जोडी ( a,b ) क्रमित जोडी ( b, a ) पेक्षा भिन्न आहे.
जर A व B हे दोन अ-रिक्त ( रिक्तेतर ) संच असतील, तर A मधील घटक पहिल्या स्थानी व B मधील घटक दुसऱ्या स्थानी घेऊन ज्या क्रमित जोडया होतात, त्या सर्व क्रमित जोडयांच्या संचाला A व B या संचांचा कार्तीय गुणाकार असे म्हणतात आणि हा संच A B असा दाखवितात. उदा., A = {a, b, c} आणि B = {x, y} हे संच असतील तर, A B= { (a, x ), ( b, x), (c, x ), (a, y), ( b, y), (c, y) } हा A व B यांचा कार्तीय गुणाकार होय. कार्तीय गुणाकाराच्या व्याख्येवरून हे स्पष्ट आहे की A x B ¹ B x A, म्हणजे कार्तीय गुणाकार क्रमनिरपेक्ष नाही.
अनंत संच : अनंत संचाबद्दलची चर्चा खूप उद्बोधक ठरते. अनंत संचांमध्ये जो संच { १,२,३, . . . } या नैसर्गिक संख्यांच्या संचाशीतुल्यबल असतो त्याला गणनीय संच म्हणतात. समसंख्यांचा संच { २,४,६, . . . }, ऋण पूर्णांकांचा संच { ¾१,¾२,¾३, ¾४, . . . }, परिमेय संख्यांचा संच, बैजिक संख्यांचा संच ही गणनीय संचांची काही उदाहरणे आहेत.
गणनीय नसणाऱ्या संचांना अगणनीय संच म्हणतात. सत् संख्यांचा संच, सद्सत् संख्यांचा संच, [०,१] या अंतरालातील सर्व फलनांचा संच ही अगणनीय संचांची काही उदाहरणे होत.
संचांक : दोन संचांमध्ये एकास-एक संगती लावता येत असेल तर त्या दोन संचांचा संचांक एकच आहे असे म्हणतात. सांत संचांच्या बाबतीत, संचांमध्ये असणाऱ्या घटकांची संख्या ही त्या संचाचा संचांक होय. अनंत संचांच्या बाबतीत मात्र तसे म्हणता येत नाही, कारण अनंत संचातील घटकांची संख्या मोजता येत नाही.
नैसर्गिक संख्यांच्या संचाचा संचांक Noया अक्षराने दाखवितात. कोणत्याही गणनीय संचाची नैसर्गिक संख्यांच्या संचाशी एकास-एक संगती लावता येत असल्याने प्रत्येक गणनीय संचाचा संचांक No असतो. नैसर्गिक संख्यांचा संच व सत् संख्यांचा संच यांच्यात एकास-एक संगती लावता येत नाही. त्यामुळे सत् संख्यांच्या संचाचा संचांक Noअसत नाही. सत् संख्यांच्या संचाचा संचांक c या अक्षराने दाखविला जातो.
A हा संच B या संचाच्या एखादया सार्थ उपसंचाशी समतुल्य असेल तर A चा संचांक B च्या संचांकापेक्षा लहान आहे असे म्हणतात. यावरून Noहा संचांक c या संचांकापेक्षा लहान आहे हे उघड आहे. (No< c ).
No व c यांना सांतातीत संख्या म्हणतात. या दोन संख्यांव्यतिरिक्त सांतातीत संख्या अस्तित्वात आहेत, किंबहुना त्या अनंत आहेत असे दाखविता येते.
No व c यांच्यामध्ये एखादा संचांक आहे का, हा संच सिद्धांतातील महत्त्वाचा प्रश्न आहे. No व c यांच्या दरम्यान एकही संचांक नाही हे गणितातील महत्त्वाचे गृहीतक (परिकल्पना) असून त्याला सातत्यक गृहीतक म्हणतात.
घातसंच : कोणत्याही संचाच्या सर्व उपसंचांच्या संचाला त्या संचाचा घातसंच म्हणतात. A चा घातसंच r (A) असा दाखवितात. उदा., A = { a, b, c } या संचाचा घातसंच r (A) = {{f}, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c }} हा आहे. येथे A चा संचांक तीन असून r (A) चा संचांक आठ आहे. अशा प्रकारे कोणत्याही संचाचा संचांक त्याच्या घातसंचाच्या संचांकापेक्षा लहान असेल. उदा., R या सत् संख्यांच्या संचाचा c हा संचांक R च्या r (R) या घातसंचाच्या संचांकापेक्षा लहान आहे. r (R) या संचाचा घातसंच विचारात घेता येतात व अशा तऱ्हेने अधिकाधिक मोठे संचांक मिळतात व त्यांची संख्या अनंत होते.
No< c < r (R) चा संचांक < . . . . . . . .
उपयोग : गणितातील संकल्पना व क्रिया संचांच्या साहाय्याने सुस्पष्ट रीतीने मांडता येतात, हा संच सिद्धांताचा एक महत्त्वाचा उपयोग होय. असा दावा मांडला जातो की, गणितातील कोणतीही संकल्पना संचांच्या भाषेत मांडता येते. एन्. बूरबाकी यांनी असे विधान केले आहे की, ‘ सध्याचे सर्व गणित तर्कदृष्टया एकाच उगमापासून अनुसाधित करता येते व तो उगम म्हणजे संचविज्ञान होय ’.
अंकगणितातील अगदी प्राथमिक क्रिया ‘ बेरीज ’ ही होय. ती संचांच्या साहाय्याने मांडता येते किंबहुना, प्राथमिक शाळेत बेरीज ही क्रिया त्याच प्रकाराने शिकवितात. उदा., ३ + २ = ५ ही बेरीज संचाच्या भाषेतपुढील- प्रमाणे मांडता येते : A = {a, b, c} व B = {d, e}. हे संच घेताना AdB या संचात समाईक घटक नाही, याची काळजी घेतात. A∪ B = {a, b, c, d, e } या स्थितीत ३+२ = ५ या समानतेचा अर्थ असा लावता येतो की, A व B हे संच A∩ B = f ही अट पाळत असल्यास त्यांच्या संचांकांची बेरीज A ∪ B चा संचांक असतो.
कलनशास्त्रातील महत्त्वाची संकल्पना फलन ही होय. ही संकल्पना संचांच्या भाषेत मांडली जाते. F हे A या क्षेत्रापासून B या सहक्षेत्रावर फलन आहे, ही स्थिती F : A → B अशी दाखवितात. F हा A x B या कार्तीय गुणाकाराचा विशिष्ट उपसंच असतो. या उपसंचाची विशिष्टता खालील अटींवरून ठरते :
(१) A या संचातील a हा घटक दिला असता B या संचातील b हा घटक असा निश्र्चित करता येतो की, ( a, b ) ही क्रमित जोडी F या उपसंचात असते.
(२) ( a, b1 ) व ( a, b2 ) या दोन जोडया F या उपसंचात असतील तर b1 = b2. याचप्रमाणे गणितातील इतर मूलभूत संकल्पनाही संचाच्या भाषेत मांडता येतात.
त्रोटक इतिहास : संच ही संकल्पना ⇨ यूलिउस डेडेकिंट या गणितज्ञांनी मांडली. गणितात बरेचदा परस्परांशी संबंधित नसलेल्या वस्तूंचा एकत्र विचार करण्याची वेळ येते. ज्या वस्तूंचा एकत्र विचार केला जातो, त्यांचा एक संच बनतो, अशी डेडेकिंट यांची कल्पना होती.⇨ गेओर्क कँटर (१८४५–१९१८) या गणितज्ञांनी या संकल्पनेचा फार मोठा उपयोग केला [→ संख्या]. मुख्यत: सांत व अनंत संच यांच्या संकल्पना त्यांनी सुस्पष्ट रीतीने मांडल्या व उपयोगात आणल्या परंतु अनंत संचाच्या संकल्पनेमुळेच संच सिद्धांताला विरोध करणारा गणितज्ञांचा मोठा वर्ग तयार झाला व त्यांच्यापैकी काहींकडून कँटर यांना खूप त्रास सहन करावा लागला.
⇨ गोटलोप फ्रेग व त्यानंतर⇨ बर्ट्रंड रसेल यांनी संच सिद्धांताचा उपयोग एका बाजूने अंकगणिताची मांडणी करण्यासाठी आणि दुसऱ्या बाजूने तर्कशास्त्र व गणित यांची सांधेजोड करण्यासाठी केला. त्यामुळे संचाच्या संकल्पनेतील अनेक अडचणी लक्षात आल्या. म्हणून संच सिद्धांताची मूलतत्त्वाधारित मांडणी करण्याच्या प्रयत्नांना सुरूवात झाली. या मांडणीचा विचार प्रस्तुत नोंदीत केलेला नाही. याबाबतीत महत्त्वाचे प्रयत्न अर्नेस्ट झर्मेलो व अब्राहम ॲडॉल्फ फ्राएन्केल यांनी १९०८ मध्ये व त्यानंतर केले.
पाहा : बूलीयन बीजगणित; संख्या.
संदर्भ : 1. Bourbaki, N. Theory of Sets, 1968.
2. Cohen, P. J. Set Theory and the Continuum Hypothesis, 1966.
3. Halmos, P. R. Naive Set Theory, New York, 1961.
4. Roitman, J. Introduction to Modern Set Theory, 1990.
5. Stoll, R. R. Set Theory and Logic, 1963.
6. Vaught, R. L. Set Theory : An Introduction, 1994.
ओक, स. ज.; भावे, श्री. मा.; टिकेकर, व. ग.