सममिति नियम

सममिति नियम : अवकाशाची समदिकता आणि समांगता या सममितीच्या अगदी सोप्या प्रकारच्या संकल्पना फार पूर्वीपासून परिचित  आहेत. एकविध वेग असलेल्या सहनिर्देशक व्यूहाच्या रूपांतरणाने भौतिकीय नियम अचल ( निश्र्चल ) राहतात. यास गॅलिलीयन रूपांतरण अचलता असे म्हणतात. ही न्यूटन प्रणीत यामिकीमधील एक सुविकसित सममिती होय.

⇨ संदर्भ-व्यूहा त बदल होऊनही भौतिकी सिद्धांताच्या वर्णनात फरक  न आढळून येणे, ही गोष्ट वैश्र्विक सममितीच्या अस्तित्वाची द्योतक आहे. म्हणजेच या सममितीपासून असे स्पष्ट दिसून येते की, वस्तूच्या व्यूहाचे स्थलांतरण केले तरी त्यामध्ये पूर्वीचेच गुणधर्म राहतात. उदा., अवकाशाच्या स्थलांतरणाने रेषीय संवेगाची अचलता दिसून येते. तसेच अवकाशाच्या परिभ्रमणामुळे कोनीय संवेगाची अचलता दिसून येते. हे दोन्ही अक्षय्यतेचे नियम वरील सममितीचे परिणाम होत. म्हणून सममितीपासून अक्षय ( अविनाशी ) राशींचा तर्क करता येतो.

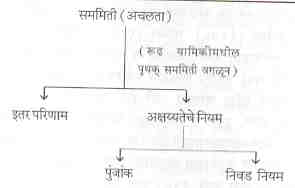
उजव्या-डाव्या सममितीचे नियम रूढ भौतिकीमध्ये वापरण्यात येत होते परंतु प्रत्यक्ष व्यवहारात त्यांना फार महत्त्व नव्हते. कारण उजवी-डावी सममिती ही पृथक् सममिती असून ती अखंड असलेल्या परिभमण सममितीपेक्षा भिन्न आहे. अखंड सममितीमुळे रूढ भौतिकीमध्ये अक्षय्यतेचे नियम निष्पन्न होतात, परंतु पृथक् सममितीमुळे ते निष्पन्न होत नाहीत. पुंजयामिकीच्या प्रस्थापनेनंतर पृथक् आणि अखंड सममितीमधील    फरक नाहीसा झाला. पुंजयामिकीमध्ये उजव्या-डाव्या सममितीच्या नियमामुळे अक्षय्यतेचे नियम निष्पन्न होतात उदा., समतेची अक्षय्यता. [→ समता -२].

समतेची अक्षय्यता म्हणजे जर व्यूहाच्या सुरूवातीच्या अवस्थेचे वर्णन करणाऱ्या तरंग फलनाची समता सम ( विषम ) असेल, तर अंतिम अवस्थेचे वर्णन करणाऱ्या तरंग फलनाची समताही समच (विषमच) असते. समतेची अक्षय्यता हाही एक सममितीचाच नियम आहे. या गोष्टीचा आणवीय संक्रमण आणि अणुकेंद्रीय विकियांशी फार महत्त्वाचा संबंध आहे.

समस्थानीय परिवलन अक्षय्यता या सममितीच्या नियमासंबंधी पुष्कळ विवरण झालेले आहे. प्रबल परस्परकिया (आंतरकिया) करणाऱ्या सर्व मूलकणांना समस्थानीय परिवलन असते. समस्थानीय अवकाशामध्ये सर्व परस्परकिया समदिक् असतात आणि समस्थानीय परिवलने अक्षय राहतात. सममितीच्या या नियमांमुळे विचित्र कणासंबंधीच्या आविष्कारामध्ये अनुभवाधिष्ठित सुव्यवस्था निर्माण झाली आहे. समस्थानीय परिवलन अक्षय्यतेच्या उगमाबाबतचे ज्ञान आणि त्याचे इतर सममितींशी कशा तऱ्हेने संपूरण करावयाचे हा उच्च ऊर्जा भौतिकीतील एक कूट प्रश्न आहे.

CPT सिद्धांत : CPT सिद्धांतानुसार( येथे C– विद्युत् भार, P– समता, T – काल ) सर्व परावर्तन सममिती परस्परसंबंधित असतात. या  सिद्धांताने असे स्पष्ट दिसून येते की, लोरेन्ट्स अचल क्षेत्र सिद्धांत हा तिन्ही परावर्तनांच्या ( भार संयुग्मन, अवकाश व्युत्कमण आणि काल प्रत्यावर्तन यांच्या ) गुणाकाराशी अचल आहे. प्रायोगिक रीतीने असे दिसून येते की,   विश्र्व ( दुर्बल परस्परकियांचा समावेश असतानासुद्धा ) काल प्रत्यावर्तनाशी तसेच भार संयुगमन आणि अवकाश व्युत्कमण यांच्या गुणाकाराशीसुद्धा ( CP किंवा एकत्रित परावर्तन याच्याशी ) पुष्कळ अचूकपणे अचल आहे.

निवड नियम : निवड नियम हे अक्षय्यता नियमांचे महत्त्वाचे निष्कर्ष आहेत. विशिष्ट विकिया अक्षय्यता नियमांची पूर्तता करतात की नाही, हे निवड नियमावरून स्पष्ट कळून येते. कोनीय संवेग आणि समता यांच्या अक्षय्यतेने प्रारणाच्या ( तरंगरूपी ऊर्जेच्या ) उत्सर्जनाचे निवड नियम सुचविले जातात.

पहा : पुंज क्षेत्र सिद्धांत फिच, व्हाल लॉग्सडॉन मूलकण यांग, चेन निंग  समता – २.

संदर्भ : 1. Lannutti, J. E. Williams, P. K., Eds., Current Trends in the Theory of Fields : A Simposium in Honour of P. A. M. Dirac, 1978.

           2. Sakurai, J. Invariance Principles and Elementary Particles, 1969.

           3. Wigner, E. Group Theory and Its Application To Quantum Mechanics of Atomic Spectra, 1959.

सूर्यवंशी, वि. ल.