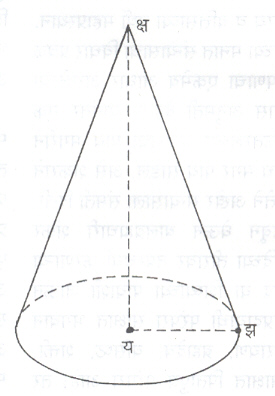
शंकुच्छेद : (शांकव). काटकोन त्रिकोणाची काटकोनाशी संलग्न असणारी कुठलीही एक बाजू स्थिर धरून काटकोन त्रिकोण त्या बाजूभोवती फिरविल्यास कर्णाने जे वक्रपृष्ठ तयार होते, त्यास शंकू किंवा अधिक काटेकोरपणे जात्य वृत्तशंकू असे म्हणतात. आ.१ मध्ये काटकोन त्रिकोण क्षयझ याची क्षय बाजू स्थिर असून त्रिकोण त्या बाजूभोवती फिरविला असता, कर्ण क्षय फिरल्याने वक्रपृष्ठ निर्माण झाले आणि तळाची बाजू यझ फिरल्याने वर्तुळ तयार झाले. भ्रमण होताना क्ष बिंदूस शंकूचे अग्र किंवा शिरोबिंदू आणि क्षय रेषेस शंकूचा अक्ष असे म्हणतात.
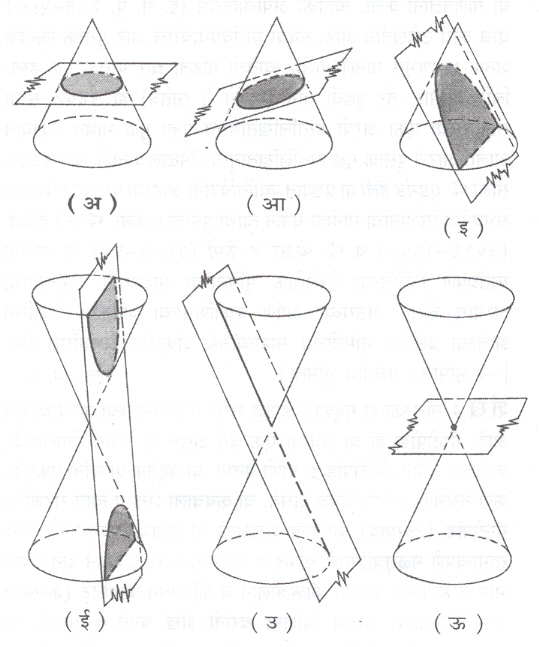
जात्य वृत्तशंकूला कोणत्याही प्रतलाने छेदल्यास ⇨वक्र मिळतो, त्याला शंकुच्छेद किंवा शांकव म्हणतात. हा छेद ⇨ वर्तुळ, ⇨ विवृत्त, ⇨ अपास्त, ⇨ अन्वस्त, दोन सरळ रेषा वा बिंदू असा सहा प्रकारचा असू शकतो: (१) आ. २ (अ) मध्ये दर्शविल्याप्रमाणे अक्षाला काटकोनात छेदणारे, पण शंकूच्या शिरोबिंदूतून न जाणारे प्रतल शंकूस वर्तुळात छेदील. (२) पण हे प्रतल अक्षाशी तिरपे असून शिरोबिंदूच्या एकाच बाजूस असलेल्या शंकुपृष्ठास छेदत असेल, तर छेद विवृत्त असतो [आ. २ (आ)]. (३) शंकूच्या एखाद्या जनक रेषेस समांतर असणाऱ्या (पण त्या रेषेतून न जाणाऱ्या) प्रतलाने मिळणारा छेद शिरोबिंदूच्या एकाच बाजूस असलेल्या शंकुपृष्ठावर असतो. (४) जर हे अक्षाशी तिरपे प्रतल शिरोबिंदूतून जात नसेल आणि शिरोबिंदूच्या दोन्ही बाजूंस असलेल्या शंकुपृष्ठास छेदत असेल, तर अपास्त असतो [आ. २ (ई).] (५) शंकूच्या जनक रेषेतून (अर्थात शिरोबिंदूतून) जाणारे प्रतल शंकूस दोन सरळ रेषांत छेदील [आ.२ (उ)]. मात्र हे प्रतल शंकूस स्पर्श करीत असेल, तर दोन सरळ रेषा एकमेकींत मिसळून एकच सरळ रेषा (जनक रेषा) मिळेल. (६) शंकूला फक्त शिरोबिंदूतच छेदणाऱ्या प्रतलछेदामुळे एक बिंदू (शिरोबिंदू) मिळेल. [आ.२ (ऊ)].
वरील विवेचन शंकुच्छेद या संज्ञेची व्युत्पत्ती देण्यापुरतेच आता उपयोगी समजले जाते. कारण वरील विवेचनात वापरलेल्या संश्लिष्ट भूमितीच्या पद्धतीने शंकुच्छेदाचा सखोल अभ्यास किचकट होतो : म्हणूनच यासाठी प्रतलीय वैश्लेषिक भूमितीच्या सोप्या पद्धती वापरतात [⟶ भूमिती]. त्यासाठी शंकुच्छेदाची व्याख्या पुढीलप्रमाणे करतात : समजा, प्रतलावर एक स्थिर रेषा (नियत रेषा) व एक स्थिर बिंदू (नाभिबिंदू) दिलेले आहेत. प्रतलावरील ज्या बिंदूने नाभिबिंदू व नियत रेषा या दोन्हीपासूनच्या अंतरांचे गुणोत्तर (विकेंद्रता) एक दिलेली स्थिर संख्या असते अशा सर्व बिंदूंच्या संचाला शंकुच्छेद म्हणतात. (आ. ३). [⟶ भूमिती: शांकव].
वरील व्याख्येतील शंकुच्छेदाचा आकार विकेंद्रितेचे मूल्य इ. यावर अवलंबून असतो. इ. <१ असेल, तर विवृत्त इ = १ असेल, तर अन्वस्त इ > १ असेल, तर अपास्त हे वक्र मिळतात [⟶ अन्वस्त अपास्त विवृत्त]. वरील व्याख्येआधारे शंकुच्छेदाचे कार्तीय समीकरण काढल्यास ते क्ष व य या दोन चल निर्देशकांचे द्विघाती समीकरण असते, असे दाखविता येते. [⟶ भूमिती: शांकव].

उलट असे कोणतेही द्वीघाती समीकरण कक्ष२ + २ जक्षय + खय२ + २टक्ष +२छय+ ग = ० घेतले, तर त्याचा आलेख एक शंकुच्छेद असतो. तो सुरुवातीस दिलेल्या सहा प्रकारच्या शंकुच्छेदांपैकी कोणताही असू शकेल. त्याचा आकार क, ज, ख, ट, छ, ग, या स्थिरांकांच्या परस्परसंबंधांवर अवलंबून असून त्याचे निकष उपलब्ध आहेत. [⟶ भूमिती : शांकव]. शंकुच्छेदाचा अधिक अभ्यास करण्यासाठी मात्र वरील लांबलचक द्विघाती समीकरण सोयीचे होत नाही. त्यासाठी नाभीपासून नियतरेषेवर काढलेल्या लंबावर क्ष-अक्ष घेऊन आणि क्ष-य अक्षांचा आदिबिंदू या अक्षावर योग्य प्रकारे निवडून शंकुच्छेदाची सुटसुटीत कार्तीय व ध्रुवीय समीकरणे मिळविता येतात. या समीकरणांच्या आधारे शंकुच्छेदाचे खालील महत्त्वाचे गुणधर्म मिळतात.
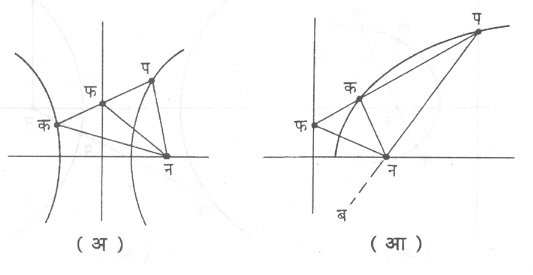
शंकुच्छेदाचे काही गुणधर्म : (१) शंकुच्छेदावरील प व क हे बिंदू जोडणारी रेषा नियतरेषेस फ मध्ये मिळते. न ही नाभी आहे, तर नफ ही रेषा आंतर्कोन पनक [आ.४ (अ)] अथवा पन वाढवून मिळालेला बाह्यकोन कनब दुभागते [आ.४ (आ)].
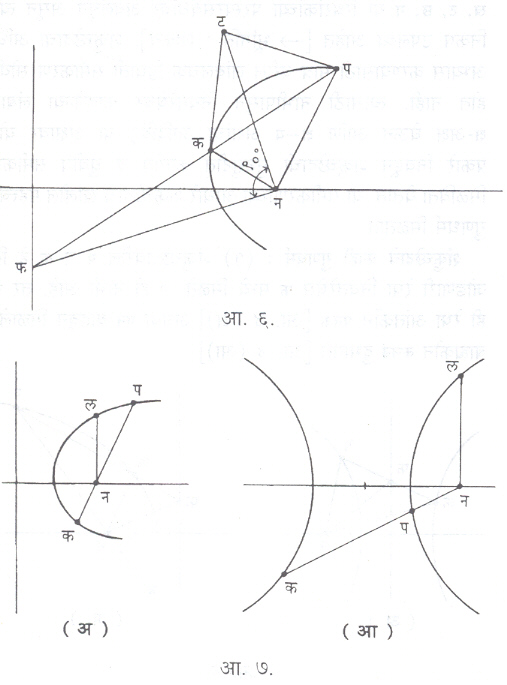
(२) शंकुच्छेदावरील प बिंदूतून काढलेली स्पर्शरेषा नियतरेषेस ट मध्ये छेदत असेल व न ही नाभी असेल, तर < पनट = ९०० (आ.५).

(३) शंकुच्छेदाबाहेरील ट बिंदूपासून टप व टक या दोन स्पर्शरेषा काढल्या व न ही नाभी असेल, तर नट ही रेषा पनक दुभागते (आ.६). तसेच पक रेषा नियत रेषेस फ मध्ये छेदत असेल, तर टनफ = ९०० .
(४) नल हा न या नाभीपासून शंकुच्छेदास काढलेला लंब आहे. न मधून जाणारी एक जीवा शंकुच्छेदास प आणि क मध्ये मिळते. नाभीपासून लंब नल आणि जीवेच्या नप व नक ह्या छेदांची लांबी ह्यात पुढील संबंध असतो.
१/नप + १/नक = २/नल (आ.७ अ)
१/नप – १/नक = २नल (आ.७ आ)
याशिवाय अन्वस्त, अपास्त, वर्तुळ, विवृत्त या प्रत्येक प्रकारच्या शंकुच्छेदांचे वेगवेगळे विशिष्ट गुणधर्म आहेत. यासंबंधीची अधिक माहिती मराठी विश्वकोशातील अन्वस्त, अपास्त, वर्तुळ व विवृत्त या नोंदीत दिलेली आहे.
उपयोग : तोफेचा गोळा, बंदुकीची गोळी अशा प्रक्षेप्यांचे मार्ग (वातावरणातील हवेत विरोध दुर्लक्षिल्यास) साधारण अन्वस्त आकाराचे असतात. झुलत्यापुलांचीरचनाही अन्वस्तआकाराची असते. सूर्यमालेतील ग्रहांचा सूऱ्याभोवतीचा मार्ग विवृत्ताकार असून सूर्य या विवृत्ताच्या नाभिस्थानी असतो. न्यूटनच्या गुरूत्वाकर्षण नियमाप्रमाणे सूर्य हा ग्रहास स्वत:कडे आकर्षित करतो. अशा प्रकारे छोट्या खगोलाचा मार्ग एक शंकुच्छेद असतो. विवृत्ताच्या एका नाभिस्थानातून उगम पावणाऱ्या प्रकाश वा ध्वनी लहरी विवृत्तावर परावर्तीत होऊन दुसऱ्या नाभिस्थानी एकत्र येतात. या गुणधर्माचा उपयोग कुजबुजणाऱ्या सज्जाच्या बांधणीत आढळतो. तोफेचा आवाज दोन ठिकाणी नोंदला असता आवाज ऐकण्याच्या वेळांतील फरकावरून ती दोन ठिकाणे व तोफेचे स्थान यामधून जाणारा अपास्त निश्चित होतो. अशा तऱ्हेचे दोन अपास्त मिळविले असता, त्यांचा छेदबिंदू म्हणजे शत्रूच्या तोफेचे स्थान निश्चित करता येते. अणुविज्ञानातील अनेक सूत्रांचे आलेख शंकुच्छेदाकार असतात.
स्वत:च्या सममिती अक्षाभोवतीच्या शंकुच्छेदाच्या भ्रमणामुळे मिळणारी अवकाश-पृष्ठे व्यवहारात सुपरिचित आहेत. वर्तुळाच्या अशा भ्रमणाने चेंडू, विवृत्ताच्या भ्रमणाने अंडे, अपास्ताच्या भ्रमणाने फेरीवाल्याचा स्टँड, तर अन्वस्ताच्या नाभिस्थानी असल्याने सर्व प्रकाश किरणांचे परावर्तन समांतर किरणांत होते.
इतिहास : ग्रीसमध्ये इ.स.पू. ४०० पासून शंकुच्छेदाचा अभ्यास ⇨ पेर्गाचे अँपोलोनियस, अरिस्टाऊस, ⇨ यूक्लिड, थेल्स, ⇨ आर्किमिडीज या गणितज्ञांनी केला. त्यांपैकी अँपोलोनियस (इ.स.पू. २६१ – २००) यांचे कार्य उल्लेखनीय आहे. त्यांची या विषयावरील आठ पुस्तके कित्येक शतके प्रमाणभूत मानली जातात. त्यातील पहिली चार पुस्तके मूळ हस्तलिखितानुसार, तर पुढची तीन (पाचवे ते सातवे) ही १६५८ साली सापडलेल्या एका अरबी हस्तलिखितावरून पुन्हा मूळ भाषेत रचण्यात आली. आठवे पुस्तक मूळ हस्तलिखितावरून मिळालेच नाही पण १७१० साली ⇨ एडमंड हॅली या प्रख्यात ज्योतिर्विदांनी आठव्या पुस्तकात येणाऱ्यासंभवनीय सिद्धांतांचा मागोवा घेऊन त्याची पुनर्रचना केली. ⇨ रने देकार्त (१५९६ –१६५०) व ⇨ प्येअर द फेर्मा (१६०१ – ६५) या दोघांनी स्वतंत्रपणे निर्मिलेल्या वैश्लेषिक भूमितीच्या साहाय्याने शंकुच्छेदांचा अभ्यास केला. अठराव्या आणि एकोणिसाव्या शतकांत विकसित झालेल्या प्रक्षेपीय झालेल्या भूमितीच्या साहाय्यानेही शंकुच्छेद अभ्यासिले गेले. [⟶ भूमिती : प्रक्षेपीय भूमिती ].
कस्तुरे, दा. य.