व्यस्तीकरण : (इन्ह्रूपर्शन). ही एक गणितीय क्रिया आहे. एकास एक संगती असलेले कोणतेही ⇨ फलन दिले असता त्यावरून व्यस्त फलन काढणे व त्याद्वारे फलन प्रतिमेतील प्रत्येक बिंदूची पूर्व प्रतिमा काढणे, या क्रियेला फलनाचे व्यस्तीकरण म्हणतात. उदा., य = २क्ष, –१ ≤ क्ष ≤ २ हे फलन दिले असता त्यावरून क्ष = य/२, –२ ≤ -य ≤ ४ हे व्यस्त फलन काढले की, व्यस्त फलन काढले की, व्यस्त फलनाच्या सर्व प्रतिमा [–१, २] या अंतरालात मिळतात. वरील फलन बैजिक आहे. भूमितीय फलनात दोन बिंदूंची एकास एक संगती दाखविण्याचा नियम किंवा समीकरण देतात. अर्थात भूमितीय व्यस्तीकरणामुळे मिळणारे फलनही भूमितीय असते. फलनाचे समीकरण व त्याचा आलेख माहीत झाला, तर भूमितीय व्यस्तीकरण हे बैजिक व्यस्तीकरणही होते.
वर्तुलीय (गोलीय) व्यस्तीकरण : हे भूमितीय व्यस्तीकरणाचे उपयुक्त आणि महत्त्वाचे उदाहरण आहे. म केंद्र व त त्रिज्या असलेल्या वर्तुळाच्या (गोलाच्या) अंतर्भागात किंवा वर्तुळावर (गोलावर) असलेला क हा कोणताही बिंदू असेल, तर मक किरणावर क’ हा बिंदू असा घ्या की मक X मक’ = त२, (आ. १.) या एकास एक संगती असलेल्या फलनामुळे प्रत्येक बिंदू क ची प्रतिमा क’ काढता येते. या फलनाचे व्यस्त फलन काढले, तर वर्तुळाबाहेरील वा वर्तुळावरील (गोलाबाहेरील वा गोलावरील) क’ या प्रत्येक बिंदूची व्यस्त प्रतिमा क वर्तुळाच्या (गोलाच्या) अंतर्भागात किंवा वर्तुळावर (गोलावर) मिळेल. या व्यस्त प्रतिमा काढण्याच्या क्रियेला वर्तुलीय (गोलीय) व्यस्तीकरण म्हणतात. दिलेल्या वर्तुळाला (गोलाला) आधार वर्तुळ (आधार गोल) म्हणतात. वर्तुलीय (भूमितीय) व्यस्तीकरणाचे बैजिक रूपांतर करण्यासाठी जर क, क’ चे ध्रुवीय निर्देशक, अनुक्रमे [र, θ] [र’, θ’] असतील, तर दिलेल्या फलनाची समीकरणे, र’ = त२/र, θ’= θ, o ≤ र ≤ त, o ≤ θ < २ π अशी असतील तर व्यस्त फलनाची समीकरणे, र = त२/र’, θ = θ’, त ≤ र’ ≤ ∞, o ≤ θ’< २ π अशी असतील. कार्तीय सहनिर्देशक पद्धती (रने देकार्त यांच्यावरून आलेले या पद्धतीचे नाव) वापरून ही समीकरणे क्ष’ = त२क्ष/(क्ष२ + य२) य’ = त२य/(क्ष२ + य२), क्ष = त२क्ष’/(क्ष’२ + य’२), य = त२य’/(क्ष’२ + य’२) अशी लिहिता येतात. अशाच प्रकारे गोलीय व्यस्तीकरणात गोलीय सहनिर्देशकांची व अवकाशातील कार्तीय सहनिर्देशकांची [→ भूमिती] समीकरणे लिहिता येतात.
व्यस्त फलन हेच दिलेले फलन आहे असे गृहीत धरले, तर क’ ची प्रतिमा क आणि क ची व्यस्त फलन प्रतिमा क’ असे म्हणता येते. म्हणूनच क व क’ यांना आधार वर्तुळाच्या (आधार गोलाच्या) संदर्भात एकमेकींच्या व्यस्त प्रतिमा म्हणतात.
वर्तुलीय व्यस्तीकरणामुळे एका वक्राची प्रतिमा दुसरा वक्र (उदा., वर्तुळकेंद्रातून जाणाऱ्या सरळ रेषेची प्रतिमा सरळ रेषा आणि वर्तुळकेंद्रातून न जाणाऱ्या सरळ रेषेची प्रतिमा एक वर्तुळ) अशी मिळते.
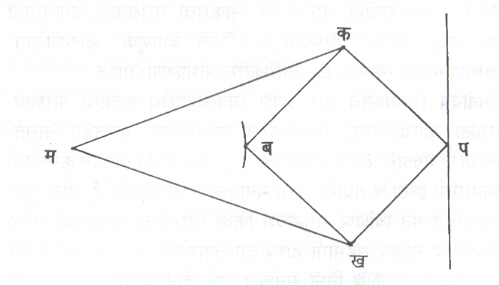वर्तुलव्यस्ताचे यांत्रिक रेखाटन : आ. २ मधील प्रत्येक दंड त्याच्या सांध्यांभोवती मुक्तपणे फिरू शकतो. तसेच मक = मख आणि कब = बख = खप = पक आहेत. प आणि ब या ठिकाणी खोबणी ठेवून त्यांत वक्र रेखाटण्याकरिता पेन्सिली बसविल्या आहेत. सर्व दंड कागदावर ठेवले, म बिंदू स्थिर केला, तर प आणि ब येथील पेन्सिली एकमेकींचे व्यस्त वक्र रेखाटतील. आ. २ मध्ये ब वर्तुळ रेखाटत आहे, तर प रेषा रेखाटत आहे.
उपयोग : एखादी दिलेली आकृती किचकट असेल, तर एकास एक संगती दाखविणार्या विशिष्ट भूमितीय फलनाच्या (रूपांतराच्या) साहाय्याने अनेक वेळा साधी नित्य परिचयाची आकृती मिळविता येते. एखादा विज्ञानातील प्रश्न जर या साध्या आकृतीसाठी सोडविता आला आणि निष्कर्ष काढता आले, तर भूमितीय व्यस्तीकरणाने रूपांतरित आकृतीवरून मूळ आकृती मिळविता येते आणि मिळालेल्या निष्कर्षांचे रूपांतरही मूळ प्रश्नासंबंधीच्या निष्कर्षात करता येते. उदा. विमानाच्या पंखांच्या आडव्या छेदाचा आकार वातपर्णासारखा [→ वायुयामिकी: वक्र] म्हणजे साधारण मासळीसारखा किचकट असतो. यावरून वाहणाऱ्या हवेचे गणित अत्यंत अवघड होते. म्हणून झुकॉव्हस्की या शास्त्रज्ञांनी एका विशिष्ट फलनाच्या साहाय्याने वातपर्णाचे रूपांतर वर्तुळात किंवा विवृत्तात केले. आता वर्तुळावरून (विवृत्तावरून) वाहणाऱ्या हवेचा गणितीय अभ्यास सोपा आहे. त्यावरून व्यस्तीकरणाचा उपयोग करून वर्तुळाचे (विवृत्ताचे) मूळ वातपर्णात, तर वर्तुळाआधारे काढलेल्या निष्कर्षाचे (उदा., उत्थापन बल) वातपर्णासंबंधीच्या निष्कर्षात रूपांतर करून विमानाच्या पंखाभोवतीच्या हवेच्या वहनासाठीचे निष्कर्ष मिळतात.
कस्तुरे, दा. य.
आपल्या मित्रपरिवारात शेअर करा..
