विवर्तन जालक

विवर्तन जालक : ही एक प्रकाशकीय प्रयुक्ती असून हिच्यात अरुंद फटी किंवा खाचा यांचा समूह असतो. यामुळे असंख्य शलाका निर्माण होऊन त्यांच्यातील व्यतिकरणातून वर्णपट निर्माण होतात. अपारदर्शक पडद्यावर समान अंतरावर पाडलेल्या असंख्य समांतर फटी ही या प्रकारची सर्वांत साधी रचना होय. प्रकाशाचे वर्णपटीय पृथःकरण (विश्लेषण) करणे आणि तरंगलांबीचे अचूक मापन करणे हा विवर्तन जालकाचा महत्त्वाचा उपयोग होय. मराठी विश्वकोशात ‘प्रकाशकी’ या स्वतंत्र नोंदीत विवर्तनाची व व्यतिकरणाची तपशीलवार माहिती दिलेली असून ‘इलेक्ट्रॉन विवर्तन’ अशीही स्वतंत्र नोंद आहे.

विवर्तन जालकावर प्रकाश पाडल्यावर मिळणारी प्रतिमा विवर्तन आणि व्यतिकरण यांच्या मिलाफातून मिळते. जालकावरील प्रत्येक फट प्रकाशाचे विवर्तन करते. विवर्तित शलाकांमध्ये व्यतिकरण होऊन अंतिम आकृतिबंध तयार होतो. विवर्तन जालकामध्ये दोषरहित आवर्ती पुनरावृत्त रचनेला फार महत्व असते. जालकाचे अपस्करण (वेगवेगळे रंग परस्परांपासून अलग करण्याचा गुणधर्म), ⇨विभेदनक्षमता इ. महत्त्वाचे गुणधर्म फटींच्या आकारावर अवलंबून न राहता त्यांच्या पुनरावृत्त रचनेवर अवलंबून असतात.

⇨टॉमस यंग यांनी यंग फट-युग्म हे साधन वापरून व्यतिकरण पट्टांच्या निर्मितीचा प्रयोग केला. या प्रयोगाद्वारे व्यतिकरणाचा आकृतिबंध मिळतो. या फटींची संख्या वाढवली, तर तो विवर्तन जालक होतो व या जालकावर प्रकाश पडला की, त्या प्रकाश उद्‌गमाचा वर्णपट विवर्तनामुळे मिळतो. हिऱ्याच्या अणकुचीदार टोकाने सपाट काचपट्टीवर समांतर आणि सारख्या अंतरांवर रेषा (ओरखडे) ओढल्या, खाचा पाडल्या, तर तो पारगम्य विवर्तन जालक होतो, तसेच काचेऐवजी धातूच्या चकचकीत पृष्ठभागावर ओढल्या (खाचा कोरल्या), तर त्यामुळे परावर्तन विवर्तन जालक तयार होतो. पारगम्य जालकामध्ये दोन रेषांमधील भागातून प्रकाश पलीकडे जाऊन तो भाग रेषा-छिद्राचे किंवा फटीचे काम करतो, तर परावर्तन विवर्तन जालकामध्ये खाचांच्या मधल्या भागांवरून प्रकाश परावर्तित होतो.

 विवर्तन जालकाची निर्मिती : परावर्तन विवर्तन जालक बनविण्याकरिता आतापर्यंत स्पेक्युलम या मुख्यतः तांबे व कथिल यांच्यापासून बनविलेल्या चकचकीत पांढऱ्या मिश्रधातूचा उपयोग केला जात असे, पण अलीकडे पारदर्शक काचपट्टीवर किंवा सायुज्जित क्वार्ट्झावर (नैसर्गिक क्वार्ट्झाचे चुरडलेले स्फटिक किंवा विशिष्ट प्रकारची क्वार्ट्झ–वाळू वितळवून बनविलेल्या काचेसारख्या निरोधक द्रव्यावर) ॲल्युमिनियमाचा थर देऊन त्यावर खाचा पाडतात. खाचा पाडल्यावर हवेचा परिणाम होऊ नये म्हणून ॲल्युमिनियमावर मॅग्नेशियम फ्ल्युओराइडाचा पातळ, पारदर्शक थर देतात. वर्णपटाच्या जंबुपार (दृश्य वर्णपटातील जांभळ्या रंगापलीकडील अदृश्य)प्रारणाच्या (तरंगरूपी ऊर्जेच्या) भागात विवर्तन जालकाचा वापर करावयाचा असल्यास ॲल्युमिनियमाऐवजी सोन्याचा थर देऊन खाचा पाडतात. कारण ॲल्युमिनियमाची परावर्तनक्षमता जंबुपार भागात कमी होत जाते.

विवर्तन जालकांवर १ मिमी. मध्ये ५०० ते १,२०० पर्यंत खाचा असू शकतात. खाचा आखण्यासाठी यंत्राचा उपयोग करतात. हिऱ्याच्या टोकाने खाच पाडल्यावर, यंत्राच्या साहाय्याने ते टोक वर उचलले जाते आणि स्क्रूच्या अत्यल्प फेऱ्याने ते टोक पुढे सरकवून दुसरी खाच पाडली जाते. काही यंत्रांमध्ये हिऱ्याचे टोक स्थिर राहते आणि खाचा पाडावयाची  काचच पुढे सरकविली जाते. यासाठी स्क्रूचे सूत्रांतर अगदी न बदलणारे पाहिजे. या पद्धतीने ⇨हेन्री ऑगस्टस रोलंड यांनी पहिला विवर्तन जालक १८८२ मध्ये तयार केला होता.  पारदर्शक पदार्थावर मूळ जालकाचा ठसा उमटवून जे जालक तयार करतात त्यांना प्रतिकृती विवर्तन जालक म्हणतात, तर खाचा पाडून तयार केलेल्या मूळ जालकाला प्रमाण विवर्तन जालक म्हणतात. ⇨योझेफ फोन फ्राउनहोफर यांनी पहिला व्यावहारिक विवर्तन जालक १८२० च्या सुमारास तयार केला. याकरिता त्यांनी अतिशय बारीक व सरळ तारा सारख्या अंतरावर अगदी जवळजवळ ठेवल्या होत्या. याच्या मदतीने त्यांनी सोडियमाच्या वर्णपटातील D रेषांची तरंगलांबी मोजली आणि काही ताऱ्यांच्या वर्णपटांचे निरीक्षणही केले.

खाचा पाडणाऱ्या यंत्रणेतील दोष म्हणजे खाच पाडत असताना स्क्रूचे सूत्रांतर अगदी तेच राहावयास पाहिजे, पण ते तसे राहत नाही. त्यामुळे ठराविक कालावधीनंतर खाचांतील अंतरात बदल पडतो. त्यामुळे जेव्हा वर्णपट घेतला जातो, तेव्हा अशा जालकाच्या वर्णपटात काही फसव्या किंवा कपट (अनिष्ट) वर्णपटरेषा आढळतात, त्या प्रकाश उद्गमापासून निघालेल्या नसतात. त्यांचे लायमन फसव्या वर्णपटरेषा आणि रोलंड फसव्या वर्णपटरेषा असे प्रकार असून विशिष्ट तंत्राने त्यांची ओळख पटविता येते, पण अलीकडे जालकावर खाचा पाडण्याचे तंत्रज्ञान बरेच विकसित झाल्याने वर उल्लेख केलेल्या दोषांचे प्रमाण खूप कमी करण्यात यश मिळाले आहे. अलीकडे ⇨लेसर किरणांच्या व्यतिकरणाच्या साहाय्याने जो सूक्ष्म असा धारींचा  आकृतिबंध तयार होतो त्यांच्या साहाय्याने व स्वलेखी तंत्राच्या साहाय्याने विवर्तन जालक बनवतात, त्यांस परावर्तित लेसरलिखित जालक असे म्हणतात.

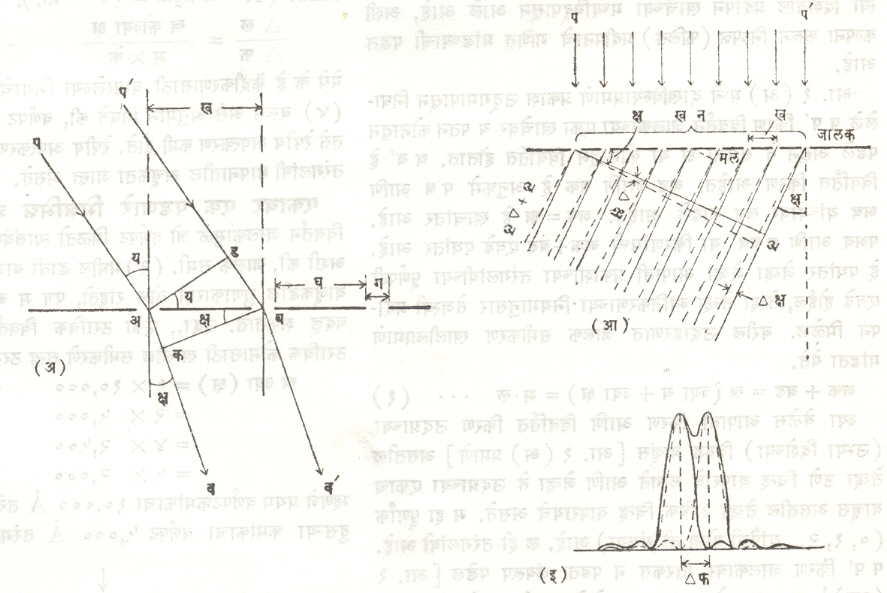
विवर्तन जालक समीकरण : अनेक समांतर, पारदर्शक, अरुंद खाचा (फटी) असलेला विवर्तन जालक आ. १ मध्ये दाखविला आहे. याच्या खाचांची रुंदी ग असून खाचांमधील अपारदर्शक भागाची रुंदी घ आहे. खाच आणि अपारदर्शक भागाची एकत्रित रुंदी ग + घ = ख इतकी आहे. ख हा जालकाचा स्थिरांक होय. जालकाच्या प्रत्येक एकक अंतरातील खाचांची संख्या म असल्यास ख = १/म होय.

अशा विवर्तन जालकावर प्रकाश पडल्यावर प्रत्येक खाच आयताकृती फट असल्याप्रमाणे कार्य करते आणि वेगवेगळ्या दिशांना प्रकाश विवर्तित करते. कोणतीही एक दिशा घेऊन खाचेच्या सर्व बिंदूंमुळे त्या दिशेतील प्रदीपन खाचेच्या मध्यबिंदूपासून आले आहे, अशी कल्पना करून निष्पन्न(फलित) प्रदीपनाचे गणित मांडण्याची पद्धत आहे.

आ. १ (अ) मध्ये दाखविल्याप्रमाणे प्रकाश उद्‌गमापासून निघालेले ष प’ किरण विवर्तन जालकाच्या एका खाचेवर य पतन कोनातून पडले असून ते समजा क्ष या कोनातून विवर्तित होतात. ब व’हे विवर्तित किरण आहेत. अड आणि बक हे अनुक्रमे प’ब आणि अव यांच्यावर लंब काढले आहेत. अब = ख हे खाचांतर आहे. पअव आणि प’बव’ या किरणांमध्ये अक + बड एवढे पथांतर आहे. हे पथांतर जेव्हा जेव्हा आपाती प्रकाशाच्या तरंगलांबीच्या पूर्णपटी एवढे होईल, तेव्हा तेव्हा व्यतिकरणाच्या नियमानुसार तेजस्वी प्रदीपन मिळेल. वरील उदाहरणात जालक समीकरण खालीलप्रमाणे मांडता येते.

अक + बड             =            ख (ज्या य + ज्या क्ष)           =            म. ल. …             (१)

ज्या वेळेस आपाती किरण आणि विवर्तित किरण उदग्राच्या (उभ्या दिशेच्या) विरुद्ध बाजूंस [ आ. १ (अ) प्रमाणे]  असतील तेव्हा उणे चिन्ह वापरावे लागते आणि जेव्हा ते  उदग्राच्या एकाच बाजूस असताल तेव्हा अधिक चिन्ह वापरायचे असते. म हा पूर्णांक (०, १, २ . . . यांपैकी योग्य ती संख्या) आहे. ल ही तरंगलांबी आहे. प प’ किरण जालकावर तिरकस न पडता लंबरूप पडेल [ आ. १ (आ)], तर पतन कोन य हा शून्य होतो व वरील समीकरण असे होते.

ख ज्या क्ष                =            म. ल                       …           …           …           (२)

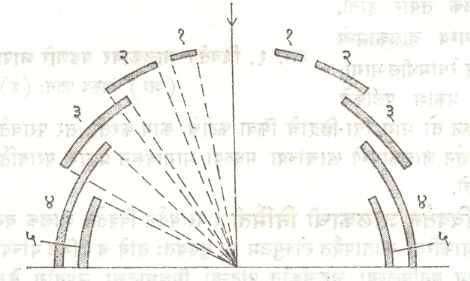
जर म = ० असेल, तर ती प्रधान प्रतिमा असते आणि म = १, २, ३, . . . इ. असल्यास प्रधान प्रतिमेच्या दोन्ही बाजूंना क्र. १, क्र. २, क्र. ३ इ. वर्णपट मिळतात (आ.२). वर्णपटमापकावर विवर्तन जालक बसवून जालकावर समांतरित्राद्वारे एखाद्या प्रकाश उद्‌गमाचे किरण लंबरूपाने पाडले, तर वर्णपटमापकातील दूरदर्शकाद्वारे प्रधान प्रतिमेच्या दोन्ही बाजूंना असलेले वर्णपट पाहता येतात (आ.२). दुसऱ्या क्रमांकाच्या वर्णपटातील रेषा प्रथम क्रमांकाच्या वर्णपटातील रेषांपेक्षा दूर दूर असतात. तिसऱ्या क्रमांकाच्या वर्णपटातील रेषा या दुसऱ्या क्रमांकाच्या वर्णपटातील रेषांपेक्षा अधिक दूर असतात. एकंदरीत वर्णपटाचा क्रमांक वाढल्यास अपस्करणही वाढते. विवर्तन जालकाद्वारे मिळणारा वर्णपट अनेक खाचांमधून प्रकाशाचे जे विवर्तन होते त्यामुळे मिळतो. यंग फट-युग्माच्या प्रयोगाचे हे वर्धित स्वरूप आहे. जसजशी खाचांची संख्या वाढत जाते, तसतसे प्रमुख कमाल रेषांचा रेखीवपणा वाढत जातो. दुय्यम कमाल रेषांची संख्या सुद्धा वाढते, पण त्यांची तेजस्विता घटते.

विवर्तन जालक अपस्करण : विवर्तन जालकावरील आपाती प्रकाश संमिश्र तरंगलांबींचा असल्यास विवर्तन प्रक्रियेमध्ये अपस्करणाने तरंगलांबी घटकांचे पृथक्करण होते. आ. १ (आ) मधील आपाती प्रकाशात समजा ल आणि ल + Δल असे घटक असल्यास विवर्तित प्रकाशात अपस्करणाने घटक वेगळे होतात. ही अपस्करण प्रक्रिया खालील समीकरणाने मांडता येते.

 याला कोणीय अपस्करण म्हणतात. कारण वेगळ्या तरंगलांबीच्या प्रकाशाचा विवर्तन कोन तरंगलांबीतील फरकाप्रमाणे वेगवेगळा असतो. विवर्तित प्रकाशाचे केंद्रीकरण केल्यास आ. १ (इ) मधील फ्राउनहोफर आकृतिबंध मिळतो. यातील वर्णपट रेषांतील अंतर  फ मिमी. असल्यास रेषीय अपस्करण (Å / मिमी.) समी. (४) प्रमाणे मिळते. (Å = ॲगस्ट्रॉम = १० ^–१० मी.).

येथे के हे केंद्रीकरणासाठी वापरलेल्या भिंगाचे केंद्रांतर होय. समी. (४) वरून असे अनुमान निघते की, वर्णपट क्रमांक म जसा वाढेल तसे रेषीय अपस्करण कमी होते. रेषीय अपस्करण जितके जास्त तितकी तरंगलांबी मापनातील अचूकता जास्त असते.

एकावर एक पडणारे भिन्नभिन्न क्रमांकांचे वर्णपट: विवर्तन जालकामुळे जो वर्णपट मिळतो त्यासंबंधी एक महत्वपूर्ण गोष्ट अशी की, जालक समी. (२) मधील डावी बाजू तीच असून उजव्या बाजूकडील गुणाकारही तोच राहतो, पण म आणि ल च्या किंमती बदलू शकतात. उदा., एका ठराविक विवर्तन जालकाद्वारे एका ठराविक कोनासाठी खालील समीकरणे सत्य ठरतात.

ख ज्या (क्ष)=        १×१०,०००            …           …           (५)

                            =        २×५,०००

                            =        ४×२,५००

                            =         ५×२,०००

म्हणजे प्रथम वर्णपटक्रमांकाचा १०,००० Å तरंगलांबीच्या  वर्णपटावर दुसऱ्या क्रमांकाचा वर्णपट ५,००० Å तरंगलांबीचा, तर चौथ्या  वर्णपटक्रमांकाचा २५०० Å तरंगलांबीचा वर्णपट पडतो. ह्यांना परस्परव्यापी भिन्नक्रमी वर्णपट म्हणतात (आ.२). ह्या एकत्रित अशा वर्णपटातून हव्या त्या वर्णपट क्रमांकाचा वर्णपट पाहिजे असल्यास तो, छायाचित्रण पटलाच्या (फिल्मच्या) संवेदनक्षमतेद्वारे किंवा गाळण्यांद्वारे किंवा वर्णपट क्रमांक पृथक्कारकाद्वारे मिळवता येतो.

 विवर्तन जालकामधून मिळणाऱ्या वर्णपटांची अनेक क्रमांकाच्या वर्णपटात वाटणी झाल्याने त्याची तेजस्विता क्षीण होते. हे टाळण्यासाठी अलीकडे विवर्तन जालकावर ज्या खाचा पाडल्या जातात त्यांना विशिष्ट कोन दिलेला असतो. ह्यास जालकातील खाचांचे कोनीकरण असे म्हणतात. कोनीकरणामुळे ठराविक क्रमांकाचा वर्णपट ठराविक कोनासाठी व तरंगलांबीला तेजस्वी असतो. जालकावरील खाचांचे कोनीकरण करण्यामागील हेतू हा की कोनीकरणानंतर प्रत्येक खाच निवडलेल्या वर्णपटक्रमामध्ये प्रकाशीय भूमितीच्या नियमानुसार आपाती प्रकाश वळवेल. पारगम्य विवर्तन जालकामध्ये कोनीकरण केलेली खाच लोलकाप्रमाणे कार्य करते, तर परावर्तन विवर्तन जालकातील अशी खाच योग्य त्या कोनामध्ये बसविलेल्या आरशाप्रमाणे कार्य करते.

ख ज्या क्ष’               =            म. ल’     …             …             …             (६)

क्ष’ आणि ल’ हे कोनीकरणाचा कोन व संबद्ध कोनीकरणाची तरंगलांबी दाखवतात. एखादा विवर्तन जालक समजा प्रथम क्रमांकाच्या वर्णपटासाठी ६००० Å तरंगलांबीला कोनीकरण केलेला आहे, तर त्याचा अर्थ असा की, दुसऱ्या क्रमांकाच्या वर्णपटात ३००० Å तरंगलांबीच्या आसपास वर्णपटाची तेजस्विता अधिक असेल. तसेच तिसऱ्या क्रमांकाच्या वर्णपटात २००० Å तरंगलांबीच्या आसपासही  वर्णपट अधिक तेजस्वी असेल. या तंत्रामुळे वाढत्या क्रमांकाचे वर्णपट छायाचित्रित करताना प्रकाशन काळाची बचत होते व कमी वेळात वर्णपटाचे चित्र घेता येते.

विवर्तन जालकाची विभेदनक्षमता : विवर्तन जालकाची विभेदनक्षमता लोलकापेक्षा हजारोपटींनी अधिक असते. त्यामुळेच वर्णपटविज्ञानात विवर्तन जालकाचा वापर अधिकाधिक होत आहे. वर्णपटरेषांचे सूक्ष्मरूप अभ्यासण्यास त्यामुळे मदत होते. विवर्तन जालकावर न एवढ्या खाचा असतील, तर

विभेदनक्षमता         =            म × न     …             …             …             (७)

(येथे म = ०, १, २, . . . वर्णपटक्रमांक). वरील समीकरणाद्वारे विभेदनक्षमता ही खाचांच्या एकूण संख्येवर अवलंबून आहे. मग एका मिमी. मध्ये ५०० खाचा असोत की १,००० असोत. विवर्तन जालकावर असलेल्या एकूण खाचांची संख्या महत्त्वाची असते. दुसरे असे की, दुसऱ्या क्रमांकाच्या वर्णपटात जालकाची विभेदनक्षमता पहिल्याच्या दुप्पट असते. तसेच तिसऱ्या क्रमांकाच्या वर्णपटात ती पहिल्याच्या तिप्पट असते, पण ही केवळ सैद्धांतिक बाजू आहे.  प्रत्यक्षात १०० टक्के विभेदनक्षमता मिळू शकत नाही. वरील सूत्राने दिलेल्या विभेदनक्षमतेच्या ६० टक्के जरी विभेदनक्षमता प्रत्यक्षात मिळाली, तरी तो उत्तम विवर्तन जालक वर्णपटलेखक समजतात.

एशलेट, एशलॉन आणि एशेल: कोनीकरण केलेल्या विवर्तन जालकाला ‘एशलेट’ म्हणतात. यामध्ये खाचा जालक प्रतलाशी जो कोन करतात तो कोनीकरणाचा कोन होय. अवरक्त (दृश्य वर्णपटातील तांबड्या रंगापलीकडील अदृश्य प्रारणाच्या) विभागातील वर्णपट अभ्यासण्यासाठी हा विवर्तन जालक विशेष उपयुक्त आहे. एशलॉन (सौपानिक) जालक एशलेटपूर्वी अस्तित्वात आले. पायऱ्यापायऱ्यांची जिन्यासारखी याची रचना असल्याने याला ‘एशलॉन’ हे नाव दिले गेले.

वर्णपट अभ्यासासाठी तरंगलांबी मापनासाठी उच्च विभेदनक्षमतेच्या विवर्तन जालकाची आवश्यकता असते. विशेषकरून वर्णपटाच्या अवरक्त विभागात याची फार आवश्यकता असते. यासाठी जालकावरील खाचांची संख्या खूप मोठी ठेवून खालच्या क्रमाचा वर्णपट अभ्यासणे हा जसा एक मार्ग आहे (समी. ७ पहा) तसेच खाचांची संख्या कमी ठेवून उच्च क्रमाचा वर्णपट अभ्यासणे हा दुसरा कल्पक मार्ग आहे. एशलॉन विवर्तन जालक हा दुसऱ्या प्रकारातील होय. यामध्ये साधारणपणे १ सेंमी. जाडीच्या सारख्या रुंदीच्या काचेच्या पट्ट्या सौपानिक (जिन्याच्या) रचनेप्रमाणे एकमेकींवर चिकटवलेल्या असतात. पट्ट्यांची लांबी १ मिमी.ने कमीकमी होत जाते. त्यामुळे पायऱ्यांसारखी रचना दिसते.

परावर्तन एशलॉन विवर्तन जालकामध्ये म ची किंमत २ ट/ल एवढी असते, तर पारगम्य एशलॉनमध्ये ती (μ-१) ट/ल इतकी असते. μ हा पट्टीचा प्रणमनांक (वक्रीभवनांक) आहे. विवर्तन जालकापेक्षा म च्या किंमती एशलॉनमध्ये खूप जास्त (१०,०००च्या जवळपास) असल्याने विभेदनक्षमताही अधिक असते. एशलॉन आणि सपाट विवर्तन जालक यांच्या दरम्यान गुणधर्म असलेला एशेल हा जालक आहे. उच्च विभेदनक्षमतेसाठी यामध्ये उच्च क्रमाचा (१०० ते १,०००) वर्णपट ४५° पेक्षा जास्त कोनातून आपाती प्रदीपन करून मिळवितात. याच्यावर दर २.५ सेंमी. मध्ये १०० ते २०० खाचा असतात, परंतु या खाचा अत्यंत सूक्ष्म असतात व वेगवेगळ्या वर्णपटक्रमांचा प्रकाश एका अरुंद पट्ट्यात परावर्तित होईल, अशी यांची रुपरेखा असते. लोलकासारख्या अपस्करण करणाऱ्या अन्य उपकरणासोबत एशेल प्रकारचा विवर्तन जालक वापरून परस्परव्यापी वर्णक्रम टाळून नेमका हवा असलेला वर्णपट मिळविता येतो.

अंतर्गोल विवर्तन जालक : सपाट विवर्तन जालकामुळे मिळणाऱ्या वर्णपटाचे भिंगाद्वारे केंद्रीकरण करावे लागते. हे टाळण्यासाठी अंतर्गोल विवर्तन जालकाचा वापर सुरू झाला. हा विवर्तन जालक रोलंड यांनी शोधून काढला.  हा परावर्तन विवर्तन जालक असतो. धातूच्या अंतर्गोल आरशावर त्याच्या जिवेला समांतर खाचा पाडतात. अंतर्गोल विवर्तन जालकांना वर्णपटाचे केंद्रीकरण करण्यासाठी, सपाट जालकांना जसे भिंग लागते, तसे लागत नाही. त्यामुळे अंतर्गोल विवर्तन जालकाचा जंबुपार विभागात विशेष उपयोग होतो. कारण भिंग वापरावे लागत नसल्यामुळे भिंगामुळे होणारे जंबुपार प्रारणाचे शोषण टाळता येते.

विवर्तन जालकाची त्रिज्या र असेल, तर र हा व्यास कल्पून जे वर्तुळ काढतात त्याला रोलंड वर्तुळ म्हणतात. विवर्तन जालक या वर्तुळाला स्पर्श करेल असा ठेवला जातो. याच वर्तुळावर असलेल्या प्रकाश उद्गमाचे किरण जालकावर पडल्यास विवर्तित प्रतिमा किंवा वर्णपटही याच वर्तुळावर केंद्रित होईल. त्यासाठी वेगळे भिंग लागत नाही.

विवर्तन जालकाची निरनिराळी स्थापने : ईगल स्थापन : अंतर्गोल विवर्तन जालकाची वेगवेगळी स्थापने आहेत. त्यांपैकी पाशेन आणि रोलंड स्थापने कालबाह्य झाली आहेत. अलीकडे ईगल स्थापनाचा वापर केला जातो. ईगल स्थापनात पाशेन आणि रोलंड स्थापनांपेक्षा कमी जागा लागते, त्यामुळे वातानुकूलिक करण्यासाठी कमी खर्च येतो. अधिक क्षेत्र व्यापणाऱ्या जागेचे तापमान स्थिर ठेवणे त्रासदायक व खर्चाचे असते. आ. ३ मध्ये दाखविल्याप्रमाणे विवर्तन जालक ग, ग’ या ठिकाणी असताना, कॅमेरा क, क’ या ठिकाणी असल्यास, तसेच उ, उ’ या ठिकाणी  प्रकाश उद्गम ठेवल्यास दर वेळी जालक, कॅमेरा व उद्गम छिद्र ही रोलंड वर्तुळाकार असतात. अ ओट्यावर विवर्तन जालक पुढेमागे करणारी यंत्रणा असते, तसेच विवर्तन जालकाचा कोनसुद्धा अचूक वाचता येतो. छायाचित्रीय पटल (फिल्म) वापरणारा कॅमेरा जालकाच्या स्थितीनुसार योग्य त्या ठिकाणी ठेवता येतो. ओट्याची उभारणी अशा रीतीने केलेली असते की,जमिनीतले हादरे वगैरे विवर्तन जालकापर्यंत पोहोचू नयेत, अन्यथा विभेदनक्षमता कमी होते. या विवर्तन जालकाच्या वक्रतेच्या त्रिज्या सु. ६ ते ९ मी. एवढ्या मोठ्या असू शकतात.

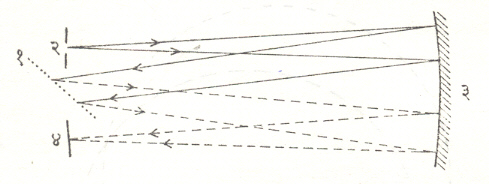
एबर्ट स्थापन : अलीकडे सपाट परावर्तन विवर्तन जालक एबर्ट स्थापन करून वर्णपटलेखकात वापरतात. आ. ४ मध्ये दाखविल्याप्रमाणे ह्या स्थापनात प्रवेश फटीतून निघालेले किरण अंतर्गोल  आरशावर पडतात. त्यावरुन ते विवर्तन जालकावर पडतात व जालकावरून विवर्तन होऊन परत त्याच अंतर्गोल आरशावर पडतात. तेथून ते कॅमेऱ्याच्या फिल्मवर केंद्रित होतात. उच्च वर्णपटक्रमांकाचे अंकन करण्यासाठी वर्णपटक्रमांक पृथक्कारक किंवा गाळण्या वापराव्या लागतात. एकच अंतर्गोल आरसा बहुद्देशीय कामे करतो. स्थापन अवर्णी आणि आटोपशीर असते. यामध्ये एकाच अंतर्गोल आरशाचे दोन भाग सारख्याच अशा बाह्य अक्षापासून दूर पद्धतीने वापरले जातात. या समप्रमाणतेमुळे कोमा नावाचा प्रतिमाविकार दोष (प्रकाशकीय प्रणालीतील त्रुटी उघड करणाऱ्या या दोषात बिंदू नासपतीसारख्या असममित ठिपक्याप्रमाणे दिसतो) नाहीसा होतो परंतु  ही दुरुस्ती फटीइतकीच अक्षबाह्य असलेल्या वर्णपटरेषेला लागू पडत असल्याने विवर्तन जालकाच्या कोणत्याही दिक् स्थितीमध्ये वर्णपटाचा थोडासाच भाग रेखीवपणे केंद्रित होतो. त्यामुळे वर्णपटाच्या विस्तृत भागाच्या लेखन/मापनासाठी एबर्ट स्थापन फारसे समाधानकारक फल देत नाही. निर्गम फट योग्य पद्धतीने ठेवून मोनोक्रोमॅटरसाठी (एकवर्णकारी वर्णपटलेखकासाठी) मात्र ते समाधानकारक ठरते.

पहा : प्रकाशकी.

संदर्भ :       1. Chang, R. Basic Principles of Spectroscopy, 1978.

            2. Hutley, M. C. Diffraction Gratings, New York, 1982.

            3. Jenkins, F. A. White, H. E. Fundamentals of Optics, New York, 1976.

            4. Maystre, D. Ed., Selected Papers on Diffraction Gratings, New York, 1993.

            5. Sears, F. W. Zeemansky, M. W. Young, H. D. University Physics, New Delhi, 1982.

            6. Tenquist, D. W. Whittle, R. N. Yarwood, J. University Optics, London, 1969

कुलकर्णी, दि. भि. बेहेरे, सुभाष

“