वर्णपटविज्ञान : (स्पेक्ट्रॉस्कोपी). द्रव्याने उत्सर्जित व शोषण केलेल्या दृश्य प्रकाश व इतर ⇨विद्युत् चुंबकीय प्रारणांचे त्यांच्या तरंगलांबीच्या संदर्भात वर्णन, विश्लेषण, मापन व स्पष्टीकरण करणारी ही विज्ञान शाखा आहे. ⇨द्रव्यमान वर्णपटविज्ञानात प्रारण व द्रव्य यांच्यातील परस्परक्रियांचा संबंध येत नाही पण त्यातील प्रदत्ताचे (मिळणाऱ्या माहितीचे) स्वरूप वर्णपटविज्ञानीय प्रदत्ताशी सदृश असल्यामुळे त्याला हे नाव देण्यात आले आहे. सूर्य, तारे, काजवे, ज्योती, तडित् यांसारख्या नैसर्गिक उद्गमांपासून आणि प्रदीप्त दिवे, ⇨लेसर, विद्युत् प्रज्योत, अनुस्फुरक (फ्ल्यूओरेसंट) दिवे यांसारख्या मानवनिर्मित उद्गमांपासून मिळणारा प्रकाश अनेक रंगांचा मिळून बनलेला असतो. सर्वसाधारण निरीक्षकाला प्रकाशाच्या या मिश्ररूपाची जाणीव बहुधा होत नाही परंतु प्रकाश लोलकातून वा अन्य प्रयुक्तीतून जाऊ देऊन घटक रंगांत त्याचे विभाजन करून हे मिश्ररूप दाखवून देता येते. एखाद्या उद्गमाने उत्सर्जित केलेल्या या रंगांचे प्रदर्शन वा वर्णन म्हणजे त्या उद्गमाचा वर्णपट असे म्हणता येईल.
वर्णपटविज्ञानात वर्णपटांचे उद्गम, मापन, विश्लेषण आणि उपयोग यांचा विचार करण्यात येतो. अनेक तांत्रिक क्षेत्रांत त्याचा व्यावहारिक उपयोग करण्यात येतो. विशेषतः प्रकाशाचे उत्सर्जन करणाऱ्या कोणत्याही उद्रमातील घटक व प्रक्रिया ओळखण्यासाठी त्याचा उपयोग होतो. उदा., वर्णपटविज्ञानीय पद्धतींनी प्रयोगशाळेत पदार्थांच्या अल्प राशीचे संघटन रासायनिक प्रक्रियांनी करता येणार नाही इतक्या अचूकतेने व जलद ओळखता येते. नमुने ओळखण्यासाठी त्यांचा तुलना करता येते. उत्पादित वस्तूंच्या अखंड मालिकेतील बदलांवर वा प्रदूषकांवर लक्ष ठेवता येते. नियंत्रित अणुकेंद्रीय विक्रियेतील तापमान मोजण्यासाठी वर्णपटविज्ञानावर आधारलेल्या उपकरणांचा उपयोग होतो. आणवीय व रेणवीय संरचनांचा विस्तृत अभ्यास करणे वर्णपटविज्ञानामुळेच शक्य झाले आहे. ज्योतिषशास्त्रात वर्णपटविज्ञानाच्या साहाय्याने सौर चुंबकीय वादळांचे भाकित करता येते व ताऱ्यांच्या रासायनिक संघटनांचे विश्लेषण करता येते.
वर्णपट : सूर्यप्रकाश काचेच्या लोलकामधून पार जाऊ देऊन भिंगांनी पडद्यावर पाडल्यास पडद्यावर सप्तरंगाचा पट्टा दिसतो. या सप्तरंगी पट्ट्याला सूर्याचा वर्णपट असे म्हणतात. या पट्ट्यामधील रंग ⇨इंद्रधनुष्याच्या रंगांप्रमाणे असतात, कारण इंद्रधनुष्य हासुद्धा सूर्याचा वर्णपटच होय. तो तयार होण्यास वातावरणातील पाण्याचे थेंब लोलकाचे कार्य करतात.
जेम्स क्लार्क मॅक्सवेल (१८२९-७९) यांनी असा सिद्धांत मांडला की, प्रकाश म्हणजे काही विशिष्ट तरंगलांब्यांचे विद्युत् चुंबकीय तरंग असतात. डोळ्यांना दिसणारा प्रकाशाचा रंग त्याच्या तरंगलांबीवर अवलंबून असतो. विशिष्ट मर्यादेत असलेले विद्युत् चुंबकीय तरंगच आपल्याला प्रकाश म्हणून भासमान होतात. तांबड्यापेक्षा जास्त अगर जांभळ्यापेक्षा कमी तरंगलांबी असलेले विद्युत् चुंबकीय तरंग डोळ्यांना प्रकाश म्हणून दिसत नाहीत. पांढरा प्रकाश हा या विशिष्ट मर्यादेतील तरंगलांब्यांचे किंवा कंप्रतांचे (दर सेकंदाला होणाऱ्या कंपन संख्यांचे) मिश्रण असते. लोलकामध्ये त्यांचे अपस्करण होते म्हणजे वेगवेगळ्या कंप्रता परस्परांपासून अलग केल्या जातात.
विद्युत् चुंबकीय तरंगांच्या कंप्रता अत्यंत कमी म्हणजे प्रती सेकंदाला एक दोन कंपनांपासून तो कोट्यवधी कंपनांपर्यंत असू शकतात. कंप्रतांच्या मूल्यांवरून त्यांना वेगवेगळी नावे दिली आहेत व त्यांचे उद्गम वेगवेगळ्या प्रकारांचे असतात. त्यांचे अभिज्ञान (ओळखणे व मापन) करण्याची साधने वेगवेगळी असतात.
यावरून वर्णपटाची व्यापक व्याख्या करता येते. कोणत्याही विद्युत् चुंबकीय तरंगांच्या उद्गमापासून निघालेल्या विविध कंप्रतांच्या तरंगांना तरंग सापेक्ष विस्तारित केले, तर मिळणाऱ्या नकाशाला त्या तरंग समुच्चयाचा वर्णपट असे म्हणतात. अशा विविध प्रकारच्या वर्णपटांचा स्थूलमानाने येथे आढावा घेतला आहे. वर्णपटातील कंप्रतांच्या मर्यादेवरून त्यांना विशिष्ट नावे दिलेली असतात उदा., गॅमा किरण वर्णपट, क्ष-किरण वर्णपट वगैरे. कित्येकदा वर्णपट उत्सर्जित करणाऱ्या वस्तूंपासून त्याचे नामकरण होते जसे आणवीय वर्णपट (अणूत उत्पन्न होणारा वर्णपट), रेणवीय वर्णपट, अणुकेंद्रीय चुंबकीय अनुस्पंदन वर्णपट (अणुकेंद्राच्या चुंबकीय अनुस्पंदनामुळे उत्सर्जित झालेला वर्णपट).
वर्णपटाची एकके : निर्वात अवकाशामध्ये सर्व प्रकारचे विद्युत् चुंबकीय तरंग c (३ × १०८ मी. /से. ) या वेगाने जातात. तरंगांची कंप्रता हर्ट्झ (Hz = एक कंपन प्रती सेकंद ) या एककात मोजतात. १,००० हर्ट् झ म्हणजे किलोहर्ट्झ व दहा लाख हर्ट्झ म्हणजे मेगॅहर्ट्झ ही एकके उच्च कंप्रता व्यक्त करण्यासाठी वापरतात.
कंप्रता व वेग यांवरून तरंगलांबी ठरविता येते. त्यासाठी मीटर, सेंटिमीटर यांखेरीज पुढील काही खास एकके वापरतात.
| १ मायक्रॉन (μ) किंवा १ मायक्रोमीटर (μm ) = | १०–४ सेंमी. = १०–६मी. |
| १ मिलिमायक्रॉन (mμ) = | १०–७ सेंमी. = १०–९मी. |
| १ अँगस्ट्रॉम (A) = | १०–८ सेंमी. = १०–१० मी. |
| १ क्ष-किरण एकक किंवा सीगवान एकक (X XU) = | १०–११ सेंमी. = १०–१३ मी. |
| १ नॅनोमीटर (नॅमी.) = | १०–७ सेंमी. = १०–९मी. |
| १ पायकोमीटर (पामी.) = | १०–१० सेंमी. = १०–१२मी. |
विद्युत् चुंबकीय तरंगांचा वेग माध्यमानुसार बदलतो परंतु विशिष्ट तरंगाची कंप्रता कोणत्याही माध्यमात तीच राहते. अशा वेळी तरंगाबद्दल चर्चा करताना कंप्रतांचा उल्लेख करणे अधिक सोईस्कर असते. विद्युत् चुंबकीय तरंगांचे वर्गीकरण कोष्टक क्र. १ मध्ये दिल्याप्रमाणे ढोबळपणे करतात परंतु हे लक्षात ठेवले पाहिजे की, त्यातील सीमारेषा पूर्णपणे स्पष्ट नाहीत. विविध तरंगलांब्यांच्या वर्णपटांच्या अभ्यासापासून एक विशिष्ट प्रकारची उपयुक्त माहिती मिळते. गॅमा किरण अणुकेंद्राच्या संरचना व अणुकेंद्रीय विक्रिया यांबद्दल उपयुक्त माहिती देतात. तसेच विश्वकिरणांतर्गत (बाह्य अवकाशातून पृथ्वीवर पडणाऱ्या भेदक किरणांतर्गत) येणाऱ्या गॅमा किरणांपासून विश्वरचनेबद्दल उपयुक्त अंदाज बांधता येतात. क्ष-किरणांच्या वर्णपटाच्या अभ्यासाविषयी ‘क्ष-किरण’ ही नोंद पहावी.
जंबुपार व दृश्य वर्णपटांपासून अणू व रेणू यांच्या संरचनेबद्दल, तर अवरक्त व सूक्ष्मतरंग वर्णपटांच्या अभ्यासावरून रेणूंच्या संरचनेबद्दल महत्त्वाची माहिती मिळते.
उत्सर्जन वर्णपट व शोषण वर्णपट : विशिष्ट प्रकाश उद्गमापासून निघणारा प्रकाश वर्णपटलेखकाच्या फटीवर पडला असता जो वर्णपट मिळतो त्याला त्या उद्गमाचा उत्सर्जन वर्णपट असे म्हणतात. शोषण वर्णपटाकरिता एक अखंड वर्णपट देणारा प्रकाश उद्गम (उदा., साधा विद्युत् दिवा किंवा सूर्य) घेऊन त्याचा प्रकाश एका विशिष्ट द्रवातून अगर घन पदार्थातून जाऊ देऊन मग तो वर्णपटलेखकाच्या फटीवर पाडतात. त्यापासून मिळणाऱ्या वर्णपटात विशिष्ट तरंगलांबीचा प्रकाश मधील द्रव अगर घन पदार्थाने शोषून घेतल्यामुळे त्या जागी प्रकाशहीनता दिसते. यामुळे हा वर्णपट अखंड न राहता त्यात काही विशिष्ट ठिकाणी काळ्या रेषा किंवा पट्टे दिसतात. अशा प्रकारे मिळणाऱ्या वर्णपटाला त्या द्रवाचा अगर घन पदार्थाचा शोषण वर्णपट असे म्हणतात. अशा काळ्या रेषांच्या कंप्रतांच्या अभ्यासावरून शोषक द्रव्याच्या अणूबद्दल वा रेणूबद्दल महत्त्वाची माहिती मिळते.
इतिहास : वर्णपट अभ्यासाची सुरुवात न्यूटन यांनी १६६४ मध्ये केली. एका लहान छिद्रातून येणारा सूर्यप्रकाश लोलकातून गेल्यानंतर पांढऱ्या पडद्यावर पडला असता सप्तरंगांचा पट्टा मिळतो. याला त्यांनी वर्णपट असे नाव दिले. हे सप्तरंग परत एकत्रित केल्यास पांढरा प्रकाश मिळतो, हे त्यांनी दाखवून दिले. यावरून सूर्यप्रकाश सात रंगांच्या प्रकाशाच्या मिश्रणाने बनलेला आहे हे सिद्ध झाले. हे सप्तरंग म्हणजे तांबडा, नारिंगी, पिवळा, हिरवा, निळा, पारवा, जांभळा हे होत. १८०० साली विल्यम हर्शेल यांना तापमापकाच्या साहाय्याने हा वर्णपट तपासून पाहता असे आढळले की, सर्वात अधिक तापमान वर्णपटातील तांबड्या रंगाच्या पलीकडील अदृश्य भागात आढळते. हा वर्णपटाचा भाग अवरक्त म्हणून ओळखण्यात येऊ लागला [⟶ अवरक्त प्रारण]. १८०२ मध्ये टॉमस यंग यांनी प्रकाशाच्या तरंग सिद्धांताच्या आधारे वर्णपटातील रंग आणि तरंगलांबी ह्यांचा परस्परसंबंध स्पष्ट केला. प्रकाश येण्यासाठी बारीक सूचिछिद्र या वर्तुळाकार रंध्र वापरण्याऐवजी अती निरुंद फट वापरून वर्णरेषा मिळविण्याचे महत्त्व ⇨विल्यम हाइड बुलस्टन यांनी १८०२ मध्ये व ⇨योझेफ फोन फ्राउनहोफर यांनी १८१४ मध्ये स्वतंत्रपणे दाखवून दिले. प्रत्येक वर्णरेषा ही फटीची प्रतिमा असून ती निराळा रंग वा तरंगलांबी निदर्शित करते. फ्राऊनहोफर यांनी अती निरुंद फटीबरोबरच वर्णपट बघण्यासाठी पडद्याऐवजी दूरदर्शक (दुर्बिण) वापरून सूर्याच्या वर्णपटाचा अभ्यास केला. या वर्णपटात विशिष्ट स्थानी काही काळ्या रेषा आढळल्या, त्या शोषण रेषा होत. या वातावरणाच्या घटकांच्या शोषण रेषा असतात. त्यांना फ्राउनहोफर रेषा अशी संज्ञा प्राप्त झाली. या रेषांना मानक (प्रमाणभूत) रेषा मानून निरनिराळ्या जातींच्या प्रकाशीय काचांमुळे पडणाऱ्या प्रकाशाच्या अपस्करणाची तुलना करण्यासाठी त्यांचा उपयोग करण्यात आला. वर्णपट मिळविण्यासाठी लोलकाऐवजी वापरण्यात येणारे ⇨विवर्तन जालक फ्राउनहोफर यांनीच प्रथम बनविले व त्या साध्या जालकाच्या साहाय्याने फ्रउनहोफर रेषांची तरंगलांबी अचूक काढली. विशिष्ट पदार्थांच्या ज्योतीच्या साहाय्याने मिळणाऱ्या काही ठळक उत्सर्जित रेषांच्या तरंगलांब्या व विशिष्ट काळ्या रेषांच्या तरंगलांब्या तंतोतंत जुळल्या आणि त्या दोहोंचा संबंध ⇨गुस्टाफ रोबेर्ट किरखोक यांनी १८५९ मध्ये विशद केला. प्रकाशाचे शोषण आणि उत्सर्जन यांच्या विशिष्ट संबंधांचा सिद्धांत त्यांनी प्रथम मांडला. किरखोक आणि ⇨रोबेर्ट व्हिल्हेल्म बन्सन यांनी अतिशुद्ध मूलद्रव्यांच्या ज्योतीच्या वा विद्युत् ठिणगीच्या साहाय्याने मिळणारे वर्णपट व फ्राउनहोफर रेषा या दोन्हींचे मूल्यमापन करून सूर्याच्या वातावरणाचे रासायनिक विश्लेषण केले. वर्णरासायनिक विश्लेषण व ⇨खगोल भौतिकी चा हा पाया होय. याच्या अभ्यासातून त्यांनी सिझियम व रुबिडियम या दोन मूलद्रव्यांचा शोध लावला. यानंतर वर्णपट संशोधनास पुष्कळच प्राधान्य मिळाले व तरंगलांबीच्या अचूक मानकांची आवश्यकता भासू लागली. असे पहिले मानक १८६८ मध्ये ⇨अंडर्स यूनास अँगस्ट्रॉम यांनी प्रचारात आणले व त्यांनी जवळजवळ १,००० फ्राउनहोफर रेषांची तरंगलांबी या एककात मोजली. हे एकक १० –१० मी. (१०–८सेंमी.) इतक्या लांबीचे असून त्याला अँगस्ट्रॉम (Å) असे नाव मिळाले.
|
कोष्टक क्र. १. विद्युत् चुंबकीय तरंगांचे वर्गीकरण |
|||||
|
वर्णपट विभाग |
अंदाजी तरंगलांबी |
कंप्रता (हर्ट्झ) |
नमुनेदार उद्गम |
अभिज्ञातक |
अभ्यासण्यात येणारी द्रव्यातील ऊर्जा संक्रमणे |
|
गॅमा |
१-१०० पामी. |
३×१०२२– ३×१०१६ |
किरणोत्सर्गी अणुकेंद्र |
गायगर गणित्र |
अणुकेंद्रीय संक्रमणे व विघटने |
|
क्ष-किरण |
६ पामी.-११०नॅमी |
५×१०१२-१×१०१३ |
क्ष-किरण नलिका (धातूंवरील इलेक्ट्रॉन भडिमार) |
गायगर गणित्र, चमक गणित्र |
आतील इलेक्ट्नाच्या स्थलांतराने होणारे आयनीकरण |
|
निर्वात जंबुपार |
१०-२०० नॅमी |
३×१०१६-१·५×१०१५ |
उच्च विद्युत् दाब विसर्जन, उच्च निर्वातातील ठिणगी |
प्रकाशगुणक नलिका |
बाहेरील इलेक्ट्रॉनाच्या स्थलांतराने होणारे आयनीकरण |
|
जंबुपार |
२००-४०० नॅमी |
१·५×१०१५-८×१०१४ |
हायड्रोजन-विसर्जन दिवा |
प्रकाशगुणक नलिका |
संयुजी इलेक्ट्रॉनांचे उद्दीपन |
|
दृश्य |
४००-८०० नॅमी |
८×१०१४-३·८×१०१४ |
टंगस्टन दिवा |
प्रकाशविद्युत् नलिका |
संयुजी इलेक्ट्रॉनांचे उद्दीपन |
|
समीप अवरक्त |
०·८-२·५mm |
३·८×१०१४-१·२×१०१४ |
टंगस्टन दिवा |
प्रकाशविद्युत् घट |
संयुजी इलेक्ट्रॉनांचे उद्दीपन रेणवीय कंपनांचे वर्चस्व. |
|
अवरक्त |
२·५-५०mm |
१·२×१०१४– ६×१०१३ |
नेर्न्स्ट दिवा, ग्लॉबर दिवा |
तपयुग्म, बोलोमीटर |
रेणवीय कंपने, ताणणे, वाकविणे व डोलणे |
|
दूर अवरक्त |
५०-१००mm |
६×१०१३-३×१०११ |
उच्च् दाबाचा पारा दिवा |
तपयुग्म, बोलोमीटर |
रेणवीय परिभ्रमणे |
|
सूक्ष्मतरंग |
०·१-३०सेंमी. |
३×१०११-१×१०९ |
क्लायस्ट्रॉन, मॅग्नेट्रॉन |
सिलिकॉन-टंगस्टन स्फटिक, बोलोमीटर |
रेणवीय परिभ्रमणे, इलेक्ट्रॉन परिवलन अनुस्पंदन |
|
रेडिओ-कंप्रता |
१०-१-१०२ |
३×१०९-३×१०५ |
रेडिओ प्रेषक |
रेडिओ ग्राही |
रेणवीय परिभ्रमणे, अणुकेंद्रीय चुंबकीय अनुस्पंदन |
ए. ए. मायकेलसन यांनी १८९२ मध्ये आपल्या व्यतिकरणमापकाच्या [⟶ व्यतिकरणमापन] साहाय्याने अँगस्ट्रॉममध्ये कॅडमियम या मूलद्रव्याच्या उत्सर्जित रेषांची तरंगलांबी मोजली. त्याचप्रमाणे शार्ल फ्रावी, आल्फ्रेद पेरॉ व आर्. बेन्वा यांनी फ्रावी-पेरॉ व्यतिकरणमापकाचा उपयोग करून १९०७ मध्ये कॅडमियम बाष्पाच्या प्रारणातील लाल रेषेची तरंगलांबी मानक मीटरमध्ये मोजली. त्याचे मूल्य (६,४३८·४६९६ Å) तरंगलांबीचे प्राथमिक मानक म्हणून सर्व देशांत १९६० सालापर्यंत प्रचारात होते. या व इतर मानकांमुळे कोणत्याही विद्युत् चुंबकीय प्रारणाच्या तरंगलांब्या अभूतपूर्व अचूकतेने मोजणे शक्य होऊ लागले. २,१०० ते १०,२०० Å दरम्यान असणाऱ्या वर्णरेषा वर्णपटाच्या दूर अवरक्त भागापासून ते अती जंबुपार भागापर्यंत पसरलेल्या आहेत. या सर्व अभ्यासाचा उपयोग रासायनिक अभिज्ञानामध्ये विवक्षित रसायनाचे अस्तित्व जाणण्यामध्ये झाला आहे व आजही होत आहे. वर्णरेषा रचनांचे विश्लेषण करणे, ⇨पुंज सिद्धांतानुसार वर्णरेषांचे विवरण करणे आणि अणू व अणुकेंद्र यांच्या संरचनेसंबंधीचे सिद्धांत मांडणे या अभ्यासास वर्णरेषा संशोधन साहाय्यभूत झाले आहे.
दुसऱ्या महायुद्धानंतर मुख्यत्वे इलेक्ट्रॉनिकी व उत्पादन तंत्रविद्या यांतील प्रगतीमुळे वर्णपटविज्ञानीय उपकरणसामग्रीचा विस्मयकारक विकास झालेला आहे. निरीक्षणाचे सरळ वाचन, स्वयंचलित नोंदणी, उत्तम स्थिरता असलेली सुधारित संवेदनक्षमता,वापरण्यातील सुलभता व विस्तारित क्षमता ही अनेक व्यापारी उपकरणांची विशेष लक्षणे असून त्यांतील अनेक उपकरणे ⇨सूक्ष्मप्रक्रियक-नियंत्रित आहेत. कित्येक नवीन उपकरणांना खास प्रदत्त प्रणाली जोडलेल्या आहेत. या उपकरण प्रगतीमुळे वर्णपटविज्ञानीय तंत्रांचा विस्तृत प्रमाणात व्यवहारात उपयोग होणे सुलभ झाले असून त्यामुळे अनुप्रयुक्त व सैद्धांतिक वर्णपटविज्ञानाची प्रगती होण्यास फार मोठी मदत झालेली आहे.
तरंगलांबी व वर्णपटविज्ञानाचे वर्गीकरण : विद्युत् चुंबकीय प्रारणाच्या समग्र वर्णपटाच्या मानाने दृश्य प्रकाशाच्या वर्णपटाचा विस्तार पुष्कळच लहान आहे, म्हणूनच प्रारणाची निर्मिती अगर त्याचा शोध यांच्या पद्धतीनुसार तरंगलांबी समुहाचे वर्णपटविज्ञानामध्ये विभाग पाडलेले आहेत. ते विभाग पुष्कळदा एक दुसऱ्यात संमिश्र झालेले दिसतात. हे विभाग येणेप्रमाणे : (अ) क्ष-किरण वर्णपटविज्ञान, (आ) जंबुपार वर्णपटविज्ञान, (इ) दृश्य वर्णपटविज्ञान, (ई) अवरक्त वर्णपटविज्ञान, (उ) सूक्ष्मतरंग वर्णपटविज्ञान, (ऊ) रेडिओकंप्रता वर्णपटविज्ञान. या प्रत्येकाचे संक्षिप्त वर्णन खालीलप्रमाणे करता येईल.
(अ) क्ष-किरण वर्णपटविज्ञान : यात तरंगलांबीची मर्यादा ०·००६ ते १,००० Å एवढी आहे. याच्या अभ्यासासाठी छायाचित्रण अनुस्फुरण (वस्तूवर एखाद्या स्वरूपातील ऊर्जा प्रवाहित झाल्याने तीतून विद्युत् चुंबकीय प्रारण बाहेर पडण्याची व ऊर्जा प्रवाह बंद झाल्यावर थांबणारी क्रिया) व आयनीभवन (विद्युत् भारित अणू, रेणू वा अणुगट यांत रूपांतर होणे)या आविष्कारांचा उपयोग केला जातो. [⟶ क्ष-किरण].
(आ) जंबुपार वर्णपटविज्ञान : या विज्ञानाची व्याप्ती सु. ६०० ते ३,८०० Å एवढी असून यात छायाचित्रण,⇨ प्रकाशविद्युत् व प्रारणमापक या साधनांचा उपयोग केला जातो. [⟶ जंबुपार प्रारण].
(इ) दृश्य वर्णपटविज्ञान : यात नावाप्रमाणेच डोळ्यास दृश्य होणाऱ्या) प्रकाशाचा अभ्यास करण्यात येतो. या प्रकाशाची तरंगलांबी सु. ३,८०० Å (जंबू) ते ७,८०० Å (रक्त) असते. याचा अभ्यास छायाचित्रण, प्रकाशविद्युत् नलिका व प्रारणमापक यांच्या साहाय्याने होतो.
(ई) अवरक्त वर्णपटविज्ञान : यातील विद्युत् चुंबकीय तरंगलांबीची मर्यादा ७,८०० Å ते १०७ Å किंवा एक मिमी. एवढी आहे. छायाचित्रणाच्या पद्धतीने होऊ शकणारा अभ्यास फक्त १०,००० Å च्या जवळपास संपतो. १०,००० Å ते ५०,००० Å दरम्यान लेड सल्फाइड अगर लेड टेल्युराइड प्रकाशविद्युत् संवाही अभिज्ञातक वापरला जातो. त्याच्या पुढच्या तरंगलांब्यांच्या अभ्यासासाठी बोलोमीटर अगर तपचिती वापरतात [⟶ अवरक्त प्रारण उष्णता प्रारण].
(उ) सूक्ष्मतरंग वर्णपटविज्ञान: याची व्याप्ती सु. १ मिमी.पासून ते ३० सेंमी. पर्यंत असते. याच्या अभ्यासासाठी अवरक्त वर्णपटविज्ञानात वापरल्या जाणाऱ्या पद्धती अगर प्रचारात असणारी रेडिओ मंडले उपयोगी पडू शकत नाहीत आणि म्हणूनच ⇨ रडारचा शोध लागेपर्यंत या सूक्ष्मतरंगांसंबंधी फारशी माहिती उपलब्ध झाली नव्हती परंतु आता वेग विरूपित इलेक्ट्रॉन शलाका चलित विवर अनुस्पंदकांचा [⟶ विवर अनुस्पंदक] वापर करून सूक्ष्मतरंग निर्माण केले जातात. ⇨तरंग मार्गदर्शकाने त्यांचे प्रेषण होते व स्फटिक एकदिशकारकाने त्यांचा अभ्यास केला जातो. [⟶ सूक्ष्मतरंग ].
(ऊ) रेडिओ-कंप्रता वर्णपटविज्ञान: यातील तरंगलांब्यांचा पल्ला सु. १० सेंमी. पासून ते कित्येक किमी. पर्यंत आहे. याची उत्पत्ती निर्वात नलिकायुक्त आंदोलकासारख्या [⟶ आंदोलक, इलेक्ट्रॉनीय] पारंपरिक रेडिओ मंडलाने केली जाते. अनुस्पंदक ग्राही मंडलाच्या [⟶ रेडिओ ग्राही] मदतीने याचा अभ्यास केला जातो. रेणवीय किंवा आणवीय शलाकाही या कामासाठी वापरल्या जाऊ शकतात.
वर्णपटीय उपकरणे व साहाय्यक साधने
प्रस्तुत नोंदीत वर्णपटाच्या अवरक्त, दृश्य वजंबुपार या भागांकरिता लागणाऱ्या उपकरणांचे व साहाय्यक साधनांचे फक्त वर्णन केलेले आहे. सूक्ष्मतरंग, रेडिओ तरंग व क्ष-किरण या भागासंबंधीचे वर्णन ‘सूक्ष्मतरंग’ व ‘क्ष-किरण’ या नोंदीत पहावे.
प्रकाश उद्गम : प्रकाश वर्णपट मुख्यत्वे दोन प्रकारचे असतात : (१) उत्सर्जन वर्णपट व (२) शोषण वर्णपट.
(१) उत्सर्जन वर्णपट : हे वर्णपट मिळविण्याकरिता खालील प्रकाश उद्गम उपकरणे वापरतात.
(अ)ज्योती : बन्सन ज्वालकाची [⟶ ज्वालक] ज्योत निळसर असताना तिचे तापमान सु. १८००° से. असते. लवणाच्या विद्रावात भिजविलेली ॲस्बेस्टसाची वात ज्योतीच्या निळसर भागात धरतात(आ.१), त्यामुळे त्या लवणातील मूलद्रव्यांचे अणू उत्तेजित होऊन ते काही विशिष्ट वर्णरेषांचे उत्सर्जन करतात. हा प्रकाश उद्गम तितकासा प्रखर नसतो. त्यामुळे वर्णरेषांची संख्या कमी असते कारण ती तापमानावर अवलंबून असते. वर्णरेषांचा रेखीवपणाही तापमानावर अवलंबून असतो. ऑक्सि-ॲसिटिलीन ज्योत वापरल्यास तापमान सु. २,५००° से. मिळू शकते व त्या अणूंच्या वर्णरेषा विस्तारित प्रमाणात मिळतात. एच्. लुंदेगार्द यांच्या प्रयोगात विद्रावाचा फवारा या ज्योतीवर सोडतात. या पद्धतीने जवळजवळ ३४
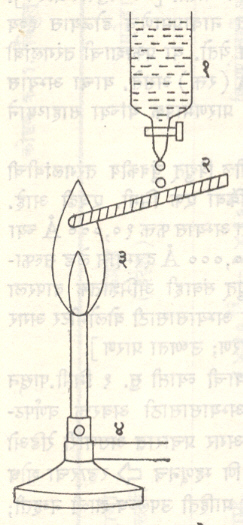
मूलद्रव्यांचे वर्णपट वर्णपटमापकाच्या साहाय्याने चांगले अभ्यासिता येतात. या उद्गमापासून मिळणाऱ्या निरनिराळ्या वर्णपटांचे स्वरूप आणवीय संरचनेशी संबंधित असल्यामुळे या वर्णपटाला आणवीय वर्णपट म्हणतात.
(आ)विद्युत् प्रज्योत: या उद्गमाचा प्रकाश प्रखर असतो व तापमान ३,०००° ते ८,०००° से. असते. या वर्णपटांच्या रेषा अरुंद व रेखीव नसतात. ज्या धातूचा वर्णपट पाहिजे असेल तिच्या कांड्या १००-२०० व्होल्ट आणि ३-१० अँपिअरच्या एकदिश विद्युत् पुरवठ्याला जोडतात. एकसरीत एक विद्युत् रोधकही ठेवतात. दोन्ही कांड्या एकमेकींना स्पर्श करून थोड्या दूर केल्यास त्यांच्या दरम्यान एक प्रखर ज्योत (प्रज्योत) निर्माण होते व तिच्यातून विद्युत् प्रवाह चालू राहतो. ज्या मूलद्रव्याच्या कांड्या करणे कठीण असते त्यांच्याकरिता कार्बनाच्या कांड्यांची प्रज्योत पेटविता येते. कार्बनाच्या कांड्यांवर आवश्यक ती मूलद्रव्ये ठेवल्यास अशा मूलद्रव्यांचे वर्णपट मिळविता येतात. (आ. २). याकरिता कार्बनाच्या कांड्या घेऊन त्यांतील धनाग्र कांडीला खळगा करून त्या खळग्यात मूलद्रव्याचे अगर त्याच्या लवणाचे तुकडे अगर विद्राव भरतात. ही कांडी खालील बाजूस असते व वरची कांडी या कांडीला टेकवून नंतर थोडी दूर करून प्रज्योत पेटवितात. अशा प्रकाश उद्गमात त्या मूलद्रव्याच्या वर्णरेषा मिळतात.
अशा प्रज्योतीत विशिष्ट अणूपासून मिळू शकतील त्या जवळजवळ सर्व रेषा उत्सर्जित होतात. यातील मुख्य दोष म्हणजे प्रज्योत बिंदू एका ठिकाणी स्थिर न राहता कांडीच्या टोकावर एकसारखा बदलत असतो. त्यामुळे प्रकाशकिरण वर्णपटमापकाच्या फटीवर केंद्रित करणे कठीण जाते. अशीच प्रज्योत १,००० व्होल्ट प्रत्यावर्ती (मूल्य व दिशा दर सेकंदास वारंवार उलटसुलट बदलणाऱ्या) विद्युत् प्रवाहावर चालविल्यास प्रज्योत बिंदूची अस्थिरता पुष्कळशी कमी होते.
(इ) विद्युत् ठिणगी : १०,००० ते १५,००० व्होल्ट विद्युत् दाब मिळेल अशा आरोहित्राच्या (विद्युत् दाब वाढविणाऱ्या साधनाच्या) द्वितीयक गुंडाळीला विद्युत् प्रज्योतीच्या कांड्या जोडतात व कांड्यांच्या अनेकसरीत एक विद्युत् धारित्र विद्युत् भार साठवण्याकरिता ठेवतात. अशा रचनेता फायदा असा की, कांड्या भराभरा जळत नाहीत व त्यांत अणूंचे अधिक उच्च दर्जाचे उत्तेजन शक्य होते. याचा परिणाम अणूपासून विस्तारित वर्णपट मिळू शकतो, तसेच त्या मूलद्रव्याच्या अणूंचे एकेरी, दुहेरी वगैरे आयनीकरण होते व त्यांचेही वर्णपट अभ्यासिता येतात. अर्थात यात उच्च दर्जाचे उत्तेजन शक्य होते. याचा परिणाम अणूपासून विस्तारित वर्णपट मिळू शकतो, तसेच त्या मूलद्रव्याच्या अणूंचे एकेरी, दुहेरी वगैरे आयनीकरण होते व त्यांचेही वर्णपट अभ्यासिता येतात. अर्थात यात उच्च विद्युत् दाबामुळे थोडा धोका संभवतो.
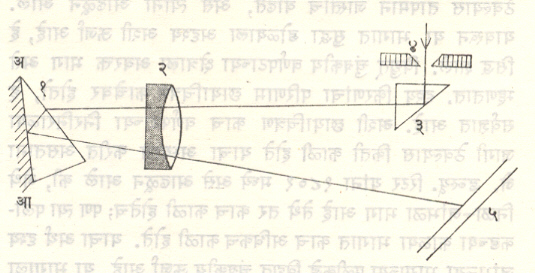
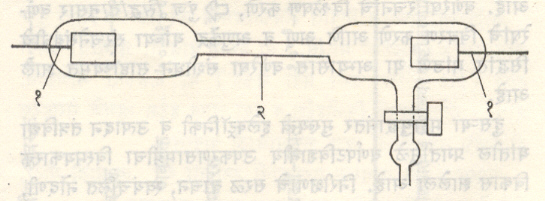(ई) गाइसलर नळी : या नळीचा शोध हाइन्रिक गाइसलर या जर्मन भौतिकीविज्ञांनी लावला. वायुरूप द्रव्ये आ. ३ मध्ये दाखविलेल्या आकाराच्या नळीत भरतात. वायूचा दाब ०·१ ते १० मिमी. इतका ठेवून नळी बंद करतात. नळीच्या मध्यभागी असलेल्या केशनलिकेची (बारीक व्यासाच्या नळीची) लांबी जवळजवळ १० सेंमी. असते. नळीच्या रुंद भागात ॲल्युमिनियमाची अगर प्लॅटिनमाची विद्युत् अग्रे बसवितात. ही विद्युत् अग्रे ⇨ प्रवर्तन वेटोळ्याला किंवा कमी प्रदान असलेल्या आरोहित्राच्या द्वितीयक गुंडाळीला जोडली, की विद्युत् विसर्जन होते. १,५००-१०,००० व्होल्ट व १०-५० मिलिअँपिअर प्रत्यावर्ती विद्युत् प्रवाहावर चालणारी रोहित्रे गाइसलर नळीसाठी वापरतात. केशनलिकेतून विशिष्ट तरंगलांबीचा प्रकाश बाहेर पडतो व तो वायूच्या अणूंपासून किंवा रेणूंपासून उत्सर्जित होत असतो. प्रकाशाची तीव्रता तसेच तापमान फारसे नसते. यापासून मिळणाऱ्या वर्णरेषा अधिक रेखीव व अरुंद असतात. नळी द्रवरूप हवेच्या तापमानाला (–१८०° से.) ठेवल्यास हा रेखीवपणा खूपच वाढतो.
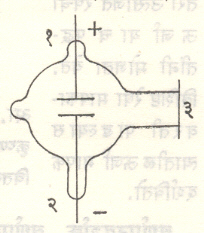
नळीच्या एका बाजूस सपाट काच अगर क्वार्ट्झ पट्टी बसवून त्या बाजूचा विद्युत् अग्र ऋण व भोक असलेला ठेवून नळी अग्रस्थितीत वापरल्यास वर्णपटदर्शकाच्या फटीवर पडणाऱ्या प्रकाशाची तीव्रता खूपच वाढविता येते (आ. ४). ऋणाग्र पोकळ नळीचा केल्यास पुष्कळसे विसर्जन या पोकळीत होऊन वर्णपटात वायूच्या अणूंच्या वर्णरेषा मिळतातच पण त्याखेरीज विद्युत् अग्र ज्या धातूचे बनलेले असेल त्याच्या अणूंच्या वर्णरेषाही मिळतात.
अग्र धातूवर नळीतील वायूची रासायनिक विक्रिया होत असल्यास अग्र गाइसलर नळीत न बसविता केशनलिकेच्या जवळच रुंद भागावर बाहेरून तांब्याच्या पट्ट्या चढवितात अगर तांब्याची तार गुंडाळतात. त्या पट्ट्या उच्च कंप्रता आंदोलकाच्या प्रदानाला जोडतात म्हणजे विसर्जन सुरू होते. या तऱ्हेने अणूंचे वा रेणूंचे वर्णपट मिळतात. उदा., एखादी रासायनिक विक्रिया सावकाश होत असल्यास ठराविक वेळापत्रकांनुसार वर्णपट तपासल्यास त्या विक्रियेच्या प्रगतीसंबंधीची माहितीही मिळविता येते.
वायूखेरीज इतर पदार्थांचे वर्णपट मिळविण्यासाठी पाहिजे असलेल्या मूलद्रव्याचे एखादे बाष्पनशील संयुग काही मिग्रॅ. इतके वायूत मिसळतात. उदा., युरेनियमाचा वर्णपट मिळविण्यासाठी युरेनियम क्लोराइड वापरतात.
(उ) अणु–झोत : निर्वात भट्टीत एक फट असलेल्या मुशीत द्रवरूप झालेले मूलद्रव्य उकळले म्हणजे त्या फटीतून त्या मूलद्रव्याच्या अणूंचा झोत बाहेर येतो. त्यावर गतिमान इलेक्ट्रॉनांचा झोत टाकल्यास त्याच्यापासून अणूंच्या वर्णरेषा मिळतात. या वर्णरेषांची तीव्रता कमी असली, तरी त्या अतिशय रेखीव असतात. वर्णपटाच्या अभ्यासात रेखीव वर्णरेषा मिळविणे फार महत्त्वाचे असते.
(ऊ) लेसर : यात एका विशिष्ट परिस्थितीत एकच वर्णरेषा उत्सर्जित करण्यास अणूंना भाग पाडून त्यांचे जरूर तेवढेच उत्तेजन होईल अशी व्यवस्था करतात. त्यापासून मिळणारे किरण बाजूला समांतर आरसे लावून पुन्हा पुन्हा प्रकाशाचे विवर्धन केल्यास एक सुसंगत प्रकाश स्पंद तयार होऊन बाहेर पडतो. हा प्रकाश झोत अतिशय प्रखर, एकवर्णी व सुसंगत असतो.⇨रामन परिणामाचा सखोल अभ्यास करण्यासाठी हा प्रकाश उद्गम अत्यंत उपयोगी ठरला आहे. [⟶ लेसर].
(२) शोषण वर्णपट: असा वर्णपट अभ्यासण्यास सर्ववर्णी प्रकाश लागतो. दृश्य भागाकरिता ५०० ते १,००० वॉटचा टंगस्टन दिवा वापरतात. असाच दिवा किंवा ग्लॉबर दिवा अवरक्त भागाकरिता वापरतात. अती जंबुपार भागाकरिता हायड्रोजनयुक्त गाइसलर नळी वापरतात. तीत हायड्रोजनाचा दाब १ ते ५ मिमी. असतो व ती नळी ८०० ते १,००० व्होल्ट प्रत्यावर्ती विद्युत् प्रवाहावर चालवितात. अशा प्रकाश उद्गमाला ३ ते ४ अँपिअर विद्युत् प्रवाह लागतो.
प्रकाश उद्गमापासून निघणारे किरण एक किंवा अधिक योग्य तऱ्हेची भिंगे वापरून वर्णपटदर्शकाच्या फटीवर अशा रीतीने केंद्रित करतात की, संबंध फट सम प्रमाणात प्रकाशित होईल. उद्गम व दर्शक यांमध्ये एका नळीत वायुरूप विद्राव अगर घनरूप लवण ठेवल्यास दर्शक सवर्णीय प्रकाशात काही काळा भाग दाखवितो. हा शोषण वर्णपट होय.
उत्सर्जन व शोषण वर्णपटांचे उपप्रकार : या वर्णपटांचे मुख्यत्वे तीन उपप्रकार असतात.
(१) रेषा वर्णपट: काळोख्या पार्श्वभूमीवर निरनिराळ्या रंगांच्या रेषा मापकाच्या दर्शक भागातून दिसतात. या रेषा वर्णपटदर्शकातून मिळणाऱ्या फटीच्या प्रतिमा होत. असे वर्णपट मुख्यत्वे अणूंमुळे मिळतात.
(२) पट्ट वर्णपट: विशिष्ट संगती दर्शविणारे तुटकतुटक रंगीत लहान लहान पट्ट वर्णपटदर्शकात दिसतात. या पट्टांची एक कड रेखीव असून दुसऱ्या कडेला पट्टाचे विकीर्णन (रेखीवपणा कमी होणे) होत जाते. विकीर्णनाची दिशा काही वर्णपटांत निळ्या बाजूला, तर काहींत तांबड्या बाजूला असते. मोठ्या विभेदनक्षमतेच्या (अगदी जवळजवळच्या वर्णरेषा अलग करू शकणाऱ्या) वर्णपटदर्शकातून हे पट्ट पाहिल्यास असे दिसते की, कोणताही पट्ट अखंड नसून त्यात अनेक रेषा अगदी जवळजवळ असल्याने ते पट्टांसारखे भासतात. असे वर्णपट रेणूंमुळे मिळतात.
(३) अखंड वर्णपट: यात अवरक्त, दृश्य व जंबुपार प्रकाशाचा एक अखंड पट्टा मिळतो. असा वर्णपट मिळण्याची अनेक कारणे आहेत.
वर्णपटांचे स्थूलमानाने उत्सर्जन वर्णपट व शोषण वर्णपट असे दोन भाग करता येतात. ज्या मूलद्रव्याचा उत्सर्जन वर्णपट हवा असेल त्याचा प्रकाश उद्गम तयार करून त्याने वर्णपटदर्शकाची फट प्रकाशमान करतात. यात दोन गोष्टींकडे विशेष लक्ष द्यावे लागते. एक म्हणजे तापमान वाढल्यास वर्णरेषांचा रेखीवपणा खूपसा कमी होतो व दुसरे म्हणजे रेणूंचा उत्सर्जन वर्णपट असल्यास तापमानामुळे रेणूंचे वियोजन होण्याची (तुकडे होण्याची) शक्यता असते. याकरिता प्रकाश उद्गमाची योग्य निवड व उद्गमाचे योग्य नियंत्रण फार आवश्यक असते.
शोषण वर्णपटात ज्या माध्यमाचा शोषण वर्णपट मिळवावयाचा असेल त्यामधून सर्ववर्णी प्रकाश पाठविल्यास शोषण झाल्यानंतर जो प्रकाश उरतो तो वर्णपटदर्शकाच्या फटीवर टाकतात. शोषणामुळे अखंड वर्णपटात काळ्या रेषा अगर पट्टे दिसतात. हे अनुक्रमे अणूंमुळे वा रेणूंमुळे मिळतात. म्हणून त्यांच्या अभ्यासाने अणू व रेणू यांच्या संरचनेसंबंधीची माहिती मिळविता येते.
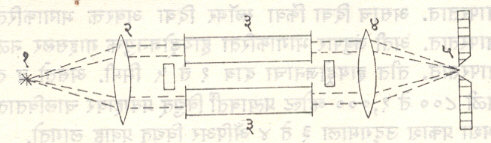
प्रयोगाची सर्वसाधारण मांडणी आ. ५ मध्ये दाखविल्याप्रमाणे असते. माध्यम वायुरूप किंवा द्रवरूप असेल, तर ते काचेच्या सपाट बाजू असलेल्या नळीत ठेवतात. शोषण वर्णपटाचा अभ्यास अधिक सूक्ष्म रीतीने करण्याकरिता सारख्याच जातीच्या दोन नळ्या घेतात. एक नळी निर्वात असते व दुसरी माध्यमाने भरलेली असते. एकाच उद्गमापासून दोन्ही नळ्यांमधून सारखाच प्रकाश गेल्यामुळे दोन वर्णपट शेजारी शेजारी मिळतील अशी व्यवस्था केल्यास शोषण वर्णपटाचे मापन करता येते. शोषणाचे मापन निर्वात नळीतून गेलेल्या प्रकाशाची प्रखरता विशिष्ट प्रमाणात कमी करून शोषणमापन करता येते. द्रवरूप माध्यमाकरिता डब्ल्यू. बेली यांची नळी वापरून माध्यमाची लांबी बदलता येते व शोषणमापन करता येते. आधुनिक उपकरणांत या गोष्टी आपोआप होतील अशी व्यवस्था असते व त्यांची आलेखस्वरूपात नोंदही मिळते. वर्णपटाच्या निरनिराळ्या भागांतील शोषण मिळण्यास निरनिराळे प्रकाश उद्गम वापरावे लागतात.
अखंड वर्णपटातील ऊर्जेचे वितरण व मापन : कोणत्याही प्रकारच्या विद्युत् चुंबकीय ऊर्जेचे शोषण झाल्यास तिचे रूपांतर उष्णतेत होते व शोषण करणाऱ्याऊ वस्तूचे तापमान वाढते. तापमानातील वाढ मोजता आल्यास उष्णताही मोजता येते व त्यावरून ऊर्जेचे मापन करता येते.
सौर वर्णपटातील ऊर्जेचे वाटप मोजण्याकरिता एस्. पी. लँग्ली यांनी बोलोमीटर उपकरण बनविले. यात मापनासाठी वापरण्यात येणाऱ्या ⇨व्हीट्स्टन सेतूतील एक विद्युत् रोधक अगदी अरुंद पट्टीचा केलेला असतो. पट्टी तांब्याची अगर प्लॅटिनमाची असते व तिच्यावर काजळीचा लेप देतात. काळ्या पट्टीवर ऊर्जेचे संपूर्ण शोषण होऊन पट्टीचे तापमान बदलते व तिचा विद्युत् रोधही वाढतो. परिणामी संतुलित विद्युत् मंडलातील विद्युत् दर्शक विचलित होतो. या उपकरणाचे इयत्तीकरण (योग्य मानकावरून दर्शकावरील अंशांची केलेली तपासणी) केले असल्यास त्यावरून ऊर्जेचे सरळ मापन करता येते. काळ्या केलेल्या पट्टीवर वर्णपटातील निरनिराळे भाग पाडल्यास त्या त्या भागातील ऊर्जेचे वाटप कसे झाले आहे, हे समजते. असा मापक मुख्यत्वे अवरक्त वर्णपट भागाकरिता वापरतात. [⟶ उष्णता प्रारण].
हल्ली ऊर्जामापनाकरिता प्रकाशविद्युत् घट [⟶ प्रकाश विद्युत्] मुख्यत्वे वापरला जातो. प्रकाशविद्युत् घट वर्णपटाच्या काही भागांकरिता कार्यक्षम असल्याने योग्य प्रकाशविद्युत् घट
निवडणे महत्त्वाचे असते. प्रकाशविद्युत् घटामध्ये अनेक पटींनी मापन वृद्धी करता येते. हल्ली दहा लाख पटींनी जास्त कार्यक्षम असलेली प्रकाश गुणक नलिका [⟶ इलेक्ट्रॉनीय प्रयुक्ति] उपलब्ध आहे. तिच्या साहाय्याने अतिशय कमी ऊर्जासुद्धा मोजता येते.
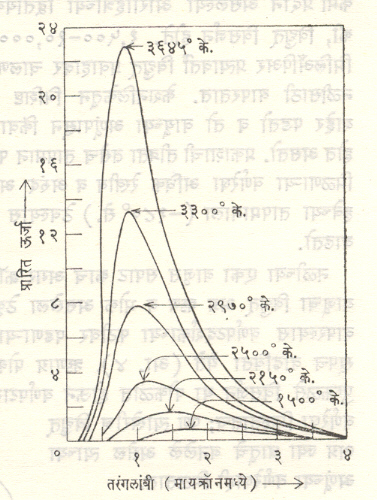
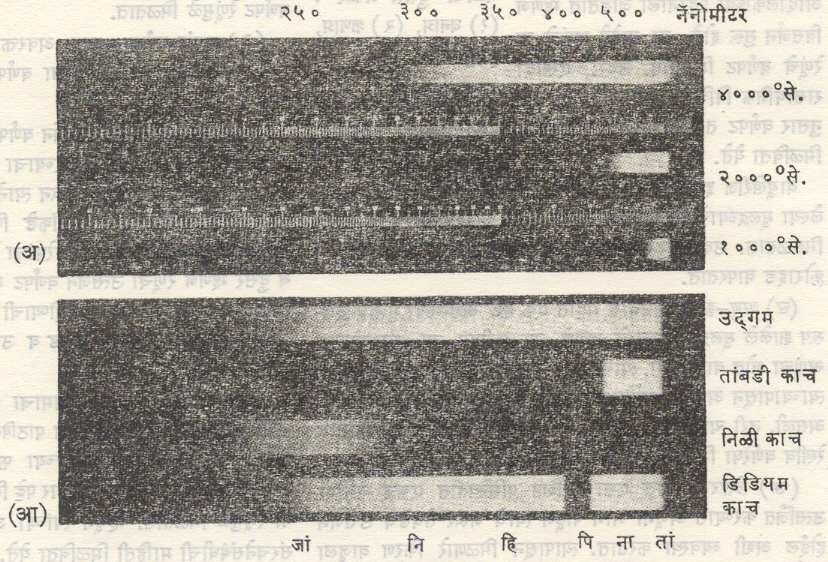
सौरवर्णपटाप्रमाणे, कोणताही ⇨कृष्ण पदार्थ तापविल्यास त्यापासून मिळणारा वर्णपट अखंड असतो व त्यातील ऊर्जेचे वितरण त्याच्या तापमानावर अवलंबून असते. याचे संशोधन बरेच विस्ताराने झाले आहे व त्यासंबंधीचा आलेख आ. ६ मध्ये दिला आहे. आ. ७ मध्ये कृष्ण पदार्थांचे वर्णपट दाखविले आहेत. [⟶ उष्णता प्रारण].
वर्णपट रेषांचा बनलेला असला, तरी उत्सर्जित रेषेची ऊर्जा याच पद्धतींनी मोजता येते. विशिष्ट रेषा मापकावरती पाडल्यास त्यातील ऊर्जा मापक दर्शवितो.
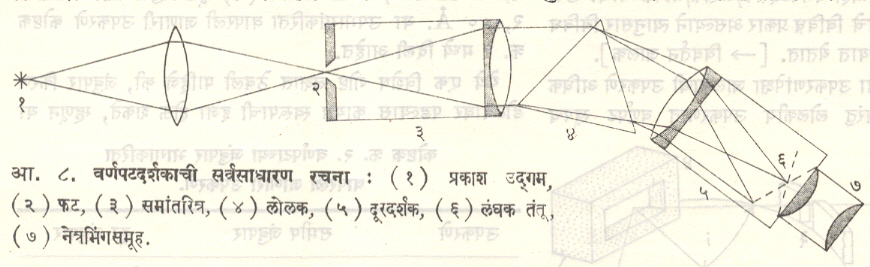
वर्णपटदर्शक, वर्णपटलेखक व वर्णपटमापक : ही तिन्ही साधने वर्णपटांच्या अभ्यासाकरिता वापरतात. साध्या डोळ्यांनी वर्णपट पहावयाचा असेल तेव्हा वर्णपटदर्शक वापरतात (आ. ८). यात दूरदर्शकाद्वारे वर्णपट बघता येतो. वर्णपटलेखकाद्वारे वर्णपटाचे छायाचित्र येऊन नंतर तो अभ्यासिता येतो. वर्णपटमापकावर कोन मोजण्याची व्यवस्था असते व त्यावरून तरंगलांबीत सरळ रूपांतर करता येते. यात कुठलाही मापक वापरता येतो.
रचना : वर्णपट अभ्यासाच्या उपकरणाचे मुख्यत्वे तीन भाग असतात : (१) समांतरित्र, (२) लोलक [⟶ प्रकाशकी] किंवा ⇨विवर्तन जालक ठेवण्याकरिता बैठक आणि (३) अभिज्ञातक (दूरदर्शक, कॅमेरा किंवा मापक).
(१) शुद्ध वर्णपट मिळवण्याकरिता समांतरित्राची जरूरी असते. त्यात एक विवर्णी भिंग व त्याच्या केंद्राशी फट ठेवलेली असते. उद्गमापासून निघालेला प्रकाश फटीवर केंद्रित करतात. समांतरित्रातून बाहेर पडणारे किरण समांतर होऊन पुढे लोलकावर पडतात. रेखीव वर्णपट मिळण्याकरिता फटीची बनावट फार महत्त्वाची असते. फटीच्या कडा धारदार असतात आणि तिची रुंदी व लांबी कमी-जास्त करता येते.
(२) अपस्करणाकरिता लोलक किंवा विवर्तन जालक वापरतात. लोलकाची बैठक फिरविण्याची व्यवस्था असते व तिचे स्थान मोजण्याकरिता बैठकीला कोनमापक लावलेला असतो. समांतर किरण लोलकावर किंवा जालकावर पडल्यावर त्यांचे अपस्करण होते.
(३) अपस्करणानंतर प्रकाशाचे विस्तारण होते व त्याचा अभ्यास करण्याकरिता वेगवेगळे अभिज्ञातक वापरता येतात. एक दूरदर्शक त्या जागी ठेवल्यास वर्णपट दृश्य स्वरूपात दिसतो व एका अक्षाभोवती दूरदर्शक फिरविल्यास निरनिराळ्या तरंगलांब्यांचे प्रकाशकिरण दूरदर्शकात शिरतात. लोलक व दूरदर्शक यांच्यातील सापेक्ष कोन मोजल्यास तरंगलांबी काढता येते. दूरदर्शकाचे दुसरे टोक असलेले नेत्रभिंग काढून त्या ठिकाणी कॅमेरा लावल्यास वर्णपटाचे संपूर्ण छायाचित्र काढता येते व ह्या उपकरणास वर्णपटमापक म्हणतात. कॅमेऱ्याऐवजी प्रकाशविद्युत् घट योग्य मंडलामध्ये लावल्यास प्रत्येक वेळी विशिष्ट तरंगलांबीची ऊर्जा मोजून सबंध वर्णपटाचा ऊर्जा आलेख काढता येतो.
प्राथमिक स्वरूपाचा वर्णपटदर्शक ४० ते ५० सेंमी. लांब असतो तर खगोलीय अभ्यासासाठी वापरण्यात येणारा वर्णपटदर्शक कित्येक मीटर लांब असतो. सखोल अभ्यासासाठी वापरण्यात येणाऱ्या लोलकीय वर्णपटलेखकाची लांबी १५०-२०० सेंमी., तर विवर्तन जालकाच्या वर्णपटलेखकाची लांबी ७ मी. पर्यंत असू शकते.
वर्णपटलेखकाची विभेदनक्षमता मुख्यत्वे दोन गोष्टींवर म्हणजे (१) लोलकाच्या पायाची रुंदी अगर जालकावरील एकूण रेषा व (२) दूरदर्शकाच्या वस्तुभिंगाचा व्यास यांवर अवलंबून असते.
निरनिराळ्या लोलकांसंबंधीची माहिती ‘प्रकाशकी’ या नोंदीत व प्रस्तुत नोंदीत खाली दिलेली असून विवर्तन जालकांसंबंधीची माहिती त्या शीर्षकाच्या स्वतंत्र नोंदीत दिलेली आहे. येथे खाली काही विशिष्ट तऱ्हेच्या वर्णपटदर्शक/मापक/लेखक यांची माहिती दिली आहे.
सरल-दृष्टी वर्णपटदर्शक : या उपकरणातून सरळ प्रकाश उद्गमाकडे पाहिले असता वर्णपट दिसू शकतो, म्हणून याला सरल-दृष्टी ही उपाधी लावलेली आहे. लोलक किंवा दूरदर्शक फिरवून वर्णपट शोधीत बसावे लागत नाही. त्यामुळे पुष्कळशा वर्णपटांचे जलद परीक्षण करताना हा फार सोयीचा पडतो.
यात समांतरित्र व दूरदर्शक एकाच सरळ नळीत बसविलेले असून त्यांच्या दरम्यान जी. बी. आमिची यांनी शोधून काढलेला सरलदृष्टी लोलक (आ.१४) बसविलेला असतो. हा लोलक म्हणजे खरोखर तीन (केव्हा केव्हा पाच) लोलकांची मालिकाच असते. तीत दोन वेगवेगळ्या प्रकारच्या काचांचे लोलक, एकाआड एक व उलटसुलट असे बसविलेले असतात. या लोलकांचे प्रणमनांक व शिरोकोन [⟶ प्रकाशकी] असे निवडलेले असतात की, त्यांच्यामधून जाताना पिवळ्या रंगाच्या प्रकाशाचे विचलन (वर किंवा खाली वळणे) न होता तो सरळ रेषेत बाहेर येतो. त्याच्या एका बाजूला नारिंगी व तांबडा आणि दुसऱ्या बाजूला हिरवा ते जांभळा या रंगांचे प्रकाश किरण वळतात व वर्णपट तयार होतो. काही उपकरणांत तरंगलांबीदर्शक मोजपट्टी वर्णपटावरच दिसावी अशी योजना केलेली असते.
स्थिरापगमन वर्णपटमापक : या उपकरणात पी. पेलिन व ए. ब्रॉका यांनी शोधलेला खास आकाराचा लोलक (आ. १३) वापरून पिवळ्या किरणांचे विचलन बरोबर ९०° व्हावे, अशी योजना केलेली असते म्हणून समांतरित्र व दूरदर्शक हे परस्परांना लंब दिशेने पक्के बसविलेले असतात. लोलकाची बैठक एका मळसूत्राच्या साहाय्याने फरवून इष्ट ती वर्णरेषा दूरदर्शकाच्या दृष्टिक्षेत्राच्या मध्यावर आणता येते. या मळसूत्राच्या डोक्याला एक जाड दंडगोल जोडून त्याच्यावर वर्णरेषांची तरंगलांबी दर्शविणारी मोजपट्टी खोदलेली असते.
या वर्णपटमापकाच्या उपयोगाने डोळ्यांनी पाहून दृश्य वर्णरेषांच्या तरंगलांब्या कोणतेही गणितकृत्य न करताच मिळतात, हा त्याचा मुख्य गुण आहे. अशा प्रकारच्या काही उपकरणांत
दूरदर्शकाच्या जागी कॅमेरा बसवून वर्णपटांची छायाचित्रे घेण्याची सोय केलेली असते. त्याचप्रमाणे समांतरित्र व लोलक यांच्या दरम्यान महत् विभेदनक्षमता असलेले उपकरण ठेवण्याची सोय केलेली असते. असे उपकरण [ उदा., फाब्री-पेरॉ ईटॅलॉन ⟶ व्यतिकरणमापन] ठेवून वर्णरेषांची सूक्ष्मरचना अभ्यासिता येते.
लोलकीय लिट्रो वर्णपटलेखक : (आ ९). यात लोलकाच्या अआ या पृष्टभागात आरसा बसविलेला असतो, म्हणून लोलक अर्धा असूनही सबंध लोलक वापरल्याचा फायदा होतो. तसेच यात समांतरित्र व कॅमेरा या दोहोंसाठी एकच विवर्णी भिंग वापरले असल्याने त्याचे आकारमान एवढ्याच क्षमतेच्या वर्णपटलेखकापेक्षा लहान असते. हा वापरण्यास सोपा असतो. त्यात एक दोष म्हणजे भिंगावरून परावर्तित झालेला अतिरिक्त प्रकाश छायाचित्रण काचेवर पडतो. भिंग व छायाचित्रण काच यांमध्ये योग्य तऱ्हेने अडथळे वापरल्यास हा त्रास पुष्कळच कमी होतो. लोलकाच्याऐवजी सपाट पारदर्शक विवर्तन जालकही वापरतात.
विवर्तन जालक वापरूनही वर्णपटदर्शक/लेखक/मापक याचा उपयोग करता येतो. जालकांचे विविध प्रकार असल्याने त्यानुसार विविध प्रकारची उपकरणे बनविण्यात येतात. [⟶विवर्तन जालक].
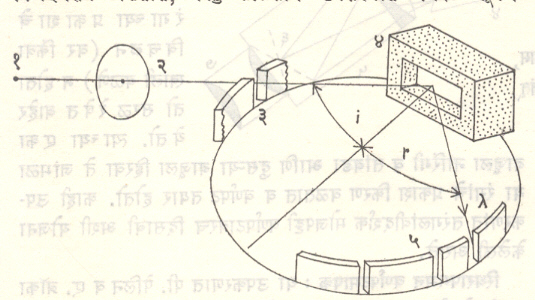
साधारणपणे लोलकाच्या उपकरणांपेक्षा जालकाची उपकरणे अधिक विभेदनक्षम असतात परंतु लोलकीय उपकरणात वर्णपट खूपच अधिक प्रकाशमान दिसतात. जालकाचे आकारमान पुष्कळ मोठे करता येते व वर्णपटलेखक अनेक मीटर लांब करता येतो. पुष्कळदा अंतर्गोल जालक वापरूनसुद्धा वर्णपटलेखक तयार करतात. (आ.१०).
वर्णपटाचे विशिष्ट भाग व त्यांकरिता वापरण्यात येणारी उपकरणे : वर्णपटदर्शकातून विद्युत् दिव्याचा अगर पेट्रोमॅक्स दिव्याचा वर्णपट पाहिल्यास जांभळा ते तांबडा पट्टा दिसतोच आणि त्याच्या अलीकडे व पलीकडे डोळ्याला काळोख दिसतो. हर्शेल यांनी तापमापक वर्णपटांत फिरविला तेव्हा तांबड्या प्रकाशात तापमान वाढलेले दिसलेच पण त्याच्या अलीकडच्या काळ्या भागात तापमापक ठेवल्यास तापमान जास्तीच वाढते, असे त्यांना आढळून आले. यावरून या भागात सुद्धा डोळ्याला अदृश्य अशी ऊर्जा आहे, हे सिद्ध झाले. विद्युत् चुंबकीय वर्णपटाच्या क्षेत्राला अवरक्त भाग असे म्हणतात. दृश्य किरणांचा परिणाम छायाचित्रण काचेवर होतो, हे सर्वज्ञात आहे. अशी छायाचित्रण काच वर्णपटाच्या निरनिराळ्या जागी ठेवल्यास किती काळी होते याचा अभ्यास करीत असताना जे. डब्ल्यू. रिटर यांना १८०१ मध्ये असे आढळून आले की, जेथे निळा-जांभळा भाग आहे तेथे तर काच काळी होतेच पण त्या पलीकडच्या काळ्या भागात काच अधिकच काळी होते. याचा अर्थ दृश्य जांभळ्या भागाच्या पलीकडे विद्युत् चुंबकीय ऊर्जा आहे. या भागाला जंबुपार भाग म्हणतात. अशा रीतीने वर्णपटाची एकंदर कक्षा वाढली व त्याचा अभ्यास करण्याची उपकरणेही शोधून काढण्यात आली.
तरंगलांब्यांच्या भाषेत दृश्य भाग ४,००० Å ते ८,००० Å इतका आहे. ४,००० Å हा जांभळा भाग आणि त्या आधी १०० Å ते ४,००० Å इतका कक्षेचा जंबुपार भाग, तसेच ८,००० Å ते १,००,००,००० Å (०·८ मायक्रॉन ते १,००० मायक्रॉन) एवढ्या कक्षेत अवरक्त भाग पसरलेला आहे. या भागांचा अभ्यास करण्याची विशिष्ट उपकरणे असतात.
जंबुपार भाग : याचे दोन उपभाग पडतात : (१) समीप जंबुपार २,००० Å ते ४,००० Å आणि (२) दूर जंबुपार १०० Å ते २,००० Å. या उपभागांकरिता वापरली जाणारी उपकरणे कोष्टक क्र. २ मध्ये दिली आहेत.
येथे एक विशेष गोष्ट लक्षात ठेवली पाहिजे की, जंबुपार किरण डोळ्यावर पडल्यास कायम स्वरूपाची इजा होऊ शकते, म्हणून या भागावर काम करताना सदैव काळा चष्मा वापरणे
|
कोष्टक क्र. २. वर्णपटाच्या जंबुपार भागाकरिता वापरली जाणारी उपकरणे. |
||
|
उपकरणे |
समीप जंबुपार |
दूर जंबुपार |
|
प्रकाश उद्गम |
पाऱ्याची विद्युत् प्रज्योत, कॅडमियमाची विद्युत् ठिणगी, हायड्रोजन विसर्जन नळी, लेसर. |
निर्वात विद्युत् ठिणगी |
|
समांतरित्र आणि अपस्करण साधने |
क्वार्ट्झाची भिंगे व लोलक |
अंतर्गोल आरसे, परावर्तक जालक, निर्वात केलेले वर्णपटलेखक. |
|
अभिज्ञातक |
प्रकाशविद्युत् घट, छायाचित्रण काचा, तपयुग्मे वा तपचिती. |
निर्वात प्रकाश विद्युत् घट अगर प्रकाशगुणक नलिका. |
आवश्यक असते. [⟶ जंबुपार प्रारण].
अवरक्त भाग : याचेही दोन उपभाग पडतात : (१) समीप अवरक्त म्हणजे ०·८ मायक्रॉन ते २५ मायक्रॉन व (२) दूर अवरक्त म्हणजे २५ मायक्रॉन ते १,००० मायक्रॉन. या उपभागांकरिता वापरली जाणारी उपकरणे कोष्टक क्र. ३ मध्ये दिली आहेत.
|
कोष्टक क्र. ३. अवरक्त भागाकरिता वापरली जाणारी उपकरणे |
||
|
उपकरणे |
समीप अवरक्त |
दूर अवरक्त |
|
प्रकाश उद्गम |
टंगस्टनाचा दिवा अगर ग्लॉबर दिवा. |
नेर्न्स्ट दिवा, ग्लॉबर दिवा. |
|
समांतरित्र आणि अपस्करण साधने |
क्वार्ट्झाच्या अगर सैंधवाच्या स्फटिकांचे लोलक व भिंगे. |
अंतर्गोल आरसे व तारांचे विवर्तन जालक अगर परावर्तन जालक. |
|
अभिज्ञातक |
गोले घट, तपचिती, तपयुग्म, थर्मिस्टर, प्रकाशविद्युत् घट, विशिष्ट छायाचित्रण काचा |
निर्वात तपचिती |
अवरक्त वर्णपटमापक : आ. ११ व १२ मध्ये दोन प्रकारचे अवरक्त वर्णपट दाखविले आहेत. यांत भिंगांच्या ऐवजी अंतर्गोल आरसे वापरलेले आहेत, कारण काच अवरक्त किरण शोषून घेते. तसेच दृश्य भागाकरिता केलेले केंद्रीकरण अवरक्त भागालाही चालते.
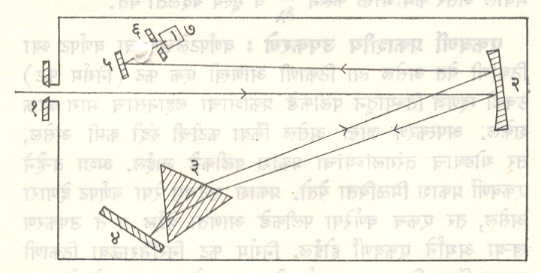
यात इयत्तीकरण महत्त्वाचे आहे. याकरिता सपाट जालक वापरून कोन-अपगमन मोजतात व d sinq = nl या सूत्रावरून [⟶ विवर्तन जालक] तरंगलांबी काढतात. अशा तऱ्हे ने काही विशिष्ट प्रकाश उद्गमांतील विशिष्ट वर्णरेषांच्या तरंगलांब्या प्रमाणित करतात. कोन व तरंगलांबी यांचा आलेख काढून इयत्तीकरण करतात. तयार मिळणाऱ्या वर्णपटमापकात इयत्तीकरणाच्या खुणा ज्या भागाचे परिभ्रमण होते त्या भागावरच करतात. या वर्णपटमापकात अभिज्ञातक म्हणऊ तपयुग्म , तपचिती किंवा बोलोमीटर वापरतात. यातील विद्युत् प्रवाहमापकाच्या विचलनाची वाचने व तरंगलांबी यांचा तयार कागदावर आलेखच मिळतो. अर्थातच असा वर्णपटमापक वापरणे सोपे असते. वातावरणातील वायू अवरक्त भागाचे शोषण करतात म्हणून पूर्ण वर्णपटमापक निर्वात करावा लागतो. [⟶ अवरक्त प्रारण].
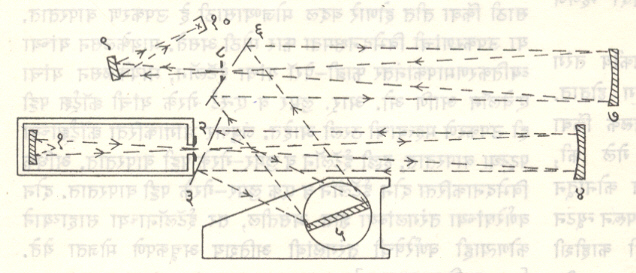
लोलक : प्रकाशाचे अपस्करण होण्यासाठी लोलक (किंवा विवर्तन जालक) लागतो. वर्णपटदर्शकात साधारणपणे ६०° शिरोकोनाचा त्रिकोणी लोलक वापरतात. मोठ्या आकारमानाचा लोलक जास्त प्रकाश संकलित करू शकतो व त्यामुळे वर्णपटाची तीव्रता वाढते. लोलकाचा पाया जितका रुंद तितकी वर्णपटमापकाची विभेदनक्षोमता जास्त असते. तसेच लोलकाच्या द्रव्याचा प्रणमनांक जितका जास्त तितकी त्याची अपस्करणक्षमता जास्त असते. अपस्करणक्षमता तरंगलांबीवरही अवलंबून असते. साधारणपणे तरंगलांबी जशी वाढते तशी अपस्करणक्षमता कमी होते.
लोलकाचे द्रव्य अतिशय शुद्ध व एकजिनसी असावे लागते. तसेच त्याचे पृष्ठभाग प्रकाशीय दृष्ट्या सपाट असावे लागतात. वर्णपटाच्या निरनिराळ्या भागांकरिता निरनिराळ्या द्रव्यांचे लोलक वापरतात, कारण ती द्रव्ये त्या त्या भागाकरिता पारदर्शक असतात. अतिशय घन फ्लिंट काच दृश्य भागाकरिता चांगली असते. क्राऊन काच २,००० Å ते ३,५०० Å या भागाकरिता चालते. दृश्य भागातही
|
कोष्टक क्रं ४. लोलकांसाठी वापरण्यात येणारी काही द्रव्ये |
||
|
द्रव्य |
पारदर्शकेतेची कक्षा (तरंगलांबी मायक्रॉनमध्ये) |
प्रणमनांक (सोडियमाच्या ५,८९३ Å या रेषेकरिता) |
|
पोटॅशियम आयोडाइड (KI) |
०·२५ – ३१ |
१·६६३४ |
|
पोटॅशियम ब्रोमाइड (KBr) |
०·२१-३० |
१·५५८१ |
|
लिथियम फ्ल्युओराइड (LiF) |
०·१२-६ |
१·३९१७७ |
|
कॅल्शियम फ्ल्युओराइड (CaF2) (फ्ल्युओराइट) |
०·१२-९ |
१·४३३८५ |
|
क्वार्ट्झ (स्फटिकी)(SiO2) |
०·१८५-३·५ |
१·५४४२६ |
|
सैंधव (NaCl) |
०·२-१७ |
१·५४४३१ |
|
सिल्व्हाइट (पोटॅशियम क्लोराइड,KCl) |
०·२-२१ |
१·४९०३८ |
|
थॅलियम ब्रोमोआयोडाइड |
०·५-४० |
२·६३१६ |
ती वापरतात. लोलकांसाठी वापरण्यात येणाऱ्या काही द्रव्यांची माहिती कोष्टक क्रं. ४ मध्ये दिली आहे.
कोष्टकावरून असे दिसून येते की, लोलक वापरून ४० मायक्रॉनांपेक्षा पुढे अभ्यास करता येत नाही. याकरिता विवर्तन जालकाचा उपयोग करता येतो.
क्वार्ट्झ हे द्रव्य ध्रुवण प्रतलाचे घूर्णन करते [⟶ ध्रुवणमिति]. दोन प्रकारची क्वार्ट्झ द्रव्ये असून एक उजवीकडे धूर्णन करते, तर दुसरे डावीकडे. म्हणून दोन्ही प्रकारच्या क्वार्ट्झांचे ३०°, ६०° व ९०° कोनांचे दोन लोलक घेऊन ते एकत्र चिकटवून प्रत्येकी ६०° कोन असलेला लोलक तयार करतात. याला ए. कॉर्नू यांचा लोलक (कॉर्नू लोलक) म्हणतात. अशा तऱ्हेचा लोलक जंबुपार भागाकरिता वर्णपटदर्शकात वापरतात.
लिट्रो वर्णपटलेखकात ३०°, ६०°, ९०° कोन असलेल्या लोलकात ६०° कोनासमोरील पृष्ठभाग परावर्तनक्षम केल्याने ३०° कोनातून किरण दोनदा प्रवास करतो. अशा तऱ्हेने ६०° चे कार्य होते. (आ.९).
स्थिरापगमन लोलक : हा जणू काही तीन लोलकांचा मिळून बनलेला लोलक असतो (आ. १३). D अआई मध्ये Ðअ = ६०°, Ðआ = ३०°, Ð इ = ९०° D आइफ मध्येÐआ = ६०°, Ð इ = ३०°, Ð फ = ९०° D इईफ मध्ये Ð इ = ४५°, Ð ई = ४५°, Ð फ = ९०°. अशा तऱ्हेने तयार होणाऱ्या लोलकात किरण एकूण ९०° तून फिरतात. हे कोणत्याही तरंगलांबीच्या किरणांना लागू आहे. निरनिराळ्या तरंगलांब्यांच्या किरणांना निरनिराळे आपाती कोन लागतात व त्याकरिता लोलकाचे परिभ्रमण करतात. यामुळे अपस्करणही मिळून वर्णपटदर्शक बनविता येतो.
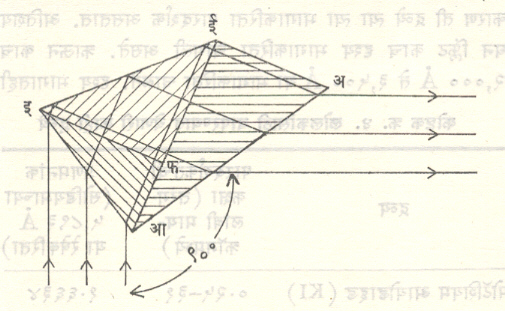आमिची लोलक : दोन क्राऊन काचेच्या लोलकांत एक फ्लिंटचा लोलक किंवा तीन क्राऊन लोलकांत दोन फ्लिंटचे लोलक बसवून एक लोलक समूह तयार करतात (आ.१४). विचलनरहित अपस्करण मिळविणे हा याचा उद्देश असतो. वर्णपटातील मधल्या तरंगलांबीच्या किरणापुरते हे घडल्यास इतर तरंगलांब्यांच्या किरणांचे दोन्ही बाजूंना अपस्करण होऊन वर्णपट मिळतो. यात महत्त्वाचा फायदा म्हणजे प्रकाश उद्गमाकडे सरळ पाहता येते.
अपस्करण : निरनिराळ्या तरंगलांब्यांचे विद्युत् चुंबकीय तरंग निरनिराळ्या कोनांतून वळल्यामुळे परस्परांपासून अलग होतात. याला अपस्करण म्हणतात. अपस्करण होण्याकरिता लोलक किंवा विवर्तन जालक वापरतात. प्रकाशकिरण लोलकामधून गेले की, प्रकाशाचे निरनिराळ्या तरंगलांब्यांचे किरण निरनिराळ्या कोनांतून वळतात व पडद्यावर वर्णपट मिळतो. हा साधा सिद्धांत वापरून न्यूटन यांनी वर्णपटविज्ञानाचा पाया घातला. जालकामध्येही काहीशी अशीच प्रक्रिया होते. त्यांतील फरक म्हणजे लोलकाच्या बाबतीत जसजशी तरंगलांबी वाढते तसतसा विचलन कोन कमीकमी होत जातो, म्हणूनच लोलकाच्या पायाकडे जांभळा आणि शिरोकोनाकडे तांबडा रंग दिसतो. जालकामध्ये त्याच्या रेषांवरती प्रकाश पडल्यास विवर्तन होते व त्याबरोबरच व्यतिकरण होऊन प्रकाश तरंगलांबीच्या प्रमाणात वर्णपट देतो. जालकामध्ये होणारा फरक लोलकांच्या उलट असतो म्हणजे तरंगलांबी वाढते, तसा विचलन कोनही वाढतो.
लोलक किंवा जालक यांची अपस्करणक्षमता (δ∅/δl) या गुणांकाने देतात (येथे δl हा तरंगलांबीतील बदल असून δ∅ हा त्यानुसार अपस्करण कोनात होणारा अल्प बदल आहे). लोलकाच्या बाबतीत ती ऋण असते. तर जालकाच्या बाबतीत ती धन असते. (δ∅/δl) चे मूल्य लोलकाच्या वर्णपटामध्ये सर्व तरंगलांब्यांकरिता एक नसते.∅ व lयांचा आलेख सरळ रेषेत मिळत नाही म्हणजे वर्णपट सुसम नसतो. याउलट सपाट जालकात d.sin = nl या सूत्राप्रमाणे sin व lयांचा आलेख सरळ रेषेत असतो (येथे d हा जालक स्थिरांक आहे). जालकामध्ये (δ∅/δl) याचे मूल्य जालकावर प्रती सेंमी. काढलेल्या रेषांवर अवलंबून असते. लोलकामध्ये अपस्करणाचे मूल्य जंबुपार भागात जास्त असल्याने त्या भागाच्या अभ्यासाकरिता लोलकीय वर्णपटदर्शक वापरणे फायदेशीर असते. जालकावरील दोन रेषांमधील अंतर कमीजास्त करून (δ∅/δl) चे मूल्य बदलता येते.
एकवर्णी प्रकाशीय उपकरणे : वर्णपटलेखकाचा वर्णपट ज्या ठिकाणी येत असेल त्या ठिकाणी आणखी एक फट (निर्गम फट) ठेवली म्हणजे तिच्यातून पलीकडे प्रकाशाचा लहानसाच भाग जाऊ शकेल. अपस्करण जास्त असेल किंवा फटीची रुंदी कमी असेल, तर थोड्याच तरंगलांब्यांचा प्रकाश पलीकडे जाईल. अशा तऱ्हेने एकवर्णी प्रकाश मिळविता येतो. प्रकाश उद्गम रेषा वर्णपट देणारा असेल, तर एकच वर्णरेषा पलीकडे आणता येईल व ते उपकरण खऱ्या अर्थाने एकवर्णी होईल. निर्गम फट निरनिराळ्या ठिकाणी हलवून किंवा स्थिरापगमन वर्णपटलेखकात लोलक हलवून वेगवेगळ्या तरंगलांब्यांचा एकवर्णी प्रकाश मिळविता येतो.
मूलद्रव्यांच्या लाक्षणिक वर्णरेषा ज्या ठिकाणी येतात त्या ठिकाणी निर्गम फटी ठेवून त्यामागे अभिज्ञातक ठेवतात. अशा तऱ्हेने प्रकाश उद्गमात ती मूलद्रव्ये आहेत की नाहीत ते चटकन समजते. तसेच अभिज्ञातकांच्या विचलनांवरून त्या त्या मूलद्रव्यांचे प्रकाश उद्गमामध्ये किती प्रमाण आहे हेही समजते. याला अनेकवर्णी प्रकाशीय उपकरण म्हणता येईल. हल्ली अशा उपकरणाचा उद्योगधंद्यामध्ये सर्रास वापर करण्यात येतो.
व्यतिकरणमापक : वर्णरेषांच्या सूक्ष्म रचनेचा अभ्यास करण्यासाठी किंवा तीत होणारे बदल मोजण्यासाठी हे उपकरण वापरतात. या उपकरणांची विभेदनक्षमता फार मोठी असते. मायकेलसन यांच्या व्यतिकरणमापकानंतर फाब्री-पेरॉ यांचा ईटॅलॉन, मायकेलसन यांचा एचेलॉन आणि ओ. आर्. लुमर व एर्न्स्ट गेरके यांची क्वार्ट्झ पट्टी ही उपकरणे महत्त्वाची ठरली आहेत. जंबुपार भागाकरिता क्वार्ट्झच्या पट्ट्या वापरतात, हल्ली ईटॅलॉन व लुमर-गेरके पट्टी वापरतात. अधिक विभेदनाकरिता दोन ईटॅलॉन व एक लुमर-गेरके पट्टी वापरतात. दोन वर्णरेषांच्या तरंगलांब्या ज्ञात असतील, तर ईटॅलॉनाच्या साहाय्याने कोणत्याही वर्णरेषेची तरंगलांबी अतिशय अचूकपणे मोजता येते. [⟶ व्यतिकरणमापन].
विभेदनक्षमता : वर्णपटातील l व l+δl या दोन नजीकच्या तरंगलांब्यांच्या वर्णरेषा जेव्हा वर्णपटमापक वेगवेगळ्या दाखवितात तेव्हा त्याला विभेदन म्हणतात. lया तरंगलांबीच्या एका वर्णरेषेचा प्रकाश फटीवर टाकल्यास फटीची प्रतिमा विवर्तनामुळे कशी दिसते हे आ. १५ मध्ये अखंड रेषेने दाखविले आहे. टिंबाटिंबांनी काढलेला आलेख हा l+δl या वर्णरेषेची प्रतिमा दाखवितो. अखंड रेषेच्या किमान बिंदूच्या बाजूला जर टिंबांकित रेषेचा कमाल बिंदू आला, तर दोन्ही मिळून मिळणारी प्रतिमा आकृतीत खालील बाजूस दाखविली आहे. दोघांमधील खोलगट भागाची तीव्रता कमाल बिंदूला असलेल्या तीव्रतेपेक्षा १९ टक्क्यांनी कमी असते व लॉर्ड रॅली यांच्या म्हणण्याप्रमाणे डोळ्यांना हा फरक जाणवेल आणि दोन वर्णरेषा स्पष्ट दिसतील. मात्र त्यापेक्षा दोन वर्णरेषा जास्त जवळ असल्यास त्या वेगळ्या दिसणार नाहीत. विभेदनक्षमताl/δl या गुणोत्तराने काढतात. लोलकाकरिता tδm/δl हे गुणोत्तर वापरतात. येथे t म्हणजे लोलकातून जाणाऱ्या दोन कडेच्या किरणांचा प्रकाशीय मार्गातील फरक असून m हा लोलक द्रव्याचा प्रणमनांक आहे. जालकाकरिता विभेदनक्षमता N.n इतकी असते. (N = जालकातील रेषांची संख्या व n= विवर्तित रेषासमूहाचा क्रमांक) वर्णपटलेखकाची विभेदनक्षमता १,००० पासून दोन-तीन लाखांपर्यंत असू शकते. [⟶ विभेदनक्षमता].
वर्णपटाची मापने : मिळालेल्या वर्णपटाचा उपयोग करण्यासाठी सामान्यतः पुढील मापने करावी लागतात : (१) वर्णरेषांच्या तरंगलांब्या, (२) प्रत्येक वर्णरेषेची तीव्रता, (३) वर्णरेषांची सूक्ष्म रचना, (४) वर्णरेषांवर होणारा चुंबकीय क्षेत्राचा परिणाम (झीमान परिणाम) व विद्युत् क्षेत्राचा परिणाम (श्टार्क परिणाम). यांपैकी पहिल्या दोन मापनांसंबंधीच येथे विवरण केलेले असून झीमान परिणामाकरिता ‘अणुकेंद्रीय व आणवीय परिबले’ ही स्वतंत्र नोंद पहावी व श्टार्क परिणामाकरिता ‘श्टार्क परिणाम’ ही स्वतंत्र नोंद पहावी. वर्णरेषांच्या सूक्ष्मरचनेसंबंधी प्रस्तुत नोंदीतच ‘आणवीय वर्णपटविज्ञान’ या विभागात विवरण दिलेले आहे.
तरंगलांबीचे मापन : स्थिरापगमन वर्णपटमापक वापरला असता त्याच्या मोजपट्टीवरुन वर्णरेषांच्या तरंगलांब्या सरळ वाचता येतात. काही वर्णपटदर्शकांत व लेखकांत वर्णपटावर आरोपित मोजपट्टी आपोआप दिसण्याची योजना केलेली असते. परंतु या पद्धतीत तरंगलांबी काळजीपूर्वक इयत्तीकरण केलेल्या मोजपट्टीवरून विनासायास मिळत असली, तरी तिच्यात १ Å पेक्षा जास्त अचूकता येऊ शकत नाही. अधिक अचूक म्हणजे ०·०१ Å किंवा त्यापेक्षाही जास्त अचूक तरंगलांबी मोजायची असेल, तर जे. हार्टमान यांची अंतर्वेशन [⟶ अंतर्वेशन व बहिर्वेशन] पद्धत वापरावी लागते. यासाठी लोह, तांबे अगर इतर मूलद्रव्यांच्या वर्णपटाचे मानक संदर्भ तक्ते वापरतात (आ. १६). या तक्त्यांवर त्या त्या मूलद्रव्याच्या वर्णरेषा निर्देशित केलेल्या असतात. इष्ट वर्णपट (PQR….) व मानक वर्णपट (ABC ….) यांतील वर्णरेषा समोरासमोर येतील अशा प्रकारे त्यांचे छायाचित्र छायाचित्रण काचेवर घेण्यात येते. समजा, आपणास एखाद्या (Q) वर्णरेषेची तरंगलांबी काढावयाची असेल, तर तिच्या दोन बाजूंस शक्य तितक्या जवळ असतील अशा दोन रेषा (A व B) मानक वर्णपटातून निवडतात. मानक वर्णरेषांच्या तरंगलांब्या l1 व l 2 या मानक वर्णपट तक्त्यावरून आधीच माहीत असतात. तरंगलांबी काढावयाच्या वर्णरेषेबरोबर घेतलेले या वर्णरेषांचे छायाचित्र चल सूक्ष्मदर्शकाखाली ठेवून A व Q यांमधील अंतर (a) व Q आणि B यांमधील अंतर (b) मोजतात. नंतर l = l1 +l2 – l1/a+b.a या सूत्रावरून इष्ट वर्णरेषेची तरंगलांबी (l) काढता येते. हे सूत्र जालक वर्णपटमापका करिता आहे. लोलक वर्णपटाकरिता तरंगलांबीचे मापन करण्याची पद्धत पुढीलप्रमाणे आहे. याकरिता हार्टमान सूत्र वापरतात: l= l० + A/B+m यात l०, A व B हे जो वर्णपटमापक वापरला असेल त्याचे स्थिरांग आहेत. m हे तरंगलांबी मोजावयाच्या वर्णरेषेचे वाचन (निरीक्षण) आहे. A व B हे मानक वर्णपटाच्या पूर्व निर्धारित वर्णरेषांवरून काढतात.
तरंगलांबी व तरंगांक : मापनावरून तरंगलांबी मिळत असली, तरी सद्धांतिक कामासाठी तरंगांक (n) म्हणजे एक सेंटिमीटरमधील तरंगलांब्यांची संख्या ही राशी जास्त सोईची ठरते. तरंगलांबी l सेंमी. असेल, तर ν = I/l सेंमी.–१ हे सूत्र वापरून तरंगांक काढता येतो. हा तरंगांक मुख्यत्वेकरून अवरक्त भागातील वर्णपटांकरिता वापरतात. आणखी एक राशी सैद्धांतिक कामासाठी वापरतात व ती म्हणजे कंप्रता (n) ही होय. ती c = ν.l या सूत्रावरून काढतात. येथे c हा विद्युत् चुंबकीय तरंगांचा वेग आहे. ही राशी ऊर्जा काढण्याकरिता उपयोगी पडते, कारण h. n यावरून अर्ग अगर वॉटमध्ये त्या तरंगलांबीची ऊर्जा मिळते (येथे h हा प्लांक स्थिरांक आहे).
वर्णरेषांच्या तीव्रतेचे मापन : (वर्णपट प्रकाशमापन). वर्णरेषांच्या तीव्रतेचे म्हणजेच तेजस्वितेचे मापन ही एक महत्त्वाची बाब आहे, कारण यावरूनच पुढे वर्णपटीय रासायनिक विश्लेषण करण्यात येते. तीव्रतेचे मापन मुख्यत्वे तीन पद्धतींनी करता येते. कारण यावरूनच पुढे वर्णपटीय रासायनिक विश्लेषण करण्यात येते. तीव्रतेचे मापन मुख्यत्वे तीन पद्धतींनी करता येते.
(१) दृश्य मापन : डोळ्यांनी दिसणारे तौलनिक तीव्रतेचे मापन आजूबाजूच्या रेषांच्या मानाने करता येते. याहून जास्त बिनचूक मापनासाठी प्रकाशाच्या तीव्रतेला संवेदनाशील असे एखादे उपकरण (उदा., प्रकाशविद्युत् घट, बोलोमीटर, तपचिती, गोले घट) वापरावे लागते.
(२) छायाचित्रण पद्धती : या पद्धतीत प्रथम इष्ट वर्णपटाचे काचेवर छायाचित्र घेतात. या छायाचित्रात जितकी रेषेची तीव्रता जास्त तितका तिचा छायाचित्राचा काळेपणा जास्त असतो. याच्या मापनाकरिता या छायाचित्रावर प्रकाश झोत टाकून आरपार गेलेला प्रकाश एका अरुंद फटीतून जाऊन पलीकडील प्रकाश विद्युत् घटावर पडतो. जितकी विशिष्ट रेषेची तीव्रता जास्त तितका तिच्या छायाचित्रातून पलीकडे जाणारा प्रकाश कमी तीव्रतेचा असेल. प्रकाशविद्युत् घटाला विद्युत् मापक जोडलेला असतो. प्रकाशविद्युत् घटातून जाणारा विद्युत् प्रवाह त्याच्यावर पडणाऱ्या प्रकाशाच्या सम प्रमाणात असतो. त्यामुळे विद्युत् मापकाचे विचलन हे वर्णरेषेच्या तीव्रतेचे मापच असते. फटीसह प्रकाशविद्युत् घट छायाचित्रण काचेला समांतर सरकवून तो निरनिराळ्या वर्णरेषांच्या छायाचित्रासमोर आणता येतो व त्यांची तीव्रता मोजता येते. या पद्धतीत एक दोष म्हणजे छायाचित्राचा काळेपणा व प्रकाश तीव्रता यांमधील संबंध बराच गुंतागुंतीचा आहे. यामुळे काही त्रुटी उत्पन्न होतात पण काळेपणाच्या एका विशिष्ट सीमेपर्यंत तीव्रता व काळेपणा सम प्रमाणात असतात. म्हणून वर्णपट मिळविताना छायाचित्रण एका विशिष्ट काळेपणापर्यंत येऊ शकेल याची काळजी घ्यावी लागते. ही पद्धत दृश्य, अवरक्त व जंबुपार या तीनही वर्णपटांसाठी वापरता येते.
(३) वर्णपटावरून सरळ मापन : या पद्धतीत वर्णपटदर्शकाच्या दूरदर्शकातील नेत्रभिंग काढून तेथे एक निरुंद फट व तिच्या मागे एक निर्वात तपचिती (किंवा बोलोमीटर वा गोले घट) अगर प्रकाशविद्युत् घट बसवितात. दूरदर्शक फिरवून कोणतीही वर्णरेषा त्या फटीवर आणता येते व तपचिती किंवा प्रकाशविद्युत् घट यांना जोडलेल्या विद्युत् मापकावरून वर्णरेषेची तीव्रता मोजता येते. तपचितीत निर्माण होणारा विद्युत् प्रवाहकारक वर्णरेषेच्या तीव्रतेच्या सम प्रमाणात असतो. त्यामुळे तपचितीद्वारे मापन करणे खूपच अचूक व अगदी सोपे असते. प्रकाशविद्युत् घट वापरल्यास त्याची निरनिराळ्या तरंगलांब्यांकरिता प्रती एकक ऊर्जा संवेदनक्षमता वेगळी असते. त्यामुळे त्याने केलेले मापन संवेदना आलेखावरून वाचावे लागते.
वरील संक्षिप्त वर्णनाखेरीज विविध प्रकारांच्या वर्णपट प्रकाशमापकांचे वर्णन ‘प्रकाशमापन’ या नोंदीत दिलेले आहे.
वर्णपटविज्ञानाचे काही उपयोग :तरंगलांबीचे निरपेक्ष मापन: इंटरनॅशनल कमिटी ऑन वेट्स अँड मेझर्स या आंतरराष्ट्रीय समितीने मीटर हे लांबीचे प्रमाण ठरविले आहे. अशा प्रमाण मीटरच्या मानक प्रतिकृती मुख्यतः पॅरिसमध्ये व इतर काही ठिकाणी सुरक्षित ठेवलेल्या आहेत. वस्तुनिष्ठ लांबीचे परिमाण हे केव्हाही नैसर्गिक लांबीच्या परिमाणापेक्षा शास्त्रशुद्ध असू शकत नाही म्हणूनच काही विवक्षित तरंगलांब्यांच्या सूक्ष्मतर वर्णरेषा वापरून लांबीचे निरपेक्ष मापन होऊ शकते. प्रथम १८९३ साली मायकेलसन यांनी त्यांचा व्यतिकरणमापक वापरून पॅरिसमधील प्रमाण मीटरच्या संदर्भात कॅडमियमाच्या वर्णरेषांची तरंगलांबी मोजली. त्यापेक्षा क्रिप्टॉनाची लाल नारिंगी वर्णरेषा खूपच रेखीव आहे व म्हणून १९६० मध्ये ती आद्य प्रमाण मानली गेली. तिची तरंगलांबी ६,०५७·८०२१ Å आहे. या आद्य मानकावरून पुष्कळशा वर्णरेषांच्या तरंगलांब्या दुय्यम मानक म्हणून ठरविल्या आहेत. त्यांत लोह विद्युत् प्रज्योतीतील ३०६, निऑनाच्या २० व क्रिप्टॉनाच्या २० वर्णरेषा आहेत. पारदर्शक विवर्तन जालक वर्णपटमापक वापरून तरंगलांबीचे निरपेक्ष मापन करता येते. [⟶ मेट्रिक पद्धति].
वर्णपटीय रासायनिक विश्लेषण : वर्णपटविज्ञानाचा उपयोग वर्णपटात आढळणाऱ्या रेषा व पट्ट यांवरून तो वर्णपट देणारी मूलद्रव्ये व संयुगे यांच्यासंबंधी ज्ञान मिळविणे हा होय. कोणते अणू , रेणू व मूलके (रासायनिक संघटनांमध्ये अभेद्य राहणारे अणुसमुच्चय उदा., SO4, NO3) उद्गमात आहेत, उद्गमांच्या स्थानी व उत्सर्जनाच्या वेळी त्यांची कोणती उत्तेजित स्थिती आहे, त्यांचे प्रमाण किती आहे वगैरे प्रश्नांची उत्तरे मिळविणे हा एक दृष्टिकोन झाला. मिळालेल्या वर्णपटात पूर्वी न आढळलेल्या वर्णरेषा सापडतात काॽ माहीत नसलेल्या ऊर्जा अवस्थांपासून काही संक्रमणे मिळालेली आहेत काॽ वर्णपट देणाऱ्या पदार्थात काही इतर पदार्थ मिश्रित आहेत काॽ इ. प्रश्नांची उत्तरे मिळविणे हा दुसरा दृष्टिकोन झाला. दोन्ही प्रकारच्या अभ्यासांत वर्णपटामध्ये आढळणारी रेषा वा पट्ट कोणत्या अणू व रेणूपासून आलेला आहे याच गोष्टीस महत्त्व आहे.
प्रत्येक रेषेचे असे मूलद्रव्याशी वा संयुगाशी नाते ठरविताना निरनिराळ्या शास्त्रज्ञांनी मोठ्या परिश्रमाने तयार केलेली शुद्ध पदार्थांच्या वर्णपटात आढळून येणाऱ्या रेषांची व पट्टांची कोष्टके व तक्ते फार उपयोगी पडतात. सर्व मूलद्रव्यांच्या मिळून एक अँगस्ट्रॉम लांबीमध्ये अंदाजे १४ रेषा आढळून येतात. यावरून कितीही मोठी विभेदनक्षमता असलेले उपकरण वापरले, तरी प्रश्न किती जिकिरीचा असू शकतो याची कल्पना येईल. एखाद्या रेषेकरिता असे विविध पदार्थ या तक्त्यांवरून ओळखणे शक्य असले, तरी हे सर्वच पदार्थ उद्गमस्थानी नसतात. उद्गमस्थानी कोणते पदार्थ वापरले आहेत या माहितीवरून व त्याच्यात शक्य असणाऱ्या अशुद्ध पदार्थांचा अंदाज घेऊन ही यादी बरीच लहान करता येते. राहिलेल्या यादीतील पदार्थांच्या वर्णपटात नेहमी आढळून येणाऱ्या अतितीव्र रेषा आढळतात का हे मोजलेल्या तरंगलांबीवरून सांगता येते. ज्या पदार्थांच्या रेषा व पट्ट आढळत नाहीत ते अणू वा रेणू उद्गमात नाहीत, हे निश्चित सांगता येते. तीव्र रेषांच्या अभ्यासाने काही निश्चित अनुमाने काढल्यानंतर कमी तीव्रतेच्या रेषा विचारात घेता येतात. तीव्र रेषांवरून ठरलेल्या मूलद्रव्यांच्या इतर कमी तीव्र व निस्तेज रेषा तक्त्यांवरून पाहून त्या आढळतात का हे मोजमापांशी ताडून पाहिले जाते. या पद्धतीने बऱ्याच रेषांचे व पट्टांचे उद्गम ठरविता येतात. एवढे केल्यानंतर राहिलेल्या ओळख न पटलेल्या रेषा बहुधा अतिनिस्तेज असतात. त्या कोष्टकातून वा तक्त्यातून आढळत नाहीत याचे कारण अगोदरच्या प्रयोगाच्या वेळी उद्गमांची असलेली अवस्था आपल्या प्रयोगाच्या वेळी कदाचित नसते किंवा आपल्या प्रयोगात मूळ पदार्थांमध्ये अतिसूक्ष्म प्रमाणात इतर पदार्थांचे मिश्रण झालेले असण्याची शक्यता असते. या पदार्थांच्या नेहमी आढळणाऱ्या रेषा त्यांचे वर्णपट घेतल्यास जरी तीव्र आढळल्या, तरी आपल्या प्रयोगात त्या पदार्थांचे प्रमाण अत्यंत कमी असल्याने त्या अतिनिस्तेज आढळणे शक्य असते. येथे गुणात्मक अभ्यासाने जास्त माहिती सांगणे कठीण असल्याने परिमाणात्मक अभ्यासाची गरज भासते. यावरूनच वर्णपटीय रासायनिक विश्लेषण पद्धती केवळ रासायनिक विश्लेषण पद्धतीपेक्षा किती जास्त उपयुक्त आहे, हे लक्षात येते. कारण केवळ रासायनिक पद्धतीने जितके सूक्ष्म प्रमाण निश्चित करता येते त्याच्या किती तरी अधिक पटींचे सूक्ष्म प्रमाण वर्णपटीय पद्धतीने निश्चित करता येते.
वर्णरेषांच्या तीव्रतामापनावरून करण्यात येणाऱ्या रासायनिक विश्लेषणाला सैद्धांतिक व औद्योगिक प्रयुक्तींत फार महत्त्व आहे. उदा., पोलादासारख्या मिश्रधातूतील सूक्ष्म प्रमाणात असलेल्या इतर धातू व अधातू ओळखता येतात आणि सोन्यासारख्या धातूच्या एक कोटी भागांत एक भाग इतक्या सूक्ष्म प्रमाणात असलेले हीणही निश्चितपणे मोजता येते. याकरिता प्रमाणित मिश्रधातूतील जी धातू मोजावयाची असेल तिची वर्णपट तीव्रता काढून तिचे आलेख तयार करतात. नंतर ज्या मिश्रधातूचे विश्लेषण करायचे असेल तिचा वर्णपट काढून त्यावरून मिश्रधातूत त्या धातूचे प्रमाण ठरविता येते. या पद्धतीचा उपयोग खनिजे, वनस्पती आणि जीवविज्ञान या क्षेत्रांत होतो. या पद्धतीने जवळजवळ ४० धातूंचे व अधातूंचे मापन करता येते.
याच पद्धतीचा अधिक प्रगत उपयोग म्हणजे आणवीय शोषण वर्णपटविज्ञान होय.
या पद्धतीमध्ये जी धातू मोजावयाची असेल तिचा पोकळ ऋणाग्र दिवा प्रकाश उद्गम म्हणून वापरतात. वर्णपटमापक व प्रकाश उद्गम यांमध्ये एक ८००° ते १,०००° से. तापलेली ग्रॅफाइट भट्टी ठेवतात. या भट्टीमध्ये विश्लेषण करावयाच्या मिश्रणाचा विद्राव सूक्ष्म फवाऱ्याद्वारे सोडतात. उद्गमापासून निघालेल्या वर्णरेषेचे भट्टीत उत्तेजीत झालेल्या मूलद्रव्याच्या अणूंमध्ये शोषण होते व त्या रेषेची तीव्रता वर्णपटमापकाने मोजतात. आधीच तयार असलेल्या आलेखावरून मूलद्रव्याचे प्रमाण काढता येते. या पद्धतीने जवळजवळ ७० मूलद्रव्ये मोजता येतात व मोजता येणारे न्यूनतम प्रमाण इतर विश्लेषण पद्धतींपेक्षा १०० ते १,००० पट सूक्ष्म असते.
या पद्धतीचा उपयोग करणारी काही प्रातिनिधिक क्षेत्रे पुढीलप्रमाणे आहेत : (१) खाणीतून मिळणारी धातुके, मिश्रधातू, धातुमळी, विविध प्रकारच्या काचा, रंग, रसायने, रासायनिक औषधी द्रव्ये इत्यादींचे विश्लेषण करणे (२) न्यायवैद्यकाशी संबंधित रासायनिक विश्लेषण करणे [⟶ न्याय रसायनशास्त्र] (३) प्रदूषणावर लक्ष ठेवणे व ते कोठे होते ते शोधणे (४) शेतजमीन, खते, कीटकनाशके तसेच वनस्पती आणि प्राणी यांतील कोशिकांचे (पेशींचे) रासायनिक विश्लेषण करणे (५) अणुभट्टीतील युरेनियमाच्या समस्थानिकांच्या (अणुक्रमांक तोच पण भिन्न अणुभार असलेल्या त्याच मूलद्रव्याच्या प्रकारांच्या) परस्पर प्रमाणावर लक्ष ठेवून भट्टीची कार्यक्षमता कमाल मर्यादेत ठेवण्यास मदत करणे (६) अतिशुद्ध रसायनांमध्ये अत्यल्पही अशुद्ध द्रव्ये असल्यास त्यांचा शोध घेणे.
आणवीय वर्णपट
अणू व विद्युत् चुंबकीय प्रारण (प्रकाश) यांच्यामधील ऊर्जेच्या देवघेवीमुळे आणवीय वर्णपट निर्माण होतात. जेव्हा अणू आपली काही ऊर्जा प्रकाश तरंगांच्या स्वरूपात बाहेर टाकतो तेव्हा उत्सर्जन वर्णपट मिळतात. याउलट जेव्हा विशिष्ट विद्युत् चुंबकीय तरंगांच्या स्वरूपात बाहेर ऊर्जेचे शोषण करतो तेव्हा शोषण वर्णपट मिळतो. आणवीय वर्णपट हे साधारणतः रेषा वर्णपट असतात पण अणूचा इलेक्ट्रॉन बंधनमुक्त होतो व अणू जेव्हा आयन होतो तेव्हा वर्णपट पट्टारूप होतो. उत्सर्जन रेषा वर्णपटात काळ्या पार्श्वभूमीवर विविध तरंगलांब्यांच्या रेखीव वर्णरेषा १०० Å ते १ मायक्रॉन या मर्यादेत असतात.
अशा वर्णपटाच्या रेषांची मांडणी, त्यांच्या तरंगलांब्या व तीव्रता या उत्सर्जक अणूच्या रचनेवर आणि गुणधर्मांवर अवलंबून असतात. त्यामुळे त्या वर्णपटाच्या अभ्यासावरून आणवीय संरचनेबद्दल महत्त्वाची माहिती उपलब्ध होते. आणवीय संरचनेच्या सध्याच्या ज्ञानामध्ये आणवीय वर्णपटाच्या अभ्यासाचा वाटा फार मोठा आहे.
काही मूलभूत माहिती : वरवर पाहिल्यास एखादा आणवीय वर्णपट असंख्य वर्णरेषांचा बनलेला दिसतो. या सर्व रेषांचे पारस्परिक संबंध वर्णपट अभ्यासाने निश्चित करता येतात व त्यावरून या रेषांमध्ये एक सुसूत्रता दिसून येते. साधारणतः वर्णरेषांचे काही विशिष्ट गटांत वर्गीकरण करता येते व त्या गटांमध्ये पारस्परिक संबंध असतात. वर्णरेषांच्या अशा गटांना श्रेणी असे म्हणतात. पुष्कळदा काही श्रेणींना त्यांच्या स्वरूपावरून अगर त्यांच्या संशोधकाच्या नावांवरून खास नावे दिली आहेत.
योग्य परिस्थितीत विशिष्ट मूलद्रव्याचे अणू काही विशिष्ट वर्णरेषाच उत्सर्जित करतात, मग ते मूलद्रव्य शुद्ध स्वरूपात असो अगर संयुगाच्या स्वरूपात असो. विशिष्ट अणू ज्या तरंगलांब्यांच्या अगर कंप्रतांच्या रेषा उत्सर्जित करतो त्या सर्व रेषा जशाच्या तशा दुसरा कोणताही अणू उत्सर्जित करू शकत नाही म्हणजे वर्णरेषा या अणूच्या व्यवच्छेदक लक्षणच म्हटले पाहिजे. उदाहरण द्यावयाचे झाल्यास सोडियम धातूच्या वर्णपटात मिळणाऱ्या दोन पिवळ्या तेजस्वी रेषा (यांना D रेषा म्हणतात) घेऊ. त्यांच्या तरंगलांब्या ५,८९६ Å व ५,८९० Å अशा निश्चित झाल्या आहेत. पारा, हीलियम, लोह वगैरे अनेक मूलद्रव्यांच्या वर्णपटातही पिवळ्या वर्णरेषा असतात पण बरोबर तितक्याच तरंगलांबीच्या रेषा सोडियमाशिवाय दुसरे मूलद्रव्य देऊ शकत नाही. सोडियम कुठल्याही स्वरूपात असला, तरी या दोन प्रखर वर्णरेषा प्रकर्षाने दिसतात.
रेषा वर्णपटांच्या अभ्यासावरून एक महत्त्वाची गोष्ट लक्षात आली व ती म्हणजे ज्या मूलद्रव्यांचे रासायनिक गुणधर्म एकसारखे असतात, त्यांच्या वर्णपटांत पुष्कळसे साम्य आढळते. समान गुणधर्मांची मूलद्रव्ये ⇨आवर्त सारणीत एकाच स्तंभात येतात. उदा., पहिल्या स्तंभात हायड्रोजन, लिथियम, सोडियम, पोटॅशियम ही एकसंयुजी (इतर मूलद्रव्यांशी संयोग पावण्याची क्षमता १ असलेली ) क्षारीय मूलद्रव्ये आहेत. त्यांचे रेषा वर्णपट आ. १७ मध्ये दाखविले आहेत. त्यांच्यातील साम्य स्थळे लक्षात घेण्यासारखी आहेत. इतकेच नव्हे, तर आवर्त सारणीच्या दुसऱ्या स्तंभातील मूलद्रव्यांतील (उदा., बेरिलियम, मॅग्नेशियम) एक इलेक्ट्रॉन काढून टाकला, तर उरलेल्या आयनाच्या वर्णपटांचे स्वरूप वरील वर्णपटांसारखेच असते. तसेच तिसऱ्या स्तंभातील अणूंतील दोन इलेक्ट्रॉन काढून उरलेल्या आयनांचे वर्णपट त्याच स्वरूपाचे मिळतात. यावरून रेषा वर्णपट व अणूच्या सर्वांत बाहेरच्या भागातील इलेक्ट्रॉन कक्षेचा संबंध लक्षात येतो. पुष्कळदा मूलद्रव्यांची आवर्त सारणीतील स्थाने निश्चित करण्यासाठी व त्यांतील इलेक्ट्रॉनांचा आराखडा निर्धारित करण्यासाठी वर्णपटविज्ञानाचा उपयोग करावा लागला.
हायड्रोजनाच्या अणूमध्ये अणुकेंद्राभोवती फक्त एक इलेक्ट्रॉन फिरत असतो. ही संरचना सर्वात साधी असली, तरी हायड्रोजनाचा वर्णपट गुंतागुंतीचा असतो. या वर्णपटातील एका श्रेणीच्या रेषा (बाल्मर श्रेणी) आ. १८ मध्ये दाखविल्या आहेत. त्यांमधील परस्परसंबंध तरंगलांबी अगर तरंगांक यापैकी कोणत्याही एका परिमाणाने व्यक्त करता आले म्हणजे त्यांचा संबंध स्पष्ट होतो. या रेषांना तांबड्या बाजूकडून Ha, H∅ वगैरे नावे आहेत. त्यांच्या तरंगलांब्यांमधील अंतर लागोपाठ कमीकमी होत जाऊन विशिष्ट रेषेपाशी ती श्रेणी संपते. त्या रेषेला श्रेणी सीमा म्हणतात. या श्रेणीतील तरंगांकांबद्दल १८८४ साली प्रयोगावरून⇨योहान याकोब बाल्मर यांनी खालील सूत्र निश्चित केले.
⊽ = RH (1/22 –1/n12) … … … (१)
येथे RH = हा स्थिरांक (RH = १,०९,६७७·५८१ सेंमी.–१ ) असून n1 हा पूर्णांक (= ३, ४, ५, . . . .) आहे. बाल्मर श्रेणीतील वर्णरेषांचे तरंगांक वरील सूत्रांवरून अचूकपणे मिळतात पण या सूत्राची सैद्धांतिक बैठक तेव्हा माहीत नव्हती.
बाल्मर श्रेणीव्यतिरिक्त हायड्रोजनाच्या आणखी काही वर्णरेषा जंबुपार व अवरक्त विभागांत मिळतात. त्यांची पण श्रेण्यांमध्ये विभागणी करता येते व त्या श्रेण्यांना योग्य अशी बाल्मर सूत्रासारखी सूत्रे देता येतात. त्यावरून असे दिसून येते की, बाल्मर सूत्र अधिक व्यापक स्वरूपात खालीलप्रमाणे मांडता आल्यास
⊽ = RH (1/n22 –1/n12 ) … … … (२)
या सूत्रात त्या श्रेण्या बसतात. यात प्रत्येक श्रेणीसाठी n2 हा स्थिर पूर्णाक धरून n1 ही n2 पेक्षा मोठी पूर्णांकी मूल्ये घेणारी चल संख्या आहे. n1 व n2 यांना वेगवेगळी मूल्ये दिल्यास हायड्रोजनाच्या विविध श्रेण्यांमधील वर्णरेषांचे तरंगांक मिळतात. या श्रेण्यांची नावे आणि त्यांच्या n1 व n2 ची मूल्ये कोष्टक क्र. ५ मध्ये दिली आहेत. श्रेण्यांची नावे त्या त्या संशोधकांच्या नावांवरून देण्यात आलेली आहेत.
कोणत्याही श्रेणीसाठी n1 = ¥ घातल्यास श्रेणी सीमा तरंगांक RH/n22 मिळतो. (याखेरीज हायड्रोजन अणू विशिष्ट रेडिओ कंप्रतांच्या
|
कोष्टक क्र.५. हायड्रोजन वर्णपटातील वर्णरेषांच्या श्रेण्या. |
|||
|
श्रेणीचे नाव |
n2 |
n1 |
वर्णपट विभाग |
|
लायमन श्रेणी |
१ |
२, ३, ४, .. |
जंबुपार |
|
बाल्मर श्रेणी |
२ |
३. ४, ….. |
दृश्य (बहुतांशी) |
|
पाशेन श्रेणी |
३ |
४,५,६,… |
अवरक्त |
|
ब्रॅकेट श्रेणी |
४ |
५,६,७,८,. |
अवरक्त |
|
फुंड श्रेणी |
५ |
६,७,८,… |
अवरक्त |
|
हंफ्रीज श्रेणी |
६ |
७,८,९,१०, |
अवरक्त |
वर्णरेषाही उत्सर्जित करतो परंतु त्यांच्याकरिता n2 मूल्ये फार मोठी म्हणजे ९०, १०९, १५८, १६६ वगैरे घ्यावी लागतात).
या सर्व विवेचनावरून आणवीय वर्णपटाच्या अभ्यासाची सामान्य रूपरेषा लक्षात येईल. ती म्हणजे प्रथम विशिष्ट वर्णरेषांची वेगवेगळ्या श्रेण्यांमध्ये विभागणी व मग त्या श्रेण्यांसाठी बाल्मर सूत्रासारखे एखादे सूत्र शोधून काढणे.
आणवीय वर्णपटातील श्रेण्यांची उपपत्ती समजण्यासाठी अणूची संरचना समजणे आवश्यक आहे, हे नील्स बोर यांनी ओळखले. त्यांनी हायड्रोजनाच्या आणवीय संरचनेसंबंधी ⇨ पुंज सिद्धांतावर आधारलेला सिद्धांत १९१३ मध्ये मांडला [⟶ अणु व आणवीय संरचना]. या सिद्धांतावरून अभ्यासिलेल्या श्रेण्यांचे पारस्परिक संबंध तर स्पष्टपणे कळलेच पण काही संभाव्य श्रेण्यांची शक्यता वर्तविता आली व पुढे त्या श्रेण्या प्रयोगांत प्रत्यक्ष आढळूनही आल्या. बोर सिद्धांतानुसार हायड्रोजनाच्या अणूत अणुकेंद्राभोवती एकच इलेक्ट्रॉन विशिष्ट कक्षांतून फिरत असतो. एका उच्च ऊर्जेच्या कक्षेतून (उच्च ऊर्जा पातळीतून ) इलेक्ट्रॉन जेव्हा नीच ऊर्जा पातळीत जातो तेव्हा त्या पातळ्यांतील ऊर्जा फरकाइतक्या ऊर्जेची (E) वर्णरेषा उत्सर्जित होते व तिची कंप्रता (ν) ही E2– E1 = hν या सूत्राने दिली जाते परंतु
ν/C = ⊽ किंवा ν = c⊽ म्हणून E = hc ν म्हणजे
⊽ = E/hc = 1/hc (E2 – E1 ) … … (३)
येथे c हा प्रकाश वेग, h हा प्लांक स्थिरांक आहे.
या सूत्रांनी (E2-E1) या ऊर्जा फरकामुळे मिळणाऱ्या रेषेचा तरंगक ⊽ मिळतो. बाल्मर सूत्राशी तुलना करता असे दिसते की, RH/n12 व RH/n22 ही हायड्रोजन अणूच्या उत्सर्जनाच्या आधीच्या व नंतरच्या ऊर्जेची मूल्ये आहेत. कुठल्याही वर्णरेषेचा तरंगांक RH/n12 व RH/n22 यासारख्या पदांच्या फरकाने दिला जातो. असेच सूत्र इतर अणूच्या वर्णपटांनाही लागू पडते. या पदांना ‘वर्णपट पदे’ असे म्हणतात.
रिट्स-रिडबर्ग संयोग तत्त्व : समी. (२) मधील कोणतेही वर्णपट पद Tn = RH/n2 (यात n = 1, 2, 3, . . . . . . . . . ,¥) या स्वरूपात देता येते. हायड्रोजनाकरिता n ला 1, 2, 3, . . . . . . . . अशी वेगवेगळी मूल्ये देता येतात व दोन योग्य त्या पदांच्या संयोगाने म्हणजे दोन पदांच्या पदमूल्यांतील फरकामुळे हायड्रोजन
वर्णपटातील कोणत्याही रेषेचा तरंगांक मिळतो. उदा., लायमन श्रेणीतील पहिल्या रेषेचा तरंगांक ⊽1,2 = T1 –
T2 तसेच बाल्मर श्रेणीतील चौथ्या रेषेचा तरंगांक ν2,6 , = T2-T6 असा मिळेल. इतर अणूंच्या बाबतीतही योग्य त्या वर्णपट पदांच्या मूल्यांच्या संयोगाने अशाच प्रकारे कोणत्याही वर्णरेषेचा तरंगांक मिळतो. हा महत्त्वाचा नियम डब्ल्यू. रिट्स व जे. आर्. रिडबर्ग यांनी प्रायोगिक माहितीवरून शोधून काढला. सूत्र स्वरूपात तो
⊽ = T-T’… … (४)
असा देता येईल.
ग्रोटियन आलेख : कोणताही अणू आपल्या मूळ स्थितीत असताना त्याची अंगभूत ऊर्जा किमान पातळीत असते. या ऊर्जेचे निरपेक्ष मापन करता येत नाही. मूळ स्थितीतील अणूवर विविध प्रक्रिया (उदा., दुसरा इलेक्ट्रॉन आदळणे, विद्युत् चुंबकीय प्रारण टाकणे) करून त्याला ऊर्जा देता येते व अशा ऊर्जेचे शोषण करून अणू ऊर्जेच्या क्षुब्धावस्थेत जातो. क्षुब्धावस्थेतील अणूची ऊर्जा मूळ स्थितीतील त्याच्या ऊर्जेपेक्षा साहजिकच जास्त असते. क्षुब्धावस्थेतील अणू जेव्हा परत मूळ स्थितीप्रत येतो तेव्हा तो वर्णरेषांच्या स्वरूपात विद्युत् चुंबकीय ऊर्जा बाहेर टाकतो. ही क्रिया एकाच संक्रमणाने किंवा टप्प्याटप्प्याने होऊ शकते. त्यानुसार एक किंवा अनेक वर्णरेषांचे उत्सर्जन होते. या उत्सर्जनाला समी. (४) लागू पडते.
वर्णरेषांच्या उत्सर्जन-शोषण क्रियांची यंत्रणा स्पष्ट करण्यासाठी व्होल्फगांग ग्रोटियन यांनी ऊर्जा पातळी आलेखाची कल्पना काढली. प्रत्येक अणूसाठी असा वेगळा आलेख काढावा लागेल. आ. १९ मध्ये हायड्रोजनाच्या अणूचा ग्रोटियन आलेख दाखविला आहे. यातील प्रत्येक रेषा ऊर्जा पातळी दाखविते व उभ्या रेषा दोन ऊर्जा पातळ्यांतील फरक आणि तदनुसार मिळणारी वर्णरेषा दाखविते.
या आकृतीत हायड्रोजनाच्या अणूचे संपूर्ण आयनीकरण म्हणजेच त्यातील इलेक्ट्रॉन अणुकेंद्रापासून पूर्णपणे अलग झाला असता त्या स्थितीला शून्य ऊर्जा मानले आहे. त्यामुळे या अणूच्या मूळ स्थितीत किंवा कोणत्याही क्षुब्धावस्थेत त्याचे ऊर्जामूल्य ऋण येईल. ऊर्जामूल्य = hc × तरंगांक, म्हणून तरंगांकही ऋण येतील.
n = 1, 2, 3, . . . . . . . . वगैरे प्रमुख पुंजांकांशी संबद्ध असलेल्या ऊर्जा पातळ्या आडव्या रेषांनी दाखविल्या आहेत. एका ऊर्जा पातळीतून दुसऱ्याव पातळीत संक्रमण होऊन वर्णरोषांच्या वेगवेगळ्या श्रेण्या निर्माण होतात. त्या उभ्या बाणयुक्त रेषांनी दाखविल्या आहेत. अणूचे संपूर्ण विदलन झालेली स्थिती n = ¥ या जाड रेषेने दाखविली आहे. या स्थितीत संकेतानुसार ऊर्जा व म्हणून तरंगांक शून्य येतो. उभ्या अक्षावरील तरंगांक ऋण असून सोयीसाठी ऋण चिन्ह गाळले आहे. प्रत्येक ऊर्जा पातळी एकाच रेषेने दाखविली आहे पण प्रत्यक्षात ती एकापेक्षा अधिक ऊर्जा पातळ्यांनी बनलेली असते. या सूक्ष्म विभाजनासंबंधी खाली विविरण केलेले आहे.
वर्णरेषांची सूक्ष्म रचना : बोर यांची हायड्रोजन वर्णपटाची उपपत्ती प्रथम समाधानकारक वाटली, तरी तीत जास्त अभ्यासानंतर पुष्कळ वैगुण्ये आढळून आली. त्यामुळे बोर यांनी सुचविलेल्या मूळ आणवीय संरचनेच्या कल्पनेत अनेक सुधारणा करणे भाग पडले. [⟶ अणु व आणवीय संरचना].
अधिक विभेदनक्षमता असलेल्या वर्णपटदर्शकातून प्रत्येक हायड्रोजन वर्णरेषेचे निरीक्षण केल्यास ती दुहेरी असते, असे दिसून येईल. इतर मूलद्रव्यांच्या वर्णरेषांच्या बाबतीत सुद्धा दुहेरी, तिहेरी किंवा अधिक सूक्ष्म रेषांचे पुंजके आहेत, असे आढळते. या संरचनेला वर्णरेषांची सूक्ष्म रचना म्हणतात. बोर यांच्या सिद्धांतानुसार इलेक्ट्रॉन अणुकेंद्राभोवती फक्त वर्तुळाकार कक्षांतच फिरतो ही मांडलेली आणवीय संरचनेची कल्पना वर्णरेषांच्या सूक्ष्म रचनेचा खुलासा करण्यास अपुरी ठरली. याकरिता आर्नोल्ट झोमरफेल्ड यांनी बोर सिद्धांताचा विस्तार केला व अणूतील इलेक्ट्रॉनाच्या कक्षा विवृत्तीय चपटेपणाशी निगडित असा/हा विवृत्त कक्षेचा परिभ्रमण पुंजांक आणवीय संरचनेच्या कल्पनेत समाविष्ट करण्यात आला. विशिष्ट पुंजांक n साठी / = n-I , n-2, . . . . ., 0 अशी पूर्णांकी मूल्ये असू शकतात. / = n-I ही कक्षा वर्तुळाकार असते व जसजसे / चे मूल्य कमी होत जाते तशी कक्षा जास्त चपटी होते. विशिष्ट कक्षेत इलेक्ट्रॉनाच्या कोनीय परिभ्रमण संवेगाचे (कोनीय गतीचे मान दर्शविणाऱ्या राशीचे) मूल्य = परिभ्रमण परिबल = /h/2p = /h असते. ह्या कल्पनेनुसार हायड्रोजनाच्या वर्णरेषांच्या सूक्ष्म रचनेचा खुलासा मिळत असला, तरी या सिद्धांताच्या आधारे इतर अणूंच्या वर्णरेषांच्या सूक्ष्म रचनेचा पूर्ण खुलासा देता येईना, म्हणून जी. ऊलेनबेक व एस्. गाउडश्मिट यांनी पुढील उपपत्ती दिली. इलेक्ट्रॉन पृथ्वीच्या दैनंदिन परिवलनाप्रमाणे स्वतःच्या अक्षाभोवती परिवलन करीत असतो. त्यामुळे त्याला आणखी एक कोनीय संवेग प्राप्त होतो व याचे मूल्य = परिवलन परिबल = sh असते. s हा परिवलन परिबलदर्शक तिसरा पुंजांक असून त्याचे मूल्य 1/2 असते. त्यानंतर वर्णरेषांच्या सूक्ष्म रचनेचे समाधानकारक स्पष्टीकरण देता आले. या शेवटच्या पुंजांकाने हायड्रोजनाच्या ऑर्थो व पॅरा या दोन आढळलेल्या स्थितींचे योग्य समर्थन होते.
कोष्टक क्र. ६ मध्ये आवर्त सारणीतील वेगवेगळ्या स्तंभांतील मूलद्रव्यांच्या वर्णपटांत वर्णरेषांचे गट कसे मिळतात, हे दाखविले आहे.
जितके वर्णरेषांचे गट असतात तितक्याच ऊर्जा पातळ्यांत ग्रोटियन आलेखात एका रेषेने व्यक्त केलेली प्रत्येक ऊर्जा पातळी विभागली जाते. याला वर्णपट पदांचे बहुगुणनत्व म्हणतात. सामान्यतः जसजसा अणुक्रमांक वाढत जातो तसतसे सूक्ष्म रचनांतर्गत रेषा गटांतील अंतर वाढत जाते (कोष्टक क्र. ७). त्याचप्रमाणे जसजसा रेषांचा तरंगांक कमी होत जातो तसतसे सूक्ष्म रचनांतर्गत सक्ष्म रेषांतील अंतर वाढते.
अणूच्या / या पुंजांकाच्या मूल्यानुसार त्याच्या ऊर्जा पातळीला म्हणजे इलेक्ट्रॉनाच्या कक्षेला एक-अक्षरी नामाभिधान देण्याचा वर्णपटविज्ञानात प्रघात आहे. /= 0 असल्यास (n चे मूल्य काहीही असो) त्या इलेक्ट्रॉनाला s इलेक्ट्रॉन म्हणतात. कोष्टक क्र. ८ मध्ये ही नामाभिधाने दिली आहेत.
इलेक्ट्रॉनाच्या / च्या मूल्यावरून त्या इलेक्ट्रॉनाला व त्यातून उत्पन्न होणाऱ्या वर्णपटाला तेच अक्षर दिले जाते. जसे s इलेक्ट्रॉन, p इलेक्ट्रॉन वगैरे. वर्णपट पदे अशा तऱ्हेने व्यक्त करण्याच्या या पद्धतीवरून संबंधित इलेक्ट्रॉनाची अणूतील स्थिती आपोआप व्यक्त होते व त्यासाठी हा एक संकेत वापरला जातो.
इलेक्ट्रॉनांच्या परिवलनावरून रेषांच्या सूक्ष्म रचनेचे स्पष्टीकरण देता येते. अणूमधील प्रत्येक इलेक्ट्रॉनाला कक्षीय परिभ्रमण परिबल /h इतके असते. या परिबलांचा दर्शक सदिश परिभ्रमण कक्षेला लंब असतो. अणूतील सर्व इलेक्ट्रॉनांच्या परिभ्रमण परिबलांची बेरीज लिहिता येते. आवर्त सारणीच्या अभ्यासावरून असे दिसून येते की, n = १, २ . . . . ही मुख्य कवचे जसजशी भरत जातात तसतसा अणुक्रमांक वाढत जातो. यातील परिभ्रमण परिबलांची बेरीज काढण्याकरिता फक्त शेवटच्या गटातील इलेक्ट्रॉनांचा विचार करणे पुरेसे होते. कारण गट पूर्ण भरला की, परिभ्रमण परिबल आपोआप ० होते. अशा इलेक्ट्रॉनांचे संयुक्त परिभ्रमण परिबल काढतात व हे पुंजांकित असते. त्याचा संबंधित पुंजांक L या चिन्हाने दर्शवितात. L हा नेहमी पूर्णांक असतो. L = ० असल्यास वर्णपट पदाला S पद, L = १ असल्यास P पद, L = २ असल्यास D पद वगैरे. याप्रमामे मोठ्या म्हणजे कॅपिटल अक्षरांनी वर्णपट पद दिग्दर्शित केले जाते. या पुंजांकाकरिता फक्त अपूर्ण कवचातील इलेक्ट्रॉनांचा/मूल्यांचाच संयोग करणे पुरेसे असते. उदा., वेगवेगळ्या / मूल्यांच्या दोन इलेक्ट्रॉनांमुळे निर्माण होणारी Lची संभाव्य मूल्ये व वर्णपट पदे कोष्टक क्र. ९ मध्ये दाखविली आहेत.
यावरून इलेक्ट्रॉनांची वैयक्तिक / मूल्ये /1 व /2 असतील, तर L ची संभाव्य मूल्ये खालीलप्रमाणे मिळतात.
L = /1 + /2, /1 + /2 – /, /1 + /2-२, . . . . . , ∣ /1 – /2 ∣. ∣ /1 – /2 ∣ याने /1 व /2 यांतील घन फरक दर्शविला आहे.
इलेक्ट्रॉनांचे संयुक्त परिवलन परिबल : वरीलप्रमाणेच इलेक्ट्रॉनांच्या परिवलन परिबलांचीही सदिश पद्धतीने बेरीज करून त्यावरून सबंध अणूचे संयुक्त परिवलन परिबल काढता येते. हे संयुक्त परिवलन
|
कोष्टक क्र. ६. आवर्त सारणीतील स्तंभ क्रमांक व त्यांतीलमूलद्रव्यांच्या वर्णरेषांच्या सूक्ष्म रचनेतील रेषांची संख्या. |
|
|
आवर्त सारणीतील स्तंभ क्रमांक १ २ ३ ४ ५ ६ ७ ८ |
वर्णरेषांच्या सूक्ष्म रचनेतील रेषांची संख्या २ १, ३ २, ४ १, ३, ५ २, ४, ६ १, ३, ५, ७ २, ४, ६, ८ १, ३, ५, ७, ९ |
|
कोष्टक क्र. ७ काही दुहेरी रेषांमधील वर्णरेषांच्या तरंगलांब्यांतील फरक. |
||
|
मूलद्रव्य |
अणुक्रमांक |
पहिल्या जोडरेषेतील तरंगलांब्यांमधील |
|
लिथियम |
३ |
०·१५ |
|
सोडियम |
११ |
६ |
|
पोटॅशियम |
१९ |
३४ |
|
रुबिडियम |
३७ |
१४७ |
|
सिझियम |
५५ |
४२२ |
परिबल विशिष्ट पुंजांक S ने दर्शवितात. प्रत्येक उपकवचात दोन इलेक्ट्रॉन असतात व त्यांच्या वैयक्तिक पुंजांक s चे मूल्य 1/2 असते. दोन परिवलनांचे दर्शक सदिश एकाच दिशेने असले, तर दोघांच्या s चे मूल्य धन असते व एकमेकांच्या विरुद्ध असल्यास एकाचे धन आणि दुसऱ्यायचे ऋण असेल. यावरून असे दिसेल की, अपूर्ण कवचात दोन इलेक्ट्रॉन असतील, तर S ची मूल्ये S = + 1/2 +1/2 = 1 किंवा S = +1/2 – 1/2 = 0 ही दोन असू शकतील. जर अपूर्ण कवचातील इलेक्ट्रॉन असतील, तर तिघांचीही दिशा एकच असल्यास S = 1/2 + 1/2 + 1/2 = 3/2 आणि दोघांची एक व तिसऱ्याची विरुद्ध असल्यास
| कोष्टक क्र. ८ अणूंच्या / पुंजांकाच्या मूल्यानुसार ऊर्जा पातळ्यांना देण्यात येणारी नामाभिधाने. | |
|
/ चे मूल्य |
ऊर्जा पातळीचे नामाभिधान |
|
० १ २ ३ ४ ५ |
S P D F G वगैरे |
|
कोष्टक क्र. ९. वेगवेगळ्या /च्या मूल्यांच्या दोन इलेक्ट्रॉनांमुळे निर्माण होणारी Lची संभाव्य मूल्ये वर्णपट पदे |
|||
|
/1, |
/2 |
L |
वर्णपट पदे |
|
० १ १ २ |
१ १ २ २ |
१ २, १, ० ३, २, १ ४, ३, २, १, ० |
P D, P, S F, D, P G, F, D, P, S |
S = 1/2 + 1/2 – 1/2 = 1/2 अशी त्यांची संयुक्त परिवलन परिबल मूल्ये येतील. यावरून अपूर्ण कवचातील इलेक्ट्रॉनांच्या निरनिराळ्या संख्यांनुसार येणारी S ची संभाव्य मूल्ये कोष्टक क्र. १० मध्ये दिली आहेत.
|
कोष्टक क्र. १०. अपूर्ण कवचातील इलेक्ट्रॉनांच्या निरनिराळ्या संख्यांनुसार येणारी S ची संभाव्य मूल्ये व वर्णरेषांचे बहुगुणनत्व |
|||
|
आवर्त सारणीतील स्तंभ |
अपूर्ण कवचातील इलेक्ट्रॉनांची संख्या |
Sची संभाव्य मूल्ये |
बहुगुणनत्व (= 2S +1) |
|
१ २ ३ ४ ५ ६ ७ ८ |
१ २ ३ ४ ५ ६ ७ ८ |
१/२ ०,१ १/२, ३/२ ०, १, २ १/२, ३/२, ५/२ ०,१, २, ३ १/२, ३/२, ५/२, ७/२ ०,१, २, ३,४ |
२ १, ३ २, ४ १, ३, ५ २, ४, ६ १, ३, ५, ७ २, ४, ६,८ १, ३, ५, ७, ९ |
वरील कोष्टकावरून असे दिसून येते की, संबंधित वर्णपट पदाचे बहुगुणनत्व 2S + 1 या सूत्राने दिले जाते.
अपूर्ण कवचातील एकूण इलेक्ट्रॉनांचे परिभ्रमण परिबल L h/2p व परिवलन परिबल S h/2p यांची सदिश बेरीज ही इलेक्ट्रॉनांचे निष्पन्न परिबल देते. त्यांचे मूल्य J h/2p असते. J हा नवीन पुंजांक असून त्याची मूल्ये १/२ च्या पूर्णांकी पटीतच म्हणजे १/२ २/३, ३/२ . . . . वगैरे असू शकतात. J ची ही संभाव्य मूल्ये L व S यांची मूल्ये व त्यांच्यामधील कोन यांवर अवलंबून असतात. ही मूल्ये खालील प्रमाणे मिळतात.
J = L + S, L + S -1, L + S-2,. . . . . . , L– S
यावरून असे दिसते की, विशिष्ट L व S साठी J च्या एकूण संभाव्य मूल्यांची संख्या (2 S + 1) असते. तसेच L नेहमी पूर्णांक असतो पण सम संख्येच्या इलेक्ट्रॉनांसाठी पूर्णांक असतो, तर विषम संख्येच्या इलेक्ट्रॉनांसाठी तो १/२ च्या पूर्ण पटीत असतो. त्यानुसार J ची मूल्ये पूर्णांक किंवा १/२ च्या पूर्ण पटीत असतात.
दोन पदांमध्ये प्रमुख पुंजांक n व परिभ्रमम पुंजांक L यांची मूल्ये समान असली, तरी त्यांनी दिग्दर्शित होणाऱ्या अणूंच्या ऊर्जा सारख्या नसतात J च्या मूल्यानुसार या ऊर्जा मूल्यांत थोडा फरक पडतो. निम्म्यापेक्षा कमी भरलेले अपूर्ण कवच किमान J मूल्याशी संलग्न असलेल्या अणुस्थितीची ऊर्जा किमान असते परंतु कवच निम्म्यापेक्षा जास्त भरलेले असल्यास किमान ऊर्जा स्थिती कमाल . J मूल्याशी संलग्न असते.
J च्या या परिणामामुळे ऊर्जा मूल्ये व तत्संलग्न वर्णपट पदे ही जवळजवळ समान मूल्ये असलेल्या उपपातळ्यांचे समुदायच होतात. एका उपपातळीतून दुसऱ्या उपपातळीत संक्रमणे झाल्यामुळे परस्परांच्या अगदी निकट असलेल्या वर्णरेषांचे गट उत्सर्जित होतात. हीच वर्णरेषांच्या सूक्ष्म रचनेची उपपत्ती होय.
वरील विवेचनात J काढण्यासाठी प्रथम सर्व / मूल्यांची सदिश बेरीज करून L काढला व त्याप्रमाणेच बेरजेने S काढला आणि L व S यांच्या संयोगाने J काढला. या पद्धतीला एच्. एन्. रसेल व एफ्. ए. साँडर्स या संशोधकांच्या नावांवरून रसेल-साँडर्स संयोग असे म्हणतात किंवा L–S संयोग असेही म्हणतात.
उच्च भाराच्या अणूमध्ये असे दिसते की, इलेक्ट्रॉनाचे परिभ्रमण परिबल व परिवलन परिबल परस्परांशी घनिष्ठपणे संलग्न झालेली असल्याने त्या त्या इलेक्ट्रॉनाच्या / व s यांचा संयोग होऊन व्यक्तिगत j मिळतो. सर्व इलेक्ट्रॉनांचा j चा परत संयोग होऊन संयुक्त J मिळतो. या पद्धतीला j-j संयोग म्हणतात. संपूर्णपणे j-j संयोग फारसा आढळत नाही, तर L–S संयोग जेव्हा लागू पडत नाही, तेव्हा बहुधा या दोन संयोगांच्या मधली स्थिती असते.
पहा : वर्णपटविज्ञान १
“