वंटन सिद्धांत

वंटन सिद्धांत : प्रयोग, निरीक्षण इ. प्रकारे विविध प्रकारची जी सांख्यिकीय माहिती अथवा आकडेवारी गोळा होते तिचा विचार करून तिच्यापासून योग्य अंदाज आणि अनुमाने काढण्यासाठी सांख्यिकीय सिद्धांताचे साहाय्य घ्यावे लागते. आधुनिक वैज्ञानिक पद्धतीत सांख्यिकीय सिद्धांताला महत्त्वाचे स्थान आहे. सांख्यिकीय सिद्धांत आणि त्याचे गणित, म्हणजे गणितीय सांख्यिकी, हे ⇨संभाव्यता सिद्धांत या शुद्ध गणिताच्या शाखेवर आधारलेले असून गणितीय सांख्यिकीला अनुप्रयुक्त गणिताची शाखा समजतात. ऐतिहासिक दृष्ट्या संभाव्यता सिद्धांत बराच जुना आहे पण गणितीय सांख्यिकी ही अलीकडच्या काळातील असून तिचा विशेष विकास साधारणपणे १९२० नंतर झालेला आहे.

वंटन सिद्धांत हा गणितीय सांख्यिकीतील मूलभूत महत्त्वाचा भाग आहे. त्यात संभावी चल व त्यांची वंटने (वितरणे) यांचा विचार होतो. इंग्रजी भाषेत रँडम (random) या शब्दाचा वापर (१) संभाव्यतायुक्त म्हणजे संभाव्यता असलेला आणि (२) क्रमरहित म्हणजे विशिष्ट क्रम नसलेला अशा दोन अर्थांनी केलेला आहे. या दोन्ही अर्थांत अप्राक्कथनीयकता म्हणजे भाकीत करता न येणे हा साधारण गुण आहे. संभाव्यता सिद्धांतात क्रमविरहिततेची अथवा यदृच्छतेची कल्पना कोणत्या ना कोणत्या अवस्थेला पूर्वज्ञानाधिष्ठित गृहीत कल्पना मानावी लागते. अशा रीतीने हे दोन अर्थ एकमेकांशी निगडित असले, तरी पुढील विवेचनात अर्थसुलभतेसाठी पहिल्या अर्थी ‘संभावी’ (उदा., संभावी चल) आणि दुसऱ्याअर्थी ‘यदृच्छ’ (उदा., यदृच्छ निवड, यदृच्छ प्रतिदर्श अथवा नमुना) हे शब्द वापरले आहेत.

संभावी चल : यालाच ‘चर’ अशीही संज्ञा वापरतात. यापुढील विवरणात संभावी चल याऐवजी नुसतीच ‘चल’ ही संज्ञा काही ठिकाणी वापरली आहे. संभावी चलाचा मुख्य गुण असा की, त्याच्या शक्य मूल्यांपैकी, तो विवक्षित प्रसंगी कोणते विवक्षित मूल्य अथवा मूल्ये धारण करील हे सांगता येत नाही, पण त्याविषयी संभाव्यतात्मक विधाने करता येतात. अशा चलाच्या वंटनाचा विचार करताना त्याचा गणितीय स्वभाव अथवा गुणधर्म यांचा म्हणजे त्याची शक्य मूल्ये कोणती, त्यांची संभाव्यता किती, संभाव्यतेचा गणितीय नियम कोणता, इतर गणितीय गुमधर्म कोणते इत्यादींचा विचार होतो.

प्रथम संभावी चलाची कल्पना स्पष्ट होण्यासाठी दोन उदाहरणे घेऊ. (१) तीन नाणी एकदम फेकली, तर फेकीत मिळालेल्या छापांची संख्या ०, १, २, ३ यांपैकी कोणतीही असू शकेल. विविक्षित फेकीत हे मूल्य अप्राक्कथनीय असले, तरी कोणते मूल्य किती संभाव्य असेल हे सांगणे शक्य असते. उदा., नाणी निरभिनत म्हणजे निर्दोष (कोणतीही विशिष्ट बाजूच वर येण्यास अनुकूल नसलेली) असल्यास छापांची संख्या अनुक्रमे ०, १, २, ३ असण्याची संभाव्यता १/८, ३/८, ३/८, १/८ असेल हे संभाव्यता सिद्धांतातील सोपी प्रमेये वापरून समजते. (२) सहा बाजूंवर १, २, ३, ४, ५, ६ अंक अथवा ठिपके असलेला घनाकृती फासा फेकला, तर विविक्षित फेकीक कोणते दान पडेल हे निश्चितपणे सांगणे अशक्य आहे पण फासा निरभिनत असल्यास यांपैकी कोणतेही दान पडण्याची संभाव्यता १/६ असते. वरील उदाहरणांतील छापांची संख्या व फाशाचे दान हे संभावी चल आहेत. संभावी चल केवळ नाणीफेक, फासाफेक यांसारख्या सापेक्षतया अल्प महत्त्वाच्या घटनांत आढळतात, असे समजू नये. अंमळ विचार केल्यास सहज कळून येईल की, किरणोत्सर्गी अणूतून निघणारे विद्युत् भारित कण, वाटाण्याच्या शेंगेतील दाणे, कुटुंबातील मुले, परीक्षेतील गुण, दुकानातील दैनंदिन विक्री, वार्षिक पर्जन्यमान, दर दिवशी अथवा सप्ताहात एखाद्या शहरात घडलेले अपघात इ. विविध क्षेत्रांत आढळणारी सांख्यिकीय लक्षणे ही सर्व संभावी चलाची उदाहरणे आहेत. ज्या घटनांची वारंवार आवृत्ती होते पण ज्यांचे परिणाम अप्राक्कथनीय स्वरूपाचे असतात, अशा कित्येक घटनांचा अभ्यास करताना त्यांच्याशी निगडित असलेल्या मोजण्याजोग्या अथवा मापण्याजोग्या सांख्यिकीय लक्षणांना संभावी चल मानणे प्राप्त असते.

संभावी चलाविषयीची आधुनिक विवरण पद्धतीत व्याख्येकरिता घटना अवकाशाच्या कल्पनेचा आधार घेतात. संतत चलांचा विचार करताना ही कल्पना करावी लागते आणि माप सिद्धांताचे [⟶ माप व समाकलन] साहाय्य घ्यावे लागते. वंटन सिद्धांताच्या प्राथमिक विवेचनासाठी इतक्या खोलात न शिरता पुढील व्याख्या पुरेशी होते. एखाद्या सत्-मूल्यी [⟶संख्या] चलाविषयी तो धारण करू शकत असलेल्या मूल्यांबद्दल संभाव्यता विधाने मांडता येत असली, तर त्याला संभावी चल म्हणावे.

संभावी चलाविषयी मूलभूत महत्त्वाचे गणितीय फलन [गणितीय संबंध ⟶फलन] म्हणजे वंटन फलन F (x). संभाव्यता सिद्धांतातील संकेत चिन्हे वापरून याची व्याख्या पुढीलप्रमाणे : संभावी चल X एकमितीय असल्यास त्याचे वंटन फलन

           F (x) = P(X ≤ x)                …           …           (१)

येथे उजव्या बाजूचा अर्थ X हा x हून लहान अथवा समान मूल्य घेण्याची संभाव्यता असा आहे. (संभावी चल मोठ्या अक्षराने व त्याचे मूल्य लहान अक्षराने दाखविण्याचा संकेत आहे. सोयीसाठी कित्येकदा फक्त लहान अक्षरही वापरण्यात येते). वंटन फलनाचे पुढील गुणधर्म त्याच्या व्याख्येवरून सहज मिळतात.

              

शेवटच्या समीकरणावरून दिसून येते की, वंटन फलन हे न-ऱ्हासी (ऱ्हास न पावणारे) फलन असते.

प्रकार : संभावी चलाचे मुख्य प्रकार दोन : (१) पृथक व (२) संतत. प्रारंभी दिलेली दोन्ही उदाहरणे पृथक संभावी चलाची होती.  

पृथक् संभावी चल : या प्रकारचा चल x₁, x₂, ….x_j… याप्रमाणे फक्त पृथक् मूल्ये घेऊ शकतो आणि त्यांची संख्या सांत अथवा अनंत असल्यास गणनीय असते. त्याचे वंटन

                    P_i = P (x_i)=P (X =x_i) (i = 1, 2, . . .)  … (३)

या संभाव्यता श्रेणीने पूर्णपणे निर्देशित होते. त्याला पृथक् संभाव्यता फलन अथवा वारंवारता फलन असे म्हणतात. त्याचे पुढील गुणधर्म सरळच आहेत. 

               

संतत संभावी चल : उंची, वजन, तापमान यांसारखे अनेक संभावी चल संतत स्वरूपाचे असतात. व्यवहारात चलाच्या व्याप्तीचे (कक्षेचे) सांत भाग पाडून त्यांना पृथक मानता येते पण गणितीय सैद्धांतिक काटेकोरपणा सांभाळण्यासाठी माप सिद्धांताचा आधार घ्यावा लागतो याचा उल्लेख वर आलाच आहे. ते सर्व गृहीत धरून संतत संभावी चलाची व्याख्या अशी: जर F (x) सर्वत्र संतत असेल आणि F'(x) =f(x) हा अवकलज [⟶ अवकलन व समाकलन] सर्वत्र अस्तित्वात असून (अपवादात्मक मूल्ये सोडल्यास) संतत असेल, तर त्या चलाला संतत चल म्हणतात. यांवरून

 

---

हे सूत्र निघते. व्याख्येवरून P (x &lt X ≤ x + δx) = F'(x) δ x= f (x) δ x म्हणून P(X = x) =0 हा सीमा निष्कर्ष निघतो. यामुळे संभावी चल संतत असल्यास P (a &lt X ≤ b) व P (a &lt X &lt b) यांची मूल्ये समान होऊन

हे सूत्र मिळते. फलन f(x) याला संभाव्यता घनता फलन अथवा वारंवारता फलन म्हणतात. या प्रकाच्या चलाचे वंटन F (x) किंवा f (x) फलनाने पूर्णपणे निर्देशित होते.

हे निष्कर्ष सहजसिद्ध आहेत. 

रीमान समाकलाऐवजी लबेग समाकल [⟶ माप व समाकलन] योजून पृथक् व संतत चलांची सूत्रे (४) आणि (५) यांत दिलेली वंटन फलने F (x)

 

वर उल्लेखिलेल्या संतत व पृथक् संभाव्यतांचे अखंड द्रव्यमान असलेला गज आणि खंडित द्रव्यमान बिंदू असलेली तार यांच्याशी जे सादृश्य आहे त्यामुळे वंटन विषयात संभाव्यतेच्या घनतेची कल्पना स्वाभाविकपणे आली. हे सादृश्य इतर विवेचनातही काही अंशी दिसून येईल, उदा., द्रव्यमान मध्य आणि माध्य (सरासरी). याच अनुरोधाने या वंटनांना रेखा वंटने अथवा एकमितीय वंटने असेही म्हणतात.

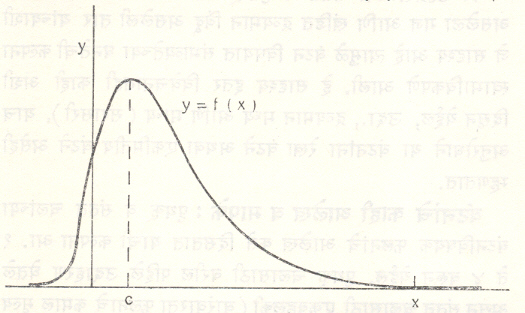
वंटनांचे काही आलेख व मापके : पृथक् व संतत चलांच्या वंटनविषयक फलनांचे आलेख कसे दिसतात याची कल्पना आ. १ ते ४ वरून येईल. पृथक् चलासाठी वरील पहिले उदाहरण घेतले असून संतत चलासाठी एकबहुलकी (वारंवारता फलनाचे कमाल मूल्य देणारे संभावी चलाचे एकच मूल्य असलेले) विषम वंटन घेतले आहे. 

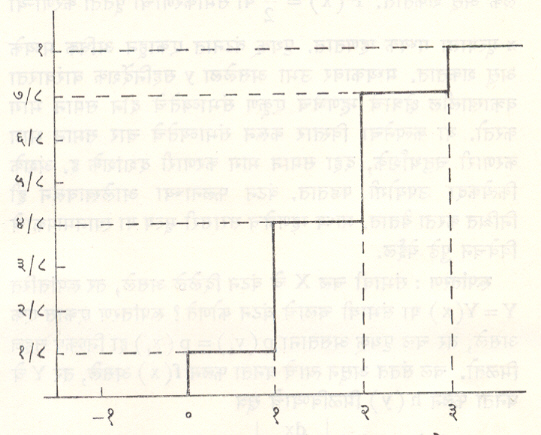
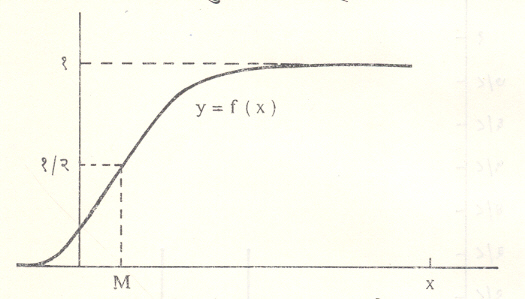
पृथक् चलाच्या संभाव्यता फलनाचा आलेख स्तंभालेख असतो आणि वंटन फलनाचा आलेख पायऱ्यांनी युक्त असतो. संतत चलाचे घनता वक्र संतत वक्र असून त्याखालचे क्षेत्रफळ एक एकक असते. त्याच्या वंटन वक्राचा आकार इंग्रंजी अक्षर S ताणल्यासारखा दिसतो. त्याला ‘ओजाइव्ह वक्र’ म्हणतात.

येथे बहुलक व मध्यक या स्थानमापकांचा उल्लेख करणे सोयीचे होईल. वारंवारता फलनाचे f (x) चे किंवा p (x) चे कमाल मूल्य देणाऱ्या x मूल्याला संभावी चलाचा बहुलक म्हणतात. महत्त्वाची अनेक वंटने एकबहुलकी आहेत पण काहींना एकापेक्षा अधिक बहुलके असू शकतात. F(x) =¹/₂ या समीकरणाची पूर्तता करणाऱ्या x मूल्याला मध्यक म्हणतात. पृथक् वंटनात एकाहून अधिक मध्यके असू शकतात. मध्यकावर उभा असलेला Y सहनिर्देशक वारंवारता वक्राखालील क्षेत्राचे म्हणजेच एकूण संभाव्यतेचे दोन समान भाग करतो. या कल्पनेचा विस्तार करुन संभाव्यतेचे चार समान भाग करणारी चतुर्थांशके, दहा समान भाग करणारी दशांशके इ. अंशके कित्येकदा उपयोगी पडतात. वंटन फलनाच्या आलेखावरून ही निश्चित करता येतात. माध्य म्हणजेच सरासरी मूल्य या स्थानमापकाचे विवेचन पुढे येईल.

---

रूपांतरण : संभावी चल X चे वंटन दिलेले असले, तर रूपांतरित Y=Y(x) या संभावी चलाचे वंटन कोणते? रूपांतरण एकास-एक असले, तर चल पृथक् असताना P(Y_i)=P(X_i) हा निष्कर्ष सहज मिळतो. चल संतत असून त्याचे घनता फलन f(x) असले, तर Y चे घनता फलन h(y) मिळविण्याचे सूत्र

असल्याचे सिद्ध करता येते. बहुमितीय संभावी चलासाठी वरील सूत्राचे व्यापकीकरण होऊ शकते. 

माध्य अथवा अपेक्षित मूल्ये : X संभावी चलाचे फलन g(X) यासंबंधीच्या खालील निश्चित समाकलाला अथवा श्रेढीला g(x) चे माध्य किंवा गणितीय अपेक्षित म्हणतात व ते E या संकेत चिन्हाने दर्शवितात.

चल संतत असला, तर समाकल आणि पृथक् असला, तर श्रेढी मिळते. काटेकोरपणाने पाहिले, तर अपेक्षिताच्या अस्तित्वासाठी सूत्र (९) मधील समाकल अथवा श्रेढी केवल अभिसारी असावी लागतात. गणितीय अपेक्षित हे संभाव्याता हे संभाव्यता भार देऊन काढलेले भारित माध्य असते. गणितीय अपेक्षिताविषयी खालील सूत्रे महत्त्वाची आहेत.

(१) X व Y हे संभावी चल असले, तर

E [g(X)+h(Y)] = E [g(X)]+E[h(Y)]…..(१०)

(२) आणि ते निरवलंबी (परस्परांवर अवलंबून नसलेले) संभावी चल असले, तर

E [g(X).h(Y)]=E [g(X)].E[h(Y)]…..(११)

(वरील सूत्रातील चल बहुमितीय आहेत, त्यांचे अधिक विवेचन याच नोंदीत पुढे येणार आहे). या सामान्य सूत्रावरून निघणारी सोपी सूत्रे अशी.

         E(aX+b)=aE(X)+b

         E(X+Y)= E(X)+E(Y)   …             …             (१२)

आणि X, Y निरवलंबी असता,

         E (XY)=E(X).E(Y)        …            …             (१३)

परिबल : खालील गणितीय अपेक्षिते विशेष महात्तवाची आहेत. 

याला r कोटीचे परिबल म्हतात [परिबल ही संज्ञा येथे यामिकीतील परिबल संकल्पनेशी असलेल्या सादृश्यावरून वापरलेली आहे ⟶ यामिकी]. यांपैकी पहिल्या कोटीच्या परिबलाला E(X)=m ला संभावी चलाचे माध्य असे नाव आहे(आरंभीच्या दोन उदाहरणांतील माध्ये अनुक्रमे ^३/_२ व ^७/_२ आहेत हे ∑X_iP_i या बेरजेवरून निघते). माध्य हे रेखीय संभाव्यता द्रव्यमानाचे द्रव्यमान मध्य म्हणता येईल.

परिबले कोणत्याही आदिबिंदूभोवती घेता येतात. सूत्र (१४) मधील परिबले शून्य आदिबिंदूभोवती आहेत. आदिबिंदू c असता परिबल E(X-c)^r होईल. दोन वेगळ्या आदिबिंदूंभोवती घेतलेल्या परिबलांचे एकमेकांत रूपांतर करता येते. आदिबिंदू m कल्पून काढलेली परिबले विशेष महत्त्वाची असून त्यांना केंद्रीय परिबले म्हणतात आणि ती μ_r या चिन्हाने दर्शवितात.उदा., 

           μ_० =1 μ₁ =0 μ_r =E(X-m)^r r ≥ 2 … (१५)

द्वितीय केंद्रीय परिबलाला विचरण असे नाव असून त्याला 

                   Var(X)= μ₂ =E(X-m)² …..        ….(१६)

याप्रमाणे चिन्हांकित करतात. विचरण हे रेखीय द्रव्यमान वंटनाचे द्वितीय परिबल (म्हणजेच निरूढी परिबल) म्हणता येईल. विचरणाचे वर्गमृळ √μ₂ = σ यास प्रमाण विचलन म्हणतात. ही दोन्ही मापके चलाची चलनशीलता दर्शवितात. तिसरी व चौथी केंद्रीय परिबलेही महत्त्वाची समजतात. त्यांवर आधारलेली γ₁ =( μ₃/ μ₂^3/2) आणि γ₂ =( μ₄/ μ₃²)-3 या मापकांना अनुक्रमे विषमतांक आणि ककुदतांक अशी नावे आहेत. वंटन सममित असल्यास त्याचा μ₃ आणि म्हणून γ₁ शून्य असतात, यामुळे शून्येतर γ₁ घनता वक्राची विषमता दर्शवितो, ही पहिल्या मापकामागील कल्पना आहे. घनता वक्र अधिक उन्नत असल्यास γ₂ अधिक होईल आणि कमी उन्नत असल्यास γ₂ कमी होईल, यावर हे दुसरे मापक आधरले आहे. सी, एफ्. गौस (१७७७-१८५५) यांच्या प्रसामान्य (नॉर्मल) वंटनात ही दोन्ही शून्य असतात. तेव्हा दिलेल्या घनता वक्राची या बाबतीत प्रसामान्य वक्राशी तुलना करणारी ही मापके आहेत. प्रसामान्य वंटनाचे विवरण पुढे दिले आहे. या दोन मापकांऐवजी β₁ = μ₃²/ μ₂³ आणि β₂ = μ₄/ μ­₂² ही मापकेही वापरतात. 

परिबल जनक फलन, लक्षण फलन : अपेक्षिताचा एक महत्त्वाचा

 

या परिबल जनक फलन म्हणतात, कारण त्याचा विस्तार केल्यास

अशी सूत्रे मिळतात. या विस्तारात याचे सहगुणक असतात. म्हणून वरील नाव सार्थ आहे. परिबल जनक फलनापासून  

असे फलन घेऊन त्याचा विस्तार केल्यास मिळणाऱ्या k_r सहगुणकांना संचयक असे नाव आहे. M (θ) च्या विस्तारातील सहगुणक X च्या आदिबिंदूवर अवलंबून असतात पण K (θ) मधील सहगुणक (K₁ हा पहिला संचयक सोडल्यास) आदिबिंदूवर अवलंबून नसतात हा संचयकांचा विशेष गुण आहे. संचयक व परिबले यांचे एकमेकांत रूपांतर होते. उदा., केंद्रीय परिबल घेतल्यास k₁= m₁ k₂ = μ₂ k₃ = μ₃ k₄ = μ₄-3 μ₂²

k₅ = μ₅– 10 μ₂μ₃

K₆ = μ₆ – 15 μ₂μ₄ – 10 μ₃² + 30 μ₂³ वगैरे … (१९) 

संचयकांचा उपयोग केल्यास γ₁ =K₃/k₂^3/2 γ2  = K₄/k₂² अशी या मापकांना सुटसुटीत रूपे मिळतात .

परिबल जनक फलनातθ =  it घेऊन  मिळणाऱ्या

Φ(t)= E(e^itx)

या फलनास वंटनाचे लक्षण फलन म्हणतात. याचाही उपयोग परिबले शोधण्यासाठी होतो पण त्याचा विशेष गुण असा की, हा समाकल नेहमीच अभिसारी असतो. तसेच साधारणपणे असे म्हणता येते की, कोणत्याही वंटनाचे विशिष्ट असे खास लक्षण फलन असते आणि उलटपक्षी प्रत्येक लक्षण फलनास अनुरूप असे एकमेव वंटन असते. हे वंटन मिळविण्याचे गणिती सूत्रही सांगता येते, ते असे

याला व्यस्तीकरण सूत्र म्हणतात. परिबल जनक व लक्षण फलन हे घनता फलनाची अनुक्रमे लाफ्लास व फूर्ये रूपांतरे आहेत व त्यांचा त्या दृष्टीने विचार करणे कित्येकदा सोयीचे असते[⟶ समाकल समीकरणे व रूपांतरे]. 

---

चेविशॉव्ह असमा : वंटन फलन F (x) पूर्णपणे माहीत असेल तेव्हा संभावी चल निरनिराळ्या अंतरालांत असण्याची संभाव्यता किती हे सूत्र (२) वरून सांगता येते. पण F (x) माहीत नसून वंटनाची केवळ पहिली काही परिबले अथवा तत्सम लक्षणे माहित असता अशी संभाव्यता विधाने करणे सोपे नाही. पी. एल्. चेविशॉव्ह (१८२१-९४) या रशियन गणितज्ञांनी अशा अपुऱ्या ज्ञानाच्या आधारानेही कित्येक संभाव्यता विधाने असमांच्या स्वरूपात सिद्ध केली. त्यांपैकी एक महत्त्वाची असमा अशीः संभावी चल X याचे माध्य m आणि प्रमाण विचलन s असल्यास  

ही असमा माध्यापासून दूरचे मूल्य धारण करण्याच्या संभाव्यतेचा ऊर्ध्व बंध देते. अशा तऱ्हेचा संभावी चल माध्याहून दूर दूर अंतरावर असण्याची संभाव्यता कमी कमी होत जाते, हेही तिच्यावरून स्पष्ट होते. बहुतेक वंटनांच्या बाबतीत हे ऊर्ध्व बंध अंतरालीय संभाव्यतेच्या यथार्थ मूल्यापेक्षा खूपच मोठे असतात, असे प्रत्ययास येते. पण याचे कारण म्हणजे या असमेत वंटनांच्या पुऱ्या ज्ञानाचा, F (x) चा, उपयोग न करता त्रुटित ज्ञानाचा, केवळ माध्य व प्रमाण विचलन यांचाच, उपयोग केलेला आहे. फार काय एवढे त्रुटित ज्ञान असता ही असमा सर्वोत्कृष्ट आहे आणि त्या ज्ञानाच्या जोरावर याहून सूक्ष्म संभाव्यता विधाने करता येणार नाहीत, हेही सिद्ध करता येते.

महत्त्वाची वंटने : महत्त्वाच्या वंटनांविषयी ठळक माहिती खाली दिली आहे, प्रथम पृथक् वंटनांचे व नंतर संतत वंटनांचे विवरण केलेले आहे.

महत्त्वाची पृथक् वंटने : द्विपदी वंटन: समजा अनेकदा आवृत्ती होणारी एखादी घटना फक्त दोन प्रकारे घडते: इष्ट प्रकारे घडणे म्हणजे ‘यश’ आणि दुसरा प्रकार म्हणजे ‘अपयश’. दरवेळी यशाची संभाव्यता p आणि अपयशाची q = 1 – p आहे असे समजू. अशा तऱ्हेच्या पुनरावृत्त होणाऱ्या घटनेला द्विपदी ‘खेळी’ म्हणण्याची प्रथा आहे. उदा., नाण्याच्या दर फेकीला द्विपदी खेळी म्हणता येईल. अशा n खेळीत मिळणाऱ्या यशांची संख्या याचे मूल्य ०, १, २, ……, n यांपैकी कोणतेही असू शकते. संभाव्यात सिद्धांताची तत्त्वे वापरून या चलाचे संभाव्यता फलन

P (x) = P (X = x) = C (n, x) p^x q^n-x

        X = 0, 1, 2, ….. , n  … … (२२)

याप्रमाणे मिळते. येथे C (n, x) हा द्विपदी सहगुणक आहे, त्यांचे मूल्य n! / x! (n-x)! आहे. उजवीकडील पद (q + p)ⁿ या द्विपदी विस्तारात आढळते, म्हणून या संभावी चलाला द्विपदी चल म्हणतात. तसेच म्हणजे वंटनांची दुसरी अटही पूर्ण होते. प्रस्तुत नोंदी लेखातील आरंभीचे पाहिले उदाहरण n = 4, p= ¹/₂ ने निर्दिष्ट होणाऱ्याद्विपदी चलाचे आहे. व्यवहारात द्विपदी चलाचे प्रतिमान पुष्कळदा उपयोगी पडते. n व P या प्रचलांच्या वेगवेगळ्या मूल्यांप्रमाणे द्विपदी चलाची P (x) व F (x) ही फलने देणारी अनेक प्रकारची विस्तृत कोष्टके उपलब्ध आहेत. द्विपदी चलाचे गणितीय विशेष असेः E (x) = np Var (X) = npq μ₃ = npq (q – p)

μ₄=3n²p² q² + npq (1-6pq). तसेच जेव्हा n ⟶∞γ₁⟶ 0 γ₂ ⟶ 0. लक्षण फलन φ(t) = (q + pe^it)ⁿ आणि त्यापासून वरील परिबले सहज मिळतात.

द्विपदी चलाविषयी पुढील निष्कर्ष महत्त्वाचे आहेत : (१) अनुक्रमे (n₁, p) व (n₂, p) याप्रमाणे समान p असलेल्या दोन निरवलंबी द्विपदी चलांची बेरीज हा द्विपदी चल (n₁ + n₂,p) असतो. याला जननाचा गुणधर्म म्हणतात. याच्या आधाराने समान यश संभाव्यता असलेले स्वतंत्र खेळींचे गट एकत्र करून त्यांचा मोठा गट बनविता येतो. (२) यश-संख्येची वारंवारता x/n ही n ⟶∞ असता सीमेत p प्रत जाते. याकोप बेर्नुली (१६५४-१७०५) या फ्रेंच गणितज्ञांच्या नावावरून याला बेर्नुली प्रमेय म्हणतात. यश-संख्येची वारंवारता x/n ही मोठी असल्यास p या यश-संभाव्यतेहून फारशी वेगळी असण्याचा फारसा संभव नाही असा याचा अर्थ असल्यामुळे सांख्यिकीय अनुमान मीमांसेत हा निष्कर्ष मूलभूत महत्त्वाचा आहे. (३) द्विपदी चल X वरून कल्पिलेला प्रमाणित चल (X- np) / √npq याचे वंटन n ⟶ ∞ असता सीमेत प्रसामान्य वंटनाप्रत पावते. [संभावी चल X चे माध्यम m व प्रमाण विचलन σ असल्यास (X-m) / σ या चलास प्रमाणित चल म्हणतात]. हे प्रमेय केंद्रीय सीमा प्रमेयावरून अथवा अन्य प्रकारे सिद्ध करता येते. त्याला आब्राआम द ग्वाव्हर (१६६७-१७५४) या गणितज्ञांच्या नावावरून द ग्वाव्हर प्रमेय म्हणतात. सैद्धांतिक महत्त्वाप्रमाणे त्याला व्यावहारिक महत्त्वही आहे. कारण त्यामुळे n मोठा असता द्विपदी संभाव्यतेचे अंदाजी गणन प्रसामान्य वंटनाच्या कोष्टकावरून करता येते (प्रसामान्य वंटन व केंद्रीय सीमा प्रमेय यांचे विवेचन पुढे दिले आहे).

प्वासाँ वंटन : याचे नाव सिमेआँ देनिस प्वासाँ (१७८१-१८४७) या फ्रेंच गणितज्ञांच्या नावावरून पडले आहे. हा चल ०, १, २, … …, ∞ ही अनंत मूल्ये

           P(x) = e^-m m^x/x !  …  …      (२३)

या नियमानुसार घेतो. या वंटनाचे माध्य व विचरण समान म्हणजे m एवढे असून सर्व संचयकही m एवढे असतात, ही या वंटनाची वैशिष्ट्यपूर्ण लक्षणे समजली जातात. लक्षण फलन

φ (t) = exp (-m +me^it) यावरून वरील निष्कर्ष सहज निघतात. हे वंटन द्विपदी वंटनावरून सीमा-क्रियेने निघते, हा त्याचा दुसरा विशेष होय. द्विपदी (n, p) वंटनात n ⟶∞ P ⟶ 0 np = m अशी सीमावर्ती प्रक्रिया योजिल्यास हे सिद्ध होते. याचा व्यावहारिक उपयोग असा की, अनेकदा आवृत्त होणाऱ्या दुर्मिळ घटनांचा विचार करण्यासाठी प्वासाँ प्रतिमान वापरता येते. किरणोत्सरर्गि अणूतून निघणारे विद्युत् कण, ठराविक अवधित होणारे अपघात, दूरध्वनी केंद्रात ठराविक कालांतरात येणाऱ्या संदेशांची संख्या इ. चलांचे वंटन या प्रकारचे असल्याचे दिसून येते. स्थलावकाश व कालावकाश यांमध्ये घडणाऱ्या कित्येक ⇨यदृच्छ प्रक्रियांत आढळणारी सीमावर्ती वंटने या स्वरूपाची असतात. या वंटनाचे p(x) व F(x) या फलनांची m च्या वेगवेगळ्या मूल्याप्रमाणे विस्तृत कोष्टके उपलब्ध आहेत. या वंटनालाही जनन गुणधर्म आहे : माध्य m₁ व m₂ असलेल्या दोन निरवलंबी प्वासाँ चलांची बेरीज m₁ + m₂ माध्य असलेला प्वासाँ चल असते.

अतिगुणोत्तरीय वंटन : एकूण N वस्तूंपैकी Np व वस्तू एका तऱ्हेच्या असल्या व राहिलेल्या Nq = N (l – p) दुसऱ्या तऱ्हेच्या असल्या आणि या N वस्तूंमधून n वस्तू यदृच्छपणे निवडल्या व त्यांमध्ये x पहिल्या तऱ्हेच्या व n-x दुसऱ्या तऱ्हेच्या आढळल्या, तर x चे संभाव्यता वंटन

असते. यातील उजवीकडील पद अतिगुणोत्तरीय श्रेढीच्या [⟶श्रेढी] विस्तारात येते, यावरून वंटनास हे नाव मिळाले आहे. याचे माध्य n p व विचरण (N-n) npq / (N-1) आहे. वरील वंटनापासून N ⟶∞ असता नेहमीचे (n, p) द्विपदी वंटन मिळते.

या दोन वंटनांकडे पाहण्याचा आणखी एक दृष्टिकोन असा : वर उल्लेखिलेल्या निवडीत सर्व वस्तू समान संभाव्यतेने निवडलेल्या असून एकदा निवडलेली वस्तू पुन्हा N वस्तुसंचात समाविष्ट केलेली नसते. अशा निवडीला पुनःस्थापनरहित निवड म्हणतात. उलट निवडलेली वस्तू दर वेळी पुन्हा N वस्तुसंचात टाकली, तर त्या निवडीली पुनःस्थापनसहित निवड म्हणतात. पहिल्या प्रकारात अतिगुणोत्तरीय व दुसऱ्यात द्विपदी वंटन मिळते. कारखान्यात तयार झालेल्या वस्तूंतील दोषयुक्त वस्तूंचे प्रमाण शोधण्याकरिता व्यवहारात ही दोन्ही प्रतिमाने उपयोगी पडतात.

---

महत्त्वाची संतत वंटने : आयताकृती अथवा एकविध वंटन : या वंटनाचे घनता फलन  

 

असून F (x) = (x-a) / (b-a) असते. याचा घनता वक्र आयताकृती दिसतो. याचे माध्य ½ ( a + b) आणि विचरण 1/12 (b-a)² असून ही मूल्ये एक एकक द्रव्यमान असलेल्या (b-a) लांबीच्या एकविध गजाचे अमुक्रमे द्रव्यमान मध्य व केंद्रीय निरूढी परिबल यांच्या बरोबर आहेत. पुष्कळदा सांख्यिकीय सिद्धांतात वरील वटनांऐवजी (-१/२, १/२) किंवा (०, १) या अंतरातील एकविध वंटने उपयोगी पडतात. उदा., y = F (x) या रूपांतरणाने कोणताही संतत प्रभावी चल (०, १) या अंतरावरील एकविध संभावी चलात रूपांतरित होतो.

गौस प्रसामान्य वंटन : या वंटनास सांख्यिकीय असाधारण महत्त्व आहे. व्यवहारात वजन, उंची , परीक्षांतील गुण इ. अनेक मापनीय लक्षणांची वारंवारता वजन, उंची परीक्षांतील गुण इ. अनेक मापनीय लक्षणांची वारंवारता वंटने या स्वरूपाची असल्याचे अनुभवास येते. अनेक प्रतिदर्शी वंटने याच मूळ वंटनावर आधारेलली आहेत. प्रसामान्य वंटनांची मूळ कल्पना द ग्वाहर यांची (१७३३) होती पण गौस (१८०९) व लाप्लास (१८१२) यांनी मापनभिन्नतेच्या (त्रुटीच्या) सिद्धांतासाठी त्याचा उपयोग केला. तेव्हापासून त्याला गणितात महत्त्वाचे स्थान प्राप्त झाले. या वंटनाचा विशेष विकास अर्थातच विसाव्या शतकात झाला. या वंटनाचे घनता फलन

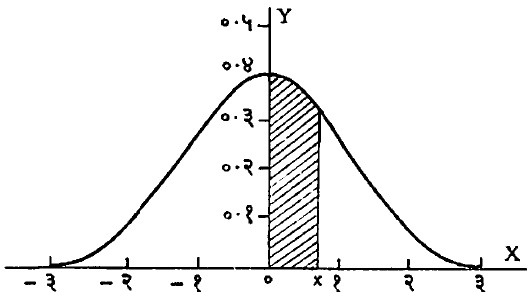
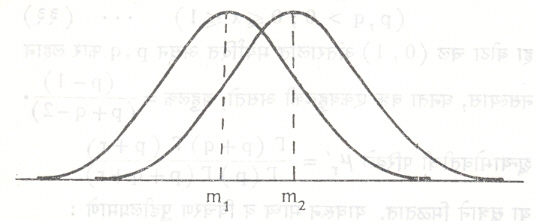असे असून माध्य m व प्रमाण विचलन σ हे त्याचे प्रचल होत. हे वंटन दर्शविण्यासाठी N(m, σ) हे संकेत चिन्ह वापरतात. उदा., (x-m) / σ या प्रमाणित चलाचे वंटन N (0, 1) असते. याला प्रमाण किंवा एकक प्रसामान्य वंटन म्हणतात. याच्या संभाव्याता घनता फलनाचा आलेख आ. ५ मध्ये दिला आहे. प्रथम प्रसामान्य वंटनाचे मुख्य गुणधर्म पाहू. घनता वक्र मध्याभोवती सममित असून त्याचे मध्यक व बहुलक माध्यापाशी आहेत. वक्र दोन्ही बाजूंना अतिशय जलद अक्षाशी अनंतवर्ती होतो. त्याला m ±σ हे दोन नतिवर्तन बिदू (एकाद्या स्थिर अक्षाच्या सापेक्ष वक्राचा आकार अंतर्गोलापासून बहिर्गोलात बदलतो असे बिंदू) आहेत. माध्य बदलल्यास वक्राचा आकार न बदलता फक्त स्थान बदलते (आ. ६) पण प्रमाण विचलन बदलल्यास चलाचे एकक अथवा मापप्रमाण बदलून त्याचा आकार बदलतो (आ. ७). वक्राखालचे क्षेत्र नेहमी एक एकक राहावयाचे असल्यामुळे σ लहान झाले, तर वक्र मध्यभागी उंच होऊन संभाव्यतेचा बराच मोठा भाग माध्यापाशी गोळा होतो. उलटपक्षी σ मोठे झाल्यास वक्र मघ्यभागी ठेंगणा होऊन संभाव्यता माध्यामापासून दूर पसरते.

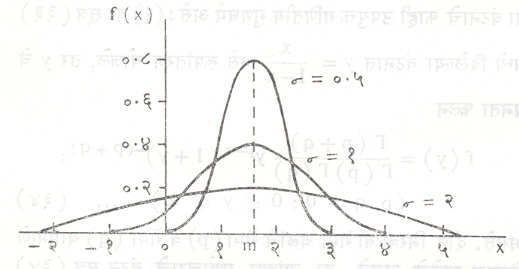घनता वक्र सममित असल्यामुळे विषम कोटीची सर्व केंद्रीय परिबले शून्य असतात. सम कोटीची परिबले μ_2r = 1. 3. 5…………. (2r-1) σ^2r या सूत्राने मिळतात. विषमतांक व ककुदतांक γ₁ व γ₂ हे शून्य होतात. अनुक्रमे N (m, σ) व N(0,1) वा वंटनांची लक्षण फलने

  

असून यांतील दुसरे रूप संभाव्यता सिद्धांतात व गणितीय सांख्यिकीत अनेकदा वापरलेले आढळते. माध्य व विचरण यांशिवाय सर्व संचयक शून्य असतात हा प्रसामान्य वंटनाचा वैशिष्ट्यपूर्ण गुणधर्म आहे. प्रसामान्य वंटनाच्या ठायी जननाचा गुणधर्म आहे: दोन प्रसामान्य चलांची बेरीज प्रसामान्य चल असते, शिवाय ते निरवलंबी असले, तर बेरीज-चलाचे माध्य एकेक चलांच्या माध्यांच्या बेरजेएवढे व त्याचे विचरण विचरणांच्या बेरजेएवढे  असते.

प्रसामान्य वंटनांच्या विशेष महत्त्वामुळे त्यासंबंधी अनेक प्रकारची कोष्टके तयार करण्यात आलेली आहेत. ती सर्व अर्थातच प्रमाण वंटनाविषयीची, N (0,1) विषयीची, आहेत. घनता व वंटन फलने 

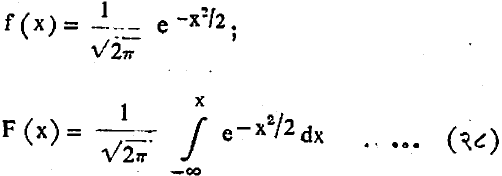
या दोन्हीची विस्तृत कोष्टके उपलब्ध आहेत.कित्येक कोष्टकांत F (x) ऐवजी F (x)-F (0) = F (x)-1/2 याचे (आ. ५ मधील छायांकित क्षेत्राचे) आकडे दिलेले असतात. सममिततेचा उपयोग करून या कोष्टकावरून कोणत्याही अंतरालातील प्रसामान्य संभाव्यता काढता येते. कित्येकदा प्रसामान्य संभावी चल त्याच्या माध्यापासून K*हून अधिक अंतरावर असण्याची संभाव्यता किती ही माहिती इष्ट असते. ही संभाव्यता

  

---

म्हणजे वक्राच्या दोन्ही बाजूंच्या पुच्छांखालील क्षेत्राएवढी असते. तिचे P=p/100 असे टक्क्यांत रूपांतर केल्यास तिला अनुरूप k च्या मूल्याला p- शतमान मूल्ये (अथवा p-शतमान बिंदू) म्हणतात. म्हत्त्वाची शतमान मूल्ये पुढीलप्रमाणेः 

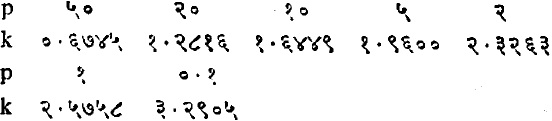
 कधीकधी m±kσ या अंतरालात k च्या वेगवेगळ्या मूल्यांप्रमाणे किती संभाव्यती असेल ही माहिती हवी असते. वरील सूत्र (२९) च्या भाषेत ही संभाव्यता (1 – P) इतकी असते. या अंतरालांना kσ अंतराले म्हणतात. माध्यापासून σ, २σ, ३σ व ४σ अंतरालांतील संभाव्यता अनुक्रमे ०.६८२६८, ०. ९५४५०, ०.९९७३० व ०.९९९९४ एवढ्या असतात.

प्रसामान्य वंटनाला सांख्यिकीत इतके महत्त्व प्राप्त होण्याचे कारण व्यवहारात अनेक वारंवारत वंटने प्रसामान्य किंवा प्रसमान्यप्राय असतात, एवढेच केवळ नाही. त्याला एक महत्त्वाचे गणितीय कारण आहे, ते म्हणजे केंद्रीय सीमा प्रमेय होय. त्याची स्थूल प्रतिज्ञा अशी : X1, X2, …….., Xn  या श्रेणीतील संभावी चल काही (विवक्षित) सामान्य स्वरूपाच्या गणितीय अटी पूर्ण करीत असल्यास, त्यांची बेरीज

या प्रमेयाच्या सिद्धतेत अथवा अटींच्या तपशीलात न शिरता असे म्हणतात येईल की, अनेक चल श्रेणींना हे प्रमेय लागू पडते म्हणजे कित्येक श्रेणींतील चलांच्या बेरजेचे वंटन प्रसामान्य किंवा प्रसामान्याच्या जवळ असते. शास्त्रीय घटनांत आढळणारे अनेक चल, त्यांना कारणीभूत झालेल्या अनेक चलांचा परिपाक अथवा बेरजेसारखे असतात हे त्यांच्या अंगी दिसणाऱ्या प्रसामान्य वंटनाचे कारण असावे, असे अनेकदा म्हटले जाते. त्यांच्या युक्तायुक्ततेत शिरले नाही, तरी ही गोष्ट खरी की, गणितीय व आनुभविक या दोन्ही कारमांमुळे प्रसामान्य वंटनाला सांख्यिकीत अनन्यसाधारण स्थान प्राप्त झाले आहे.

गॅमा वंटन : कलनशास्त्रातील गॅमा फलनावरून [⟶ अवकलन] निघालेल्या या वंटनाचे घनता फलन खालीलप्रमाणे आहे.  

  

या वक्राची आकृती p&gt¹ असता एकबहुलकी, विषम व उजवे पुच्छ अक्षाला अनंतवर्ती अशी असते. गॅमा व (पुढे दिलेली) बीटा वंटने जीवविज्ञानातील कालावलंबी प्रक्रियांचा सांख्यिकीय विचार करताना प्रतिमाने म्हणून उपयोग पडतात. लक्षण फलन φ(t) = (1-it)^-p यापासून परिबले व संचयक सहज मिळतात. उदा., माध्य व विचरण समान असून त्यांचे मूल्य p आणि संचयकांचे सूत्र k _r= (r-l)!p. गॅमा वंटन फलन F(x) याची कोष्टके उपलब्ध आहेत.

गॅमा वंटनांचे दोन महत्त्वाचे गुणधर्म असे : (१) जननाचा गुणधर्म म्हणजे P₁, P₂ यांनी निर्देशिलेल्या दोन निरवलंबी गॅमा चलांची बेरीज ही p₁+p₂ ने निर्देशिलेला गॅमा चल असते. (२) सूत्र (३०) मध्ये p=n/2 (n पूर्णांक) व x ऐवजी x/2 चल घेऊन येणारे गॅमा वंटन काय-वर्ग (X²) वंटन म्हणून प्रसिद्ध आहे. सांख्यिकीय विश्लेषणासाठी ते विविध प्रकारे वापरतात. त्याचे घनता फलन

असून लक्षण फलन φ(t) = (1-2it)^-n/2, माध्य = n व विचरण =2n. प्रचलन n ला मुक्तता मात्रा अशी संज्ञा आहे. प्रसामान्य वंटनाशी या वंटनाचा संबंध जोडता येतो, तो असा : निरवलंबी n प्रसामान्य N(0, 1) चलांच्या वर्गाच्या बेरजेचे काय-वर्ग (n) वंटनाप्रमाणे वितरण झालेले असते. काय-वर्ग वंटनाला जननाचा गुणधर्म आहेच. या वंटनाची n च्या वेगवेगळ्या मूल्यांप्रमाणे कोष्टके उपलब्ध आहेत आणि p(x &gt x_p) = p/100 ने निर्देशिलेले शतमान बिंदूही दिलेले असतात. मुक्तता मात्रा n⟶∞ असता काय-वर्ग वंटन सीमेत प्रसामान्य वंटन होते.

आणखी एक वंटन, t-वंटन येथेच सांगणे सोयीचे होईल. डब्ल्यू. एस्. गॉसेट या इंग्रज सांख्यिकीविज्ञांनी  ‘स्टूडंट’ (विद्यार्थी) या टोपण नावाने याचा प्रथम १९०८ मध्ये निर्देश केला, यावरून त्याला स्टूडंटचे t – वंटन असेही म्हणतात. त्याची व्याख्या  : X हा प्रसामान्य N(0, 1) चल असून Y हा n मुक्तता मात्रांचा निरवलंबी काय-वर्ग चल असेल, तर t= X/√Y/n या चलाला n मुक्तता मात्रांचा t – चल असे म्हणतात. त्याचे घनता फलन

असून तो t = 0 भोवती सममित असतो, तेथेच त्याचे माध्य, मध्यक व बहुलक आहेत. विषम परिबले शून्य व सम परिबलाचे सूत्र

  

आहे. विचरण = n/(n-2) असून ते एकक प्रसामान्य चलाच्या विचरणापेक्षा अधिक आहे. घनता वक्राचा आकार n लहान नसल्यास, बराचसा प्रसामान्य वक्रासारखा असतो आणि n⟶∞ असता t – वंटन सीमेत प्रसामान्य N (0, 1) वंटनाप्रत जाते. वंटन 

यांनी निश्चित केलेले शतमान बिंदूही n च्या वेगवेगळ्या मूल्यांप्रमाणे दिलेले असतात.

बीटा वंटन : कलनशास्त्रातील बीटा फलनावरून कल्पिलेल्या या वंटनाचे घनता फलन पुढीलप्रमाणे :  

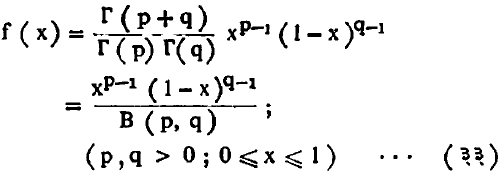
हा बीटा चल (0, 1) अंतरालात मर्यादित असून p, q फार लहान

---

या वंटनाचे काही उपयुक्त गणितीय गुणधर्म असे : (१) वर सूत्र (३३) मध्ये दिलेल्या वंटनात y = x/1-x असे रूपांतरण योजले, तर y चे घनता फलन

असते. दोन निरवलंबी गॅमा चलांचे गॅमा (p) व गॅमा (q) याप्रमाणे वितरण झालेले असले, तर त्यांच्या गुणोत्तराचे वंटन सूत्र (३४) प्रमाणे असते, दोन निरवलंबी काय-वर्गांच्या गुणोत्तराचे वंटनही याच प्रकारचे असते मात्र p, q च्या ऐवजी त्यांच्या मुक्तता मात्रांचे अर्ध येतात.

(२) अशा तऱ्हेचे आणखी एक वंटन प्रतिदर्शी वंटनाxच्या विचारात महत्त्वाचे आहे. त्याचे नाव जी. डब्ल्यू स्नेडेकर यांचे F- वंटन होय. दोन निरवलंबी काय-वर्ग चल x  व y अनुक्रमे m व n मुक्तता 

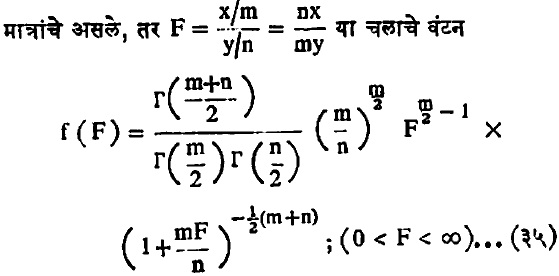
  या घनता फलनाने मिळते. हे वंटन सूत्र (३४) हून फारसे वेगळे नाही. याच्या शून्याभोवतीच्या परिबलांचे सूत्र   

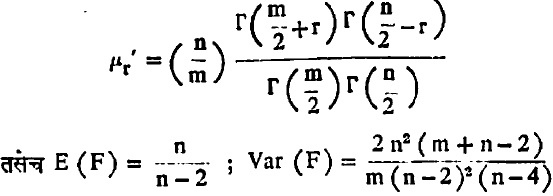
  उजवीकडे अनंतवर्ती पुच्छ असलेले असे हे एकबहुलकी विषम वंटन आहे. याच्या वंटन फलनाची व शतमान बिंदूंची कोष्टके प्रचल m, n यांच्या निरनिराळ्या मूल्यांप्रमाणे दिलेली असतात.

कोशी वंटन : ए. एल्. कोशी (१७८९–१८५७) या फ्रेंच गणितज्ञांच्या नावाने ओळखण्यात येणाऱ्या या वंटनातील कोशी चल हा गणितीय सैद्धांतिक दृष्ट्या विशेष महत्त्वाचा आहे. याचे घनता फलन व लक्षण फलन खालीलप्रमाणे आहेत :  

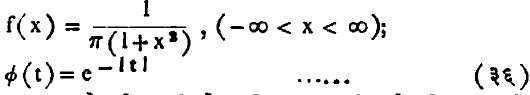
माध्यासकट कोणतीच परिबले अस्तित्वात नाहीत, हे कोशी चलाचे वैशिष्ट्य आहे. घनता वक्र शून्याभोवती सममित असून तेथेच त्याचे मध्यक व बहुलक आहेत. वंचन फलनाचे रुप फारच सोपे :

अधिक व्यापक रूप म्हणजे x=(y-m)/a या रूपांतरणाने मिळणाऱ्या y चलाचे वंटन होय. त्याचे घनता फलन

 

असून त्याचे मध्यक m आहे. कोशी वंटनास जननाचा गुणधर्म आहे: प्रचल (m₁, a₁) व (m₂, a₂) यांनी निर्देशिलेल्या दोन निरवलंबी कोशी चलांच्या बेरजेचे वंटन (m₁ +m₂, a₁ + a₂) ने निर्देशिलेले कोशी वंटन असते.

पीअर्सन वंटन : कार्ल पीअर्सन (१८५७–१९३६) या इंग्रज सांख्यिकीविज्ञांनी व्यवहारात आढळून येणाऱ्या विविध आकृतींच्या वारंवारता वंटनांना अनुरुप असे गणितीय वक्र शोधण्याच्या द्दष्टीने ही वंटने सुचविली. 

या ⇨अवकल समीकरणापासून निघणारी विविध घनता फलने f(x) म्हणजे पीअर्सन वंटने होत. याचे अनेक प्रकार कल्पिले आहेत. वरील विवेचनात आलेली सर्व संतत वंटने (३८) या सूत्रात वसतात, म्हणजे ती पीअर्सन वंटनांची विशिष्ट रूपे आहेत.

द्विमितीय व बहुमितीय वंटने : कित्येकदा अनेक परस्परावलंबी चलांचा एकत्र विचार करावा लागतो. फुलातील पाकळ्या व पुंकेसर, व्यक्तीचे वजन व उंची, स्क्रूची लांबी व व्यास इ. जोड्यांतील चल परस्परावलंबी संभावी चल असतात. यांना द्विमितीय संभावी चल अथवा संभावी द्विचल किंवा द्विचर म्हणू. एकमितीय वंटनाच्या व्यापकीकरणाने (X, Y) या संभावी द्विचलाचे वंटन फलन

F (x, y )= P (X ≤x, Y≤ y)                 ….            ….            (३९)

या द्विचल फलनाने निदर्शित होते. द्विचल वंटनांचे मुख्य प्रकार दोन : (१) पृथक् व (२) संतत. 

पृथक् द्विचल वंटने : द्विचलांतील प्रत्येक चल X व Y पृथक् मूल्ये घेत असल्यास त्याच्या संभाव्यता फलनाची व्याख्या खालीलप्रमाणे : 

 

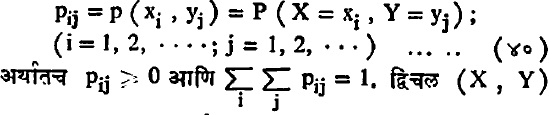
याचा विचार करताना दोन प्रश्र उपस्थित होतात: (१) केवळ X चे वंटन कोणते व ते कसे कोणते व ते कसे काढावयाचे? (२) समाजा Y हा y_j मूल्यावर स्थिर केला, तर X  चे वंटन कोणते व ते कसे काढावयाच्या? पहिल्या प्रश्रात P(X=x_i), मग Y  कितीही असो. संभाव्यता तत्त्वे वापरून तिचे मूल्य 

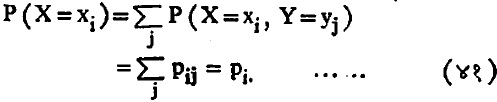
असे मिळते. याला X चे उपांत वंटन म्हणतात. ज्या अर्थी   

 दुसऱ्या प्रश्रात P(X = _xi | Y = y_j) ही सशर्त संभाव्यता अभिप्रेत आहे. संभाव्यता तत्त्वांच्या साहाय्याने तिचे मूल्य 

 निघते. याप्रमाणे Y हा y_j वर स्थिर असतानाचे X चे सशर्त वंटन सूत्र (४२) मधील संभाव्यता फलनाने मिळते. ज्या अर्थी 

 त्या अर्थी हेही खरोखरीच संभाव्यता फलन आहे. द्विचलातील X व Y हे निरवलंबी असले, तर P (x_i | y_j) = P (x_i) म्हणून निरवलंबतेची अट अशी :

P_ij=P (x_i , y_j) P(x_i).P(y_j)= P _i. P._{j  …}                  (४३)

त्याचप्रमाणे वंटन फलनाचेही दोन अवयव पडतात, असे :

F(x, y) = P (X≤ x, Y≤ y) = P (X ≤x) P(Y≤ y)

              = F₁(x) F₂ (y)     …  ….                          (४४)

संतत द्विचल वंटने : संभावी द्विचल संतत असता त्याचे वंटन फलन F(x, y) हे सर्वत्र संतत असते आणि त्याचा

  

---

हा अवकलज सर्वत्र निष्पन्न होतो. यातील f (x, y) ला पूर्वीप्रमाणे संभाव्यता घनता अथवा वारंवारता फलन म्हणतात. पुढील निष्कर्ष सहज निघतात :

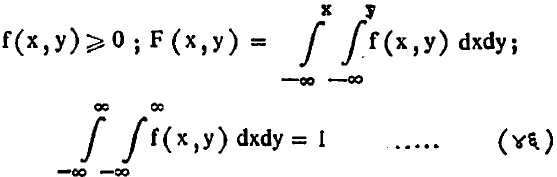
यापासून निघणारी उपांत व सशर्त वंटने (स्पष्टीकरण गाळून) पुढे दिली आहेत. उपांत वंटने 

आणि सशर्त वंटने 

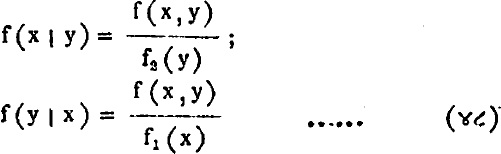
या घनता फलनांनी मिळतात. द्विचलाच्या निरवलंबतेची अट f(x, y) = f₁(x) f₂(y) हे रूप धारण करते.

अपेक्षित मूल्ये इत्यादी : यांची व्याख्या द्विचल संतत असता एकचल वंटनाप्रमाणे 

बेरजेने होते. पूर्वीच्या विवेचनात आलेली निरवलंबी चलांच्या अपेक्षितांविषयीची (११) व (१३) ही सूत्रे (४९) सूत्रावरून सिद्ध होतात. आता द्विचलाच्या परिबलांचा विचार करू. परिबलाची व्याख्या μ’rs = E (xrys). द्विचलाला E (x)= m1, E (y)= m2 अशी माध्यांची जोडी असेल. हे उघड आहे. त्यांचा उपयोग करून μ _rs = E (x – m₁)^r (y-m₂)^s ही केंद्रीय परिबले निघतात. दुसऱ्या कोटीच्या (r+s=2) परिबलांचा विचार करता

        Var (x) = E (x-m₁)² = σ1²

        Var (y) = E (y-m₃)³ = σ2²  ….           (५०)

या विचरणांसमवेत 

Cov (x, y) = E (x – m₁) (y – m₂)  …           (५१)

असे आणखी एक परिबल मिळते, त्याला सहविचरण म्हणतात. त्यावर आधारलेल्या 

 

या गुणांकाला सहसंबंधांक म्हणतात. त्याचा उपयोग करून सहविचरण = ρσ₁σ₂ याप्रमाणे सुटसुटीतपणे चिन्हांकित करता येते. सहसंबंधांकाचे मूल्य नेहमी – 1≤ p ≤+ 1 या असमेत सामावलेले असते. जेव्हा X व Y हे निरवलंबी असतात तेव्हा

E (x –m₁) (y –m₂) = (x –m₁) E (y –m₂) = 0 आणि p = 0 होतो. म्हणून हा गुणांक द्विचलाची अवलंबिता दर्शविण्यासाठी वापरला जातो.

द्विचलाचे लक्षण फलन φ(t₁, t₂) = E (e^it1 x+it₂y) असून द्विचल निरवलंबी असल्यास φ(t₁, t ₂) = φ₁(t₁) φ₂(t₂) अशी नित्यसमा मिळते. येथे φ₁(t₁) व φ₂(t₂) ही X व Y यांची लक्षण फलने आहेत.

बहुचल किंवा बहुचर वंटने : याच पद्धतीने बहुमितीय वंटनाचा विचार करता येतो. (X₁, Xऋ, …. Xऋ) या k- मितीय बहुचलाच्या वंटन फलनाची व्याख्या अशी:

F(x₁, x₂, ….x_k)= P (X₁ ≤ x₁, X₂ ≤ x₂,

                           …, X_k ≤ x_k)        …             (५३)

बहुचल पृथक् असल्यास त्याचे संभाव्यता फलन   

आणि संतत असल्यास त्याचे घनता फलन 

 

याप्रमाणे व्याख्या करून अपेक्षित मूल्ये, परिबले, लक्षण फलन इत्यादींचे विवेचन करता येते. द्विचल मीमांसेचे हे स्वाभाविक व्यापकीकरण असल्यामुळे त्याच्या विशेष तपशिलात न शिरता येथे फक्त दोनच गोष्टींचा उल्लेख केला आहे. वरील (X, X, …. X) बहुचलाचे माध्य m₁, m₂, ….m_k हा E (X_i)= m_i वरून       मिळालेला K-मितीय बिंदू असेल. तसेच विचरण व सहविचरण यांकरिता 

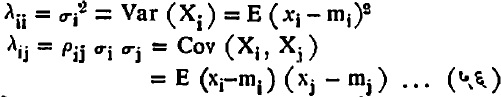
 ही चिन्हे वापरून A = (λ_ij) आणि P = (ρ_ij) हे दोन आव्यूह मिळतात [⟶आव्यूह सिद्धांत]. पहिल्याला विचरण-सहविचरण आव्यूह व दुसऱ्याला सहसंबंध आव्यूह म्हणतात. दुसऱ्याला सहसंबंध आव्यूह म्हणतात. दुसऱ्याच्या रचनेत ρ_ij=1 हे मूल्य घेतलेले असते. बहुचल वंटनांचा विचार करताना या आव्यूहांचा अतिशय उपयोग होतो. महत्त्वाच्या दोन बहुचल वंटनांची माहिती थोडक्यात खाली दिली आहे.

(१) बहुपदी वंटन : समजा एखादी घटना k प्रकारे घडते. पहिल्या प्रकारे घडण्याची संभाव्यता P₁, दुसऱ्याची P₂,…….., k व्या प्रकारची संभाव्यता P_k आहे आणि P₁+P₂+….+P_k=1 आहे. या घटनेची n वेळा आवृत्ती झाली असता ती पहिल्या प्रकारे X₁ वेळा, दुसऱ्या प्रकारे X₂ वेळा, ….., k व्या प्रकारे X_k वेळा घडली (X₁+ X₂ + …. + X_k = n). अशा प्रतिमानातून निघालेल्या (X₁+X₂+,……,X_k) या संभावी बहुचलाला बहुपदी चल म्हणतात. त्याचे संभाव्यता फलन

आहे, हे दाखविता येते. उजवीकडील पद हे

[P¹+P²+…+P^k]ⁿ

---

 या बहुपदीच्या विस्तारात आढळत असल्यामुळे त्याचे नाव या वंटनास मिळाले आहे. बहुपदी वंटन हे द्विपदी वंटनाचे व्यापकीकरण आहे आणि व्यवहारात ते तशाच प्रकारे उपयोगी पडते. बहुपदीचे एक सोपे उदाहरण असे : एखादा निरभिनत फासा n वेळा टाकला, आणि १, २, ३, ४, ५, ६ ही दाने अनुक्रमे X₁, X₂, X₃, X₄, X₅, X₆ वेळा पडली, तर ( X₁, X₂, ….X₆) हा P₁ =P₂ … P₆ = ¹/₆ असलेली बहुपदी चल होईल. बहुचलांचे माध्य व विचरण-सहविचरण यांची सूत्रे अशी :

 

 (२) द्विचल प्रसामान्य वंटन : हे द्विचल संतत वंटन एकमितीय प्रसामान्य वंटनाचे व्यापकीकरण असून व्यवहारात आढळणाऱ्या अनेक द्विचलांची वारंवारता या तऱ्हेची असते. याचे घनता फलन  

दाखविता येते. या वंटनाचे महत्त्वाचे गुणधर्म थोडक्यात दिले आहेत. प्रथम माध्य व विचरणे :

E(x)=m₁ , E(y)=m₂                                                                                                     …          (६०)

Var(x)=σ₁² Var (y)= σ₃²

 Cov (x, y)=ρσ₁σ₂                                                                                                        ……      (६१)

अर्थात ρहा सहसंबंधांक आहे. याचे लक्षण फलन

f(t₁,t₂)= exp[m₁it₁+m₂it₂-1/2(σ₁²t₁²+σ₂²t₂²+2ρσ₁σ₂t₁t₂)]                                   …… (६२)

असे आहे. द्विचलापासून निघणारी x व y यांची उपांत वंटने

                                f₁ (X)=1/√2πσ₁  e–1/2(x-m₁/σ₁)²

                                 f₂(y)=1/√2πσ₂  e-1/2(y-m₂/σ₂)²                                             ….. (६३)

 

याप्रमाणे N (m₁, σ₂) आणि N (m₂, σ₂) अशी एकमितीय प्रसामान्य आहेत. यावरून निरवलंबतेची आवश्यक तशीच पुरेशी अट r = 0 असल्याचे सिद्ध करता येते. तसेच उपांत वंटने वापरून सूत्र (४८) च्या साहाय्याने सशर्त वंटने निघतात. उदा., f(y|x) हे माध्य m₂+ ρσ₂/ρσ₁ (x-m₁) आणि विचरण σ₂²(1-r²) असलेले,  प्रसामान्य वंटन असते. यावरून y चे सशर्त माध्य

                E(y|x)=m₂+ ρσ₂/ρσ₁(x-m₁)                           ……. (६४)

 

या स्वरूपात लिहिता येते. याचा आलेख सरळ रेषाकृती आहे. या रेषेला y ची x वरची समाश्रयण रेषा म्हणतात. याचप्रमाणे रेषा म्हणतात. याचप्रमाणे x ची y वरची समाश्रयण रेषा काढता येईल. या रेषा (m₁, m₂) या माध्य बिंदूतून जातात. सामान्यपणे त्या अलग असतात पण r = ± 1 असल्यास त्या तादात्म्य होतात. माध्य m₁ = m₂ = 0 आणि σ₁= σ₂ = 1 असलेल्या द्विचल प्रसामान्य वंटनाला प्रमाणित द्विचल प्रसामान्य वंटन म्हणतात. त्याच्या वंटन फलनासंबंधी F (h, k) – F (0, 0) ची कोष्टके आहेत.

 

आव्यूह पद्धतीने (५९) मधील सूत्र z = (x, y), m = (m₁, m₂) हे स्तंभ सदिश [⟶सदिश अवकाश] आणि  Λ=λ_ij  हा सहविचरण आव्यूह ही संकेत चिन्हे वापरून

f(z)= 1 / 2π |Λ|^1/2 e^–1/2(z-m)’Λ^–1(z-m)                    …  (६५)

 

या सुटसुटीत स्वरूपात लिहिता येते. याचे व्यापकीकरण करून k मितीय बहुचलाचे घनता फलन लिहिता येईल ते असे :

  f(x)= 1 / (2π)^k/2 |Λ|^1/2 e^–1/2(x-m)’Λ^–1(x-m)          …. (६६)

 

येथे X=(x₁, x₂,….,x_k) हा बहुचलाचा स्तंभ सदिश, m=(m₁, m₂,….,m) हा माध्य आणि Λ =(λ_ij)=(ρ_ijσ_iσ_j) हा त्याचा सहविचरण आव्यूह आहे आणि E (x_j)=m_ij Var (x_i)= σ_i²= λ_ij Cov (x_i, x_j)=ρ_ijσ_iσ_j = λ_ijइ. संकेत अभिप्रेत आहेत. 

---

प्रतिदर्शी वंटने: सांख्यिकीय सिद्धांताचा मुख्य प्रश्न म्हणजे प्रतिदर्शनावरून मूळ समष्टीविषयी (समुदायाविषयी) अनुमान करणे. येथे समृष्टी हा शब्द मानवसमुदाय या मर्यादित अर्थाने योजिलेला नाही. ज्याला वंटन मानता येईल असा कोणताही लक्षणसमुदाय अथवा निरीक्षणसमुदाय या व्यापक अर्थाने तो योजिला आहे. प्रतिदर्श हा मूळ समष्टीचा केवळ भाग असल्याने त्यातील माहिती अपुरी असणार आणि म्हणून त्यावरून काढलेल्या अनुमानांत अनिश्चितता असणार, हे उघड आहे. सांख्यिकीय सिद्धांतात ही अनिश्चितता संभाव्यतेच्या स्वरूपात सांगितलेली असते. अनुमाने मुख्यतः दोन तऱ्हेची: (१) मूळ समष्टीच्या वंटनाविषयी अथवा त्यातील प्रचलांविषयी आकलन करणे (२) तद्विषयक गृहीतकांची कसोटी घेणे. यासाठी प्रतिदर्शातील निरीक्षणांचे एक अथवा अनेक अनुरूप फलने योजतात. निरीक्षणांच्या फलनाला संख्यानक म्हणतात. प्रतिदर्श वंटनांचा विचार म्हणजे प्रतिदर्श संख्यानकांच्या वंटनांचा विचार होय.

 

सांख्यिकीय अनुमान पद्धतीत सामान्यपणे प्रतिदर्शाची यदृच्छता गृहीत धरलेली असते. संभाव्यतेच्या दृष्टीने पाहिले, तर प्रतिदर्श यदृच्छ आहे याचा अर्थ प्रतिदर्शातील x₁, x₂,  ….., x_n ही निरीक्षणे मूळ अनंत समष्टीचे वंटन अनुसरणारे निरवलंबी चल आहेत असा होतो (सांत समष्टीविषयीच्या विवेचनासाठी ‘प्रतिदर्श सर्वेक्षण सिद्धांत’ही नोंद पहावी). सोयीसाठी मूळ वंटन f(x) घनता फलन असणारे संतत वंटन मानले, तर

                 f(x₁, x₂, ……, x_n) = f(x₁) f(x₂)…f (x_n) …. (६७)

हे प्रतिदर्शनाच्या यदृच्छेतेचे गणितीय रूप होईल.

 

अशा विवेचनात तीन वेगवेगळ्या तीन वेगवेगळ्या प्रकारच्या वंटनांचा कित्येकदा उल्लेख होतो, हे ध्यानात ठेवावे. मूळ वंटन व संख्यानकाचे प्रतिदर्शाचे वंटन या दोघांचा खुलासा वर आला आहे. उल्लेख येणारे तिसरे वंटन म्हणजे म्हणजे प्रतिदर्शातील निरीक्षणांचे वारंवारता वंटन. याला प्रत्यक्ष अनुभवसिद्ध वारंवारता वंटन असेही म्हणतात. हे वंटन P (X=x_i) = 1/n  या व्याख्येने, म्हणजे प्रतिदर्शातील निरीक्षणांची संख्या n असता प्रत्येक निरीक्षणाला 1/n ही समान संभाव्यता देऊन कल्पलेले पृथक वंटन होय. प्रतिदर्श यदृच्छ असून पुरेसा मोठा असला, तर संभाव्यता सिद्धांतानुसार असे सांगता येते की, अनुभवसिद्ध वंटन म्हणजे प्रतिदर्शाचे वारंवारता वंटन मूळ वंटनाच्या समीप असते. यामुळे मूळ वंटन व त्याचे प्रचल यांविषयी अनुमान करण्यासाठी प्रतिदर्शाचे वारंवारता वंटन व त्याची अनुरूप संख्यानके योजणे स्वाभाविक होय. उदा., मूळ वंटनाचे माध्य व विचरण यांविषयी अंदाज व्यक्त करण्यासाठी प्रतिदर्श माध्य व प्रतिदर्श विचरण

***X=1/n ∑x_i m₂=1/n _i ∑(x_i-x***)2     ….   (६८)

 

या संख्यानकांचा उपयोग केला जातो, म्हणून शक्य असल्यास अशा संख्यानकांची वंटने शोधून काढणे इष्ट असते.

 

प्रतिदर्शावर आधारलेल्या u = u (x₁,x₂, …, x_n) यासारख्या संख्यानकाचे वंटन शोधावयाचे म्हणजे मूळ वंटन f(x) दिलेले असता सूत्र (६७) लक्षात घेऊन त्याचे वंटन फलन

G(u )= P (u (x) &lt u )

                =ò……òf(x₁)….. f(x_n)dx₁….  Dx_n  u (X)&ltu

 

या समाकलाचे मूल्य काढणे होय. गणितीय संकेत चिन्हात हे पद सोपे वाटते पण प्रत्यक्षात हे समाकलन साधणे अवघड होऊन बसते. त्यासाठी सरळ समाकलन पद्धतीशिवाय फूर्ये रूपांतर, बहुमितीय भूमिती [⟶ भूमिति], समचयात्मक पद्धती [⟶ समचयात्मक विश्लेषण] इ. गणितीय युक्त्या-प्रयुक्त्या उपयोगात आणतात. इतके करूनही फार थोडी प्रतिदर्श वंटने सोप्या गणितीय स्वरूपात मिळाली आहेत. तसेच या संख्यानकांचे माध्य, विचरण व (शक्य असल्यास) इतर परिबले काढणे उपयुक्त असते. काही महत्त्वाच्या संख्यानकांचा विचार उदाहरणादाखल खाली केला आहे.

 

प्रतिदर्श माध्य (x***) : मूळ वंटनाचे माध्य m व विचरण s² असल्यास E (x***) = m Var (x***) = σ²/n  ……. (६९)

हे निष्कर्ष सहज मिळतात. प्रतिदर्शातील निरीक्षण संख्या n जसजशी मोठी होईल तसतसे x***  चे विचरण ऱ्हास पावेल आणि x* मूळ वंटनाचे माध्य m याच्या समीप असेल. हे यावरून उघड होते. या गुणधर्मामुळे x*** हे m साठी आकल (अंदाजित मूल्य) म्हणून वापरतात. केंद्रीय सीमा प्रमेयामुळे याहून सूक्ष्म निष्कर्ष निघतो तो असा की, अनेक मूळ वंटनांच्या बाबतीत x*** चे सीमा वंटन प्रसामान्य N(m, σ/√n) असते. हा निष्कर्ष मोठ्या प्रतिदर्शाच्या वेळी वापरता येतो.

 

मूळ वंटनास जननाचा गुणधर्म असला (उदा., द्विपदी, प्वासाँ, प्रसामान्य), तर ∑x_i या प्रतिदर्श बेरजेचे सम्यक् वंटन सांगता येते, मग n केवाढाही असो, त्यावरून x***चे सम्यक् वंटन मिळते. उदा., मूळ वंटन प्रसामान्य N(m, σ) असेल, तर x*** चे वंटन प्रसामान्य N (m, σ/√n ) असते. विचरण σमाहीत असल्यास m या समष्टी माध्याविषयीचा अंदाज व्यक्त करण्यासाठी याचा उपयोग करता येतो आणि m बद्दलची गृहीतके तपासून पाहता येतात.

 

प्रतिदर्श विचरण (m₂) :मूळ वंटनाचे विचरण μ₂ अथवा (σ²) असेल, तर प्रतिदर्श विचरण m₂ चे माध्य E (m₂) = (n-1) μ₂ /n असते. त्याच्या विचरणाची पदावली अधिक मोठी आहे पण मूळ वंटन प्रसामान्य असल्यास Var (m₂) = 2(n-1) σ⁴/ n² असल्याचे दाखविता येते. प्रतिदर्शातील निरीक्षण संख्या मोठी होत जाईल, तसे m₂ हे μ₂ प्रत पोचू लागते, तसेच अनेक मूळ वंटनांच्या बाबतीत त्याचे सीमा वंटन प्रसामान्य असते पण प्रतिदर्श लहान असल्यास आणि मूळ वंटन प्रसामान्य नसल्यास m₂ चे सम्यक् वंटन काढणे अवघड आहे. मूळ वंटन प्रसामान्य असून त्याचे विचरण σ² असेल, तर ∑(x₁-x***)² / σ² चे वंटन n-1 मुक्तता मात्रा असलेले काय-वर्ग वंटन असते. याचा उपयोग σ² विषयी अंदाज करण्यासाठी व त्याबद्दलची गृहीतके तपासण्यासाठी करता येतो.

 

प्रतिदर्शावर आधारलेली t व F वंटने: मूळ वंटन प्रसामान्य N (m, σ) असता आणखी दोन उपयुक्त प्रतिदर्शी वंटने मिळतात. अशा प्रसामान्य प्रतिदर्शाची x*** व ∑(x_i-x***)²  यांची वंटने वर सांगितली आहेत. शिवाय हे संभावी चल निरवलंबी असल्याचे सिद्ध  करता येते म्हणून s²=∑(x_i-x***)² /  n-1 हे संकेत चिन्ह वापरून √n(x***-m)/s हे संख्यानक रचिल्यास त्याचे वंटन n-1 मुक्तता मात्रा असलेले t– वंटन असते. याचा उपयोग असा की, मूळ वंटनाचे विचरण σ² माहीत नसतानासुद्धा त्याचे माध्य m याविषयी अंदाज व्यक्तविता येतात व गृहीतके तपासता येतात. याच कल्पनेचा थोडा विस्तार करून दोन मूळ प्रसामान्य वंटनांची विचरणे समान असल्यास त्यांच्या माध्यांच्या तुलनेकरिता t – वंटन वापरता येते.

 

मूळ वंटने σ₁² व σ₂² विचरणे असणारी प्रसामान्य वंटने असली आणि त्यांपासून n₁ व n₂ निरीक्षण संख्या असलेले प्रतिदर्श घेऊन त्यांपासून वर सांगितल्याप्रमाणे s₁² आणि s₂² काढले, तर त्यांच्या गुणोत्तराचे प्रतिदर्शी वंटन सांगता येते. वर पाहिल्याप्रमाणे          (n₁-1) s₁²/σ₁² आणि (n₂-1) s₂²/σ₂² यांची वंटने काय-वर्ग वंटने असतात, शिवाय ते चल निरवलंबी असतात, यामुळे s₁²/σ₁²  / s₂²/σ₂² =  s₁² σ₂²/s₂‑σ₁² या गुणोत्तर चलाचे वंटन n₁–1, n₂–1 या मुक्तता मात्रा असलेले F– वंटन होते, म्हणून मूळ विचरणांचे गुणोत्तर σ₁²/σ₂² याविषयी अंदाज व्यक्तविण्यासाठी आणि तद्विषयक गृहितके तपासण्यासाठी s₁² / s₂² या संख्यानकाचा उपयोग होऊ शकतो. उदा., त्याच्या साहाय्याने σ₁²=σ₂² या गृहीतकाची कसोटी पाहता येते.

 

याहून अधिक अवघड संख्यानके घेतली की, त्यांची प्रतिदर्शी वंटने निश्चित करणे, विशेषतः मूळ वंटन प्रसामान्य नसताना प्रतिदर्शी वंटने शोधणे अवघड असते (गणितीय सांख्यिकीतील अनेक चालू संशोधने या विषयावर आहेत). मग वंटनाच्या अभावी या संख्यानकांची परिबले मुख्यातः माध्य व विचरण यांवर समाधान मानून घ्यावे लागते आणि अनेकदा ही संख्यानके सीमेत प्रसामान्य वंटनाप्रत जात असल्यामुळे प्रतिदर्श मोठा असल्यास या अपुऱ्या ज्ञानाचाही मूळ वंटनाविषयी अनुमाने करण्यासाठी उपयोग होतो.

 

द्विचल आणि बहुचल मूळ वंटनांपासून मिळालेल्या बहुचल प्रतिदर्शी संख्यानकांच्या वंटनांचाही विचार याच पद्धतीने केला जातो. हे काम अर्थातच आधिक अवघड व गुंतागुंतीचे होते. सांख्यिकीविज्ञांनी मूळ बहुचल प्रसामान्य मानून काही महत्त्वाच्या बहुचल संख्यानकांची वंटने शोधून काढली आहेत आणि बहुचल आकडेवारीच्या विश्लेषणासाठी त्यांचा उपयोग केला गेला आहे. व शेवटी एकचल प्रतिदर्शातील क्रमित निरीक्षणांचे थोडक्यात विवचन खाली दिले आहे.

 

क्रमित निरीक्षणे : समजा प्रतिदर्शातील निरीक्षणे त्यांच्या मूल्यांवरून संख्यानुक्रमाने पुढे दिल्याप्रमाणे लावली:

x₍₁₎ &lt x ₍₂₎ &lt…………………………….&lt x _(n).  क्रमवार लावलेल्या या निरीक्षणांना क्रमित निरीक्षणे म्हणतात. उदा., x_(r) हे r क्रमांकाचे क्रमित निरीक्षण आहे (वंटन संतत असल्यास कोणतीही दोन निरीक्षणे समान असण्याची संभाव्यता शून्य असल्याचे सिद्ध करता येते). मूळ संतत वंटनाचे f (x) व F (x) ही फलने दिलेली असल्यास क्रमित निरीक्षणांचे वंटन काढता येते. उदा., x _(r) = u याचे घनता फलन असे :

  g(u)= n!/(r-1)! (n-r)! (F(u))^r–1 × (1-F(u))^n–rf(u)         …..        (७०)

 

यावरून वंटन फलन G (u) सुद्धा सहज निघते. या सूत्रात अनुक्रमे r=1 आणि r = n घालून लघुतम निरीक्षण x₍₁₎ व महत्तम निरीक्षण x _(n) यांची वंटने मिळतात. याच पद्धतीने x _(r) = u, x _(s)=v, (r&lts) या दोन क्रमित निरीक्षणांच्या संयुक्त द्विचल वंटनाचे घनता फलन

                h(u,v) =n! / (r-1)! (s–r–1)! (n–s)!..(F(u))^r–1

                (F(v)–F(u)^s–r–1 (1–F(v))n–3f(u)f(v)                   ..…..       (७१)

 

असल्याचे दाखविता येते. या सूत्रात r=1, s=n घेतले, तर x₍₁₎ व x _(n) या अंत्य निरीक्षणांचे द्विचल फलन मिळते ते असे :

                h(u,v)=n(n–1)(F(v)–F(u))^n–2  f(u) f(v)…….. (७२)     

               

यापासून प्रतिदर्श व्याप्ती x_(n) –x₍₁₎= v–u =w हिचे वंटन निघू शकते. क्रमित निरीक्षणे व त्यांवर आधारलेले प्रतिदर्श संख्यानके आकडेमोडीच्या दृष्टीने वापरावयास सोपी असतात म्हणून अनुमान सिद्धांतात त्यांना अधिकाधिक महत्त्व प्राप्त होत आहे. विशेषतः अंत्य निरीक्षणे व प्रतिदर्श व्याप्ती ही संख्यानके पुष्कळदा वापरली जातात.

 

पहा: सांख्यिकीय अनुमानशास्त्र.

 

संदर्भ: 1. Cramer, H. Mathematical Methods of Statistics, Princeton, 1961.

           2. Fisher, R. A. Yates, F. Statistical Tables for Biological, Agricultural and Medical Research, London, 1963.

           3. Hoel, P. G. Introduction to Mathematical Statistics, New York, 1971.

           4. Kendall, M. G. Stuart, A. Advanced Theory of Statistics, Vol. I: Distribution Theory London, 1969.

           5. Mood, A. M. Graybill, F. A. Boes D. S. An Introduction to the Theory of Statistics, New York, 1973.

           6. Wilks, S. S. Mathematical Statistics, New York, 1962.

 

 

                                                                                कामत, अ. रा.

“