रामन परिणाम : पारदर्शक माध्यमामधून जेव्हा प्रकाश जातो, तेव्हा त्याचे प्रकीर्णन (विखुरण्याची क्रिया) होते. माध्यमातून बाहेर पडणाऱ्या प्रकाशाचे वर्णपटलेखकाद्वारे [⟶ वर्णपट-विज्ञान] विश्लेषण केले असता त्यामध्ये मूळ आपाती प्रकाशाच्या कंप्रतेशिवाय (दर सेकंदास होणाऱ्या कंपनांच्या संख्येस कंप्रता म्हणतात) अत्यंत कमी तीव्रतेच्या अशा अनेक भिन्न प्रकाश कंप्रता आढळतात. हा शोध सर चंद्रशेखर व्यंकट रामन व सर कार्यमाणिक्कम श्रीनिवास कृष्णन या भारतीय शास्त्रज्ञांनी कार्बन टेट्राक्लोराइड, क्लोरोफॉर्म, बेंझीन इ. द्रवांवर प्रयोग करून १९२८ साली लावला. या शोधाबद्दल रामन यांना १९३० मध्ये भौतिकीचे नोबेल पारितोषिक देण्यात आले. प्रकीर्णनामुळे निर्माण झालेल्या काही कंप्रता मूळ प्रकाश कंप्रतेपेक्षा कमी मूल्याच्या तर काही अधिक मूल्याच्या असतात, असे प्रयोगान्ती कळते. यांपैकी कमी कंप्रतेच्या प्रकाश वर्णपट रेषांस स्टोक्स रेषा, तर अधिक कंप्रतेच्या रेषांस प्रतिस्टोक्स रेषा अशा संज्ञा जी. जी स्टोक्स या ब्रिटिश भौतिकीविज्ञांच्या नावावरून दिल्या जातात. नव्या प्रकाश कंप्रतेची मूल्ये आपाती प्रकाश कंप्रता व प्रकीर्णक पदार्थाचे स्वरूप या दोहोंवर अवलंबून असतात पण नव्या वर्णपट रेषांच्या मूळ वर्णपट रेषेपासून आढळणाऱ्या स्थानच्युतींचा संबंध पदार्थांच्या रेणूंच्या इलेक्ट्रॉनीय कंपन अथाव परिभ्रमणी ऊर्जा पातळ्यांशी असल्याने ही स्थानच्युती मूल्ये फक्त प्रकीर्णन करणाऱ्या पदार्थाच्या स्वरूपामुळे निश्चित होताना आढळतात. त्यांचे मूल्य आपाती प्रकाश कंप्रतेवर अवलंबून नसते.
द्रवरूप हायड्रोजन या द्विआणवीय रेणूकरिता मिळणाऱ्या रामन वर्णपटाचा अभ्यास करून जे. सी. मल्केनन यांनी रामन कंप्रता स्थानच्युती आणि रेणूच्या कंपन व परिभ्रमण ऊर्जा पातळ्या यांमध्ये सरळ संबंध आहे, हा महत्त्वाचा शोध लावला. मक्लेनन यांच्या संशोधनापासून आणखी एका महत्त्वाच्या गोष्टीचा खुलासा झाला. अती नीच तापमानाच्या हायड्रोजन रेणूकरिता ऑर्थो व पॅरा अशा दोन स्वतंत्र अपरिवर्तनीय अवस्था आहेत, असे दाखविले गेले. हायड्रोजन रेणूच्या ऊष्मीय गुणधर्मावरून असे काहीतरी घडत असावे, असे सूचित होत होते पण याकरिता प्रत्यक्ष पुरावा रामन परिणामावरील प्रदत्तावरून (माहितीवरून) मिळाला. असाच एक महत्त्वाचा निष्कर्ष एफ्. रॅझेटी यांना द्रव नायट्रोजन रेणूच्या रामन वर्णपटाच्या अभ्यासावरून मिळाला. या काळापर्यंत न्यूट्रॉनाचा शोध लागला नव्हता. त्यामुळे सर्व पदार्थाच्या अणुकेंद्रात प्रोटॉन व इलेक्ट्रॉन हे निरनिराळ्या संख्येत उपस्थित असतात, असे त्या वेळी मानले जात होते. अणुकेंद्रात जे घटक कण असतात त्यांना प्रत्येकी विशिष्ट अशी परिवलन गती (स्वतःभोवती फिरत राहण्याची परिभ्रमण गती) असते. या सर्व घटकांच्या परिवलन गतींची जर सदिश बेरीज [⟶ सदिश] केली, तर त्यावरून संपूर्ण अणुकेंद्राच्या परिवलन गतीचे ज्ञान मिळू शकते. रॅझेटी यांच्या रामन परिणामावरील प्रदत्तामुळे हे सूचित झाले की, गृहीत धरलेले अणुकेंद्रीय इलेक्ट्रॉन अणुकेंद्राच्या परिवलन गतीमध्ये सहभागी होत नाहीत. अणुकेंद्रात इलेक्ट्रॉन नसतातच या स्पष्ट निष्कर्षापर्यंत यावयास भौतिकीला आणखी काही अवधी लागला, हे खरे असले तरी या प्रमेयाची सुरूवात परिणामावरील संशोधनामुळे झाली, हे तितकेच सत्य आहे. रेणूच्या संरचनेबद्दल फक्त नव्हे, तर अणुकेंद्राच्या संरचनेबद्दल सुद्धा रामन यांच्या शोधामुळे कशी माहिती उपलब्ध झाली, ही उल्लेखनीय गोष्ट आहे. अशा प्रकारे विविध क्षेत्रांत महत्त्वाची माहिती या नव्या शोधामुळे उपलब्ध होण्याच्या या घटनेमुळे प्रभावित होऊन रामन यांना नोबेल पारितोषिक समितीने पारितोषिक द्यावयाचे ठरवले, हे उघड दिसते.
एकंदर प्रकीर्णन प्रक्रियेचा रामन आविष्कार हा एक अत्यंत कमी संभाव्यतेचा असा एक भाग आहे, हे लक्षात घेणे आवश्य आहे. पदार्थामधून जाणाऱ्या प्रकाशाचे प्रकीर्णन फार मोठ्या प्रमाणात रॅली प्रक्रियेद्वारे होत असते [⟶ प्रकाशकी]. या प्रक्रियेमध्ये आपाती व प्रकीर्णित प्रकाशाच्या कंप्रतांमध्ये बदल होत नाही व या दोन प्रकाशांमध्ये एक निश्चित प्रकारचा कलासंबंध (ठराविक संदर्भापासून मोजल्या जाणाऱ्या गतिविषयक स्थितीतील संबंध) पण आढळतो. प्रकाशाचे गुणधर्म कंप्रता, तीव्रता व कला या तीन राशींमुळे ठरतात.
प्रकाशाचा रंग त्याच्या कंप्रतेमुळे (ν) निश्चित होतो. त्याच्या फोटॉनामध्ये (विद्युत् चुंबकीय ऊर्जेच्या अविभाज्य व अत्यल्प मूल्य असलेल्या कणामध्ये व पुंजकणामध्ये) असणाऱ्या ऊर्जेचे मूल्यसुद्धा कंप्रतेवरच अवलंबून असते (hν; h – प्लांक स्थिरांक). प्रकाश तीव्रतेमुळे एका एकक क्षेत्रफळावर पडणाऱ्या एकंदर प्रकाश ऊर्जेविषयी कल्पना मिळते, तर दोन फोटॉनांमध्ये होणाऱ्या परस्परक्रियेचे स्वरूप त्यंच्या विशिष्ट कलामूल्यावरून ठरत असते. कंप्रता (ν), तरंगलांबी (λ) व प्रकाशवेग (c) यांमध्ये λ ν = c हा सूत्रमय संबंध असतो आणि तरंगसंख्या ![]() असेल, तर
असेल, तर ![]() प्रकाश कंप्रतेचे मूल्य
प्रकाश कंप्रतेचे मूल्य ![]() तरंगसंख्येच्या स्वरूपात देण्याचा आधुनिक प्रघात आहे, हीच पद्धत प्रस्तुत नोंदीमध्ये वापरली आहे, हीच पद्धत प्रस्तुत नोंदीमध्ये वापरली आहे.
तरंगसंख्येच्या स्वरूपात देण्याचा आधुनिक प्रघात आहे, हीच पद्धत प्रस्तुत नोंदीमध्ये वापरली आहे, हीच पद्धत प्रस्तुत नोंदीमध्ये वापरली आहे.
रामन परिणामामध्ये आपाती व प्रकीर्णित प्रकाशांच्या कलांमध्ये यदृच्छ प्रकारचे बदल होताना आढळतात. रॅली प्रकीर्णनामध्ये जर आपाती प्रकाश ध्रुवित (एकाच प्रतलात कंपने होत असलेल्या) स्वरूपाचा असेल, तर या क्रियेमुळे तो अंशतः विध्रुवित होतो. काही पदार्थांच्या विशिष्ट ऊर्जा पातळ्यांच्या बाबतीत रामन प्रकीर्णनामुळे नैसर्गिक आपाती प्रकाशाचे ध्रुवीकरण होताना आढळते. रॅली प्रक्रियेच्या योगे पदार्थांच्या रेणूंपासून प्रक्रीर्णित होणाऱ्या प्रकाशाची तीव्रता त्या रेणूंची अवकाशीय स्थाने व त्यांचा दिक्विन्यास (दिशांची मांडणी) यांवर अवलंबून राहतात. हे दिक्विन्यास ज्या प्रमाणात यदृच्छ स्वरूपाचे असतील त्या प्रमाणात ही तीव्रता सर्वांत कमी मूल्याची असते, तर कमी घनतेच्या वायूमध्ये हे प्रमाण सर्वांत जास्त असते, असे प्रयोगान्ती आढळते. पुढे दाखविल्याप्रमाणे रामन प्रकीर्णित प्रकाशाची तीव्रता रेणूच्या पुंज ऊर्जा पातळ्यांमधील संक्रमण संभाव्यतेवर सरळपणे अवलंबून रहात नाही.
काही पदार्थांमधून प्रकाश गेला असता त्यांपासून आपाती प्रकाश कंप्रतेपेक्षा भिन्न कंप्रतेचा अनुस्फुरित (आपाती प्रकाशामुळे निर्माण होणारा व आपाती प्रकाश थांबल्यास निर्मिती बंद होणारा) प्रकाश उत्सर्जित केला जातो. अनुस्फुरित प्रकाश कंप्रतेचे मूल्य आपाती प्रकाश कंप्रतेवर अवलंबून नसते. अशा प्रकारे रामन प्रकीर्णन, रॅली प्रकीर्णन व अनुस्फुरण या तीन आविष्कारांमधील भेद स्पष्ट होतो. द्रवामध्ये रामन प्रकीर्णनाचा परिणाम रॅली प्रकीर्णनाच्या सु. हजार पटींनी कमी असतो. रामन प्रकीर्णनामध्ये मिळणाऱ्या प्रकाशाची तीव्रता आपाती प्रकाश तीव्रतेच्या सु. एक कोटी पटींनी कमी असते. या गोष्टीवरून या परिणामाचा शोध लागण्यास विलंब का लागला, हे लक्षात येते.

रामन व कृष्णन यांनी १९२८ मध्ये या परिणामावरील आपला संशोधन निबंध प्रसिद्ध केल्यानंतर काही महिन्यांनंतर रशियामध्ये जी. एस्. लँड्सबर्ग व एल्, आय्. मांडेलस्टाम यांनी असाच परिणाम आपणास क्वॉर्ट्झ स्फटिकामध्ये मिळाल्याचे प्रसिद्ध केले. रामन व कृष्णन यांचा या विषयावरील निबंध आधी प्रसिद्ध झाला होता आणि तो जास्त सविस्तर व निर्णायक स्वरूपाचा असल्यामुळे या शोधाचे जनकत्व रामन यांनाच देण्यात येते.

⇨ पुंज सिद्धांतावर आधारित अशी अपस्करणाची (प्रकाशाचे निरनिराळ्या कंप्रतेच्या घटकांत अलगीकरण करणाऱ्या प्रक्रियेची) मीमांसा करून ए. श्मेकाल यांनी १९२३ मध्ये पारदर्शक माध्यमामध्ये प्रकाशाचे प्रकीर्णन झाले असता त्यायोगे आपाती प्रकाश कंप्रतेहून भिन्न अशा नव्या कंप्रता निर्माण होऊ शकतील, असा निष्कर्ष काढला होता, हे या संदर्भात नमूद केले पाहिजे. या कारणाकरिता या नवीन परिणामाचा ‘श्मेकाल-रामन परिणाम’ असा पण उल्लेख काही वेळा केला जातो. एच्. ए. क्रॅमर्स व डब्ल्यू. हायझेनबेर्क यांच्या १९२५ साली मांडलेल्या अपस्करण मीमांसेपासून रामन परिणामाविषयी संपूर्ण स्पष्टीकरण मिळू शकते. रामन परिणामामध्ये आढळणाऱ्या सर्व अंगांकरिता जे सैद्धांतिक विशदीकरण जी. प्लाकझेक यांनी १९३४ मध्ये दिले त्याचे विवेचन पुढील भागात केले आहे.
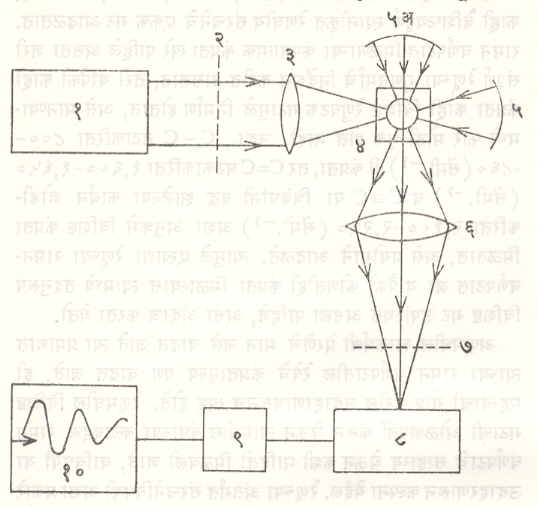
रामन परिणामाचे निरीक्षण करण्याकरिता उपकरण योजना : आर्. डब्ल्यू. वुड यांनी वापरलेली उपकरण योजना या कार्याकरिता वापरणे सोईस्कर ठरते (आ. १).
प्रकीर्णित प्रकाशाचे विश्लेषण करण्याकरिता या योजनेत छायाचित्रण काच असलेला वर्णपटलेखक (६) दाखविलेला आहे. छायाचित्रण काचेऐवजी प्रकाशगुणक नलिकेचा [⟶ इलेक्ट्रॉनीय प्रयुक्ति] क्रमवीक्षक (क्रमाक्रमाने प्रत्येक बिंदूचे पद्धतशीरपण निरीक्षण करणारी प्रयुक्ती) म्हणून पण उपयोग करता येतो. या योजनेमध्ये पुढील महत्त्वाचे विभाग असतात : (१) उच्च तीव्रतेचा विस्तारित प्रकाश उद्गम (सामान्यपणे पाऱ्याची विद्युत् प्रज्योत), (२) आपाती प्रकाशाला एकवर्णी करण्याकरिता प्रकाशीय गाळणी, (३) नमुना द्रवाकरिता धारक. धारकाचा एका बाजूचा भाग (आकृतीमध्ये दाखविल्याप्रमाणे) काळा केलेला असतो. या काळ्या पार्श्वभूमीवर प्रकीर्णित प्रकाशाचे अभिलेखन करणे सुलभ होते. प्रकीर्णित प्रकाशाचे निरीक्षण मूळ प्रकाश दिशेच्या उदग्र (उभ्या) दिशेत करण्याकरिता द्रव धारकाच्या दुसऱ्या टोकाला सपाट काच बसविलेली असते, (४) प्रकीर्णित प्रकाशाला वर्णपटलेखकाकडे वळवून एकत्रित करण्याकरिता संधनक भिंग योजना. (५) छायालेखन प्रतलावर आपाती प्रकाशाचे अतिउद्भासन होऊ नये म्हणून या प्रकाशीय गाळणीच्या साहाय्याने प्रकाशाची तीव्रता कमी केली जाते.
प्रकीर्णित प्रकाशाच्या ध्रुवीकरण अवस्थेविषयी माहिती मिळविणे जेव्हा आवश्यक असते तेव्हा वर्णपटलेखकाच्या जोडीला प्रकाशाच्या मार्गात द्विप्रणमनी लोलक [⟶ प्रकाशकी] ठेवून त्याद्वारे समांतर व उदग्र या दिशांत ध्रुवित झालेल्या प्रकाश घटकांचे एकाच वेळी अभिलेखन करून त्यांचे मूल्यमापन केले जाते. प्रकाशाचे वर्णपटलेखकामुळे जे काही प्रमाणात ध्रुवीकरण होते ते विचारात घेऊन त्याकरिता मिळालेल्या प्रदत्ताची संशुद्धी करावी लागते. रामन वर्णपट रेषेची ध्रुवण अवस्था p या संख्येद्वारे निर्देशित केली जाते. ही संख्या अशा प्रकारे व्याख्यात केली जाते की, जेव्हा p = 0 असेल तेव्हा रेषेत संपूर्ण ध्रुवण असते आणि जेव्हा p = 1 असेल तेव्हा तदनुरूप रेषेमध्ये ध्रुवणाचा संपूर्ण अभाव असतो.
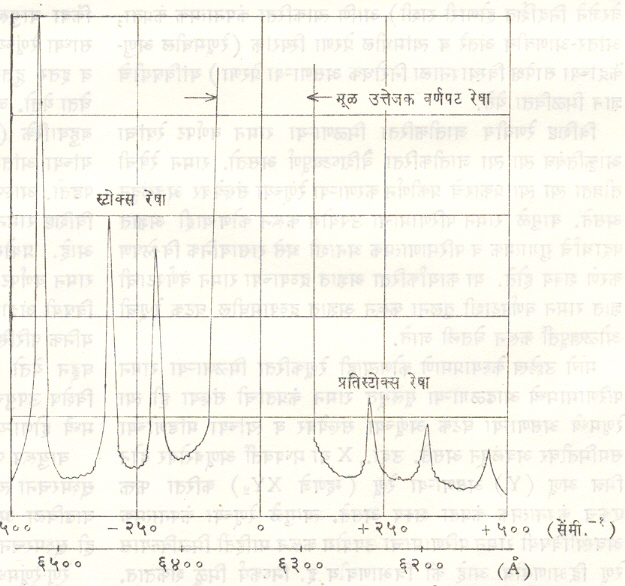
रामन वर्णपटाचे स्वरूप : कार्बन टेट्राक्लोराइडाकरिता मिळालेला प्रत्यक्ष रामन वर्णपट आ. २ मध्ये दाखविला आहे. आकृतीमध्ये ४,३५८ Å आणि ४,०४६·५ Å या उत्तेजक वर्णपट

रेषांकरिता मिळालेले काही प्रदत्त दाखविले आहेत. आकृतीमध्ये दाखविलेली कंप्रता स्थानच्युती मूल्ये ही मागे नमूद केल्याप्रमाणे तरंगसंख्येच्या स्वरूपात दिली आहेत. आकृतीवरून स्टोक्स व प्रतिस्टोक्स वर्णपट रेषांच्या स्थानांविषयी पण चांगली कल्पना येईल. कार्बन टेट्राक्लोराइडाकरिता रामन स्थानच्युती मूल्ये व तदनुरूप अवरक्त (दृश्य वर्णपटावरील तांबड्या रंगाच्या अलीकडील अदृश्य) शोषण पट्टातील कंप्रता यांमधील परस्परसंबंध कोष्टक क्र. १ वरून स्पष्ट होतो.
आ. ३ मध्ये तीन स्टोक्स व तीन प्रतिस्टोक्स रामन वर्णपट रेषा दाखविल्या आहेत. आकृतीमधील रेषांच्या तरंगलांब्या तदनुरूप वर्णपट रेषांच्या तीव्रतेचे निर्देशन करतात. याच रेणूच्या वर्णपट रेषांकरिता मिळालेली p गुणकाची मूल्ये कोष्टक क्र. २ मध्ये दाखविली आहेत.
उत्तेजक रेषेपासून रामन वर्णपट रेषांकरिता मिळणारी कंप्रता स्थानच्युती मूल्ये ही त्या रेणूच्या शोषण पट्टाच्या कंप्रतांच्या समान असतात, ही रामन परिणामामध्ये स्पष्टपणे दिसणारी अशी गोष्ट आहे. येथे हे स्पष्ट केले पाहिजे की, प्रत्येक रामन वर्णपट रेषेला अनुरूप अशी अवरक्त शोषण पट्ट रेषा असतेच असे आढळत नाही. याउलट काही अवरक्त शोषण वर्णपट रेषांकरिता तदनुरूप रामन वर्णपट रेषा मिळत नाहीत, असे पण आढळते. रामन वर्णपट रेषांकरिता मिळणाऱ्या कंप्रता स्थानच्युती रेणूनच्या आंतरिक ऊर्जा बदलामुळे (इलेक्ट्रॉनीय अथवा कंपन किंवा परिभ्रमणी) निर्माण होतात, हे मक्लेनन यांनी प्रथम दाखविले. प्रकाशाकरिता फोटॉन किंवा तरंग प्रतिरूपाचा उपयोग करून रामन परिणाम विशद करता येतो.

रामन परिणामाचे विशदीकरण : प्रकाशतरंग संकल्पनेनुसार : माध्यमामधून जेव्हा विद्युत् चुंबकीय तरंग प्रसारित होतो तेव्हा त्याच्या अणु-रेणूंमधील शिथिलपणे बद्ध असलेले इलेक्ट्रॉन दोलायमान होतो तेव्हा तो विद्युत् चुंबकीय तरंगाचे प्रेषण करतो. इलेक्ट्रॉनाची आंदोलन कंप्रता तरंगामधील विद्युत् क्षेत्र सदिशाच्या कंप्रतेएवढीच असते. त्यामुळे अशा आंदोलनामुळे निर्माण होणाऱ्या तरंगाची कंप्रता मूळ तरंग कंप्रतेएवढीच राहते. रॅली प्रकीर्णन प्रक्रियेमध्ये प्रकाशाचे उत्सर्जन या प्रकारे होते.
रेणूमध्ये बंधित इलेक्ट्रॉनांमुळे ऋण विद्युत् भार केंद्रे, तर त्यांमधील अणुकेंद्रामुळे धन विद्युत् भार केंद्रे निर्माण होत असतात. रेणूच्या संरचनेनुसार दोन गोष्टींची शक्यता असते : (१) रेणूला शाश्वत स्वरूपाचे द्विध्रुवी विद्युत् परिबल (विद्युत् भार वितरणाचे वैशिष्ट्य दर्शविणारी आणि विद्युत् भार व त्याचा स्थान सदिश यांच्या गुणाकारांची सर्व विद्युत् भारांसाठी घेतलेल्या सदिश बेरजेबरोबर असणारी राशी) असेल, तर त्याला ध्रुवी रेणू अशी संज्ञा दिली जाते. (२) रेणूला शाश्वत द्विध्रुवी परिबल नसेल, तर अशा रेणूला विध्रुवी रेणू असे म्हणतात. आपाती विद्युत चुंबकीय प्रारणाकरिता या दोन प्रकारच्या रेणूंच्या प्रतिसादांमध्ये फरक असतो.

ध्रुवी रेणूवर जर विद्युत् चुंबकीय ऊर्जेचे आपतन झाले, तर या प्रकारचा रेणू या ऊर्जेचे शोषण करण्याच्या अवस्थेत असतो. पुंज सिद्धांताप्रमाणे रेणूला पृथक् इलेक्ट्रॉनीय वा कंपन किंवा परिभ्रमणी ऊर्जा पातळ्या असतात. त्यामुळे तो विद्युत् चुंबकीय ऊर्जेचे काही ठराविक परिमाणामध्येच शोषण करू शकतो. रेणूच्या शोषण वर्णपटाचा अभ्यास केला असता या प्रकारच्या ऊर्जा पातळ्यांविषयी माहिती मिळविता येते. आपाती प्रकाशामध्ये मिळणाऱ्या विवेचक विवेचक शोषणावरून ही माहिती उपलब्ध होते. या कार्याकरिता रेणूच्या अवरक्त शोषण वर्णपटाचा पण उपयोग करता येतो.
विध्रुवी रेणूद्वारा आपाती विद्युत् चुंबकीय प्रारणाचे शोषण होत नाही. या प्रकारच्या रेणूमध्ये एक निराळ्या प्रकारची प्रक्रिया घडून येते, असे प्लाकझेक यांनी १९३४ मध्ये दाखविले. आपाती प्रारणामधील विद्युत क्षेत्रामुळे रेणूमधील धन व ऋण विद्युत् भारांचे विस्थापन होऊन त्यामुळे त्यामध्ये प्रवर्तित स्वरूपाचे द्विध्रुवी परिबल निर्माण होते. रेणूमधील या दोन प्रकारच्या विद्युत भार केंद्राची एकमेकांच्या सापेक्ष विस्थापन होण्याची क्षमता ही रेणूच्या ध्रुवणक्षमता (α) या स्थिरांकामुळे निश्चित होते. या स्थिरांकाचे मूल्य रेणूच्या निव्वळ स्वरूपावर सरळपणे अवलंबून नसते. विद्युत् क्षेत्राची कंप्रता, रेणूचा दिक्विन्यास आणि रेणूच्या अंतर्गत होणाऱ्या इलेक्ट्रॉन व अणुकेंद्रे यांच्या हालचाली या सर्वांचा α वर परिणाम होतो. इलेक्ट्रॉन व अणुकेंद्र यांची हालचाल परत रेणूच्या कंपन व परिभ्रमणी गतीमुळे प्रभावित होत असते. परिभ्रमणी व कंपनशील रेणूंनी भरलेल्या माध्यमातून जेव्हा प्रकाश जातो तेव्हा त्यामधील विद्युत् चुंबकीय ऊर्जेचा मोठा भाग इलेक्ट्रॉनांच्या आंदोलनामुळे मूळ कंप्रतेच्याच प्रकाशाची पुनर्निर्मिती करण्यामध्ये खर्च केला जातो. ध्रुवणक्षमतेद्वारे प्रकाशाची अल्प प्रमाणात रेणूबरोबर परस्परक्रिया होऊन त्याची रामन प्रकीर्णन प्रक्रियेत परिणती होते. अशा प्रकारे नव्या कंप्रता निर्माण होतात. रामन प्रकीर्णित प्रकाशाच्या तीव्रतेकरिता α ही राशी फार महत्वाची असते. या दृष्टिकोनाप्रमाणे थोडक्यात असे म्हणता येते की, अवरक्त वर्णपट प्राप्त होण्याकरिता रेणूच्या द्विध्रुवी विद्युत् परिबलात फरक पडावा लागतो, तर रेणूच्या ध्रुवणक्षमतेत बदल झाल्याशिवाय रामन वर्णपट उपलब्ध होत नाही. प्लाकझेक मीमांसेनुसार प्राथमिक स्वरूपाचे विवेचन वर दिले आहे. या मीमांसेप्रमाणे देण्यात येणारे जास्त तर्ककठोर विशदीकरण पुढे दिले आहे.
फोटॉन संकल्पनेप्रमाणे : क्ष-किरण फोटॉन व धातूमधील मुक्त इलेक्ट्रॉन यांमध्ये होणाऱ्या आघात प्रक्रियेचा विचार ⇨ कॉम्पटन परिणाम विशद करण्याकरिता केला जातो. याच न्यायाने रामन परिणाम विशद करण्याकरिता केला जातो. याच न्यायाने रामन परिणाम विशद करण्याकरिता त्यामध्ये फोटॉन व रेणू यांमध्ये घडून येणारी आघात क्रिया मूलभूत स्वरूपाची आहे, असे मानले जाते. फोटॉन व रेणू हे जेव्हा एकमेकांवर आघात करतात तेव्हा यांपैकी बहुसंख्य आघात स्थितिस्थापक (ज्यात आघातापूर्वीची एकूण गतिज ऊर्जा व आघातानंतरची एकूण गतिज ऊर्जा या समान असतात असे) स्वरूपाचे होतात. यामध्ये ऊर्जा-विनिमय होत नाही. त्यामुळे या आघातानंतर फोटॉनच्या ऊर्जेत व त्यामुळे त्याच्या कंप्रतेत काही फरक पडत नाही. अशा प्रक्रियेमुळे रॅली प्रकीर्णन घडून येते. एकंदर आघात संख्येच्या अत्यंत अल्प अशा प्रमाणामध्ये फोटॉन आणि रेणू यांमध्ये उर्जेची देवघेव होते म्हणजे हे आघात अस्थितिस्थापक स्वरूपाचे होतात. यामध्ये होणारा ऊर्जा-विनिमय दोन प्रकारचा असतो. पहिल्या प्रकारात रेणूला फोटॉनपासून ऊर्जा मिळत असल्यामुळे फोटॉनची ऊर्जा कमी होऊन त्याच्या कंप्रतेमध्ये घट होते व यामुळे स्टोक्स वर्णपट रेषा उत्सर्जित केल्या जातात. मिळालेल्या उर्जेमुळे रेणू उत्तेजित होतो. अतिरिक्त ऊर्जेचे उत्सर्जन किंवा अन्य प्रक्रियेद्वारे ऱ्हास होऊन रेणू आपल्या निम्नतम पातळीवर परतो येतो. याउलट ही परस्परक्रिया उत्तेजित रेणू व फोटॉन यांमध्ये होऊन जर फोटॉनाला ऊर्जा लाभ झाला, तर त्याच्या कंप्रतेमध्ये वाढ होते व या विक्रियेमुळे प्रतिस्टोक्स वर्णपट रेषांचे उत्सर्जन होते. उत्तेजित रेणूंची संख्या ही निम्नतम अवस्थेमधील रेणुसंख्येपेक्षा निसर्गतः कमी असल्यामुळे प्रतिस्टोक्स रेषांची तीव्रता स्टोक्स रेषांपेक्षा कमी का असते, हे लक्षात येते.
तत्त्वतः पाहिले असता रामन वर्णपट रेषा रेणूच्या आंतरिक इलेक्ट्रॉनीय कंपन किंवा परिभ्रमणी अवस्थेत होणाऱ्या बदलामुळे निर्माण होतात, असे जरी मानता आले, तरी प्रत्यक्षात आढळणारे परिणाम बहु-आणवीय रेणूच्या कंपन व परिभ्रमणी अवस्थांमध्ये घडून येणाऱ्या बदलामुळेच मुख्यत्वेकरून होताना आढळतात. निव्वळ परिभ्रमणी ऊर्जा बदलामुळेच मुख्यत्वेकरून होताना आढळतात. निव्वळ परिभ्रमणी ऊर्जा बदलामुळे निर्माण होणाऱ्या रामन वर्णपट रेषा सहसा मिळत नाहीत. कारण अशा प्रक्रियेत होणारे बदल अत्यंत कमी मूल्याचे असतात व त्यामुळे त्यांचे निरीक्षण करणे सोपे नसते. या प्रकारचे बदल फक्त वायुरूपी रेणूमध्येच घडून येण्याची शक्यता असते. द्रवरूप पदार्थामध्ये रेणूच्या अशा परिभ्रमणी गतीला विरोध होतो व त्यामुळे या अवस्थेमधील रेणूंकरिता पृथक् ऊर्जामूल्ये आढळून येत नाहीत. कारण अशा प्रक्रियेत होणारे बदल अत्यंत कमी मूल्याचे असतात व त्यामुळे त्यांचे निरीक्षण करणे सोपे नसते. या प्रकारचे बदल फक्त वायुरूपी रेणूमध्येच घडून येण्याची शक्यता असते. द्रवरूप पदार्थामध्ये रेणूच्या अशा परिभ्रमणी गतीला विरोध होतो व त्यामुळे या अवस्थेमधील रेणूंकरिता पृथक् ऊर्जामूल्ये आढळून येत नाहीत. घन पदार्थाकरिता रामन परिणामाचे स्वरूप खूप वेगळे असते कारण अशा पदार्थाकरिता होणारे परस्परक्रिया स्फटिक जालक व फोटॉन यांमध्ये घडून येते, असे प्रयोगाने आढळते.
अवरक्त वर्णपटापासून रेणूच्या ऊर्जा अवस्थांबद्दल जी माहिती उपलब्ध होते, तीकरिता रामन परिणामापासून मिळणारी माहिती पूरक ठरते. या दोन प्रकारच्या संक्रमणांकरिता यथार्थ असणारे निवड नियम भिन्न असू शकतात. या दोन्ही प्रकारांमधील भेद केंद्रीय सममिती असणाऱ्या रेणूच्या बाबतीत सर्वांत जास्त स्पष्ट असतो. अशा रेणूकरिता अवरक्त शोषण वर्णपटात मिळणाऱ्या रेणू-कंप्रता रामन वर्णपटामध्ये मिळत नाहीत आणि याचप्रमाणे रामन वर्णपटात मिळणाऱ्या कंप्रता अवरक्त शोषण वर्णपटात उपस्थित नसतात. संक्षेपाने असे म्हणता येते की, एखाद्या रेणूमध्ये जर N अणू असतील, तर त्याकरिता ३N – ६ एवढ्या मूलभूत कंप्रता शक्य असतात. ज्या कंप्रता उत्सर्जनामध्ये रेणूच्या द्विध्रुवी परिबलामध्ये बदल होतो त्याविषयीची माहिती अवरक्त वर्णपटावरून मिळू शकते. ज्या कंप्रता उत्सर्जनामध्ये रेणूच्या ध्रुवणक्षमतेत म्हणजे प्रवर्तित परिबलात फरक पडतो त्याकरिता फक्त रामन वर्णपटच शक्य असतो.
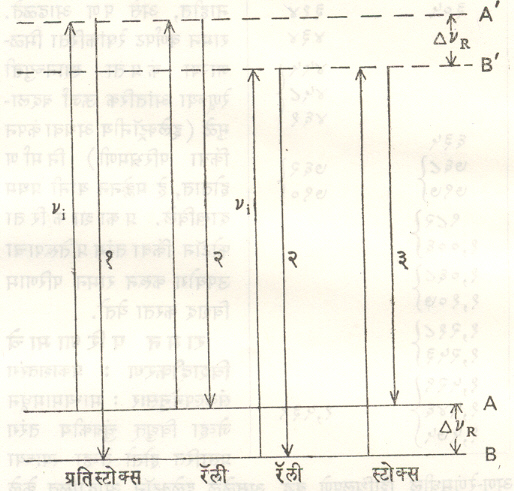
अवरक्त वर्णपटामध्ये मिळणाऱ्या इलेक्ट्रॉनीय वा कंपन अथवा परिभ्रमणी ऊर्जा बदलामुळे मिळणाऱ्या वर्णपट रेषांकरिता जे निवड नियम आहेत ते सर्वज्ञात आहेत [⟶ रेणवीय भौतिकी]. रामन संक्रमणाकरिता ज्या विशिष्ट अटी यथार्थ ठरतात त्यांचे समाधानकारक स्पष्टीकरण प्लाकझेक यांच्या पुंज-सैद्धांतिक तर्ककठोर मीमांसेपासून मिळते. रामण संक्रमण वर्णपट रेषेची तीव्रता या तदनुरूप दोन पातळ्यांकरिता मिळणाऱ्या संक्रमण संभाव्यता मूल्यावर मुळीच अवलंबून राहत नाही, असे प्रयोगाने जे आढळते त्याचा खुलासा या मीमांसेपासूनच मिळतो. तदनुरूप शोषण वर्णपट रेषेची तीव्रता या संक्रमण संभाव्यता मूल्यावरच अवलंबून असते, हे या संदर्भात नमूद करण्याजोगे आहे. रेणूच्या दोन ऊर्जा पातळ्यांमध्ये रामन संक्रमण सिद्ध होण्याकरिता एक तिसरी ऊर्जा पातळी पण आवश्यक होते. ही तिसरी ऊर्जा पातळी विशिष्ट गुणधर्माची असावी लागते. कारण नेहमीच्या निवड नियमानुसार पहिल्या दोन ऊर्जा पातळ्यांपासून या तिसऱ्या ऊर्जा पातळीपर्यंत संक्रमणे शक्य असावी लागतात म्हणजे त्या अनुज्ञात असाव्या लागतात. आपाती फोटॉन व रेणू यांमध्ये घडून येणाऱ्या रामन परस्परक्रियेच्या पहिल्या टप्प्यात रेणू व फोटॉन एक आभासी संलग्न उत्तेजित अवस्था निर्माण होते. रेणू व फोटॉन यांची ही एक तात्पुरती संलग्न अवस्था असल्यामुळे या अस्थेला आभासी ही संज्ञा दिली जाते. विवेचनाच्या सुलभतेकरिता रेणूच्या उत्तेजित अवस्थेमध्ये त्यामधील इलेक्ट्रॉनांच्या उर्जेत बदल होतो, असे गृहीत धरले आहे. बहुसंख्य इलेक्ट्रॉन या नव्या आभासी अवस्थेपासून आपल्या मूळ अवस्थेकडे झटकन परत येतात त्यामुळे संलग्न फोटॉन परत मुक्त होऊन मार्गक्रमण करू लागतो. या प्रक्रियेमुळे रॅली प्रकीर्णन मिळते. दशलक्ष ते दशकोटी इतक्या एकूण आभासी अवस्थांमधील सरासरीने एक इलेक्ट्रॉन मूळ ऊर्जा पातळीपर्यंत न येता रेणूच्या मधल्या ऊर्जा पातळीवर येऊन थांबतो व त्यामुळे रामन वर्णपट रेषेचे उत्सर्जन होते. रामन संक्रमणामद्ये ज्या विविध प्रकारच्या प्रक्रिया दिसतात त्यांचा खुलासा आ. ४ वरून होईल.
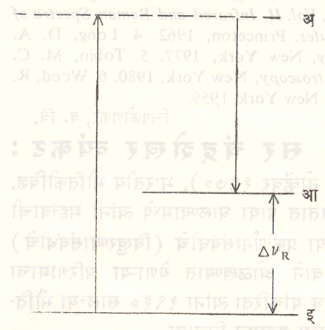
A व B या दोन रेणू ऊर्जा पातळ्या असून त्यांमधील उर्जा फरकामुळे आपाती वर्णपट रेषेपासून (कंप्रता υi) ΔνR कंप्रता स्थानच्युती असलेल्या स्टोक्स व प्रतिस्टोक्स रामन वर्णपट रेषा मिळतात असे गृहीत धरले आहे. A’ व B’ या दोन आभासी अशा वरच्या ऊर्जा पातळ्या आहेत. (१) येथे दाखविलेल्या संक्रमणामुळे प्रतिस्टोक्स रेषा, (२) येथे निर्देशित केलेल्या संक्रमणामुळे रॅली प्रकीर्णन, तर (३) या ठिकाणी दाखविलेल्या संक्रमाणामुळे स्टोक्स रेषांचे उत्सर्जन होते. वरील यंत्रणेचा उपयोग करून असे दाखविता येते की, J या परिभ्रमणी पुंजांकाकरिता ΔJ = 0, +१, + २ असा निवड नियम रामन संक्रमणाकरिता मिळतो. या यंत्रणेचा उपयोग करून रामन वर्णपट रेषांच्या तीव्रतेबद्दल पण समाधानकारक खुलासा मिळतो.
मूळ प्रकाशाच्या उदग्र दिशेत प्रकीर्णनाने मिळणाऱ्या रामन वर्णपट रेषांकरिता ध्रुवण अवस्था ही एक महत्त्वाची राशी असते. मीमांसेप्रमाणे वर्णपट रेषांकरिता ध्रुवणाचे प्रमाण एकाच मूल्याचे नसते कारण हे मूल्य प्रकीर्णन करणाऱ्या रेणूच्या संरचनेमधील सममितीवर अवलंबून असते (पहा:कोष्टक क्र.२). हेच विधान जास्त अचूकपणे करावयाचे झाल्यास रामन रेषांचे ध्रुवण त्याच्याशी निगडित असलेल्या रेणूच्या कंपन ऊर्जा पातळ्यांच्या सममितीमुळे निर्धारित होते, असे म्हणता येते. या संदर्भात असा एक नियम देता येतो की, संपूर्णपणे सममित असणाऱ्या कंपन ऊर्जा पातळ्यांकरिता रामन रेषा ध्रूवित असतात, तर याउलट संपूर्णपणे असममित ऊर्जा पातळ्यांकरिता या रेषा विध्रुवित स्वरूपात मिळतात. रामन रेषांच्या ध्रुवणाचे मापन करून तदनुरूप ऊर्जा पातळ्यांच्या सममितीबद्दल माहिती मिळविणे शक्य होते.
रामन परिणामापासून मिळणाऱ्या माहितीचे स्वरूप : आतापर्यंतच्या विवेचनावरून हे स्पष्ट होते की, रामन व अवरक्त वर्णपट या दोहोंचा अभ्यास करून मुख्यत्वे रेणूच्या कंपन अवस्थेविषयी माहिती उपलब्ध होते. निरनिराळ्या प्रणालींच्या ज्या ऊर्जा पातळ्यांविषयीची माहिती सर्वसामान्य शोषण (यामध्ये अवरक्ताचा अंतर्भाव होतो) व उत्सर्जन वर्णपटीय तंत्राद्वारे मिळविणे शक्य होत नव्हते, अशा प्रणालींच्या ऊर्जा पातळ्यांचे विश्लेषण करण्याकरिता रामन परिणामामुळे एक प्रभावी पद्धत उपलब्ध झाली, हा त्याच्या शोधामुळे झालेला सर्वांत मूलभूत व महत्त्वाचा असा फायदा होय, असे म्हणता येते.
रामन वर्णपटावरून रेणवीय निरूढी परिबल (रेणूच्या प्रत्येक घटकाचे द्रव्यमान व निर्दिष्ट अक्षापासून त्याच्या अंतराचा वर्ग यांचा गुणाकार करून सर्व घटकांकरिता अशा गुणाकारांच्या घेतलेल्या बेरजेने निदर्शित होणारी राशी) आणि त्याकरिता कंपनात्मक कंप्रता, आंतर-आणवीय अंतरे व त्यांमधील प्रेरणा स्थिरांक (रेणूमधील अणुकेंद्रांच्या सापेक्ष विस्थापनाला विरोधक असणाऱ्या प्रेरणा) यांविषयीचे ज्ञान मिळविता येते.
विशिष्ट रेणवीय जातीकरिता मिळणाऱ्या रामन वर्णपट रेषांचा आकृतिबंध त्या त्या जातीकरिता वैशिष्ट्यपूर्ण असतो. रामन रेषेची तीव्रता त्या त्या प्रकारचे प्रकीर्णन करणाऱ्या रेणूंच्या संख्येवर अवलंबून असते. यामुळे रामन परिणामाचा उपयोग करून कोणत्याही अज्ञात पदार्थाचे गुणात्मक व परिमाणात्मक अनाशी असे रासायनिक विश्लेषण करणे शक्य होते. या कार्याकरिता अज्ञात द्रव्याच्या रामन वर्णपटाची ज्ञात रामन वर्णपटाशी तुलना करून अज्ञात द्रव्यामधील घटक रेणूची ओळखपूर्ती करून घेतली जाते.
मागे उल्लेख केल्याप्रमाणे कोणत्याही रेणूकरिता मिळणाऱ्या रामन परिणामामध्ये आढळणाऱ्या मूलभूत रामन कंप्रतांची संख्या ही त्या रेणूमध्ये असणाऱ्या घटक अणूंच्या संख्येवर व त्यांच्या मांडणीच्या सममितीवर अवलंबून असते. उदा., X या मध्यवर्ती अणूबरोबर दोन भिन्न अणू (Y) असणाऱ्या रेणू (म्हणजे XY2) करिता फक्त एकच कंपनात्मक कंप्रता शक्य असते. त्यामुळे रेणूच्या कंपनात्मक अवस्थांविषयी रामन परिणामाचा उपयोग करून माहिती मिळविल्यास रेणू द्विआणवीय आहे की त्रिआणवीय इ. निष्कर्ष मिळू शकतात. एवढेच नव्हे, तर त्याच्या संरचनेबद्दलदेखील काही अनुमाने करता येतात. उदा., रामन परिणामाच्या अभ्यासावरून H2O, H2S व SO2 हे रेणू त्रिकोणी आहेत, NH3 हा प्रसूचीच्या (पिरॅमिडाच्या) आकाराचा आहे, तर फॉस्जीन (COCI2 अथवा कार्बोनिल क्लोराइड) या रेणूचा स्वरूपाकार इंग्रजीमधील Y या अक्षराच्या आकारासारखा असतो, असे दाखविता येते.
काही रेणूंमध्ये मिथिल कार्बोनिल, C-C, C=C C ≡ C इ. काही वैशिष्ट्यपूर्ण स्थानीकृत रेणवीय संरचनेचे एकक गट आढळतात. रामन वर्णपटात मिळणाऱ्या कंपनात्मक कंप्रता खरे पाहिले असता जरी संपूर्ण रेणूच्या गुणधर्माचे निर्देशन करीत असतात, तरी यांपैकी काही कंप्रता काही विशिष्ट रेणुघटक गटामुळे निर्माण होतात, असे मानण्यामध्ये फार मोठी चूक होत नाही. उदा., C-C गटाकरिता ८००-८६० (सेंमी.-१) ही कंप्रता, तर C=C घटकाकरिता १,६००-१,६५० (सेंमी.-१) व C ≡ C या त्रिबंधांनी बद्ध झालेल्या कार्बन जोडीकरिता २,१००-२,२५० (सेंमी-१) अशा अनुक्रमे विशिष्ट कंप्रता मिळतात, असे प्रयोगाने आढळते. त्यामुळे एखाद्या रेणूच्या रामनवर्णपटात जर यांपैकी कोणतीही कंप्रता मिळाल्यास त्यामध्ये तदनुरूप विशिष्ट गट उपस्थित असला पाहिजे, असा अंदाज करता येतो.
अणूमधील आकर्षणी प्रेरणेचे मान जसे वाढत जाते त्या प्रमाणात त्याच्या रामन वर्णपटातील रेषेचे कंप्रतामूल्य पण वाढत जाते, ही महत्त्वाची गोष्ट वरील उदाहरणावरूनच स्पष्ट होते. रेणूमधील विशिष्ट गटाची ओळखपूर्ती करून घेऊन त्यामधील बंधाच्या बलाबद्दल रामन वर्णपटाचे साहाय्य घेऊन कशी माहिती मिळवली जाते, याविषयी या उदाहरणावरून कल्पना येईल. रेणूच्या अंतर्गत संरचनेविषयी अशा प्रकारे माहिती मिळविण्याचे कार्य संतृप्त (ज्यांत मुक्त संयुजा नाहीत म्हणजेच द्विबंध वा त्रिबंध नाहीत अशी) व असंतृप्त हायड्रोकार्बने, कीटोने, आल्डिहाइडे इ. रासायनिक संयुगांकरिता विशेष उपयुक्त ठरते.
रामन परिणामाचा उपयोग करून रेणवीय विक्रिया, विनिमय विक्रिया (ज्यांत दोन निरनिराळ्या रेणूंतील वा एकाच रेणूतील दोन अणू वा आयन-विद्युत् भारित अणुगट-आपल्या जागांची अदलाबदल करतात अशा विक्रिया), प्रावस्था (भौतिक प्रणालीतील पूर्णपणे एकजिनसी असलेला व इतर भागांपासून अलग करता येणारा घन, द्रव किंवा वायुरूप भाग) संक्रमण विक्रिया, बहुवारिकीकरण (लहान, साध्या रेणूंच्या संयोगाने जटिल रेणू बनण्याची विक्रिया) यांसारख्या व इतर द्रुतगती रासायनिक विक्रियांच्या गतिविज्ञानाचा मागोवा घेता येतो. जीवरसायनशास्त्रात प्रथिने, ⇨न्यूक्लिइक अम्ले व समबहुवारिके (एकाच एकवारिकाच्या संयोगाने बनणारी बहुवारिके) यांच्या आंतरिक संरचनेचा शोध घेण्याकरिता रामन परिणाम उपयोगी पडतो. आल्फा सर्पिल व इतर प्रकारच्या प्रथिन रेणूंकरिता मिळणाऱ्या विशिष्ट रामन वर्णपट रेषांची एक सविस्तर सूची बनविण्यात आली आहे. प्रयोगात मिळालेल्या कोणत्याही प्रथिनाकरिता मिळालेल्या रामन वर्णपट रेषा व ही सूची या दोहोंचा वापर करून त्या प्रथिनाविषयी अंदाज करणे सुलभ रीतीने शक्य होते. भौतिक किंवा रासायनिक परिस्थितीत झालेल्या बदलामुळे प्रथिनाच्या स्वरूपात जो बदल घडून येतो त्याचे संशोधन करण्याकरिता रामन परिणामाची पद्धत विशेष उपयुक्त ठरते. सर्वत्र वापरण्यात येणाऱ्या व्हिनिल बहुवारिकामध्ये होणाऱ्या बदलाचे ज्ञान याच पद्धतीच्याद्वारे मिळविता येते.
वायुरूप पदार्थाच्या रेणूमधील परिभ्रमणी गतीमुळे निर्माण होणारी सूक्ष्मरचना त्याच्या कंपनात्मक रामन वर्णपटात मिळते. वायूचा दाब वाढविला असता रामन वर्णपट रेषांची रुंदी वाढत जाते व त्यामुळे ही सूक्ष्मरचना अस्पष्ट होत जाते.
रेणु-रेणूंमधील सरासरी अंतर कमी झाल्यामुळे त्यांमधील परस्परक्रियेचे परिणाम वाढते व हा त्याचाच परिणाम असावा असे मानले जाते. काही थोड्या द्रवांचा (उदा., द्रवरूप हायड्रोजन, अमोनियाचा पाण्यातील विद्राव) अपवाद सोडला असता सामान्यपणे द्रवाच्या रामन वर्णपट रेषेत परिभ्रमणी गतीमुळे निर्माण होणारी सूक्ष्म रचना आढळत नाही.
घन स्फटिकामध्ये रामन प्रकीर्णन प्रक्रिया रेणू व फोटॉन यांमध्ये घडून न येता ती स्फटिक जालक व फोटॉन यांमध्ये होताना आढळून येते. स्फटिकाच्या रामन परिणामामुळे स्फटिक जालकाच्या वर्तनाबद्दल उपयुक्त माहिती मिळते. बहु-आणवीय रेणूंकरिता मिळणाऱ्या कंपनात्मक कंप्रता मात्र पदार्थ घन किंवा द्रवरूप आहे या गोष्टीवर अवलंबून राहत नाहीत, असे प्रयोगान्ती आढळते.
उपकरण योजनेच्या मर्यादेमुळे १९६२ सालापूर्वी झालेले रामन परिणामावरील संशोधन-कार्य द्रव किंवा घन यासारख्या उच्च घनतेच्या पदार्थांवर करण्यात आले होते. या सालानंतर उपलब्ध झालेल्या ⇨ लेसर उद्गमामुळे कमी दाबाच्या वायूंवर रामन परिणामविषयक संशोधन करणे शक्य झाले आहे. या संशोधनामध्ये काही नवीन स्वरूपाचे आविष्कार पण आढळले आहेत.
लेसर उद्गमाच्या साहाय्याने रामन परिणाम : लेसर प्रकाश उद्गमामध्ये पुढील विशेष गुण प्रामुख्याने आढळतात. उच्च वर्णपटीय तीव्रता, प्रकाशकिरण रेषा समांतर असतात, प्रकाशाची एकवर्णीयता उच्च प्रकारची असते, त्यामध्ये आदर्श कलामेलन (निरनिराळ्या बिंदूंमध्ये निश्चित स्वरूपाचा कलासंबंध असलेले) असते व प्रकाश एका प्रतलात ध्रुवित झालेला असतो. या सर्व गुणधर्मांमुळे लेसर प्रकाश किरण केंद्रित करून त्याची तीव्रता आणखी मोठ्या प्रमाणात वाढविता येते. १९६२ मध्ये सतत कार्यकारी लेसर उद्गमाचा शोध लागल्यापासून रामन परिणामाचा अभ्यास करण्याकरिता त्याचा पूर्वीच्या काळी वापरात असणाऱ्या पाऱ्याच्या प्रज्योतीच्या ऐवजी सर्रास उपयोग होऊ लागला आहे. प्रकाशाची तीव्रता खूप मोठ्या प्रमाणात वाढल्यामुळे परीक्षण करावयाच्या पदार्थाच्या नमुन्याचे आकारमान मोठ्या प्रमाणात कमी करता येते. सूक्ष्म प्रमाणात उपलब्ध असलेल्या पदार्थाकरिताही रामन वर्णपट रेषा मिळविणे या योजनेमुळे शक्य झाले आहे. पूर्वी जे कार्य करण्याकरिता अनेक तास, तर काही वेळा काही दिवस लागत असत, तेच कार्य लेसरच्या साहाय्याने काही मिनिटांमध्ये उरकणे शक्य झाले. प्रयोगाकरिता वापरला जाणारा पदार्थ पारदर्शक व रंगहीन असावा अशी जी पूर्वी अट होती ती पण आता आवश्यक नाही. अपारदर्शक किंवा रंगीत पदार्थ-नमुन्याकरिता लेसर शलाका व पदार्थ यांमध्ये सापेक्ष गतीचा उपयोग करण्याची पद्धत वापरली जाते. यामध्ये पदार्थ जर स्थिर असेल, तर त्यावर हालती लेसर शलाका क्रमवीक्षण करते किंवा शलाका जर स्थिर ठेवावयाची असेल, तर पदार्थ-नमुना प्रयोगामध्ये स्वतःभोवती त्वरेने फिरविला जातो. या क्रियेचा उद्देश आपाती प्रकाश ऊर्जेच्या सतत शोषणाने पदार्थकणाचे तापमान वाढू नये हा असतो. प्रकीर्णित प्रकाशाच्या उदग्र व क्षैतिज (क्षितिजसमांतर) दिशांत ध्रुवित झालेल्या घटकांचे मापन केले असता रेणूच्या अवकाशातील दिक्विन्यासाविषयी माहिती मिळू शकते.
लेसरपासून मिळणारा प्रकाश एका प्रतलात ध्रुवित असतो, हे या संदर्भात लक्षात घेण्याजोगे आहे.
लेसर उद्गम वापरून रामन परिणामाचा अभ्यास करण्याकरिता उपयुक्त अशी उपकरण योजना आ. ५ मध्ये दाखविली आहे. यामध्ये (१) हा लेसर उद्गम आहे. (२) या प्रकाशीय गाळणीद्वारे बाहेरून येणाऱ्या अनाहूत प्रकाश कंप्रता बाजूस केल्या जातात. (३) ही संघनक भिंग योजना प्रकाश किरणांस (४) या पारदर्शक पात्रात ठेवलेल्या पदार्थावर केंद्रित करते. प्रकीर्णित प्रकाश (५) या अंतर्गोल आरशाच्या साहाय्याने (८) या क्रमवीक्षण वर्णपटलेखकाकडे वळविला जातो. (५ अ) हा अंतर्गोल आरसा -९०° दिशेमध्ये प्रकीर्णित झालेला प्रकाश एकत्र करून +९०° दिशेत परावर्तित करतो व एकूण प्रकीर्णित प्रकाश वृद्धिंगत करतो. याच कार्यास मदत करण्याकरिता (६) ही भिंग योजना वापरली जाते. (७) हा ध्रुवण विश्लेषक आहे. (९) मध्ये प्रकाशगुणक नलिका व इलेक्ट्रॉनीय विवर्धक यांचा समावेश होतो. या योजनेपासून मिळालेल्या प्रदत्ताचे दर्शन सरळ (१०) या पट्टी-तक्ता-आलेखकावर मिळते. यात स्थिर वेगाने गतिमान असलेल्या पट्टी-तक्त्यावर लेखणीने वा इतर प्रयुक्तीने प्रदत्त आलेखित केला जातो. रामन प्रकीर्णन जरी सर्व दिशांत सारख्या प्रमाणात होत असले, तरी ते आपाती प्रकाशाच्या उदग्र दिशेत सामान्यपणे मोजावयाचा प्रघात आहे. मूळ प्रकाश व प्रकीर्णित प्रकाश यांमध्ये अशा मापनात भेद करणे विशेष सोईस्कर ठरते. ध्रुवण विश्लेषक (७) या उपकरणाच्या साहाय्याने प्रकीर्णित प्रकाशामध्ये आपाती प्रकाशाच्या समांतर व उदग्र दिशांत ध्रुवित झालेल्या घटकांची तीव्रता मूल्ये मोजता येतात.
लेसर उद्गम म्हणून हीलियम-निऑन लेसर (प्रकाश तरंगलांबी ६३२८ Å) अथवा हीलियम कॅडमियम लेसर (तरंगलांबी ४४१५ Å ते ३२५० Å) म्हणून वापर केला जातो. दृश्य व अती जंबुपार (दृश्य वर्णपटातील जांभळ्या रंगाच्या अती पलीकडील अदृश्य) वर्णपट विभागातील कोणतीही इष्ट ती तरंगलांबी मिळविण्याकरिता जे रंजक द्रव्ययुक्त लेसर आता उपलब्ध झाले आहेत त्यांचा पण मोठ्या प्रमाणात उपयोग केला जातो. कार्बन टेट्राक्लोराइडाकरिता या पद्धतीने मिळालेला पट्टी-तक्ता आ. ६ मध्ये दाखविला आहे.
आकृतीतील आलेखन प्रकाशविद्युत् रीतीने केलेले आहे. हीलियमनिऑन लेसरपासून मिळणारी ६३२८ Å तरंगलांबीची रेषा उत्तेजक वर्णपट रेषा म्हणून वापरलेली आहे. उत्तेजक वर्णपट रेषेची तीव्रता तदनुरूप रामन रेषेपेक्षा हजार पटींनी जास्त आहे. त्यामुळे तिचे महत्तम मूल्य आलेखाच्या बाहेर गेले आहे. आलेखात रामन रेषांकरिता तरंगलांबी व तरंगसंख्या (आडव्या अक्षावर) आणि तीव्रता (उभ्या अक्षावर) या राशी दाखविल्या आहेत. रामन रेषांची स्थाने मूळ उत्तेजक रेषेपासून मिळणाऱ्या स्थानच्युतीच्या स्वरूपात दाखविली आहेत.
याशिवाय लेसरसारख्या उच्च तीव्रता प्रकाश उद्गमाचा वापर केल्यामुळे नैकरेषीय परिणामामुळे [⟶ नैकरेषीय आविष्कार] व इतर काही कारणांमुळे जे काही विशेष आविष्कार आढळतात, त्यांचे वर्णन खाली केले आहे.
अनुस्पंदनी रामन परिणाम : प्लाकझेक यांच्या सैद्धांतिक मीमांसेपासूनच या आविष्काराविषयीची कल्पना मिळते. जेव्हा आपाती प्रकाशाची कंप्रता प्रकीर्णन करणाऱ्या रेणूच्या इलेक्ट्रॉनीय शोषण पट्ट्यात येते तेव्हा या प्रकारचा रामन परिणाम घडून येतो. प्रकीर्णित प्रकाशाच्या तीव्रतेत शंभर ते हजार पटींनी वाढ होणारी वाढ हे या परिणामाचे मुख्य वैशिष्ट्य असते. यामुळे या परिणामाचा विशेष उपयोग रेणूची ओळखपूर्ती करून घेण्याकरिता केला जातो.
लेसर प्रकाश स्वभावतःच प्रतल ध्रुवित असतो. प्रकीर्णित प्रकाशाच्या ध्रुवणाचे विश्लेषण करण्याकरिता जर विश्लेषक वापरला, तर मूळ प्रकाशाच्या सापेक्ष समांतर व उदग्र दिशेत ध्रुवित झालेल्या प्रकीर्णित प्रकाशघटकाच्या तीव्रता मापता येतात. अनुस्पंदनी परिणामामध्ये काही वर्णपट रेषांच्या बाबतीत उदग्र दिशेत ध्रुवित झालेल्या घटकाची तीव्रता त्याच रेषांच्या समांतर दिशेत ध्रुवित झालेल्या घटक तीव्रतेपेक्षा जास्त मूल्याची आढळते. या परिणामास ‘व्यस्त ध्रुवण’ अशी संज्ञा दिली जाते.
अधिरामन परिणाम : लेसर उद्गमाचा वापर केला असता माध्यमातील एकक घनफळातून एका सेकंदामध्ये संचरण करणाऱ्या फोटॉनांच्या संख्येत फार प्रचंड वाढ होते व प्रकाशीय नैकरेषीय परिणाम मिळण्याची शक्यता निर्माण होते. अशा प्रक्रियेमध्ये एका रेणूची दोन फोटॉनांबरोबर एकाच वेळी परस्परक्रिया होते असे दिसते पण प्रकीर्णन होताना मात्र ते एकत्रित होतात. त्यामुळे प्रकीर्णित प्रकाशाची कंप्रता मूळ कंप्रतेच्या जवळजवळ दुप्पट होते. जवळजवळ म्हणण्याचे कारण या प्रक्रियेत रेणूला ∆ E एवढी ऊर्जा मिळते व त्यामुळे एकत्रित प्रकीर्णित फोटॉनांची कंप्रता (येथे सूत्र आहे.)एवढी होते. प्रक्रियेच्या पहिल्या टप्प्यात दोन फोटॉन व एक रेणू असे घटक असतात, तर या प्रक्रियेच्या शेवटल्या टप्प्यात एक उत्तेजित रेणू व एक बृहत् फोटॉन बाहेर पडतो. अशा प्रकारच्या संक्रमणाकरिता यथार्थ असणारे निवड नियम नेहमीच्या नियमांपेक्षा निराळे असतात, हे येथे स्पष्ट केले पाहिजे.
उत्तेजित रामन परिणाम : आ. ७ मध्ये अ, आ व इ या रेणूच्या तीन कंपनात्मक ऊर्जा पातळ्यांचे निर्देशन करतात. या रेणूच्या कंपनात्मक ऊर्जा पातळ्यांमधील प्रभावी संक्रमणामुळे मागे वर्णन केल्याप्रमाणे ∆ƲR ही कंप्रता स्थानच्युती असलेली रामन वर्णपट रेषा उत्सर्जित होते. साध्या प्रकाशाऐवजी Ʋ1 कंप्रतेचा लेसर प्रकाश जर रेणूंवर टाकला, तर त्यांतील बरेच रेणू अ या उच्च ऊर्जा पातळीपर्यंत उत्तेजित होतील. लेसर प्रकाश हा प्रकाशीय पंप म्हणूनही येथे कार्य करतो हे लक्षात ठेवण्याजोगे आहे [⟶ लेसर]. रामन प्रकीर्णनामुळे त्याचे स्टोक्स (कंप्रता Ʋ1 – ∆ƲR ) व प्रतिस्टोक्स (कंप्रता Ʋ1 + ∆ƲR) या कंप्रतेच्या प्रकाशाचे उत्सर्जन होईल.Ʋ2 = Ʋ1 – ∆ƲR अथवा Ʋ1 + ∆ƲR या दोन कंप्रतांच्या उच्च तीव्रतेच्या व कलामेलित प्रकाशास उत्तेजित रामन परिणाम असे म्हणतात. काही परिस्थितींमध्येƲ1 + ∆ƲR या वर्णपट रेषेची तीव्रता तदनुरूप स्टोक्स वर्णपट रेषेच्या तीव्रतेपेक्षा जास्त असू शकते.
लेसर प्रकाशाची मोठ्या प्रमाणातील शक्ती रेणूची कंपनात्मक ऊर्जा उत्तेजित करण्यामध्ये खर्च होत असल्यामुळे याशिवाय आणखी ऊर्जा पातळ्यांचे उत्तेजन करणे त्यास शक्य होत नाही. परिणामतः या प्रक्रियेमुळे उत्सर्जनामध्ये एकच वर्णपट रेषा सामान्यपणे मिळते.
या आविष्कारावर संशोधन करण्याच्या पर्यायी पद्धतीमध्ये रेणूवर Ʋ1 व Ʋ2 या कंप्रतेच्या दोन लेसर प्रकाश शलाका एकाच वेळी टाकल्या जातात. यांपैकी Ʋ1 लेसर शलाका प्रकाशीय पंपाचे कार्य करते, तर दुसरी लेसर शलाका एषणी (शोध घेणारी) म्हणून कार्य करते, वर वर्णन केलेल्या उत्तेजित रामन परिणामामुळे एषणी लेसर शलाकेच्या तीव्रतेत विवर्धन मिळते.
वरील परिणाम नैकरेषीय वर्तनामुळेच मिळतो हे येथे नमूद केले पाहिजे. आणखी एक महत्त्वाचा नैकरेषीय परिणाम म्हणजे कलामेलित प्रतिस्टोक्स रामन वर्णपटविज्ञान हा होय. उत्तेजित रामन परिणामाचा तो एक विशेष प्रकार आहे.
कलामेलित प्रतिस्टोक्स रामन वर्णपटविज्ञान : ज्यामध्ये प्रकाशाच्या कंप्रतेत पाहिजे तेवढा सतत बदल घडवून आणणे शक्य असते अशी लेसर उपकरणे आधुनिक काळात निघाली आहेत. रामन वर्णपटविज्ञानाच्या या पद्धतीमध्ये दोन लेसर वापरले जातात. यांपैकी एकाची कंप्रता स्थिर असते, तर दुसऱ्याची कंप्रता अखंडितपणे बदलता येण्याजोगी असते. प्रयोगामध्ये या दोन लेसरपासून मिळणाऱ्या प्रकाश शलाका एकमेकींशी एक लहान कोन (≈ २°) करून रेणूवर एकाच वेळी पडतील अशी योजना कार्यान्वित केली जाते. जेव्हा जेव्हा दोन लेसर उपकरणांमधील प्रकाशामध्ये रेणूच्या रामन कंप्रता संक्रमणाएवढा कंप्रता फरक पडतो, तेव्हा तेव्हा त्यांपासून उच्च तीव्रतेचा कलामेलित असा प्रकाश उत्सर्जित केला जातो. या प्रकाशामध्ये स्टोक्स व प्रतिस्टोक्स या दोन्ही प्रकारच्या प्रकाश कंप्रतांचा समावेश असतो. लेसरची कंप्रता सतत सारखी वाढवीत गेल्यास रेणूच्या समग्र रामन वर्णपटाविषयी माहिती मिळविणे शक्य होते.
संदर्भ :
- Clark, A. S. J., Hester, R. E. Ed., Advances in Infrared and Raman Spectroscopy, Vols. 1-7, 1975-80.
- Clothup, N. B., Introduction to infrared and Raman Spectroscopy, New York, 1964.
- Herzberg, G., Molecular Spectra and Molecular Structure, Vol. II, Infrared and Raman Spectra of Polyatomic Molecules, Princeton, 1962.
- Long, D. A., Raman Spectroscopy, New York, 1977.
- Tobin, M. C., Laser Raman Sepectroscopy, New York, 1980.
- Wood, R. W., Physical Optics, New York, 1959.
लेखक : चिपळोणकर, व. त्रिं.