ब्राउनीय गति

ब्राउनीय गति : ब्रिटिश वनस्पतिशास्त्रज्ञ ⇨ रॉबर्ट ब्राउन यांनी १८२७ साली पाण्यातील निलंबित (लोंबकळत्या) स्वरूपातील परागकणांचे सूक्ष्मदर्शकाखाली निरीक्षण केले तेव्हा त्यांना परागकण आपोआपच इतस्ततः स्वैरपणे हालचाल करीत असल्याचे आढळले. ही हालचाल अविरतपणे होत असते. ब्राउन यांच्या पूर्वी साठ वर्षे जे. टी. नीडम व एफ् डब्ल्यू. फोन ग्लेझेन या शास्त्रज्ञांनी सुद्धा परागांच्या अशा हालचालींची नोंद करून ठेवली होती. परागकणांच्या अशा हालचालींमुळे त्यांना जीव असतो अशी त्या वेळी समजूत होती. शंभर वर्षांपूर्वीच्या परागकणांमध्येही अशी हालचाल आढळल्याने पराग इतकी वर्षे सजीव राहू शकतात, असे त्या वेळी अनेक शास्त्रज्ञांचे मत झाले होते. पुढे धूर किंवा खनिजांच्या निलंबनामध्येही खनिज कण अशाच प्रकारे सर्वत्र हालचाल करताना आढळल्यावर ही कल्पना बदलावी लागली. सी. वीनर व जी. एल्. गॉय यांनी याबाबत अधिक पद्धतशीर संशोधन केले. या सूक्ष्मकणांच्या हालचालींचे कारण ऊष्मीय संनयन (उष्णतेने कण तापून हलके झाल्यामुळे वर जाणे व थंड कण त्यांच्या जडपणामुळे खाली सरकणे) किंवा ⇨ केशिकता हे नसते त्याचप्रमाणे त्यामागे कोणतीही रासायनिक किंवा विद्युत् क्रिया नाही, असेही त्यांनी दाखवून दिले. कणांचे आकारमान जितके लहान, तसेच ज्या द्रवात ते निलंबित केलेले असतील त्याची श्यानता (दाटपणा) जितकी कमी तितकी कणांची हालचाल जास्त जोरदार असते. निलंबित स्वरूपातील सूक्ष्मकणांच्या या हालचालीला जास्त जोरदार असते. निलंबित स्वरूपातील सूक्ष्मकणांच्या या हालचालीला ब्राउनीय गती असे नाव देण्यात आलेले आहे. एफ्. एम्. एक्सनर यांनी सूक्ष्मकणांची हालचाल अथवा गती ही त्यांच्या आकारमानावर आणि तापमानावर अवलंबून असते, असे सूक्ष्मकणांच्या छायाचित्रांच्या साहाय्याने १९०० साली दाखवून दिले. एच्. झीडेन्टोफ आणि आर्. झिगमोंडी यांनी साध्या सूक्ष्मदर्शकातून न दिसणाऱ्या कलिली कणांचे [→ कलिल] अतीत सूक्ष्मदर्शकाच्या (पदार्थाची स्थिती समजण्यासाठी प्रकाशाच्या विखुरण्याच्या गुणधर्माचा उपयोग करणाऱ्या सूक्ष्मदर्शकाच्या) साहाय्याने निरीक्षण करून त्यांची गतिमानता गॉय यांनी केलेल्या संशोधनाला पुष्टी देणारीच आहे, असे दाखवून दिले. झिगमोंडी यांनी ब्राउनीय गतीचे या नव्या तंत्राचे संशोधन केले.

पराग अथवा कलिल कणांच्या हालचालीचे कारण: द्रवातील निलंबित सूक्ष्मकणांच्या हालचालींचे कारण वीनर यांनी द्रवातील ‘अंतर्गत हालचाली’ हे दिले आहे, तर डेल्सॉक्स यांनी अधिक स्पष्टपणे सांगितले की, द्रवाच्या रेणूंच्या हालचालींमुळे निलंबित कणांची हालचाल होत असते. एकोणिसाव्या शतकाच्या उत्तरार्धात वायूच्या गत्यात्मक सिद्धांताचा [→ द्रव्याचा गत्यात्मक सिद्धांत] विकास झाला. शून्य निरपेक्ष तापमानाच्या वरच्या कोणत्याही तापमानास वायूचे किंवा द्रवाचे रेणू इतस्ततः स्वैर संचार करीत असतात व त्यांची दिशा अगोदर निश्चित करता येत नाही. वाढत्या तापमानाबरोबर त्यांची गती वाढत जाते व तो एक प्रकारे तापमानाचे गमकच असते. फरक इतकाच की, वायूंमधील रेणूंपेक्षा द्रवामधील रेणू एकमेकांच्या जास्त जवळ असतात. त्यामुळे द्रवात दोन रेणूंमधील आघातांमध्ये (टकरींमध्ये) रेणूने ओलांडलेले माध्य (सरासरी) अंतर वायूपेक्षा फार कमी असते.

निलंबित कलिल कणांवर द्रवरेणूंचे सर्व बाजूंनी आघात होत असतात. सर्व द्रवरेणूंचा वेग सारखा नसतो. त्यामुळे कणाला मिळणाऱ्या संवेगांची (कणांचे-येथे आघात करणाऱ्या कणांचे-द्रव्यमान व त्यांचा वेग यांच्या गुणाकाराने दर्शविल्या जाणाऱ्या राशींची) दिशा व महत्ता निरनिराळी असणार. त्यामुळे हा निलंबित कण सतत निरनिराळ्या दिशांनी व वेगाने इकडे तिकडे जात असतो. कॅटोनी व ओएल यांनी काचेच्या दोन पातळ पट्ट्यांमध्ये बंदिस्त केलेल्या निलंबित कणांमधील ब्राउनीय हालचालीत संपूर्ण वर्षभर कोणताही फरक पडला नाही, असे दाखवून दिले.

द्रवात (किंवा वायूत) निलंबित केलेले कलिल कण वायूंना लागू होणाऱ्या नियमांचे पालन करतात, असे गृहीत धरून ब्राउनीय गतीच्या आविष्कारावरून ॲव्होगाड्रो संख्येचे [N चे ग्रॅमरेणू भाराइतक्या द्रव्यातील रेणूंच्या संख्येचे→ द्रव्याचा गत्यात्मक सिद्धांत] मूल्य काढता येते. इतर पद्धतींनी काढलेल्या N च्या मूल्याशी हे मूल्य जुळते. ब्राउनीय गतीची वरील उपपत्ती बरोबर असल्याचे हे निदर्शक आहे.

द्रव कणांच्या माऱ्यामुळे निलंबित कण इकडे तिकडे असा जातो म्हणजेच त्याचे स्थानांतरण होते. अशा गतीला ‘स्थानांतरण ब्राउनीय गती’ म्हणतात परंतु केव्हा केव्हा या आघातांमुळे निलंबित कणांचे घूर्णनही (परिभ्रमणही) होते. त्याला ‘घूर्णन ब्राउनीय गती’ असे नाव देतात. उदा., यामुळे अती संवेदनशील ⇨ गॅल्व्हानोमीटराचे (अल्प विद्युत् प्रवाहाचे अस्तित्व दर्शविण्यासाठी वा तो मोजण्यासाठी वापरण्यात येणाऱ्या उपकरणाचे) टांगलेले वेटोळे स्थिर न राहता सु. १०-६ अरियमान एवढ्या कोनातून फिरत असते. यामुळे अशा उपकरणांच्या अचूकतेवर एक नैसर्गिक मर्यादा येते.

आइन्स्टाइन व पेरँ यांचे कार्य : इ. स. १९०५-०८ ला ॲल्बर्ट आइन्स्टाइन यांनी ब्राउनीय गतीला द्रव्याचा गत्यात्मक सिद्धांत लावून मिळणारी काही समीकरणे मांडली. या समीकरणांचा प्रायोगिक पडताळा पाहण्याचे कार्य पुढे जे. बी. पेरँ आणि इतर संशोधकांनी केले.

उदग्र दिशेने कण संस्थेचे वितरण: पृथ्वीच्या पृष्ठभागापासून जसजसे जास्त जास्त उंचीवर जावे तसतसा वातावरणीय दाब कमी होत जातो. कारण वाढत्या उंचीबरोबर प्रती एकक घनफळातील वायूच्या रेणूंची संख्या घटत जाते. यांमुळे वातावरणातील एकक घनफळातील रेणुसंख्येचे एक विशिष्ट वितरण प्रस्थापित होते. याबद्दलचे खालील समीकरण वायूच्या गत्यात्मक सिद्धांतानुसार काढता येते.

n = n_oe – {Nmg/RT (Z-Z₀)}    … … … (१)

येथे n व no अनुक्रमे Z व Zo या उंचीवरील प्रती एकक घनफळातील रेणुसंख्या, e स्वाभाविक लॉगरिथमचा आधारांक, N ॲव्होगाड्रो संख्या, R वायू स्थिरांक, mg एका रेणूचे वजन आणि T निरपेक्ष तापमान दर्शवितात.

एकाच आकारमानाच्या निलंबित कणांनाही हे समीकरण लावता येईल. प्रत्येक कणाची त्रिज्या r व घनता d असून ज्यात कण निलंबित केले आहेत त्या द्रवाची घनता d असेल, तर एका कणाचे परिणामी वजन 4/3 πr3 (d-d’) इतके होईल आणि मग वरील समीकरण खालील रूप घेईल.

n = n_oe ^{–{N 4/3 πr3 (d–d’) (Z–Z0) g /RT}} … … … (२)

व यावरून

N = 3 RT/4 π r³(d-d’)g (Z-Z0) · log n₀/n … … … (३)

हे समीकरण मिळते.

पेरँ यांचा प्रयोग: या समीकरणावरून N चे मूल्य काढण्यासाठी पेरँ यांनी पुढीलप्रमाणे अनेक प्रयोग केले. प्रयोगातील मुख्य अवघड भाग म्हणजे (अ) सर्व कण एकाच आकारमानाचे असतील असे निलंबन (द्रव्य माध्यमात घन पदार्थाचे सूक्ष्म कण निलंबित स्वरूपात ठेवून मिळणारे मिश्रण) मिळवणे. याकरिता पेरँ यांनी डिंक व रेझीन यांचे मिश्रण असलेला गँवोज हा वनस्पतिजन्य पदार्थ अल्कोहॉलात विरघळवून मग तो विद्राव भरपूर पाण्यात ओतला. त्यामुळे पाण्यात गँबोजाचे विविध आकारमानाचे कण निलंबित झाले. या निलंबनाचे मग त्यांनी भागशः केंद्रोत्सारण करून सर्व कण एकाच आकारमानाचे असलेले निलंबन मिळविले.

(आ) समी. (३) मधील उजव्या बाजूतील r, n व no या राशी मोजणे अवघड आहे. r चे मूल्य काढण्यासाठी पेरँ यांनी जी. जी. स्टोक्स यांच्या नियमाचा [⟶श्यानता] वापर केला. दुसऱ्या पद्धतीत पेरँ यांनी अनेक कण सरळ रेषेत एकापुढे एक असे जोडून ठेवले व सूक्ष्मदर्शकाच्या साहाय्याने या कणमालिकेची लांबी मोजली. या लांबीला मालिकेतील कणसंख्येने भागून एका कणाचा व्यास व त्यावरून r चे मूल्य काढले.

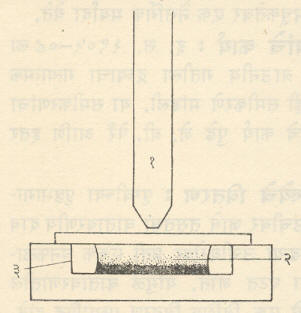
n व n0 मोजण्यासाठी वरील प्रमाणे तायर केलेल्या निलंबनाचा एक थेंब एका कोष्ठिकेत ठेवून कोष्ठिका उच्च वर्धनक्षमतेच्या सूक्ष्मदर्शकाखाली धरली (आ. १). सूक्ष्मदर्शक वर किंवा खाली सरकवून वेगवेगळ्या खोलींवरील निलंबन स्तरावर केंद्रित केला, सूक्ष्मदर्शकाच्या पदार्थभिंगाची क्षेत्र खोली (भिंगासमोरील क्षेत्र खोली अंतरातून स्थलांतरित करूनही मिळणाऱ्या प्रतिमा रेखीव दिसतात त्या अंतराला क्षेत्र खोली म्हणतात) अल्प असल्याने त्यातून एकावेळी एका अत्यंत पातळ क्षितिज समांतर स्तरातील कणच स्पष्ट दिसू शकतात. एकेका स्तरांची सूक्ष्मदर्शकातून छायाचित्रे घेऊन त्यांत उमटलेल्या कणांसी संख्या मोजून सरासरी n (प्रत्येक स्तरासाठी अलग) काढण्यात आला. तापमान (T) सहज मोजता येते व R हा वैश्विक वायू स्थिरांक आह. अशा तऱ्हेने समी. (३) वरून N चे मूल्य काढता ते ६.८२ X१०२३ आले (अपेक्षित मूल्य६.०२ X १०२३).

स्थानांतरणीय ब्राउनीय गती : ब्राउनीय गतीत ज्याप्रमाणे निलंबित कणाचे स्थानांतरण होते त्याचप्रमाणे (द्रवाच्या) ⇨विसरणात (रेणू एकमेकांत मिसळण्याच्या क्रियेत) रेणूंचे स्थानांतरण होत असते. यावरून असे लक्षात येते की, हे दोन आविष्कार एकमेकांशी निगडित असले पाहिजेत.

समजा की, एका निलंबित कणाचे एका विशिष्ट दिशेने (ही दिशा आपण क्ष अक्ष घेऊ) होणारे स्थानांतरण t या ठराविक कालखंडानंतर मोजले व त्यांचा माध्य वर्ग (∆x)2 काढला. द्रवाचा विसरण गुणांक D असल्यास आइन्स्टाइन व एम्. फोन स्मॉलुकॉव्हस्की यांनी (स्वतंत्रपणे) असे दाखविले की,

D = 1/2t (∆x)² … … … (४)

त्याचप्रमाणे गत्यात्मक सिद्धांतावरून,

D = RT / 6 π h r N … … … (५)

येथे R वायू स्थिरांक, T निरपेक्ष तापमान, hश्यानता गुणांक, r कणांची त्रिज्या, N ॲव्होगाड्रो संख्या दर्शवितात.

समी. (४) व (५) वरून

N = RTt/3 π h r(∆x)² … … … (६)

हे समीकरण मिळते. (∆x)2 चे मापन प्रयोगावरून केले असता या समीकरणाच्या साहाय्याने N चे मूल्य काढता येईल.

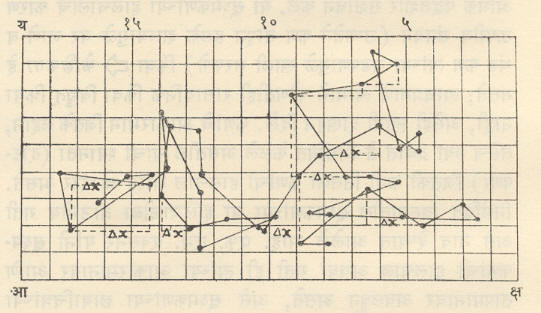
यासाठी पेरँ यांनी सूक्ष्मदर्शक व कॅमेरा ल्यूसिडा [⟶ कॅमेरा ऑब्स्क्यूरा व कॅमेरा ल्यूसिडा] यांचा एकत्रित उपयोग केला. सूक्ष्मदर्शक एका विशिष्ट कणावर केंद्रित करून कॅमेरा ल्यूसिड्याच्या साहाय्याने त्या कणाची स्थाने दर ३० सेकंदा नंतर एका आलेखपत्रावर त्यांनी नोंदली (आ. २). यातील १६ भाग ५.० X १०-३ सेंमी. दर्शवितात. लागोपाठचे स्थानदर्शक बिंदू जोडत गेले असता आकृतीत दाखविल्याप्रमाणे आकृती मिळते. यांपैकी काही स्थानांतरणांचे क्ष अक्षाच्या दिशेतील घटक (∆x) आकृतीत तुटक रेषांनी दाखविले आहेत. या आकृतीवरून (∆x)2 चे मूल्य काढता येते. या प्रयोगावरून N चे मूल्य ६.८८ X १०२३ इतके मिळाले. वायूमध्ये निलंबित केलेल्या कणाच्या ब्राउनीय गतीवरून N चे मूल्य फारच अचूक म्हणजे ६.०६ X १०२३ इतके मिळाले.

द्रव्याच्या रेणूंच्या ऊष्मीय गतीबद्दल ब्राउनीय गती हा एकमेव प्रत्यक्ष पुरावा आहे. ब्राउनीय गतीच्या अभ्यासामुळे पदार्थ रेणूंपासून बनलेले असतात ही कल्पना पूर्णपणे प्रस्थापित झाली.

संदर्भ : 1. Einstein, A. Investlgations on the Theory of Brownian Movement, New York, 1956.

           2. Mcc. A. J. Physical Chemistry, London, 1962.

           3. Saha, M. N. Srivastava, B. N. A Treatise on Heat, Allahabad, 1965.

           4. Taylor, H. S. Glasstone, S. A Treatise on Physical Chemistry, Vol.2, New York, 1952.

कारेकर, न. वि. पुरोहित, वा. ल.

“