बेर्नुली संख्या : याकोप बेर्नुली (१६५४ – १७०५) या स्विस गणितज्ञाच्या नावावरून या विशिष्ट संख्यांना `बेर्नुली संख्या’ हे नाव पडले आहे. मात्र त्यांचे हे संशेधन त्यांच्या मरणोत्तर Ars conjectandi या त्यांच्या ग्रंथात १७१३ मध्ये प्रसिद्ध झाले.
बेर्नुली संख्या या परिमेय (म्हणजे क/ख, ख ०, अशा स्वरूपात लिहिता येणाऱ्या) संख्या असून त्यांच्या श्रेणीची व्याख्या अनेक प्रकारे करता येते. ऐतिहासिक दृष्ट्या पहिली व्याख्या म्हणजे बेर्नुली यांनी स्वतः लिहिलेल्या व्याख्या ही यर =१र २र …. (स – १)र अशा प्रकारच्या सात श्रेढीच्या बेरजांच्या ( श्रेढी) संदर्भात उद्‌भवते. बेर्नुली संख्या ब ०, ब १, ब २, ……, ब स,…… याप्रमाणे दर्शविल्यास वरील बेरीज
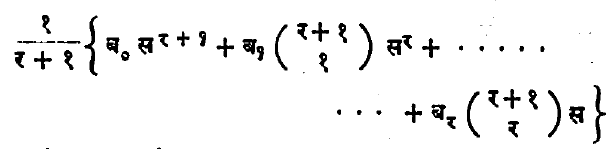
अशी मांडून बेर्नुली संख्यांची व्याख्या बेर्नुली यांनी दिली. येथे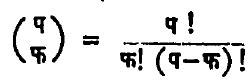 
होय. म्हणजे र-वी
बेर्नुली संख्या बर = यर मधील स चा सहगुणांक होय .[य र = फ (स) अशी बहुपदी म्हणून लिहावयाचे आहे].
काही लेखक य र =१र २र …. सर असे घेतात पण ही बेरीज स च्या बहुपदीच्या रूपात मांडल्यावर तिच्यातील स चा सहगुणक पूर्वीसारखाच राहिल कारण आपण सर या पदाची भर घातली आहे. तुर्त य र =१र २र …. (स – १)र असे मानू.
वरील व्याख्या बेर्नुली संख्या प्रत्यक्ष काढण्याच्या दृष्टीने गैरसोईची आहे. त्या ऐवजी खालील पद्धतीने निराळी व्याख्या मिळवीतात :
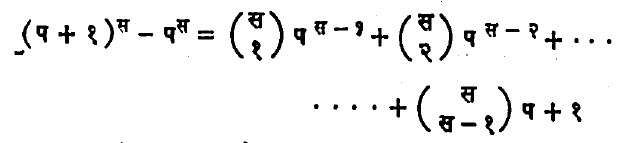
या नित्य समीकरणात क्रमाने प ऐवजी १, २,….., (स – १) घालून बेरीज केल्यास खालील समीकरण मिळेल :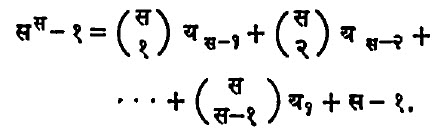 
केवळ सच्या सहगुणकांचा विचार केल्यास
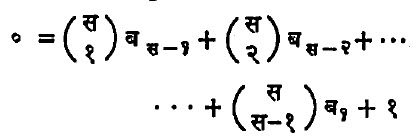
असे सुत्र मिळेल. हे प्रतिकरूपात व्यक्त करणे सोईचे होते. दोन्ही बाजूस ब स मिळवून आणि उजव्या बाजूस ब र = बर असे लिहून सुत्र थोडक्यात ब स = (ब १)स असे लिहीतात. येईल. यात अर्थात उजवीकडील द्विपदीचा विस्तार केल्यावर बर ऐवजी ब र लिहावयाचे हा संकेत वापरावयाचा आहे. अशी पद्धत गणित शास्त्रात पुष्कळवेळा वापरतात. वरील सुत्राने बेर्नुली संख्या मिळवीणे सोपे जाते. ब ० = १ आणि ब १ = – १/२ यापुढील विषम कोटीच्या सर्व बेर्नुली संख्या शुन्य असतात, असे दिसून येईल सम कोटीच्या काही बेर्नुली संख्या पुढीलप्रमाणे :
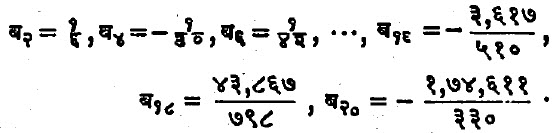
या संख्या एकाआड एक धन व ऋण असल्याचे दिसते. प्रारंभीच्या बेर्नुली संख्या जरी लहान वाटत असल्या, तरी त्या घात – फलनापेक्षाही [ →फलन] अधिक वेगाने अनंताप्रत जातात. स चे मुल्य पुरेसे मोठे असेल, तर जवळजवळ 
असे दाखविता येते. (येथे (इंग्रजी) हा स्वभाविक लॉगरिथमाचा आधारांक होय इ (इंग्रजी)). काही लेखक बेर्नुली संख्याची व्याख्या करताना त्यांचे चिन्ह गाळून व्याख्या करतात. तसेच विषम कोटीच्या सर्व ( ब १ वगळून) बेर्नुली संख्या शुन्य असल्याने त्यांचा उल्लेख गाळतात आणि ब ० व ब १ वगळून ब २ पासून आरंभ करतात पण त्यांना नावे ब १, ब २ , …. अशी
देतात म्हणेच । ब २स स। ऐवजी ब स लिहितात. 
बेर्नुली संख्या मिळवीण्याचे आणखी एक सूत्र खालील प्रमाणे आहे :
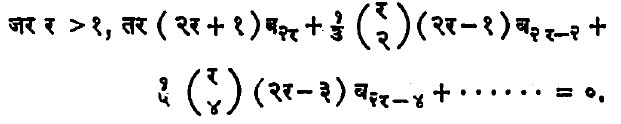
र सम किंवा विषम असेल त्यानुसार या सूत्रात शेवटी बर किंवा (र + २) बर + १ राहील. जर र = १ असेल, तर वरील सुत्रातील उजवी बाजू १/२ घ्यावी.
बेर्नुली संख्याच्या आणखी काही व्याख्या खालील श्रेढींच्या सहाय्याने करतात :
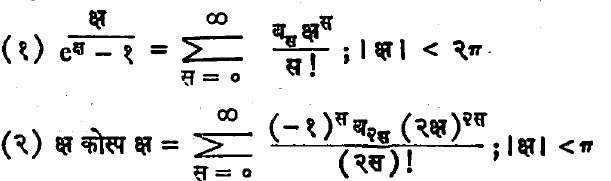
लेनर्ड ऑयलर यांनी बेर्नुली संख्या स्वतंत्रपणे १७४८ मध्ये शोधून काढल्या व त्यांची प्रत्यक्ष सूत्रे खालीलप्रमाणे मांडली :
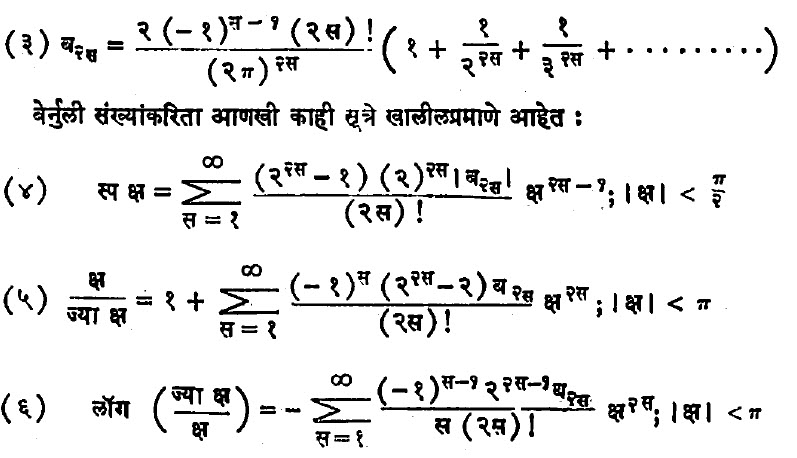
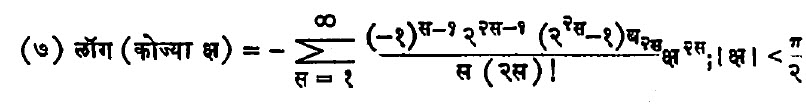
गुणधर्म : प्येअर द फेर्मा (१६०१ ? – ६५) यांचे शेवटचे प्रमेय : [→गणितातील अनिर्वाहित प्रश्न]. क्षस + यस = झस या समीकरणाला स >=3 असेल, तर परिमेय उत्तर मिळत नाही. हे फेर्मा यांचे प्रमेय अद्याप सिद्ध झालेले नाही पण स = प ही एक विषम अविभाज्य संख्या असून तिने ब२ , ब४ …… , बप – ३ या बेर्नुली संख्यांच्या अंशांना भाग जात नसेल, तर क्षस + यस = झस या समीकरणाला परिमेय उत्तर मिळत नाही, असे ई. ई. क्युमेर (१८१० – ९३) या जर्मन् गणितज्ञांनी सिद्ध केले आहे. विसाव्या शतकातील बेर्नुली संख्यावरील पुष्कळसे संशोधन या प्रमेयाशी निगडीत आहे.
फोन स्टाउट – क्लाउझेन प्रमेय : (के. जी. सी. फोन स्टाउट व टॉमस क्लाउझेन या गणितज्ञाच्या नावावरून ओळख्यण्यात येणारे प्रमेय). बेर्नुली संख्या
या संख्या अविभाज्य असून २ स च्या भाजकापेक्षा १ ने मोठ्या आहेत आणि अस हा पुर्णंक धन किंवा ऋण आहे. उदा.,
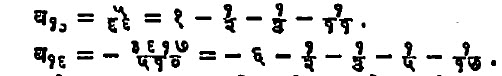
हा गुणधर्म विलक्षण असून त्याचे कित्येक उपयोग आहेत.
एक बहुपदी मानली, तर खालील महत्वाचे गुणधर्म मांडता येतात.
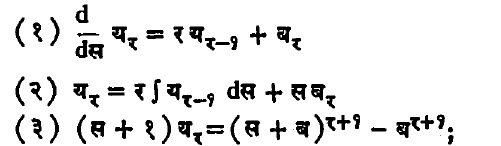
या प्रमेयाला बेर्नुली प्रमेय म्हणतात.
बस या बेर्नुली संख्या देणारी पुष्कळ सूत्रे प्रसिद्ध आहेत, तरी प्रत्यक्षात फार मोठ्या फार थोड्या बेर्नुली संख्याचे संगणक करण्यात आले आहे.एस्‌. ए. सरेब्रनिकॉफ योनी आयलर यांच्या सुत्राचा उपयोग करून ब१८४ चे संगणक केलेले आहे. १९३६ साला पर्यंत पहिल्या ११० बेर्नुली संखयाचे संगणक केले गेले होतं. जे. डल्ब्यु. एल्‌. ग्लेशर यांनी २५० पर्यंतच्या बेर्नुली संखयाचे १० आकडी लॉगरिथम आणि ४ सार्थ संखयापर्यंत प्रत्यक्ष मूल्य देणारे कोष्टक केले आहे. ही मूल्ये ऑयलर सुत्रावरूनच काढण्यात आली.
जी. ए. गव्हन यांनी बेर्नुली संक्ष्या अंनत समाकलाच्या रूपात खालीलप्रमाणे दिल्या आहेत.
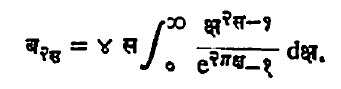
संदर्भ : 1. Bernard, S. Child, J.M.Higher Algebra, London, 1960.
2. Chrystal, G. Algebra, London, 1904.
3. Davis, H. T. Tables of the Higher Mathematical Functions, Vol.II, 1935.
4. Gibson, G. A. Advanced Calculus, London,1958.
राईलकर, म.रा.
“