प्रत्यावर्ती विद्युत् प्रवाह

प्रत्यावर्ती विद्युत् प्रवाह : एखाद्या संवाहकातून वाहणाऱ्या विद्युत् प्रवाहाचे मूल्य व दिशा दर सेकंदास वारंवार उलटसुलट बदलत असेल, तर त्या प्रवाहास ‘प्रत्यावर्ती प्रवाह’ म्हणतात. एकदिश प्रवाहाच्या बाबतीत संवाहकातून वाहणाऱ्या प्रवाहाची दिशा सतत तीच असते [⟶ एकदिश विद्युत् प्रवाह]. प्रत्यावर्ती प्रवाहाचे तसेचदाबाचे तात्कालिक मूल्य हे कालानुरूप प्रथम एका दिशेस शून्यापासून महत्तम मूल्यापर्यंत व पुन्हा शून्य (धन मूल्य), तसेच नंतर विरुद्ध दिशेस शून्यापासून महत्तम मूल्यापर्यंत व पुन्हा शून्य (ऋण मूल्य) असे सतत बदलत असते. बदलते मूल्य व काल यांच्या आलेखास प्रवाहाचा किंवा दाबाचा तरंगाकार असे म्हणतात. धन मूल्ये व ऋण मूल्ये यांच्या एका संचास ‘आवर्तन’ अशी संज्ञा आहे. दर सेकंदास पूर्ण होणाऱ्या आवर्तन संख्येस प्रत्यावर्ती प्रवाहाची अगर दाबाची ‘कंप्रता’ असे म्हणतात. एक आवर्तन पूर्ण करण्यास लागणाऱ्या कालखंडास ‘आवर्तन काल’ म्हणतात. अमेरिकेच्या संयुक्त संस्थानांत वापरल्या जाणाऱ्या प्रत्यावर्ती प्रवाहाची ‘मानक (प्रमाणभूत) कंप्रता’ ६० हर्ट्‌झ व इतर सर्व देशात ५० हर्ट्‌झ ठरविलेली आहे. व्यावहारिक उपयोगासाठी ४० हर्ट्‌झपेक्षा कमी कंप्रतेचा प्रत्यावर्ती प्रवाह वापरल्यास विद्युत् दिव्यामध्ये ‘लुकलुक’ निर्माण होऊन स्थिर प्रकाश मिळत नाही व डोळ्यांना त्रास होतो. अधिक कंप्रतेचा प्रवाह वापरल्यास विद्युत् साधनांत होणारा लोहिक व्यय (बदलत्या चुंबकीय क्षेत्रामुळे चुंबकीय द्रव्यात होणारा ऊर्जचा व्यय) वाढतो व त्यांची कार्यक्षमता कमी होते.

आज जगात निर्माण होणाऱ्या एकूण विद्युत् शक्तीपैकी ९५ टक्क्यांपेक्षा जास्त विद्युत् शक्ती प्रत्यावर्ती प्रवाहाच्या स्वरूपातच निर्माण केली जाते आणि औद्योगिक, व्यापारी व घरगुती अशा विविध उपयोगांसाठी वितरणही प्रत्यावर्ती प्रवाहाच्या स्वरूपातच केले जाते. याचे खालीप्रमाणे अनेक फायदे आहेत.

(१) प्रत्यावर्ती प्रवाहाचा विद्युत् दाब रोहित्राचा उपयोग करून जरूरीप्रमाणे पाहिजे तितका वाढविता येतो अगर कमीही करता येतो [⟶ रोहित्र]. या प्रवाहाद्वारे विद्युत् शक्ती दूर अंतरावर पाठविताना प्रेषण मार्गातील संवाहक तारांमधील विद्युत् दाब आवश्यक त्या प्रमाणात वाढवून त्यांमधील विद्युत् प्रवाह त्या प्रमाणात कमी करता येतो. यामुळे प्रेषण मार्गातील संवाहक तारांवरील भांडवली खर्च खूपच कमी होतो व संवाहक तापून होणारा ऊर्जेचा क्षय कमी होतो. [⟶ शक्तिप्रेषण, विद्युत्].

(२) प्रत्यावर्ती प्रवाहाच्या पद्धतीत जनित्राचा [यांत्रिक शक्ती वापरून विद्युत् शक्ती निर्माण करणाऱ्या साधनाचा ⟶ विद्युत् जनित्र] विद्युत् दाब शक्य तेवढा जास्त असून तो पुन्हा आरोहित्राच्या (विद्युत् दाब वाढविणाऱ्या रोहित्राच्या) साहाय्याने पाहिजे तितक्या प्रमाणात वाढवून विद्युत् शक्तीचे जरूर तेवढ्या दूर अंतरावर प्रेषण करणे आर्थिक दृष्ट्या सुलभ व कार्यक्षम ठरते. प्रेषित विद्युत् शक्तीचा जेथे प्रत्यक्ष उपयोग करावयाचा असेल तेथे अवरोहित्राच्या (विद्युत् दाब कमी करणाऱ्या रोहित्राच्या) साहाय्याने विद्युत् दाब आवश्यकतेनुसार कमी करून ती विद्युत् शक्ती योग्य त्या सुरक्षित दाबाखाली विशिष्ट कामासाठी वापरणे सहज शक्य होते.

(३) प्रत्यावर्ती प्रवाह निर्माण करणारी जनित्रे व त्यावर चालणारी चलित्रे (विद्युत् शक्तीचा उपयोग करून यांत्रिक शक्ती निर्माण करणारी साधने मोटर्स) व उपकरणे यांचा अभिकल्प (आराखडा) सोपा व रचना सुटसुटीत व बळकट करता येते.

(४) बऱ्याच विद्युत् साधनांत रोहित्र व रोधनिका वेटोळ्याचा (शक्तीचा व्यव न होता प्रत्यावर्ती प्रवाह मर्यादेत ठेवण्यासाठी वापरण्यात येणाऱ्या वेटोळ्याचा) उपयोग करतात त्यासाठी प्रत्यावर्ती प्रवाहच आवश्यक ठरतो.

(५) सतत ठराविक वेगाने फिरणाऱ्या चलित्रांमध्ये एकदिश चलित्रापेक्षा प्रत्यावर्ती त्रिकला प्रवर्तन चलित्राची [⟶ विद्युत् चलित्र] कार्यक्षमता जास्त असते. त्याची रचना साधी असून ते दीर्घकाळ चांगले काम देते.

(६) एखाद्या प्रदेशात अनेक ठिकाणी लागणारी विद्युत् शक्ती निरनिराळ्या ठिकाणी उत्पन्न करण्यापेक्षा मोजक्याच ठिकाणी उत्पन्न करून प्रत्यावर्ती पद्धतीने त्या त्या ठिकाणी पाठविणे हे कमी खर्चाचे असते म्हणून आता त्रिकला प्रत्यावर्ती प्रवाह पद्धती (हिचे स्पष्टीकरण पुढे दिले आहे) बहुतेक सर्व ठिकाणी मानक पद्धत म्हणून वापरण्यात येते.

(७) प्रत्यावर्ती प्रवाह एका आवर्तनात दोन वेळा शून्याप्रत येत असल्याने मोठ्या विद्युत् शक्तिगृहांतून मंडल खंडित करण्यासाठी वापरल्या जाणाऱ्या मंडल खंडक उपकरणांचे [⟶ विद्युत् मंडल खंडक] कार्य निर्धोक व सोयीस्करपणे करता येते.

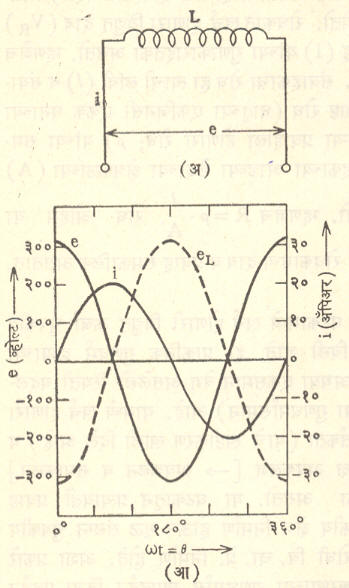
‘ज्या’ तरंगाकार :[त्रिकोणमितीय ज्या – sine – फलनाच्या आलेखासारखा आकार असणाऱ्या तरंगाला ‘ज्या तरंग’ म्हणतात ⟶ त्रिकोणमिति]. आ. १ मध्ये दाखविल्याप्रमाणे व्यवस्थित अक्षावर बसविलेले संवाहक तारेचे वेटोळे एकविध (सर्वत्र एकसारखे असलेल्या) चुंबकीय क्षेत्रामध्ये ठराविक वेगाने फिरविले असता चुंबकीय क्षेत्ररेषा कापल्या जाऊन वेटोळ्यामध्ये विद्युत् चालक प्रेरणा (विद्युत् प्रवाह वाहण्यास कारणीभूत होणारी प्रेरणा वि. चा. प्रे.) उत्पन्न होते. तिचे मूल्य वेटोळ्याच्या तात्कालिक स्थितीशी निगडित असून ते खालील सूत्राने काढता येते.

संवाहकातील तात्कालिक वि. चा. प्रे. e = Blv sin θ (व्होल्ट). या सूत्रात B चुंबकीय स्रोत घनता

[वेबर/मी.^२ ⟶ चुंबकत्व], I संवाहकाची चुंबकीय क्षेत्रातील लांबी (मीटर), v संवाहकाची रैखिक गती (मी./से.) [ v = ω.r ω कोनीय गती व r वेटोळ्याची त्रिज्या], θ फिरणाऱ्या वेटोळ्याचे क्षणिक प्रतल व चुंबकीय क्षेत्राशी लंब असणारे मूल प्रतल यांमधील कोन या राशी आहेत. ω r sin θ हा चुंबकीय क्षेत्रास लंब असणारा रैखिक गतीचा प्रक्षेप आहे.

---

ज्या वेळी θ हा ९०° असेल त्या वेळी (म्हणजे आकृतीत २ या आकड्याने दर्शविलेली वेटोळ्याची स्थिती असेल त्या वेळी) संवाहकातील वि. चा. प्रे. महत्तम असेल. महत्तम वि. चा. प्रे. E_m = B/vयावरून तात्कालिक वि. चा. प्रे. खालील सूत्राने काढता येते.

e =  E_m sin θ (व्होल्ट)

वरील वर्णनात तात्कालिक वि. चा. प्रे. ऐवजी तात्कालिक विद्युत् प्रवाह i व महत्तम विद्युत् प्रवाह I_m या राशी वापरल्यास वरील सूत्र i = I_m sin θ असे येईल. म्हणून प्रत्यावर्ती प्रवाहाचा तरंगाकार आ. १ (आ) मध्ये दर्शविल्याप्रमाणे ‘ज्या’ कार असतो.

‘ज्या’ तरंगातील परमप्रसराला (तरंगकारातील शून्य रेषेपासून जास्तीत जास्त दूर गेलेल्या बिंदूच्या अंतराला) ‘महत्तम मूल्य’ (दोलविस्तार किंवा शिखर मूल्य) म्हणतात. हे मूल्य आ. २ (अ) मध्ये पम या लंब रेषेने दाखविले आहे. प्रत्यावर्ती राशीचे सरासरी मूल्य शून्य असते परंतु फक्त धन मूल्य संचातील अगर ऋण मूल्य संचातील कालखंडाचे समान उपखंड करून त्या त्या वेळच्या सर्व मूल्यांच्या बेरजेला उपखंडाच्या संख्येने भागून येणाऱ्या मूल्यास ‘माध्य मूल्य’ म्हणतात.

प्रत्यावर्ती प्रवाहाचे मूल्य सतत बदलत असल्यामुळे एकदिश प्रवाहाशी तुलना करताना, त्याचे परिणामी मूल्य ठरविण्यासाठी प्रत्यावर्ती प्रवाहामुळे एखाद्या रोधकात काही वेळात जेवढी ऊर्जा निर्माण होते तेवढीच ऊर्जा त्याच रोधकातून तितक्याच वेळात निर्माण करणाऱ्या एकदिश प्रवाहाचे मूल्य हे सममूल्य धरतात. ज्या वेळी प्रत्यावर्ती प्रवाह रोधकातून वाहत असतो त्या वेळी विद्युत् शक्तीही पूर्ण आवर्तनातून बदलत असते व कोणत्याही क्षणी ही शक्ती तात्कालिक प्रवाह आणि तात्कालिक दाब यांच्या गुणाकाराइतकी असते. एका आवर्तनातील सरासरी शक्ती प्रवाह^२ व रोध यांच्या गुणाकाराइतकी असते. प्रत्यावर्ती प्रवाहांचे परिणामी मूल्य खालील पद्धतीने काढता येते. [आ. २ (आ) पहा].

(१) आकृतीत प्रत्यावर्ती प्रवाहi ‘ज्या’ तरंगाच्या स्वरूपात दाखविला आहे. (२) त्याच्या तात्कालिक मूल्यांचा म्हणजेच I_m sin θ या राशीचा वर्ग काढून या वर्गाचा आलेख काढला आहे. हा आलेख विद्युत् शक्तीचाही तरंग दाखवितो व त्याची कंप्रता प्रवाहाच्या कंप्रतेच्या दुप्पट असते. (३) या आलेखात गघ ही रेषा i² तरंगामधील लंबांच्या माध्याइतक्या अंतरावर काढली आहे. कग ही लांबी (I_m sin θ)² या राशीच्या माध्य मूल्य दाखविते. (४) हे मध्य मूल्य समतुल्य उष्णता निर्माण करण्यासाठी लागणाऱ्या एकदिश प्रवाहाच्या मूल्याच्यावर्गाबरोबर असते. (५)(I_m sin θ)²या राशीच्या माध्यमूल्याचे वर्गमूळ हे प्रवाहाचे परिणामी मूल्य (I_rms) असते. (६) हे मूल्य कख या रेषेने दाखविले आहे.

गणितीय पद्धतीने ०° ते १८०° यांमधील महत्तम मूल्याच्या’ज्या’ च्या वर्गांचा माध्य काढून त्याचे वर्गमूळ घेतल्यास परिणामी मूल्य काढता येते. ‘ज्या’ तरंगाकार प्रवाहाचे (अगर दाबाचे)परिणामी मूल्य खालील सूत्राने काढता येते.

Irms (परिणामी मूल्य) =	महत्तम प्रवाह मूल्य	=०·७०७Im
	√ 2

आणि माध्य मूल्य व तात्कालिक मूल्य खालील सूत्रांनी काढता येतात.

Iav (माध्य मूल्य)=	महत्तम प्रवाह मूल्य	= ०·६३७ Im
	π /2

i (तात्कालिक मूल्य)= महत्तम प्रवाह मूल्य  X sin θ = I_m sin θ

परिणामी प्रवाह मूल्य	= १·११
माध्य प्रवाह मूल्य

या गुणोत्तरास ‘आकार गुणक’ म्हणतात. 

---

कला : आवर्तनातील कोणत्याही बिंदूच्या विशिष्ट क्षणाच्या स्थितीस कला असे म्हणतात. प्रत्यावती प्रवाहाची (किंवा दाबाची) कला ही तो प्रवाह (किंवा दाब) संपूर्ण आवर्तनाच्या प्रमाणभूत स्थितीपासून किती कालकोनानंतर (कालदर्शक कोनानंतर) सुरू झाला हे दर्शविते. बहुधा प्रारंभबिंदूपासून हे अंतर मोजतात. प्रवाह हा i=I_m sin θ या सूत्राने दाखविला जात असेल, तर त्याची कला शून्य अंश असते परंतु जर i=I_m cos θ अशा सूत्राने प्रवाह दाखविला जात असेल, तर त्याची कला ९०° म्हणजे ^१/_४ आवर्तनाइतकी असते. कला हा शब्द सर्वसाधारणपणे कालकोनातील अंतराच्या संदर्भात वापरला जातो. दोन प्रत्यावर्ती राशी एकाच कंप्रतेच्या असून एकमेकींशी अनुरूप असतील, तर त्या समकालिक असतात. म्हणजेच त्यांची शून्य व महत्तम मूल्ये एकाच समयी प्राप्त होतात. जर असे होत नसेल, तर त्या राशी भिन्नकालिक समजाव्यात. म्हणजेच त्यांच्यामध्ये कलांतर असते. हे कलांतर अंशामध्ये दर्शवितात.

प्रत्यावती प्रवाह उत्पन्न करणाऱ्या जनित्रात संवाहक तारांची तीन एकसारखी वेटोळी १२०° चे अंतर सोडून स्वतंत्रपणे बसविलेली असतात. त्यामुळे या वेटोळ्यांतून निर्माण होणारा विद्युत् दाब एकाच क्षणी उत्पन्न न होता प्रत्येकी १२०° च्या कलांतराने निर्माण होतो व हे कलांतर कायम राहते. अशा जनित्रास त्रिकला जनित्र म्हणतात. [⟶विद्युत् जनित्र].

प्रत्यावर्ती पद्धतीत बहुतेक एकाच संवाहकातून जाणारा विद्युत् प्रवाह व त्यावरील विद्युत् दाब विशिष्ट परिस्थितीमुळे एकमेकांशी अनुरूप नसतो. संवाहकाच्या वेटोळ्याला विद्युत् दाब लावल्यानंतर काही कालाने प्रवाह सुरू होतो. म्हणजेच प्रवाह दाबाला अनुसरतो (मागे असतो). याउलट धारित्रापासून [विद्युत् ऊर्जा साठवून ठेवणाऱ्या साधनातून ⟶विद्युत् धारित्र] जाणारा प्रवाह दाबाच्या पूर्वीच सुरू होतो. म्हणजे प्रवाह दाबास पुरोगामी (पुढे जाणारा) असतो. अशा वेळी दाब व प्रवाह यांच्या तरंगांतील आरंभाच्या बिंदूतील अंतरास कलांतर म्हणतात व ते अंशात मोजतात.

विद्युत् जनित्रामध्ये चुंबकीय क्षेत्राचा मार्ग नुसत्या हवेतून नसून त्याचा बराचसा भाग पोलादी सांगाड्यांत व खाचा पाडलेल्या पोलादी गाभ्यामध्येच असतो. त्यामुळे चुंबकीय क्षेत्र निर्माण करण्यास लागणारी चुंबकीय चालक प्रेरणा व चुंबक उत्तेजक प्रवाह कमी करता येतो. अशा रचनेत स्थिर भाग व फिरता भाग यांमधील हवेच्या फटीत ‘ज्या’कार चुंबकीय क्षेत्र असले, तरी पोलादी गाभ्यातील खाचांमुळे स्रोत घनता शुद्ध ‘ज्या’ स्वरूपात राहत नाही व वि. चा. प्रेरणाही शुद्ध ‘तरंगाकार’ स्वरूपाची नसते. पोलादाच्या संपृक्ततेमुळेही (पोलादातून शक्य तेवढ्या जास्त चुंबकीय रेषा जाऊ दिल्यामुळेही) या स्वरूपात बदल होतो. तरीही प्रत्यक्ष व्यवहारात हा ‘ज्या’ तरंगाकार मानला जातो.

सध्या वापरात असलेले मोठ्यात मोठे प्रत्यावर्ती जनित्र सु. १,५०० मेगॅवॉट शक्तीचे आहे. २० हर्ट्‌झ ते २० किलोहर्ट्‌झ या कंप्रतेस श्राव्य कंप्रता व ५०० किलोहर्ट्‌झ ते १,५०० किलोहर्ट्‌झ या कंप्रतेस ‘रेडिओ कंप्रता’ म्हणतात. असा प्रत्यावर्ती प्रवाह विशिष्ट कारणांसाठीच वापरतात.

 प्रत्यावर्ती प्रवाह मंडलातील घटक : एकदिश प्रवाह मंडलांचा विचार करताना फक्त विद्युत् रोधाचाच विचार करतात व जी. एस्. ओहम यांच्या नियमाप्रमाणे त्यातील प्रवाह 

I =	E (दाब)
	R (रोध)

या सूत्राने काढता येतो. प्रत्यावर्ती प्रवाह मंडलाचा विचार करताना तीन प्रकारच्या घटकांचा विचार करावा लागतो : (१)  विद्युत् रोधक, (२) प्रवर्तक व (३) धारित्र.

विद्युत् रोधक : संवहकातून जाणाऱ्या प्रवाहास रोध झाल्यामुळे संवाहक गरम होतो. ज्याप्रमाणे यंत्राच्या विविध भागांमध्ये घर्षण होऊन त्यांतील यांत्रिक ऊर्जेचे उष्णतेत रूपांतर होते, त्याचप्रमाणे संवाहकातून विद्युत् प्रवाह पाठविताना खर्च होणाऱ्या विद्युत् ऊर्जेचे उष्णतेत रूपांतर होते. हा संवाहकाचा प्राकृतिक गुणधर्म आहे. रोधक हा घटक संवाहकच असून त्याचा रोध ठराविक मूल्याचा असतो व त्याचा उपयोग प्रवाह ठराविक मर्यादेत ठेवण्यासाठी वा ठराविक दाबपात (संवाहकातून प्रवाह जात असताना होणारा दाबातील बदल) मिळविण्यासाठी करण्यात येतो. रोधकात खर्च होणारा विद्युत् दाब (V_R) हा रोध (R) व प्रवाह (I) यांच्या गुणाकाराइतका असतो. म्हणजेच V_R =I·R (व्होल्ट). संवाहकाचा रोध हा त्याची लांबी (I ) व संवाहकाच्या धातूचा विशिष्ट रोध (धातूच्या एकजिनसी एकक घनाच्या विरुद्ध पृष्ठांतून जाणाऱ्या प्रवाहाला होणारा रोध p) यांच्या समप्रमाणात आणि संवाहकाच्या आडव्या छेदाच्या क्षेत्रफळाच्या (A) व्यस्त प्रमाणात बदलतो.म्हणजेच

R = p·	I
	A

रोध ‘ओहम’ या एककामध्ये मोजतात. रोधकामध्ये दाब व प्रवाह समकालिक असतात. [⟶ विद्युत् रोधक ]. 

---

प्रवर्तक : या मंडल घटकामध्ये खर्च होणारी विद्युत् ऊर्जा चुंबकीय क्षेत्राच्या रूपात साठविली जाते. हा प्राकृतिक गुणधर्म द्रव्याच्या जडत्वासमान (स्थिर अथवा एकसमान वेग असलेली स्थिती बदलण्यास विरोध करण्याच्या गुणधर्मासमान) आहे. यामध्ये खर्च होणारा दाब हा घटकाची प्रवर्तकता (याचे स्पष्टीकरण खाली दिले आहे) व प्रवाहाचा काल सापेक्ष अवकलज [⟶ अवकलन व समाकलन] यांच्या गुणाकाराइतका असतो. या घटकातून प्रत्यावर्ती प्रवाह गेल्यामुळे बदलते चुंबकीय क्षेत्र निर्माण होऊन मूळ संलग्न चुंबकीय क्षेत्र बदलल्यामुळे विरोधी वि. चा. प्रे. निर्माण होते. अशा प्रकारे विद्युत् दाब निर्माण करण्याच्या गुणधर्मास स्वप्रवर्तन किंवा प्रवर्तन म्हणतात. प्रवर्तनाच्या मूल्याला प्रवर्तकता म्हणतात व ते ‘हेन्री’ या एककात दाखवितात. प्रवर्तनामुळे निर्माण होणाऱ्या रोधास प्रवर्तनी अवरोध म्हणतात.

प्रवर्तक हा तारेच्या अनेक वेढ्यांनी बनलेल्या वेटोळ्याच्या स्वरूपात असतो. या वेटोळ्याचा गाभा त्याच्या उपयोगानुसार चुंबकीय द्रव्याचा (उदा., सिलिकॉन पोलादाच्या पट्ट्यांचा) अथवा अचुंबकीय द्रव्याचा (उदा., सेरॅमिक, प्लॅस्टिक इ.) असतो. प्रवर्तकाची प्रवर्तकता (L) पुढील सूत्राने मिळते.

प्रवर्तकता =	वेटोळ्यातील वेढ्यांची संख्या Xचुंबकीय क्षेत्र	(हेन्‍री)
	विद्युत् प्रवाह

प्रवर्तनी अवरोधाचे (X_L) सूत्र खालीलप्रमाणे आहे.

X_L = 2 π f L (ओहम)

येथे f ही प्रवाहाची कंप्रता व L ही प्रवर्तकाची प्रवर्तकता आहे. प्रवर्तनी अवरोधात खर्च होणाऱ्या दाबाचे (E) सूत्र खालीलप्रमाणे आहे.

E = 2 π f LI (व्होल्ट)

लेंट्स नियम : एखाद्या वेटोळ्यामधून वाहणाऱ्या बदलत्या विद्युत् प्रवाहामुळे संलग्न स्रोत बदलत असेल, तर मायकेल फॅराडे यांच्या नियमानुसार त्यात वि. चा. प्रे. निर्माण होते. ही वि. चा. प्रे. मूळ प्रवाहाच्या बदलास विरोध करणारी असते. म्हणजेच मूळ दाबाच्या विरुद्ध असते, असे एच्. एफ्. ई. लेंट्स यांनी १८३३ मध्ये सूत्ररूपाने खालीलप्रमाणे मांडले.

वेटोळ्यातील स्वपवर्तनी विद्युत् दाब e_L = – L ^di/_dt.

येथे L प्रवर्तकता व ^di/_dt प्रवाहाचा काल सापेक्ष अवकलज आहे. ऋण चिन्हाने स्वप्रवर्तनी वि. चा. प्रे. मूळ दाबाच्या विरुद्ध दिशेस असल्याचे दाखविले जाते.

आ. ३ मध्ये दाखविल्याप्रमाणे स्वप्रवर्तनी विद्युत् दाब हा त्याला निर्माण करणाऱ्या प्रवाहास π / 2 अरीयमानाने किंवा ९०° ने अनुसरतो. म्हणजेच फक्त प्रवर्तकाचा समावेश असलेल्या मंडलातील विद्युत् दाब व प्रवाह यांच्यामध्ये ९०° चे कलांतर असते. खर्च होणारा विद्युत् दाब स्वप्रवर्तनी दाबाच्या १८०° विरुद्ध असतो. त्यामुळे शुद्ध प्रवर्तनी मंडलातून वाहणारा प्रवाह त्याला लावलेल्या दाबाला ९०° नी अनुसरतो. 

---

धारित्र : या घटकामध्ये खर्च होणारी विद्युत् ऊर्जा विद्युत् क्षेत्ररूपाने साठवली जाते. ⇨ विद्युत् अपारक पदार्थाने निरोधित केलेल्या धातूच्या दोन समांतर पट्ट्या अशी याची सर्वसाधारणपणे रचना असते. विद्युत् संवाहक पट्ट्यावरील विद्युत् भार व विद्युत् दाब यांच्या गुणोत्तरास ‘धारकता’ म्हणतात. ही मोजण्याचे एकक ‘फॅराड’ हे आहे. हे एकक फारचमोठे असल्याने व्यवहारात मायक्रोफॅराड (१०^-६ फॅराड) किंवा याहून लहान धारकता मोजण्यासाठी पिकोफॅराड (१०^-१२ फॅराड) हे एककही वापरतात. या घटकात खर्च होणारा (तात्कालिक) विद्युत् दाब (e_C) खालील सूत्राने मिळतो.

eC =	1	∫	I dt (व्होल्ट)
	C

 

धारित्रामुळे मंडलात निर्माण होणाऱ्या रोधास धारक अवरोध (X_C) म्हणतात व तो खालील सूत्राने मिळतो.

XC =	I	(ओहम)
	2 π f C

येथे f प्रवाहाची कंप्रता व C ही धारित्राची धारकता आहे. धारित्रात खर्च होणारा परिणामी विद्युत् दाब (E) खालील सूत्राने मिळतो.

E =	I	= I· XC (व्होल्ट)
	2 π f C

येथे I हे प्रवाहाचे परिणामी मूल्य आहे.

फक्त धारित्राचा समावेश असलेल्या मंडलातील विद्युत् प्रवाह विद्युत् दाबाच्या ९०° नी पुरोगामी असतो. (आ. ४).

याप्रकारे मंडलातील वरील तिन्ही प्रकारच्या घटकांमुळे प्रवाहाला होणारा एकत्रित रोध हा रोध आणि परिणामी अवरोध यांचा संयुक्त परिणाम असतो. प्रत्यावर्ती प्रवाह मंडलात त्याला संरोध असे म्हणतात. त्याचे एकक ओहम आहे. संरोधाचे सूत्र खालीलप्रमाणे आहे.

Z = √ R² + (X_L – X_C)²

येथे Z -संरोध, R -रोध,  X_L प्रवर्तनी अवरोध,  X_C -धारक अवरोध व X_L– X_C हा परिणामी अवरोध आहेत. मंडलातील प्रवाह (I) खालील सूत्राने मिळतो.

I = E / Z

यात E दाब असून Z संरोध आहे. 

---

आ. ५ (अ) मध्ये एकसरीत जोडलेले रोधक, प्रवर्तक व धारित्र यांचे मंडल दाखविले आहे. अशा मंडलात प्रवर्तनी अवरोध व धारक अवरोध यांचे घटक १८०° च्या कलांतरात असतात. त्यांची बैजिक बेरीज म्हणजे परिणामी अवरोध हा रोधाशी ९०°च्या कलांतरात असतो. म्हणजेच रोध व परिणामी अवरोध या काटकोन त्रिकोणाच्या दोन बाजूंनी दाखविल्यास संरोधहा कर्णाबरोबर असतो. आ. ५ (आ) मध्ये असा संरोध त्रिकोण दाखविला आहे.

 

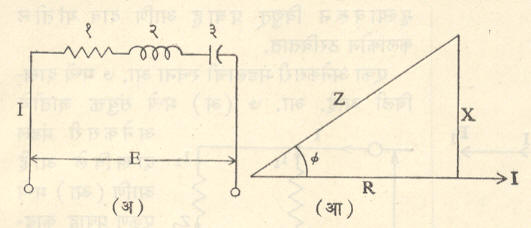
अवरोध : प्रत्यावर्ती प्रवाह मंडलातील प्रवर्तकता (चुंबकीय क्षेत्रात ऊर्जा साठवण्याची क्षमता) व धारकता (विद्युत् भार साठवून ठेवण्याची क्षमता) यांच्या रोधक परिणामास अवरोध म्हणतात. प्रवर्तनी अवरोध व धारक अवरोध यांच्या कलांमध्ये १८०° चा फरक असल्याने सदिश आरेखात [महत्ता व दिशा निर्देशक रेषांनी विविध राशी दर्शविणाऱ्या आकृतीत ⟶ सदिश], ते एकमेकांविरुद्ध दर्शवितात. त्यामुळे त्यांचे परिणामी मूल्य त्यांच्या बैजिक बेरजेबरोबरच असते. हे अवरोध ओहम या एककात मोजतात.

परिणामी अवरोध = । प्रवर्तनी अवरोध (X_L) – धारक अवरोध (X_C) । जर X_L &gt X_C, तर संरोध त्रिकोणातील Φ कोन धन असतो आणि जर X_L &lt X_C, तर Φ कोन ऋण असतो. Φ कोन धन असेल, तर प्रवाह दाबास अनुसरतो व Φ कोन ऋण असेल, तर प्रवाह दाबास पुरोगामी असतो.

   

मंडल गणन : एकदिश विद्युत् मंडले रोधकांच्या एकसरी अथवा अनेकसरी जोडणीने बनलेली असतात [⟶ एकदिश विद्युत् प्रवाह]. प्रत्यावर्ती प्रवाह मंडलांची रचनाही याच प्रकारे असते परंतु त्यामध्ये फक्त रोधकांचा विचार न करता त्याचबरोब प्रवर्तक व धारित्र यांच्या प्रवर्तनी व धारक अवरोधांचा एकत्र म्हणजे संरोधाचा विचार व्हावा लागतो.

आ.६ (अ) मध्ये विद्युत् रोधक, प्रवर्तक व धारित्र हे एकसरी पद्धतीने जोडलेले असून अशा मंडलाचा संरोध खालील सूत्राने काढता येतो.

Z = √ R² + (X_L – X_C)²

मंडलात अनेक रोधक, प्रवर्तक व धारित्रे असल्यास संरोध खालील सूत्राने मिळतो.

Z = √ (R₁ + R₂ + R₃ +…)² +  (X₁ + X₂ + X₃ +..)²

यात R₁, R₂, R₃, … हे मंडलातील रोधकांचे रोध आणि X₁,  X₂,  X₃,… हे मंडलातील परिणामी अवरोध आहेत.

[X₁ =। X_L1 – Xc₁।, X₂=। X_L2 – Xc₂।..इत्यादी].

याप्रमाणे मंडलाचा संरोध काढल्यावर व विद्युत् दाब (E) माहीत असल्यास मंडलातून वाहणारा प्रवाह (I) पुढील सूत्राने काढता येतो.

I = E/Z 

---

दाब व प्रवाह यांमधील कलाकोनΦ खालीलप्रमाणे काढतात.

tanΦ =	X1+X2+X3…	किंवा cosΦ=	(एकूण) रोध
	R1+R2+R3…		(एकूण) संरोध

मंडलातील एकूण संरोध हा एकूण रोध व परिणामी अवरोध यांच्या सदिशांच्या बेरजेबरोबर असतो.

प्रत्यावर्ती प्रवाह व दाब कालानुरूप बदलत असल्याने व मंडल गणनामध्ये निरनिराळे प्रश्न सोडविताना कलांतरांचाही विचार करावा लागत असल्याने उदाहरणे सोडविताना सदिश आरेखन पद्धती वापरल्यास सोयीचे जाते.

सदिश आरेखन पद्धती : कालानुरूप बदलणारी मूल्ये (परिणाम) व दिशा असणारी कोणतीही राशी बाणांकित प्रमाणबद्ध लांबीच्या रेषेने दाखविता येते. अशा रेषेस ⇨ सदिश म्हणतात. एकाच कोनीय वेगाने फिरणाऱ्या सदिशास कालसदिश म्हणतात. (प्रस्तुत नोंदीत ‘सदिश’ हा शब्द यापुढे ‘कालसदिश’ या अर्थाने वापरला आहे).

सदिशाची लांबी त्याच्या मूल्याच्या प्रमाणात असते आणि त्याची बाणाची दिशा त्या राशीची दिशा दर्शविते. आंतरराष्ट्रीय संकेतानुसार फिरण्याची दिशा अपसव्य(घड्याळाच्या काट्यांच्या गतीच्या विरुद्ध दिशेने) असल्यास धन व सव्य असल्यास ऋण समजतात.

एकाच कंप्रतेने बदलणाऱ्या प्रत्यावर्ती राशी साध्या (आयतनी) किंवा ध्रुवीय (कोनीय) पद्धतीने दर्शविता येतात.

प्रत्यावर्ती प्रवाह विद्युत् मंडलामध्ये एकाच वेळी अनेक विद्युत् प्रवाह व वि. चा. प्रेरणा कार्यरत असू शकतात आणि त्या सर्वांचे कलाकोन निरनिराळे असू शकतात. अशा सर्व प्रवाहांचा वि. चा. प्रेरणांचा एकत्र परिणाम अभ्यासण्यासाठी त्यांची सदिश पद्धतीने बेरीज किंवा वजाबाकी करणे सोपे जाते. सदिश पद्धती मांडलेल्या कोणत्याही राशीचे तात्कालिक मूल्य हे त्या सदिशाच्या उभ्या (य) अक्षावरील प्रक्षेपाइतके असते (या ठिकाणी सदिशाचे मूल्य महत्तम मूल्याच्या प्रमाणात असते). दोन सदिशांमधील कोनास कलाकोन म्हणतात. आरेखातील सदिशांच्या बाबतीत पुढील दोन गोष्टी आवश्यक आहेत :

(१ (१) सदिश आरेखातील प्रत्येक सदिशाचा कोनीय वेग समान असला पाहिजे. (२) आरेखातील सदिशाची लांबी त्या राशीच्या महत्तम किंवा परिणामी मूल्याच्या प्रमाणात असली पाहिजे.  

      ज्या वेळी सदिश संरोधांचे गुणाकार वा भागाकार करावयाचे असतील त्या वेळी ध्रुवीय पद्धती वापरणे सोयीचे असते. उदा., समजा  व  हे कोणतेही दोन सदिश असून ते प्रमाणभूत अक्षाशी अनुक्रमे Φ₁ व Φ₂ कलाकोन करीत असतील, तर त्यांचा गुणाकार व भागाकार खालीलप्रमाणे करता येतो. 

सदिश  = X_{1  ∠ Φ1}   सदिश   = X_2 ∠ Φ₂ 

गुणाकार :  · = X₁ · X₂  ∠ (Φ₁ +_Φ2) 

भागाकार :

	=	X1	∠ (Φ1 –Φ2)
		X2

  

कोणत्याही विद्युत् उपकरणाच्या कार्याचा अभ्यास त्याच्या मंडलाच्या सदिश आलेखावरून सुलभतेने करता येतो व त्यामुळे त्याच्या अभिकल्पनात सदिश आरेख फार उपयुक्त ठरतात. 

---

एकसरी व अनेकसरी मंडले : एकसरी मंडलामध्ये मंडलातील घटक क्रमाने एकापुढे एक असे जोडलेले असतात. त्यांमधून जाणारा प्रवाह समान असतो परंतु प्रत्येक घटकात खर्च होणारा दाब निरनिराळा असतो. या निरनिराळ्या दाबांची सदिश बेरीत एकूण विद्युत् दाबाइतकी असते. अशा प्रकारचे साधे एकसरी मंडल आ. ६ (अ) मध्ये दाखविले आहे (आ), (इ) व (ई) यांमध्ये अनुक्रमे रोधक, प्रवर्तक व धारित्र भागांतील विद्युत् दाब व प्रवाह यांतील संबंधदर्शविले असून (उ) मध्ये विविध घटकांतील विद्युत् दाबांची सदिश बेरीज करण्याची पद्धत दाखविली आहे. वरील मंडलात बाहेरून लावलेला विद्युत् दाब E व्होल्ट असेल, तर ओहम यांच्या नियमानुसार मंडलातून वाहणारा विद्युत् प्रवाह (I) खालील सूत्राने मिळतो.

I (अँपि.) =	E (व्होल्ट)
	Z (ओहम)

येथे Z हा संरोध असून तो पुढील सूत्राने काढतात.

Z = √ R² + (X_L – X_C)²

यात R रोधकाचा रोध (ओहममध्ये) असून X_L व X_C अनुक्रमे प्रवर्तनी अवरोध व धारक अवरोध आहेत.

विद्युत् दाब व प्रवाह यांमधील कलाकोनाचे (Φ) मूल्य काढण्यासाठी खालील सूत्र वापरतात.

cosΦ  =	R	किंवा tan Φ=	। XL – XC
	Z		R

ज्या ठिकाणी X_L &gt X_C असेल तेथे tan Φ आणि Φf धन असतात. या वेळी विद्युत् प्रवाह दाबाला अनुसरतो. याउलट जर X_L &lt X_C तेथे tan Φ आणि Φ ऋण असतात. या वेळी विद्युत् प्रवाह दाबाला पुरोगामी असतो. प्रत्यावर्ती प्रवाहाच्या मंडलातील अवरोध (प्रवर्तनी व धारक भागातील रोध)  प्रवाहाच्या कंप्रतेवर अवलंबून असतो. X_L व X_C यांचा परिणामी अवरोध हा त्यांच्या फरकाबरोबर असतो.परिणामी अवरोधाचे गुणधर्म X_L किंवा X_C यांपैकी जो जास्त असेल त्याप्रमाणे असतात. X_L व X_C यांमधील फरकाच्या धन वा ऋण मूल्यावरून विद्युत् प्रवाह आणि दाब यांतील कलाकोन ठरवितात.

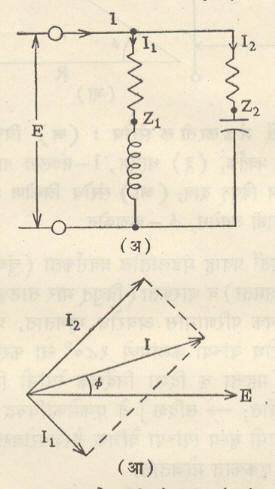
एका अनेकसरी मंडलाची रचना आ. ७ मध्ये दाखविली आहे. आ. ७ (अ) मध्ये संयुक्त जातीचे अनेकसरी मंडल दाखविले आहे आणि (आ) मध्ये एकूण प्रवाह काढण्याची सदिश पद्धत दाखविली आहे. अशा मंडलांसाठी प्रवाहांचे काढलेले सदिश आलेख हे वेगवेगळ्या शाखांतील प्रवाहांची प्रमाणबद्ध बहुभुजाकृती असते. अनेकसरी मंडलामध्ये प्रत्येक शाखामंडलाचे एक टोक विद्युत् पुरवठ्याच्या एका तारेस व दुसरे दुसऱ्या तारेस जोडलेले असते. प्रत्येक शाखामंडलाचा दाब पुरवठ्याच्या विद्युत् दाबाइतकाच असतो. मंडलातील एकूण प्रवाहाचे, दाबाशी समकला असणारा व लंब असणारा अशा दोन घटकांमध्ये विभेदन करता येते. अनेक शाखा मंडले अनेकसरीत जोडलेली असतील, तर सर्व लंब घटकांची बेरीज व सर्व समकला घटकांची बेरीज यांचे गुणोत्तर जंद tan Φ  बरोबर असते.

tanΦ =	लंब घटक प्रवाहांची बेरीज
	संपूर्ण समकला प्रवाह

या सूत्रावरून कलाकोन Φ काढता येतो.

अनेकसरी मंडलांचे गणित करताना संरोधाच्या व्यस्तांकाचा म्हणजे प्रवेशिता या राशीचा उपयोग केल्यास गणन सोपे होते.

प्रवेशिता Y = ¹ / _Z

याशिवाय संवाहिता व अनुकार्यता या दोन राशींचाही उपयोग अनेकसरी मंडलांच्या गणनात करतात. या राशींच्या व्याख्या खालील सूत्रांनी मिळतात. 

---

संवाहिता G =	R	येथे R हा रोध व Z संरोध आहेत.
	Z2

अनुकार्यता B =	X	येथे X हा अवरोध व Z संरोध आहेत.
	Z2

  

प्रवेशिता, संवाहिता व अनुकार्यता या काटकोन त्रिकोणाच्या अनुक्रमे कर्ण, क्षैतिज भुजा व उभी भुजा या क्रमाने दाखविता येतात आणि त्यावरून खालील सूत्र मिळते. 

Y = √ G² + B²

आ. ७ मध्ये दाखविल्याप्रमाणे रोधक व प्रवर्तक एका शाखेत (एकसरीत) आणि रोधक व धारित्र दुसऱ्या शाखेत (एकसरीत) जोडून या शाखा अनेकसरी पद्धतीने जोडलेल्या असतील, तस मंडलात वाहणारा एकूण प्रवाह खालील पद्धतीने काढतात.

पहिल्या शाखेकरिता G1 =	R1	, B1 =	X1
	Z12		Z12

दुसऱ्या शाखेकरिता G2 =	R2	, B2 =	X2
	Z22		Z22

यावरून परिणामी प्रवेशिता Y = √ ( G₁ +G₂)² + (B₁ + B₂)²

एकूण प्रवाह = विद्युत् दाब X प्रवेशिता = E·Y

खाली दिलेल्या j (= √-1) या कारकाचा उपयोग केल्यास हे गणन विशेष सुलभ पद्धतीने करता येते.

j पद्धती व परिमेयकरण :j पद्धती ही सदिश राशी मांडण्याची बीजगणितातील एक विशेष पद्धत आहे. यामुळे सदिश राशींची गणितकृत्ये (बेरीज, वजाबाकी, गुणाकार, भागाकार) आलेखाच्या मदतीशिवाय गणिती पद्धतीने करता येतात. ही गणन पद्धती सोपी व अचूक असते. नेहमीच्या आलेख पद्धतीतील क्षैतिज अक्षास ‘सत् अक्ष’ किंवा कालदर्शक अक्ष अगर संदर्भ अक्ष म्हणतात आणि आदिबिंदूच्या (आरंभ बिंदूच्या) उजवीकडील अंगास धन चिन्ह व डावीकडील अंगास ऋण चिन्ह लावतात. क्षैतिज अक्षास लंब असणाऱ्या व आदिबिंदूतून जाणाऱ्या अक्षास असत् अगर लंब अक्ष म्हणतात. या अक्षावर क्षैतिज अक्षाच्या वरील भागास धन चिन्ह व खालील भागास ऋण चिन्ह लावतात. काल व लंब अक्षांवरील मूल्य ओळखण्यासाठी लंब अक्षावरील मूल्यास j हे अक्षर आरंभी जोडतात. जसे एखादा बिंदू (४, ५) या मूल्याने दाखविला जात असेल, तर j पद्धतीत तो ४ + j ५ असा मांडतात (क्षैतिज अक्षापासून उजवीकडे ४ एकक व लंब अक्षापासून वर ५ एकक). j हा सहगुणक ‘कारक’ म्हणूनही वापरला जातो. याचा अर्थ असा की, सत् अक्षावरील एका सदिशास j ने गुणले, तर ती राशी ९०° तून अपसव्य दिशेने फिरते. पुन्हा j ने गुणले, तर ती राशी ९०° तून आणखी फिरेल म्हणजेच एकूण १८०° तून फिरेल आणि तिचे मूल्य तेवढेच परंतु ऋण होईल. म्हणजेच j²= -1 आणि  j = √-1 म्हणून j ही एक असत् संख्या आहे. [गणितात jऐवजी i हे अक्षर वापरतात ⟶संख्या]. कोणतीही सदिश राशी दोन अक्षांवरील सहनिर्देशकांत व्यक्त करता येत असल्याने j पद्धत बहुतेक सर्व ठिकाणी वापरता येते. अशा राशीस मिश्र राशी किंवा सदसत् राशी म्हणतात.

समजा X= A+jB ही मिश्र राशी आहे, तर तिचे मूल्य (महत्ता) X= √ A²+B² इतके असते व तिचा

कलाकोन θ, tan θ=  ^B/_A यावरून काढतात. मिश्र राशींची बेरीज व वजाबाकी खालीप्रमाणे करतात. 

---

जर X₁=A+jB व X₂ =C+jD असेल, तर

X₁ + X_{2 =}(A+C) + j(B+D)

व त्याचे मूल्य = √ (A+C)² + (B+D)²

आणि X₁ –X₂ = (A-C) +j (B-D)

व त्याचे मूल्य = √ (A-C)² + (B-D)²

मिश्र राशी एखाद्या गुणोत्तराच्या स्वरूपात असेल, तर ती A+jB अशा स्वरूपात मांडावी  लागते.

उदा., X=	1
	A+jB

ही मिश्र राशीआहे. तिच्या अंश व छेदास A-jB या राशीने गुणल्यास

X	A-jB	=	A-jB	(∵ j2 = -1)
	A2 –j2 B2		A2 +B2

म्हणून X =	A	-j	B	= A’ – jB’
	A2 + B2		A2 + B2

  

येथे A’ =	A	व B’ =	B
	A2 +B2		A2 +B2

 या क्रियेस परिमेयकरण म्हणतात. यावरून X चे निव्वळ मूल्य

X = √ A^’2 + B’²

अशा प्रकारे j पद्धतीचा उपयोग करता येतो.

 अनुस्पंदन : व्यवहारात स्थिर रोध व बदलता संरोध असलेली एकसरी मंडले जास्त प्रमाणात वापरली जातात. त्यातही विशेषेकरून प्रवर्तक किंवा धारित्र यांचा समावेश असलेली मंडले एखाद्या विशिष्ट कंप्रतेशी अनुस्पंदित करता येतात. यालाच मेलन करणे असे म्हणतात. संदेशवहन अभियांत्रिकीस विद्युत् मंडलांतील अनुस्पंदनाला अतिशय महत्त्व आहे. [⟶ अनुस्पंदन].

वास्तव व आभासी विद्युत् शक्ती आणि शक्तिगुणक : विद्युत् शक्तीच्या एका आवर्तनातील तात्कालिक बैजिक माध्य मूल्यास वास्तव, माध्य किंवा खरी (क्रियाशील) विद्युत् शक्ती म्हणतात.

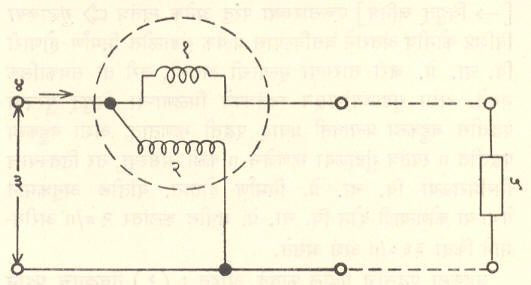
 प्रत्यावर्ती मंडलातील वास्तव शक्ती ही लावलेला विद्युत् दाब व दाबाशी समकलेत असलेला विद्युत् प्रवाहाचा घटक यांच्या गुणाकाराइतकी असते. ही शक्ती EI cos Φ या सूत्राने मिळते व ती विद्युत् शक्तिमापकाने [⟶ विद्युत् राशिमापक उपकरणे] मोजतात. प्रत्यावर्ती प्रवाहाच्या एककाला मंडलात खर्च होणारी विद्युत् शक्ती मोजण्यासाठी शक्तीमापकाची करण्यात येणारी जोडणी आ. ८ मध्ये दाखविली आहे. यामध्ये १ हे प्रवाह वाहून नेणारे वेटोळे आहे व ते ५ या भाराला एकसरीत जोडले आहे. २ हे दाब वेटोळे असून ते भाराला अनेकसरीत जोडले आहे. प्रत्यावर्ती प्रवाह मंडलात दाब X प्रवाह  (E X I)  या राशीस आभासी शक्ती म्हणतात.

---

 

 निर्धारित मूल्य : प्रत्यावर्ती प्रवाहावर चालणाऱ्या यंत्रांचे आणि साधनांचे निर्धारण म्हणजे विशिष्ट  परिस्थितीत कार्य करण्याची क्षमता दर्शविणारी मर्यादा ही त्यांमध्ये निर्माण होणाऱ्या तापमानाच्या वाढीशी निगडित असते. तापमान हे वाहणाऱ्या प्रवाहाच्या वर्गाशी संबंधितअसल्यामुळे यंत्राच्या अगर साधनाच्या वास्तव शक्तीपेक्षा प्रवाहक्षमतेवर ते अवलंबून असते व त्यामुळे शक्तिगुणकावर अवलंबून नसते. म्हणून ‘निर्धारित मूल्य’ हे आभासी शक्तीच्या स्वरूपात देतात.

निर्धारित मूल्य = दाब X प्रवाह (व्होल्ट-अँपिअर) किंवा

दाब X प्रवाह	(किलोव्होल्ट-अँपिअर)
१,०००

अशा स्वरूपात देतात.

उदा., २० अँपिअर प्रवाह घेणारे व २०० व्होल्ट दाबावर चालणारे साधन ०·८शक्तिगुणकावर

२० X ०·८ X २००	= ३·२ किलोवॉट
१,०००

शक्ती देईल आणि १ शक्तिगुणकावर

२०० X १ X २०	= ४ किलोवॉट शक्ती देईल.
१,०००

परंतु या दोन्ही बाबतींत प्रवाह २० अँपिअर असल्याने तापमान वाढ समानच राहील. म्हणून

निर्धारित मूल्य =	२००X २०	= ४ किलोव्होल्ट-अँपिअर असे येईल.
	१,०००

शक्तिगुणक : वास्तव शक्ती व आभासी शक्ती यांच्या गुणोत्तरास शक्तिगुणक म्हणतात. आभासी शक्तीला शक्तिगुणकाने गुणले, तर वास्वव शक्ती मिळते.’ज्या’ तरंग विद्युत् प्रवाह पद्धतीत शक्तिगुणकाचे मूल्य हे विद्युत् दाब व विद्युत् प्रवाह यांच्यामधील कलाकोनाच्या कोज्या (cosine) इतके असते. केवळ रोधक असलेल्या मंडलात विद्युत् दाब व प्रवाह यांमधील कलाकोन शून्य असतो म्हणून अशा मंडलात शक्तिगुणक एक असतो. केवळ प्रवर्तक वेटोळे किंवा धारित्र असलेल्या मंडलांत विद्युत् दाब व प्रवाह यांतील कलाकोन ९०° असतो म्हणून अशा मंडलांतील शक्तिगुणक शून्य असतो व अशा मंडलात खर्च होणारी शक्तीही शून्य असते. [⟶ शक्तिगुणक]. 

---

बहुकला प्रत्यावर्ती प्रवाह पद्धती : प्रत्यावर्ती विद्युत् जनित्रात [⟶ विद्युत् जनित्र] एकसारख्या परंतु अनेक स्वतंत्र ⇨ गुंडाळ्या विशिष्ट कोनीय अंतराने बसविल्यास प्रत्येक गुंडाळीत निर्माण होणारी वि. चा. प्रे. जरी सारख्या मूल्याची असली, तरी ती समकालिक नसते. अशा गुंडाळ्यांपासून स्वतंत्रपणे मिळणाऱ्या विद्युत् पुरवठा पद्धतीस बहुकला प्रत्यावर्ती प्रवाह पद्धती म्हणतात. अशा बहुकला पद्धतीत n  स्वतंत्र गुंडाळ्या म्हणजेच n कला असल्या, तर तितक्याच निरनिराळ्या वि. चा. प्रे. निर्माण होतात. यांतील अनुक्रमाने येणाऱ्या कोणत्याही दोन वि. चा. प्रे. मधील कलांतर २π /n अरीयमाने किंवा ३६०/n अंश असते.

बहुकला पद्धतीचे पुढील फायदे आहेत : (१) तेवढ्याच प्रदान शक्तीसाठी बहुकला जनित्र हे एककला जनित्रापेक्षा लहान व कमी किंमतीचे असते. (२) बहुकला प्रवाहामुळे स्थिर वेटोळ्यामधून प्रत्यावर्ती प्रवाह वापरून परिभ्रमी चुंबकीय क्षेत्र निर्माण करता येते. याचा उपयोग प्रवर्तनी प्रत्यावर्ती चलित्रात करतात. [⟶ विद्युत् चलित्र]. (३) बहुकल शक्तिप्रेषण पद्धतीत तेवढीच कार्यशक्ती नेण्यासाठी संवाहकाचे आकारमान व एकूण वजन कमी करता येते. (४) या पद्धतीत चलित्रापासून मिळणारे घूर्णी परिबल (भ्रमणगतीस कारणीभूत होणारी प्रेरणा) स्पंदरूपी नसून एकविध असते. (५) बहुकला प्रवर्तनी प्रत्यावर्ती चलित्राची कार्यक्षमता एककला चलित्रापेक्षा जास्त असते.

 या फायद्यांमुळे हल्ली व्यवहारात वापरण्यात येणाऱ्या प्रत्यावर्ती प्रवाहाचे ९०% पेक्षा अधिक वितरण व उपयोजन हे त्रिकलाप्रत्यावर्ती प्रवाहाच्या स्वरूपातच करण्यात येते. मोठ्या आकारमानाच्या जनित्रमध्ये तीन स्वंतत्र गुंडाळ्या १२०° च्या अंतराने बसवून त्यापासून त्रिकला प्रत्यावर्ती दाब निर्माण करतात.  अशा जनित्राला त्रिकला जनित्र म्हणतात. द्विकला पद्धती फारशी प्रचारात नाही. तीनपेक्षा अधिक कला वापरण्याच्या पद्धती खर्चिक असल्याने त्रिकला पद्धतच जास्त करून वापरली जाते.  अशा जनित्रात असलेल्या तीन गुंडाळ्यांमध्ये निर्माण होणारी वि. चा. प्रे. प्रत्येकी ^३६०/_३ = १२०° ने कलांतरित असते. म्हणजेच वि. चा. प्रे. १, वि. चा. प्रे. २ व वि. चा. प्रे. ३ यांमध्ये अनुक्रमे १२०° चा फरक असतो.

त्रिकला पद्धतीत गुंडाळ्यांच्या परस्परांतील जोडणीवरून तसेच भारांच्या जोडणीवरून (१) तारका पद्धत व (२) डेल्टा-जाल पद्धत असे दोन प्रकार पडतात. [अशाच जोडणी पद्धती भारांच्या बाबतीत एकदिश विद्युत् प्रवाह मंडलांतही वापरण्यात येतात ⟶ एकदिश विद्युत् प्रवाह].

तारका पद्धत : आ. ९ (अ) मध्ये दर्शविल्याप्रमाणे या पद्धतीत प्रत्येक गुंडाळीची आरंभीची अगर अखेरची टोके एकत्र जोडून इतर तीन टोकांतून दाब पुरविला जातो. या पद्धतीत पुरवठ्याच्या दोन बाहेरील तारांत मिळणारा विद्युत् दाब हा प्रत्येक गुंडाळीतील दाबाच्या √३ पट असतो. प्रत्येक गुंडाळीतील व तारेतील विद्युत् प्रवाह मात्र समान असतो.

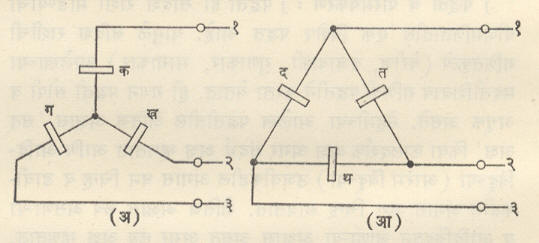
डेल्टा-जाल पद्धत : आ. ९ (आ) मध्ये दाखविल्याप्रमाणे यामध्ये तिन्ही गुंडाळ्यांची अखेरची टोके पुढील गुंडाळीच्या आरंभाच्या टोकास जोडलेली असतात. यांतील कोणत्याही दोन तारांतील विद्युत् दाब गुंडाळीतील विद्युत् दाबाइतकाच असून प्रत्येक तारेतील प्रवाह मात्र गुंडाळीतील प्रवाहाच्या √३ पट असतो.

विद्युत् पुरवठ्यासाठी किंवा वितरणाकरिता तारका पद्धत वापरतात. यामुळे गुंडाळ्यांत निर्माण करावा लागणारा दाब प्रत्यक्ष दाबाच्या (दोन तारांतील) ^१/_√३ इतकाच असतो व विद्युत् निरोधक वेष्टनावरील खर्च कमी होतो. वितरणासाठी कला तार व तटस्थ तार (तारका जोडबिंदूपासून काढलेली तार) यांमधील दाब २३० व्होल्ट मिळतो. तसेच जास्त दाबाच्या शक्तीसाठी कोणत्याही दोन कला तारांत ४०० व्होल्ट दाब मिळू शकतो. [आ. ११ (अ) पहा]. अशा पुरवठा पद्धतीत ‘त्रिकला चार तारा’ पद्धत म्हणतात. ‘त्रिकला तीन तारा’ पद्धतीत कोणत्याही दोन तारांत मिळणारा दाब पुरवठ्याच्या दाबाइतकाच असतो.

 चलित्रसाठी डेल्टा-जाल जोडणी वापरतात. यामध्ये तारेतून घेतला जाणारा प्रवाह जास्त असला, तरी प्रत्यक्ष गुंडाळीतून जाणारा प्रवाह ^१/_√३ पट इतकाच असतो आणि त्यामुळे संवाहकावरील खर्च खूपच कमी होतो. 

---

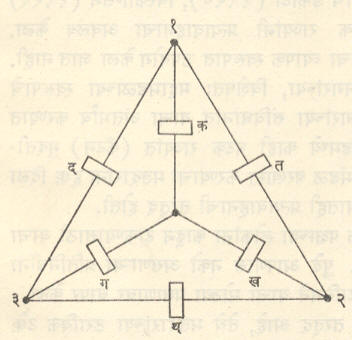
तारका पद्धतीने जोडलेल्या संरोधकाचे सममूल्य डेल्टा-जाल पद्धतीप्रमाणे व डेल्टा-जाल पद्धतीप्रमाणे जोडलेल्या संरोधकांचे सममूल्य तारका पद्धतीप्रमाणे रूपांतरित करता येते. आ. ९ (अ) मधील क, ख, क या संरोधकांची तारका जोडणी केलेली असून आ. ९ (आ) मध्ये त, थ, द या संरोधकांची डेल्टा-जाल जोडणी केलेली आहे. तारका पद्धतीचे सममूल्य डेल्टा-जाल पद्धतीत रूपांतर करण्यासाठी खालीलप्रमाणे संरोधकांची मूल्ये काढता येतात.

त =	क ख + ख ग + ग क
	ग

थ =	क ख + ख ग + ग क
	क

द =	क ख + ख ग + ग क
	ख

(आ) डेल्टा-जाल पद्धतीने सममूल्य तारका पद्धतीत रूपांतर करावयाचे असल्यास

क =	द त
	त + थ + द

ख =	त थ
	त + थ + द

ग =	थ द
	त + थ + द

 आ. १० मध्ये तारका व डेल्टा-जाल या पद्धतींची एकत्र जोडणी दाखविली आहे. तारका व डेल्टा-जाल पद्धतींमध्ये २३० व्होल्टचे दिवे लावण्याची जोडणी आ. ११ मध्ये दाखविली आहे.

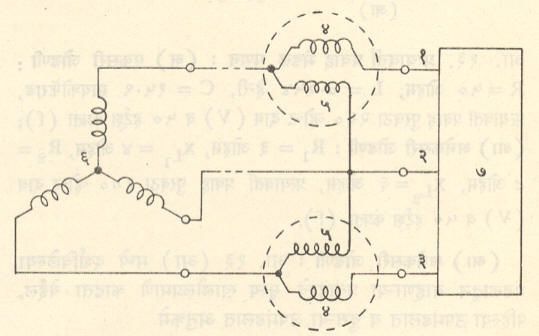
 बहुकला पद्धतीतील शक्तिमापन : त्रिकला तीन तारांच्या पद्धतीत वापरली जाणारी शक्ती खालील दोन सूत्रांनी काढता येते.

(१) शक्ती = ३ X कलेचा (गुंडाळीतील) दाब X कलेचा प्रवाह X शक्तिगुणक.

(२) शक्ती = √ ३ X तारांतील दाब X तारेतील प्रवाह X शक्तिगुणक. 

---

विद्युत् शक्ती वॉट किंवा किलोवॉट ( = १००० वॉट) या एककामध्ये मोजतात. अशा शक्तीचे मोजमाप करण्यासाठी दोन शक्तिमापक वापरावे लागतात. त्यांची जोडणी आ. १२मध्ये दाखविलीआहे. शक्तिमापकातील प्रवाह वेटोळे अनुक्रमे संवाहक तारा १ व ३ यांच्या एकसरीत जोडले असून दाब वेटोळे अनुक्रमे १ व २ आणि ३ व २ या संवाहक तारांमध्ये जोडलेले असते. आकृतीमधील दोन्ही शक्तिमापकांनी दाखविलेल्यादर्शनी मूल्यांची बैजिक बेरीज म्हणजेच मंडलात वापरली जाणारी विद्युत् शक्ती होय. भार जरी असंतुलित असला (म्हणजे तिन्ही संवाहक तारांतून समान वाटला गेलेला नसला), तरीही या पद्धतीने तीन संवाहक तारांच्या बहुकला प्रत्यावर्ती पद्धतीत खर्च होणारी शक्ती मोजता येते.

 

 

 

 

 

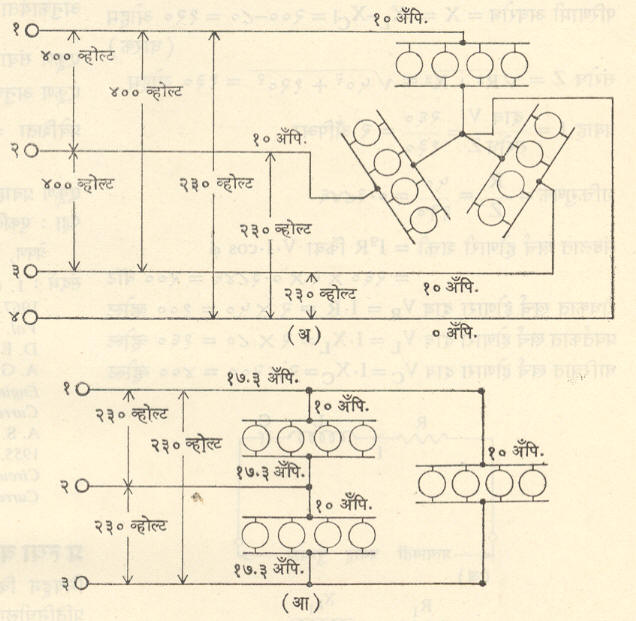
मंडल गणन पद्धतीची उदाहरणे :एकसरी जोडणी : आ. १३ (३) मध्ये दाखविलेल्या मंडलातून वाहणारा प्रवाह, तसेच शक्तिगुणक व मंडलात खर्च होणारी शक्ती या राशी खालीलप्रमाणे काढता येतात.

रोधकीय रोध R = ५० ओहम, प्रवर्तनी अवरोध X_L = २π·f·L = २ X ३·१४ X ५० X ०·२५४ = ८० ओहम

धारक अवरोध XC=	१	=	१०६	= २०० ओहम
	२π·f·c		२ x ३·१४ x ५० x १५·९

परिणामी अवरोध = X = । X_L – X_C। = २००–८० = १२० ओहम (धारक)

संरोध Z = √ R² + X² = √ ५०^२ + १२०^२ =  १३० ओहम

प्रवाह I =	दाब V	=	२६०	= २ अँपिअर
	संरोध Z		१३०

शक्तिगुणक =	R	=	५०	= ०·३८४६
	Z		१३०

  

---

मंडलात खर्च होणारी शक्ती = I²R किंवा V·I·cos Φ

                                    = २६0 x २ x ०·३८४६ = २००वॉट

रोधकात खर्च होणारा दाब V_R = I·R = २ x ५० = १०० व्होल्ट

प्रवर्तकात खर्च होणारा दाब V_L = I·X_L = २ x ८० = १६० व्होल्ट

धारित्रात खर्च होणारा दाब V_C = I· X_C = २ x २०० = ४०० व्होल्ट

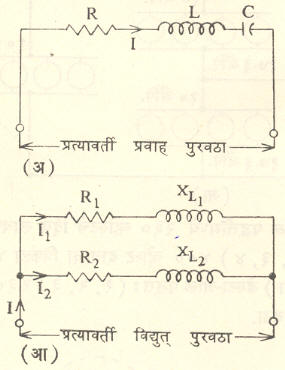
 (आ) अनेकसरी जोडणी : आ. १३ (आ) मध्ये दर्शविलेल्या मंडलातून वाहणाऱ्या प्रवाहाचे मूल्य खालीलप्रमाणे काढता येईल.पहिल्या उपमंडलात व दुसऱ्या उपमंडलात अनुक्रमे

संरोध = Z₁ = √ R₁² + X_L1²= √ ३^२ + ४^२ = ५ ओहम

प्रवाह I1 =	V	=	१००	= २० अँपि.
	Z1		५

संरोध = Z₂ = √ R₂² + X_L2²= √ ८^२ + ६^२= १० ओहम

प्रवाह I2=	V	=	१००	१० अँपि.
	Z2		१०

संवाहिता= G1 =	R1	=	३	०·१२ म्हो
	Z12		२५

संवाहिता= G2 =	R2	=	८	०·०८ म्हो
	Z22		१०२

अनुकार्यता = B1=	XL1	=	४	०·१६ म्हो
	Z12		२५

अनुकार्यता = B2=	XL2	=	६	०·०६ म्हो
	Z22		१०२

एकूण संवाहिता =G =  G₁ + G₂ = ०·१२ + ०·०८ = ०·२० म्हो

एकूण अनुकार्यता =B =  B₁ + B₂ =  ०·१६ + ०·०६ = ०·२२ म्हो

प्रवेशिता =Y = √ G² + B² = √०·२०^२ + ०·२२^२

                                    = √ ०·८८४ = ०·२९५ म्हो

एकूण प्रवाह = I = V·Y = १०० x ०·२९५ = २९·५ अँपि.

पहा : एकदिश विद्युत् प्रवाह रोहित्र विद्युत् चलित्र विद्युत् जनित्र शक्तिप्रेषण, विद्युत्.

 संदर्भ :   1. Cotton, H. Advanced Electrical Technology, London. 1967.

              2. Daws, C. L. A Course in Electrical Engineering. Vol. II, Tokyo, 1956.

              3. Fitzgerald, A. E. Higginbotham,D.E.Basic Electrical Engineering, Tokyo, 1957.

              4. Grag, A. G. Wallace, G. A. Principles and Practice of Electrical Engineering, New York, 1962.

              5.Kemp,P.Alternating Current Electrical Engineering London, 1963.

              6. Longsdorf, A. S. Theory of Alternating Current Machinery, New York, 1955.

              7.Romanowitz, H. A. Electrical Fundamentals and Circuit Analysis, New York, 1966.

              8. Say, M. G. Alternating Current Machines, London, 1972. 

  

लिमये, ग. ह. टेंबे, वि. शं.

“