अवकल समीकरणे : अवकल समीकरणांचा सिद्धांत गणिताची एक महत्त्वाची शाखा आहे. या शाखेचा शुद्ध आणि अनुप्रयुक्त गणित या दोन्ही क्षेत्रांत चांगलाच प्रभाव दिसून येतो. केवळ शुद्ध गणिताचा विचार केल्यास अनंत ðश्रेढी, अस्तित्व प्रमेये आणि फलन (निरनिराळ्या राशींमधील परस्पर गणितीय संबंध) सिद्धांत यांच्या अभ्यासात ह्या सिद्धांताचा पुष्कळ उपयोग होतो. तसेच वक्र आणि पृष्ठविषयक भूमितीत या सिद्धांताचा आधार अत्यावश्यक ठरतो. या दोन उपशाखांतून विकसित झालेली आणखी एक शाखा म्हणजे लाप्लास, फूर्ये इत्यादींच्या नावांनी ओळखली जाणारी रूपांतरणे होत. अनुप्रयुक्त गणिताच्या प्रगतीतील या सिद्धांताचे महत्त्व निःसंदिग्ध आहे. सर्व प्रकारची यांत्रिक व विद्युत् कंपने आणि ðअनुस्पंदनविषयक घटना यांच्या विवेचनात अवकल समीकरणांचा सिद्धांत आधारभूत होतो. उष्णता संवहन, विद्युत् तरंगांचे प्रेषण इ. भौतिकीय विषयांत आंशिक अवकल समीकरणांचे ज्ञान आवश्यक आहे. भौतिकीय रसायनशास्त्रातही या विषयाचे महत्त्व मोठे आहे.अवकल समीकरणांचे दोन प्रकार आहेत. पहिल्या प्रकारात एक स्वयंचल (स्वतः बदलणार्याव राशी), त्याचे फलन व त्या फलनाचे अवकलज [→अवकलन व समाकलन] यांचा संबंध असतो. जसे

या समीकरणास ‘सामान्य अवकल समीकरण’ म्हणतात. यात य हे क्ष चे फलन असून य चे क्ष सापेक्ष अवकलज ह्या समीकरणात आलेले आहेत. दुसर्या प्रकारच्या समीकरणात अनेक स्वयंचल असून त्यांचे फलन व त्या फलनाचे निरनिराळे (स्वयंचलसापेक्ष) आंशिक अवकलज यांचा समावेश असतो. अशा समीकरणास ‘आंशिक अवकल समीकरण’ म्हणतात.
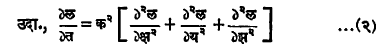






समीकरणांच्या बाबतीत चार्पिंट (१७९४) व याकोबी (१८३६) यांनी, तर उच्चतर कोटीच्या समीकरणांच्या बाबतीत लाप्लास (१७७३). माँझ (१७८४), अँपिअर (१८१४) व दार्बू (१८७०) या गणितज्ञांनी भरीव कामगिरी केलेली आहे. आंशिक अवकल समीकरणांचा सिद्धांत १८०० च्या सुमारास प्रगतावस्थेत पोचला असे म्हणण्यास हरकत नाही. प्रथमतः प्रत्येक अवकल समीकरण सोडविणे शक्य आहे अशी गणितज्ञांची समजूत होती परंतु पुढे ती चुकीची ठरली व त्यामुळे यासंबंधीचे गणितज्ञांचे परिश्रम व्यर्थ ठरले.
इ. स. १८०० नंतर हा विषय फलन सिद्धांताशी निगडित असल्याचे आढळून आले. अवकल समीकरणाचा अनंत श्रेढीच्या रूपात कोशी यांनी काढलेला निर्वाह, हा अभिसारी श्रेढीरूप असल्यामुळे अवकल समीकरणाची पूर्तता करण्यास फलनाची व्याख्या कशी करावी याविषयी अभिनव कल्पना पुढे आली. अभिसरणाचा प्रश्न तार्किक दृष्टीने महत्त्वाचा आहे व अवकल समीकरणांच्या बाबतीत तर त्याला फारच वरचे स्थान देणे आवश्यक आहे.
कोशी यांचे कार्य ब्रायो आणि बूके (१८५६) या दोघांनी पुढे चालविले. त्यांच्या संशोधनातूनच पीकार (१८९०) यांनी ‘आनुक्रमिक उपसादन पद्धती’ शोधून काढली. फुक्स (१८९६) आणि फ्रोबीनियस (१८७३) यांनी सहगुणक स्थिरांक नसलेल्या द्विकोटिक एकघाती अवकल समीकरणांचा अभ्यास केला. श्वार्त्स, क्लाइन, गूर्सा इत्यादींनी आलेखीय पद्धती वापरल्या. वाडा (१९१७) यांनी पीकार व प्वँकारे यांचे निष्कर्ष आलेखीय पद्धतीत बसविले आणि रूंगे (१८९५) यांनी अवकल समीकरणांची संख्यात्मक उपसादने (अंदाजाने जवळात जवळ असलेली मूल्ये) काढली.
पहा : अवकलन व समाकलन फूर्ये श्रेढी समाकल समीकरणे व रूपांतरे.
संदर्भ : 1. Churchill, R. V. Fourier Series and Boundary Value Problems, New York, 1941.
2. Forsyth, A. R. A Treatise on Differential Equations. London, 1961.
3. Forsyth, A. R. Theory of Differential Equations, Vols. 4, Dover, 1959.
4. Ince, E. L. Ordinary Differential Equations, London, 1927.
5. Milne, W. E. Numerical Solutions of Differential Equations, New York, 1958.
6. Piaggio, H. T. H. An Elementary Treatise on Differential Equations and Their Applications, London, 1962.
7. Ross, S. L. Differential Equations,New York, 1964. 8. Sneddon, I. Elements of Partial Differential Equations, New York, 1961.
गुर्जर, ल. वा.